Мы при дальнейшем рассмотрении пренебрегаем в силу того, что для каждой фиксированной конфигурации ядер это величина постоянная

Вид материала

Лекция

Подобный материал:

• Занятие 1 Основные понятия математики, используемые в финансовых вычислениях Процент, 95.94kb.
•            Машин много и одна лучше другой. Так что же покупать, 1003.78kb.
• У меня зазвонил… ip-телефон, 120.04kb.
• Наука прикинуться шлангом, 73.89kb.
• Сошествие Святого Духа на апостолов После вознесения Иисуса Христа наступил десятый, 220.02kb.
• Умозаключение это такая форма мышления, при которой из имеющихся посылок, из известных, 611.1kb.
• М. В. Цуциева доцент кафедры финансов и кредита виу, 124.61kb.
• М. Б. Бергельсон теория и практика межкультурного общения, 37.48kb.
• Командир электромеханической боевой части подводного атомохода это уважаемый человек,, 26.53kb.
• Доклад «О конкуренции между услугами связи для целей передачи голосовой информации, 48.46kb.

Без Nice Guy её бы не было.

Лекция 2

Электронное уравнение для стационарной задачи

Электронное уравнение:

,

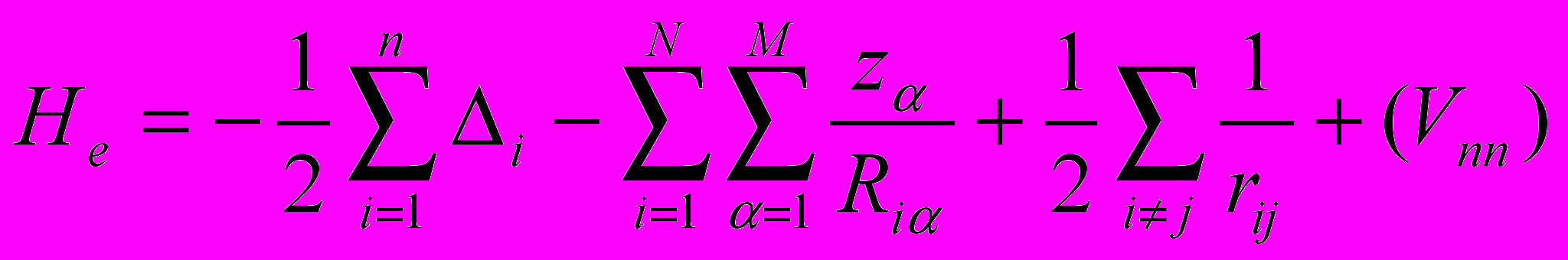где первый член в сумме – кинетическая энергия электронов (T_e), второй – потенциал взаимодействия между электронами и ядрами (V_ne), а третий – потенциал взаимодействия между электронами (V_ee). Потенциалом взаимодействия между ядрами (V_nn) мы при дальнейшем рассмотрении пренебрегаем в силу того, что для каждой фиксированной конфигурации ядер это величина постоянная.

Если бы не было члена V_ee, то гамильтониан сводился бы к:

,

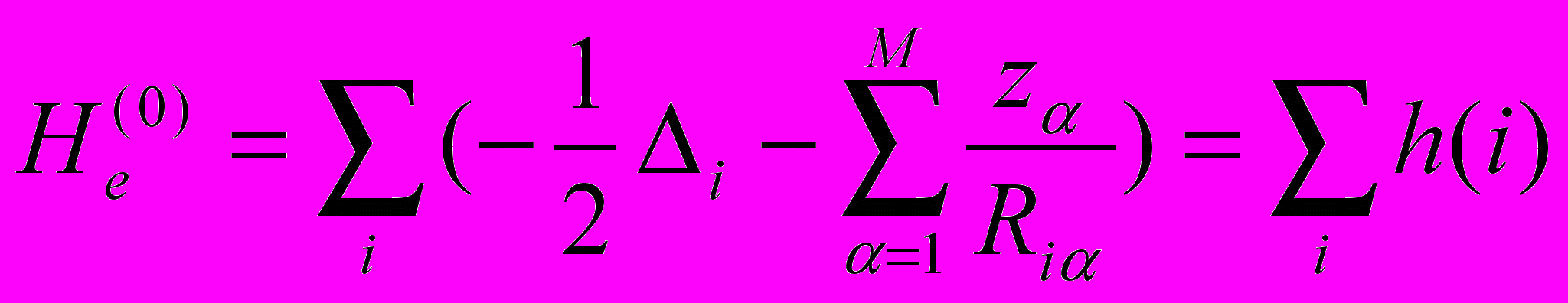где h(i) – одноэлектронный оператор.

φ'_i(i) – одноэлектронная функция (орбиталь), являющаяся решением одноэлектронного уравнения: 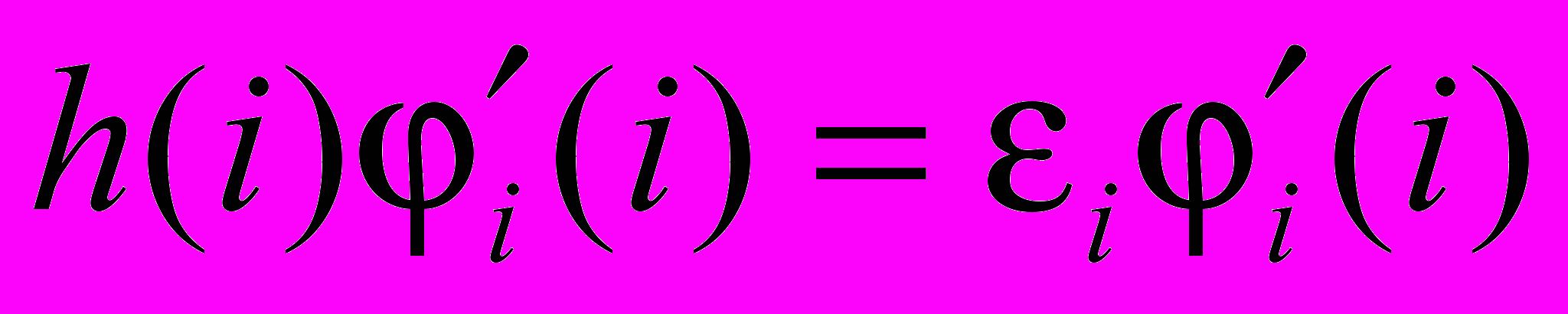. Поскольку электронный гамильтониан не зависит от спиновых операторов в используемом пока представлении, то орбиталь с учетом спина можно записать в виде φ'_i(i)σ, где σ указывает на спин (1/2 или –1/2).

При таких условиях решением уравнения 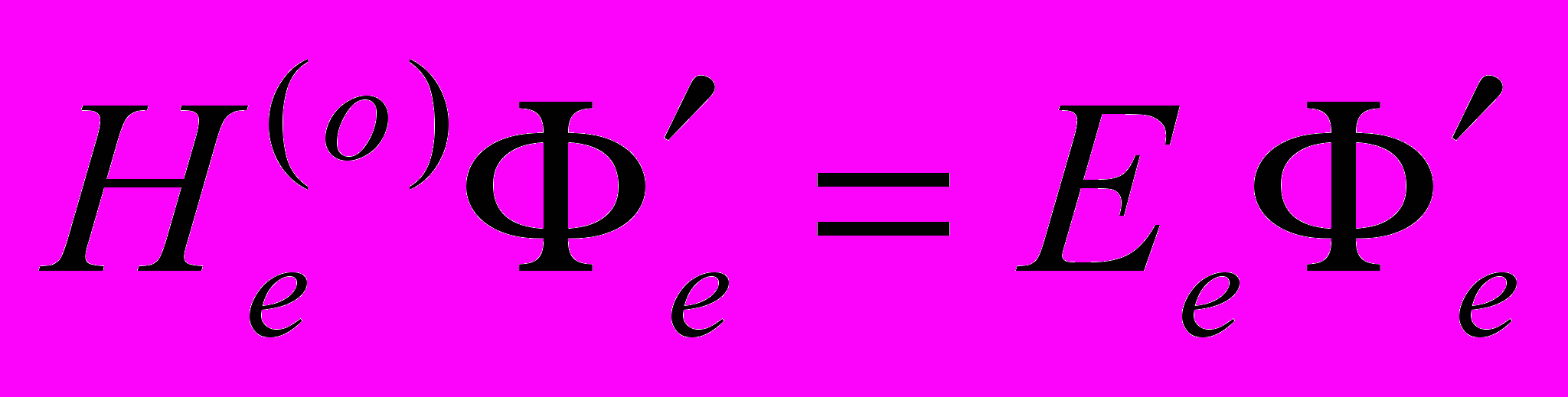будет функция, представленная в виде произведения орбиталей, или с учетом перестановочной симметрии для системы фермионов (электронов) функция в виде определителя (детерминанта) .



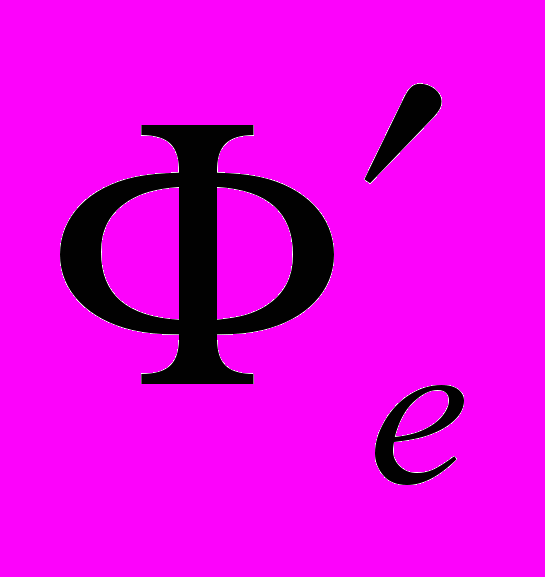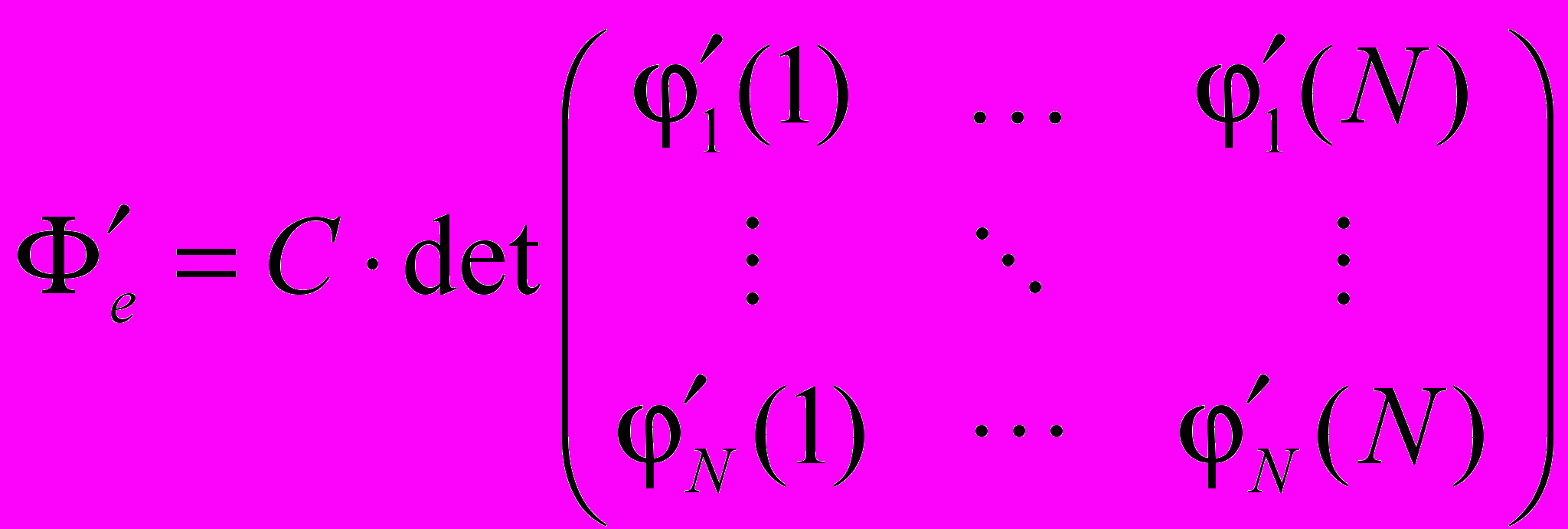
Волновая функция системы электронов, как системы тождественных частиц с полуцелым спином, должна быть антисимметрична. 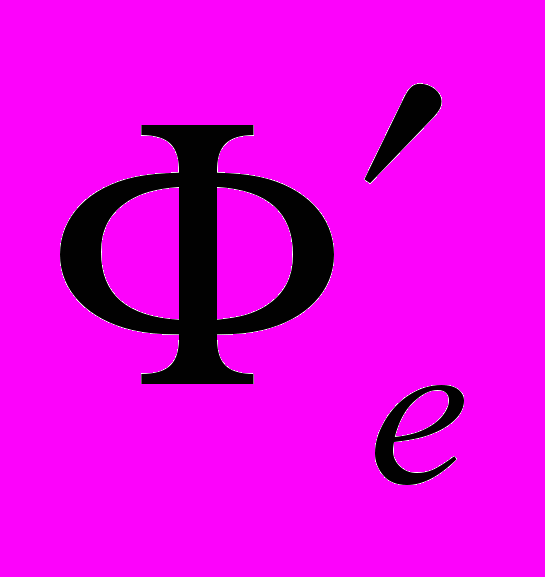- антисимметрична, что легко показать для частного случая системы двух электронов, используя одно из свойств определителя:

,

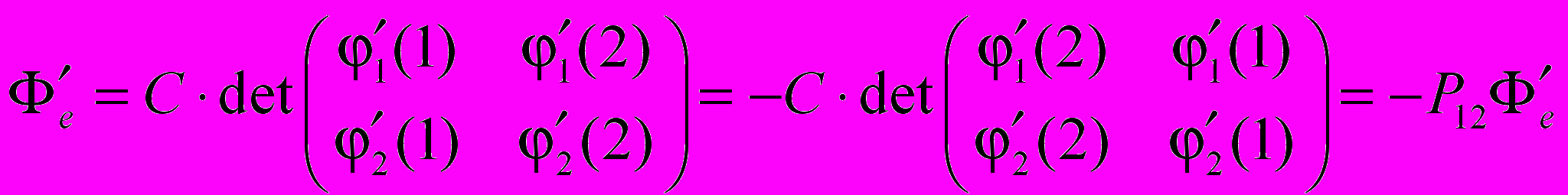где Р₁₂ – оператор, переставляющий координаты первого и второго электронов.

Если учесть межэлектронное взаимодействие V_ee и сохранить представление волновой функции в виде определителя, то далее можно воспользоваться вариационным методом для нахождения оптимальных (наилучших) орбиталей:



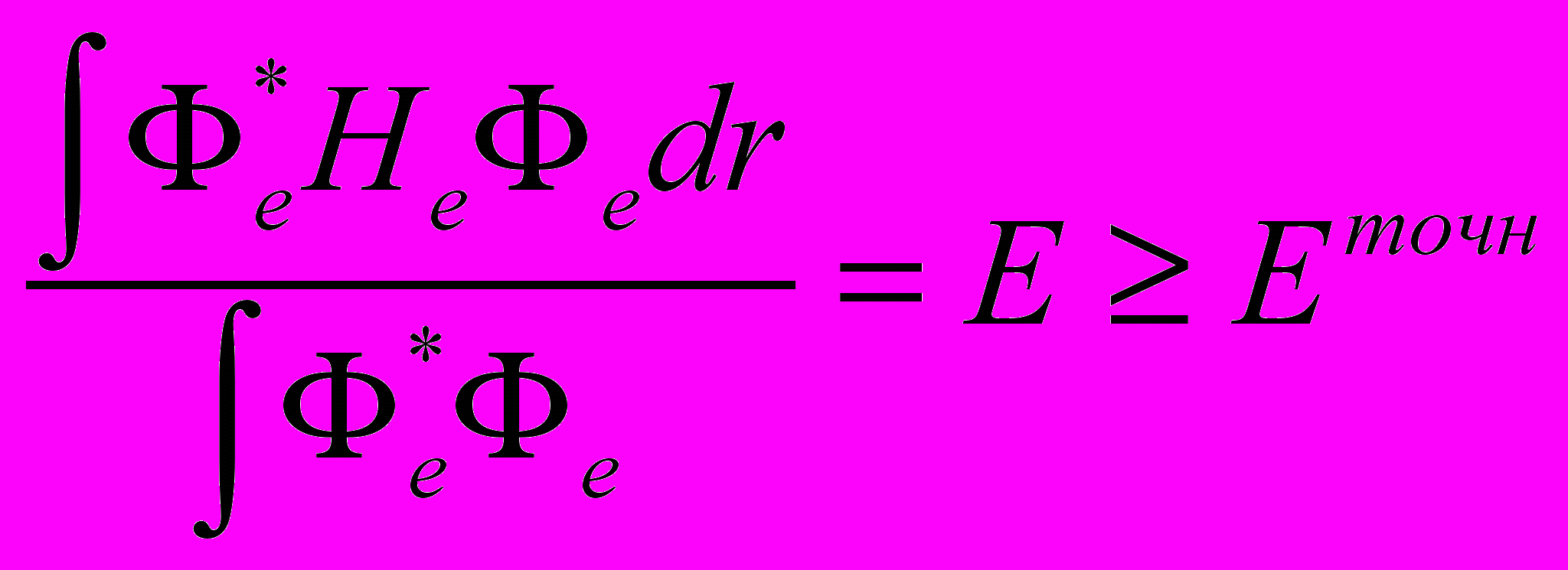
В случае представления волновой функции в виде просто произведения орбиталей это приводит к уравнениям для φ_i(i).





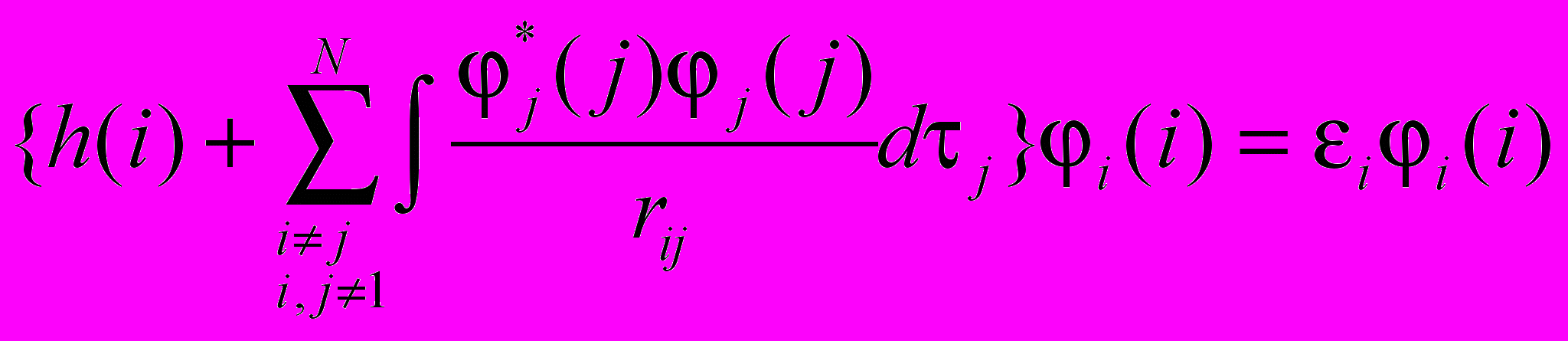
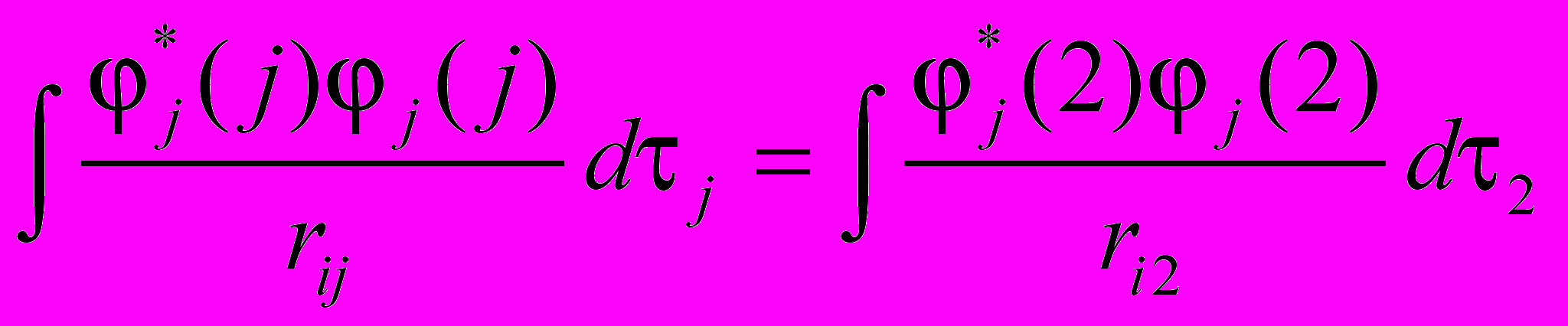
С учетом же антисимметричности волновой функции получаем уравнение:



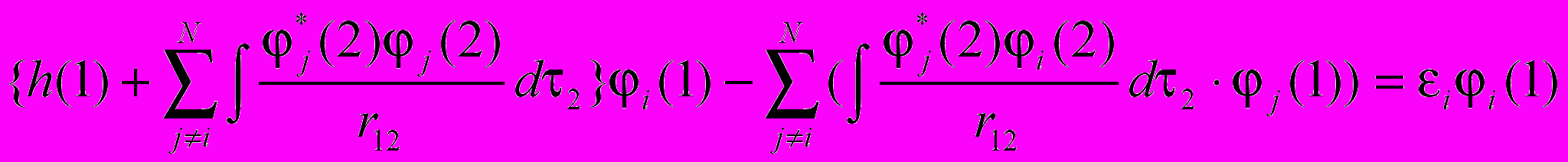
Для сокращения записи введём К_j(1) – обменный оператор и J_j(1) – кулоновский оператор.





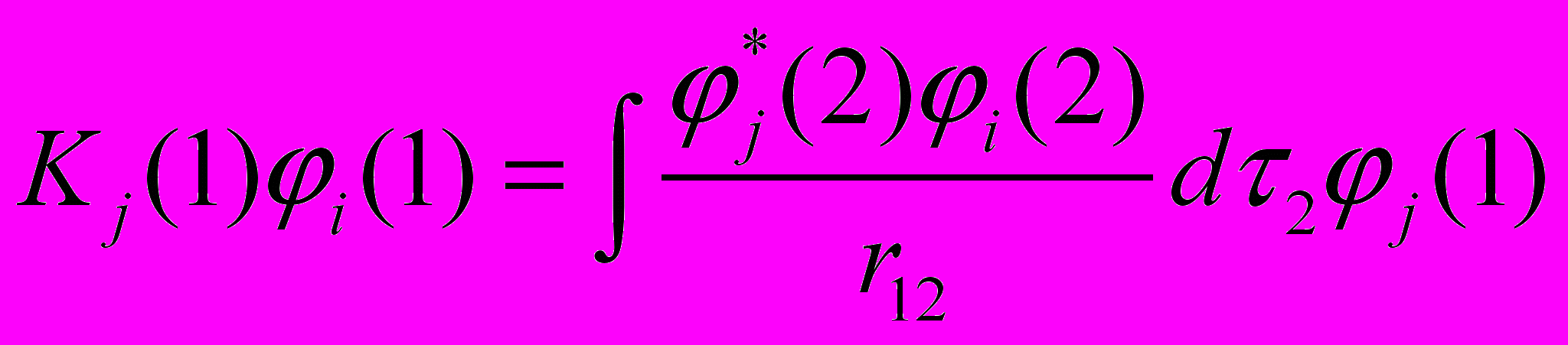
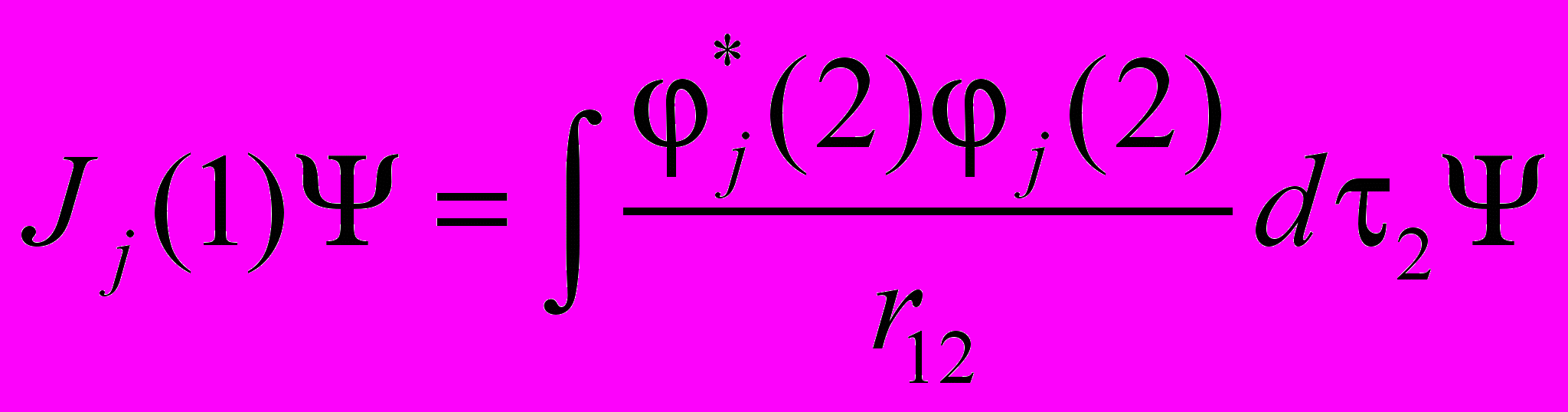
Введя операторы, получим:



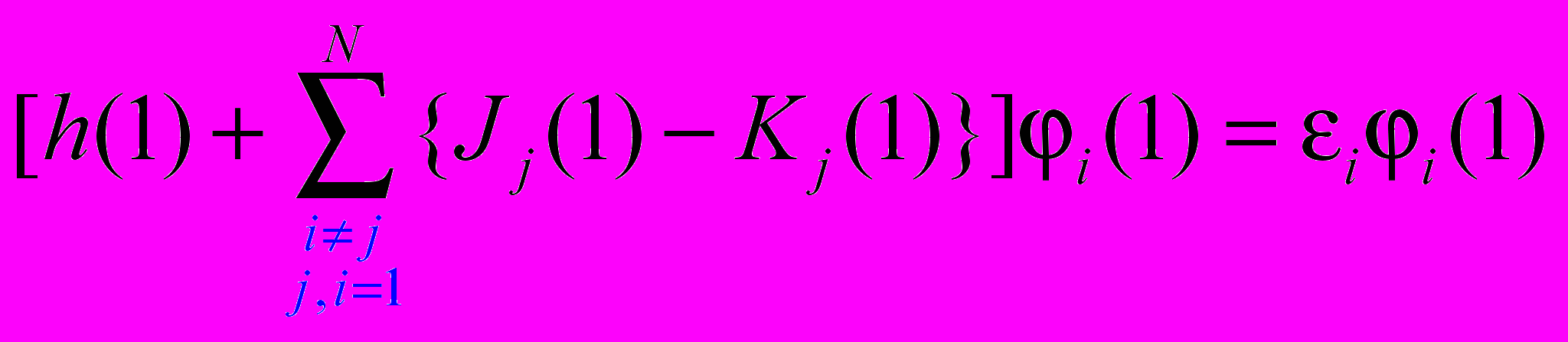
Заметим, что при j=i



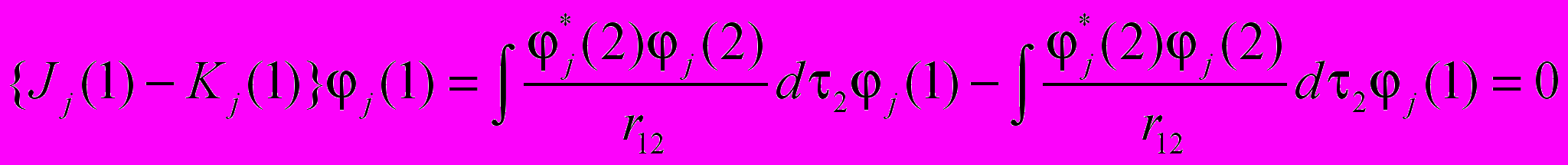
Значит, можно записать:



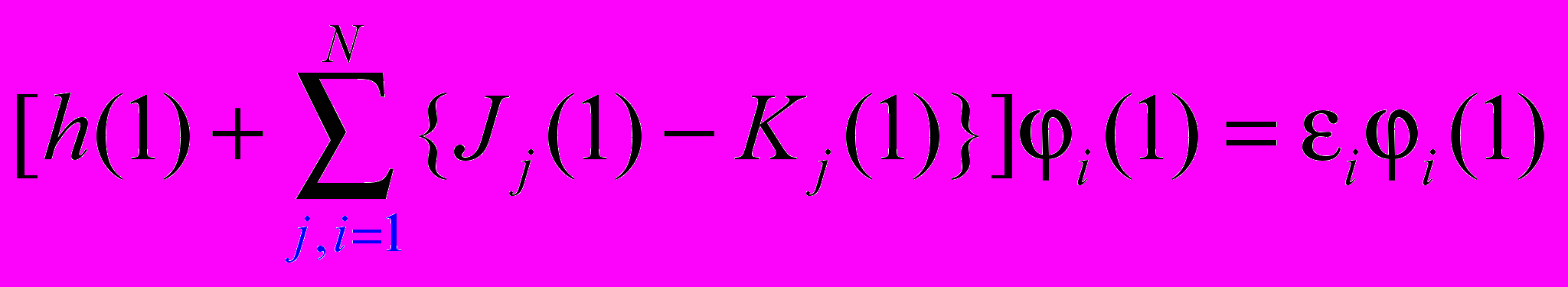
Получили систему уравнений, называемую системой уравнений Хартри-Фока, решив которую, найдем φ_i, с помощью которой найдем Ф_е:



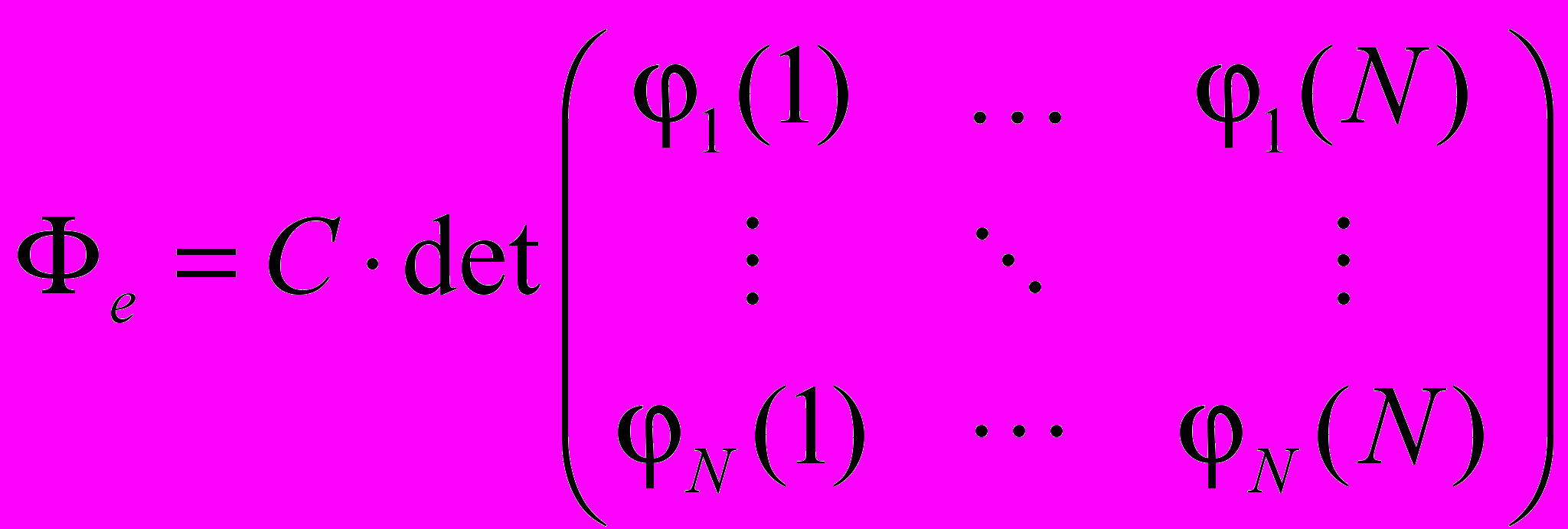
Выписанные выше уравнения Хартри–Фока получены при условии, что орбитали φ_i взаимно ортогональны, т.е



Этому условию всегда можно удовлетворить изначально, поскольку в определителе строки или столбцы можно линейно преобразовывать друг через друга, что приводит максимум к умножению исходного определителя на некоторое число, определяемое коэффициентами этих линейных преобразований. Такая возможность позволят считать орбитали нормированными и взаимно ортогональными.


Для определения нормировочной константы (С) функции Ф, подсчитаем :







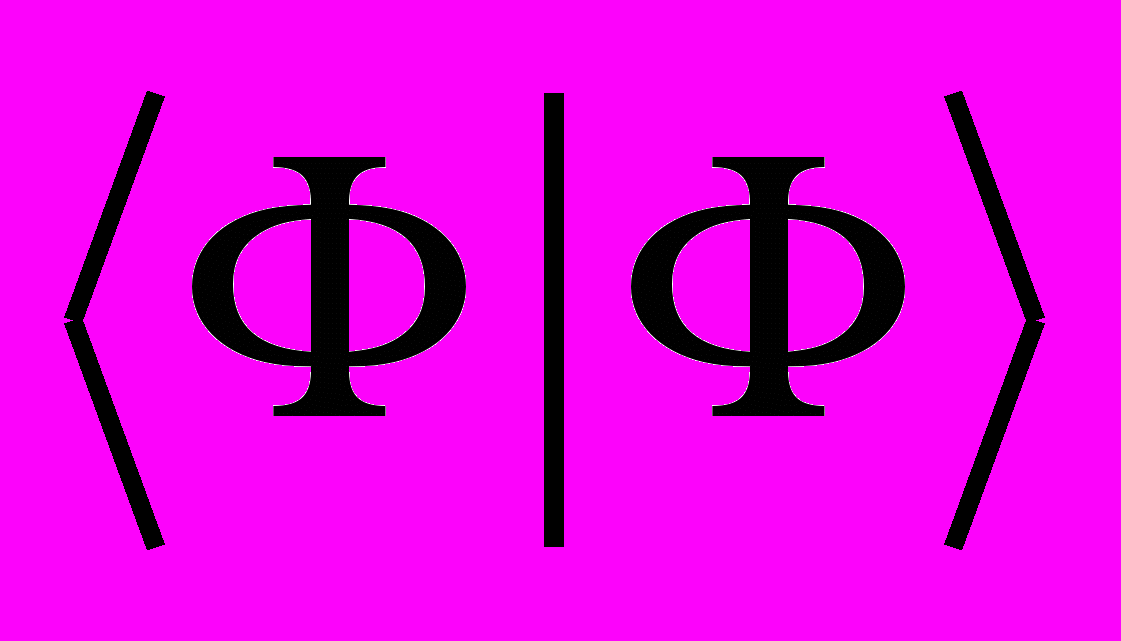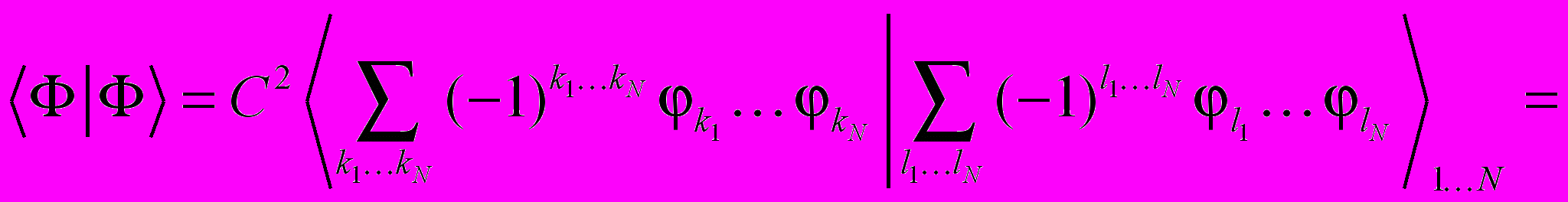
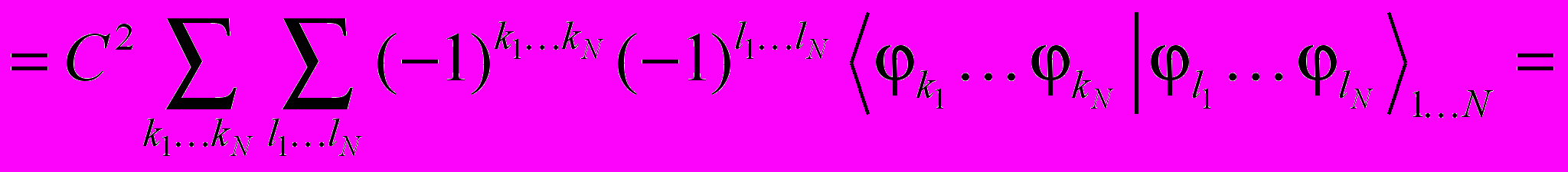
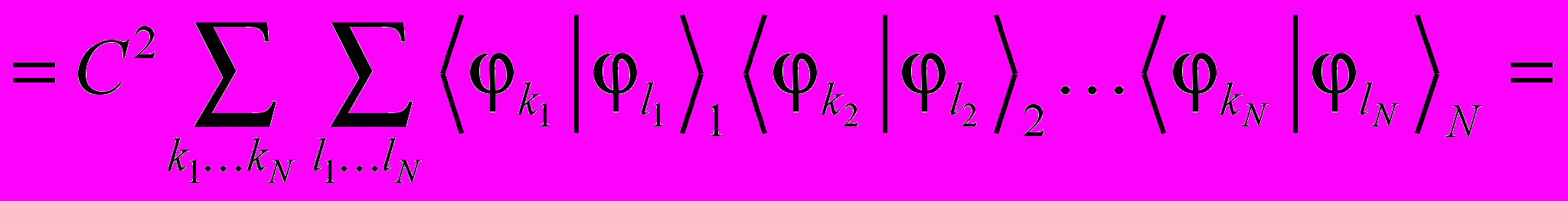
Примечание:



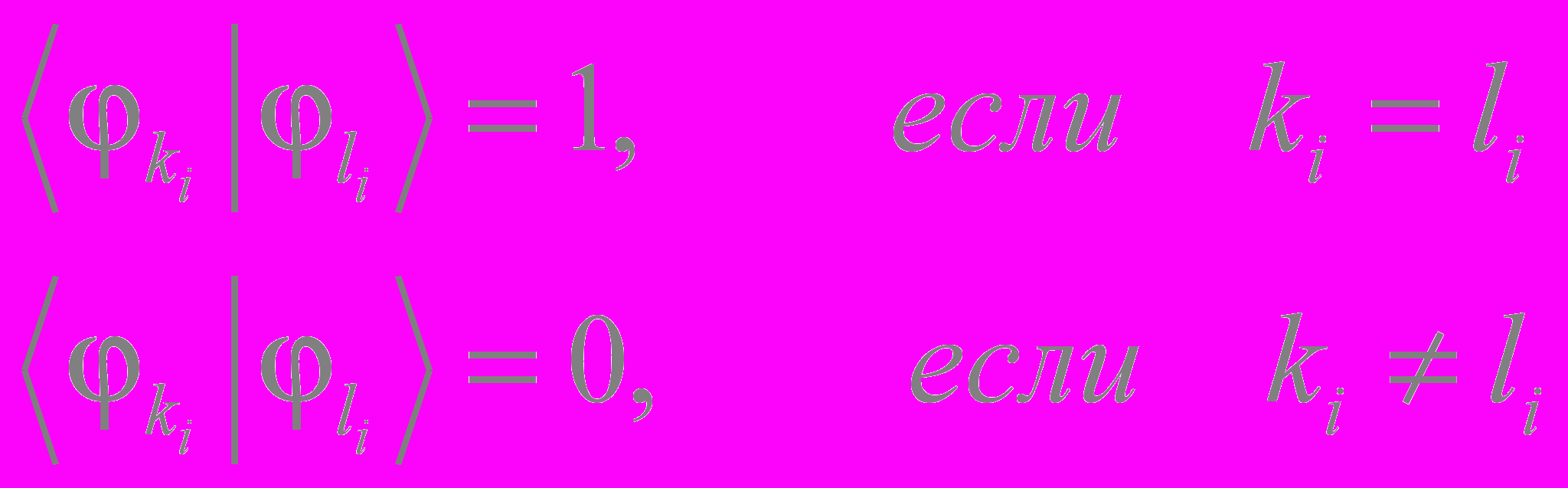
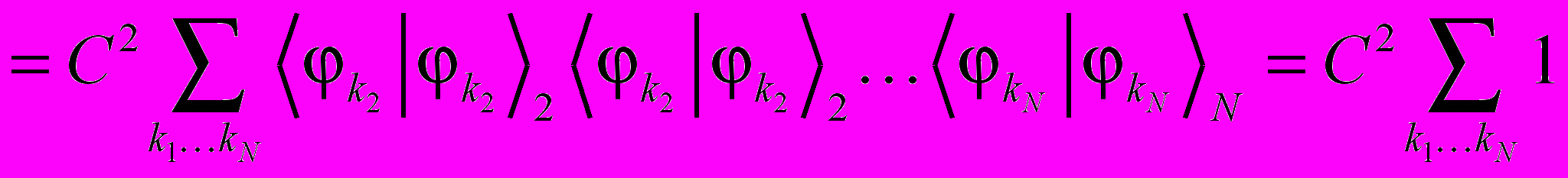
Это число перестановок из N элементов, которое равняется N!.





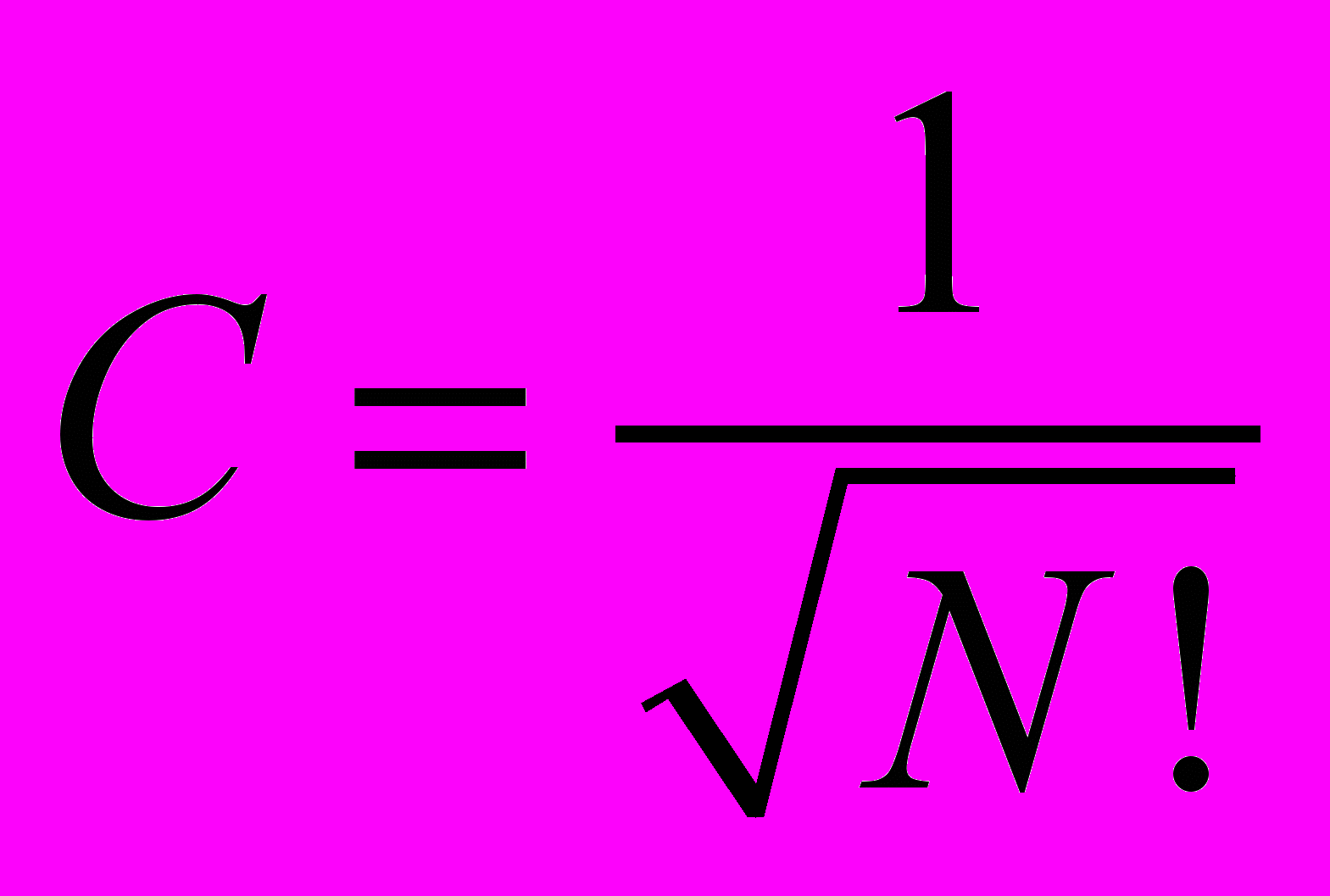
При использовании материалов лекции ссылка на ссылка скрыта обязательна.