Geum.ru

Занятие 1 Основные понятия математики, используемые в финансовых вычислениях Процент

Вид материалаДокументы

Содержание


Геометрическая прогрессия
Экономическая теория процента. Простые и сложные проценты.
6. Логика финансовых вычислений
Пример 6. Чему равна будущая стоимость одной денежной единицы через 9 лет при ставке процента 10%. Пример
Внутригодовые процентные начисления. Номинальная, эффективная ставки
Пример 4. Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно. Пример
Подобный материал:
ЗАНЯТИЕ 1

Основные понятия математики, используемые в финансовых вычислениях

Процент – это одна сотая доля величины.

Прогрессия – последовательность чисел, построенная по определенным правилам.

Арифметическая прогрессия – это числовая последовательность, для которой разность любых двух соседних чисел есть величина постоянная.

Любой член последовательности находится по формуле: an= a1+d(n-1),

где d-разность арифметической прогрессии,

n-порядковый номер элемента последовательности.

Сумма арифметической прогрессии находится по формуле: .

Геометрическая прогрессия – это числовая последовательность, для которой отношение любых двух соседних чисел есть величина постоянная.

Любой член последовательности находится по формуле: an= a1*qn-1,

где q-знаменатель геометрической прогрессии,

n-порядковый номер элемента последовательности.

Сумма возрастающей геометрической прогрессии находится по формуле: .

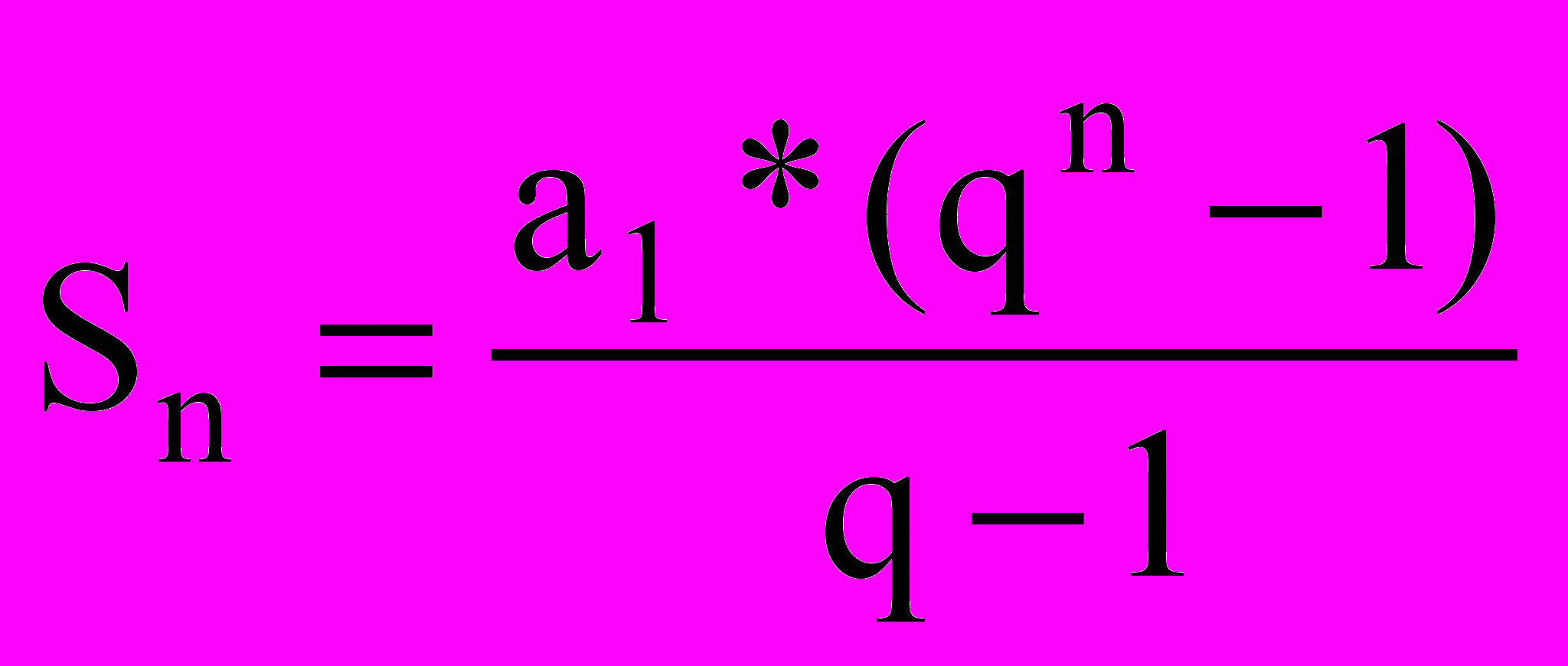Сумма убывающей геометрической прогрессии находится по формуле: .

Пример 1. Пусть S=1000руб. – это первоначальный вклад в банк, на которые начисляются простые проценты по ставке r =10%. Найти последовательность наращенных сумм за n=3 промежутка начисления.

Пример 2. Господин N старается спланировать должным образом приближающийся выход на пенсию. Брокер по ценным инвестиционным бумагам предложил схему, согласно которой господин N платит крупную сумму фирме, а в обмен получает гарантированный ежемесячный доход в 300 дол. Более того, каждый месяц доход будет увеличиваться на 40 дол. Какова будет ситуация через пять лет?

Экономическая теория процента. Простые и сложные проценты.

1. К концу n-го промежутка начисления по простым процентам наращенная сумма рассчитывается по формуле:

Fn= P(1+nr) (1).

2. Каждая следующая сумма при наращении сложных процентов по ставке r возрастает на долю r от предыдущей суммы и рассчитывается по формуле: Fn=P(1+ r)n. (2)

3. Процентные деньги (проценты) – это величина дохода, равная Dn=Fn-P (3).

4. Правило 72. Если процентная ставка есть , то удвоение капитала по такой ставке происходит примерно за 72/ лет. Это правило применяется для небольших ставок, рассчитываемых по сложным процентам.

5. Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться с помощью следующих методов:
  • По схеме сложных процентов
  • По смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года):

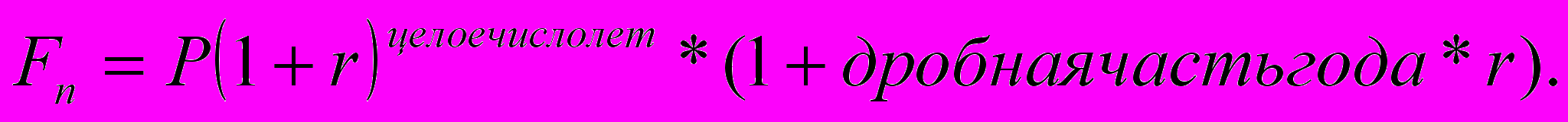
6. Логика финансовых вычислений


Существует две основные схемы финансовых вычислений:







Вопросы
  1. Определение числовой последовательности.
  2. Арифметическая прогрессия, n-й член арифметической прогрессии, сумма арифметической прогрессии.
  3. Определение геометрической прогрессии, n-й член геометрической прогрессии, сумма геометрической прогрессии.
  4. Понятие процента в математике.
  5. Чем отличаются абсолютные и относительные стоимости?
  6. Оценки эффективности финансовых операций
  7. Чем отличаются две основные схемы финансовых вычислений?
  8. Какие факторы влияют на:
    1. общий уровень процентных ставок,
    2. временную структуру процентных ставок,
    3. качественную структуру процентных ставок?
  9. В чем разница между простыми и сложными процентами?
  10. Мультиплицирующие множители, их экономический смысл.
  11. Непрерывное наращение, когда его используют?
  12. Какой тип наращения предпочтителен при хранении денег в банке?
  13. В контракте оговорены данные о сумме, которую можно получить через 3 года. Какие расчетные формулы и почему следует использовать при продаже контракта сразу после его заключения?
  14. Докажите строго, что при одной и той же ставке r наращение сложных процентов идет быстрее чем простых процентов, при длине периода наращения, более единичного, и медленнее, если период наращения менее единичного.
  15. Поясните «Правило 72». Когда его можно использовать?
  16. Какая схема начисления и почему более выгодна при начислении процентов за дробное число лет?

Пример 1.. Депозит в 200 тыс. руб. положен в банк на 4 года под 15% годовых. Найти наращенную сумму, если ежегодно начисляются сложные проценты.

Пример 2. Годовая ставка простых процентов равна 8,3%. Через сколько лет начальная сумма удвоится?

Пример.3. Пусть P=1000, r = 10%. Найти наращенную сумму за за n=3 промежутка начисления.

Пример.4. Годовая ставка сложных процентов равна r =8%. Через сколько лет начальная сумма удвоится?

Пример.5. М.Е. Салтыков-Щедрин описывает в «Господах Головлевых» такую сцену: «Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: сколько было бы у него теперь денег, если бы маменька подаренные ему при рождении дедушкой «на зубок» сто рублей не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего восемьсот рублей».

Требуется рассчитать по приведенным цифрам, какой процент платил в то время ломбард по вкладам. Возраст Порфирия в момент его расчетов примем равным пятидесяти годам.

Пример 6. Чему равна будущая стоимость одной денежной единицы через 9 лет при ставке процента 10%.

Пример 8. Пусть сумма начального вклада Р=750 у.е. наращивается по годовой ставке r=20%. Принятая схема начисления: по простым процентам. Подсчитать проценты за n=4 промежутков начисления (лет). Представить последовательность наращенных сумм за 4 года.

Пример 9. Предприниматель получил в банке ссуду в размере 25 тыс. руб. сроком на 6 лет на следующих условиях: для первого года процентная ставка равна 10% годовых, на следующие 2 года устанавливается маржа в размере 0,4% и на последующие годы маржа равна 0,7%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды по схеме простых и сложных процентов.

Пример 10. Вкладчик поместил в банк 15 тыс. руб. на след. условиях: в 1-й год процентная ставка равна 20% годовых, каждые последующие полгода ставка повышается на 3%. Найти наращенную сумму за 2 года, если проценты начисляются только на первоначальную сумму вклада.

Пример 11. Найти наращенную сумму за два года, если в предыдущем примере с изменением ставки происходит одновременно и капитализация процентного дохода.

Пример 12. Товар ценой в 3 тыс. руб. продается в кредит на 2 года под 12% годовых с ежеквартальными равными погасительными платежами, причем начисляются простые проценты. Определить долг с процентами, проценты и величину разового погасительного платежа.

Пример 13. Клиент обратился в банк 12 апреля с целью получения кредита под залог 300 ценных бумаг, причем курсовая стоимость каждой ценной бумаги на этот день составляет 100 рублей. Банк предоставляет кредит под 10% годовых на 3 месяца в размере 80% курсовой стоимости ценных бумаг. В контракте с клиентом оговаривается, что затраты банка на обслуживание долга составляют 1% от номинальной суммы кредита и удерживаются вместе с процентным платежом в момент предоставления кредита. В случае просрочки выплаты долга клиент рассчитывается с банком за каждый лишний день по ставке 12% годовых. Найти величину кредита, который получит клиент.

Пример 14. Предпринимателю необходима сумма в 40 тыс. руб. на 3 месяца. Банк предоставит ему кредит в размере 75% от стоимости залога под 12% годовых и за обслуживание долга взыщет 400 руб. Определить величину залога, если кредит взят 15 мая.

Пример 15. В 1624г. остров Манхэттен (центр Нью-Йорка) был куплен у индейского вождя за 24 долл. Чему равна это сумма в 2000 г., если средний процент по долгосрочным займам в ХХ веке в США составлял 6,3%?

Пример 16. В условиях ползучей инфляции (2-5% в год) простые проценты начисляются на вклады и кредиты сроком до года. Более того, встречаются случаи начисления простых процентов и на больший срок. Хотя в значительной мере такие проценты есть перевод результатов расчетов по сложным процентам в простые. Банкиры просто пересчитывают вклады на разные сроки по формуле сложного процента. Так если банк дает 70% годовых за месячный депозит, то чему должна быть равна трехмесячная ставка? Какой процент в этом случае должен получить банк за трехмесячный кредит (в процентах годовых).

Пример 17. Пусть некоторая величина составляет 30%. Чему будет равно увеличение доли этой величины, если произошел ее 5% рост?


ЗАНЯТИЕ 2

Внутригодовые процентные начисления. Номинальная, эффективная ставки


1. В том случае, когда продолжительность финансовой операции рассчитывается в днях, однозначного определения процента и других параметров финансовой операции нет. Решение будет зависеть от того, как рассчитывается продолжительность года и продолжительность периода финансовой операции.

Таким образом, существует два варианта процентов: точный процент и обыкновенный процент.

При расчете точного процента (exact interest) берется точное число дней в году (365, 366), в квартале (89 – 92), в месяце (28 – 31).

При расчете обыкновенного процента (ordinary) берется приближенное число дней в году (360), в квартале (90), в месяце (30).

Продолжительность периода финансовой операции (например, ссуды) исчисляется также двумя способами: расчет по дням (берется точное число дней) и расчет с приближенным числом дней в месяце (30).

Следовательно, можно выделить три способа расчета процентов :
  1. Обыкновенный процент с приближенным числом дней (360/360). Такой способ расчета практикуется в Германии, Дании, Швеции.
  2. Обыкновенный процент с точным числом дней (365/360 или АСТ/360). Такой способ расчета практикуется в Бельгии и Франции.
  3. Точный процент с точным числом дней (365/365 или АСТ/АСТ). Такой способ расчета практикуется в Великобритании и США.

В российской практике можно встретиться с различными схемами начисления процентов. Эффект от выбора зависит от суммы финансовой операции. Понятно, что использование обыкновенных процентов с точным числом дней ссуды, как правило, дает больший результат, чем применение обыкновенных процентов с приближенным числом дней ссуды.
    1. Величина наращенного капитала за n лет при m-кратном начислении процентов по сложной процентной ставке равна: , где m – количество начислений процентов за год, а r(m) - номинальная процентная ставка.
    2. Годовая эффективная ставка ref =(1+r(m)/m)m-1.
    3. Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными. Верно следующее равенство:.
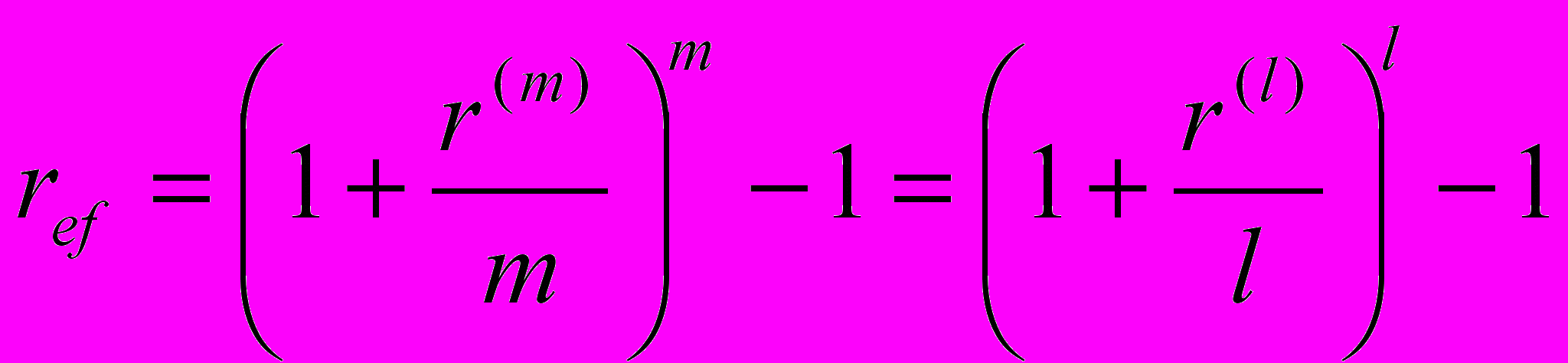    4. Номинальная процентная ставка находится из формулы: r(m)=m[(1+ref)1/m-1].
    5. Величина наращенного капитала за n лет при известной эффективной ставке: Fn=P(1+ref)n
    6. П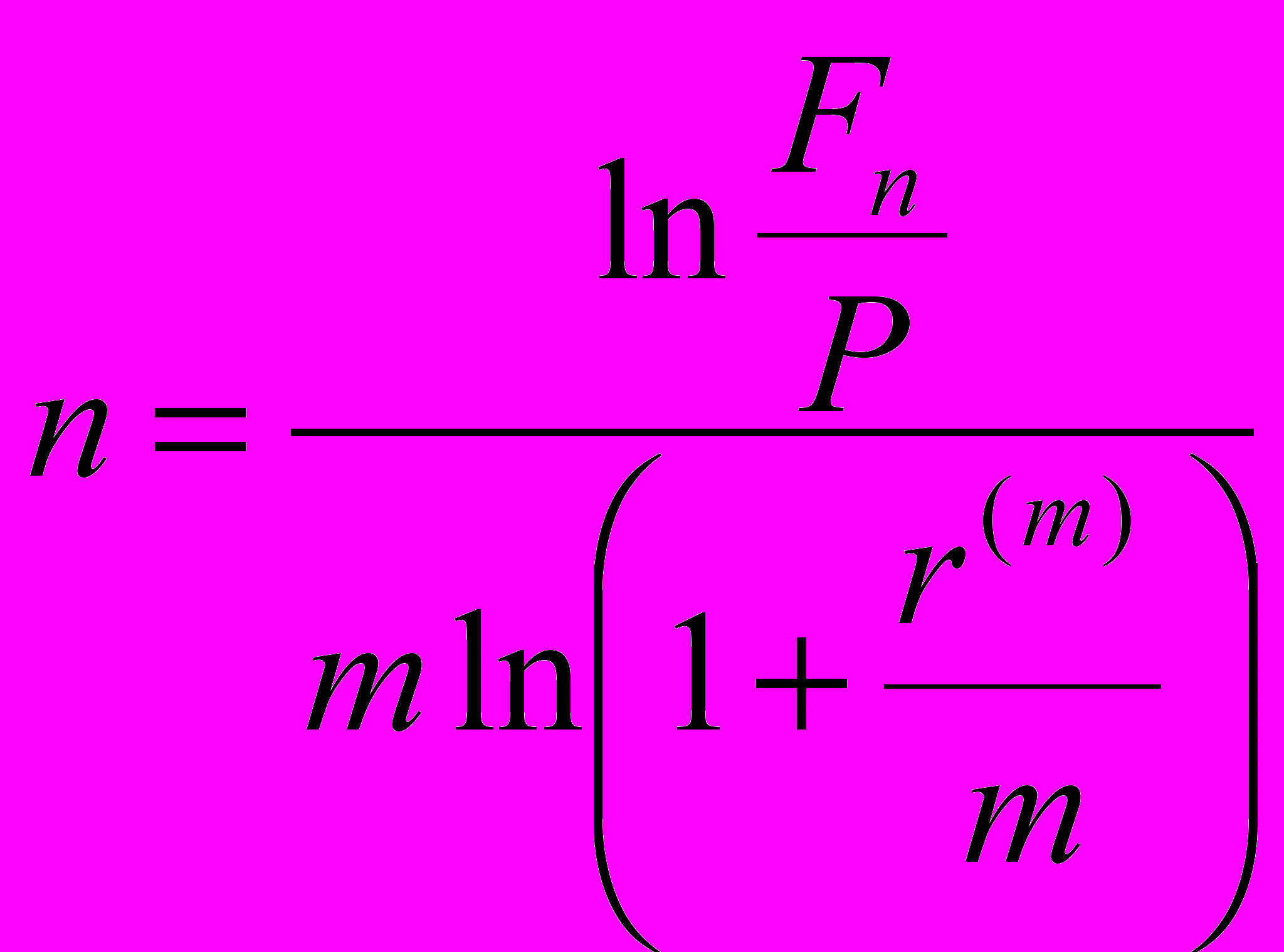ериод n, за который сумма Р при m-кратном начислении процентов в год по ставке r(m) возрастет до величины Fn, находится по формуле: .



    1. Нахождение номинальной ставки, если известны наращенная сумма и современная стоимость капитала
    2. Нахождение эффективной ставки, если известны наращенная сумма и современная стоимость капитала

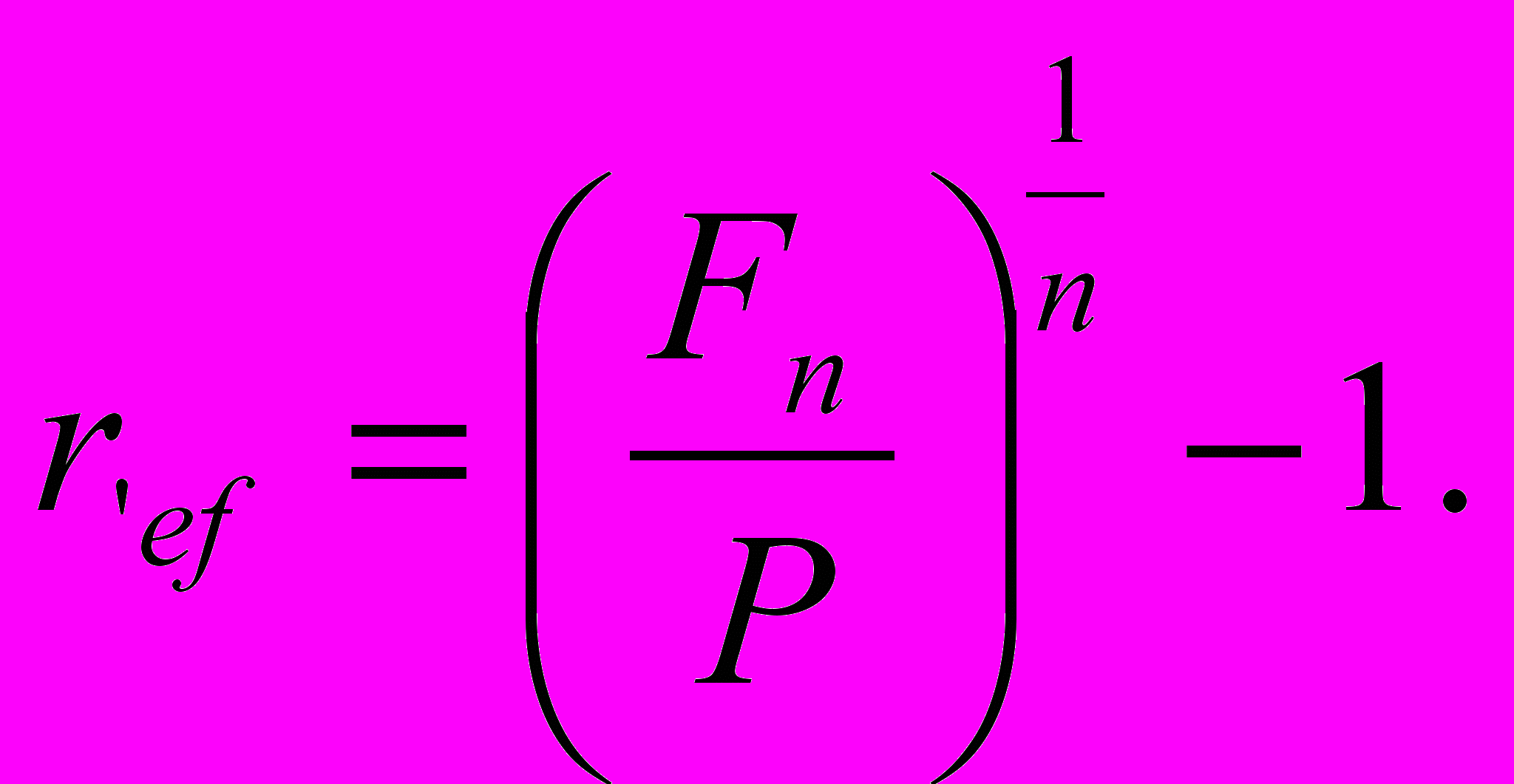
Вопросы
  1. В чем разница между точным и обыкновенным процентами?
  2. Почему нет однозначного решения задач в том случае, когда продолжительность финансовой операции не измеряется целым числом лет?
  3. Как влияет частота начисления процентов на выгодность контракта, при условии начисления по простым и сложным процентам?
  4. Докажите, что эффективная ставка всегда больше номинальной.
  5. Для каких целей используют годовую эффективную ставку?
  6. Для каких целей используют номинальную ставку?


Пример 1. Представлена ссуда в размере 7 тыс. руб. 10 февраля с погашением 10 июня под 20% годовых (простая ставка, год не високосный). Рассчитать различными способами сумму к погашению.

Пример 2. 14 марта в банк положили сумму 1000 у.е. до востребования под ставку 12% годовых сложных процентов. Какую сумму снимет вкладчик 1 сентября?

Пример 3. Предприниматель может получить ссуду а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант предпочтительнее?

Пример 4. Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.

Пример 5. Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная годовая процентная ставка равна 20%?

Пример 6. В банк вложены деньги в сумме 5 тыс. руб. на 2 года с полугодовым начислением процентов под 20% годовых. Найти наращенные суммы через 6, 12, 18, 24 месяца.

Пример 7. На вклад начисляются ежемесячно сложные проценты по номинальной годовой процентной ставке 16%. За какой срок первоначальный капитал утроится? Как изменится результат, если сложные проценты начисляются ежегодно?

Пример 8. Вкладчик хотел бы за 5 лет удвоить сумму, помещаемую в банк на депозит. Какую годовую номинальную процентную ставку должен предложить банк при начислении сложных процентов каждые полгода?

Пример 9. В долг на 2,5 года предоставлена сумма в 30 тыс. руб. с условием возврата 40 тыс. руб. Найти эффективную ставку в этой финансовой сделке.

Пример 10. Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10% и m= 1, 2, 4, 12, 365.

Пример 11.Если ссуда взята 29 января на месяц (схема 360/360), то когда ее следует отдать?

Пример 12. Ссуда взята на период с 13 июля по 19 сентября. Вычислить число дней ссуды.

Пример 13. Во сколько раз увеличится сумма долга при сроке 2 года 7 месяцев при 12% годовых? (использовать смешанный процент).

  1. Литература:

Базовые учебники:

1. Четыркин Е.М. Финансовая математика. - М.: Финансы и статистика, 2000.
Основная

  1. Капитоненко В.В. Финансовая математика и ее приложения. – М.: ПРИОР, 2000.
  2. Ковалев В.В. Сборник задач по финансовому анализу. - М.: Финансы и статистика, 2000.
  3. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. -М.: Финансы и статистика, 2001.
  4. Малыхин В.И. Финансовая математика. - М.: ЮНИТИ-ДАНА, 2000.
  5. Мелкумов Я.С. Финансовые вычисления. Теория и практика: Учебно-справочное пособие. – М.: ИНФРА-М, 2002.

Дополнительная:

  1. Уотшем Т.Дж., Паррамоу К. Количественные методы в финансах. – М.: Финансы. Изд. объединение «ЮНИТИ», 1999.
  2. Маршалл Джон Ф., Бансал Випул К. Финансовая инженерия: Полное руководство по финансовым нововведениям. – М.: ИНФРА-М,1998.