Прямолинейная регрессия, ее коэффициент и уравнение
| Вид материала | Документы |
- Решение кубичных уравнений, 38.76kb.
- Законы распределения, 20.25kb.
- Тема 2: Квадратные уравнения, 34.25kb.
- Рабочая программа учебной дисциплины ф тпу 1- 21/01 «утверждаю», 156.29kb.
- § Тема. Некоторые определения и обозначения, 1005.59kb.
- Домашнее задание. Ход урока: Устная работа На доске записаны уравнения:, 88.91kb.
- Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому, 14.77kb.
- Вопросы к экзамену по дисциплине "Статистика", 32.3kb.
- Федеральное государственное унитарное предприятие пензенское производственное объединение, 71.58kb.
- Структурные схемы операционных усилителей, 105.83kb.
ПРЯМОЛИНЕЙНАЯ РЕГРЕССИЯ, ЕЕ КОЭФФИЦИЕНТ И УРАВНЕНИЕ
При линейном типе связи между двумя изучаемыми признаками кроме расчета корреляций применяется расчет коэффициента регрессии.
В случае прямолинейной корреляционной связи каждому из изменений одного признака соответствует вполне определенное изменение другого признака. Однако коэффициент корреляции показывает эту связь лишь в относительных величинах - в долях единицы. С помощью же регрессионного анализа эту величину связи получают в именованных единицах. Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.
В отличие от корреляционного регрессионный анализ дает более широкую информацию, поскольку вычислением двух коэффициентов регрессии Rx/y и Rу/х возможно определить как зависимость первого признака от второго, так и второго от первого. Выражение регрессионной связи с помощью уравнения позволяет по определенному значению одного признака установить значение другого признака.
Коэффициент регрессии R представляет собой произведение коэффициента корреляции на отношение квадратических отклонений, вычисленных для каждого признака. Рассчитывается он по формуле
Rx/y = r
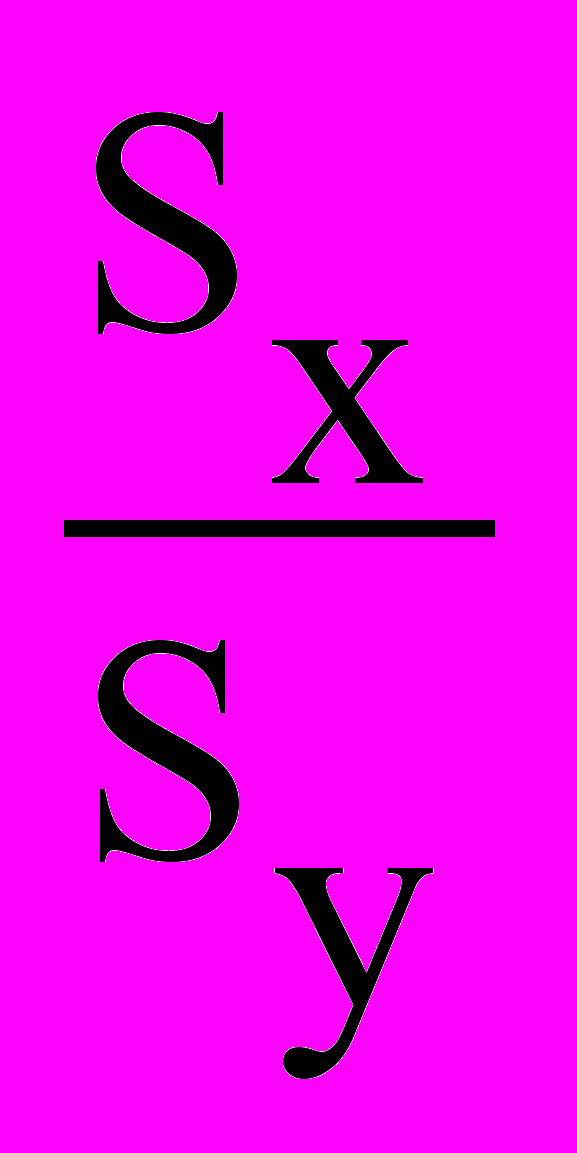
где, R - коэффициент регрессии; SХ - среднее квадратическое отклонение первого признака, который изменяется в связи с изменением второго; SУ - среднее квадратическое отклонение второго признака в связи с изменением которого изменяется первый признак; r - коэффициент корреляции между этими признаками; х - функция; у -аргумент.
По этой формуле определяется величина значения х при изменении у на единицу измерения. При необходимости обратного расчета можно найти величину у при изменении х на единицу измерения по формуле:
Rу/х = r
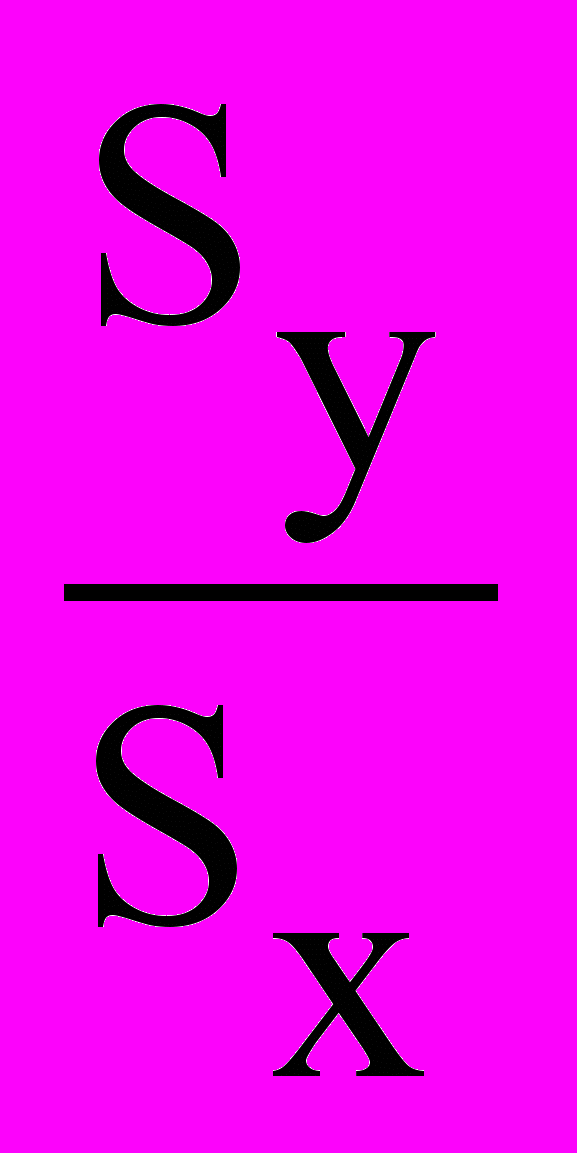
В этом случае активная роль в изменении одного признака по отношению к другому меняется, по сравнению с предыдущей формулой аргумент становится функцией и наоборот. Величины SX и SY принимаются в именованном выражении.
Между значениями г и R имеется четкая взаимосвязь, выражающаяся в том, что произведение регрессии х по у на регрессию у по х равно квадрату коэффициента корреляции, т. е.
Rx/y Ry/x = r2
Это свидетельствует, что коэффициент корреляции представляет собой среднюю геометрическую из обоих значений коэффициентов регрессии данной выборки. Данная формула может быть использована для проверки правильности расчетов.
При обработке цифрового материала на счетных машинах могут применяться развернутые формулы коэффициента регрессии:
R
или
x/y =
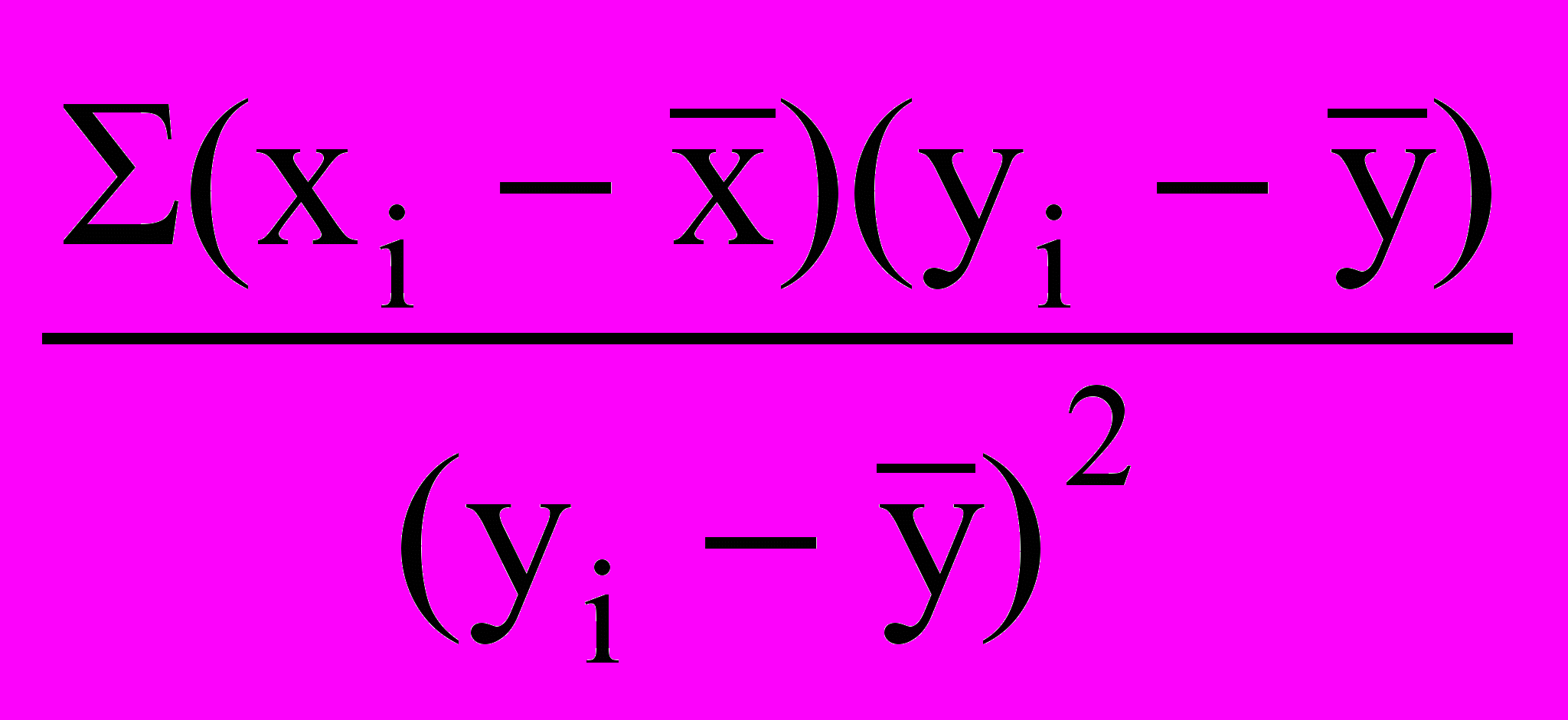 ;
;Rx/y =
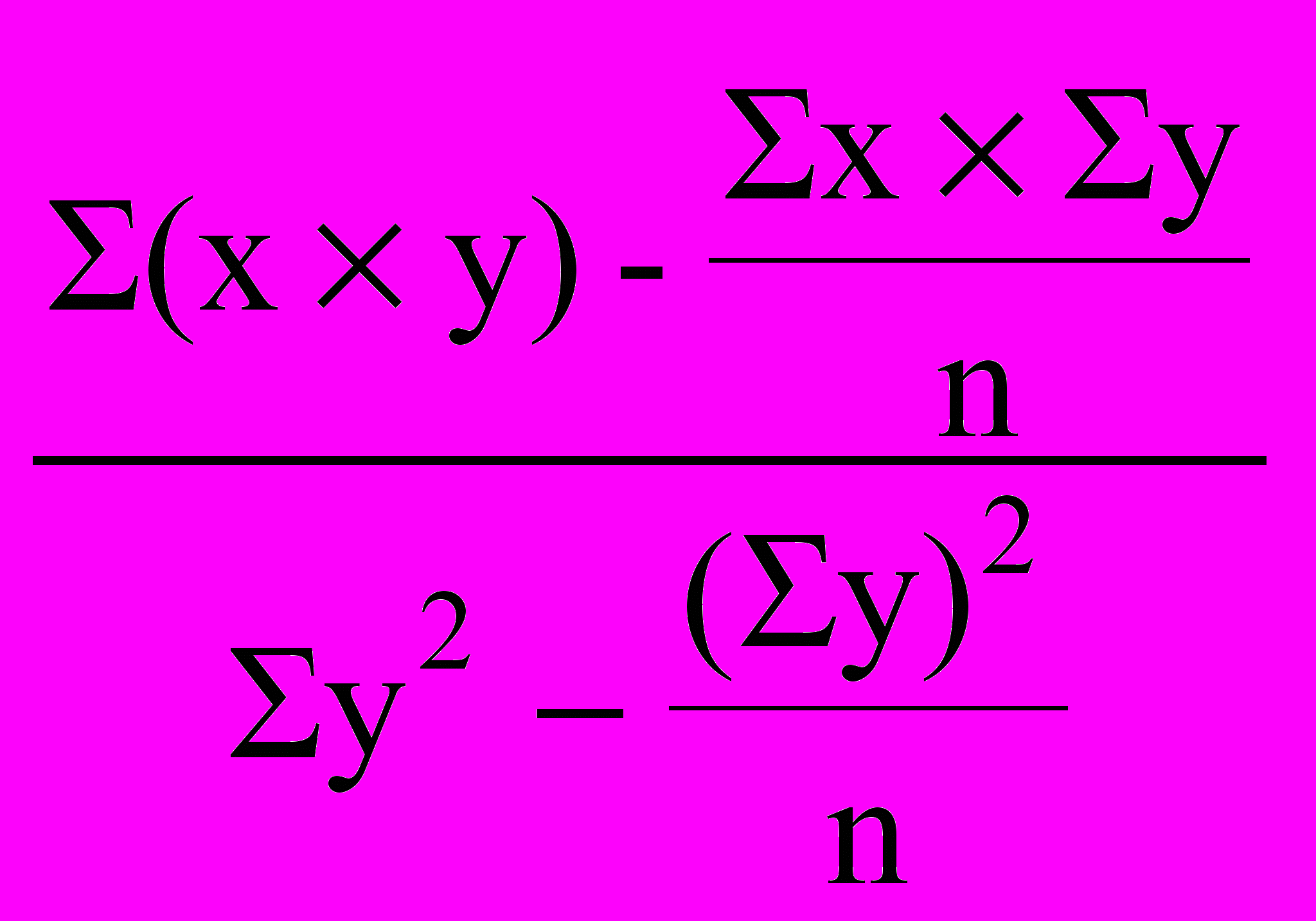
Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:
SR =
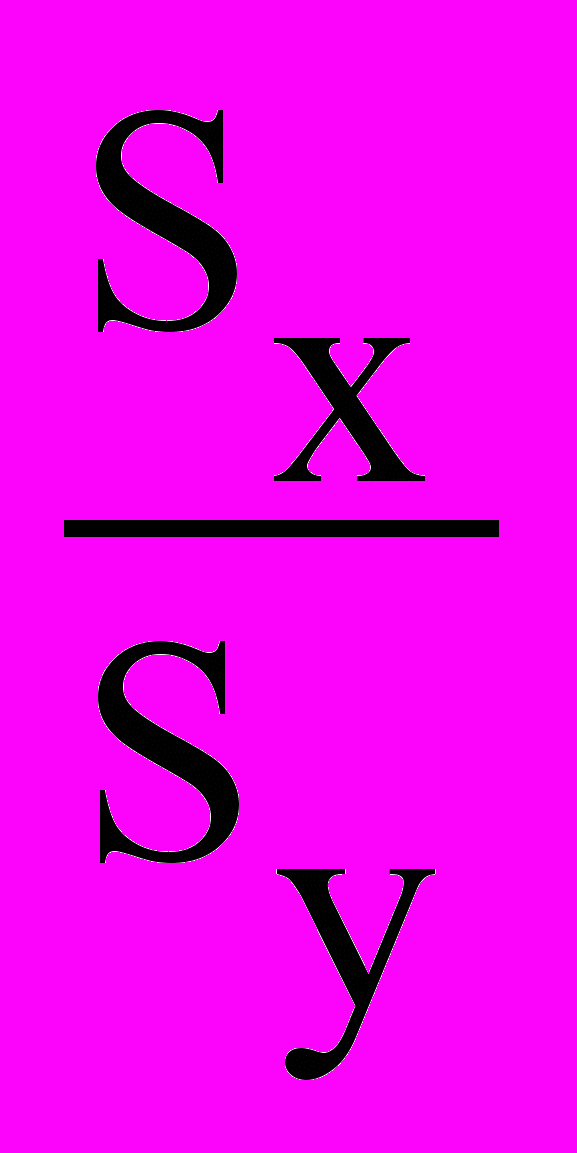 Sr =
Sr = 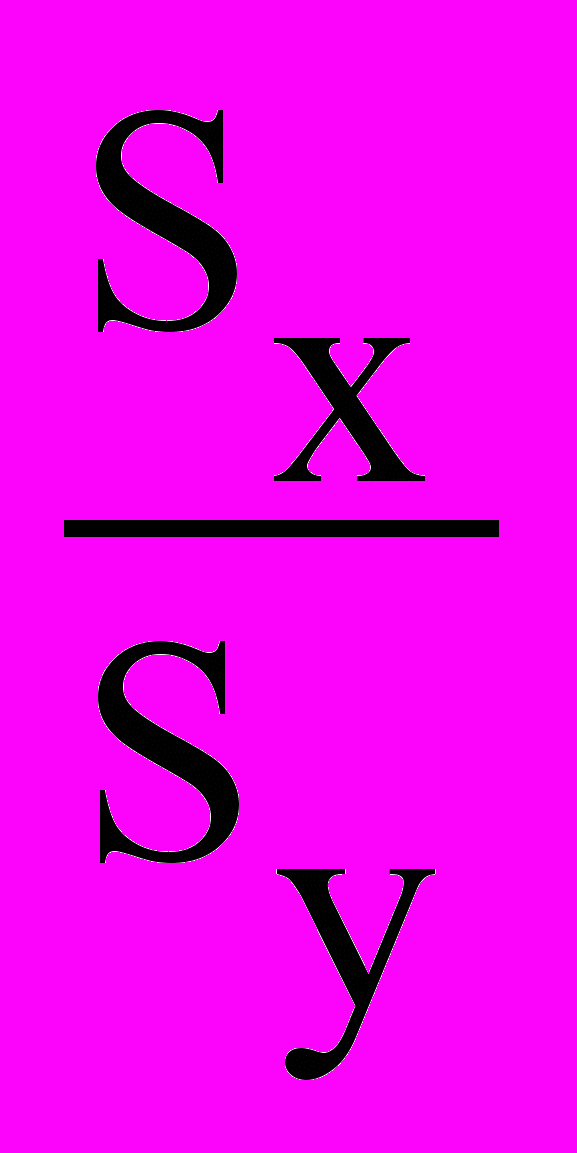
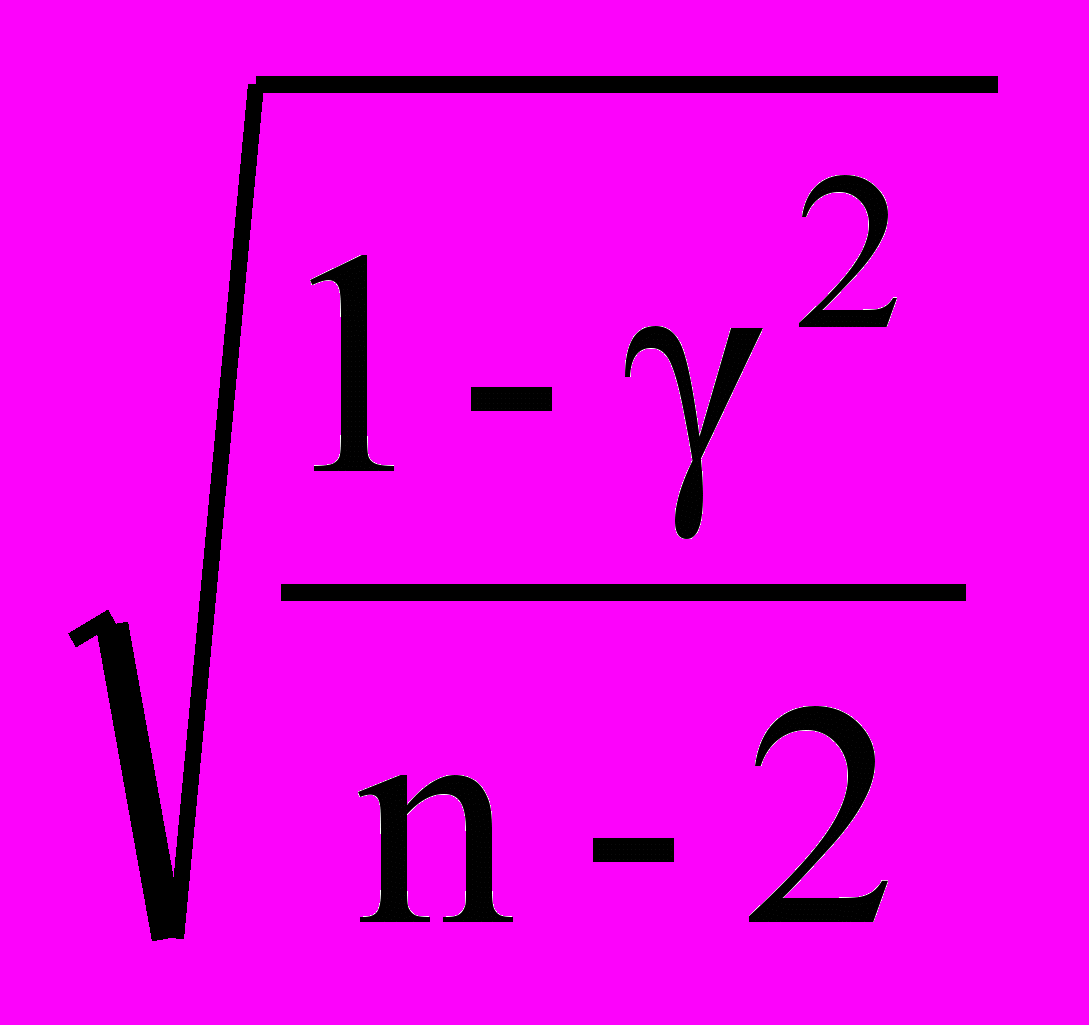
Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:
tR =
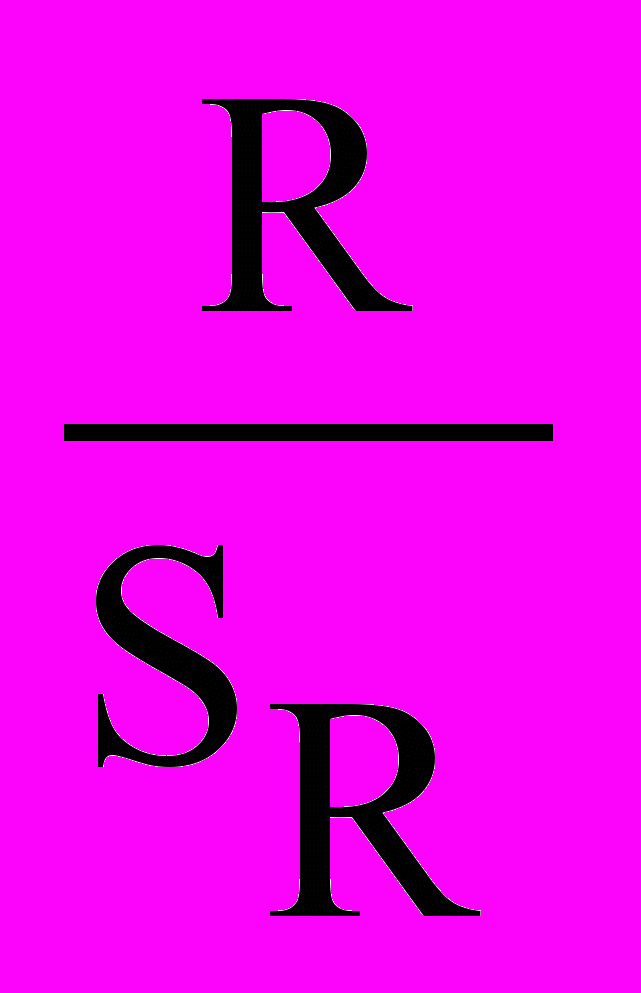
в итоге он равен критерию достоверности коэффициента корреляции:
tR =
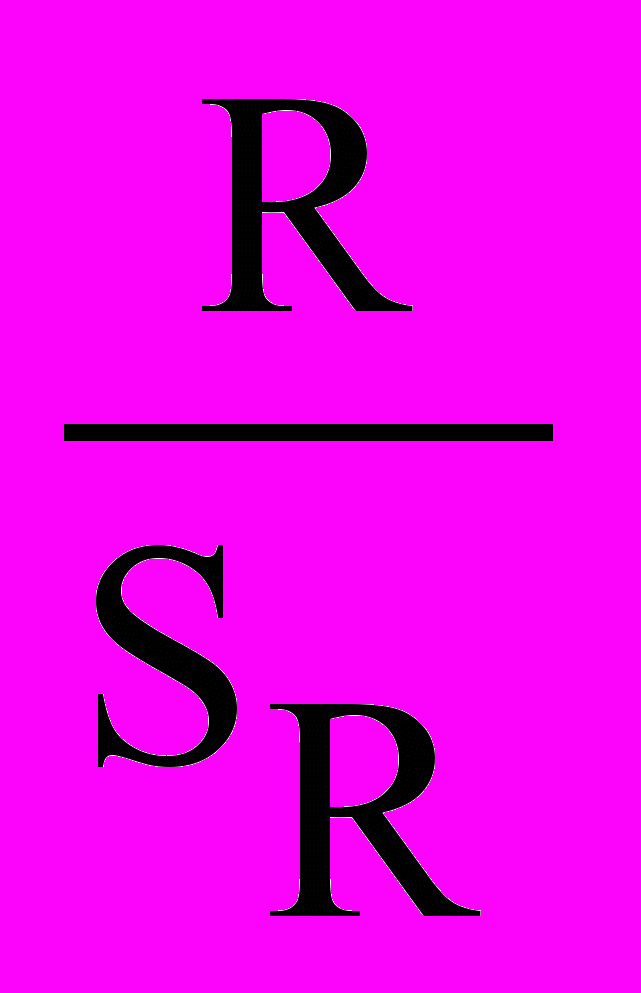 =
= 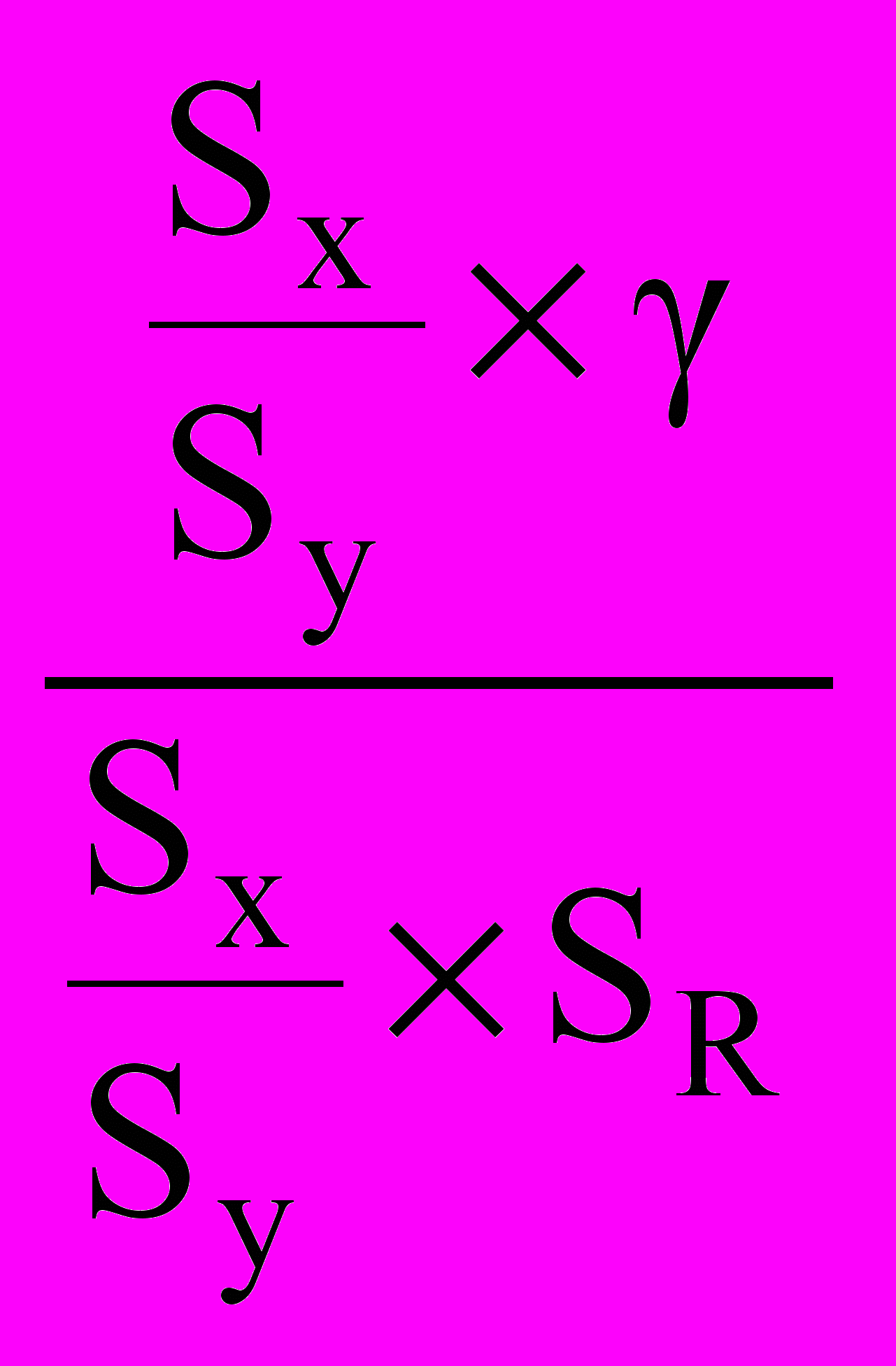 =
= 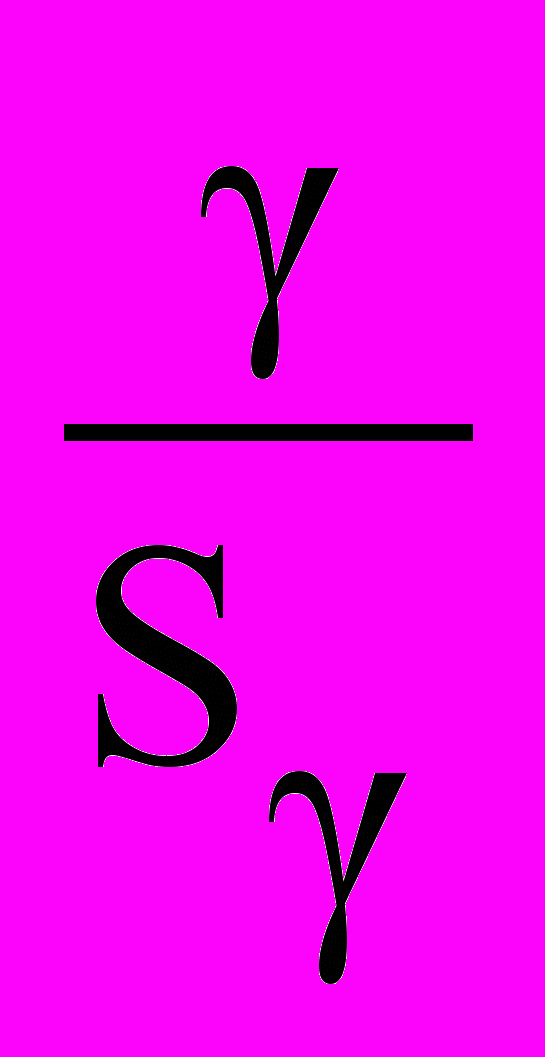 = tr
= trДостоверность величины tR устанавливается по таблице Стьюдента при = n - 2, где n - число пар наблюдений.
Предположим, что при расчете коэффициента корреляции между уровнем яйценоскости и массой яиц:
было установлено, что r = -0,46;
для показателя яйценоскости:
 = 102; S = 7,0; n = 40
= 102; S = 7,0; n = 40 для показателя массы яйца:
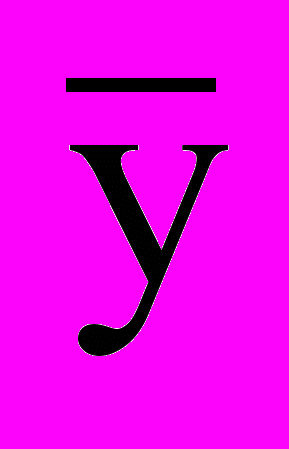 = 56,68; S = 1,94;n = 40
= 56,68; S = 1,94;n = 40регрессия первого признака по второму равна:
Rx/y =
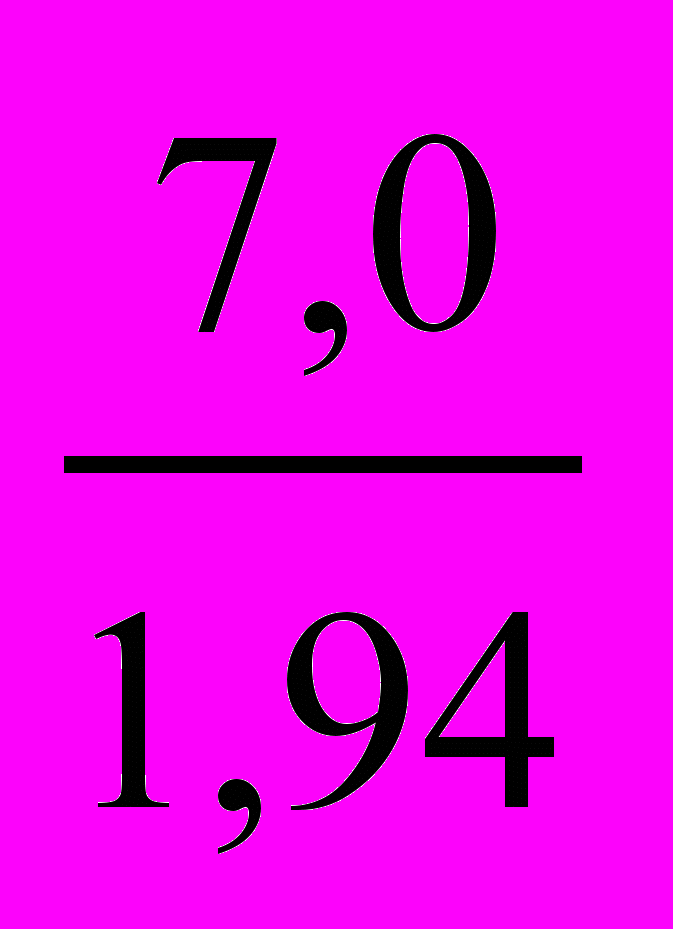 (-0,46) = 3,61(-0,46) = -1,66
(-0,46) = 3,61(-0,46) = -1,66Это означает, что увеличение массы яйца на 1 г в данной популяции кур сопровождается уменьшением яйценоскости за 5 мес. на 1,66 яйцо.
Обратный расчет:
Ry/x =
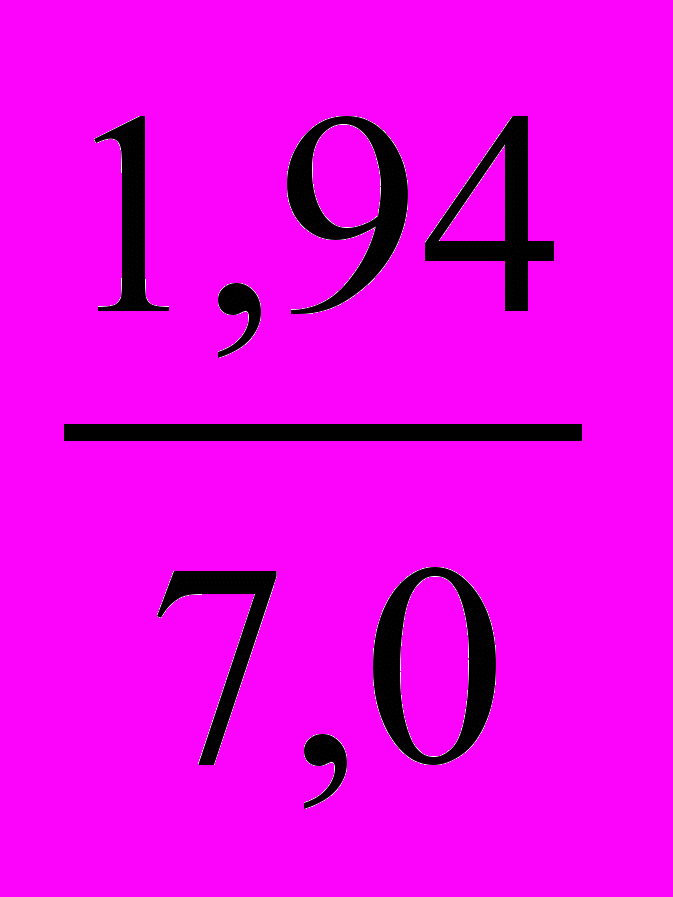 (-0,46) = 0,277(-0,46) = -0,127
(-0,46) = 0,277(-0,46) = -0,127показывает, что повышение яйценоскости на 1 яйцо за 5-месячный период в данной популяции кур сопровождается уменьшением средней массы яиц на 0,127 г.
По формуле взаимозависимости r и R можно проверить правильность расчета:
(-1,66) (-0,127) = 0,210; (-0,46)2 = 0,210.
Ошибка коэффициента регрессии Rx/y = равна
SR =
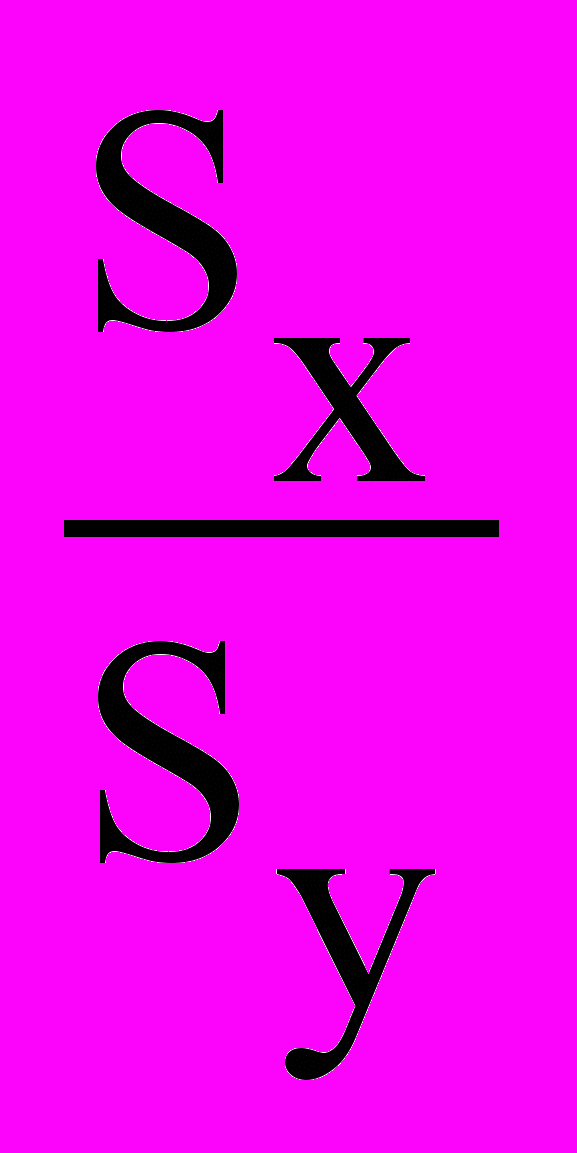 Sr =
Sr = 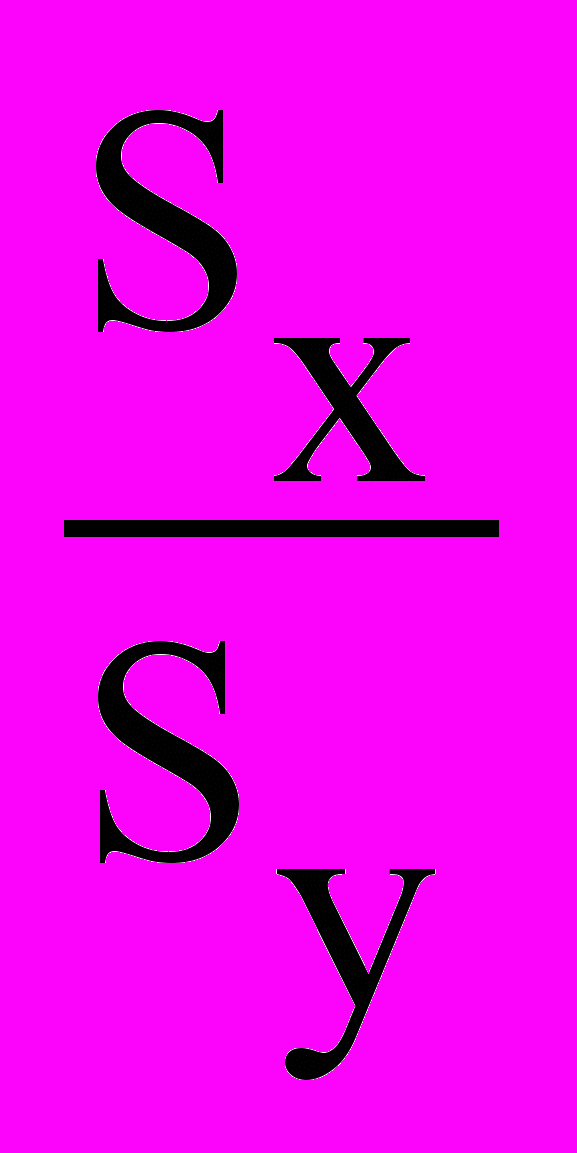
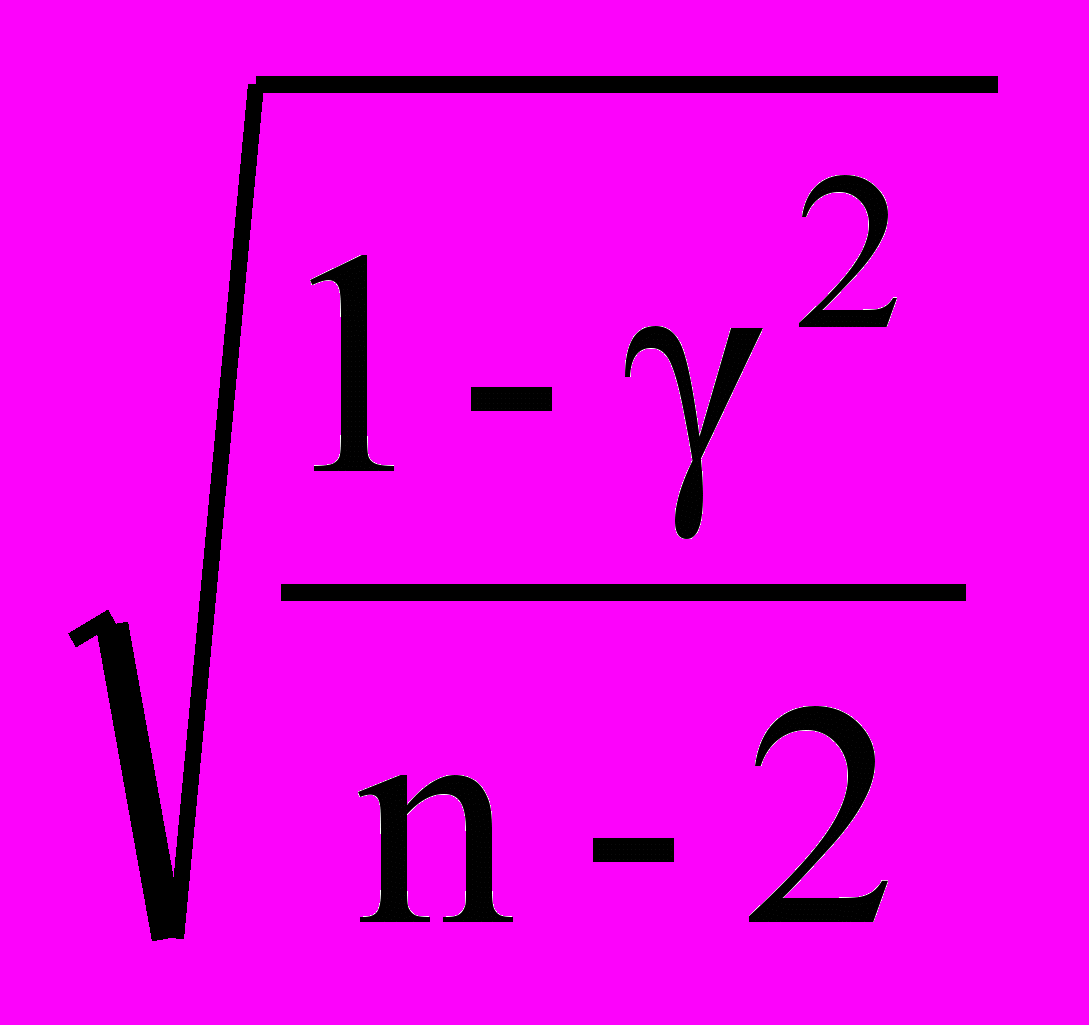
SR = 3,61
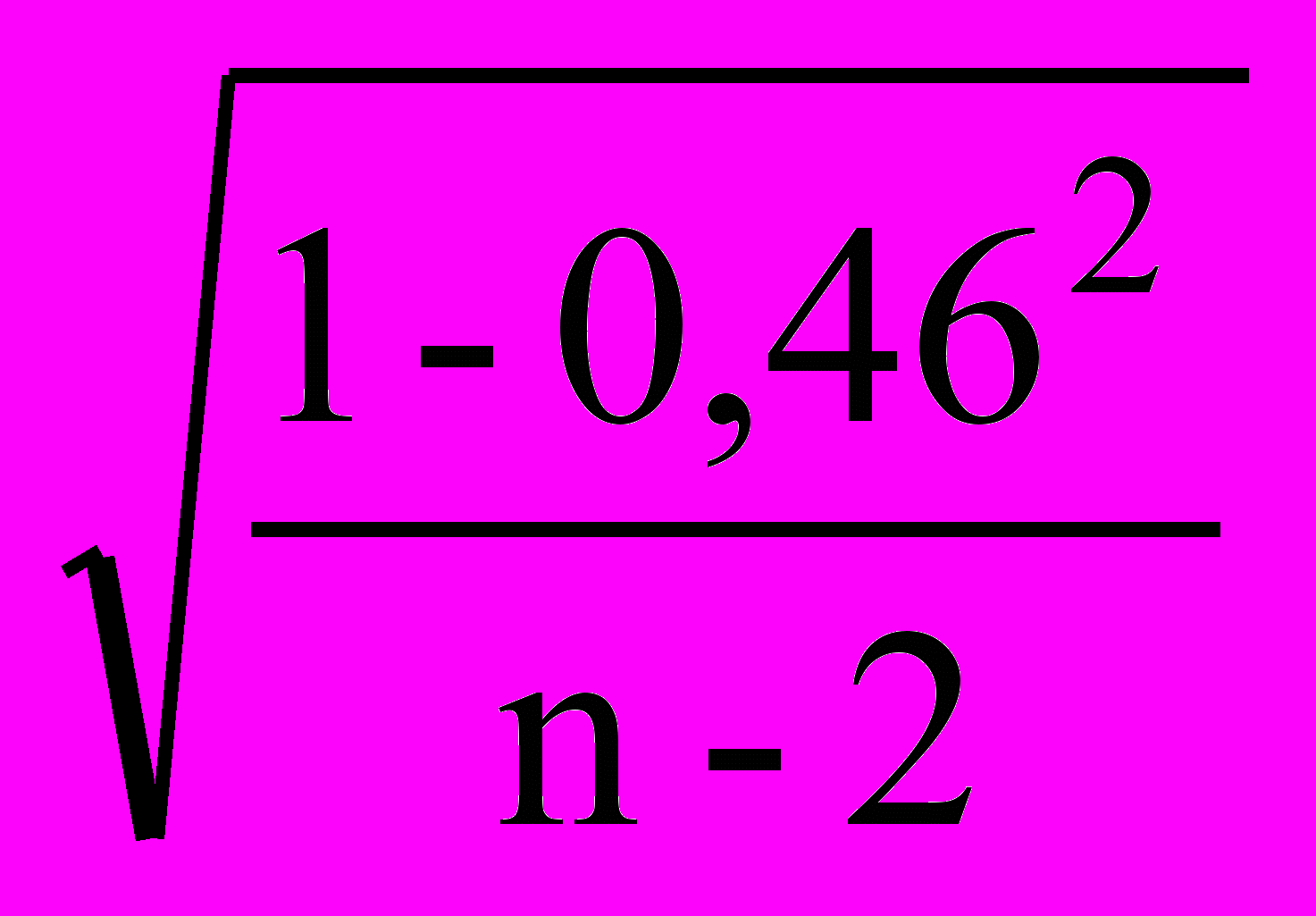 = 3,61
= 3,61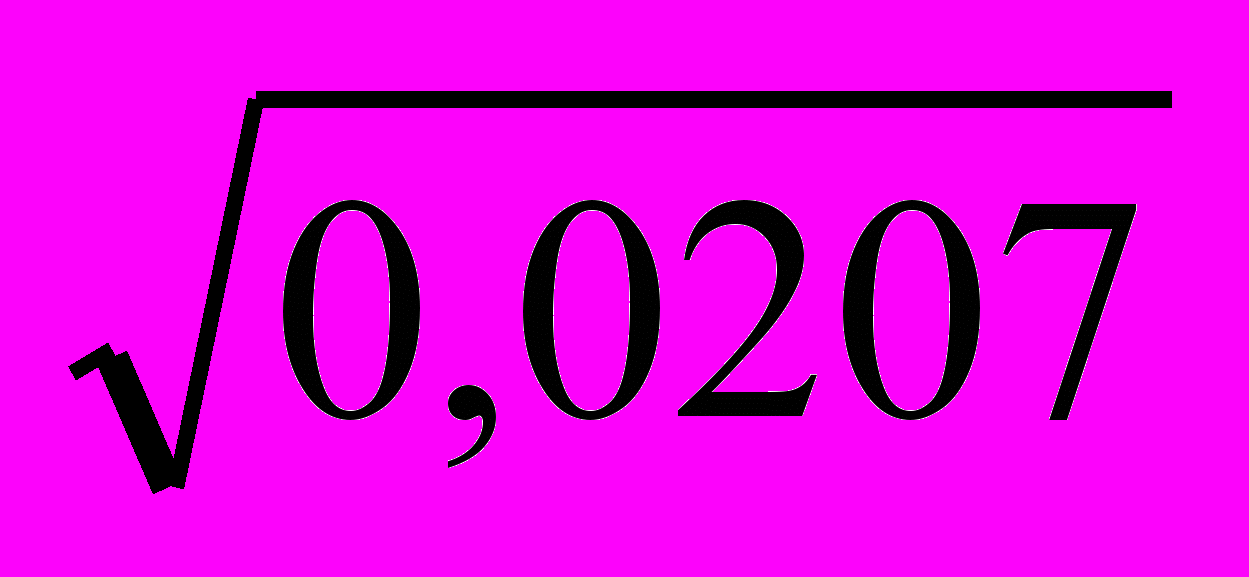 = 3,610,144 = 0,52
= 3,610,144 = 0,52SR = 0,52
Критерий достоверности Rx/y равен
tR =
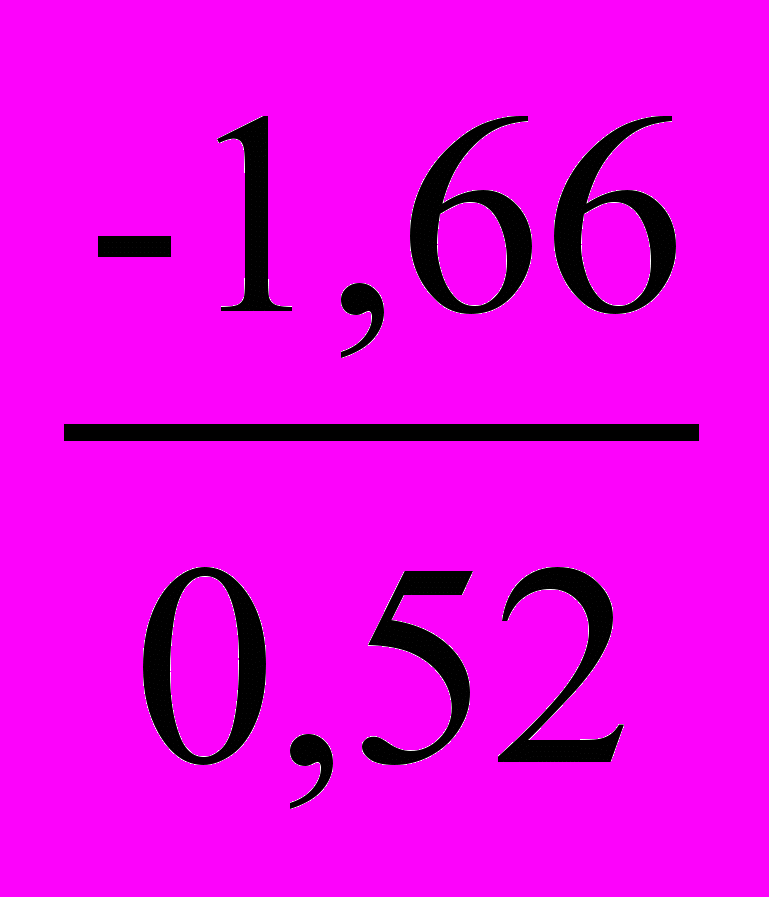 = 3,19
= 3,19По таблице Стьюдента стандартные значения t для = 38 равны 2,0-2,7-3,6. Следовательно, рассчитанный коэффициент регрессии достоверен при Р 0,99.
Более глубокий анализ связи двух признаков может быть сделан на основе расчета уравнения прямолинейной регрессии. Сущность коэффициента прямолинейной регрессии, показывающей насколько второй признак отклоняется от своей средней, если первый отклоняется от своей средней на единицу измерения, можно выразить формулой
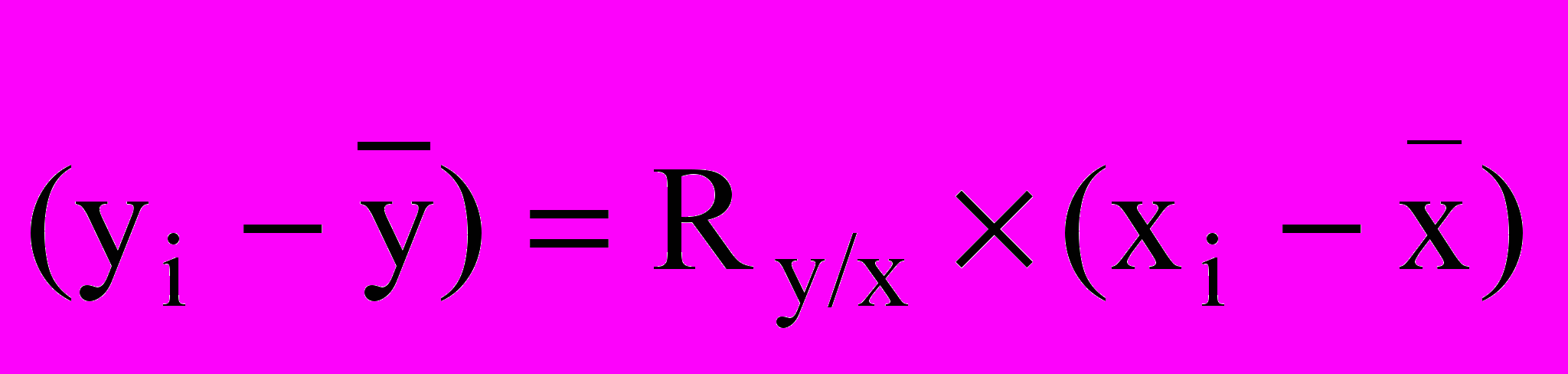
Преобразуя это уравнение, получаем рабочую формулу прямолинейной регрессии. Обозначаем Ry/x через b:
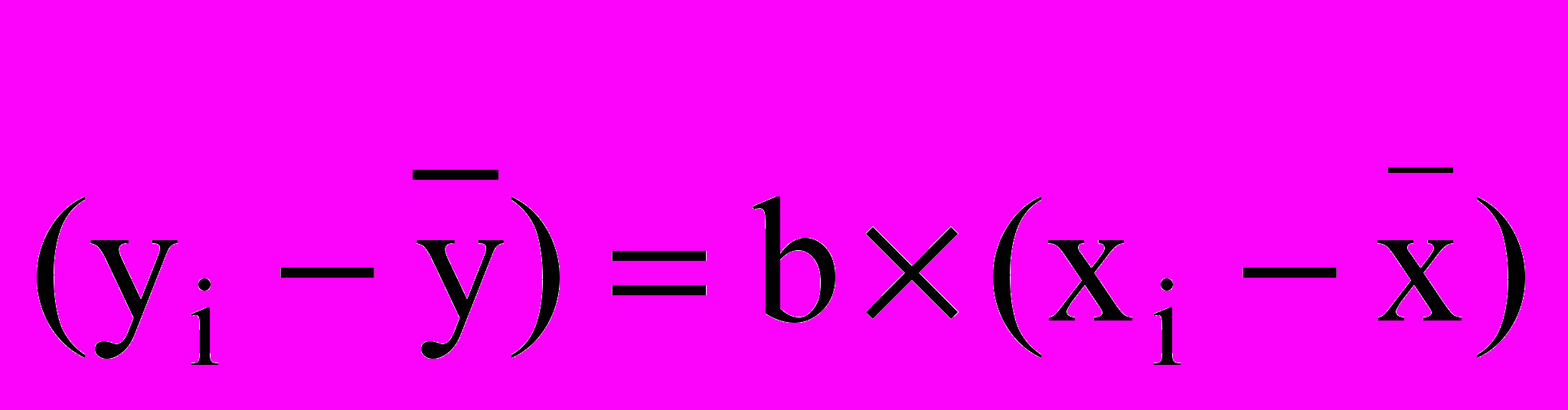
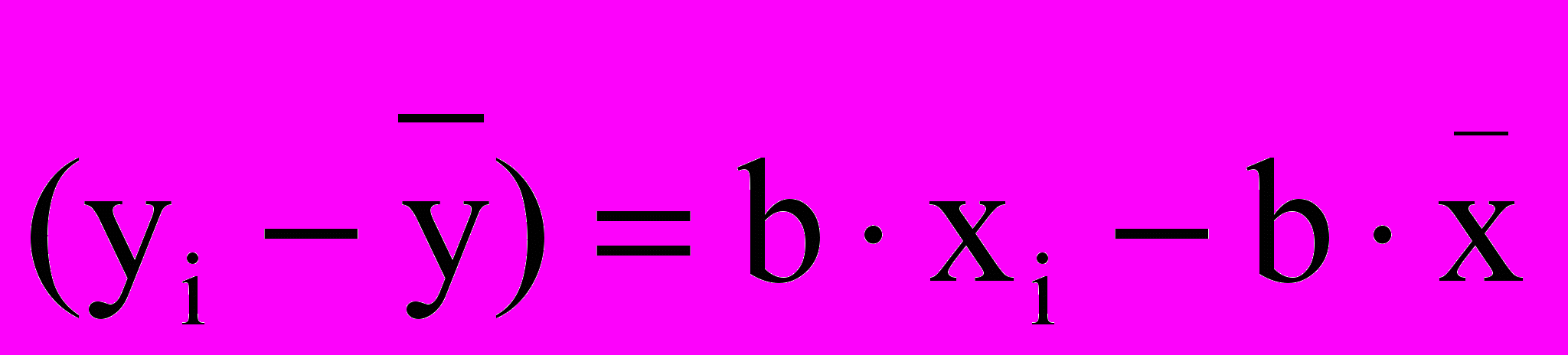
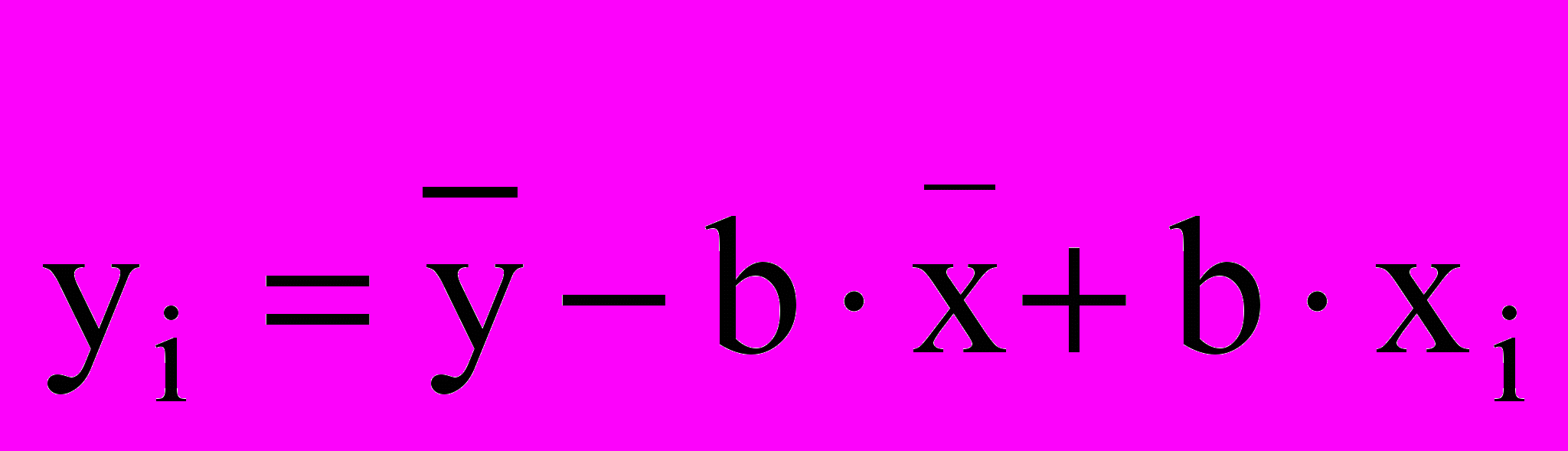
Обозначаем
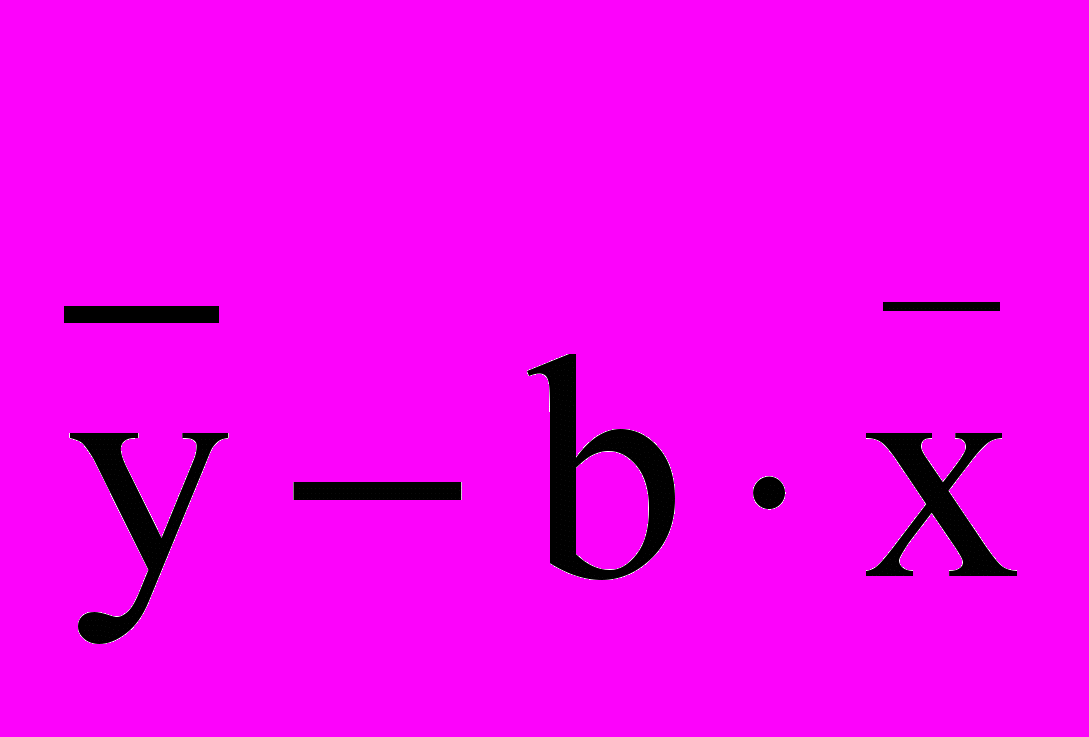 = а, следовательно
= а, следовательно 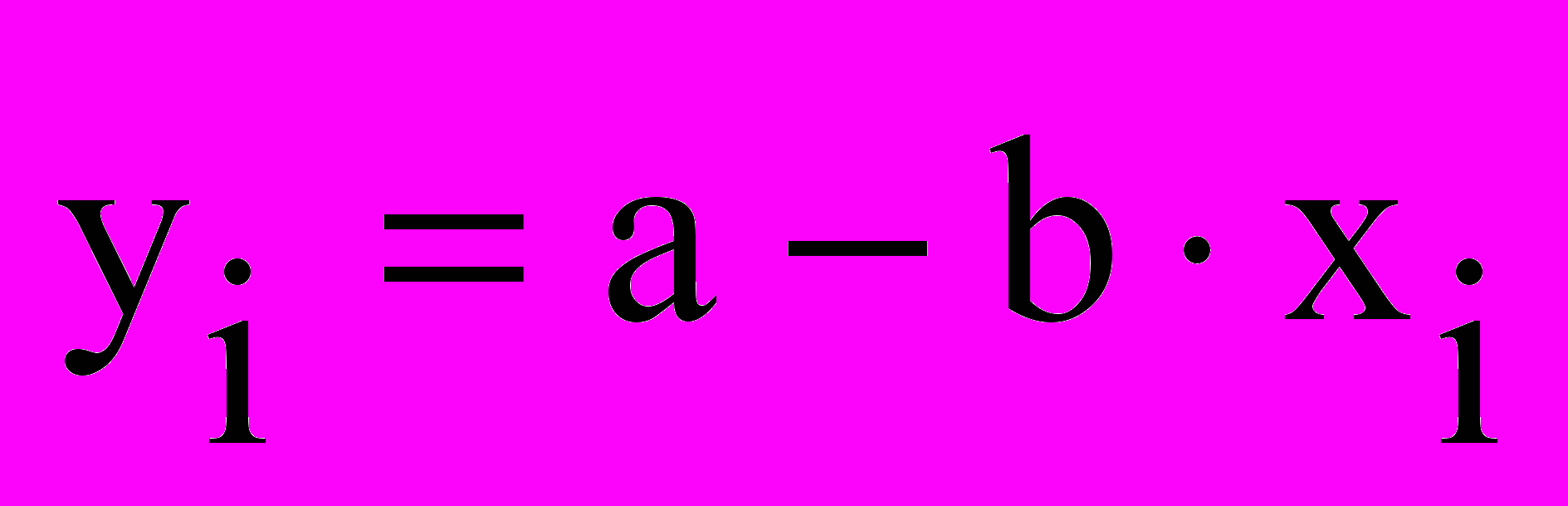
В этом уравнении х является аргументом, у - его функцией. Уравнение показывает взаимоотношение между аргументом и функцией, именно то взаимоотношение признаков, которое и образует коэффициент регрессии. По этой формуле, зная значения аргумента (х) можно определить значение его функции (у) без непосредственного ее измерения.
В рассмотренном выше примере были вычислены коэффициенты корреляции и регрессии между уровнем яйценоскости и массой яиц у кур. Если принять яйценоскость кур за аргумент, можно составить следующее уравнение прямолинейной регрессии:
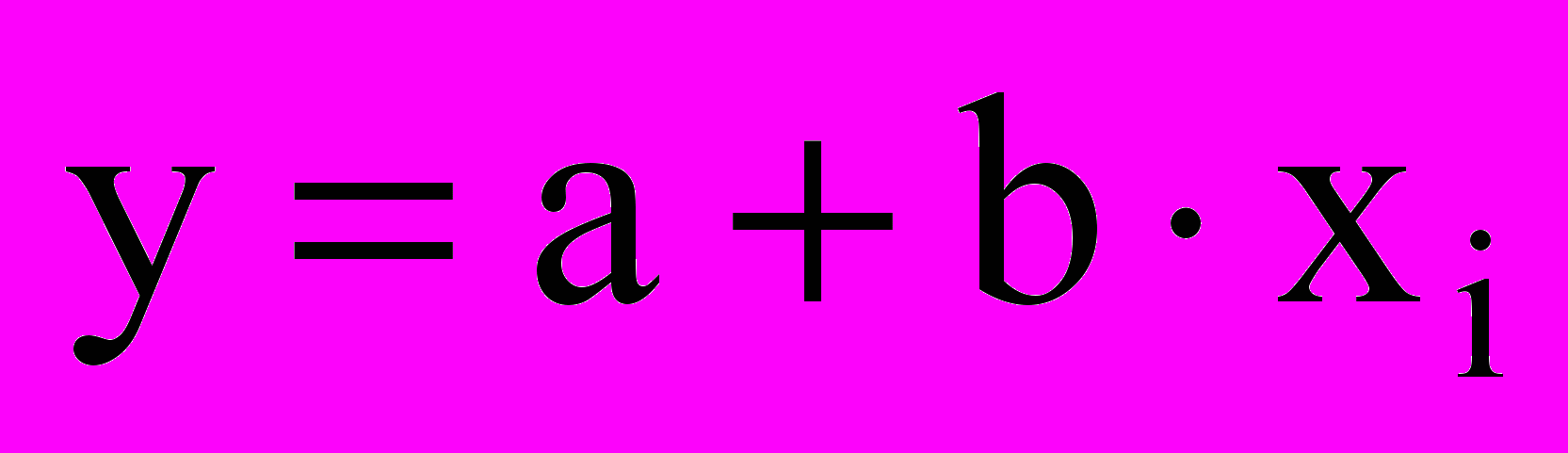 ;
; 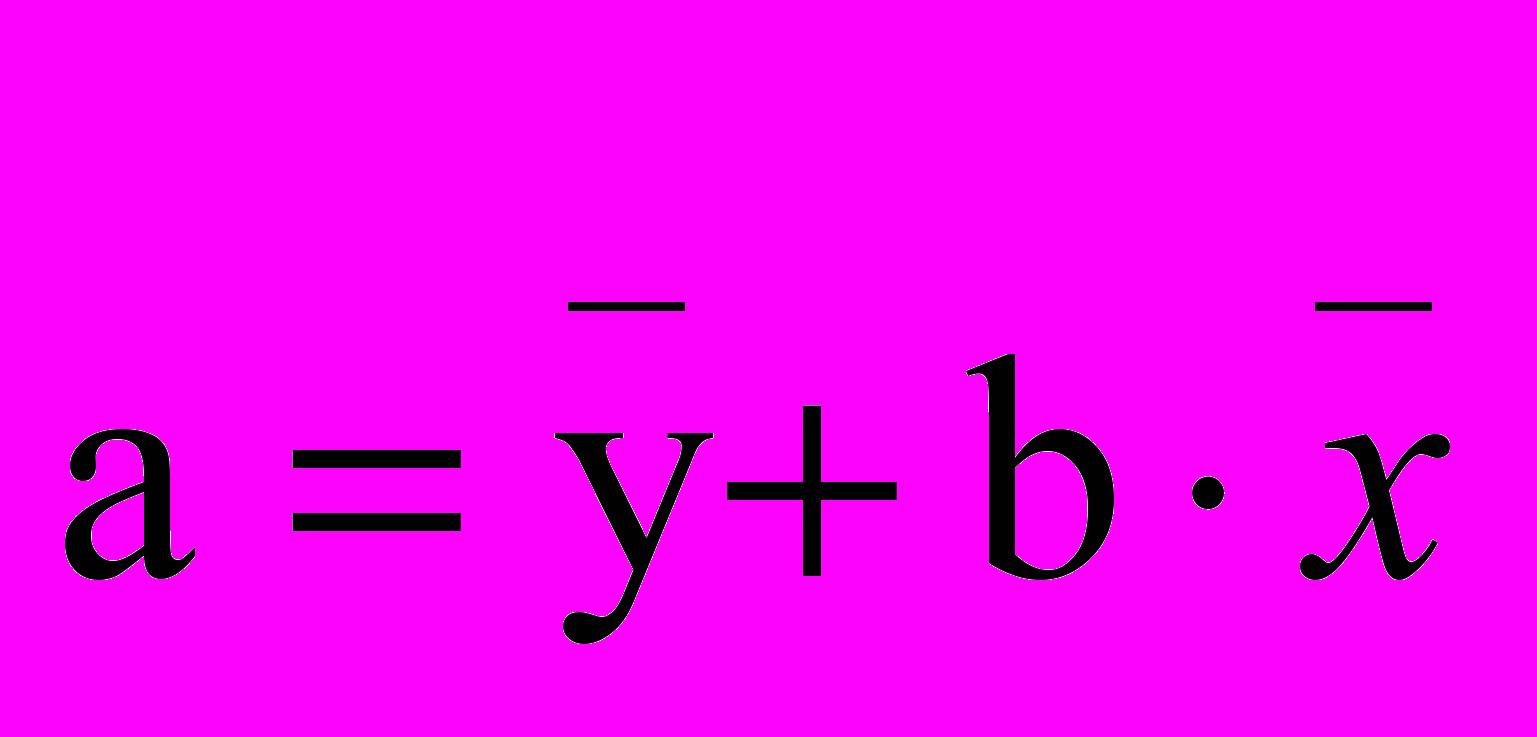
а = 56,68 - (-0,127) 102 = 56,68 + 12,95 – 69,63; а = 69,63
у = 69,63 + (-0,127) x = 69,63 – 0,127 x
Таким образом, для того, чтобы установить, какая масса яйца может соответствовать тому или иному уровню яйценоскости, нужно умножить показатель яйценоскости на коэффициент 0,127 и вычесть это произведение из числа 69,63. На основе этого уравнения можно заранее рассчитать значение функций для каждого значения аргумента. Таким образом, в частности в данном примере, можно составить ряд, показывающий регрессионные зависимости яйценоскости и массы яиц в данной популяции кур.
Таблица 30
Теоретический ряд регрессии между признаками яйценоскости кур
за 5 мес. и массой яиц
| Яйценоскость | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 |
| Масса яиц | 58,8 | 58,2 | 57,6 | 56,9 | 56,3 | 55,7 | 55,0 | 54,4 |
Эта таблица может быть полезна в селекционной работе, так как она дает основание предъявлять требования к массе яиц не вообще, а в связи с уровнем яйценоскости, т.е. на основании биологической взаимосвязи этих двух показателей. В частности, масса яйца в 57 г может быть оценена как весьма небольшая для курицы, снесшей за 5 мес. 90 яиц, но она будет очень хорошей для курицы, снесшей за тот же период 120 яиц.
Для успешной работы с той или иной популяцией животных зоотехник-селекционер может построить аналогичные таблицы по основным селекционируемым признакам.
