Рабочая программа дисциплины «методы оптимальных решений» Рекомендуется для направления подготовки 080100 Экономика
| Вид материала | Рабочая программа |
- Рабочая программа дисциплины «методы оптимальных решений» Рекомендуется для направления, 211.43kb.
- Программа дисциплины «Методы оптимальных решений» для направления 080100. 62 «Экономика», 220.95kb.
- Программа дисциплины «Методы оптимальных решений» для направления 080100. 62 «Экономика», 211.67kb.
- Рабочая программа дисциплины «математические методы и модели» Рекомендуется для направления, 140.06kb.
- Рабочая программа дисциплины «экспертные методы и системы» Рекомендуется для направления, 132.94kb.
- Программа дисциплины Методы оптимальных рещений для направления 080100. 62 "Экономика", 169.05kb.
- Рабочая программа дисциплины «институциональная экономика» Рекомендуется для направления, 398.18kb.
- Аннотация рабочей программы дисциплины методы оптимальных решений для направления подготовки, 23.52kb.
- Рабочая программа дисциплины «Оценка недвижимости» Рекомендуется для направления подготовки, 254.68kb.
- Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
«МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»
Рекомендуется для направления подготовки
080100 Экономика
Квалификация выпускника - бакалавр
Санкт-Петербург
2011 год
1. Цели и задачи дисциплины: накопление необходимого запаса сведений по математике (основные определения, теоремы, правила), а также освоение математического аппарата, помогающего моделировать, анализировать и решать экономические задачи, помощь в усвоении математических методов, дающих возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов; развитие логического и алгоритмического мышления, способствование формированию умений и навыков самостоятельного анализа исследования экономических проблем, развитию стремления к научному поиску путей совершенствования своей работы.
^ 2. Место дисциплины в структуре ООП: дисциплина «Методы оптимальных решений» относится к циклу Б.2 Математический и естественнонаучный цикл, Базовая часть. Входные знания, умения и компетенции студентов должны соответствовать дисциплинам «Линейная алгебра», «Математический анализ» и «Теория вероятностей и математическая статистика». Дисциплина «Методы оптимальных решений» является предшествующей практически для следующих дисциплин: «Математические методы и модели», «Эконометрика», «Маркетинг», «Менеджмент», «Экономика фирмы», «Управление проектами», «Бизнес-планирование», «Планирование инвестиционной деятельности с применением прикладных программ», «Экспертные методы и системы», «Финансовая математика», «Управление проектами», «Бизнес-планирование», «Организация и планирование производства и предприятия», «Управление проектами», «Экономика и организация инвестиционной деятельности предприятия», «Экономика и организация инновационной деятельности предприятия», «Управление затратами и результатами деятельности предприятия», «Инновационное управление трудом», «Инвестиции», «Международные инвестиции», «Государственное регулирование экономики», «Стратегическое планирование развития регионов и городов», «Бизнес-планирование», «Макроэкономическое планирование и прогнозирование», «Современные методы внутрифирменного планирования», «Теория игр», «Модели и методы исследования операций».
^ 3. Требования к результатам освоения дисциплины:
Процесс изучения дисциплины направлен на формирование следующих компетенций:
способен собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1);
способен выполнять необходимые для составления экономических разделов планов расчеты, обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3);
способен осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК-4);
способен выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы (ПК-5);
способен на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты (ПК-6);
способен использовать для решения аналитических и исследовательских задач современные технические средства и информационные технологии (ПК-10);
способен принять участие в совершенствовании и разработке учебно-методического обеспечения экономических дисциплин (ПК-15).
В результате изучения дисциплины студент должен:
Знать: основы методов оптимальных решений /теории игр/, необходимые для решения экономических задач;
Уметь: применять методы математического анализа и моделирования, теоретического и экспериментального исследования для решения экономических задач;
Владеть: навыками применения современного математического инструментария для решения экономических задач; методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов.
^ 4. Объем дисциплины и виды учебной работы
Общая трудоемкость дисциплины составляет 4 зачетные единицы.
| Вид учебной работы | Всего часов (четвертый семестр) |
| ^ Аудиторные занятия (всего) | 72 |
| В том числе: | - |
| Лекции | 40 |
| Практические занятия (ПЗ) | 32 |
| ^ Самостоятельная работа (всего) | 72 |
| В том числе: | - |
| Тест №1 | 14 |
| Тест №2 | 14 |
| Контрольная работа №1 | 8 |
| Экзамен | 36 |
| Общая трудоемкость час зач. ед. | 144 |
| 3+1 |
^ 5. Содержание дисциплины
5.1. Содержание разделов дисциплины
1. Линейное программирование
Тема 1. Предмет математического программирования.
Примеры экономических задач, решаемых методами математического программирования. Классификация основных методов математического программирования.
^ Тема 2. Симплекс-метод решения задач линейного программирования
Симплексные таблицы. Экономическая интерпретация элементов симплексной таблицы. Улучшение опорного решения. Определение ведущих столбца и строки.
Выбор начального допустимого базисного решения. Введение искусственных переменных.
Вырожденные задачи линейного программирования. Зацикливание и его предотвращение.
^ Тема 3. Двойственность в линейном программировании
Двойственные задачи. Экономическая интерпретация пары двойственных задач. Теоремы двойственности, их экономическая интерпретация.
^ Тема 4. Транспортные задачи
Экономическая и математическая формулировки транспортной задачи. Метод потенциалов. Основные способы построения начального опорного решения. Транспортные задачи с нарушенным балансом производства и потребления. Транспортные задачи с дополнительными условиями.
^ Тема 5. Целочисленное программирование
Постановка задачи. Примеры целочисленных моделей. Методы решения задач целочисленного программирования. Метод Гомори. Метод ветвей и границ. Постановка задачи о коммивояжере. Понятие о приближенных методах.
^ 2. Элементы нелинейного программирования и теории игр.
Тема 6. Нелинейное программирование
Методы одномерной оптимизации. Унимодальные функции. Методы поиска. Методы дихотомии и золотого сечения. Общая задача нелинейного программирования. Градиентные методы безусловной оптимизации. Выпуклое программирование. Метод штрафов.
Теорема Куна-Таккера, ее связь с теорией двойственности в линейном программировании.
^ Тема 7. Динамическое программирование
Постановка задачи. Основные определения. Принцип оптимальности. Рекуррентные уравнения Беллмана. Примеры решения задач математического программирования методом Беллмана.
^ Тема 8. Сетевое планирование
Сеть проекта. Критический путь, время завершения проекта. Резервы событий, резервы операций.
Тема 9. Теория игр – теория математических моделей принятия оптимальных решений в условиях конфликта и неопределенности
Игра как математическая модель конфликта. Основные понятия теории игр. Классификация игр. Примеры бескоалиционных игр.
Антагонистические игры. Матричные игры. Смешанные стратегии.
Графоаналитический метод решения игр.
Матричные игры и линейное программирование.
^ 5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспе-чиваемых (последую-щих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | |
| 1 | 2 | ||
| 1. | Макроэкономика | * | * |
| 2 | Математические методы и модели | * | * |
| 3 | Эконометрика | * | * |
| 4 | Маркетинг | * | * |
| 5 | Менеджмент | * | * |
| 6 | Экономика фирмы | * | * |
| 7 | Управление проектами | * | * |
| 8 | Бизнес-планирование | * | * |
| 9 | Планирование инвестиционной деятельности с применением прикладных программ | * | |
| 10 | Экспертные методы и системы | * | * |
| 11 | Финансовая математика | * | * |
| 12 | Управление проектами | * | * |
| 13 | Бизнес-планирование | * | * |
| 14 | Организация и планирование производства и предприятия | * | * |
| 15 | Управление проектами | * | * |
| 16 | Экономика и организация инвестиционной деятельности предприятия | * | * |
| 17 | Экономика и организация инновационной деятельности предприятия | * | * |
| 18 | Управление затратами и результатами деятельности предприятия | * | * |
| 19 | Инновационное управление трудом | * | * |
| 20 | Инвестиции | * | * |
| 21 | Международные инвестиции | * | * |
| 22 | Государственное регулирование экономики | * | * |
| 23 | Стратегическое планирование развития регионов и городов | * | * |
| 24 | Бизнес-планирование | | * |
| 25 | Макроэкономическое планирование и прогнозирование | * | * |
| 26 | Современные методы внутрифирменного планирования | | * |
| 27 | Теория игр | | * |
| 28 | Модели и методы исследования операций | * | * |
^ 5.3. Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Практ. зан. | СРС | Всего час. |
| 1 | Линейное программирование | 28 | 22 | 22 | 72 |
| 2 | Элементы нелинейного программирования | 12 | 10 | 14 | 36 |
^ 6. Лабораторный практикум не предусмотрен
7. Практические занятия (семинары)
| № п/п | № раздела дисциплины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
| 1 | 1 | Составление математических моделей для содержательных задач. | 2 |
| 2 | 1 | Графический метод решения задачи линейного программирования. | 2 |
| 3 | 1 | Симплекс-метод. | 2 |
| 4 | 1 | Симплекс-метод. Метод искусственного базиса. | 2 |
| 5 | 1 | Составление и решение двойственных задач. | 2 |
| 6 | 1 | Анализ на чувствительность. | 2 |
| 7 | 1 | Транспортные задачи. Построение начального плана перевозок. | 2 |
| 8 | 1 | Метод потенциалов. | 2 |
| 9 | 1 | Открытые транспортные задачи. Задачи с дополнительными условиями. | 2 |
| 10 | 1 | Метод ветвей и границ для решения целочисленных задач линейного программирования. | 2 |
| 11 | 2 | Метод золотого сечения. Градиентный метод. Метод штрафов. | 2 |
| 12 | 2 | Метод динамического программирования. Экономические примеры. | 2 |
| 13 | 2 | Сеть проекта. Критический путь, время завершения проекта. Резервы событий, резервы операций. | 2 |
| 14 | 2 | Матричные игры и линейное программирование. | 2 |
| 15 | 2 | Антагонистические матричные игры. | 2 |
| 16 | 2 | Графоаналитический метод решения матричных игр. | 2 |
^ 8. Примерная тематика курсовых работ – курсовые работы не предусмотрены.
9. Учебно-методическое и информационное обеспечение дисциплины:
а) основная литература
- Калихман И.Л. Линейная алгебра и программирование. – М.: Высшая школа, 1975.
- Калихман И.Л. Сборник задач по линейной алгебре и программированию. -М.: Высшая школа, 1975.
- Дмитриев В.Г., Дорошева Е.И., Савинов Г.В., Сорокина О.А, Основы линейного программирования: Учебное пособие / Под ред. Е.З. Хотимской. – СПб.: Изд-во СПбГУЭФ, 2006. – 95 с.
- Общий курс высшей математики для экономистов: Учебник / Под общ. Ред. В.И. Ермакова. – М.: ИНФРА-М, 2008. – 656 с.
б) дополнительная литература
- Абрамов Ю.Ш. Оптимизация функций нескольких переменных: Методические указания. – Л.: ЛФЭИ, 1979.
- Абрамов Ю.Ш. Двойственность в линейном программировании: Методические указания. – Л.: ФЭИ, 1987.
- Акулевич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
- Тернер Д. Вероятность, статистика и исследование операций. – М.: Статистика, 1976.
- Вагнер Г. Основы исследования операций. Т.1., М.: Мир, 1972; Т.2., – М.: Мир, 1973; Т.3., – М.: Мир, 1973.
- Таха Х. Введение в исследование операций. Т.1., – М.: Мир, 1985; Т.2., – М.: Мир, 1985.
- Чернов В.П., Ивановский В.Б. Теория массового обслуживания. М.: Инфра-М, 2000.
- Колемаев В.А., Математическая экономика. - М.: ИНФРА-М, 1999.
- Колемаев В.А., Математические методы принятия решения в экономике. - М.: Финстатинформ, 1999 (учебник)
- Экономико-математические методы и прикладные модели/Под ред. В.В. Федосеева. C М.: ЮНИТИ, 1999.
- Канторович Л.В., Горстко А.Б. Оптимальные решения в экономике. -М.: Наука, 1972.
в) программное обеспечение не предусмотрено.
г) базы данных, информационно-справочные и поисковые системы:
^ 10. Материально-техническое обеспечение дисциплины:
Документ-сканер, принтеры, компьютеры и пакеты программ обработки результатов тестирования.
^ 11. Методические рекомендации по организации изучения дисциплины:
Дисциплина «Методы оптимальных решений» изучается в течение одного (четвертого) семестра и заканчивается экзаменом. В процессе обучения студенты сдают два теста и делают одну расчетно-графическую (контрольную) работу. Максимальное число баллов за каждый тест равно 38. Тест считается сданным, если за него получено не менее 20 баллов. Максимальное баллов за контрольную работу равно 20, минимальное – 15. Максимальное и минимальное число баллов, которое можно получить за работу в семестре, равно, соответственно, 100 и 55. Максимальное число баллов, которое можно получить на экзамене, также равно 100. Итоговая оценка (в баллах) вычисляется по формуле
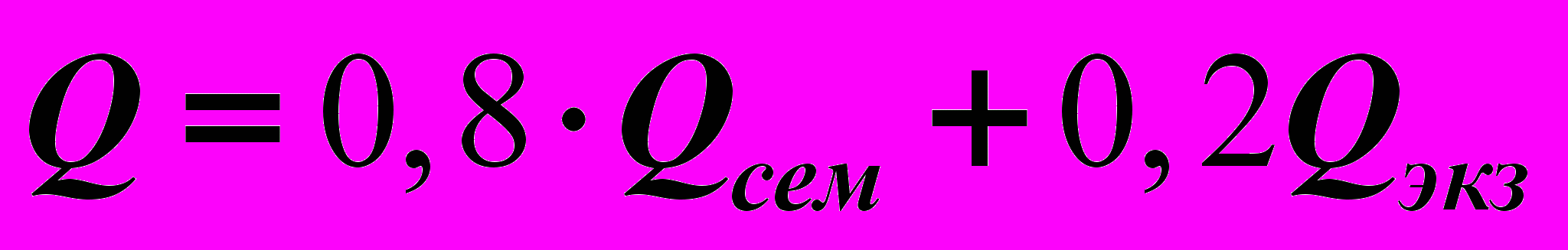 , где
, где 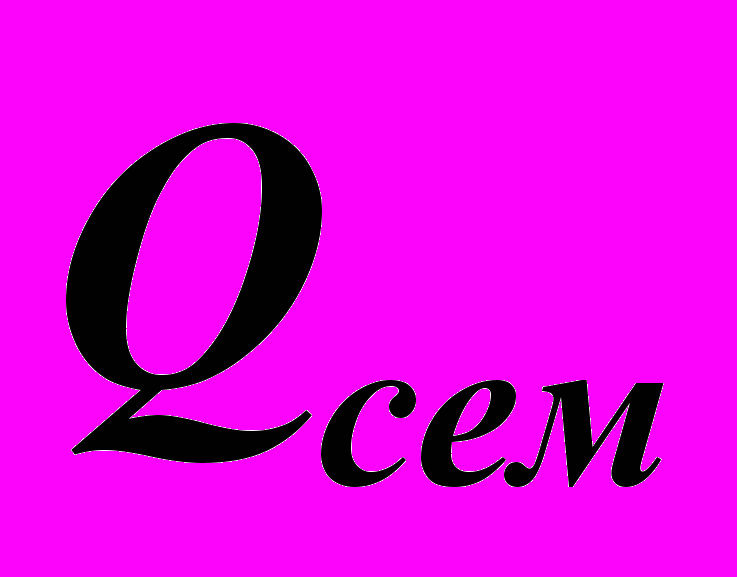 – баллы, полученные за работу в семестре, а
– баллы, полученные за работу в семестре, а 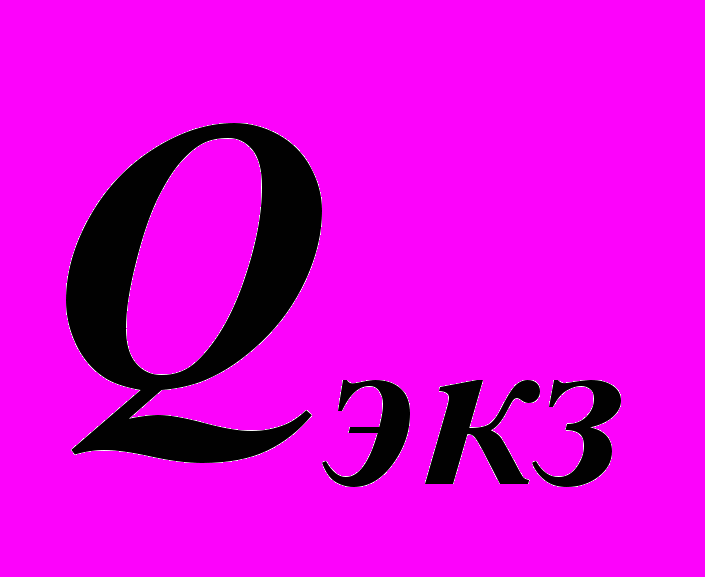 – за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:
– за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:| Итоговое количество баллов | оценка |
| до 55  | неудовлетворительно |
| от 55 до 70 | удовлетворительно |
| от 70 до 85 | хорошо |
| от 85 | отлично |
Примеры вопросов и задач теста №1.
Требуется дать ответ ДА или НЕТ.
1. Дана задача линейного программирования:
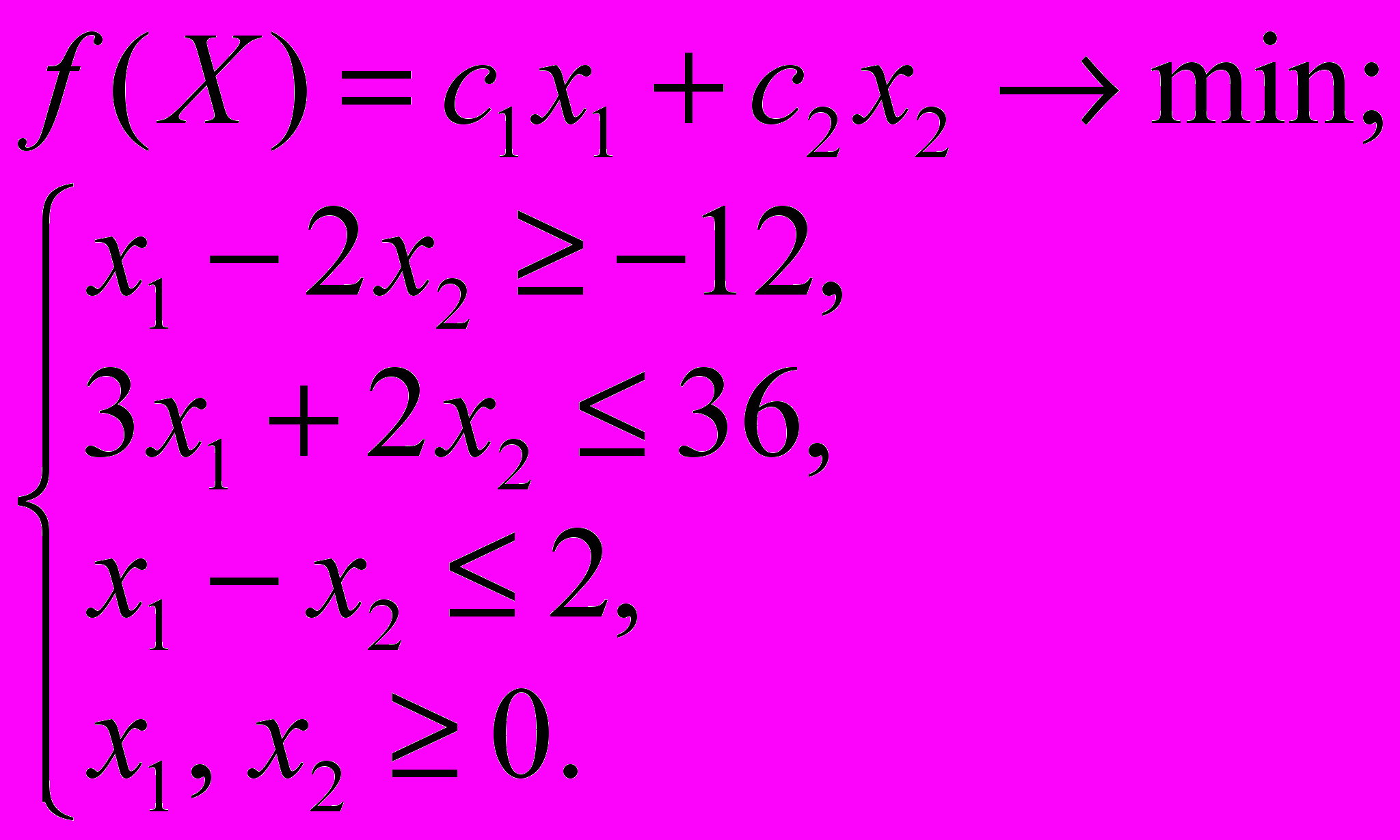
Верно утверждение:
-
 является допустимым планом данной задачи.
является допустимым планом данной задачи.
-
 является опорным (базисным) планом данной задачи.
является опорным (базисным) планом данной задачи.
-
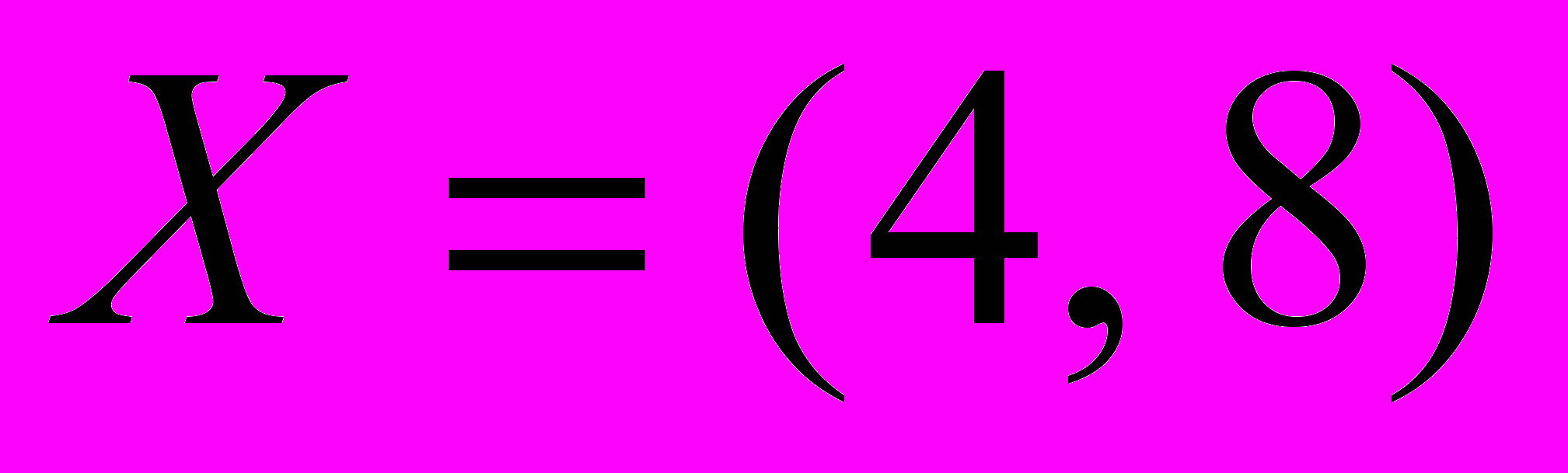 не является допустимым планом данной задачи.
не является допустимым планом данной задачи.
-
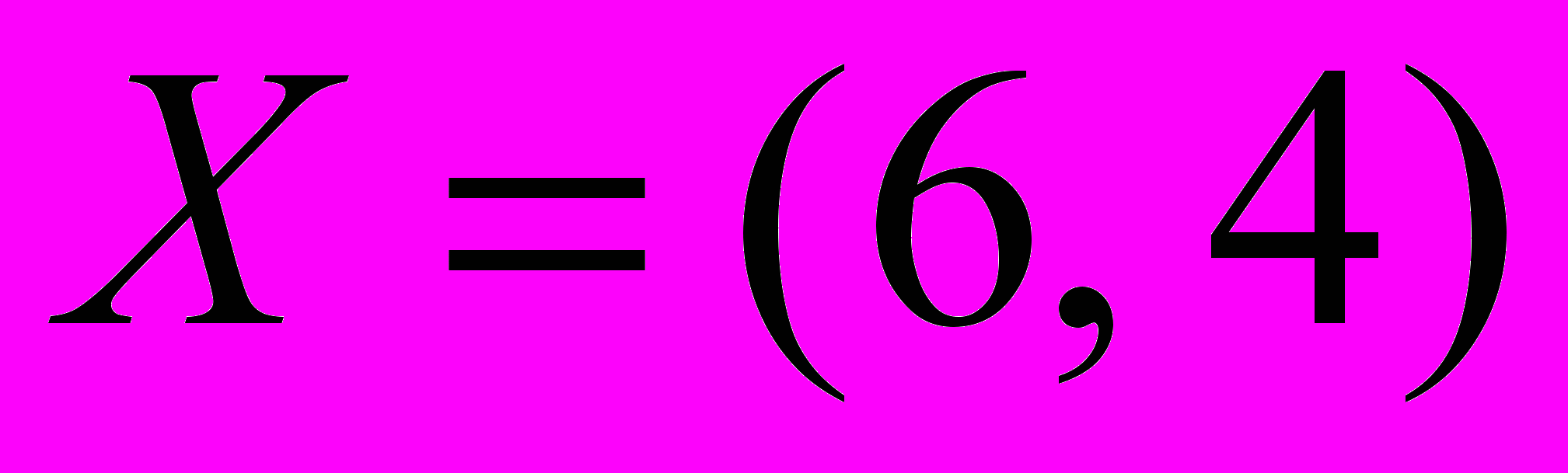 не может быть оптимальным ни при каком выборе значений
не может быть оптимальным ни при каком выборе значений  .
.
Требуется выбрать правильные ответы.
2. Дана симплекс-таблица, полученная на некотором этапе решения задачи ЛП
-
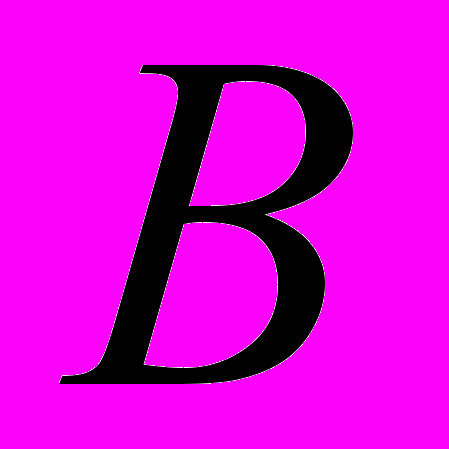
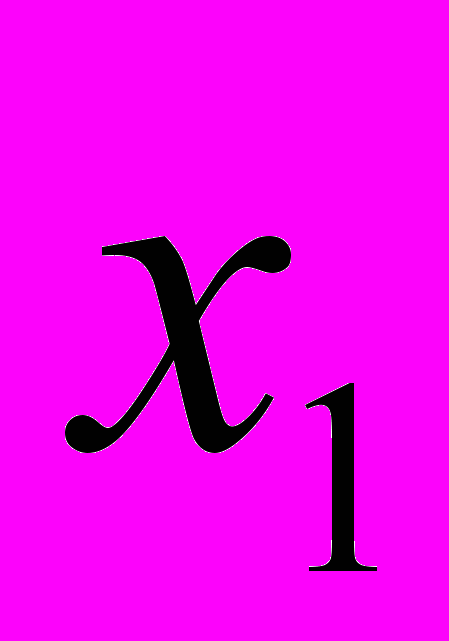

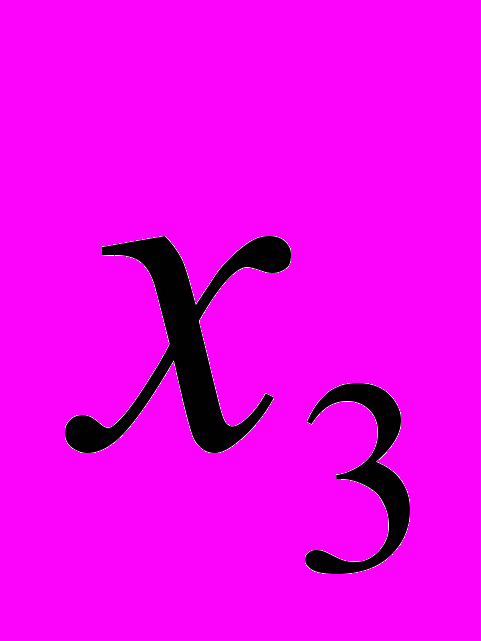
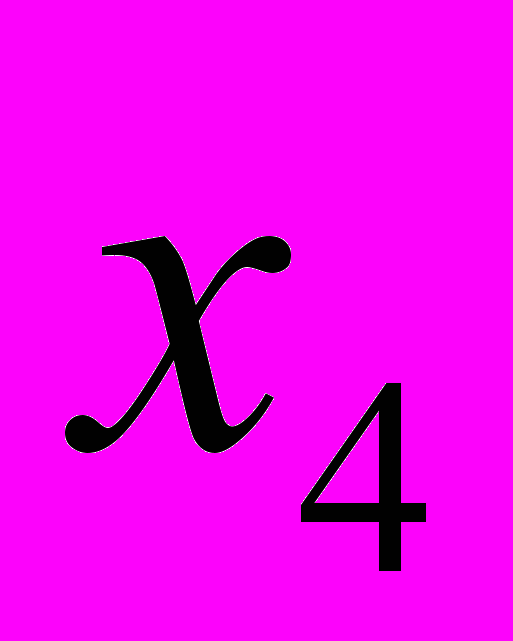
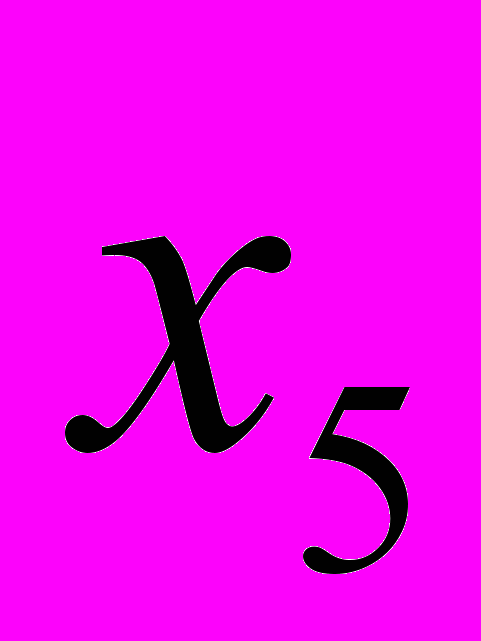
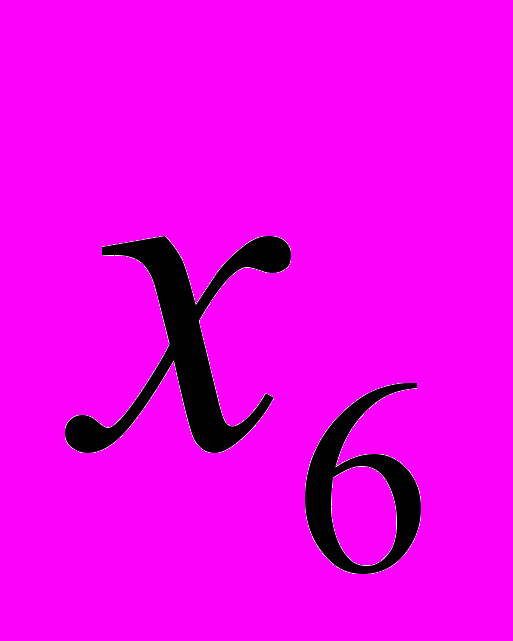
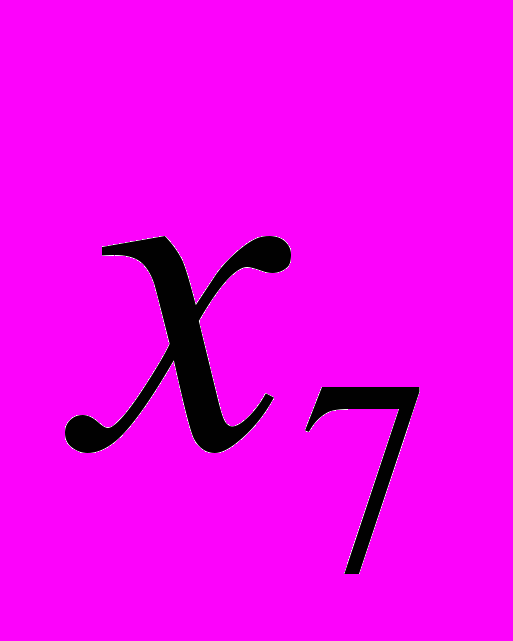

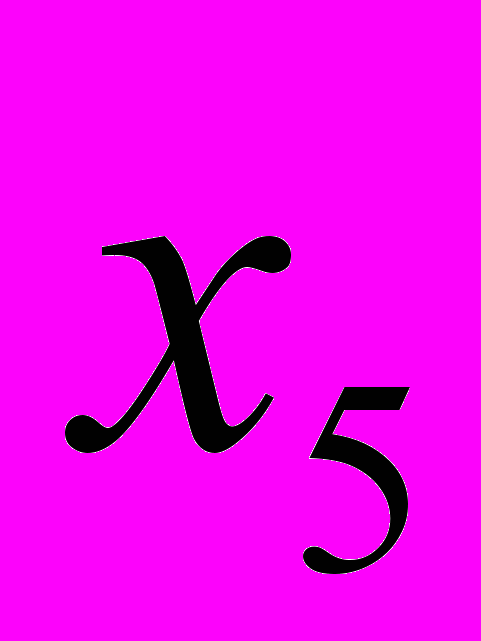
– 3
3
0
3
1
0
0
3
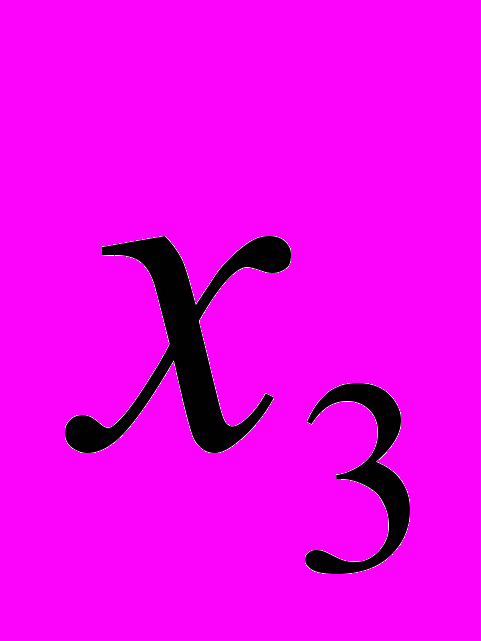
2
–1
1
– 3
0
0
0
8
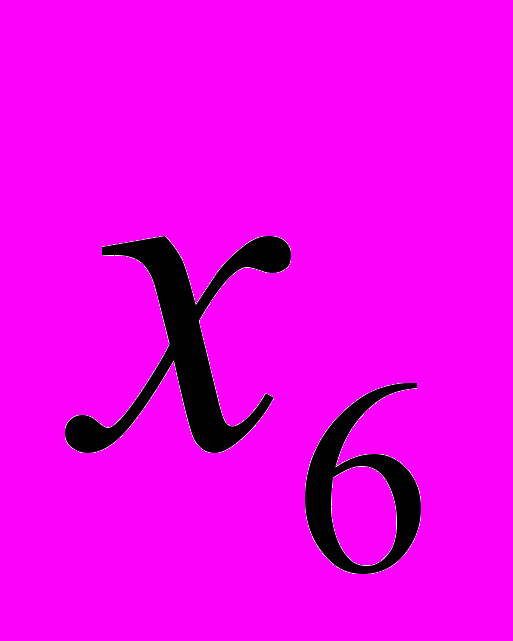
2
5
0
2
0
1
0
6
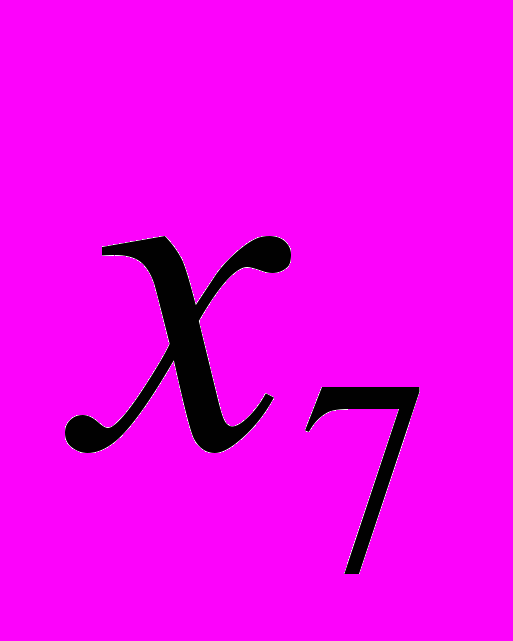
1
2
0
1
0
0
1
2
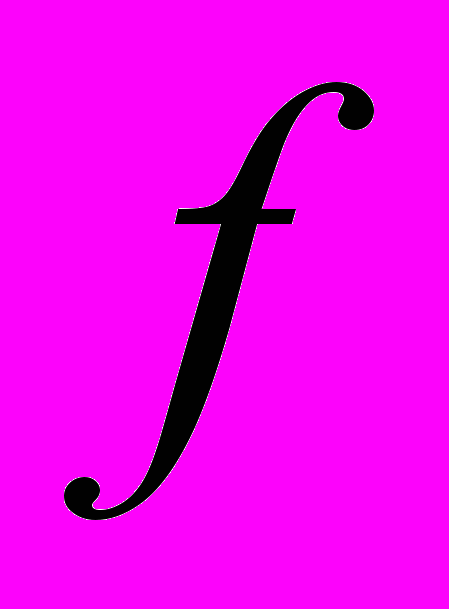
– 3
4
0
– 5
0
0
0
15
Верно утверждение:
1. Согласно данной симплекс-таблице, опорным является план
А.
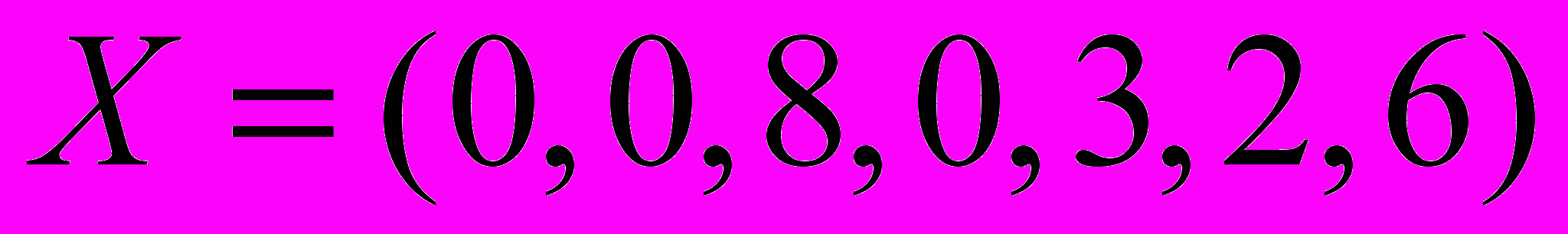 . Б.
. Б. 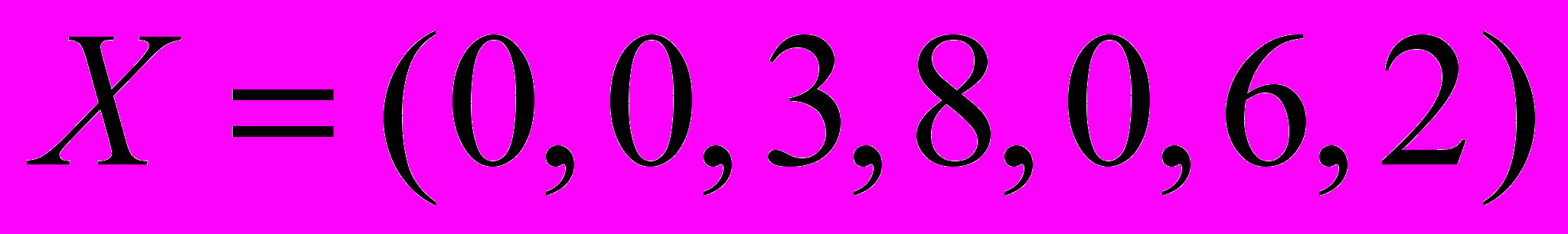 . В.
. В. 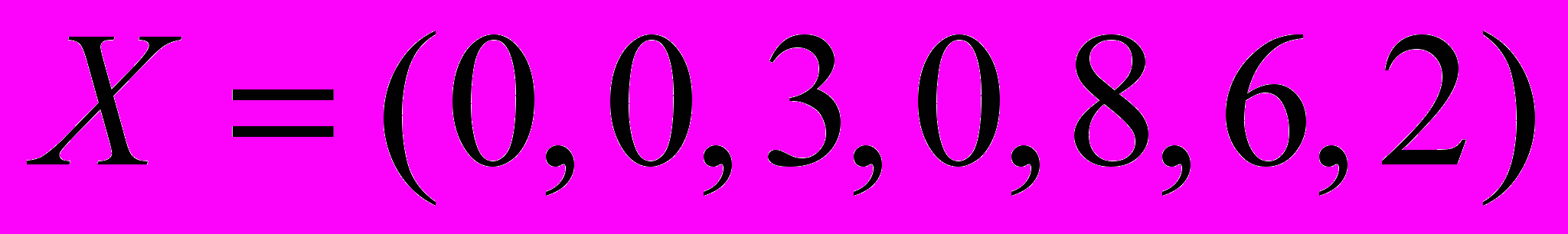 .
.Г.
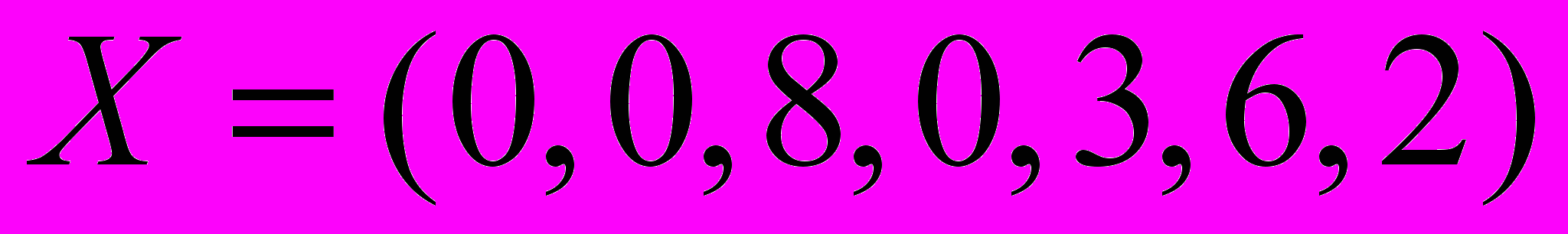 .
.2. Если ввести в базис переменную
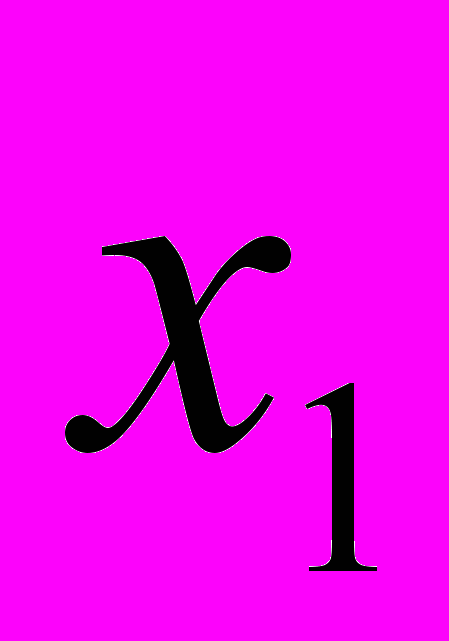 , то из базиса будет выведена переменная
, то из базиса будет выведена переменнаяА.
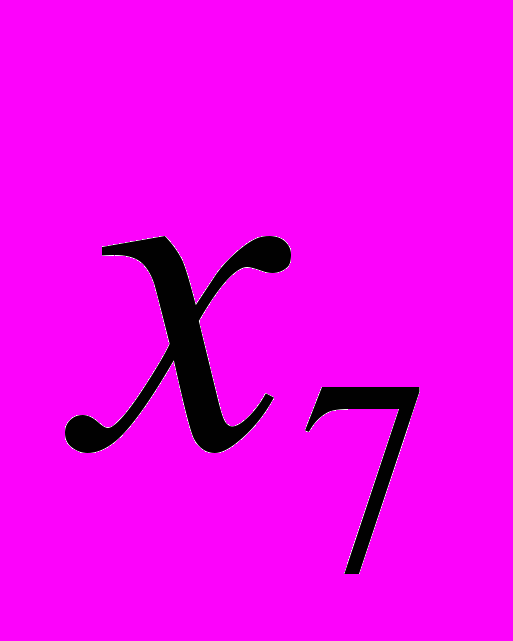 . Б.
. Б. 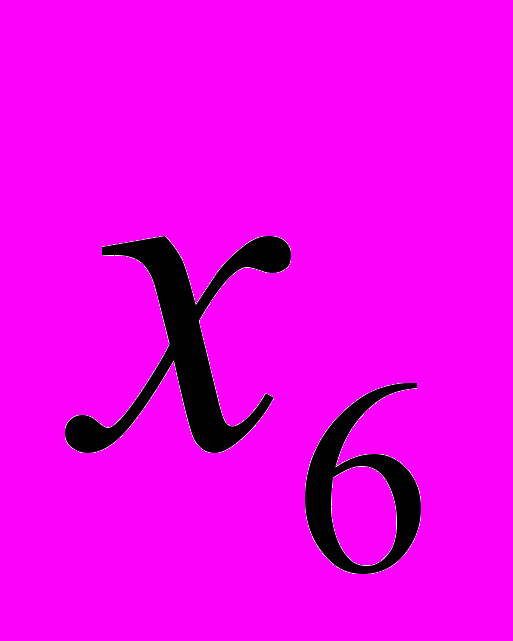 . В.
. В. 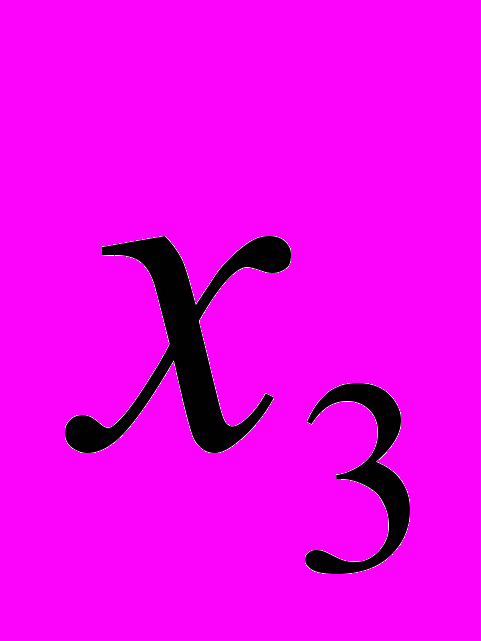 . Г.
. Г. 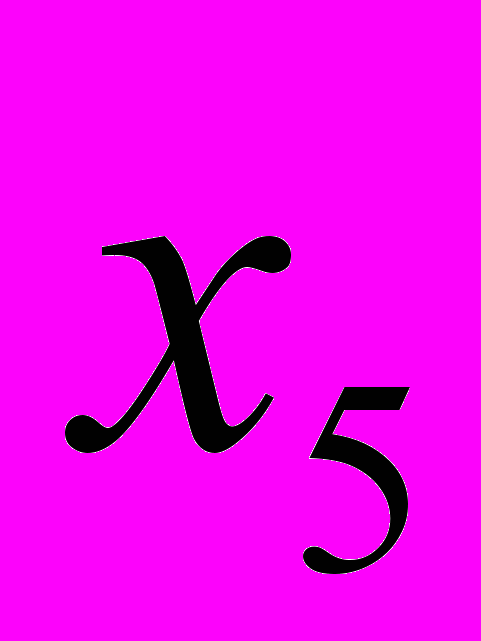 .
.3. Если ввести в базис переменную
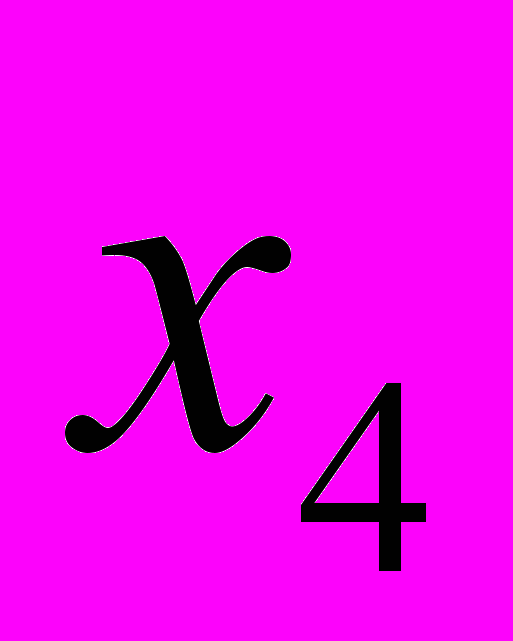 , то приращение
, то приращение 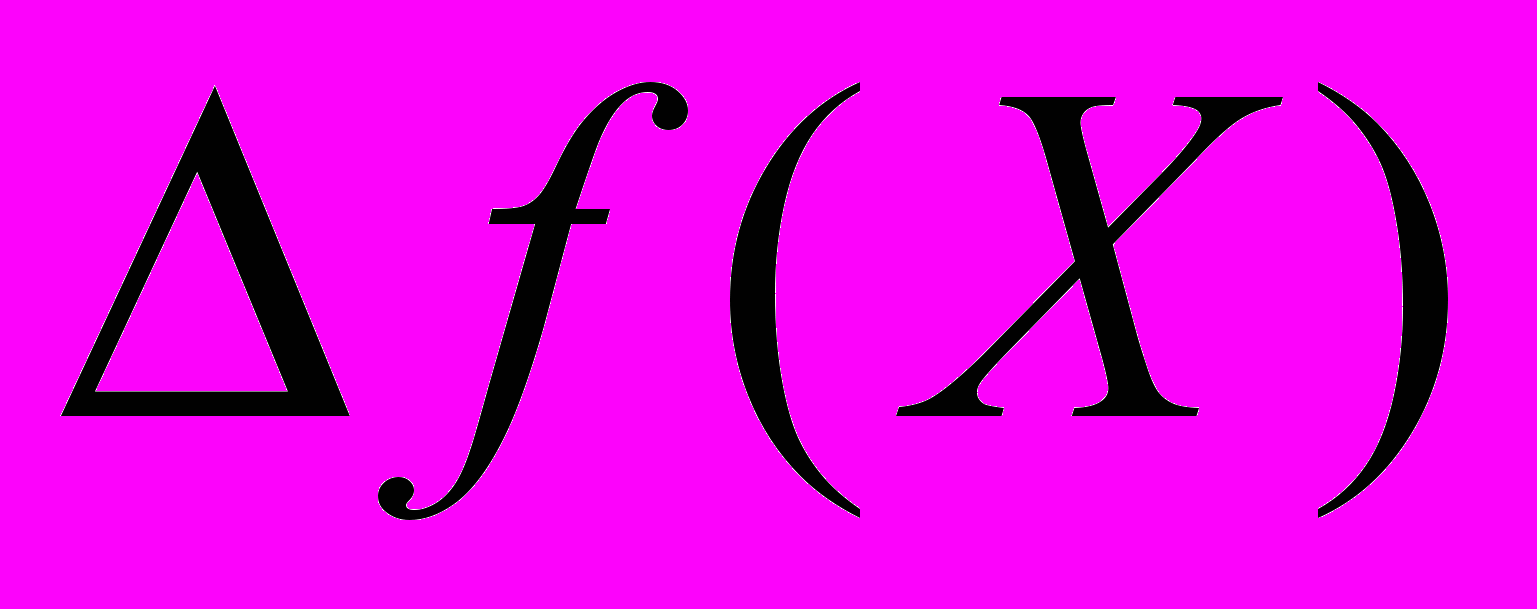 будет равно
будет равноА. 10. Б. 15. В. 20. Г. 5.
Требуется дать числовой ответ.
3. Используя метод М-задачи, решите задачу линейного программирования
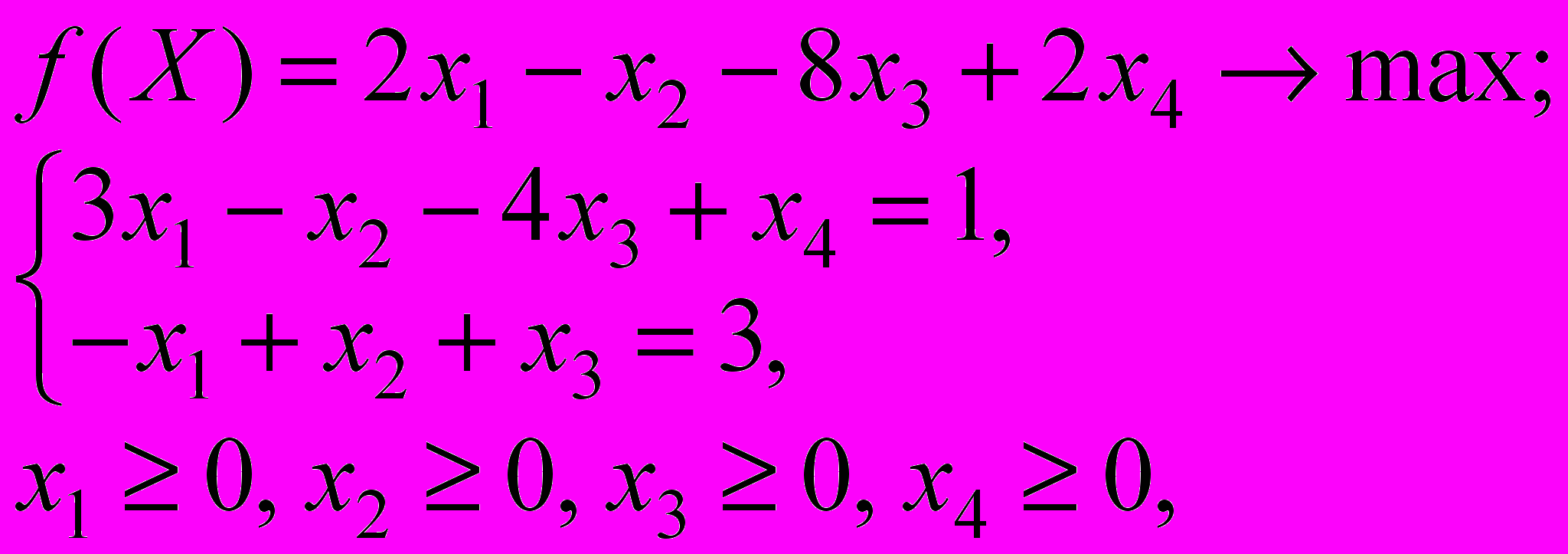
добавив одну искусственную переменную.
1. Найдите оптимальное значение целевой функции.
2. Найдите сумму компонент оптимального плана.
Примеры вопросов и задач теста №2.
Требуется дать ответ ДА или НЕТ.
1. Дана платёжная матрица
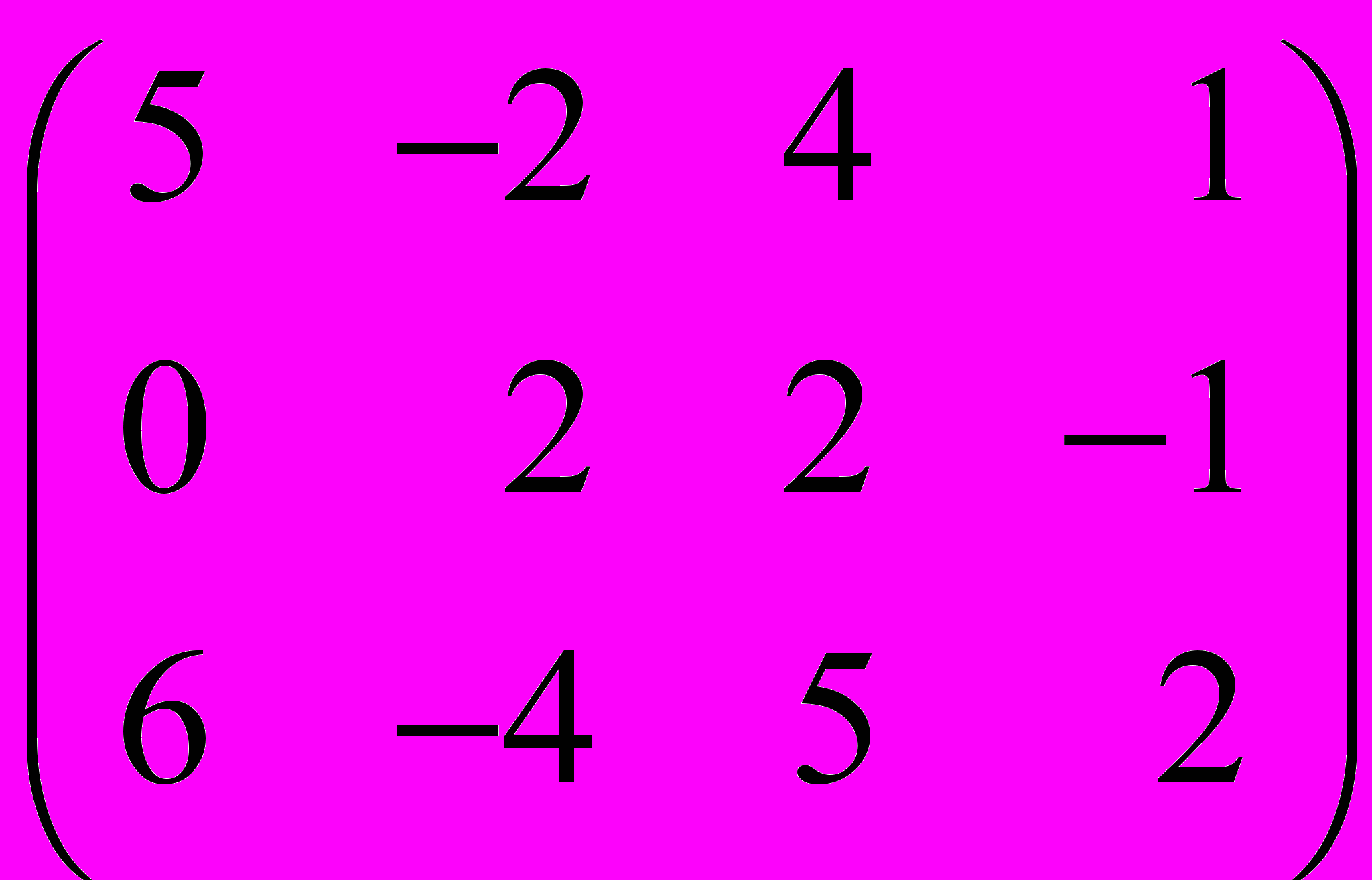 некоторой антагонистической игры.
некоторой антагонистической игры. Верно утверждение:
- Нижняя цена данной игры равна
 .
.
- Стратегия с номером 3 первого игрока доминирует стратегию с номером 1.
- Стратегия с номером 3 второго игрока доминирует стратегию с номером 2.
- Если
 и
и  смешанные стратегии первого и второго игроков соответственно, то математическое ожидание выигрыша первого игрока равно
смешанные стратегии первого и второго игроков соответственно, то математическое ожидание выигрыша первого игрока равно  .
.
Требуется выбрать правильные ответы.
2. Дана таблица, полученная на некотором этапе решения транспортной задачи
-
ПН
ПО
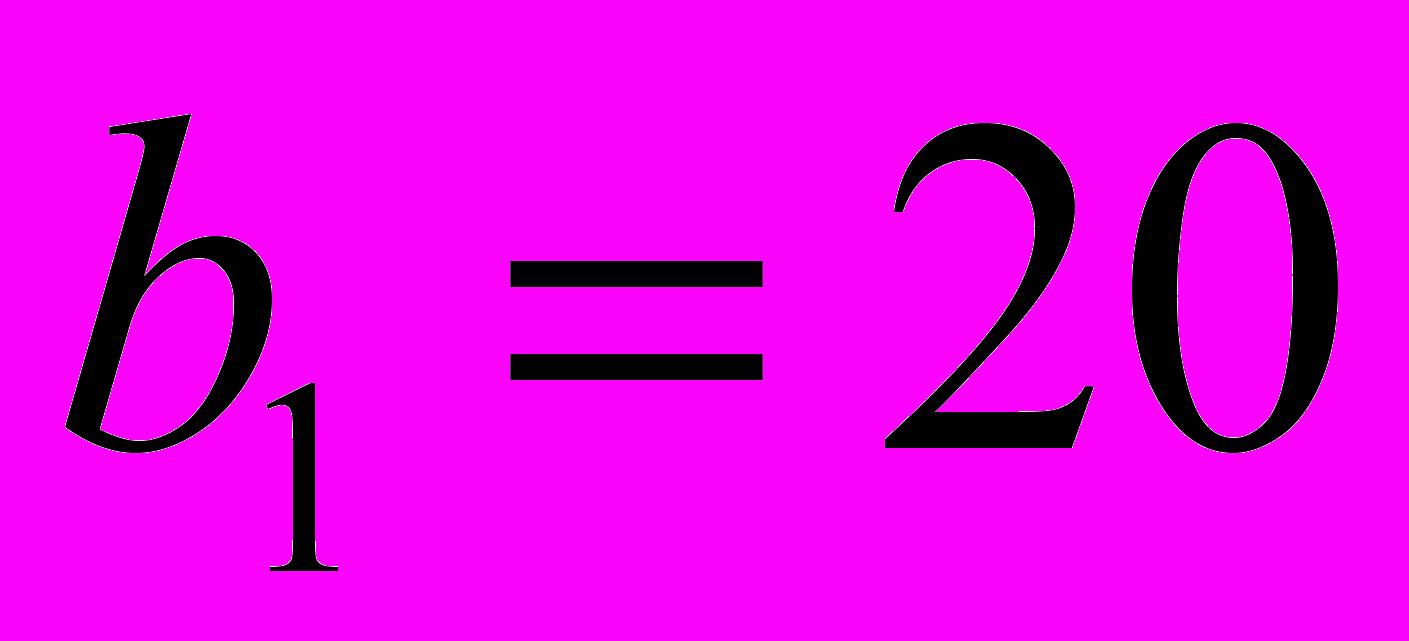
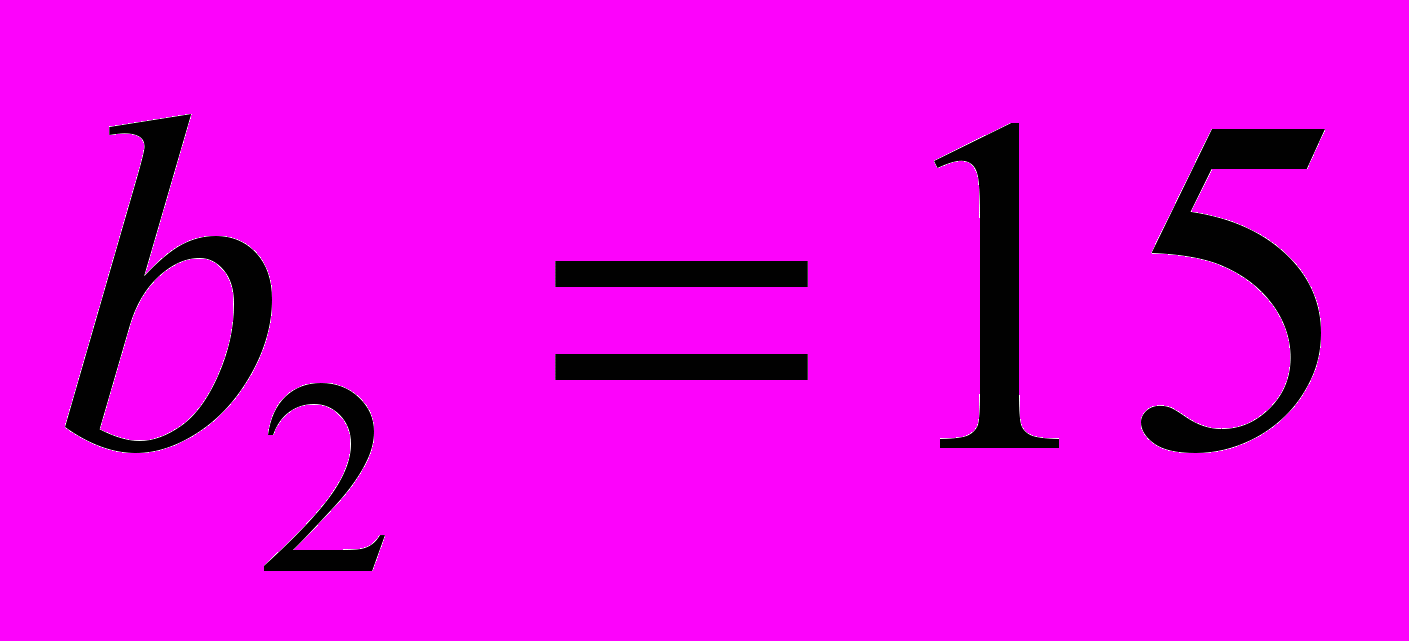


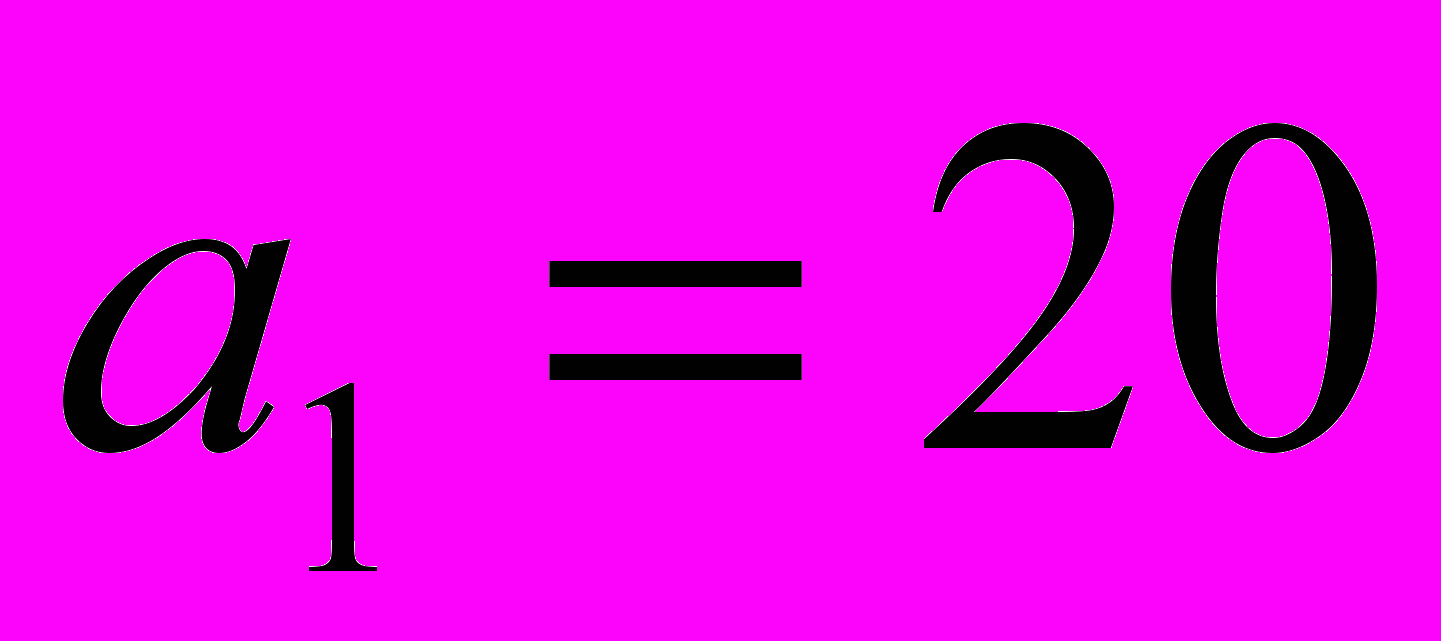
5
–
3
–
4
10
2
10
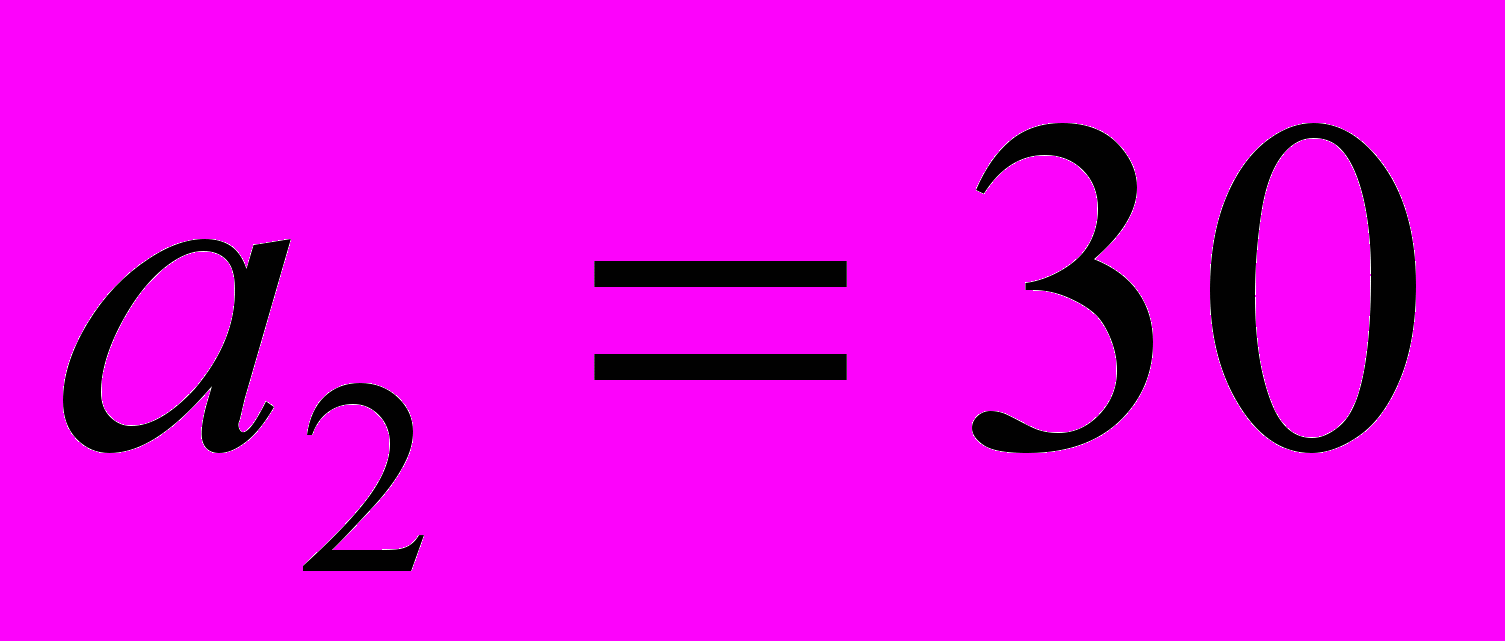
3
–
5
–
2
–
1
30
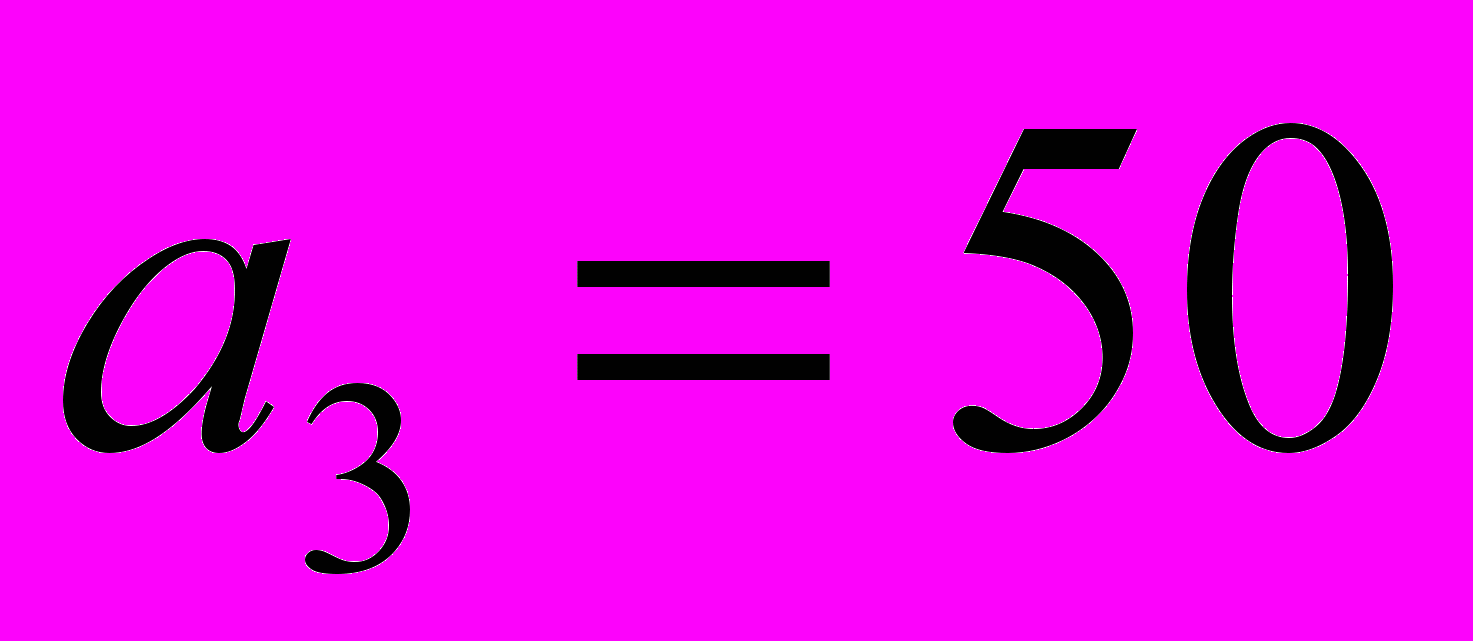
4
20
2
15
5
15
3
–
Верно утверждение:
1. Потенциалы строк
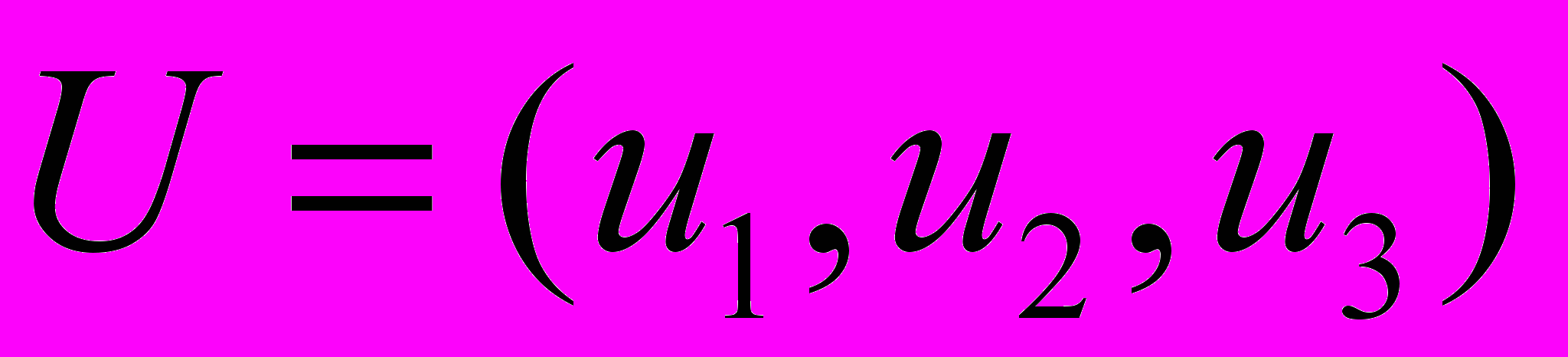 и столбцов
и столбцов 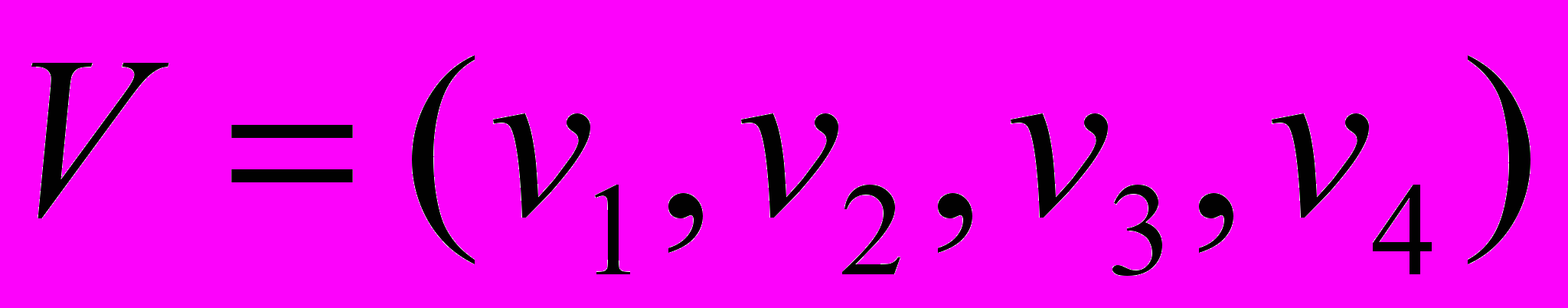 , при условии
, при условии 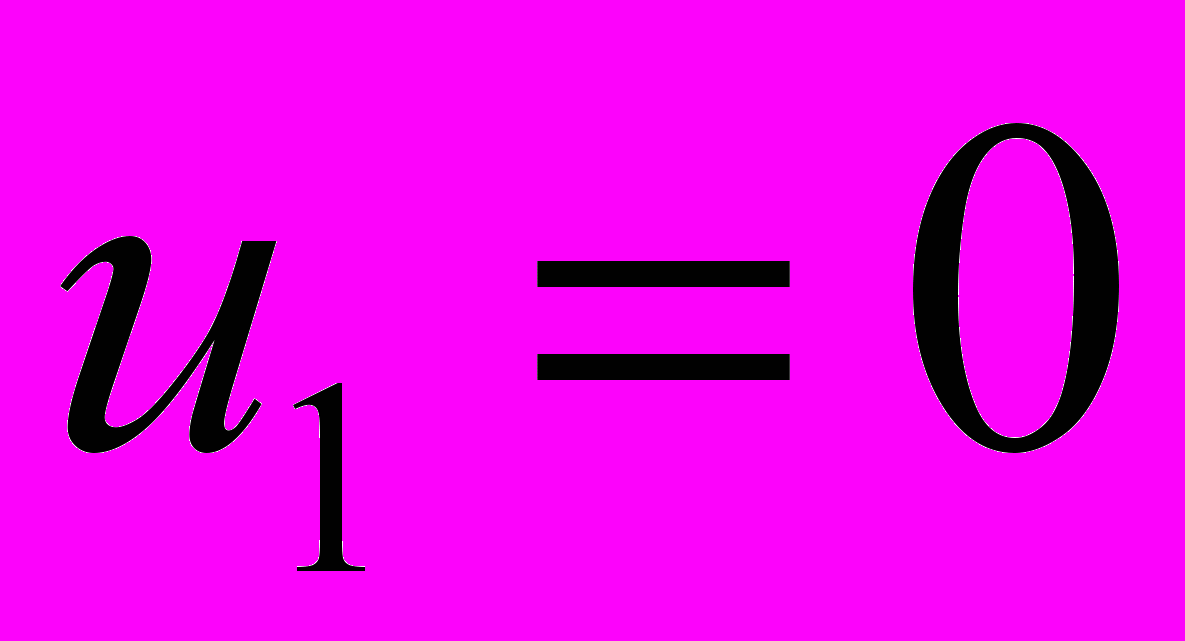 , равны
, равныА.
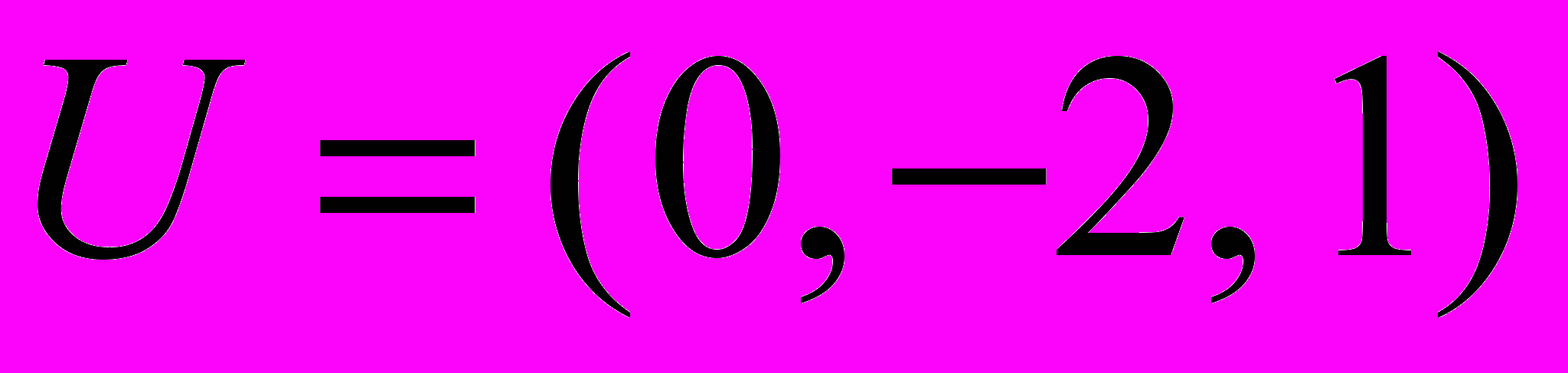 ,
, 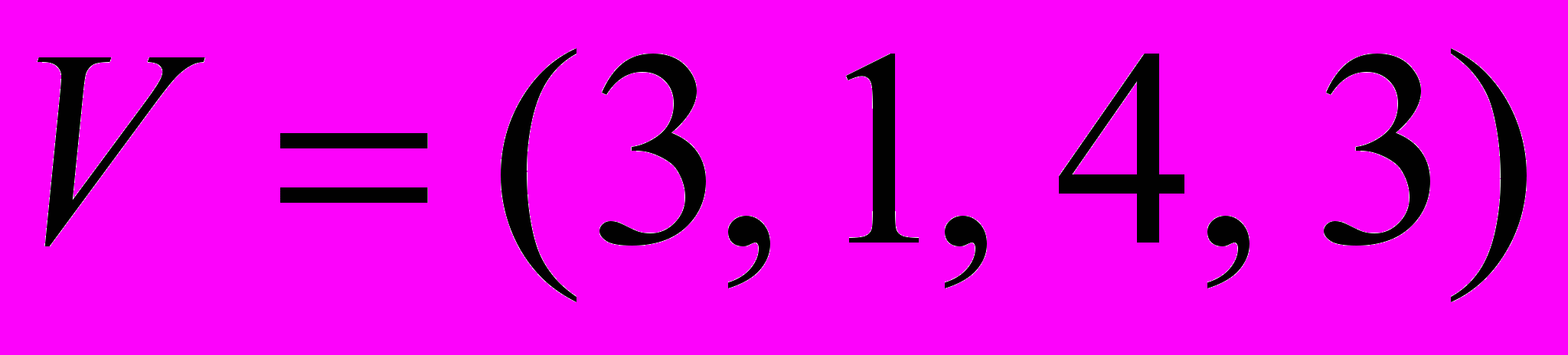 . Б.
. Б. 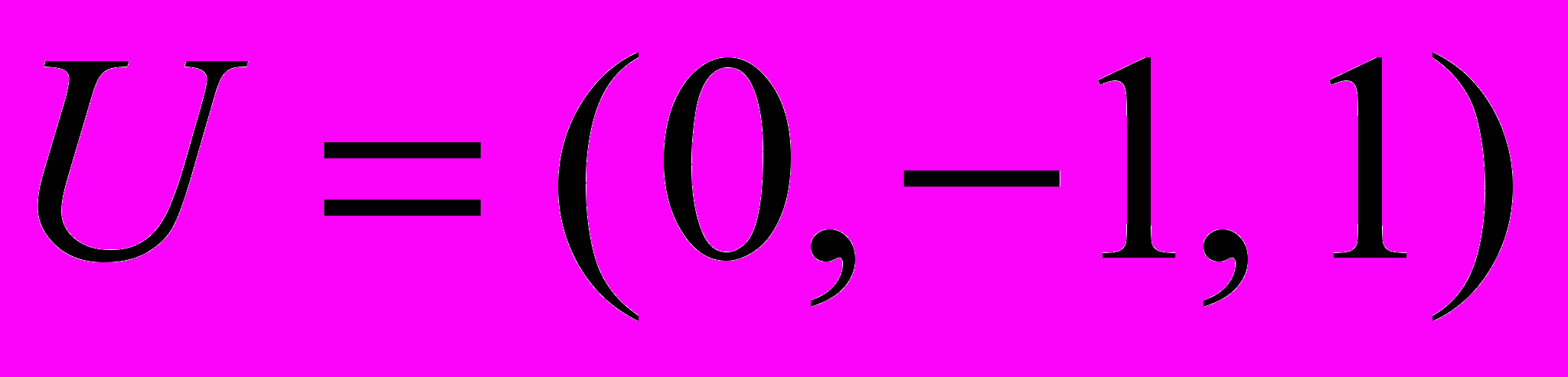 ,
, 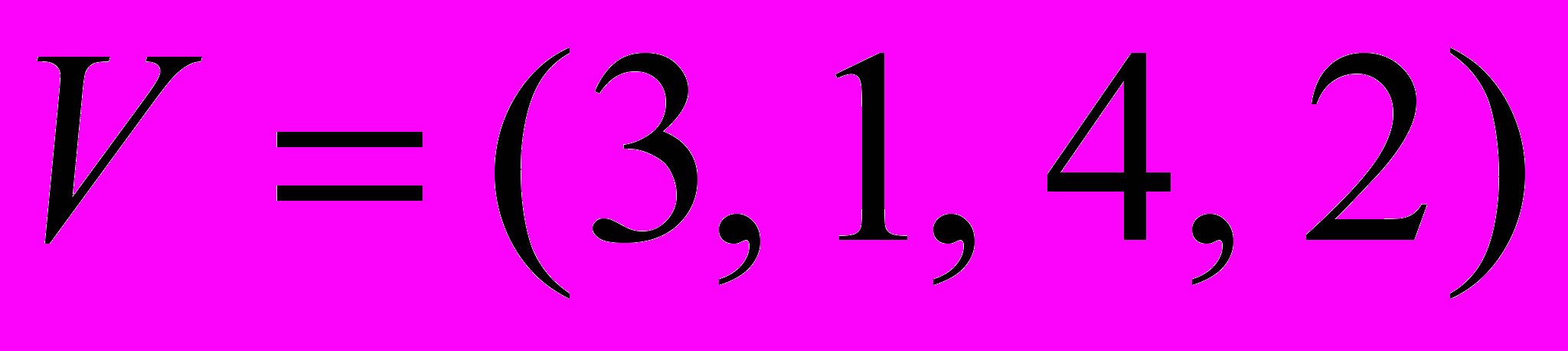 .
.В.
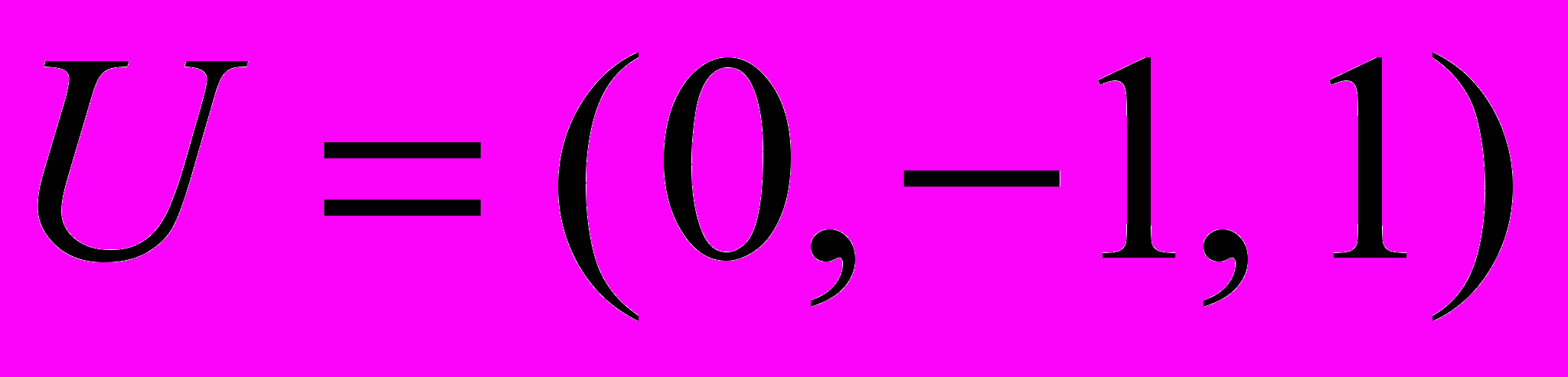 ,
, 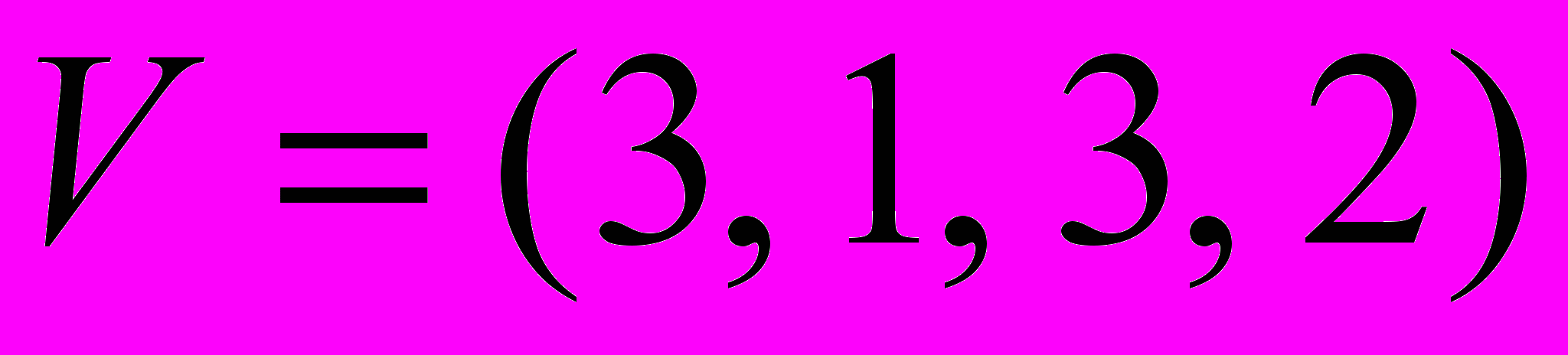 . Г.
. Г. 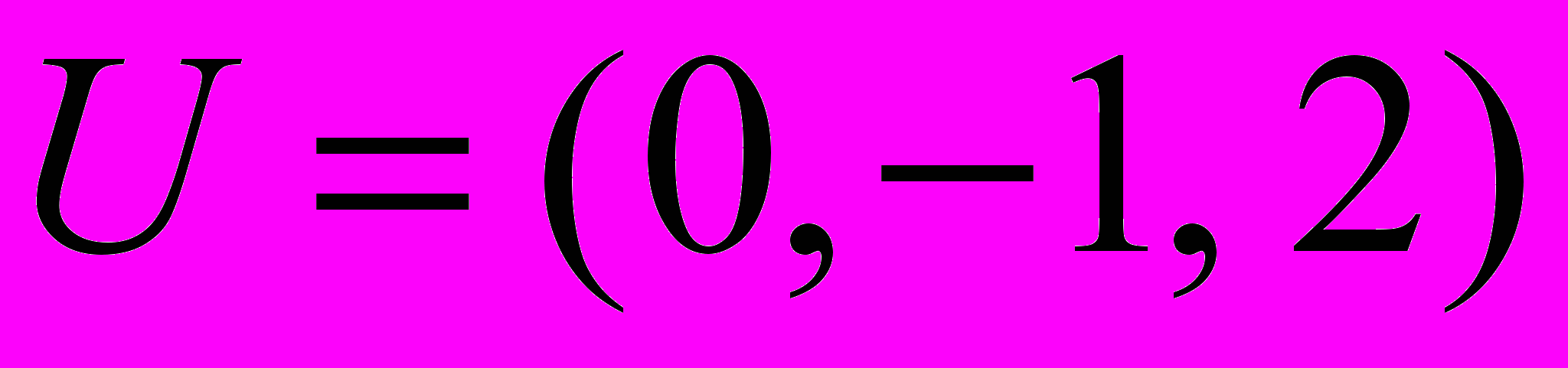 ,
, 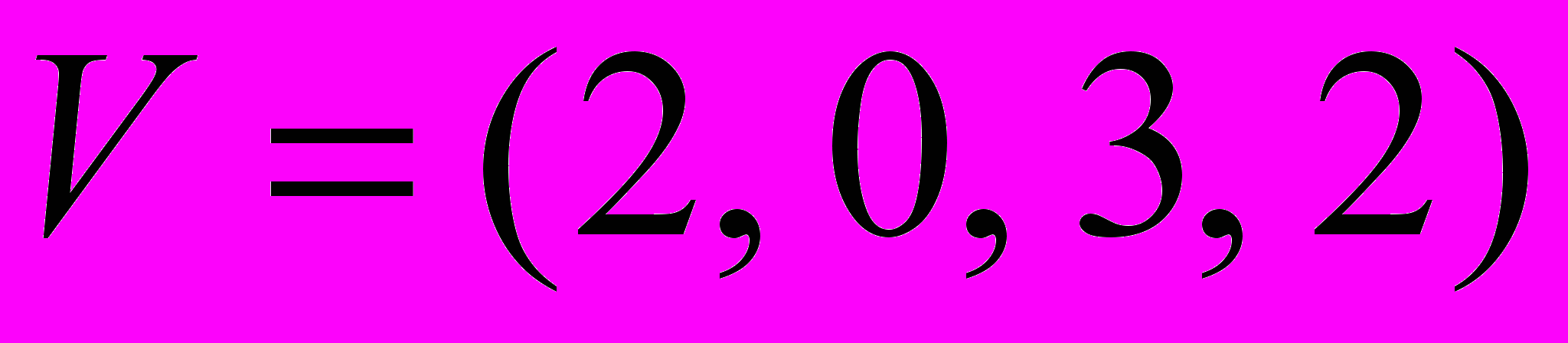 .
.2. Оценки
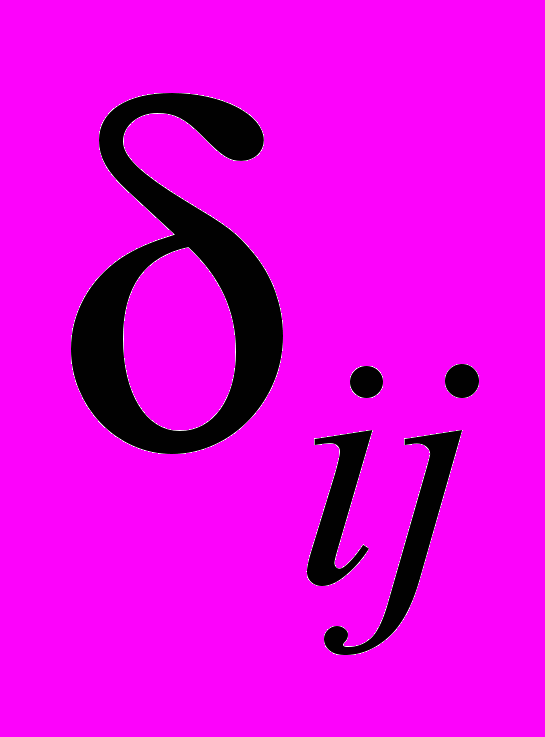 свободных переменных (клеток) равны
свободных переменных (клеток) равныА.
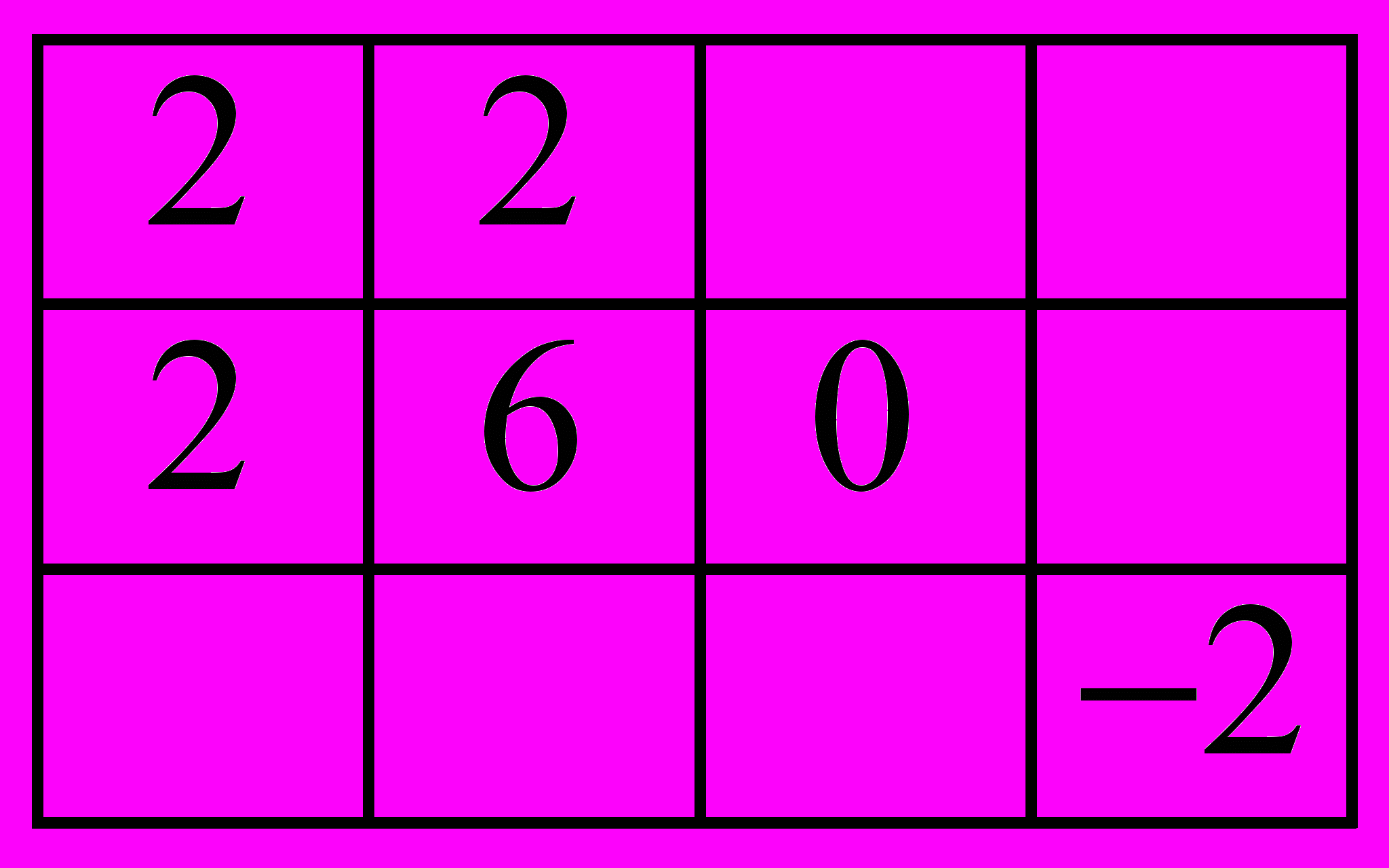 Б.
Б. 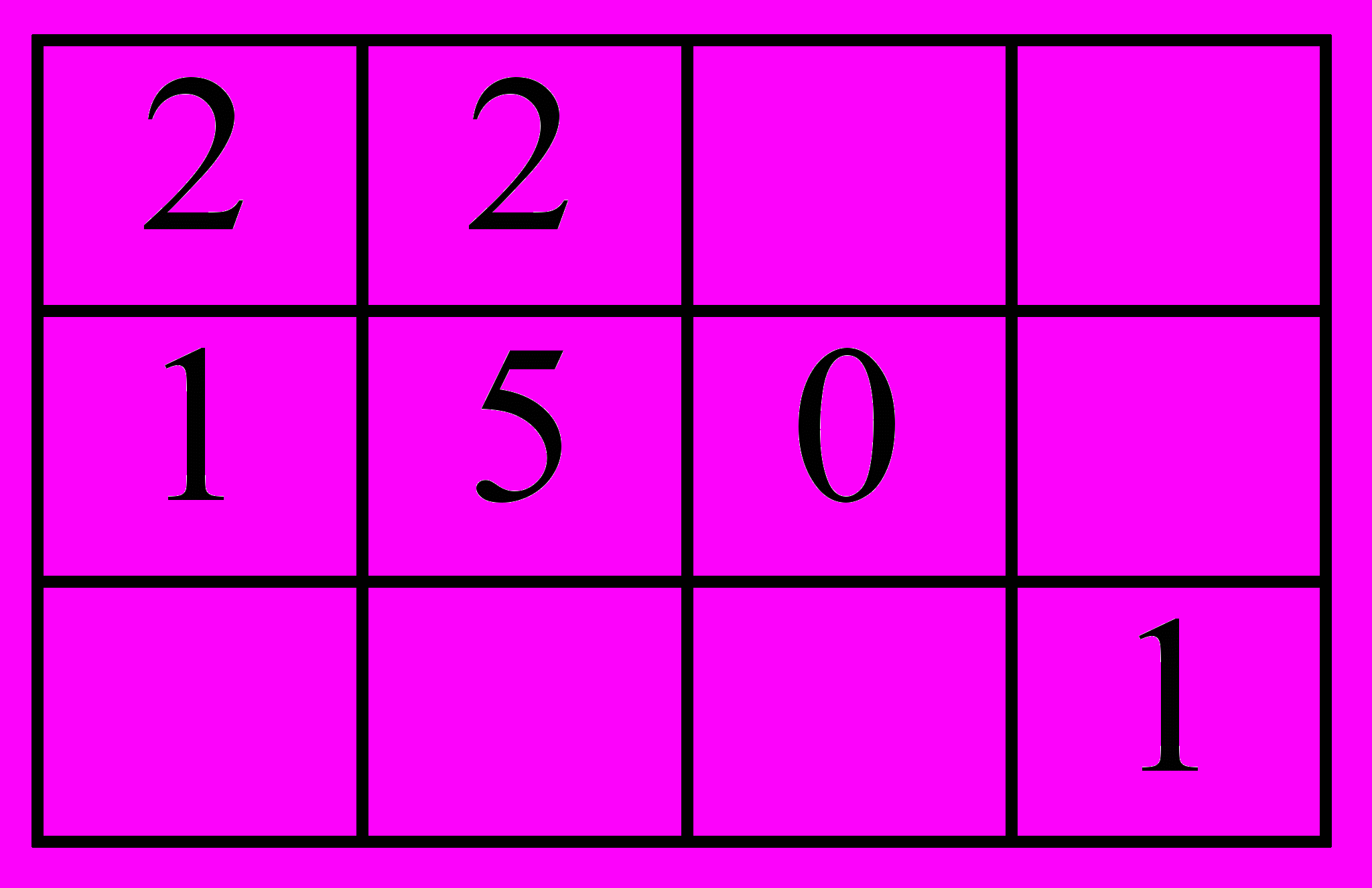 В.
В. 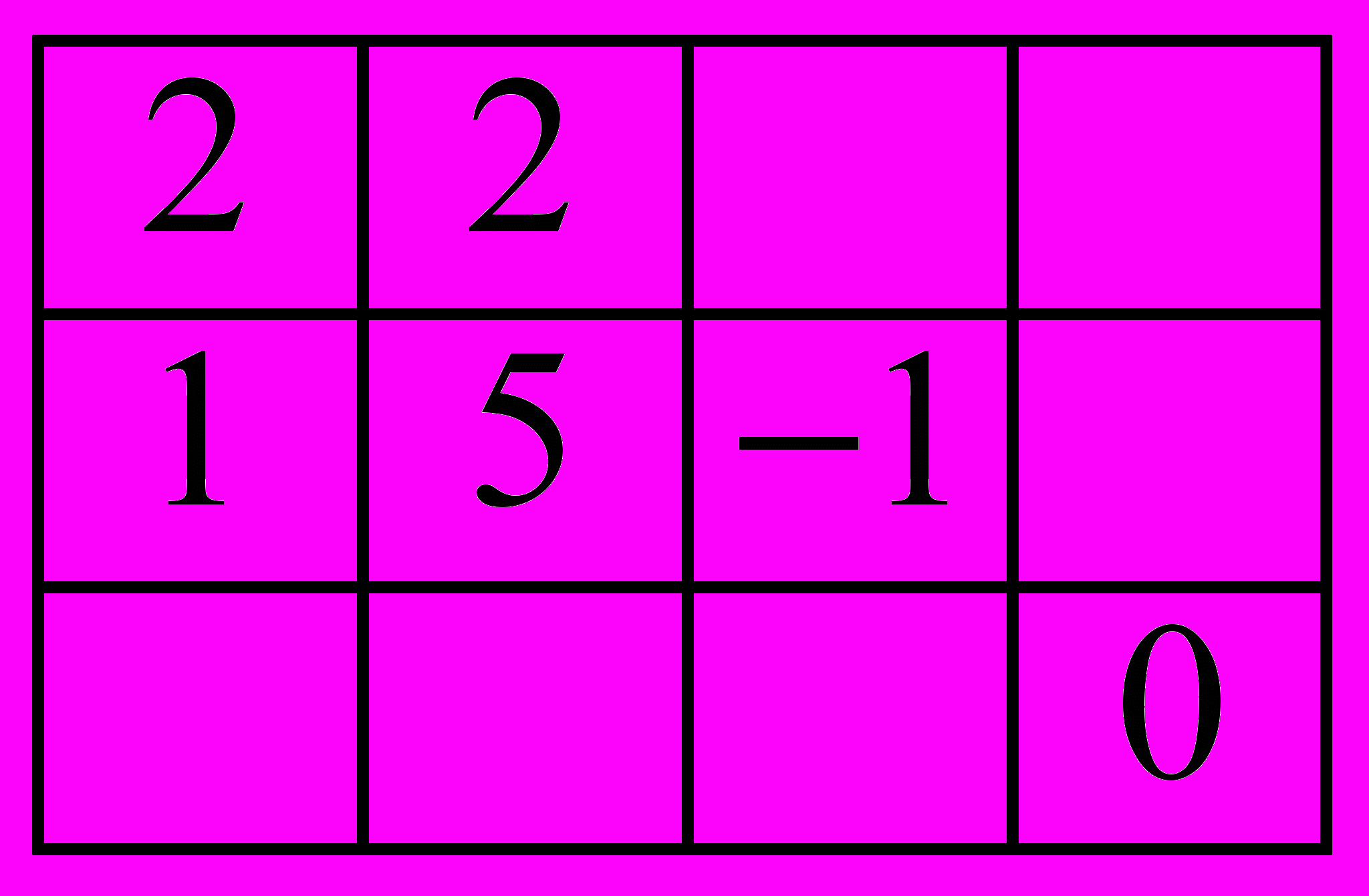 Г.
Г. 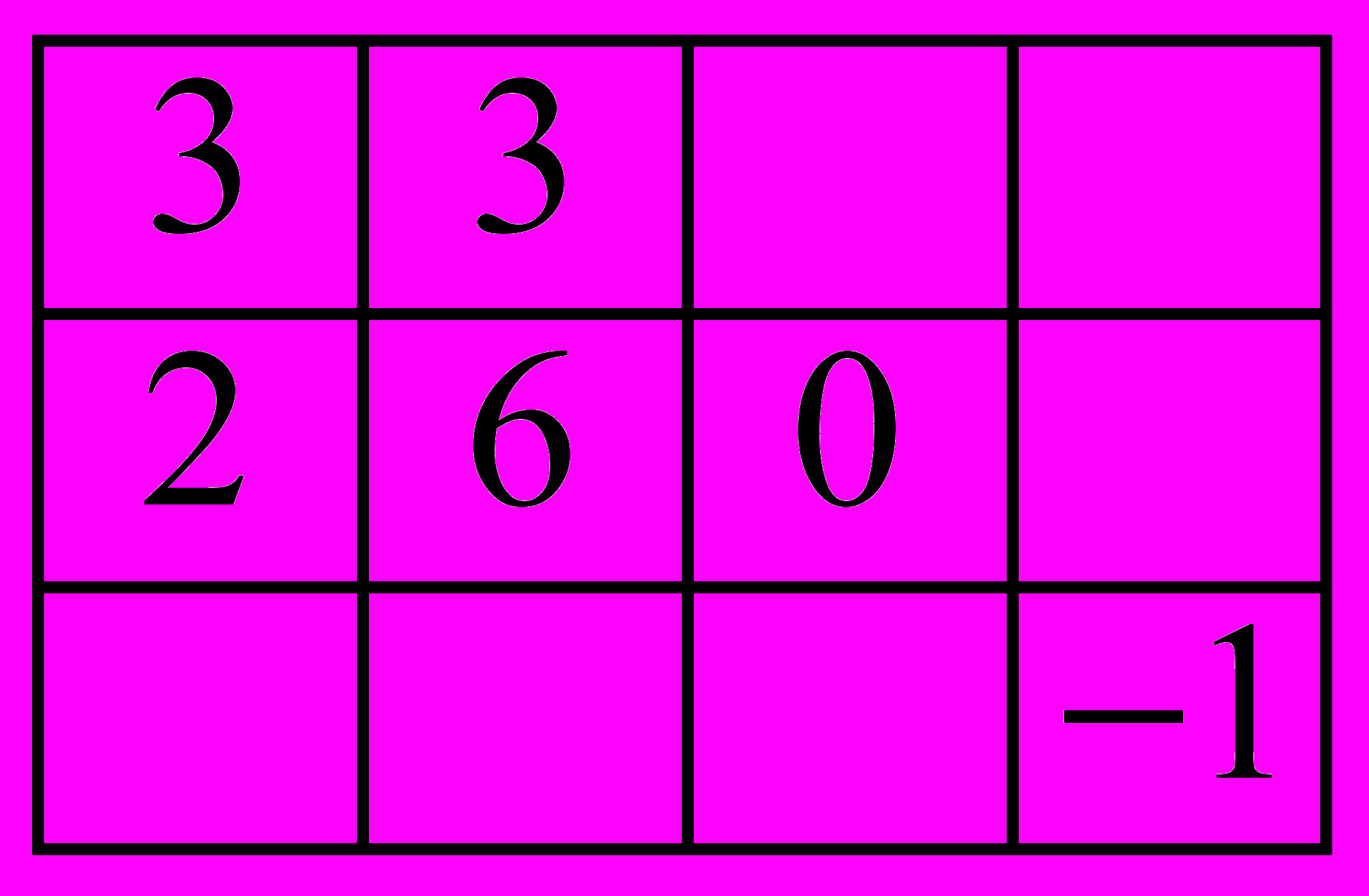
3. При переходе к новому опорному плану приращение целевой функции равно
А. –10. Б. –20. В. 0. Г. –15.
Требуется дать числовой ответ.
3
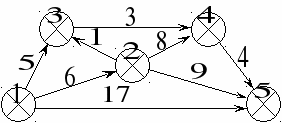
. Дан сетевой график проекта, время начала которого равно нулю.
1. Найдите полный резерв времени работы
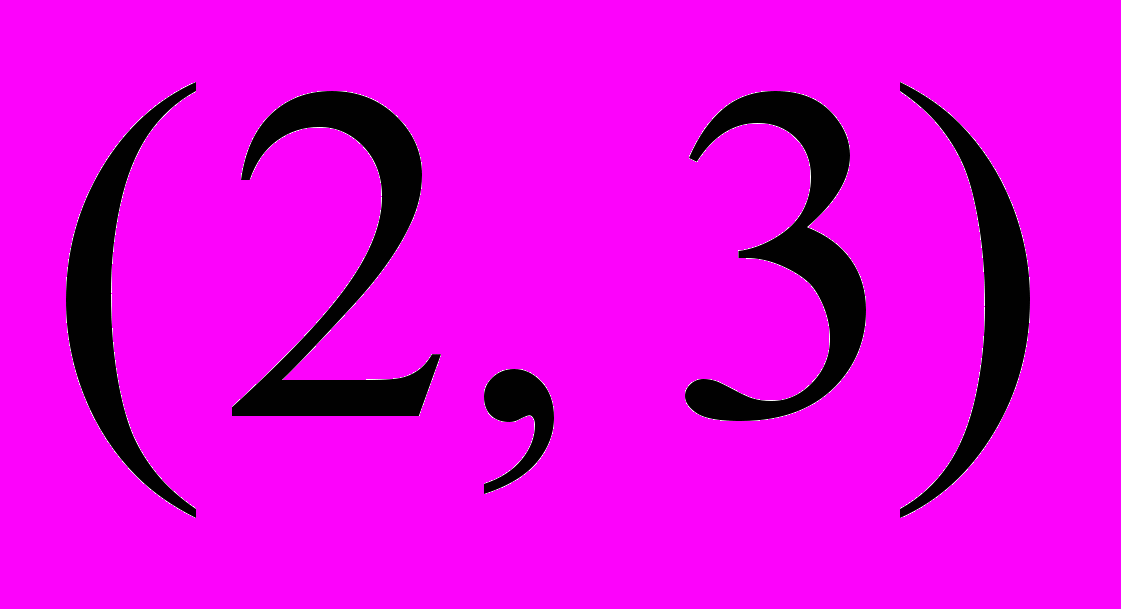 .
. 2. Найдите критическое время проекта.
Примеры задач контрольной работы №1.
1. Найти экстремум функции градиентным методом:
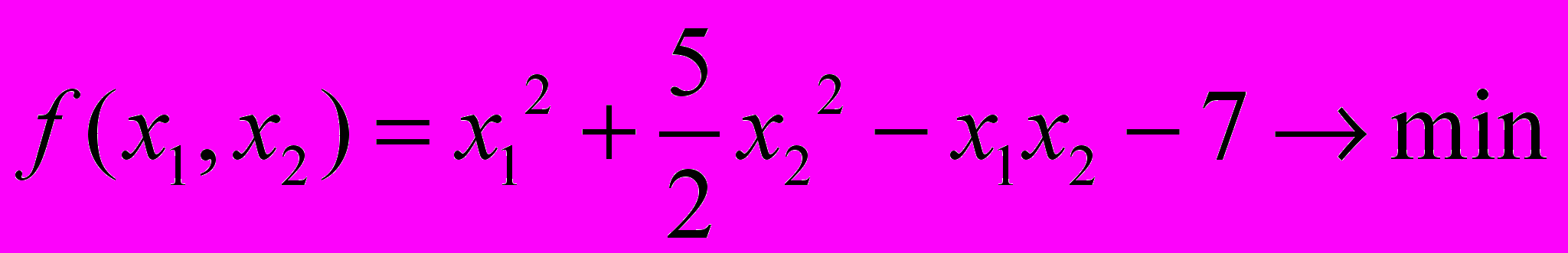 ,
, 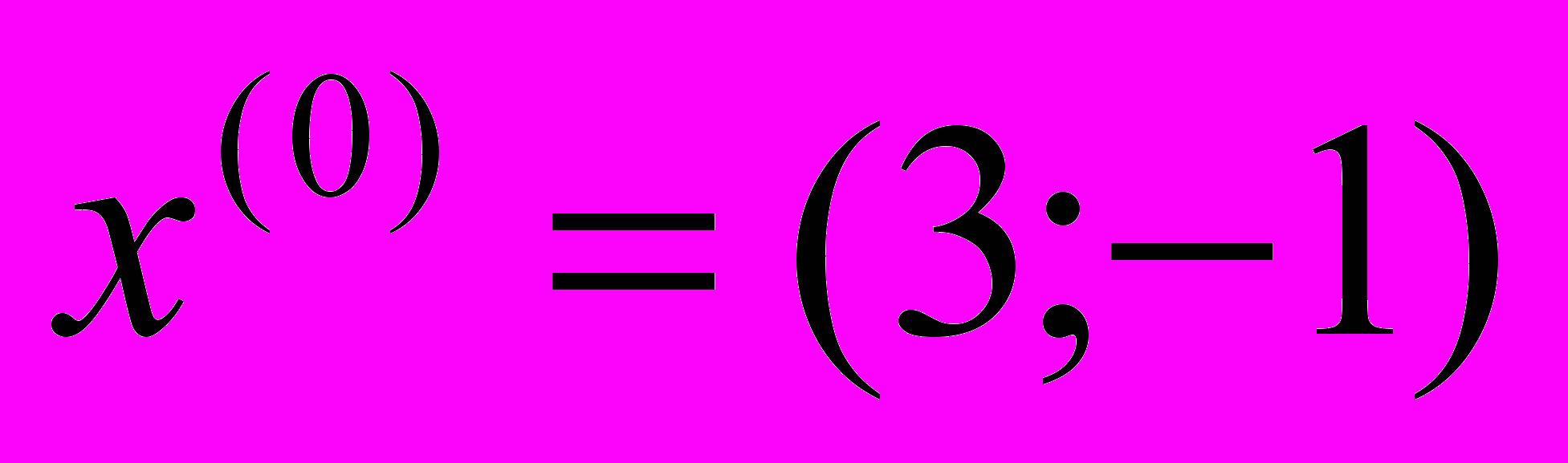 .
.2. Решить задачу о рациональном распределении ресурсов методом динамического программирования:
| Номер | Предприятие 1 | Предприятие 2 | Предприятие 3 | |||
| варианта | C1 | R1 | C2 | R2 | C3 | R3 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 5 | 2 | 6 | 2 | 5 |
| 3 | 3 | 7 | 4 | 8 | 3 | 6 |
| 4 | 4 | 8 | - | - | 4 | 7 |
| 5 | - | - | - | - | 5 | 9 |
Общая сумма капитальных вложений 8 млн. у.е.
Разработчики:
СПбГУЭФ доцент В. Г. Дмитриев
СПбГУЭФ профессор Г. В. Савинов
Эксперты:
ЭМИ РАН директор Л. А. Руховец
СПбГМТУ профессор В. Б. Хазанов
