Geum.ru

Удк 519. 63 Метод атомарных рбф и их применение при решении задач теплопроводности

Вид материалаДокументы
Подобный материал:
УДК 519.63

МЕТОД АТОМАРНЫХ РБФ И ИХ ПРИМЕНЕНИЕ ПРИ РЕШЕНИИ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ

О.Ю. Лисина

Харьковский национальный автомобильно-дорожный университет


Современные подходы к построению решений краевых задач бессеточными методами связываются с использованием в качестве базисных атомарных функций. Начало исследованиям данного класса функций положили работы В.Л.Рвачева и В.А.Рвачева, построившим в 1971 году простейшую одномерную атомарную функцию 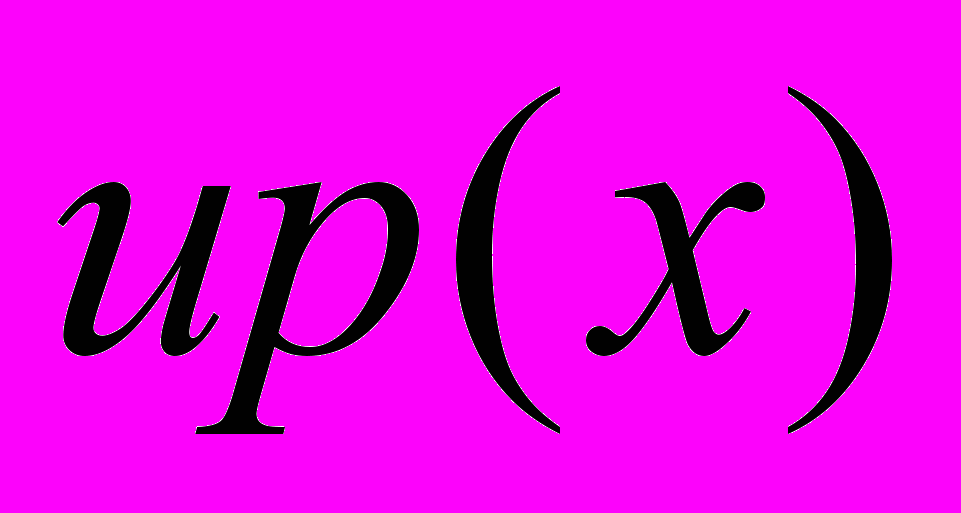[1, 2]. Бесконечная дифференцируемость и финитность функции 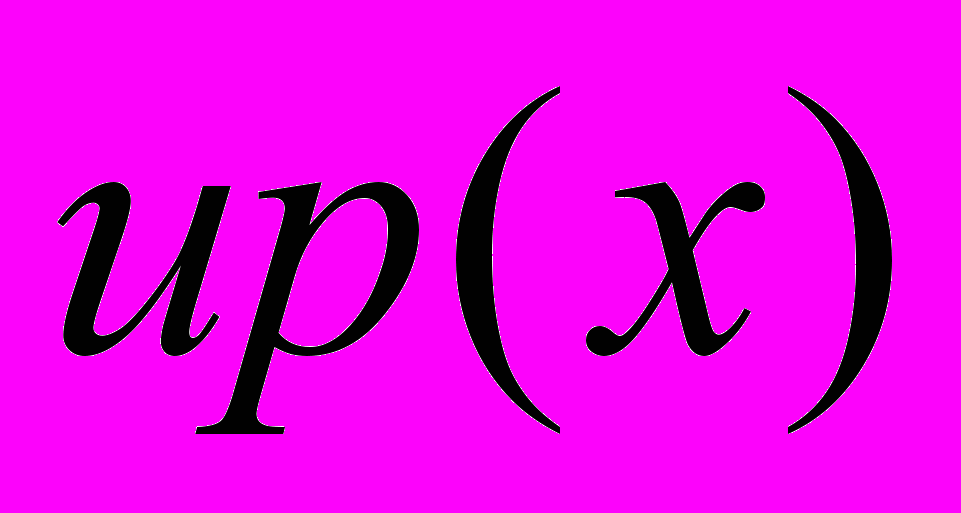позволила построить алгоритмически простые вычислительные схемы для решения задач аппроксимации функций. Атомарные функции использовались в качестве пробных при решении краевых задач на основе применения вариационных методов. Расширение понятия атомарной функции на случай многих независимых переменных (нетривиальные обобщения) связаны с исследованиями В.М.Колодяжного и В.А.Рвачева [3], которые предложили классы атомарных функций, порождаемых ФДУ специального вида [4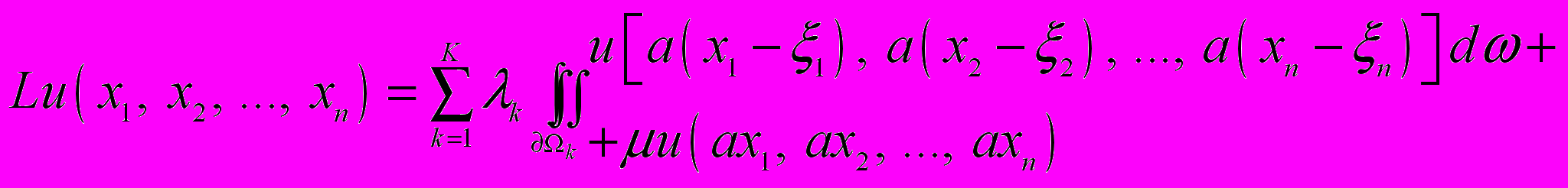, 1]:

,(1)

где 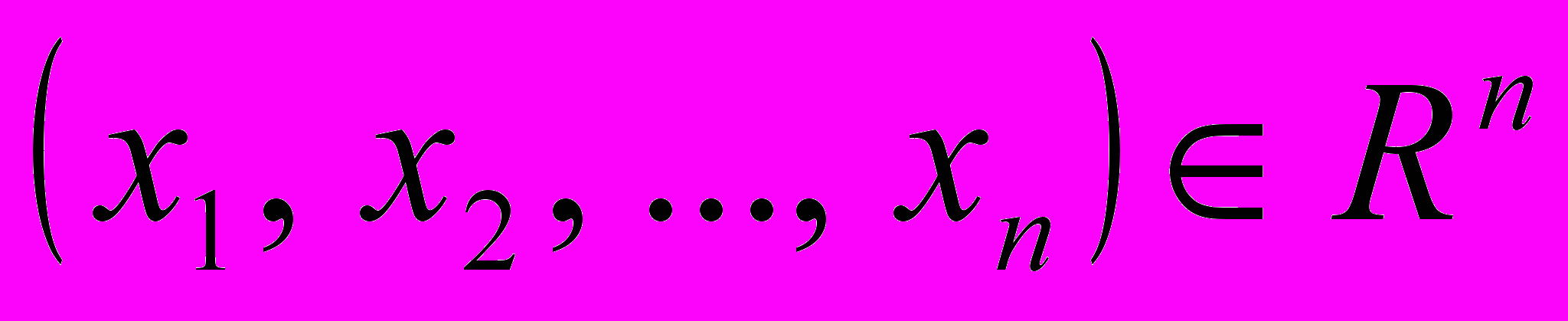, 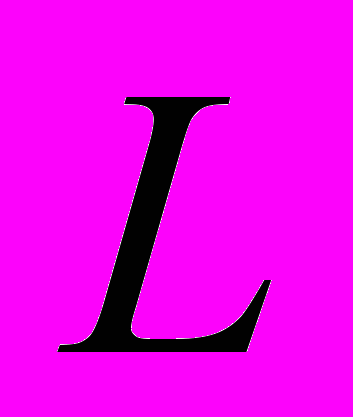– дифференциальный оператор, в качестве которого можно рассматривать дифференциальные операторы различных видов 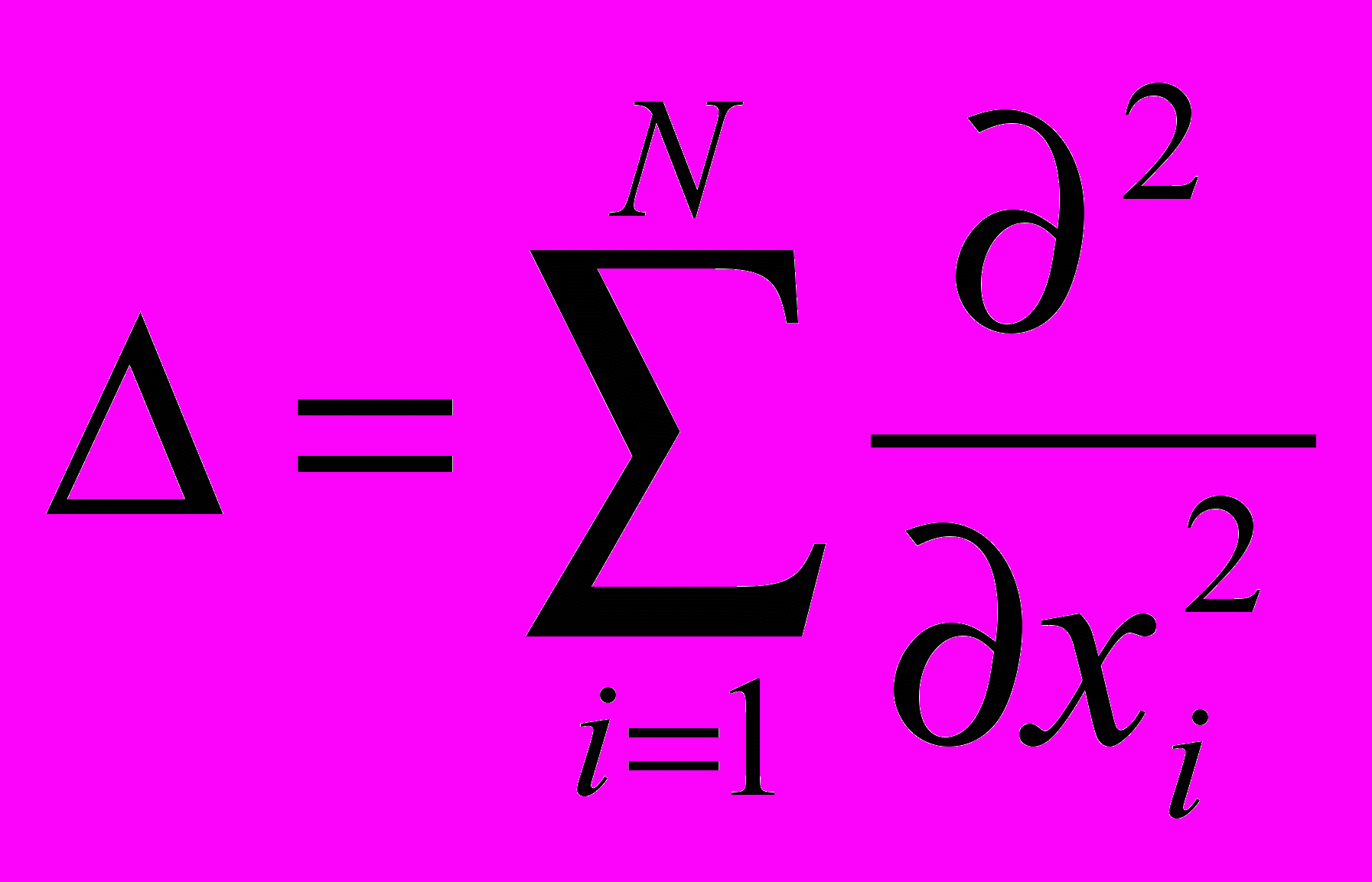– оператор Лапласа; 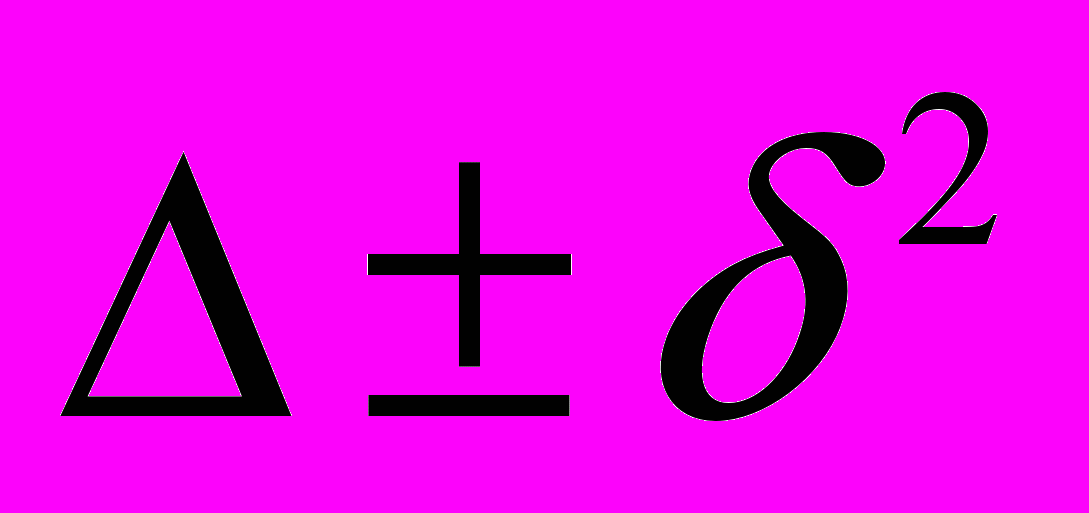– оператор Гельмгольца; 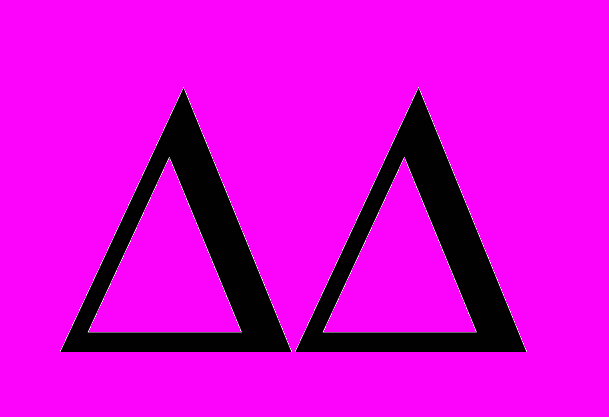– бигармонический оператор и т.д.; 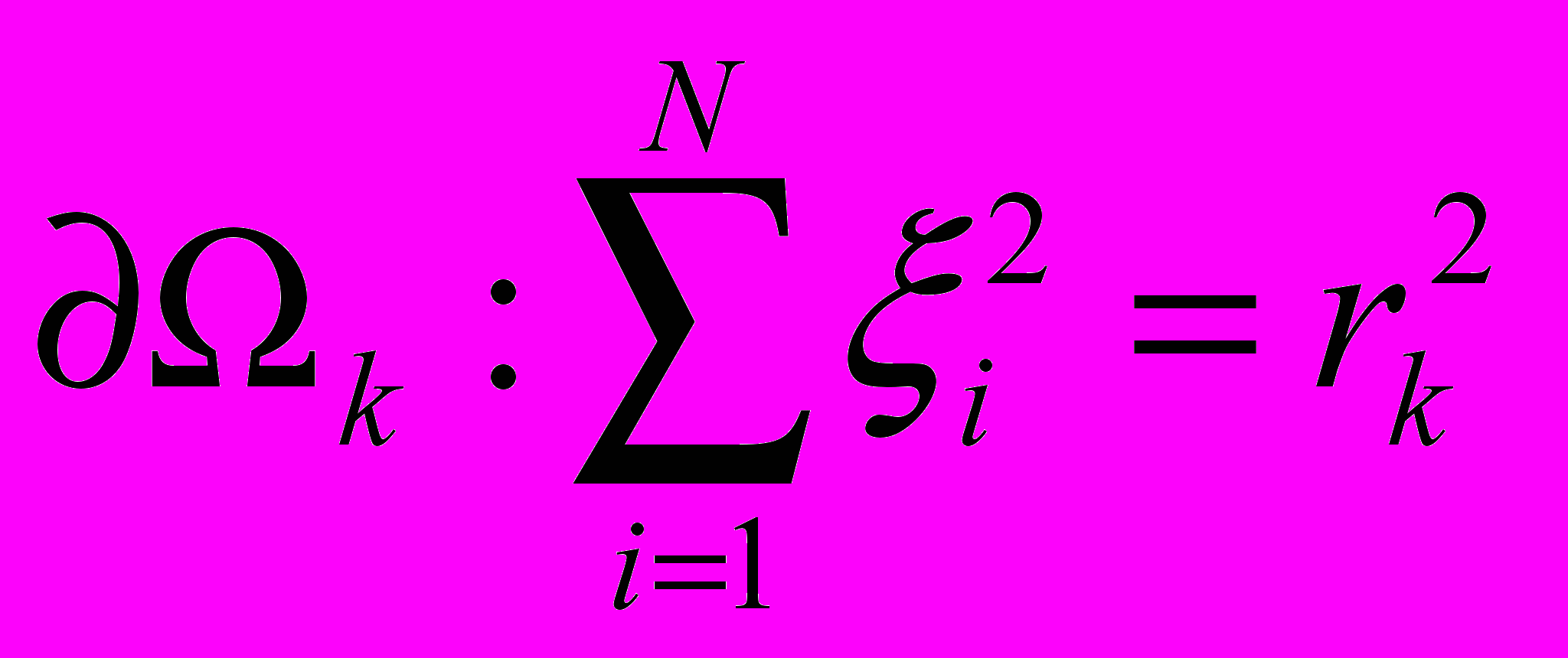– граница выпуклой области, - коэффициент сжатия. Выбор значений коэффициентов 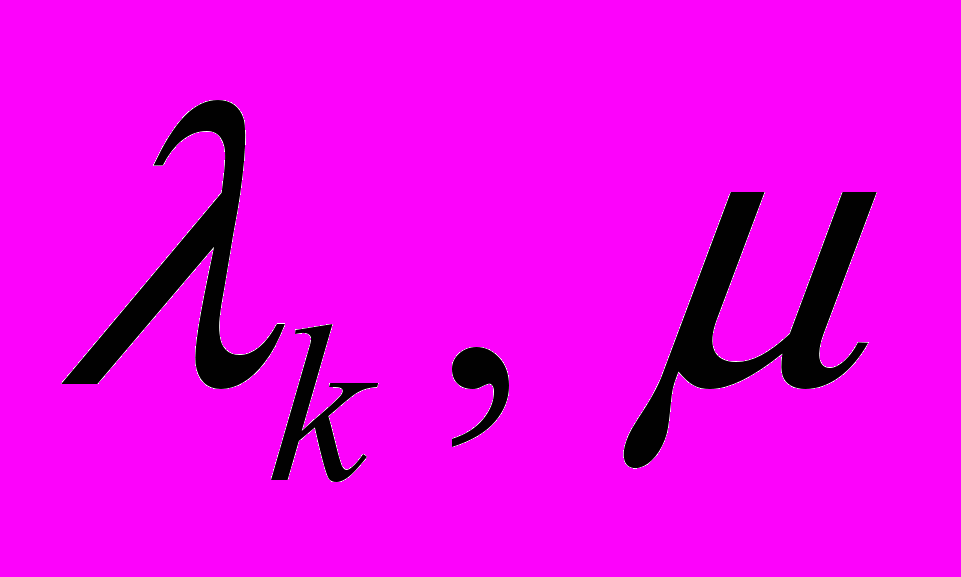осуществляется таким образом, чтобы обеспечивалось существование и единственность финитного решения соответствующих ФДУ. Функции, получаемые в результате решения ФДУ вида (1), являются бесконечно дифференцируемыми, что представляется важным при реализации численных алгоритмов решения задач математической физики. В частности, при решении задач теплопроводности такие функции могут использоваться в качестве базисных при построении приближенного решения.

Алгоритм бессеточной схемы численного решения 3D краевой задачи с помощью АРБФ 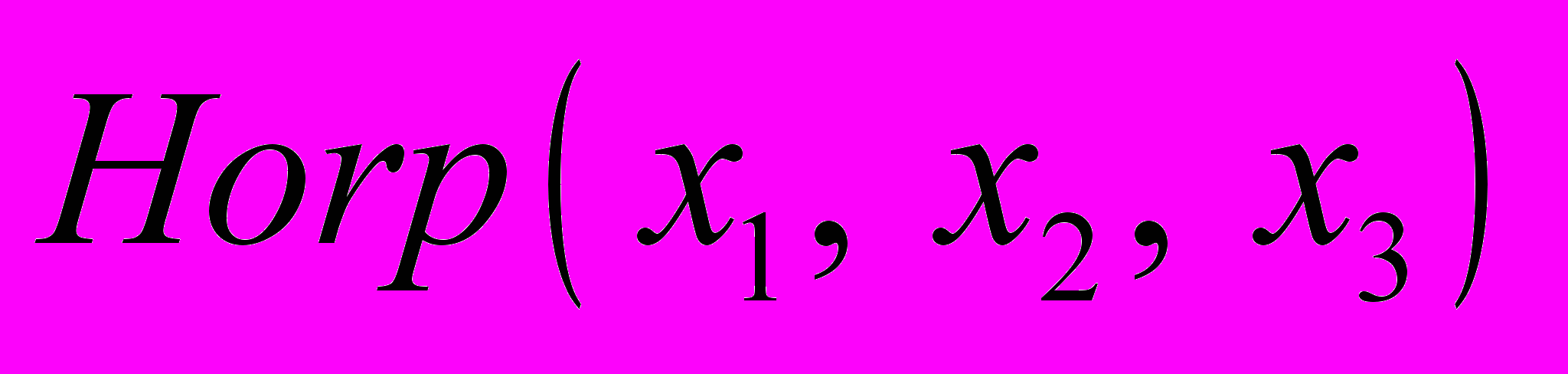рассмотрим на примере построения решения краевой задачи для дифференциального уравнения Гельмгольца, к которому легко преобразуется уравнение теплопроводности. Пусть 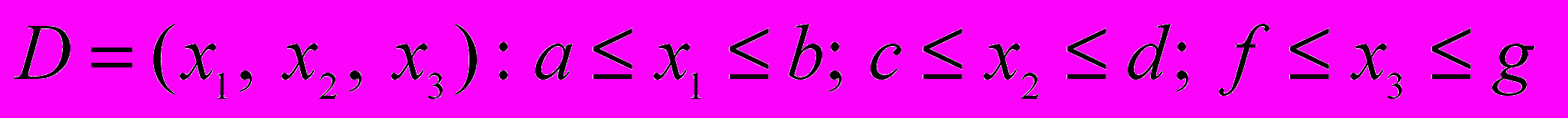куб в пространстве 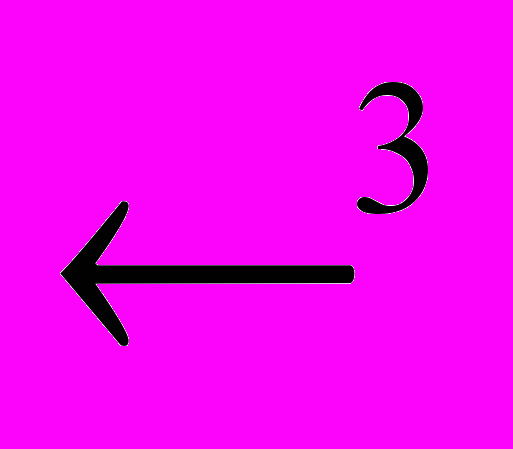. Пусть в ограниченной односвязной области 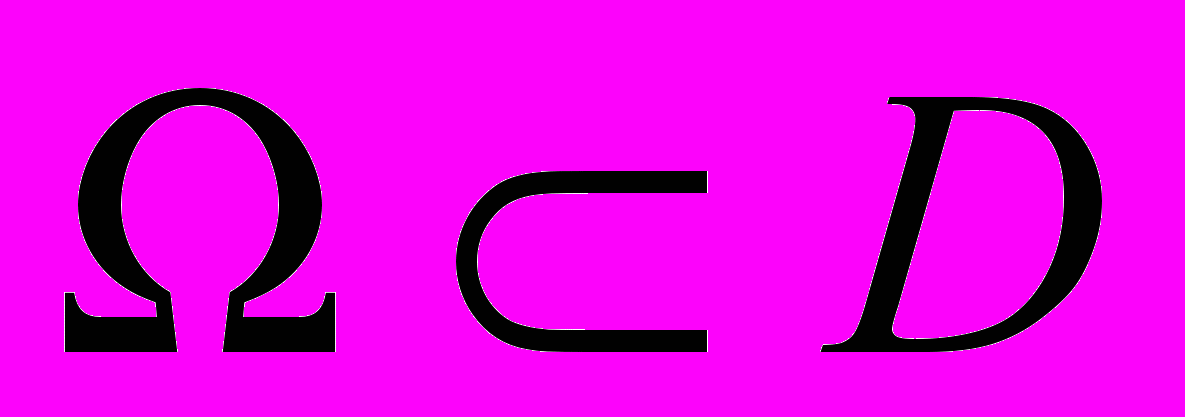задано дифференциальное уравнение

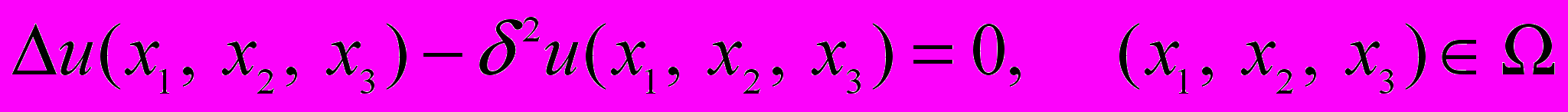(2)

а на границе 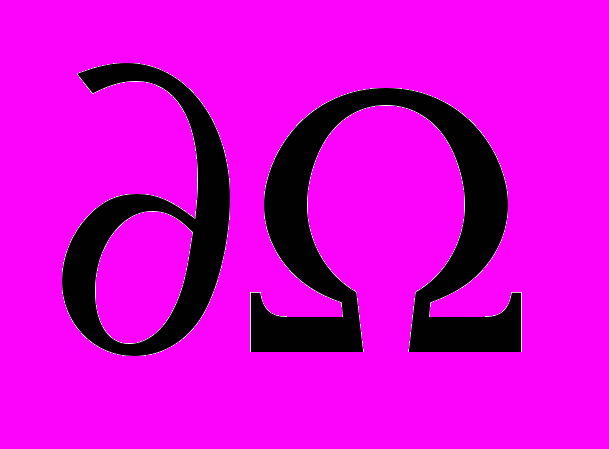области граничное условие Дирихле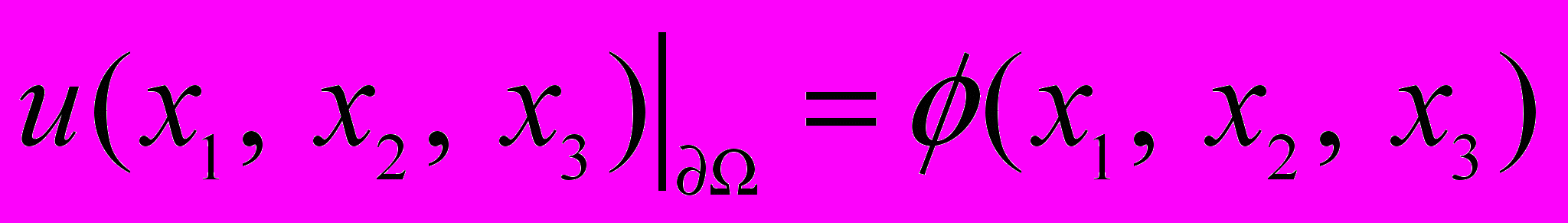

(3)

Построим в области 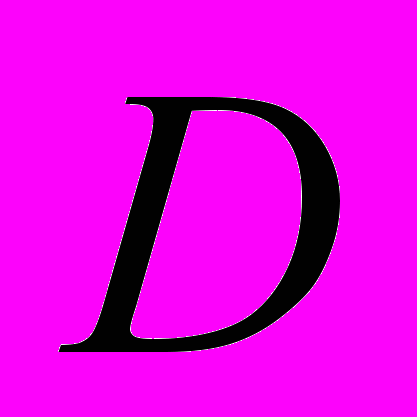множество точек 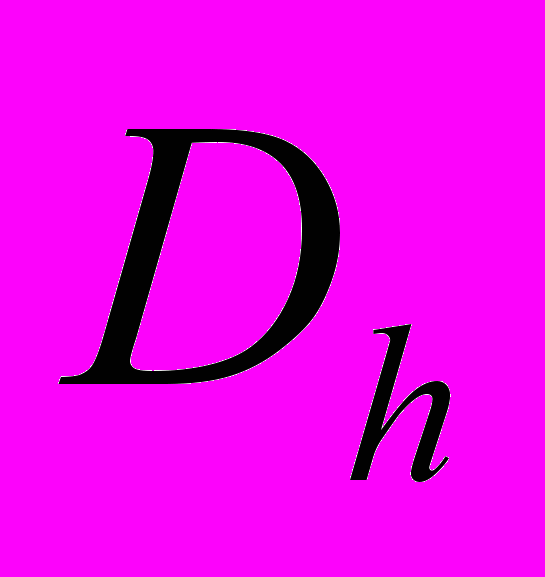, задающее сеть. Обозначим через 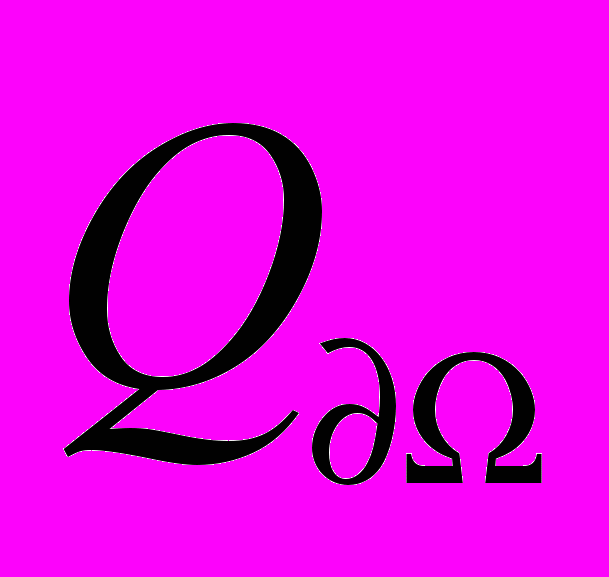множество из узловых точек множества 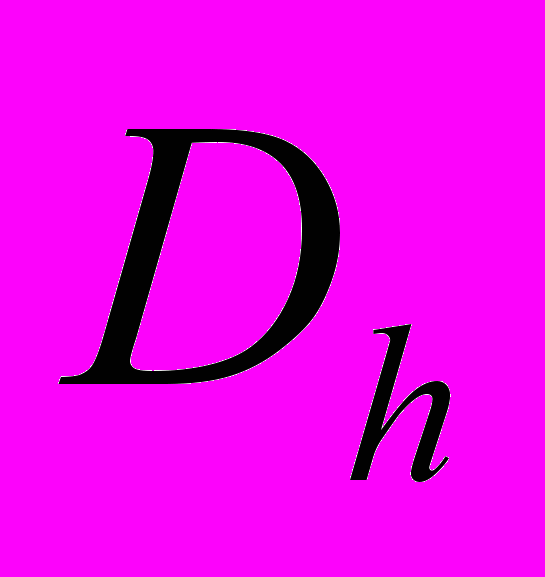, которые содержатся в области (ограничены границей 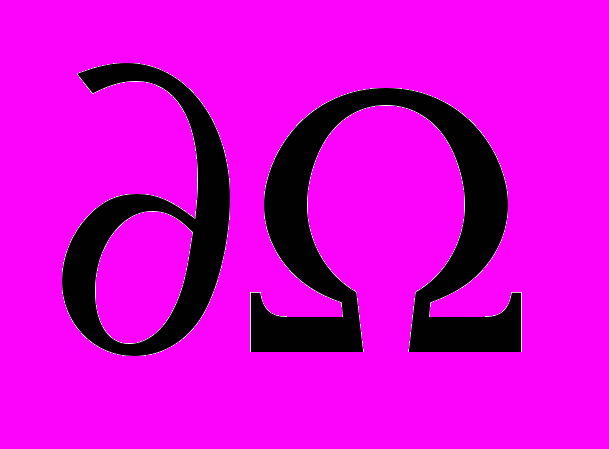). Через 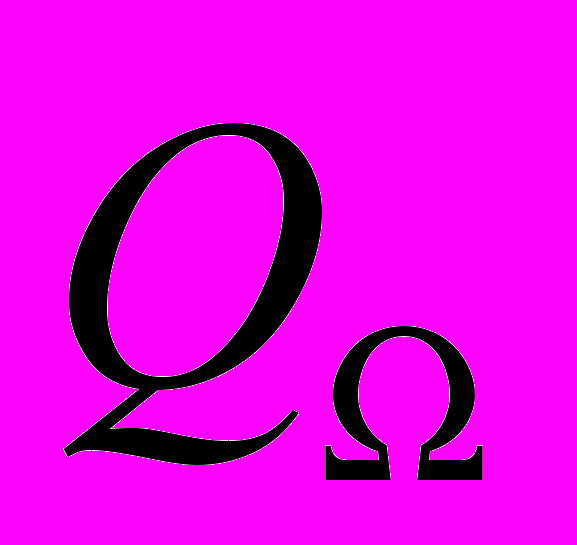обозначим множество узловых точек множества 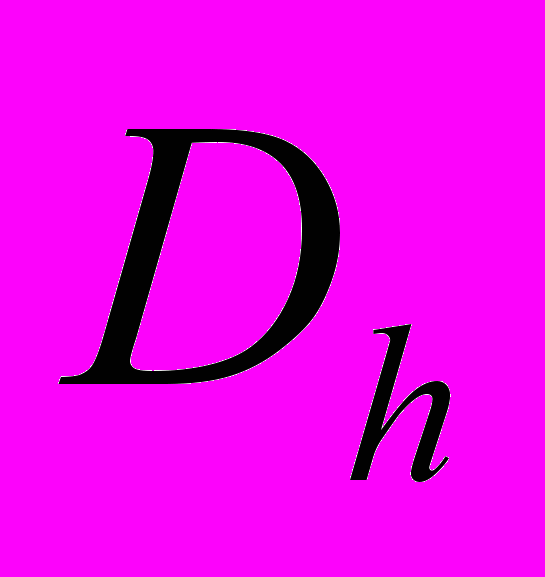, которые являются внутренними точками области . Приближенное решение задачи (2)–(3) будем отыскивать в виде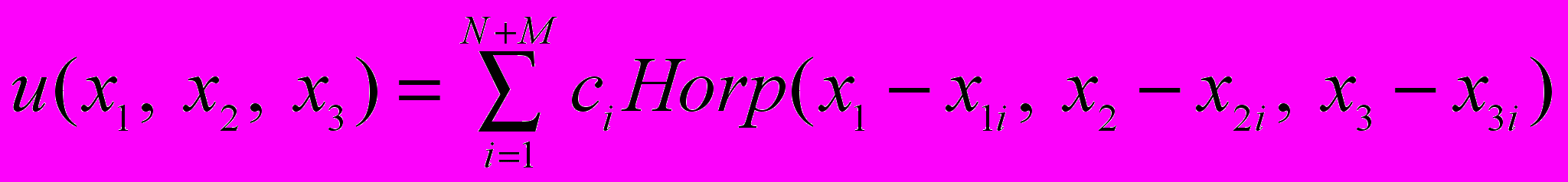

, (4)

где 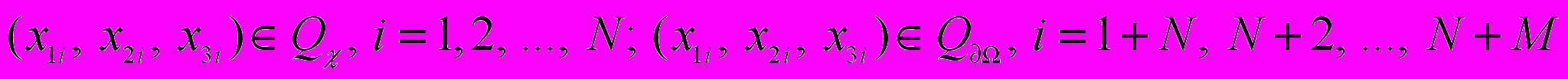, что приводит к уравнениям, необходимым для определения 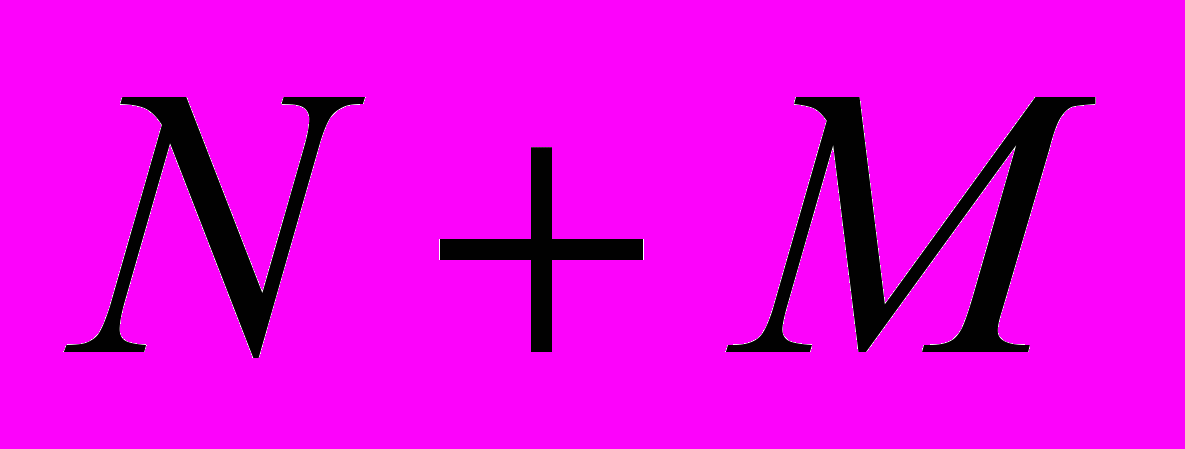коэффициентов 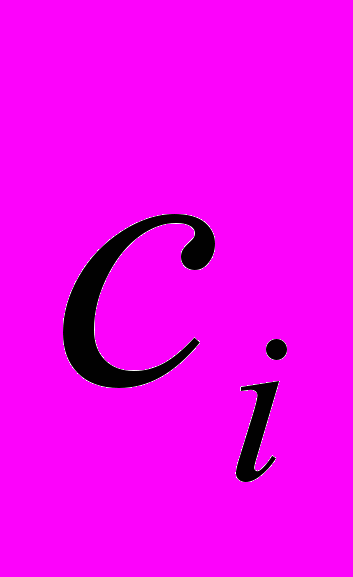. Остальные 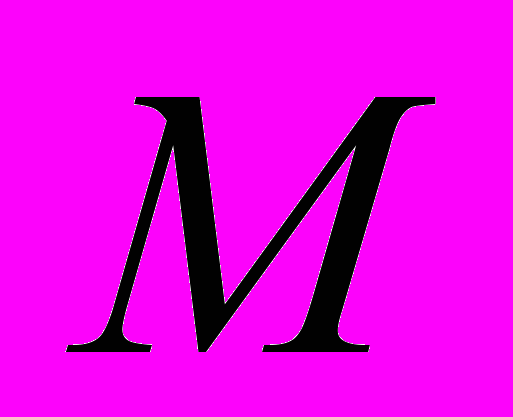уравнений получим из условия приближенного удовлетворения граничному условию (3). Характерными особенностями предлагаемого метода является, с одной стороны, использование финитных функций (свойство локальности), а с другой – полученные решения исходной краевой задачи являются бесконечно дифференцируемыми, что немаловажно для решения задач некоторых классов.

Литература
  1. Колодяжный В.М. Атомарные функции. Обобщения на случай многих переменных и перспективные направления практических приложений / Рвачев В.А. // Кибернетика и системный анализ. – 2007. – 43, N 6. – С. 155–177.
  2. Рвачев В.Л., Рвачев В.А. Теория атомарных приближений. Математика, кибернетика. – М.: Знание, 1978. – 62 с.
  3. Колодяжний В.М. Фінітні розв′язки функціонально–диференціальних рівнянь з частинними похідними/ Рвачов В.О. // Доповіді НАН України. – 2004. – № 5 – С. 17–22.
  4. Колодяжний В.М. Деякі властивості атомарних функцій багатьох змінних/ Рвачов В.О. // Доповіді НАН України. – 2005. – № 1 – С. 12–20.