Donetsk compartment of shevchenko scientific society

Вид материала

Документы

Содержание Симетрія в психіці Матеріал і методи Результати і обговорення.

Подобный материал:

• Donetsk compartment of shevchenko scientific society, 2259.73kb.
• Donetsk compartment of shevchenko scientific society, 3938.75kb.
• Donetsk compartment of shevchenko scientific society, 4086.35kb.
• Donetsk compartment of shevchenko scientific society, 3610.42kb.
• Donetsk compartment of shevchenko scientific society, 1319.59kb.
• Donetsk compartment of shevchenko scientific society, 2424.3kb.
• Донецьке відділення наукового товариства ім. Шевченка donetsk compartment of shevchenko, 3687.32kb.
• Донецьке відділення наукового товариства ім. Шевченка donetsk compartment of shevchenko, 3817.8kb.
• Донецьке відділення наукового товариства ім. Шевченка donetsk compartment of shevchenko, 3413.53kb.
• Донецьке відділення наукового товариства ім. Шевченка donetsk compartment of shevchenko, 398.96kb.

^

СИМЕТРІЯ В ПСИХІЦІ

У попередньому Віснику В.О.Максимович, М.В.Макси-мович (2004) виклали закон збереження мотивації і варіаційний принцип її організації. На відміну від генези, інваріантність (незмінність) відомих науці законів збереження в будь-якій точці простору-часу фізика пояснює наявністю у Всесвіті найбільш загального порядку, який відображається принципами (законами законів) симетрії (М.М.Мурач, 1987). Кожному перетворенню фундаментальної симетрії відповідає деякий певний закон збереження класичної фізичної величини. Однорідність простору веде до закону збереження імпульсу, однорідність часу – до закону збереження енергії, ізотропна (поворотна симетрія) простору – до збереження моменту імпульсу і т.і.

Виникає питання, якому принципу симетрії або асиметрії відповідає закон збереження мотивації. Йдеться не про збереження психіки в цілому, а про збереження усередині неї мотиваційної організації. Адже мотивація служить задатчиком, спонукачем всієї подальшої психічної активності, яка переходить у фізіологічну активність, діяльність і поведінку. Рішення цього проблемного питання могло б розкрити «геометрію» психічного світу і його зв'язок з фізичним світом. Причому розкрити значно ширше, ніж це зробила психофізика. В цілому цей напрям є об'єднання науки про психіку з сучасними точними науками.

Прямі або непрямі дослідження, у тому числі уявні експерименти, були проведені декількома вченими. З їх результатами можна ознайомитися, наприклад, в узагальненнях С.В. Петухова (1981) і В.Ю. Крилова (1990). Не дивлячись на те, що публікація В.Ю. Крилова ближча до нас за часом, ми далі цитуватимемо книгу С.В. Петухова, в якій більше особистої зацікавленості і зіставлень. Цей автор прийшов до висновку, що простір психофізичного сприйняття відповідає геометрії Лобачевського, в якому загалом діє група гіперболічних перетворень, але реально конформні відображення. Чому такий висновок задовольняє нас не повністю, буде показано подальшими результатами власних теоретичних досліджень.


^ МАТЕРІАЛ І МЕТОДИ

Матеріалом послугували теоретичні і концептуальні уявлення, що склалися в науці по проблемі симетрії і психіки. В роботі використаний аналіз і узагальнення існуючої інформації і поглядів, що склалися по даній проблемі. Крім того, був проведений уявний експеримент і конструювання варіантів рішень поставлених задач.


^ РЕЗУЛЬТАТИ І ОБГОВОРЕННЯ.

Починаючи з Ф. Клейна, геометрія Лобачевського поступово набула наочну модельну інтерпретацію. Це сприяло розумінню і прив'язці її конструкцій до фізичного світу. Перш за все, було показано, що її закономірності дотримуються усередині деякого абсолюту, обмеженого конікою, яка є замкнутою дійсною кривою другого порядку:


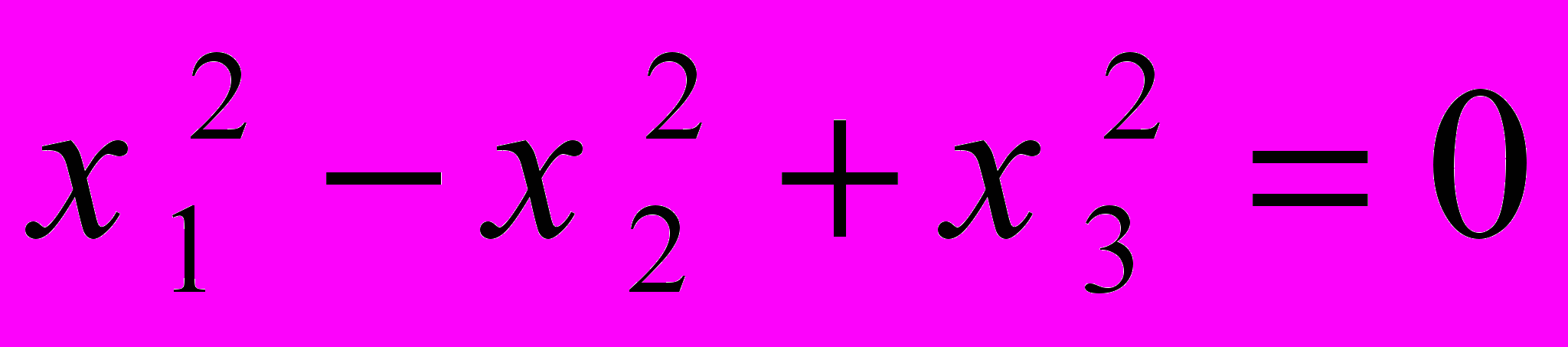(1)


Фігура усередині цієї «справжньої кривої» служить інваріантом даній геометрії. Коніку інтерпретують як «обрій», з яким не контактує, не стикається жоден, що знаходиться усередині неї, геометричний об'єкт, у тому числі найпростіші – крапка, лінія. За межами обрію існує інша геометрія з своїми об'єктами. Але потрапити туди об'єктам з коніки і навпаки неможливо. «Безконтактність» цих двох геометрій перешкоджає спілкуванню процесів в них, наприклад, фізичного і психічного світів з їх взаємопереходами і взаємодіями. Адже в цьому суть. Пригадаємо психофізику і ідеомоторику [В.А. Максимович, В.В. Мухин, С.В. Беспалова, 2001].

Розглянута перешкода усунена в геометрії Б.Рімана, принаймні, при русі з коніки за її межі. На відміну від дійсної коніки Лобачевського, у Рімана коніка повністю уявна у всіх її точках:


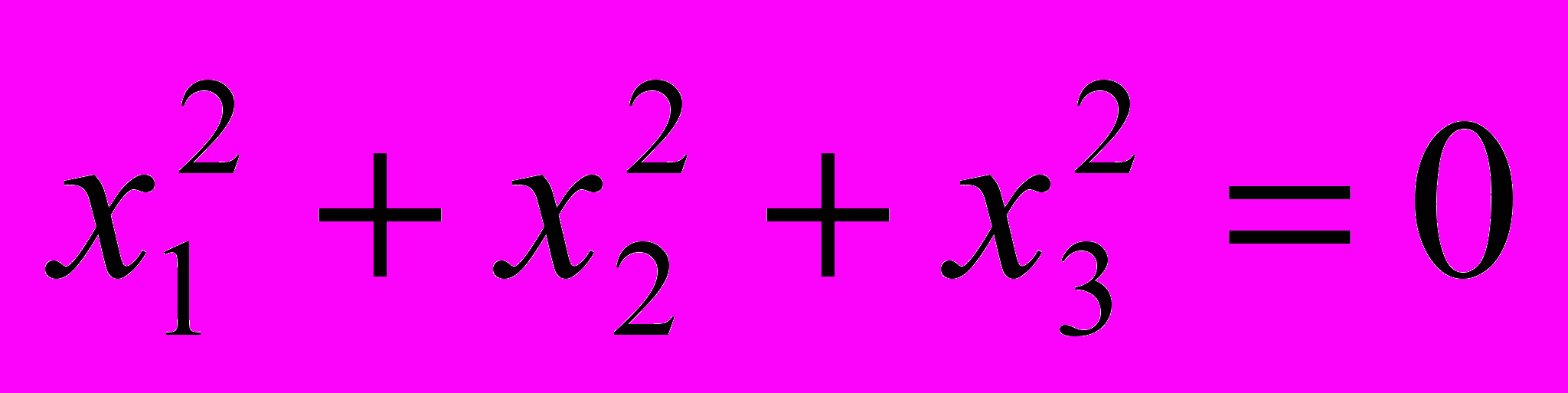(2)


В результаті будь-які об'єкти (дійсні і уявні), що знаходяться усередині уявної коніки, можуть вільно вийти за її межі і опинитися в іншому просторі. Залишилася вимога зворотного руху. Необхідно, щоб об'єкти, що знаходяться «за обрієм», могли потрапити в коніку, контактувати з нею. Потрібно, щоб був взаємообмін перетвореними об'єктами двох геометричних просторів. В книзі Р.Н. Щербакова, Л.Ф. Печуріна (1979), приведені необхідні умови. Для цього в геометрії «за обрієм», крім дійсних, потрібно ввести у фігури уявні крапки.

І усередині Рімановського абсолюту – уявної коніки, і зовні нього, «за обрієм», діє, як правило, еліптична метрика і група перетворень еліптична. Цим, в першу чергу, відрізняється наш висновок від висновку С.В. Петухова. Чи може все-таки бути і гіперболічна метрика, і яка-небудь інша. Гіпотетично, так. Наприклад, для кутів у відповідних умовах.

Декілька слів про кути. Спеціальними дослідженнями Б.М. Беспалов (1984) показав, що при операціях маніпулювання відтвореними образами пам'яті сприйняті величини кутів фігур зберігаються. Тому в перетвореннях їх величин немає потреби. Збереження величин кутів вірна ознака конформних відображень, що співпадає з думкою С.В. Петухова.

Є ще одна важлива додаткова обставина. Довжина прямої в просторі «за обрієм» обмежена діапазоном 0.... Це дуже важливо по суті явищ, які ми хочемо ототожнити з цим простором. Якщо узяти іншу одиницю вимірювання (масштаб) і ввести, наприклад, гомотетичний коефіцієнт стиснення, то величина прямої або іншої фігури може ставати скільки завгодно малою, але кінцевою. Це відповідає тому неспростовному емпіричному факту, що образи в психопросторі можуть мати дуже обмежені просторові розміри. Індивідуальний психопростір малий, в порівнянні з реальним світом, а в ньому повинні поміститися відображення величезних в матеріальному світі об'єктів. Іншими словами, масштаби координат в психопросторі стислі, згорнуті до «крапки», або (другий варіант) вони замінені якісно іншими (якісне перетворення).

Проте вищевикладене далеко не повністю характеризує симетрію психопростору (далі скорочено ПП). Емпіричними спостереженнями різних фахівців [З. Спрінгер, Р. Дейч, 1983] встановлено, що в ПП відсутня дзеркальна симетрія процесів. Процеси, що відбуваються в правій і лівій половинах ПП суб'єкта, не еквівалентні. По аналогії з мікросвітом можна сказати, що в ПП порушена Р-інваріантність. З теореми Ю. Швінгера, В. Паулі, Р. Людерса (1955) про СРТ-групу випливає, що порушення Р-інваріантності супроводжується порушенням СТ-інваріантності, тобто зарядо-часової композиції.

Не дошукуватимемося прямого або алегоричного показника тієї істинної властивості ПП, яка може бути пойменована зарядом психіки. Наведемо лише приклади двох видів потенційних кандидатів на цю роль. Першим видом кандидатів може бути баланс сили процесів збудження з антисиметричною їм силою процесів гальмування. Рівновагу сил (зарядів) цих антиподів цілком можна вважати зарядовою симетрією, С – інваріантністю, а її порушення – дисбалансом сил збудження і гальмування. Співвідношення переважання має характер вірогідності. Другим видом кандидатів – аналогів зарядового потенціалу в психології можна прийняти «добродійство суб'єкта» (його спрямованість до творення, акцентуацію на альтруїзм, на моральність і т.п.) і його антипод – «злодійство» (спрямованість до руйнування, акцентуацію на агресію, на аморальні вчинки і т.п.). Спостерігач – індивідуальний або колективний суб'єкт, оцінить першу якість як позитивну зарядженість, а другу – як негативну. Ці властивості – якості Спостерігача можна виміряти в безперервній або дискретній шкалі з наявністю нейтрального елемента, що характеризує «ні те, ні се». Обмежимося цими «прикладами».

Заряд може бути сумарним внеском обох видів, як в ядерній фізиці – сума електричного і баріонного зарядів. Можуть бути інші показники і їх комбінації. Важлива реальність зарядової інваріантності і її порушень в психіці і те, що виявлення балансу – дисбалансу має характер вірогідності.

Велику увагу учені і аматори приділяють третій складовій – часу, Т-інваріантності і її порушенням. Це не дивно. В «Роздумах про час» П. Флемінг поетизував афоризм: «В часі живучи, ми часу не знаємо». Часу присвячені безліч публікацій. В двох з них – книгах А.Д. Черніна (1987) і Є.І. Головахи, А.А. Кроника (1984), представлені відомості про фізичний і психологічний час, їх особливості і відмінності.

У фізичному макросвіті, не дивлячись на спрямованість, образно «стрілу», часу, в класичних законах механіки час симетричний. Асиметрія ж виходить з термодинаміки ентропійних процесів. В мікросвіті спрямованість пов'язана з феноменологією порушення Т-інваріантності. Метрика часу психічного миру (Б.І. Цуканов, 1992) не тільки не зводиться до фізичних вимірювань, але її одиниці здатні до стиснення і розтягування. Наприклад, при мисленні ПП властиві децентрації часу, тобто локальні зміни послідовності подій, їх перестановка, комбінаторика, яка не відповідає первинній хронології, а також інші трансформації. Загалом Т-інваріантність в психосвіті не витримується.

Чи витримується в психосвіті СРТ-інваріантність, вимагає спеціально продуманої експериментальної перевірки. В теорії перенесення (В.М. Мінаковський, 1978) подібні характеристичні комплекси називають узагальненими змінними, як, наприклад, числа Рейнольдса, Прандтля і багато ін. Вони мають межі, зони існування: то для ламінарного, то для турбулентного руху, у зв'язку з чим їх також іменують критеріями. У будь-якому випадку потрібно враховувати, що на геометрію ПП¹, ідентифіковану як «за уявним обрієм», накладені додаткові обмеження – уточнення, пов'язані з вищезгаданими асиметріями.

Отже, зі всього вищевикладеного можна зробити висновок, що геометричні властивості двох світів – фізичного і психічного, мають цілком певні відмінності. При цьому єство відповідних задач математичного моделювання психіки полягає не в тому, щоб знайти групи перетворень усередині кожної з геометрій. Це задачі математики і, в якійсь мірі, фізики. Математичній психології потрібно знайти перетворення об'єктів (явищ, подій) при переході з одного Світу в іншій, з однієї геометрії в іншу.

Перетвореннями при переході з фізичного (матеріального) світу в психічний традиційно зайнята психофізика, засновником якої 150 років тому був фізик Р. Фехнер, а головним продовжувачем З. Стівенс. Зворотними перетвореннями психічних образів в матеріальні (фізичні) явища, наприклад, в локомоції, повинна займатися інша частина науки. Умовно назвемо її психоматеріалізацією, в яку входить і ідеомоторика (О.О. Бєлкин, 1983). В психоматеріалізації математичне моделювання не розвинуто.

Почнемо з того, що здається більш простим – з психофізики. Вона, по суті, розглядає перетворення матеріальних об'єктів, що мають вигляд фізичних стимулів, які йдуть від об’єктів, в їх психічні еквіваленти. Матеріальні стимули виходять з Ріманова геометричного простору. З часів Ф.Клейна групу таких перетворень іменують еліптичною. Мабуть, до них можна віднести і перетворення засновника психофізики Р.Фехнера, а також Р. Стівенса і багатьох інших психофізиків. Повністю вписується в еліптичні перетворення застосування гіперкомплексних чисел у вигляді кватерніонів (В.А. Максимович і співавт., 2001) для складного модального сприйняття деякої події.

Перейдемо до більш важкої 2-ої частини проблеми – перетворення виникаючих у людини образів – уявлень в матеріальні (фізичні) результати. На перший погляд, здавалося б, це зворотна до психофізичної задача і її рішення можливо шляхом застосування принципу їх симетрії. Проте відповідні численні експериментальні спостереження відкидають такий висновок. Звичайно, образи за своїм змістом незрівнянно складніші за стимули, які застосовували психофізики.

Але справа в іншому. Геометрія психічного простору складніше геометрії Ріманова фізичного простору. Пригадаємо описані вище порушення в психопросторі дзеркальної, «зарядової» симетрій і часу. Невідомо, співпадає чи ні гомотетія в прямому і зворотному напрямі між просторами. Швидше ні, якщо судити, наприклад, по творах абсолютно всіх художників, на відміну від фотографів. Найімовірніше коефіцієнт зворотної гомотетії, та і прямої, і їх відношення (або якийсь їх інший аналог) мають надзвичайно індивідуальну різноманітність і мінливість. Про це, зокрема, можна судити по моделі галюцинацій (В. Максимович, 2003).

Апріорно можна затверджувати, що майже всі характеристики психопростору різноманітні і мінливі, вірогідні по своїй природі. Тому виявлення і затвердження його еліптичності, гіперболічності, параболічності, будь-якого іншого типу ніщо не дає для детермінації відповідних законів збереження. Вони (закони) принципово матимуть форму вірогідності.

Разом з тим, головні властивості психопростору можуть пояснити ряд біо- і психоявищ. Так, метрика еліптичних просторів виходить на вираз


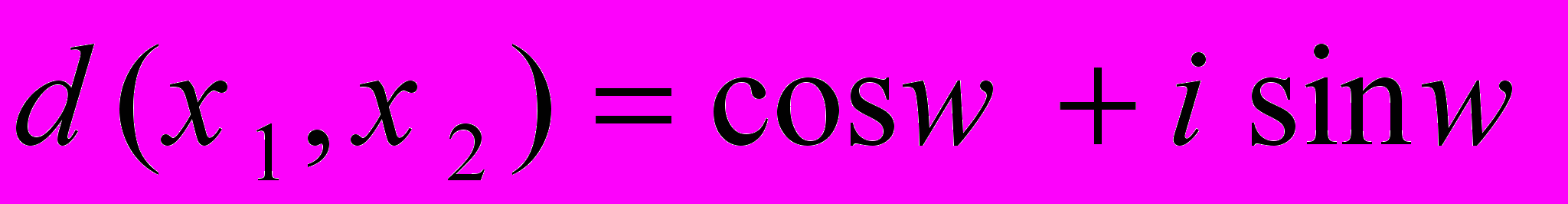(3)


Саме ця внутрішня властивість таких просторів може породжувати всім відомі біоритми. Детермінант – не зовнішнє джерело їх виникнення, а автохарактер об'єкту.

Слід зауважити, що задовго до Б. Рімана математичний зв’язок між уявними змінними та їх ритмічним коливанням був сформульований Леонардом Ейлером у посланнях (1740) до І. Бернуллі та Гольдбаха:


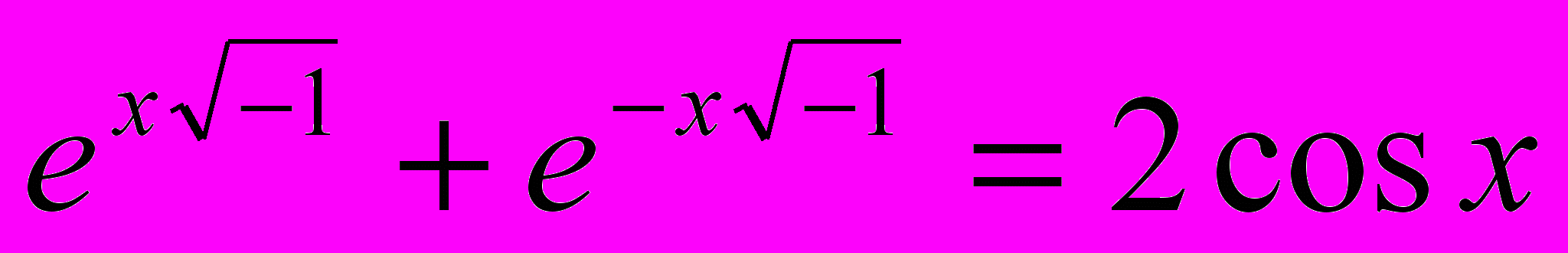(4)


Але на той час цій функціональній залежності ще не могло бути надано сучасного фізико-геометричного, тим паче, психофізіологічного сенсу.

Ще один наслідок, який, на наш погляд, не менш важливий, ніж ритмоґенерація. Ріман доводив, що презентована ним структура простору є багатолистою поверхнею. Стосовно психіки це може пояснити творче мислення, розв’язання проблем. Коли здійснюється пошук вирішення проблеми, тобто, коли відпрацьовані способи рішення традиційних (звичних) задач заводять у глухий кут, то треба перестрибнути на іншу сторінку з іншим способом розв’язування. При невдачі перехід здійснюється знов, або комбінуються сторінки на новий лист. Таким чином, розподіл на листи може відповідати класифікаційному принципу: на кожному з листів міститься група задач з об’єднуючим їх типовим шляхом вирішення.


ВИСНОВКИ

1. Виходячи з вимоги взаємодій фізичного і психічного світів, сприйманому фізичному найбільш відповідає Ріманова геометрія, а психічному – геометрія «за обрієм», в якій фігури містять уявні точки; причому обом обмінникам властива група еліптичних перетворень.
   
2. Координати сприйнятих фізичних об'єктів гомотетично стискаються в психопросторі, в ньому порушуються по окремості Р, С і Т інваріантності (дзеркальна, зарядова і часова симетрія) з відсутністю відомостей про комплексну СРТ-інваріантність.
   
3. Еліптична метрика взаємодіючих просторів може служити поясненням автоґенерації біоритмів, а багатолистна структура – поясненням джерела розв’язання проблем при його пошуку мисленням.
   

ЛІТЕРАТУРА

1. Белкин А.А. Идеомоторная подготовка в спорте. – М.: ФиС., 1983. – 128 с.
   
2. Беспалов Б.И. Действие (Психологические механизмы визуального мышления). – М.: Изд-во Моск. ун-та, 1984. – 192 с.
   
3. Головаха Е.И., Кроник А.А. Психологическое время личности. – К.: Наук. думка, 1984. – 207 с.
   
4. Крылов В.Ю. Геометрическое представление данных в психологических исследованиях. – М.: Наука, 1990. – 119 с.
   
5. Максимович В. Математичне моделювання галюцинацій. – В кн.: Донецький вісник наукового товариства ім. Шевченка. – Донецьк: Східний видавничий дім, 2003. – т. 3. – С.128–136.
   
6. Максимович В., Максимович М. Закон збереження мотивацій. – В кн.: Донецький Вісник наукового товариства ім. Шевченка. т. 5 – Донецьк: Східний видавничий дім, 2004.– С.276–282.
   
7. Максимович В.А., Мухин В.В., Беспалова С.В. Медицинская психофизика. – Донецк: Изд-во Донецкого нац. ун-та, 2001. – 152 с.
   
8. Минаковский В.М. Обобщенные переменные теории переноса. Основы теории и справочные таблицы. – К.: Вища шк., 1978. –184 с.
   
9. Мурач М.М. Геометричні перетворення і симетрія. Природа симетрії і симетрія природи. – К.: Радянська школа, 1987. – 180 с.
   
10. Петухов С.В. Биомеханика, бионика и симметрия. – М.: Наука, 1981. – 240 с.
    
11. Спрингер С., Дейч Г. Левый мозг, правый мозг. Асимметрия мозга: Пер. с англ. – М.: Мир, 1983. – 256 с.
    
12. Цуканов Б.И. Собственная единица времени в психике индивида. – Автореф.…докт. психол. наук. – К.: 1992. – 42 с.
    
13. Чернин А.Д. Физика времени. – М.: Наука. Гл. ред. Физ.-мат. лит., 1987. – 224 с.
    
14. Щербаков Р.Н., Печурин Л.Ф. От проективной геометрии – к неевклидовой (вокруг абсолюта). – М.: Просвещение, 1979. – 158 с.