Geum.ru

Лекция 8 Схемные реализации фал напоминание

Вид материалаЛекция

Содержание


Схемная реализация комбинационного двоичного сумматора.
Микропроцессорная реализация сумматора
Подобный материал:
Лекция 8

Схемные реализации ФАЛ


Напоминание: 1) ИСА (информационная структура алгоритма,) суть граф подстановок композицию функции из базовых функций; 2) ПРФ (примитивно-рекурсивная функция) имеет бесконечный граф подстановок, построенный из повторяющихся фрагментов; 3) процессорная реализация – функции ИСА реализуются либо на единственном универсальном процессоре 1П (однопроцессорное разложение), либо на п процессорах (специализированных или универсальных) – пП-разложение (универсальное), nПс-разложение (специализированное); 4) процессорная реализация имеет т хранящих регистров, где временно хранятся значения рекурсивной функции; 5) количество т регистров может быть минимизировано по теореме А.П. Ершова.

  1. ^ Схемная реализация комбинационного двоичного сумматора.

Пара чисел «а» и «b» представляются двоичными кодами. Двоичные коды имеют п разрядов и упорядочены слева направо. , .
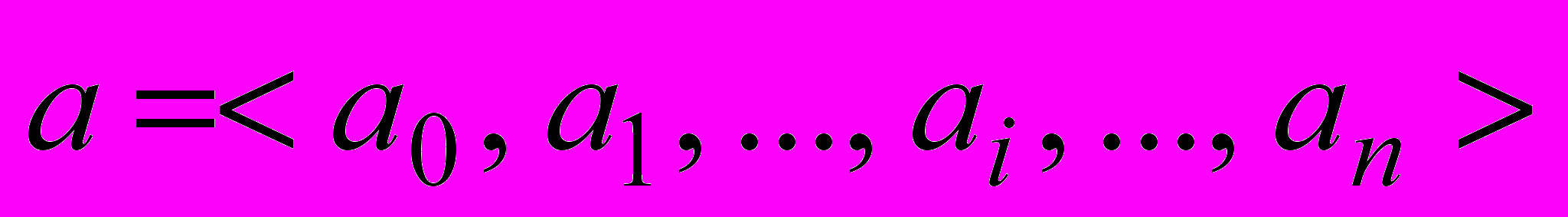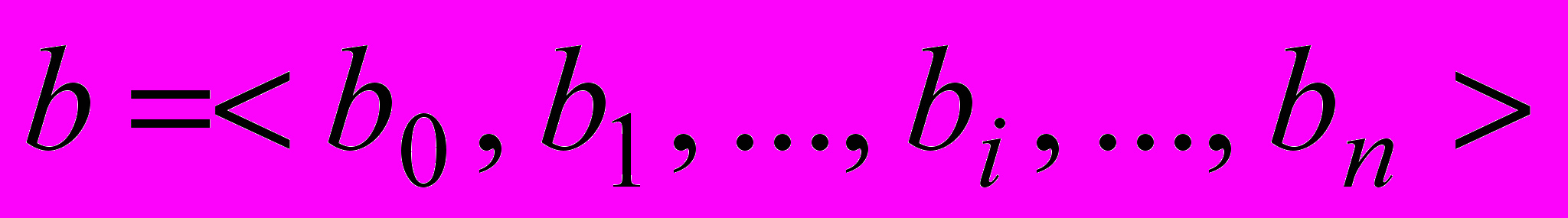
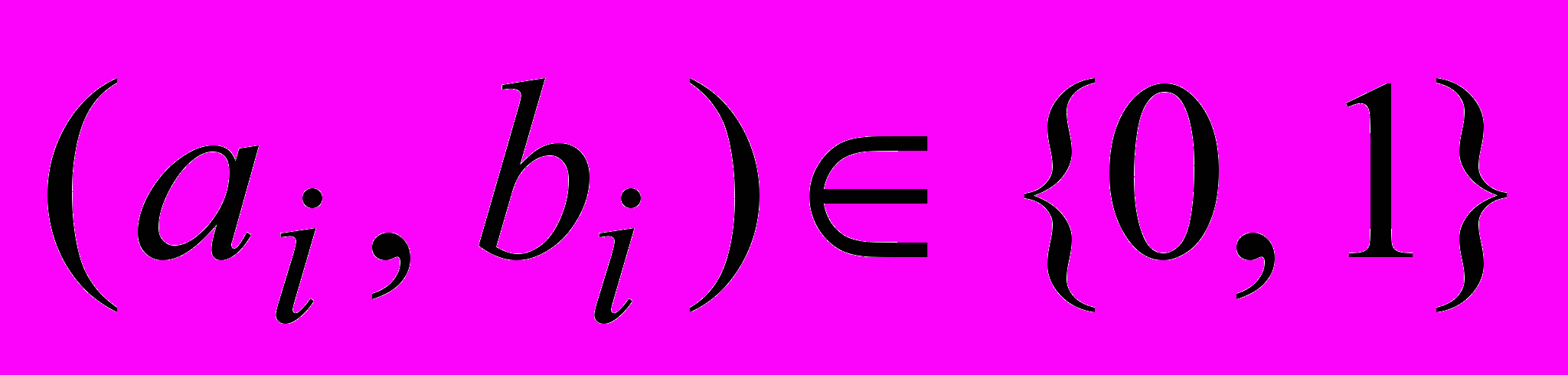  1. Примитивно-рекурсивная функция сумматора на наборе из элементарных функций {, &, }. !Заметим!, что набор не является полным (см. таблицу Поста), в данном случае требование полноты не выдвигается.

Сумматор определяется следующими функциями:



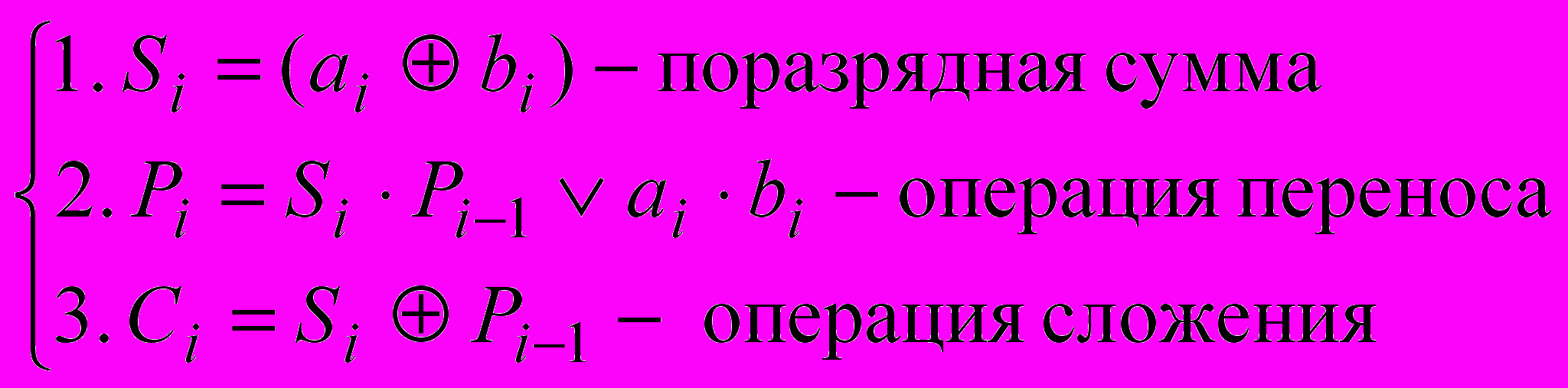
Все операции задаются соответствующими таблицами Si, Ci и Pi.

Таблицы операций поразрядной суммы переноса и сложения задаются исходя из понимания (или необходимости) получения нужных функций. (Fc – функция суммы, Fp – переноса).

Пример построения таблицы и функции Fp переноса Pi.
Pi-1
ai
bi
Pi

0
0
0
0
0

1
0
0
1
0

2
0
1
0
0

3
0
1
1
1

4
1
0
0
0

5
1
0
1
1

6
1
1
0
1

7
1
1
1
1
СДНФ Pi =






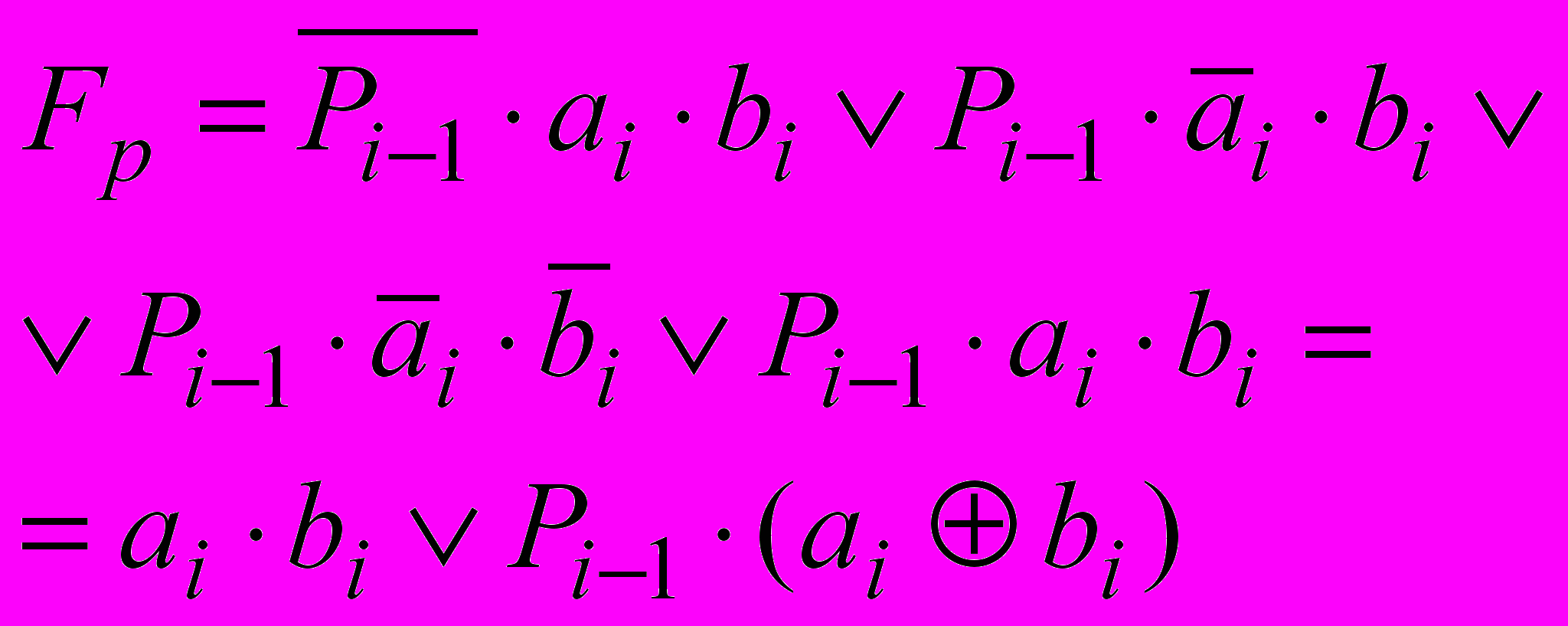
  1. Примитивно-рекурсивная функция сумматора ().

Обозначим . , где параметр рекурсии i = 0, 1, 2, …, п – количество разрядов сумматора

a) ;

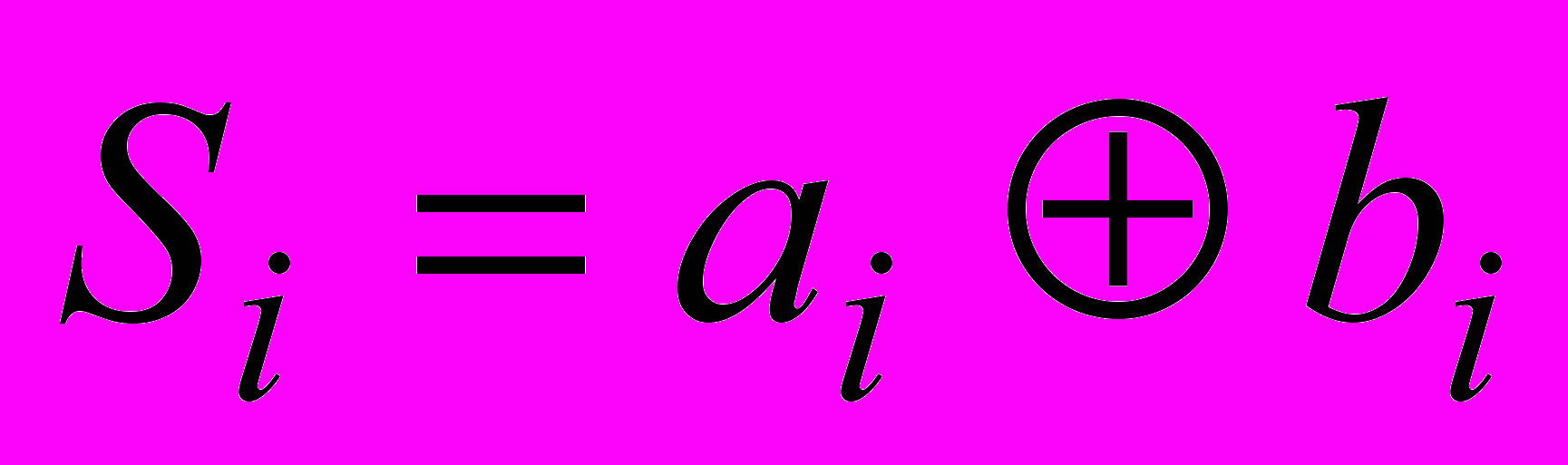б) ;

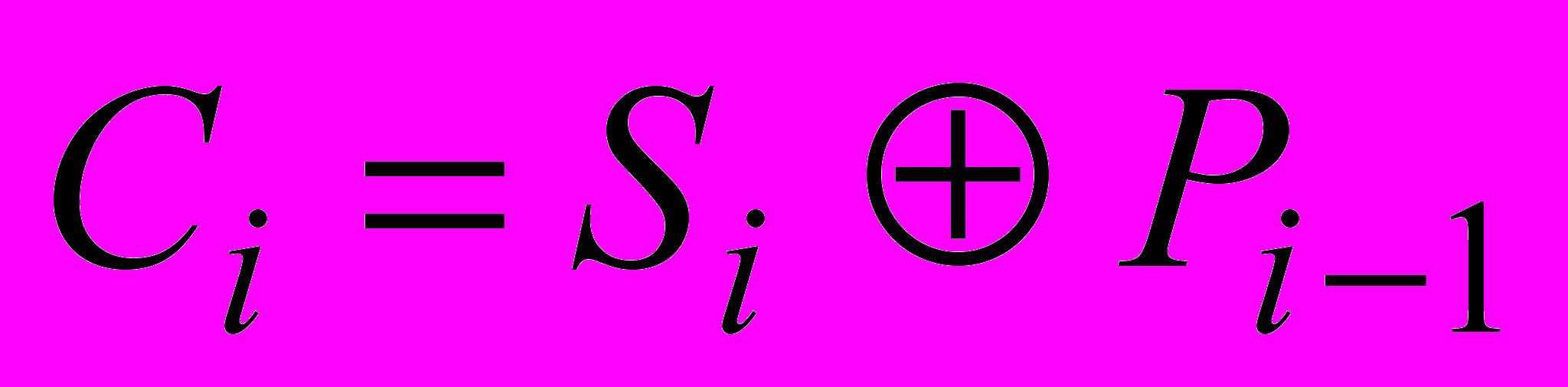
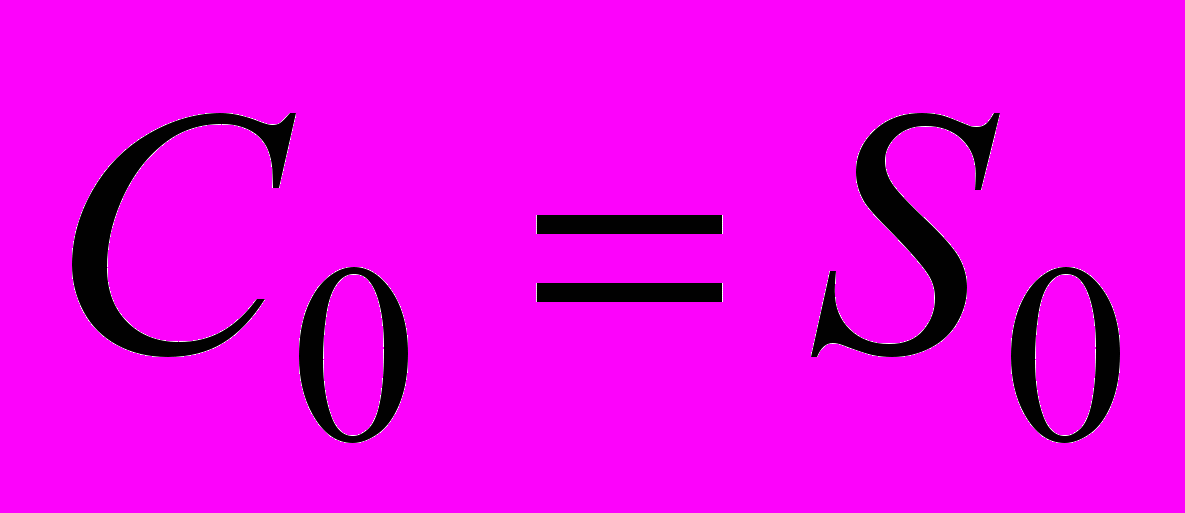в) .

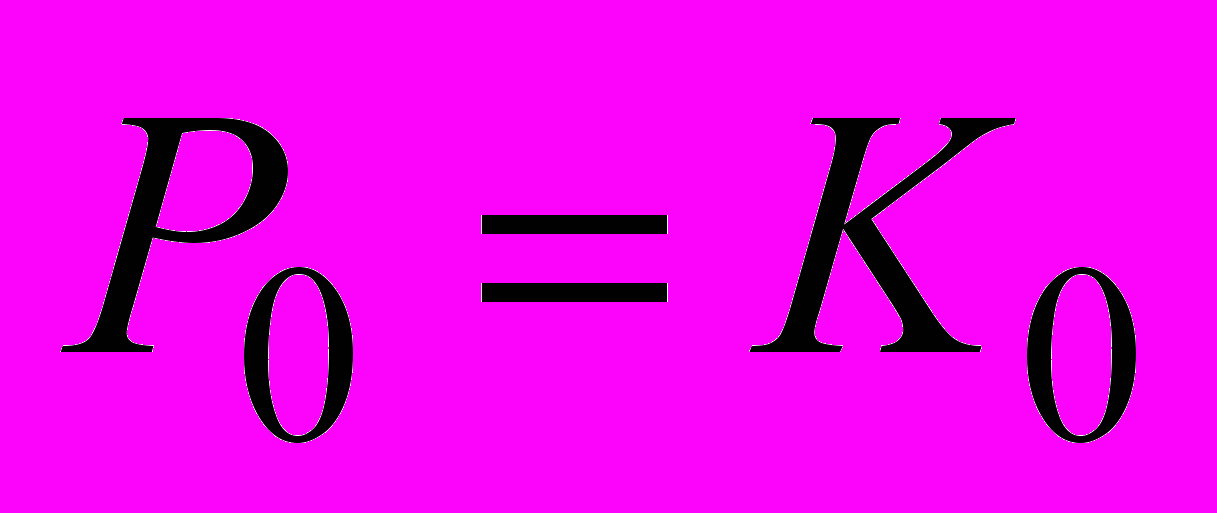  1. Комбинационный сумматор.

ИС i-го разряда в виде ЯПФ.

Комбинационная схема сумматора (1-разрядного)




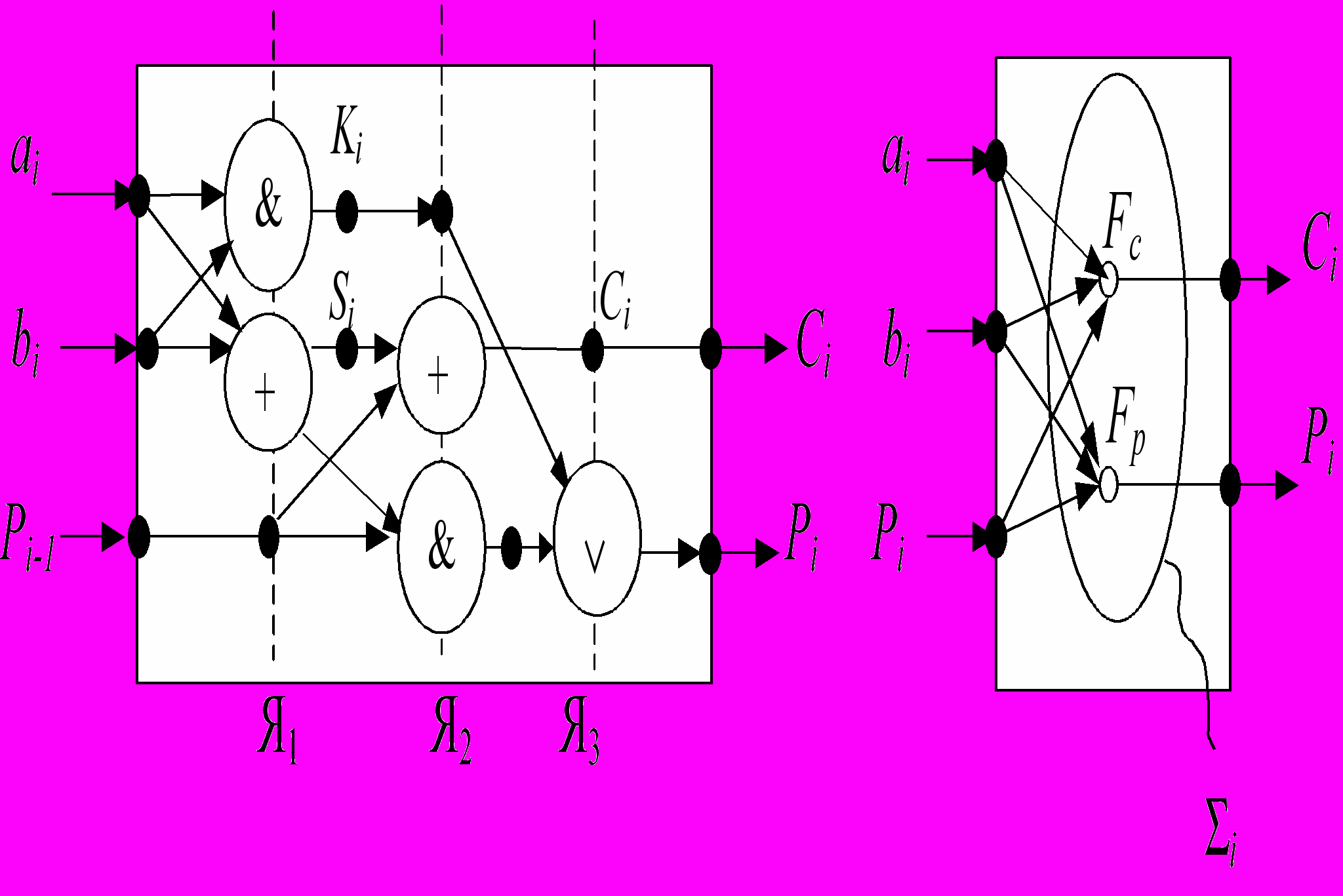
Комбинационная схема n-разрядного сумматора вычисляет сумму в каждом разряде мгновенно «со скоростью света», если одновременно поданы все входные значения <a, b>.



Затраты на оборудование комбинационных схем весьма велики. Для комбинационного п-разрядного сумматора с набором элементарных функций {, &, } число функциональных элементов – 5п, число соединительных проводов – 14п. Но, выполняется суммирование п-разрядных чисел мгновенно, с точностью до физического запаздывания в элементах схемы.
  1. ^ Микропроцессорная реализация сумматора

на трех специальных процессорах.

В данном случае в роли процессоров выступают функциональные элементы П, П, П&, работающие на общее поле памяти.

3П-разложение ИС сумматора представлено на рисунке




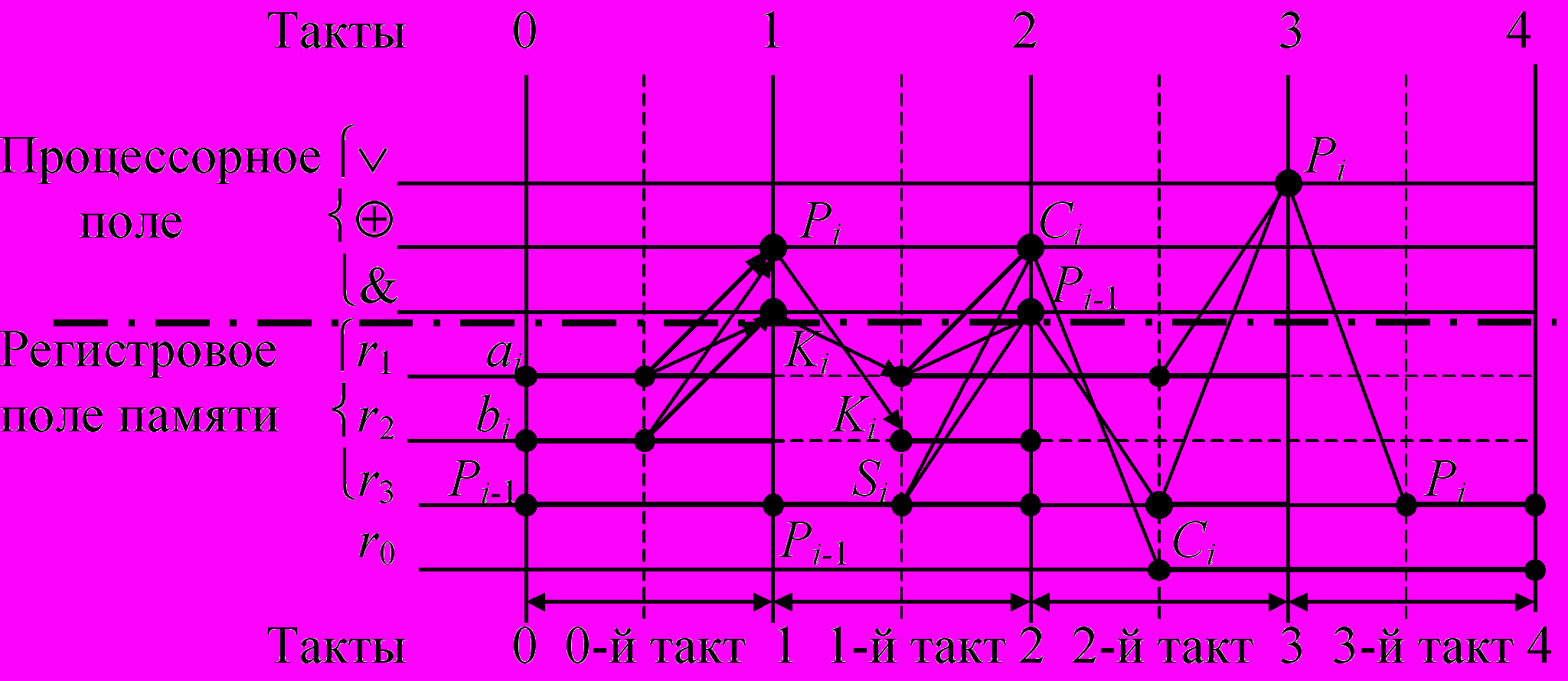
К концу 3-го такта регистр r0 хранит значение Ci, полученное во втором такте, r3 хранит значение Pi, r1 и r2 свободны и могут быть использованы для приема ai+1, bi+1 при вычислении следующих Pi+1 и Ci+1.

Таким образом строится микропроцессор из 3-х функциональных элементов и 4-х регистров, работающий за 4 такта. Заметим, что по теореме Ершова min число регистров для реализации алгоритма – три, а r0 (четвертый регистр – внешний) используется для выдачи суммы Ci во вне.

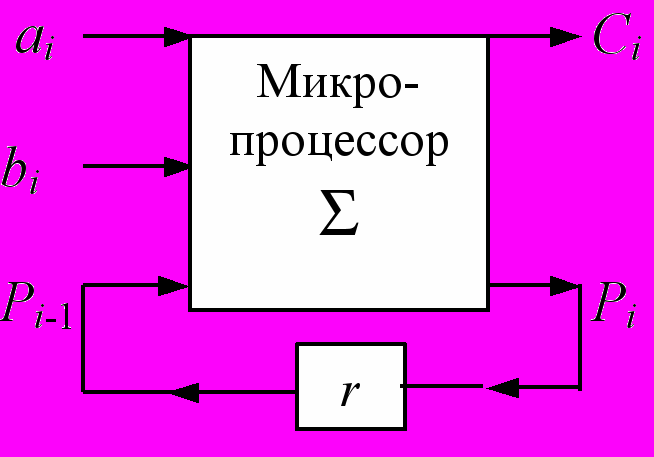Схема микропроцессора пред-

ставляет собой последователь-

ностную машину, где внешний

регистр используется для задерж-

ки Pi на один машинный такт

равный 4 микропроцессорным

тактам).