Geum.ru

Модель "затраты – выпуск"

Вид материалаИсследование

Содержание


E - целевая функция; C
Подобный материал:Модель "затраты – выпуск".

Классической моделью, позволяющей описывать внутреннюю структуру производства (технологии), а так же взаимосвязь ресурсов и готовой продукции, является модель В.В. Леонтьева "затраты – выпуск". В ней ключевыми характеристиками технологий, определяющими зависимости выпуска продукции и затрат производственных ресурсов служат коэффициенты прямых затрат (технологические коэффициенты). Метод анализа модели сводится к решению системы соответствующих линейных уравнений, устанавливающих баланс между используемыми технологиями, выпуском продукции и затратами факторов производства. [[Leontief W. The Structure of American Economy. 1919-1929. Cambridge, Mass., 1941. P. 3.; Леонтьев В. Исследование структуры американской экономики: Теоретический и эмпирический анализ по схеме: затраты-выпуск: Пер.с англ. М.:Госстатиздат. 1958, 639 с.; . Гранберг А.Г., Математические модели социалистической экономики, М.: Экономика, 1978.- 351 с.]

Несмотря на то, что этот метод изначально был разработан для макроуровня, он может так же применяться и на уровне отдельных предприятий. Василий Леонтьев характеризует метод з-в так: "это метод систематической квантификации количественных взаимосвязей между различными секторами сложной экономической системы. С помощью этого метода можно анализировать любую экономическую систему: макросистему - народное хозяйство в целом, мегасистему - мировое хозяйство как совокупность экономических взаимосвязей, промежуточную - региональную экономику отдельных материков, микросистему - экономику отдельного административного штата, области, района, предприятия. Но в любом случае подход в основном один и тот же" [ Леонтьев В.В. Экономические эссе. Теории, исследования, факты и политика: Пер. с англ. -М.: Политиздат, 1990. - 415 с.; Леонтьев В.В. Межотраслевая экономика . Экономика 1997, 361 с.;.].

Модели "затраты – выпуск" относят к моделям структурно-балансового типа. При построении микромодели (модели предприятия) в качестве отраслей рассматриваются технологические блоки экономической системы (предприятия) и моделируются процессы, связанные с движением ресурсов между блоками этой системы. Структура производственного процесса в каждом технологическом блоке представляется определенным вектором структурных коэффициентов, в котором отражается характер количественных связей между затратами и результатами (выпуском продукции данного конкретного блока). Связи представляют собой статистические данные экономики за конкретный период (год или ряд лет) в стоимостном или в натуральном выражении.

С математической точки зрения модель представляет собой систему уравнений, выражающую балансы между затратами и выпуском продукции. Каждое уравнение системы выражает требование баланса между произведенным количеством продукции и совокупной потребностью в этой продукции в каждом блоке предприятия

Иными словами, балансовые соотношения (система уравнений) отражают «приход» и «расход» каждой компоненты материально-вещественных потоков в блоках, описывающих предприятие. .[ Гранберг А.Г., Математические модели социалистической экономики, М.: Экономика, 1978.- 351 с.].

Под исходными данными понимается планируемый объем реализации продукции, а под выходными, — четко сбалансированная структура всего комплекса затрат, необходимых для того, чтобы этот объем продукции произвести. Параметрами (ключевыми характеристиками) модели являются коэффициенты затрат на производство продукции. Решение системы уравнений позволяет определить, какими должны быть выпуск и затраты в каждой отрасли, чтобы обеспечить производство конечного продукта заданного объема и структуры.

Модели «затраты-выпуск» служат двум целям: статистической и аналитической [Гранберг А.Г. Математические модели социалистической экономики. – М.: Экономика, 1978. – 351 с. ]. Они обеспечивают детальный анализ процесса производства и использования товаров и услуг, а также доходов, образующихся в результате такого производства, и создают основу для проверки согласованности статистических данных. Аналитическая функция состоит в том, что они позволяют моделировать экономическую ситуацию на основе коэффициентов прямых и полных затрат.

В классическом виде модель межотраслевого баланса «затраты-выпуск» имеет вид:

или , .

где – вектор-столбец валовых выпусков, – вектор-столбец конечной продукции, – матрица коэффициентов прямых затрат, – единичная матрица.

При необходимости модель может быть дополнена различными ограничениями, позволяющими уточнить описание условий функционирования предприятия.

На базе модели з-в выделяют такие типовые задачи прогнозирования: [Белозеров В. К., аспирант Вологодский научно-координационный центр ЦЭМИ РАН.]

- Определение сбалансированных выпусков продукции, обеспечивающих задаваемые варианты конечного спроса.

- Определение объемов конечного спроса исходя из заданных выпусков.

- Расчеты сбалансированных объемов выпуска и конечного спроса со смешанным составом неизвестных.

- Проведение структурного анализа взаимосвязей выпусков, производственных ресурсов и конечного спроса

- Модель межотраслевых зависимостей цен и добавленной стоимости

- Межотраслевые зависимости конечного спроса и добавленной стоимости.

Развитием статической межотраслевой модели являются динамические модели "затраты – выпуск". Они позволяют отражать взаимосвязи между блоками экономической системы на каждом интервале времени. При этом из состава конечной продукции выделяются производственные капитальные вложения, исследуется их структура и влияние на рост объёма производства.

В основе построения модели в виде динамической системы уравнений лежит математическая зависимость между величиной капитальных вложений и приростом продукции. Решение системы, как и в случае статической модели, приводит к определению уровней производства, но в динамическом варианте в отличие от статистического эти искомые уровни зависят от объёмов производства в предшествующих периодах.

Таким образом, решение динамической системы линейных уравнений позволяет определить выпуск продукции в последующем периоде в зависимости от уровня, достигнутого в предыдущем периоде. Связь между периодами устанавливается через коэффициенты вложений, характеризующие фондоёмкость единицы прироста продукции.

В отличие от уравнений статической модели «з-в», где конечный продукт каждой отрасли представлен одним слагаемым, здесь он распадается на два — фонд накопления и фонд непроизводственного потребления. Модель показывает, что для управления процессом решающее значение имеет соотношение между фондом накопления и фондом потребления конечной продукции.

Экономистами разрабатываются разные типы динамических моделей затраты-выпуск, примерами таких моделей могут быть:

- модели с обратной рекурсией, в которых балансы производства и распределения продукции за последний год планового периода сочетаются с уравнениями потребности в капитальных вложениях за весь плановый период.

- модели поэтапного расчета объемов производства продукции и капитальных вложений для каждого года планового периода.

- модели с явным учетом лага капитальных вложений, в которых показана прямая и обратная их связь во времени с показателями производства продукции и д.р.

Модели, которые не только описывают взаимосвязи параметров внутреннего состояния производственной системы, но и дают возможность находить оптимальные варианты функционирования предприятия, образуют класс оптимизационных моделей производства [Волков, В.Н. Информационные технологии и моделирование в организационном проектировании [Текст] / Информационные технологии и математическое моделирование: Материалы III Всероссийской научно-практической конференции (11-12 декабря 2004г.). Т1. - Томск: изд-во Том. ун-та, 2004. - 188с. - С.54-56.]. Оптимизационные модели предполагают построение целевой функции, задание критерия оптимальности (экстремума целевой функции, например, максимума прибыли, минимума затрат и т.п.) и ограничений, описывающих важнейшие условия функционирования и взаимосвязи параметров предприятия. В зависимости от вида функций, участвующих в формировании цели и ограничений, различают линейные и нелинейные, целочисленные и смешанные модели [4].

С учетом того, что эффективные методы решения задач математического программирования имеются лишь для статических задач линейного и выпуклого программирования, соответствующие модели функционирования предприятий, как правило, являются весьма упрощенными и обычно применяются для решения частных вопросов, таких, например, как оптимальное распределение ресурсов и/или использования производственных мощностей, оптимальный выбор технологических спо­собов производства заданного ассортимента продукции, определение оптимальной производственной программы и т.п. [[Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Введение в экономическую кибернетику: Учебное пособие - М.: «Экономика», 1975. – 343 с.]Вагнер, исследоване операций].

Структура оптимизационной модели состоит из переменных (управляемых и неуправляемых), соотношений, описывающих важнейшие условия функционирования объекта, (системы ограничений) и целевой функции. В общем виде оптимизационная модель выглядит следующим образом

Целевая функция:



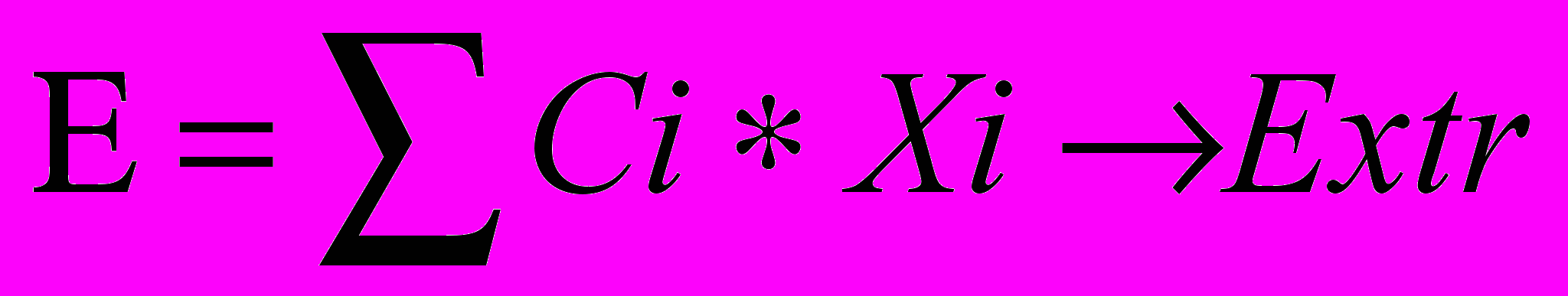
при следующих ограничениях:



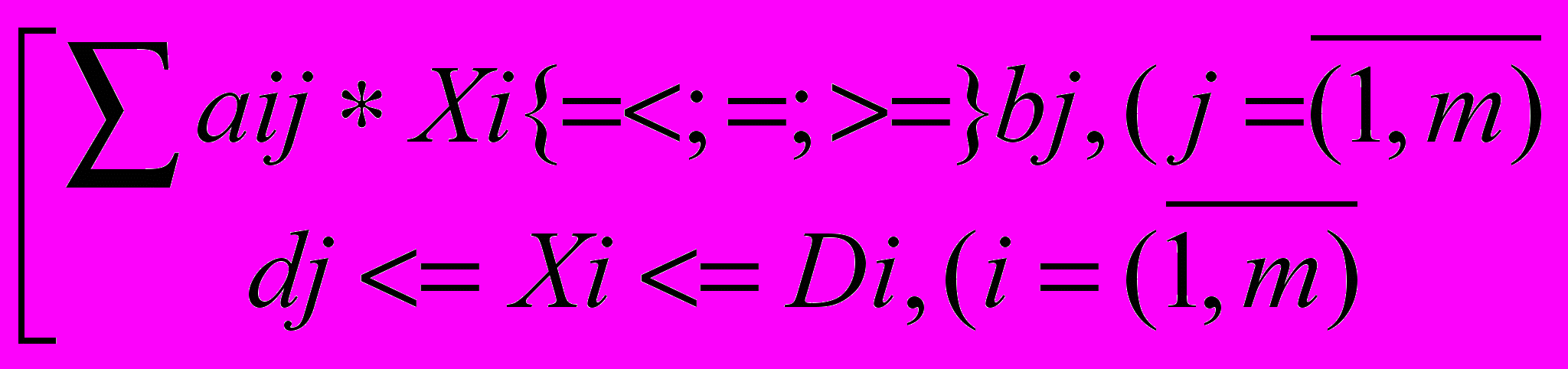
(где: E - целевая функция; Ci- коэффициенты при переменных в целевой функ­ции; Xi- переменные задачи; bj- правые части ограничений; аij- коэффициенты при переменных в ограничениях; di- минимально возможные значения переменных; Di- максимально возможные значения переменных).

Исходными данными для таких моделей являются основные показатели, описывающие функционирование предприятия: объемы ресурсов, производственные мощности и т.д. В качестве коэффициентов при переменных в целевой функции могут выступать нормативные коэффициенты показателей качества работы предприятия, например прибыль, затраты и т.д.

Зависимость межу переменными в целевой функции и ограничения может носить как линейный, так и нелинейный характер.

Соответственно различают линейные и нелинейные оптимизационные модели.

Наибольшее распространение в практике управления экономическими объектами имеют линейные оптимизационные модели. Математическая постановка задачи линейной оптимизации хорошо изучена и не представляет научных проблем. Основанием этому служат два основных момента.

Во-первых, аппарат линейных функций удобен и прост для понимания. Канторович в своей Нобелевской речи говорил, что несмотря на универсальность и хорошую точность, модель линейного программирования использует весьма элементарный инструментарий линейной алгебры и понимание и овладение ею дает возможность творческого, а не шаблонного использования предлагаемых моделью средств анализа. Во-вторых, для линейных моделей разработаны высокоэффективные методы нахождения оптимальных значений переменных.

Наиболее распространенной моделью является классическая линейная модель производства, которая позволяет представить взаимозаменяемость и комбинирование фиксированных технологических способов, считающихся основными, в некоторых пределах, обозначенных ресурсами и плановыми ограничениями. Здесь каждый технологический способ (в том числе эффективный) может быть представлен в виде линейной комбинации с положительными коэффициентами так называемых базисных производственных способов

Основное применение линейные оптимизационные модели получили при построении следующих основных классов задач: формирование производственной программы; распределение ресурсов; управление запасами; задача ремонта и замены оборудования и т.п.. Применение линейных оптимизационных методов в экономике и построенные на их базе модели предприятий и модели планирования производства широко описаны и расклассифицированы в литературе (см., например, [19] [10. Португал В. М., Семенов А. И. Модели планирования на предприятии.— М.: Наука, 1978.— 272с.; Первин Ю. А., Португал В. М., Семенов А. И. Планирование мел­косерийного производства в АСУП. М., «Наука, 1973. 22. Португал В. М., Марголин А. Л. Автоматизация оперативного уп­равления машиностроительным предприятием. М., «Статистика», 1976.;Багриновский К.А. Экономико-математические методы и модели (микроэкономика): учеб. пособие / К.А. Багриновский, В.М. Матюшок. – Изд. 2-е перераб. и доп. – М.: Изд-во РУДН, 2006. – 220 с.:],

Критерий решения задачи и управляющие переменные позволяют по-разному моделировать производство (составлять разные модели на базе одного и того же предприятия). Но, однако, чем детальнее описание предприятия, тем сложнее постановка задачи. Соответственно, тем сложнее модель и методы ее решения.

Кроме того, линейные оптимизационные модели искажают описание самого предприятия. Это связано с тем, что ограничения модели позволяют выделять лишь отдельные стороны сложной системы, которой является предприятие, а процессы, происходящие на предприятии, к тому же, далеко не всегда имеют линейный характер. Это приводит к вынужденному упрощению действительности и, соответственно полученные рекомендации по поводу оптимальных управляющих решений на деле могут оказаться неточными (достоверность полученных из модели выводов может быть подвержена сомнению).

Если в ходе производственного процесса становятся возможными значительные изменения интенсивностей технологических способов, то предположение о пропорциональности затрат ресурсов и результатов хозяйственной деятельности является, вообще говоря, неверным. Тем самым нарушается одна из важнейших предпосылок построения линейной модели и становится необходимым использовать более сложные, нелинейные оптимизационные модели производства. Наиболее естественным обобщением таких моделей является выпуклая модель производства [Данилов Н.Н. "Курс математической экономики" Высшая школа, 2006. - 407 стр.]. В ней множество  допустимых интенсивностей производства описано при помощи вогнутых функций, а для выбора наилучшего решения задается выпуклая вверх функция аргументов, которая обычно имеет смысл выпуска товарной продукции.

В оптимизационных задачах отдельно можно выделить модели календарного планирования.

Критерии оптимальности в этих задачах - минимизация затрат времени на выполнение всех работ, минимизация общего запаздывания, выполнение работ против норматива, минимизация потерь от запаздывания и т.п. [19 Португал с. стр 26]. К ним относятся модели планировании загрузки участка однотипных взаимозамещаемых станков, модели задачи теории расписаний, модели задач трех станков и д.р. В постановке этих задач обычно отсутствует такой фактор, как технология изготовления изделий, поэтому задача приво­дится к относительно нетрудоемким вычислительным схемам линейного программирования.

Преимущественно они решают задачи частного характера и разрабатываются для организации производства на каждом участке предприятия.


Вывод:

В отличие от описательных (дескриптивных) моделей, которые отражают структуру и динамику того или иного процесса нижнего уровня экономики, и имитационных задач, которые дают возможность «наблюдать» поведение исследуемой системы во времени и анализировать полученные результаты, оптимизационные задачи позволяют находить оптимальное управляющее воздействие на систему, т.е. наилучшее по сравнению со всеми другими возможными способами управления и предписывающие объекту его будущее развитие.