Е. Б. Замятина Распределенные системы и алгоритмы Курс лекций

Вид материала

Курс лекций

Содержание Лекция 6. Моделирование распределенных систем. Язык Triad Str), алгоритмов (Rout

Подобный материал:

• Века. Вопросы к семинарам и диспутам. Часть вторая е. И. Замятин. Роман-антиутопия, 78.14kb.
• С. В. Лапина Социология Курс лекций, 2085.17kb.
• Е. В. Беляева Этика Курс лекций, 693.52kb.
• С. В. Лапина Культурология Курс лекций, 3263kb.
• О. В. Свидерская Основы энергосбережения Курс лекций, 2953.76kb.
• С. М. Забелов > П. С. Забелов Административное право Курс лекций, 3268.19kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.17kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.24kb.
• Курс лекций для студентов заочного факультета самара, 1339.16kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.

Лекция 6. Моделирование распределенных систем. Язык Triad

Исследование распределенных систем – трудная задача. Прежде всего, распределенная система должна быть описана, т.е. должна быть построена модель системы. Для этой цели можно использовать различные языки: Unified Modeling Language (UML), Very large scale Hardware Description Language (VHDL) и др. Здесь мы рассмотрим средства языка Triad.

Распределенная система характеризуется распределенной структурой, т.е. набором дискретных (отделенных друг от друга) элементов или подсистем и связями между этими элементами. В соответствии с распределением элементов распределены и функции (алгоритмы работы) системы. Распределенные элементы обмениваются сообщениями (сигналами), также распределенными в пространстве.

Язык Triad предполагает самостоятельное описание структуры ( Str), алгоритмов (Rout) и сообщений (Mes). Эти описания называются слоями.

Основным слоем является слой структуры, именно он отражает распределение и связи элементов. Описание структуры основывается на теоретико-графовых средствах. Структура системы System, изображенной на рис. 1, описывается в Triad формулой

star(Server, Node[1..n]),

что означает с точки зрения теории графов структуру, представленную графом-звездой (star) с центральной вершиной Server и периферийными вершинами Node[i], нумеруемыми от 1 до n.

Структура распределенной системы, изображенной на рис. 2, описывается в Triad формулой

star(Server, Serv[a..c]) + star(Serv[a], Node[1..k]) + star(Serv[b], Node[k+1..m]) + star(Serv[c], Node[m+1..n]),

что означает с точки зрения теории графов структуру, представленную объединением (+) четырех графов-звезд. Первая звезда имеет центральную вершину Server и три периферийных вершин Serv[j], где j – переменная типа перечисления с множеством значений (a, b, c). Вершины Serv[j], в свою очередь, являются центрами трех звезд, содержащих периферийные вершины Node[1..k], Node[k+1..m] и Node[m+1..n].

Этой формуле должно быть придано необходимое языковое оформление для того, чтобы она стала описанием модели системы. Полное описание имеет вид


model System2 (k, m, n: integer) def

System2 := star(Server, Serv[a..c]) + star(Serv[a], Node[1..k]) + star(Serv[b], Node[k+1..m]) + star(Serv[c], Node[m+1..n])

enddef.


Оно задает модели имя (System2) и определяет, что модель зависит от трех целочисленных параметров k, m, n. Таким образом, эта запись определяет целое семейство однородных моделей. В частности, изображенная на рис. 2 модель может быть определена как System2 (8, 17, 28).

Заметим, что в этом описании пока нет никакой информации о том, как функционируют центральные и периферийные узлы системы.

Описание алгоритмов функционирования является предметом второго слоя, слоя рутин (routine). В этом слое, в свою очередь, нет описания связей между узлами, т.е. описания структуры.

Рутина должна быть задана для каждого узла системы (вершины графа). Если все периферийные узлы функционируют подобным друг другу образом, то для них достаточно описать только одну рутину, прикрепив ее экземпляры к каждой вершине (в Triad используется термин наложение рутины на вершину).

При описании работы узлов системы важно не только, что происходит, но и когда это происходит. Поэтому описание рутин является событийно-ориентированным. Описание рутины состоит из одной или нескольких секций описания событий (event). Считается, что все действия, описанные в событийной секции, выполняются мгновенно. При этом отдельные события состоят в причинно-следственной связи. Одно событие может повлечь за собой (через некоторое время) другое событие (в Triad используется термин планирование события e_j событием e_i).

Если в системе два узла связаны между собой, то возможно, что событие в первом узле повлечет за собой событие во втором узле. Исходя из раздельного описания слоев структуры и рутин, нельзя описать связь этих событий непосредственно с помощью оператора планирования (schedule). Вместо этого вводится понятие входного события, которое должно происходить в рутине при поступлении любого сообщения в вершину, на которую наложена эта рутина. Входное событие также описывается отдельной секцией рутины.

Рутина может инициировать входные события в других рутинах путем исполнения оператора out.

Простейшая рутина узла может выглядеть так:

routine Generator

initial

schedule (Repeat, 0.0)

endi

event Repeat;

out; schedule (Repeat, 2.4)

ende

endrout.

Здесь Generator – имя рутины, Repeat – имя события, 2.4 – интервал между событиями.

Часть initial определяет начальные условия (в том числе, начальные действия). В данном тексте – это планирование события Repeat через 0.0 единиц времени, т.е. в момент старта процесса имитационного моделирования.

В момент совершения события Repeat рутина выдает выходное сообщение, которое при наличии структуры попадет в рутины смежных вершин, став для них входным сообщением. В данном тексте никакого «значения» сообщения в операторе out нет. Оно может быть определено позже, в слое сообщений. Оно может остаться и неопределенным: иногда важен сам факт получения сообщения, а не его значение, или оно может быть ясно по умолчанию.

В этот же момент вновь планируется событие Repeat через 2.4 единицы времени.

Таким образом, рутина Generator будет, начиная с момента времени 0.0, регулярно через 2.4 единицы времени выдавать сообщения. Этот процесс неограничен и прекратится только с окончанием сеанса моделирования.

Можно задать семейство рутин, зависящих от параметра T:

routine Generator (real T)

initial

schedule (Repeat, 0.0)

endi

event Repeat;

out; schedule (Repeat, T)

ende

endrout.

Параметров может быть несколько, все они передаются по значению в момент создания экземпляра рутины и предназначены для «настройки» конкретного экземпляра.

В данном примере нет входного события, т.е. узел с рутиной Generator не реагирует ни на какие приходящие к нему сообщения. В более сложных случаях входное событие в рутине может присутствовать.

По правилам языка Triad входное событие в рутине может быть только одно. Оно не имеет имени и не может планироваться внутри данной рутины.

Следующий пример управляемого генератора ControlledGenerator показывает использование входного события.

routine ControlledGenerator (real T)

initial

Boolean Run;

Run := false

endi

event;

if Run then Run := false else begin Run := true; schedule(Repeat, 0.0) end

ende


event Repeat;

out; if Run then schedule (Repeat, T)

ende

endrout.

Событие Repeat планирует свое повторение только в том случае, если переменная Run имеет значение «истина» (true). Первоначально (в части initial) значение этой переменной установлено как «ложь» (false). Поэтому генератор не работает.

При получении сообщения (не важно какого) срабатывает входное событие, переключающее значение Run на «истину» и планирующее немедленно событие Repeat. Генератор начинает работать.

При поступлении следующего сообщения (опять не важно какого) вновь срабатывает входное событие. Но сейчас значение Run уже «истина» и тогда оно меняется на противоположное. Генератор прекращает работу. Третье сообщение вновь включает генератор, четвертое – вновь выключает и т.д.

Как видно из приведенных примеров, значения сообщений иногда не нужны, а, следовательно, можно обойтись без описания слоя сообщений. В других случаях достаточно предопределенных типов данных (integer, real, Boolean). Специального описания слоя сообщений также не требуется.

В сложных случаях моделирования при построении многоуровневых иерархических моделей требуется и построение структурных типов сообщений. Не останавливаясь здесь на этом, отметим, что оно производится подобно тому, как это делается в универсальных языках программирования (за исключением синтаксиса).

После описания структуры и рутин необходимо произвести наложение рутин на вершины графа, описывающего структуру. Делается это специальными операторами наложения, имеющими вид

routine(Node[i]) := Generator.

В нашем примере можно произвести наложение одной и той же рутины на все периферийные узлы:

for i:= 1 to n do

routine(System2.Node[i]) := Generator

endf.

При этом создается n экземпляров рутины Generator. Для каждого экземпляра рутины создается свой комплект локальных переменных. Программный код дублировать не обязательно. Дублирование программного кода может быть целесообразным в том случае, когда моделирование распределенной системы производится также в распределенном режиме. В том случае, если имитационная модель распределена по компьютерам кластера или в Grid, для балансировки нагрузки желательно сгенерировать несколько экземпляров программного кода, физически располагающихся на разных узлах кластера.

Важной особенностью языка Triad является возможность выполнения операций над моделями систем и, следовательно, возможность разработки алгоритмов, как исследования, так и синтеза моделей.

Одна из операций над структурой модели продемонстрирована, в частности, выше при описании структуры System2. Там использована операция «+» объединения графов. Могут использоваться операции добавления и удаления вершин, добавления и удаления ребер (ненаправленных связей между вершинами), добавления и удаления дуг (направленных связей между вершинами).

Например, соединение всех периферийных узлов модели System в кольцо осуществляется следующими операторами

for i:= 1 to n – 1 do

System := System + (System.Node[i]  System.Node[i + 1])

endf;

System := System + (System.Node[n]  System.Node[1])

В цикле к системе добавляются ребра между первым и вторым узлами, между вторым и третьим узлами, …, между предпоследним и последним узлами. Затем добавляется ребро между последним и первым узлами.

Точно такого же результата можно добиться более короткой записью:

System := System + cycle(Node[1..n]).

Здесь cycle – графовая константа (простой цикл). После выполнения операции получается объединение звезды с простым циклом.

Возможны операции и над рутинами. Поскольку рутина представляет собой множество событий (событийных секций), в которых производится планирование других событий из этого же множества, рутина может быть представлена графом. В этом графе вершины – события, а дуги – операторы планирования событий.

Следовательно, добавление и удаление событий – добавление и удаление вершин; введение и исключение планирования – добавление и удаление дуг. Поэтому, система операций над структурами (графами) пригодна и для обозначения операций над рутинами. Например, удаление события можно записать так:

ControlledGenerator := ControlledGenerator – Repeat;

При удалении события автоматически удаляются и все операторы планирования (schedule (Repeat, )), связанные с этим событием. Это, опять же, подобно тому, что происходит в графе при удалении вершины: удаляются все входящие в эту вершину дуги и все исходящие из этой вершины дуги.

На рисунке 9 графически изображена связь между событиями e_i некоторой рутины. Около дуг, соответствующих операторам указано значение – второй параметр оператора, задающий период времени, через который должно произойти планируемое событие.

На рисунке 10 изображена та же рутина после удаления из нее события e₂ .




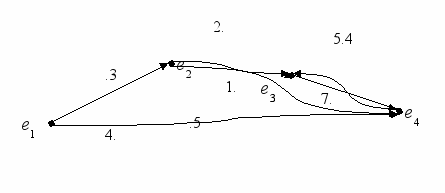
Рис. 9




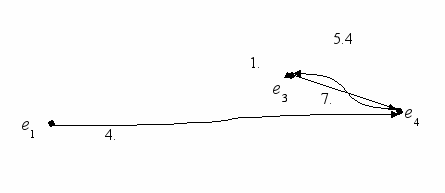
Рис. 10