Прикладная математика
| Вид материала | Лекция |
- «Математика. Прикладная математика», 366.03kb.
- Рабочая программа, 182.62kb.
- Рабочая программа, 160.99kb.
- Программа дисциплины Современная прикладная алгебра для направления 010500 Прикладная, 214.78kb.
- Цифровая обработка сигналов, 137.86kb.
- Проект постановление ученого совета сгту по вопросу: «О переименовании кафедры «Прикладная, 8.11kb.
- Программа вступительного экзамена по математике подготовки магистров по направлению, 86.94kb.
- «Прикладная математика и информатика», 3781.56kb.
- Рабочая программа дисциплины прикладная математика (Наименование дисциплины), 188.06kb.
- Программа вступительного экзамена вмагистратуру по направлению 010400 "прикладная, 204.27kb.
Прикладная математика
Лекция 2
Тригонометрия
Тригонометрические функции углов прямоугольных треугольников. Радианная мера угла. Определение тригонометрических функций произвольного аргумента. Основное тригонометрическое тождество. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы понижения степени. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Простейшие тригонометрические уравнения (
, 
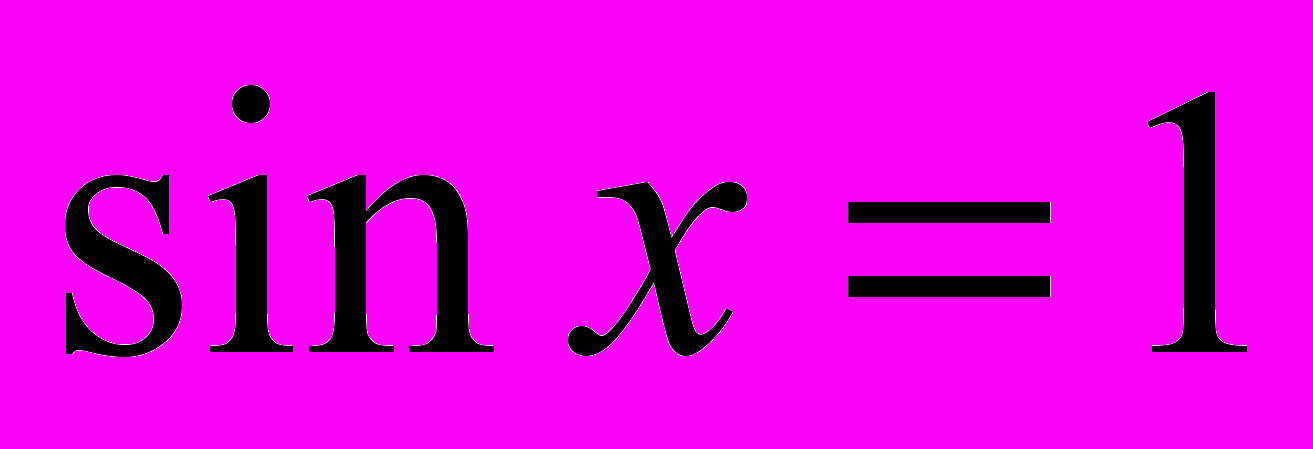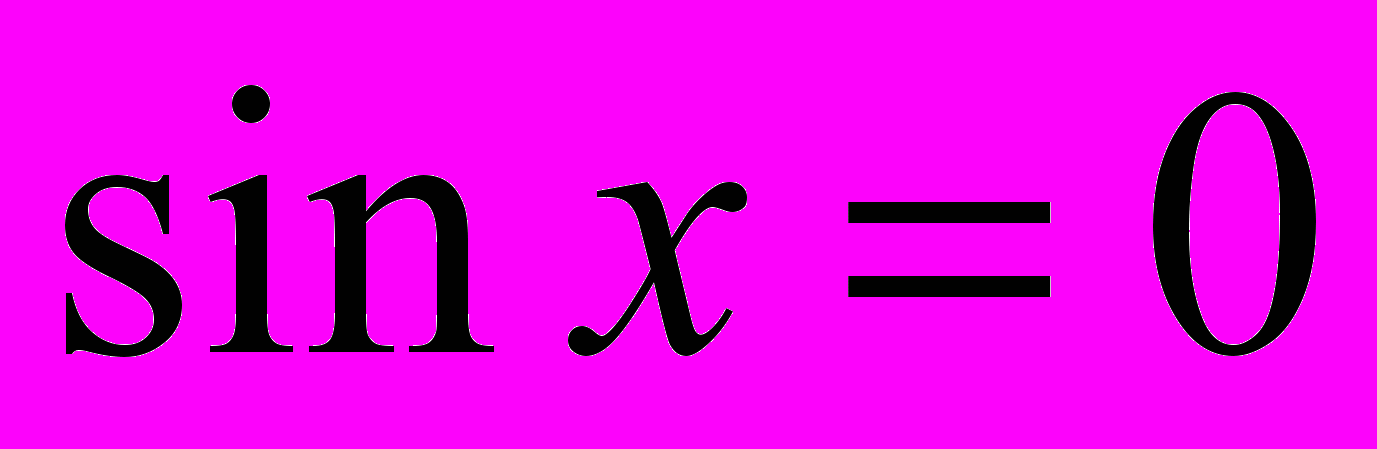и т.п.). §1. Тригонометрические функции углов прямоугольных треугольников. Основные соотношения между ними
 |
| Рис. 1. |
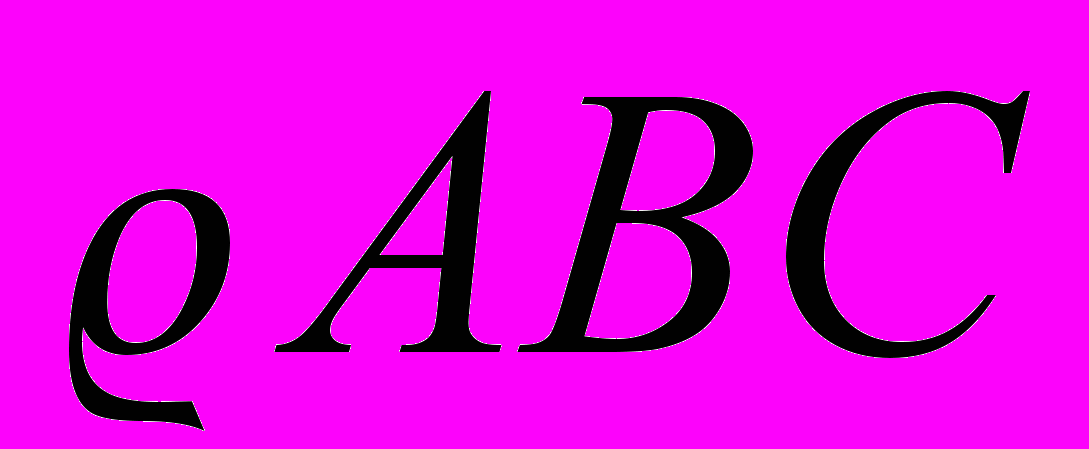(рис. 1).Синусом угла
в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе: 
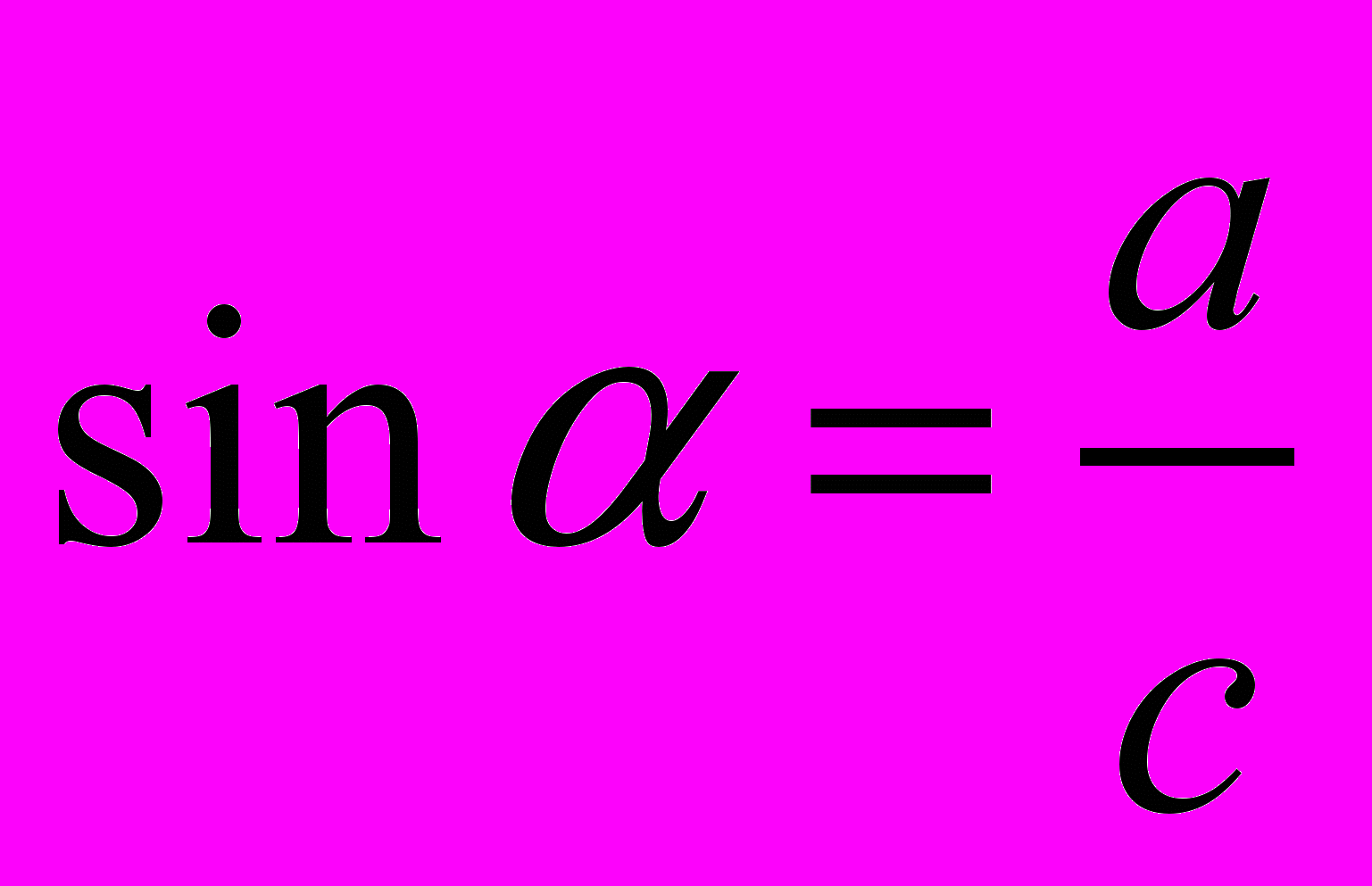.Косинусом угла
называется отношение прилежащего катета к гипотенузе: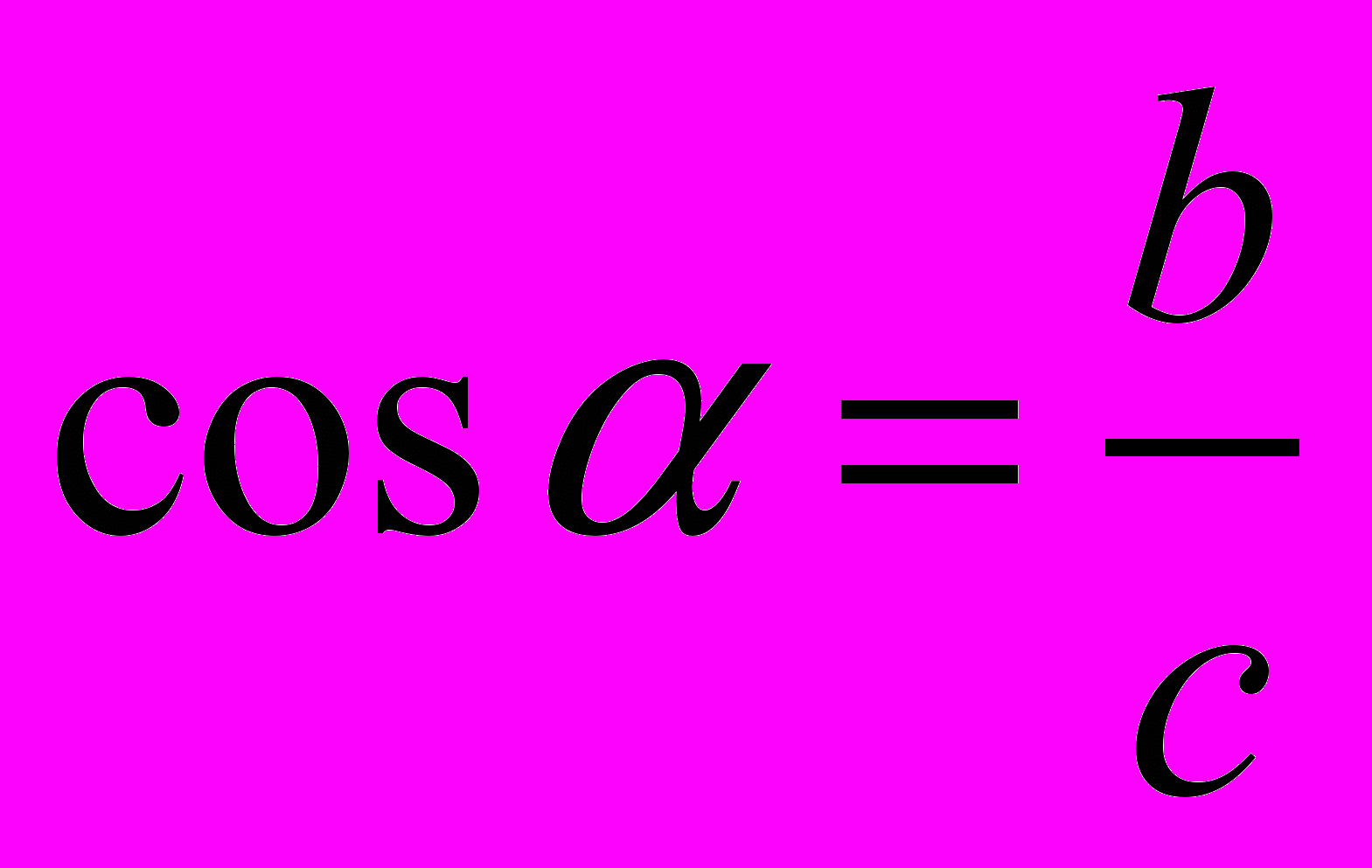
.Тангенсом угла
называется отношение противолежащего катета к прилежащему: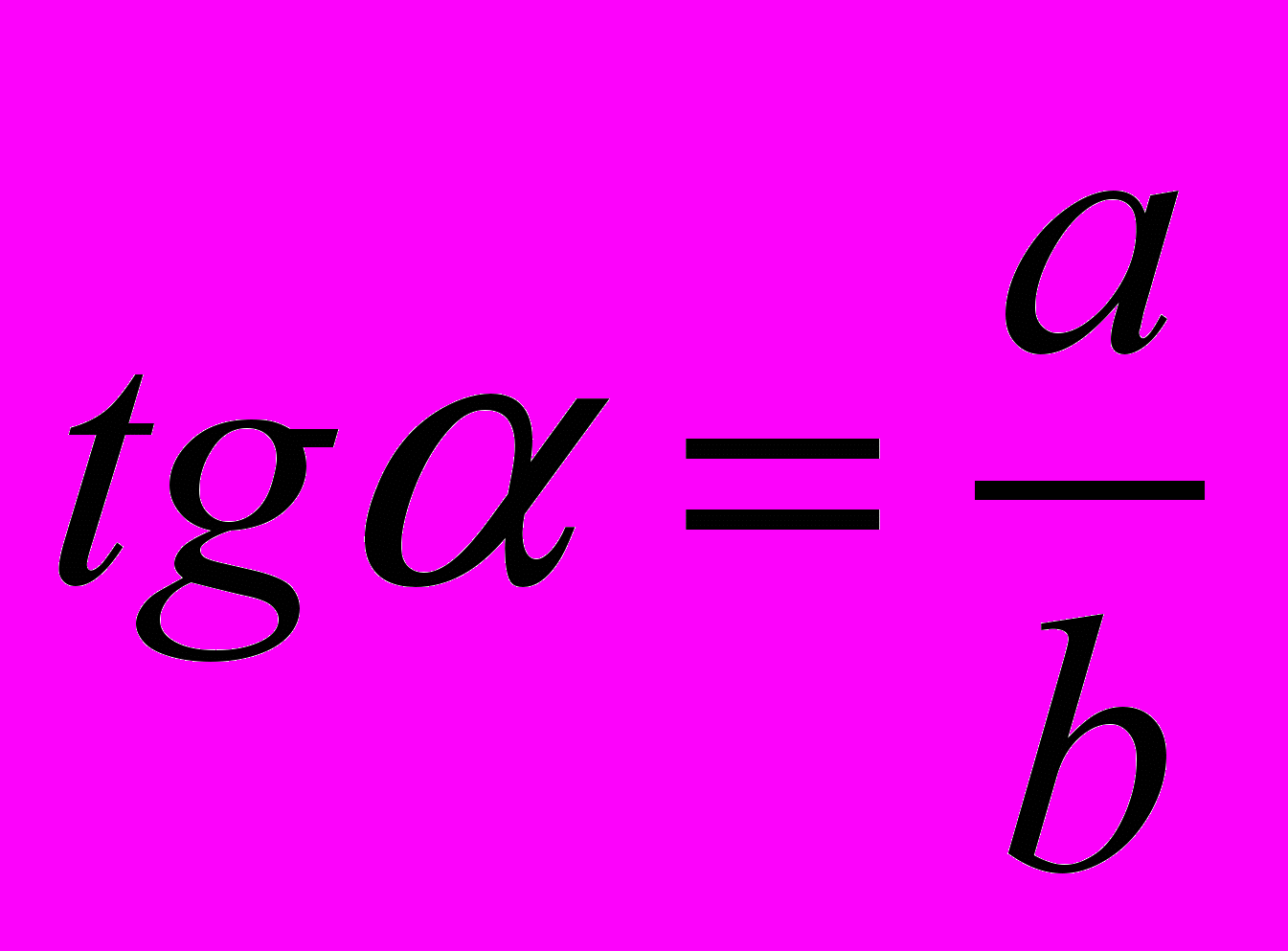
.Котангенсом угла
называется отношение прилежащего катета к противолежащему: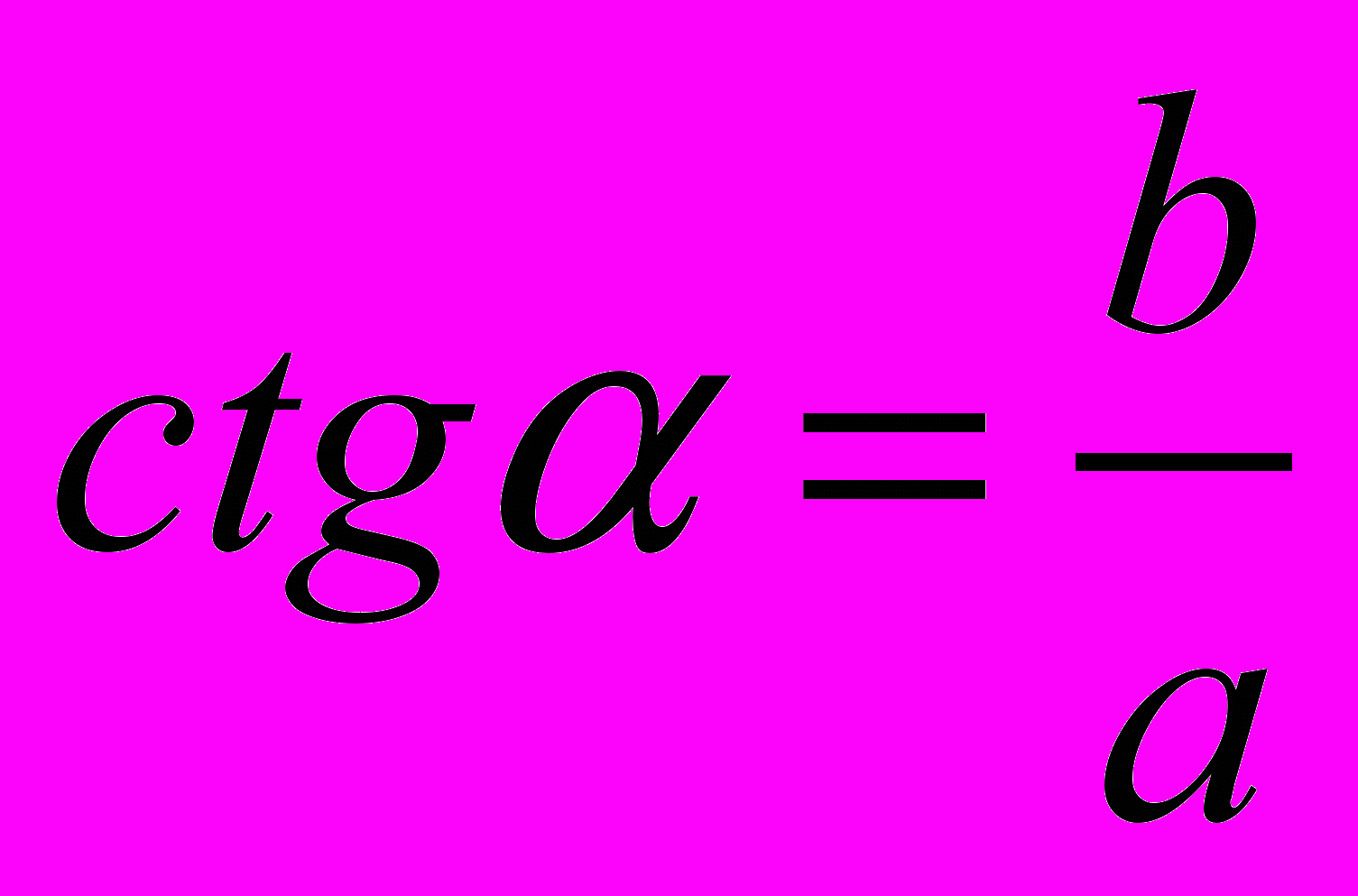
.Непосредственно из определений следуют следующие соотношения:
, 
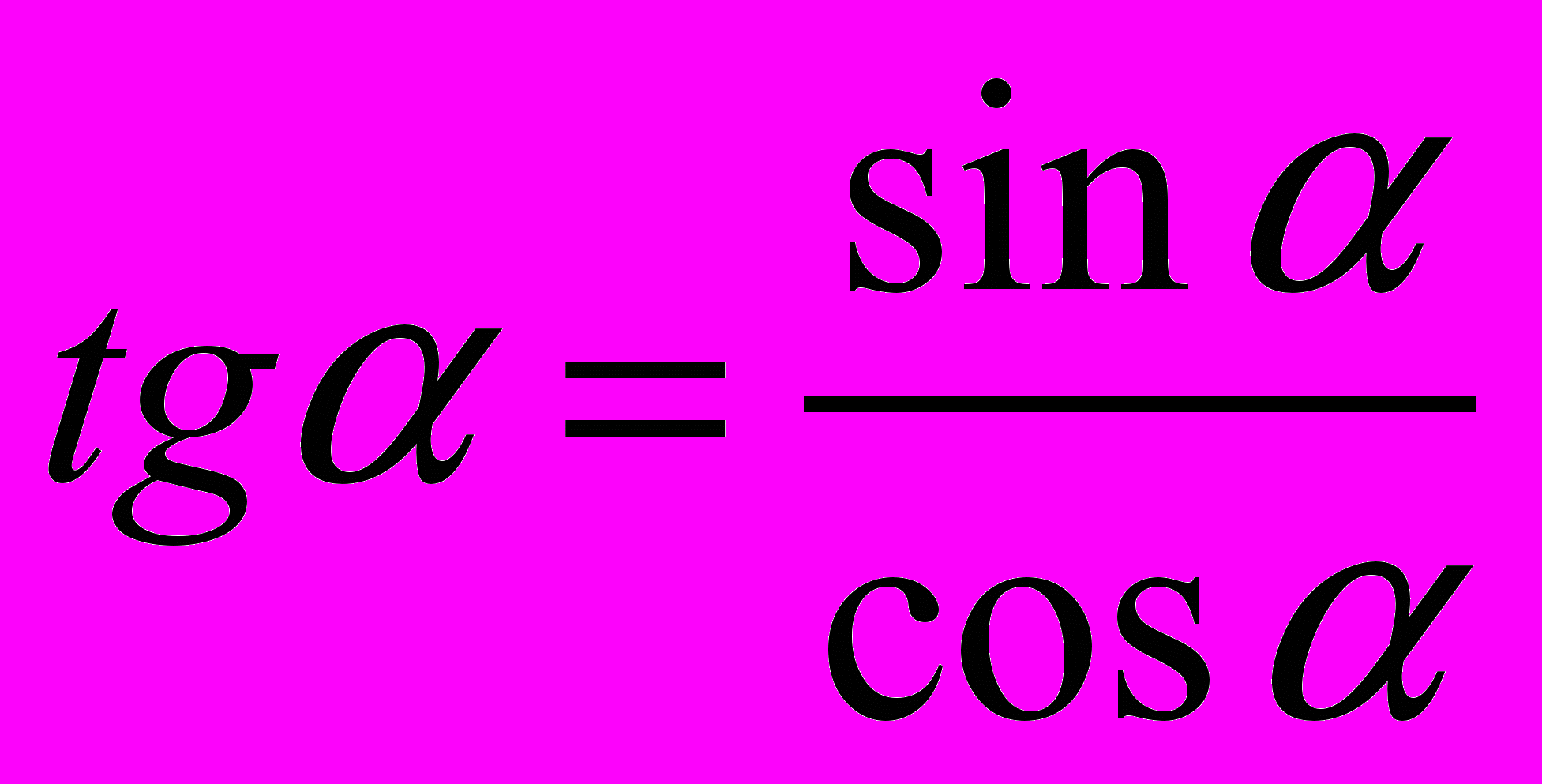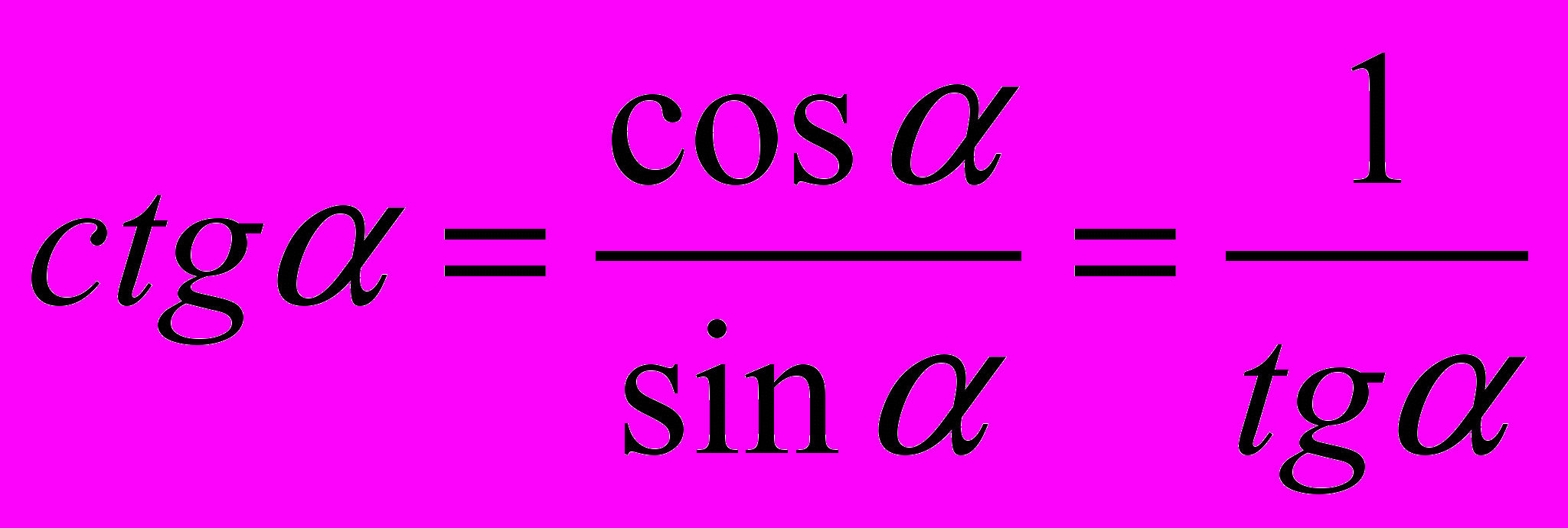.Воспользовавшись теоремой Пифагора, можно доказать основное тригонометрическое тождество:
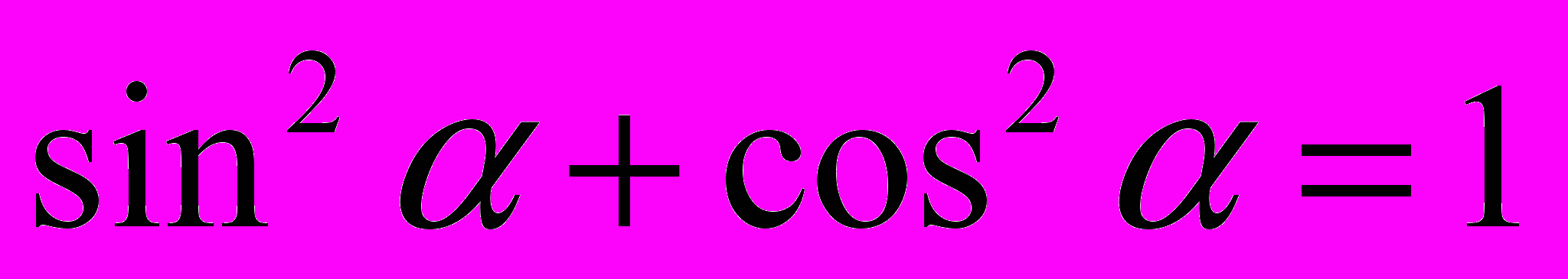.§2. Радианная мера угла. Определение тригонометрических функций
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. При этом величина угла может быть любой.
Возьмем на координатной плоскости окружность радиуса
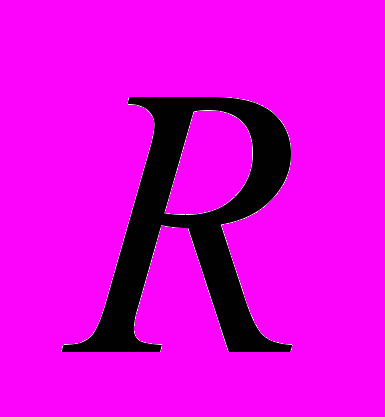с центром 
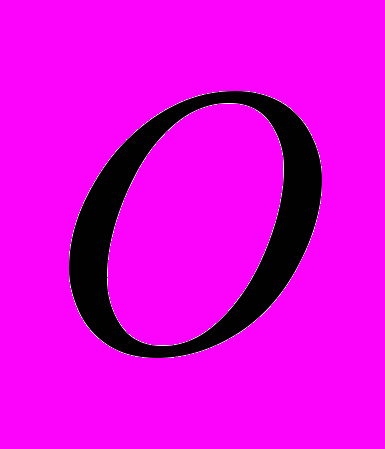в начале координат. Пусть одна сторона угла с вершиной в начале координат 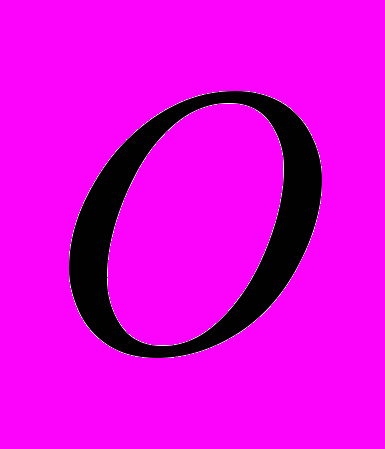идёт по оси 
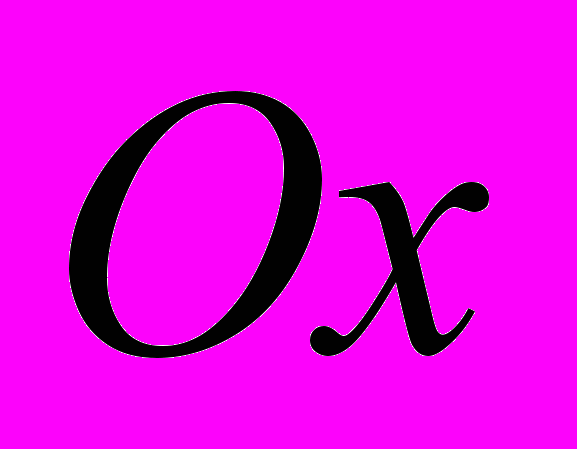, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси 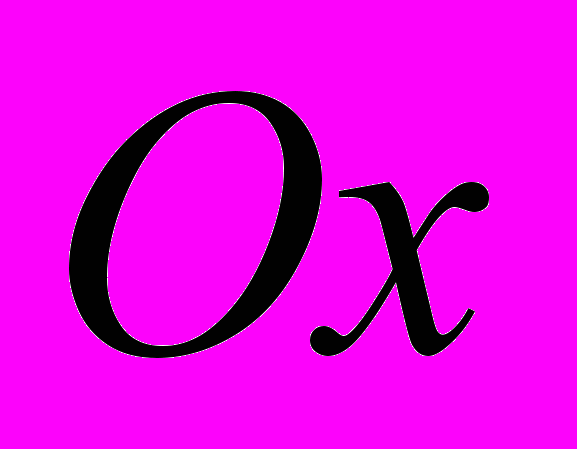. Из геометрии известно, что отношение длины дуги 
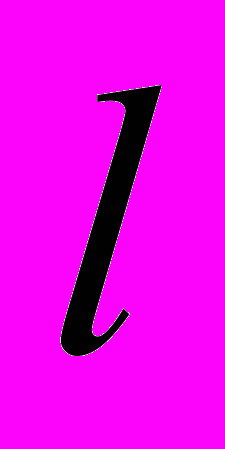, на которую опирается этот угол, к радиусу 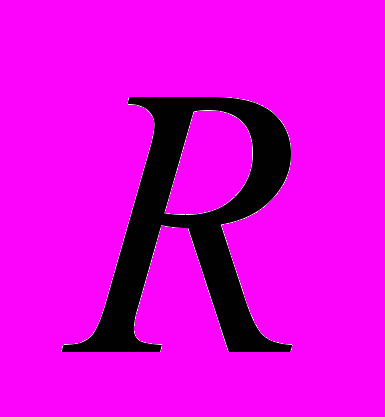этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: 
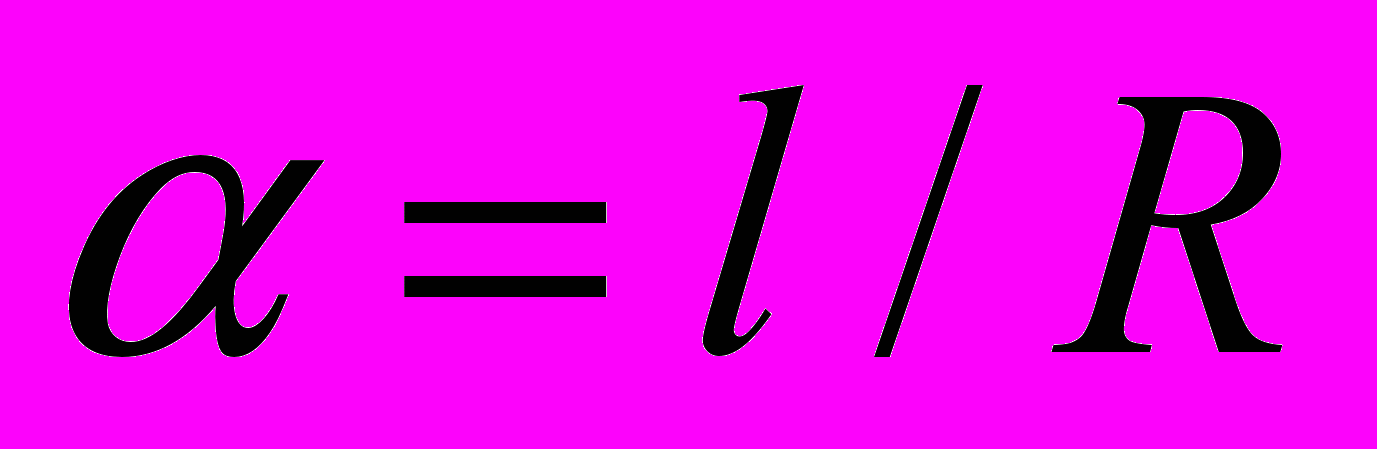. Такая мера называется радианной мерой угла. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу.Так как длина всей окружности радиуса R равна 2πR, то всей окружности соответствует угол радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует
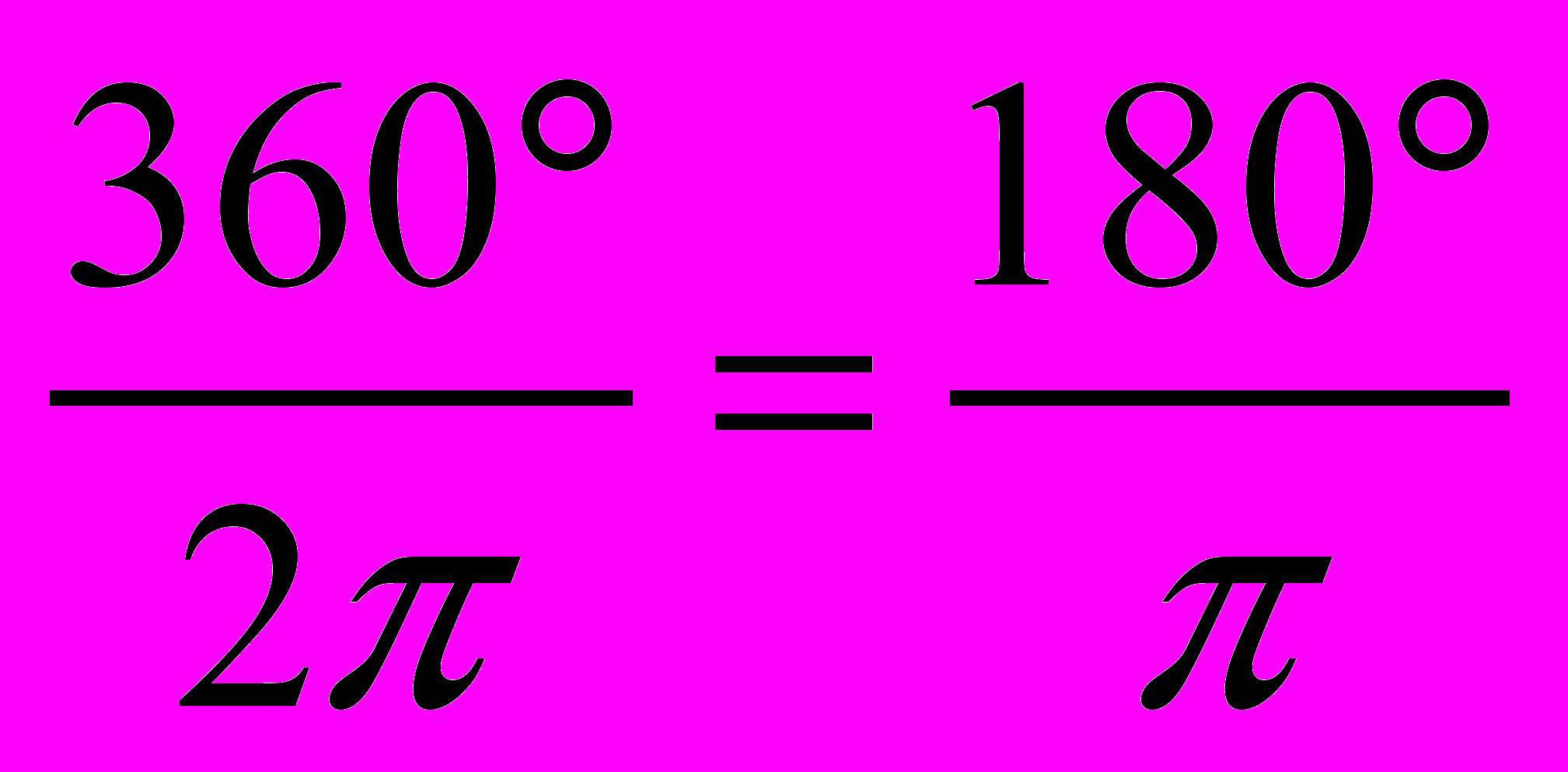градусов: 
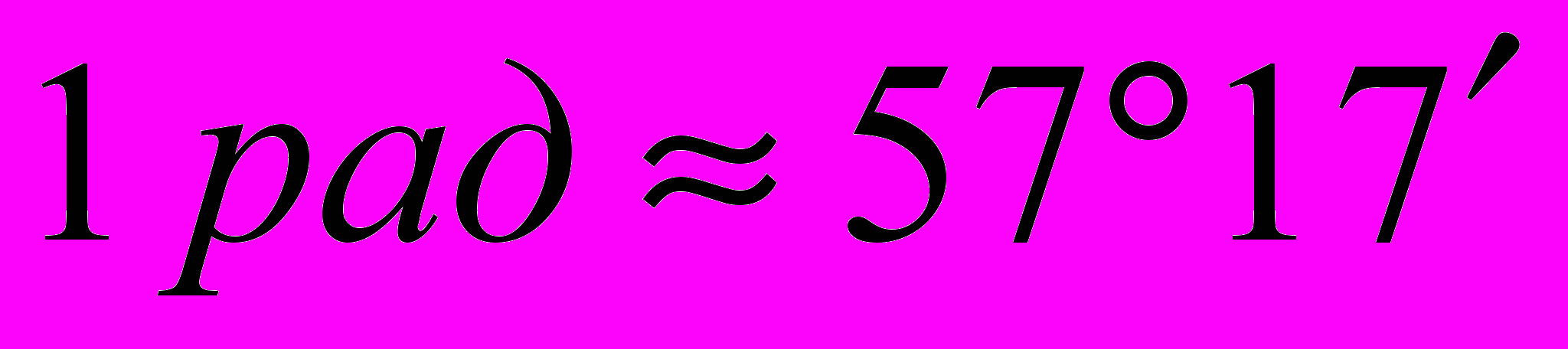.Рассмотрим на координатной плоскости окружность единичного радиуса с центром в начале координат (рис. 2). Такая окружность называется тригонометрической. Рассмотрим произвольный угол
. Изобразим его как угол поворота отрезка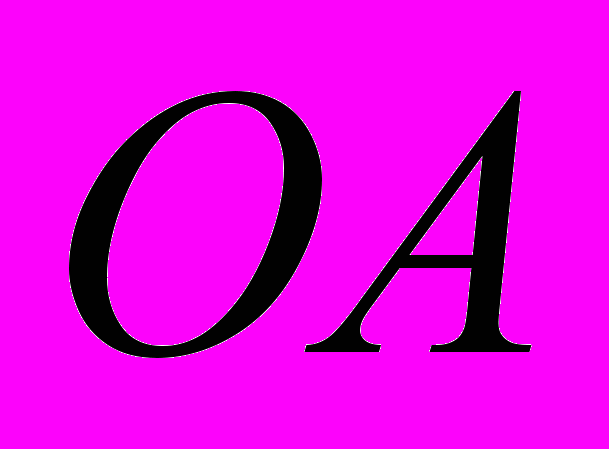 
против часовой стрелки. При таком повороте точка 
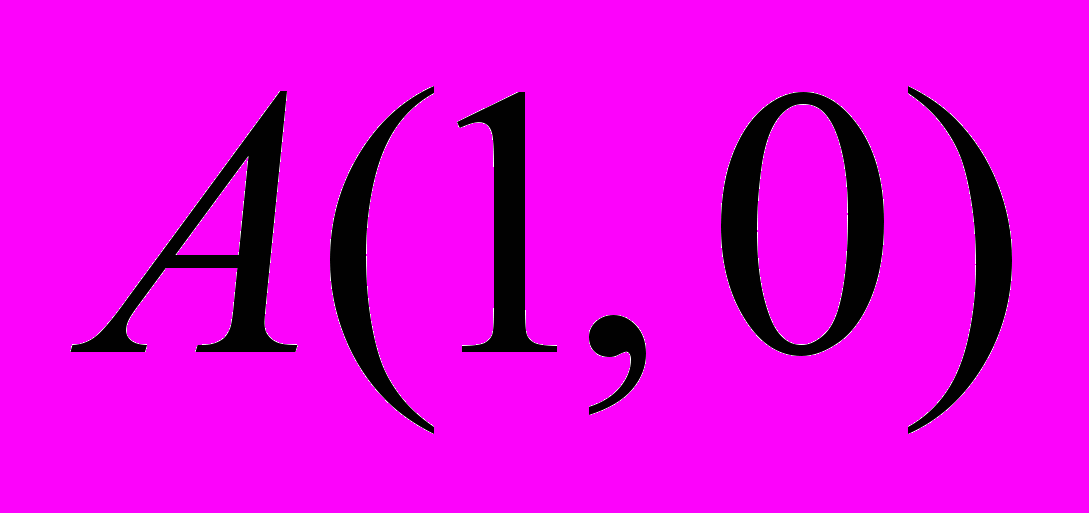перейдет в некоторую точку 
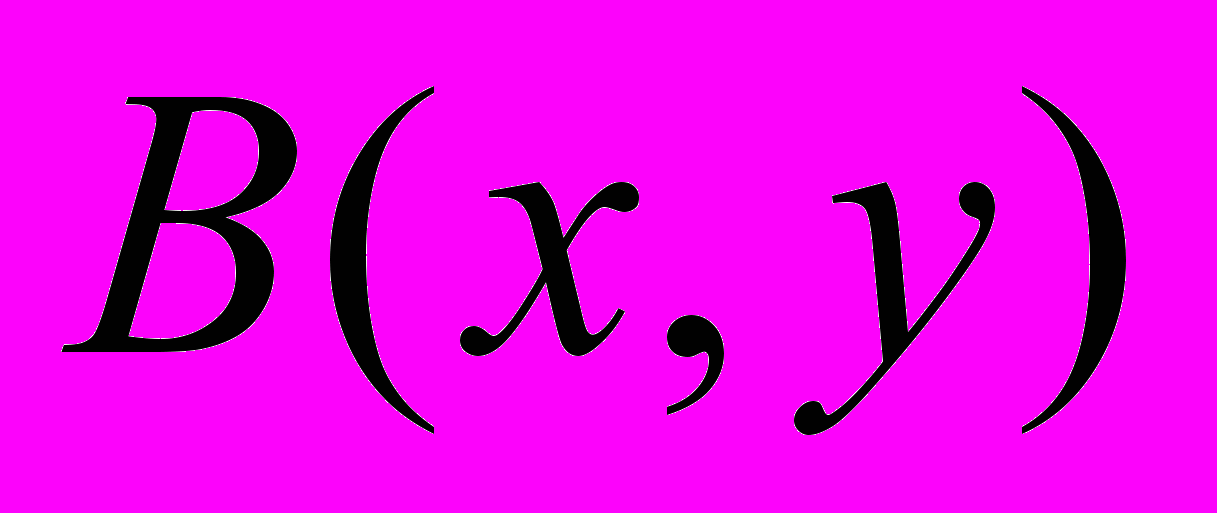. Еще раз заметим, что угол 
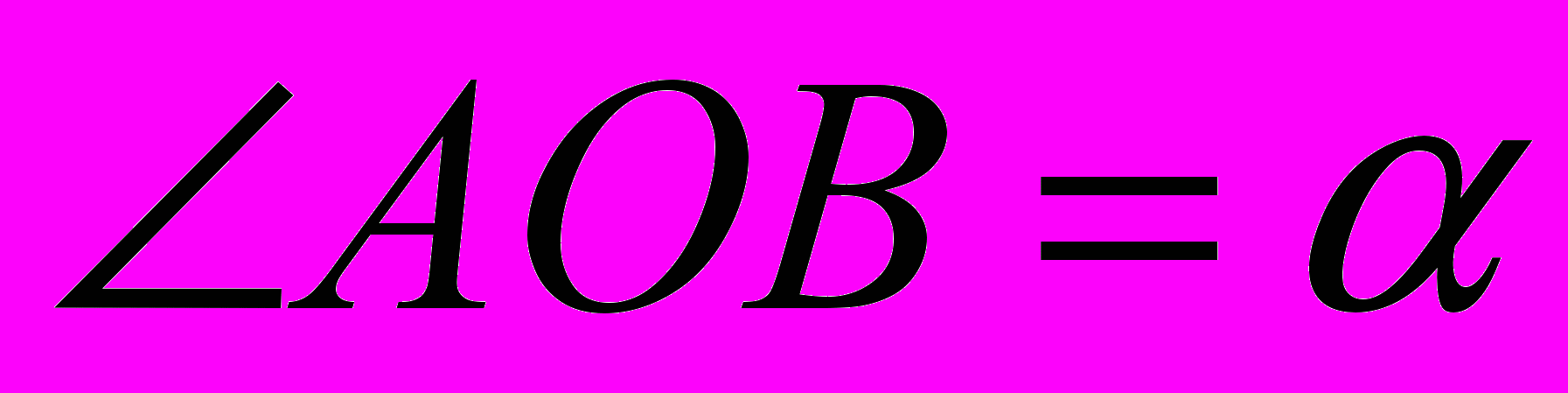может иметь произвольную величину.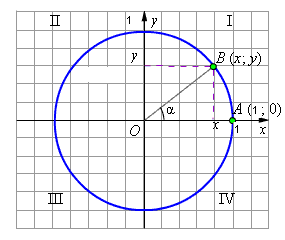
Рис. 2
Пусть сначала
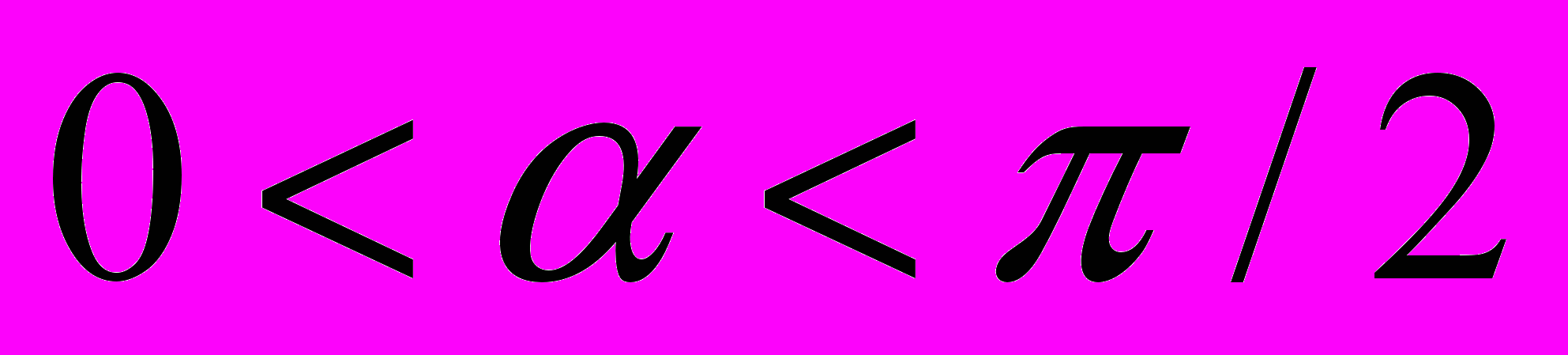. Тогда в соответствии с данными в §1 определениями 
, 
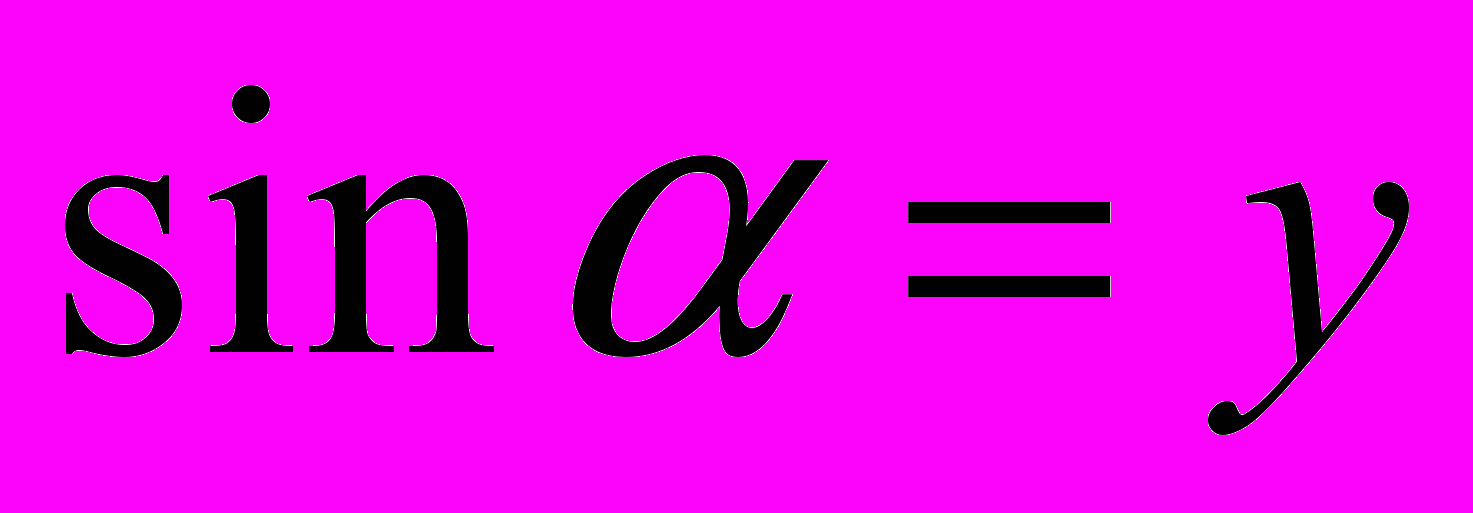и т.д. Разрешим теперь углу принимать любые значения и продолжим на них определения тригонометрических функций в соответствии с выписанными формулами. При таком определении тригонометрические функции заданы однозначно, так как каждому углу соответствует единственная точка на тригонометрической окружности. Однако функции тангенс и котангенс не определены для углов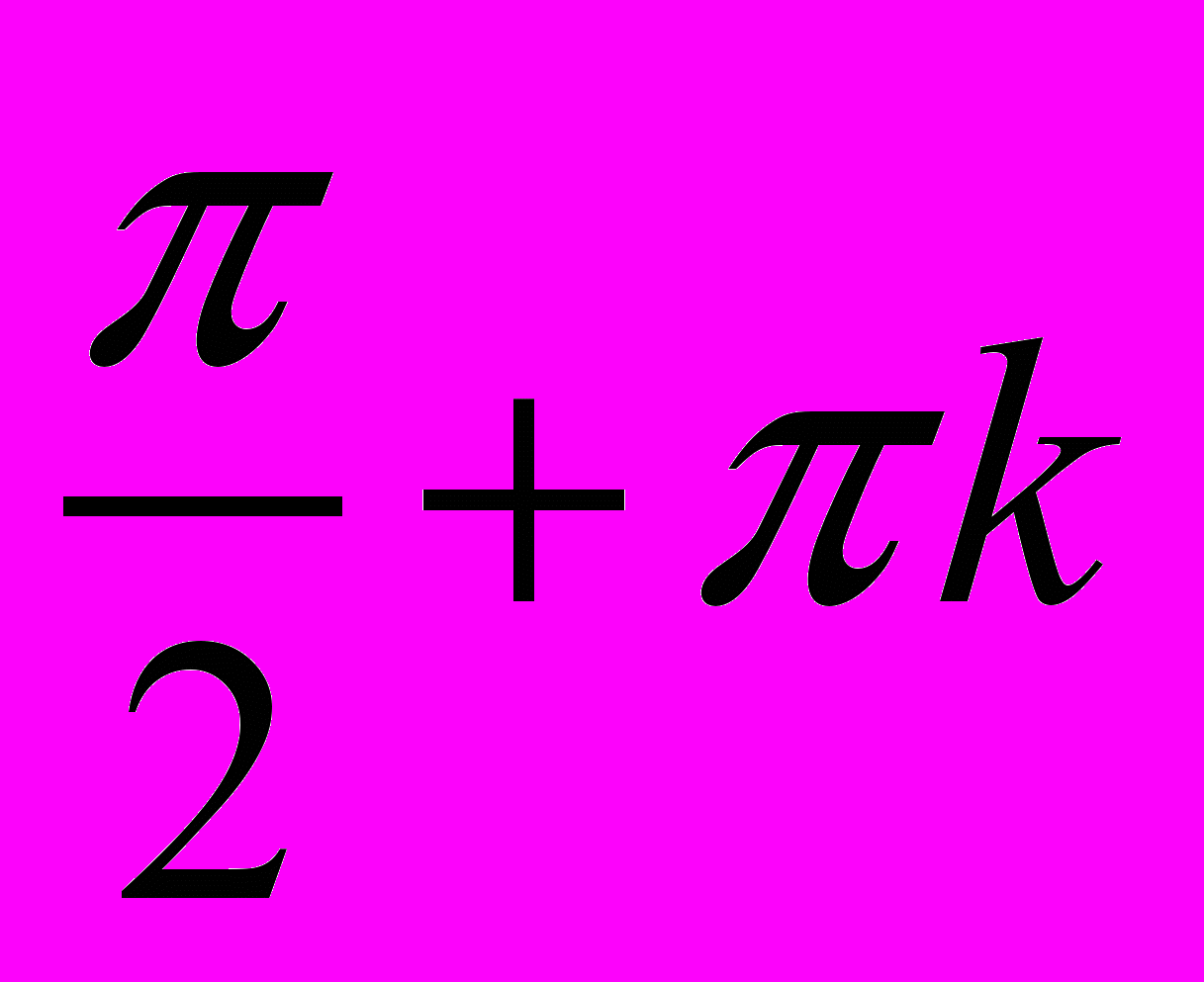 
и 
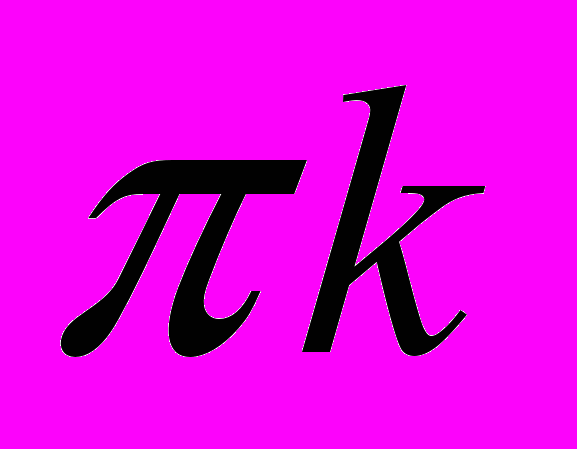, где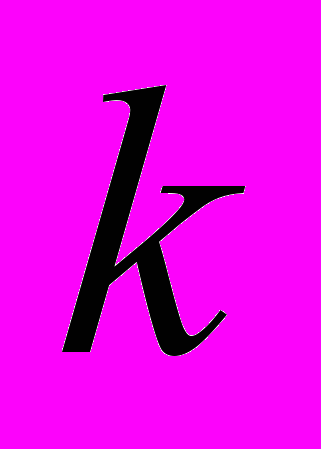 
– целое число, соответственно.§3. Формулы приведения
С помощью несложных геометрических построений можно доказать следующие формулы, называемые формулами приведения:
,
,
,
;
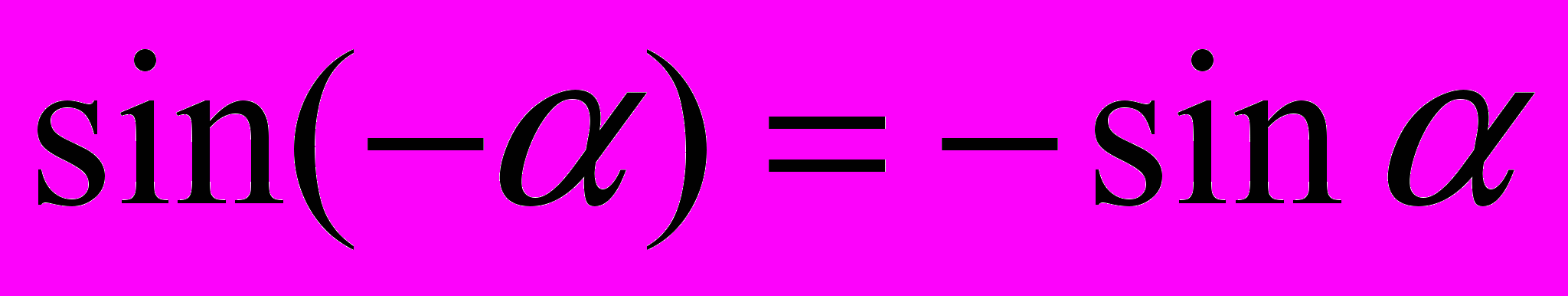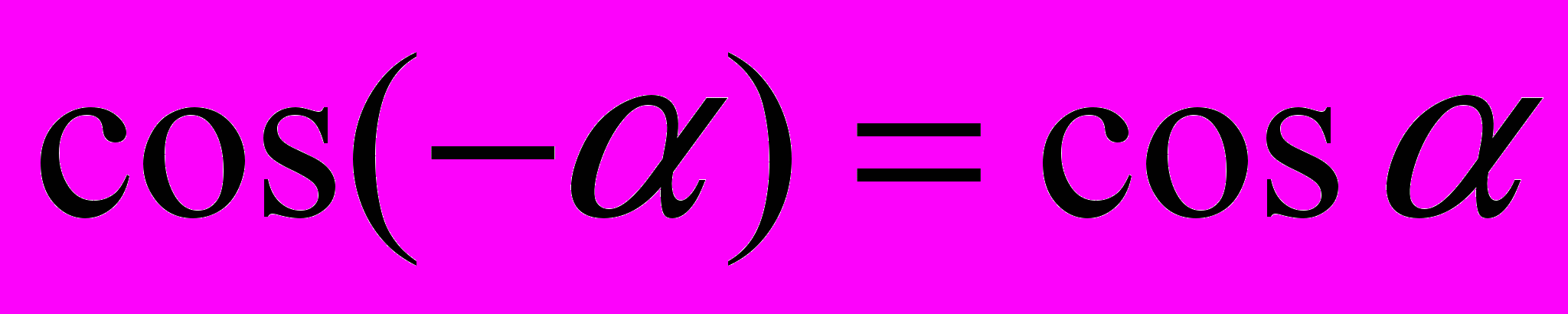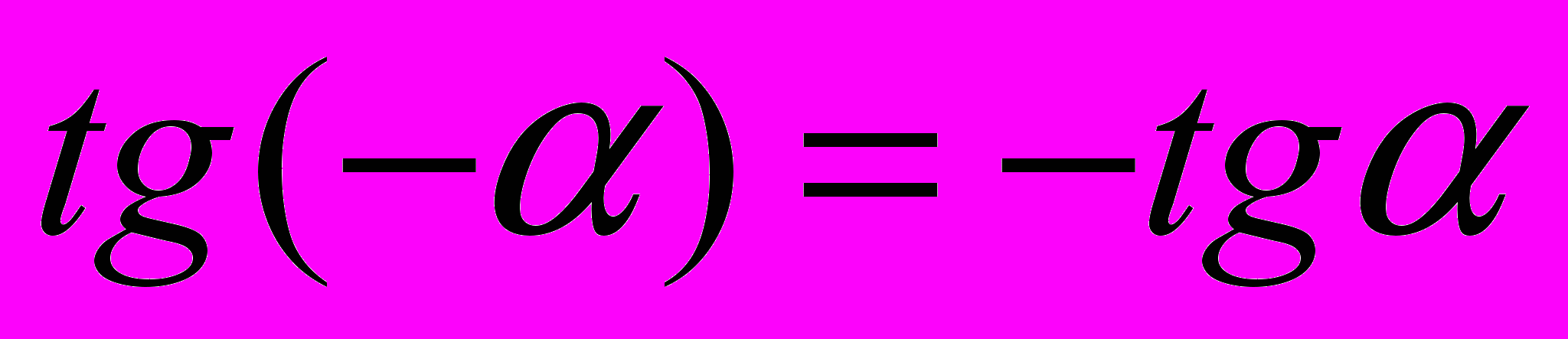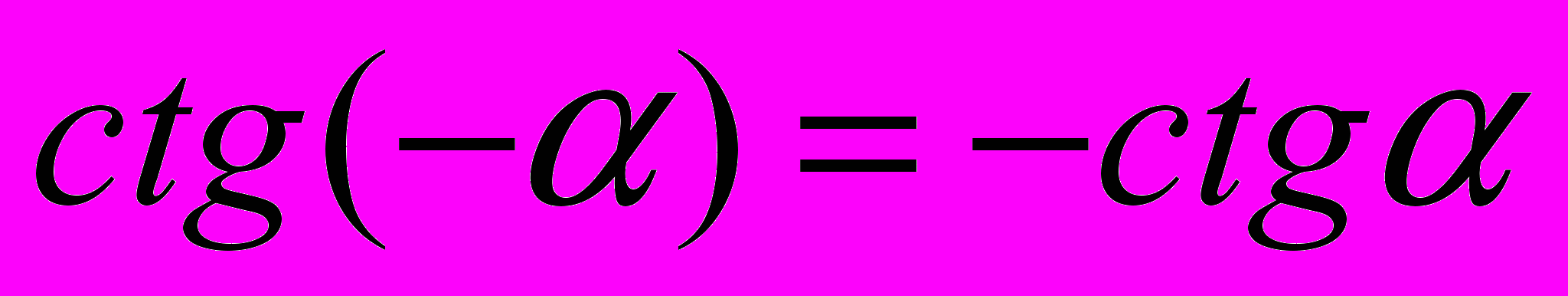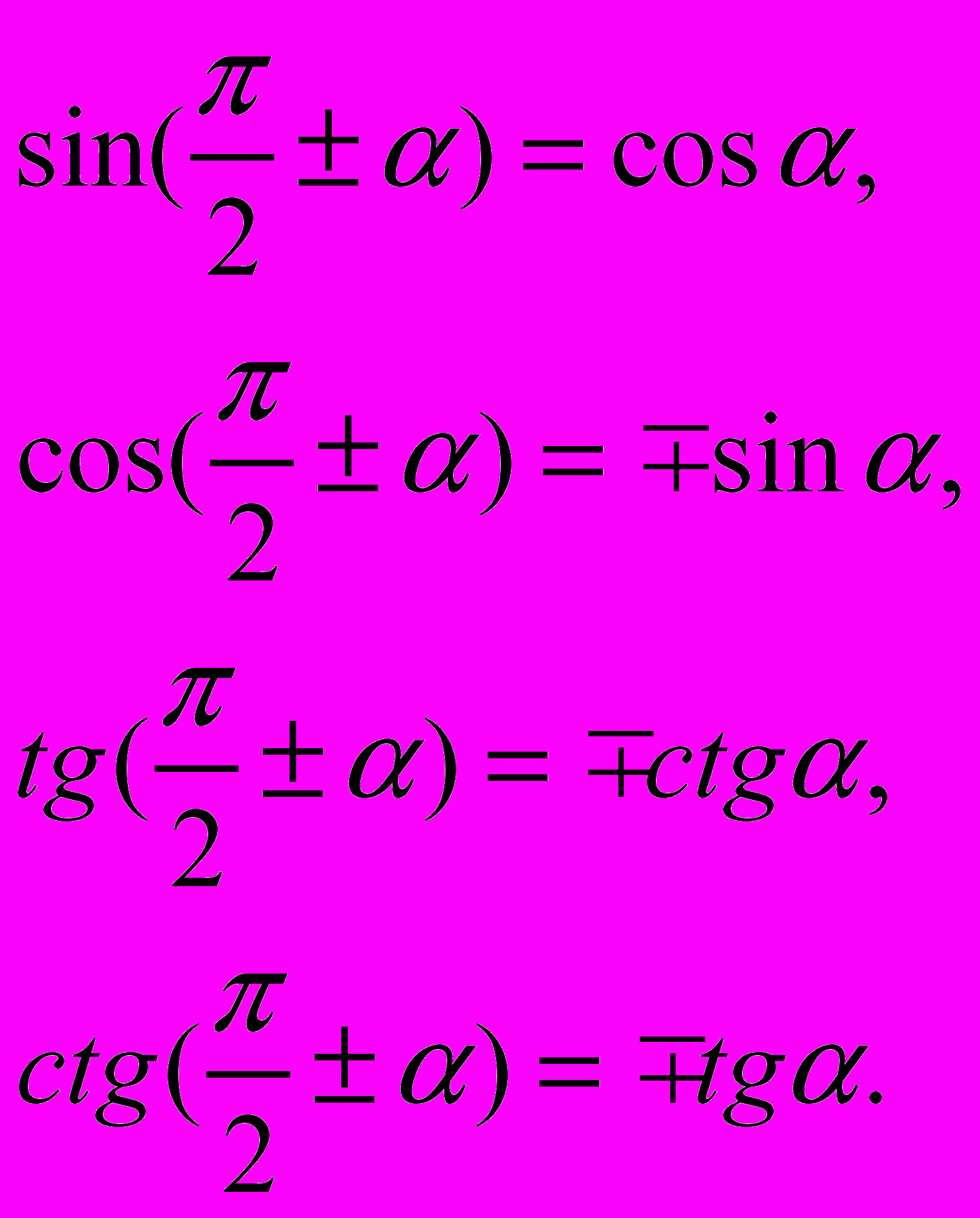
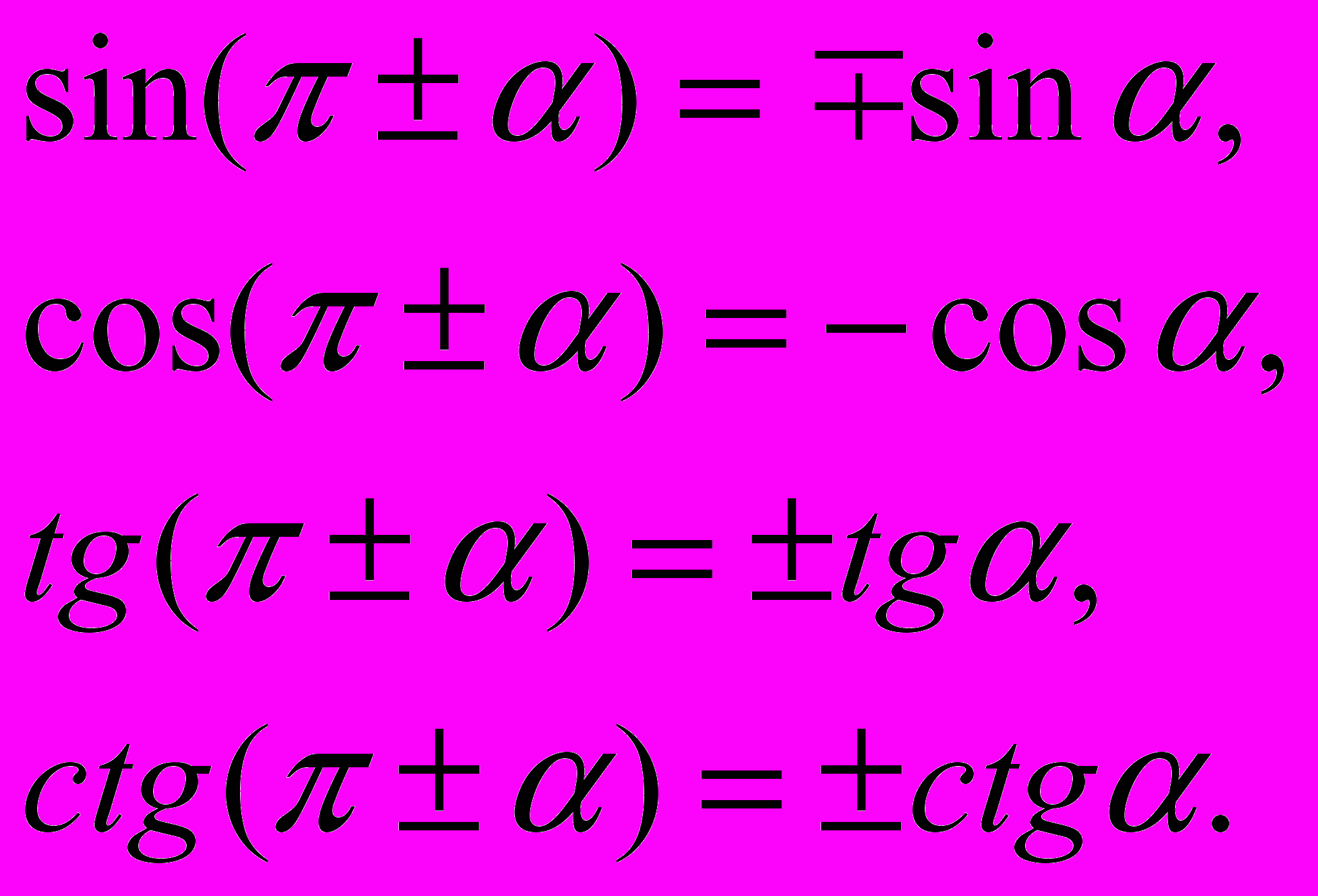
§4. Функции суммы и разности двух углов. Функции двойного угла. Формулы понижения степени
Можно доказать следующие формулы:
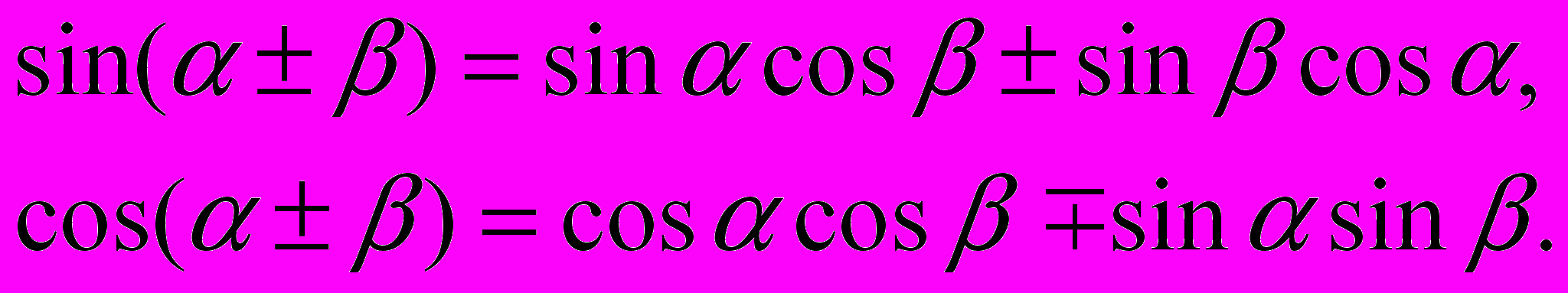
Как частный случай этих формул имеем:
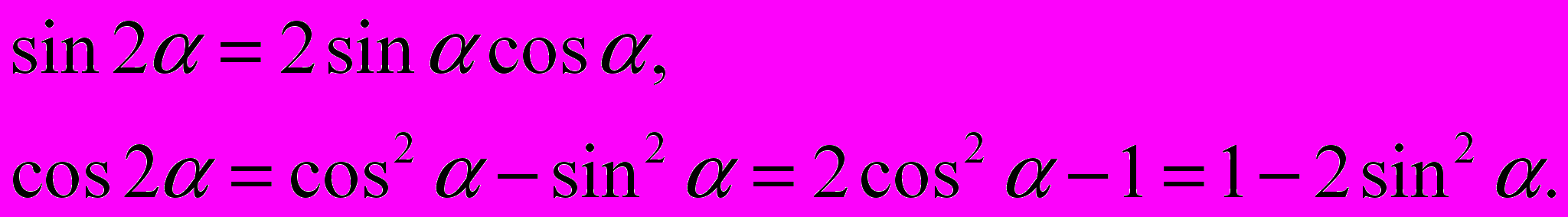
Обращая формулы для двойного угла, получаем:
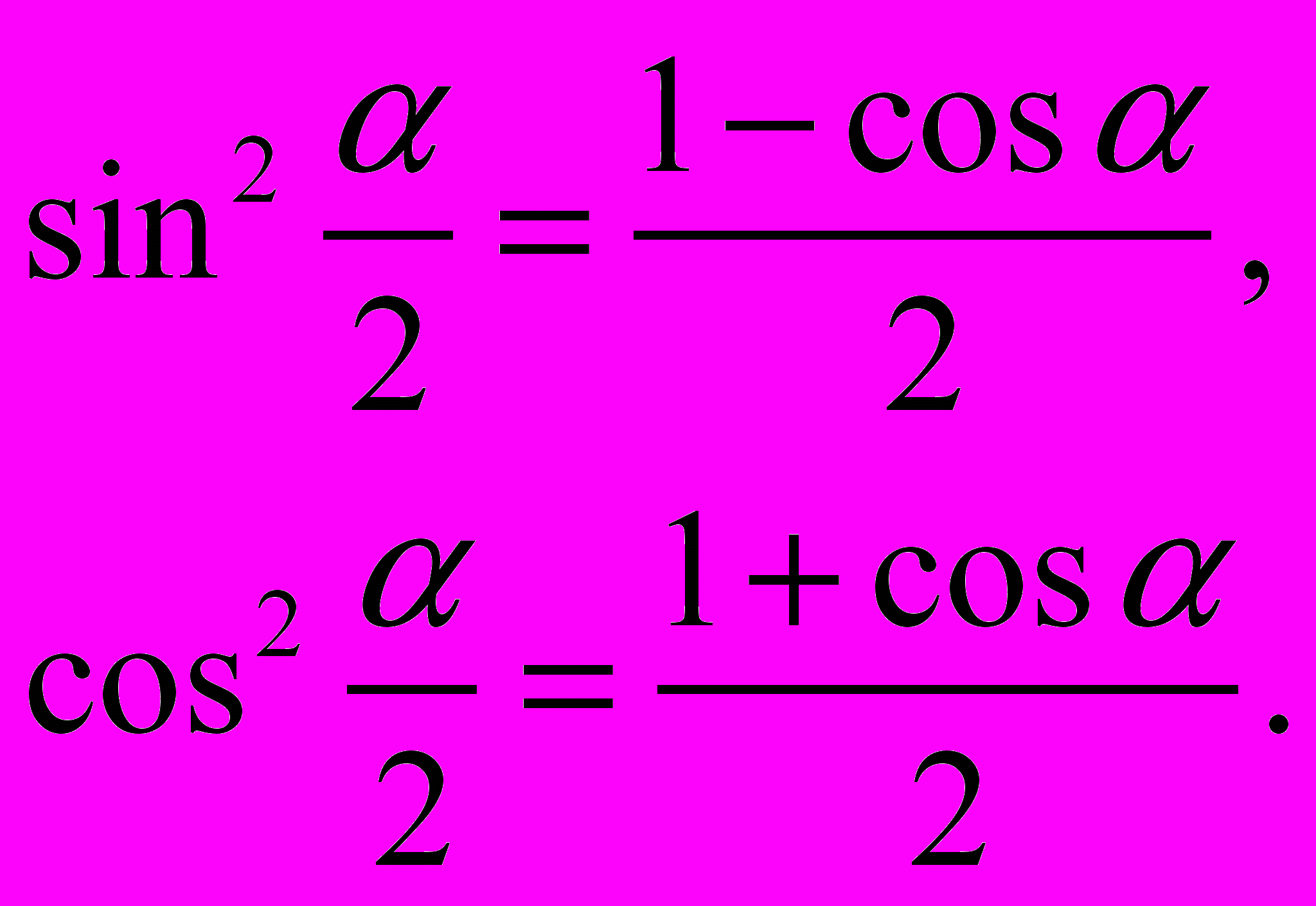
§5. Преобразование сумм в произведение и обратно
Пользуясь формулами сложения, можно доказать:
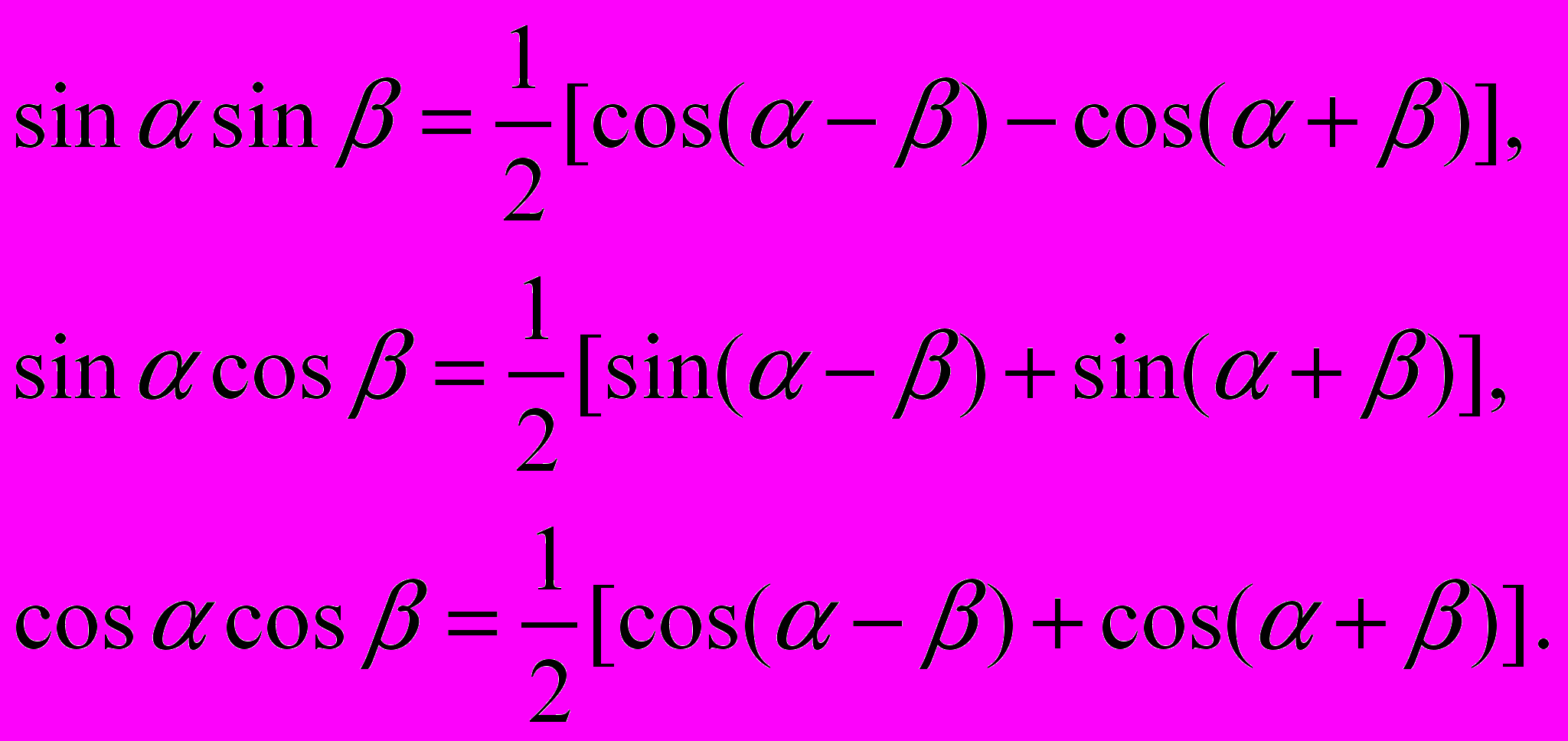
Из этих формул легко получить:
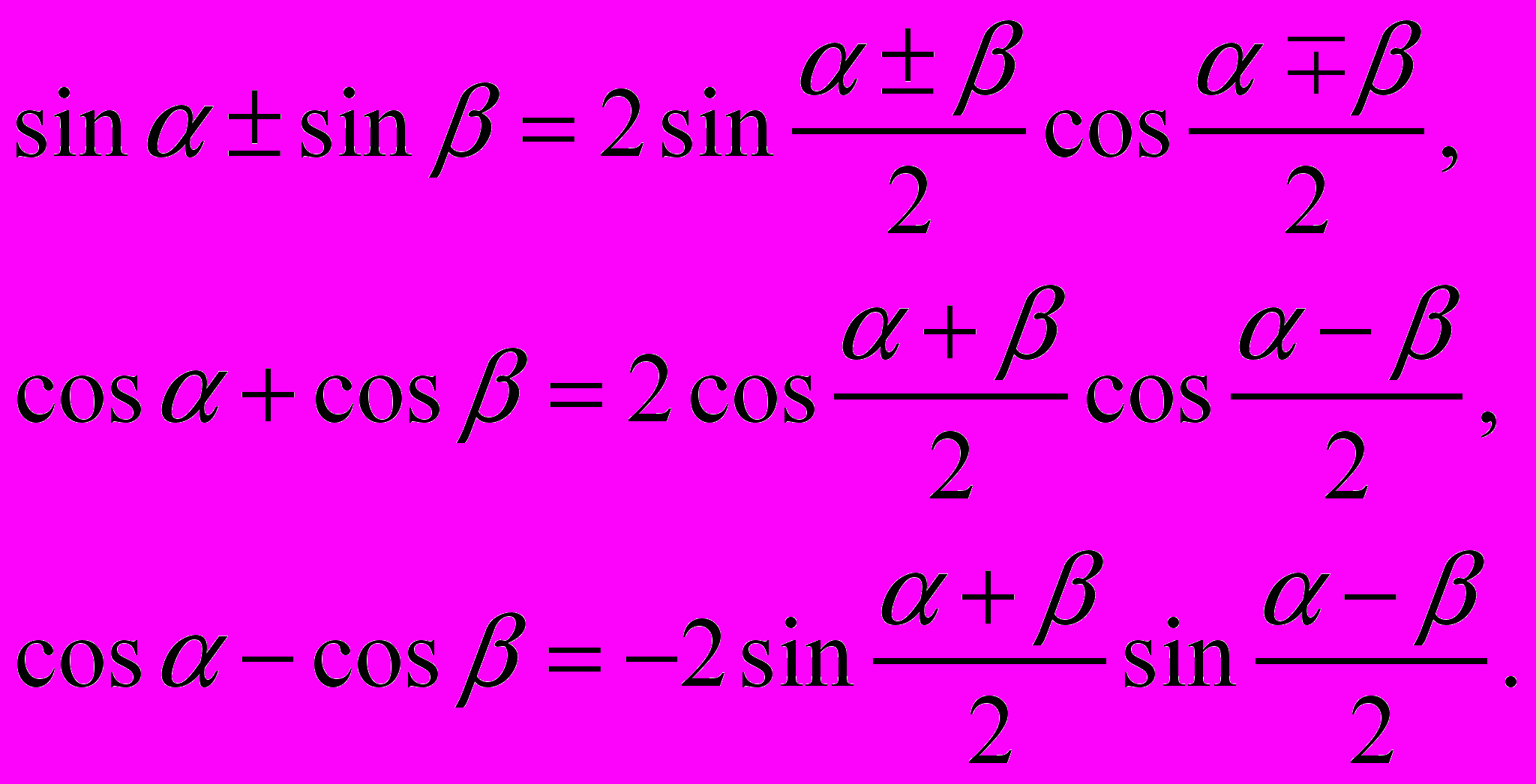
§6. Простейшие тригонометрические уравнения
В заключение рассмотрим решения простейших тригонометрических уравнений:
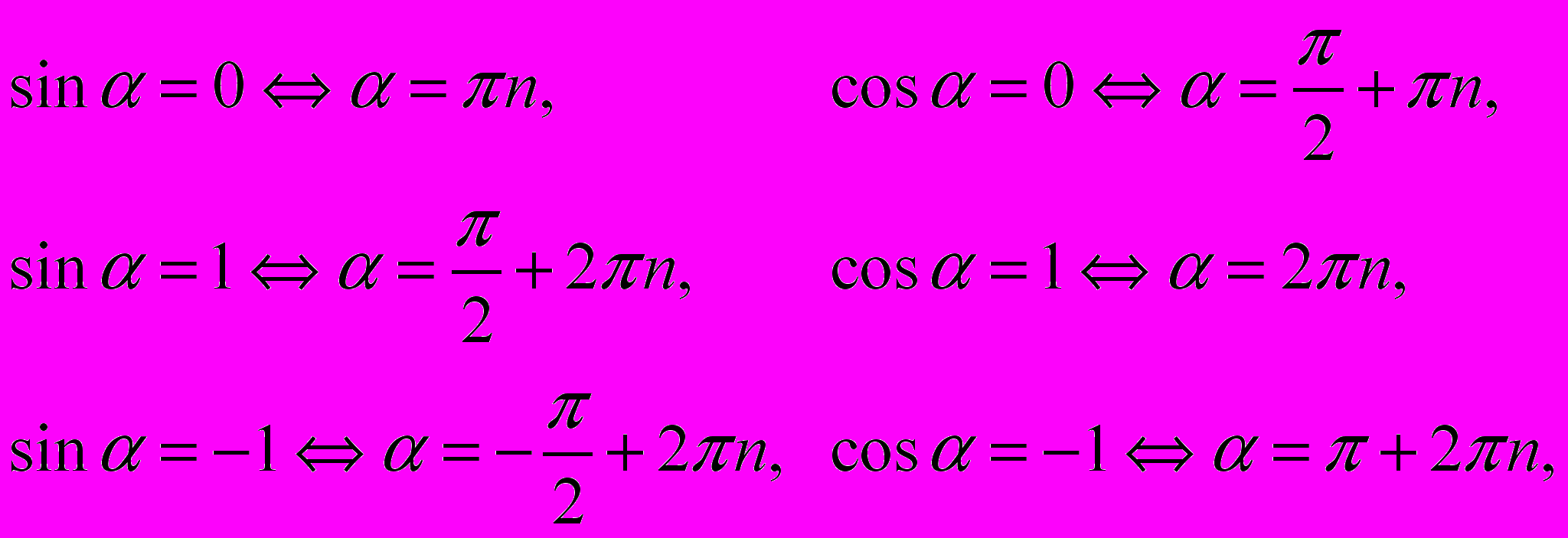
где
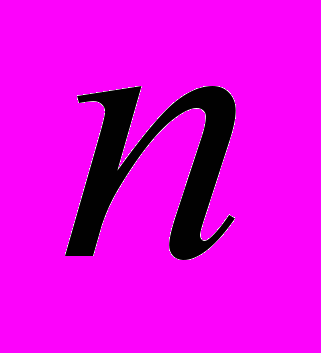– целое число.