Анфимова Наталья Геннадьевна Обсуждено на заседании мо протокол №1 От 5 ноября 2004 г. Председатель г. Волжск 2004 пояснительная записка

Вид материала

Пояснительная записка

Подобный материал:

• Мишина Наталья Анатольевна, педагог дополнительного образования вдэц. Волжск 2004 Содержание, 477.98kb.
• Вахитова Айгуль Фаритовна Базовый уровень Рассмотрено на заседании педагогического, 167.78kb.
• Программа одобрена на заседании кафедры математических и естественно-научных дисциплин, 299.17kb.
• Учебная программа (специальность 021100 «юриспруденция») москва 2005г, 274.78kb.
• А. П., Слепнёв И. Н. Памяти Андрея Матвеевича Анфимова // Россия сельская. XIX – начало, 91.68kb.
• Программа курса, темы практических занятий, рефератов и курсовых работ Казань 2004, 80.02kb.
• Председатель Ученого Совета пи юфу, Ректор ргпу, профессор В. И. Мареев пояснительная, 873.06kb.
• Председатель Ученого Совета пи юфу, Ректор ргпу, профессор В. И. Мареев пояснительная, 483.42kb.
• Учебно методическое пособие Минск 2004 удк 616. 15 053. 2: 362. 147, 619.1kb.
• 7 качество учебно-методического, информационного и библиотечного обеспечения, 99.06kb.

Министерство образования Российской Федерации
МУОО г. Волжска РМЭ
МОСШ № 4 г. Волжска РМЭ

Тригонометрические выражения и их преобразования

Элективный курс по математике

для 9 класса, на 17 часов

Разработчик программы
Анфимова Наталья Геннадьевна

Обсуждено на заседании МО Протокол № 1
От 5 ноября 2004 г. Председатель

г. Волжск

2004

Пояснительная записка

Элективный курс "Тригонометрические выражения и их преобразования" рассчитан на 17 часов для учащихся 9-х классов.

В курсе тригонометрии 8 класса были сформированы определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, были введены основные формулы тригонометрии и формулы приведения вида 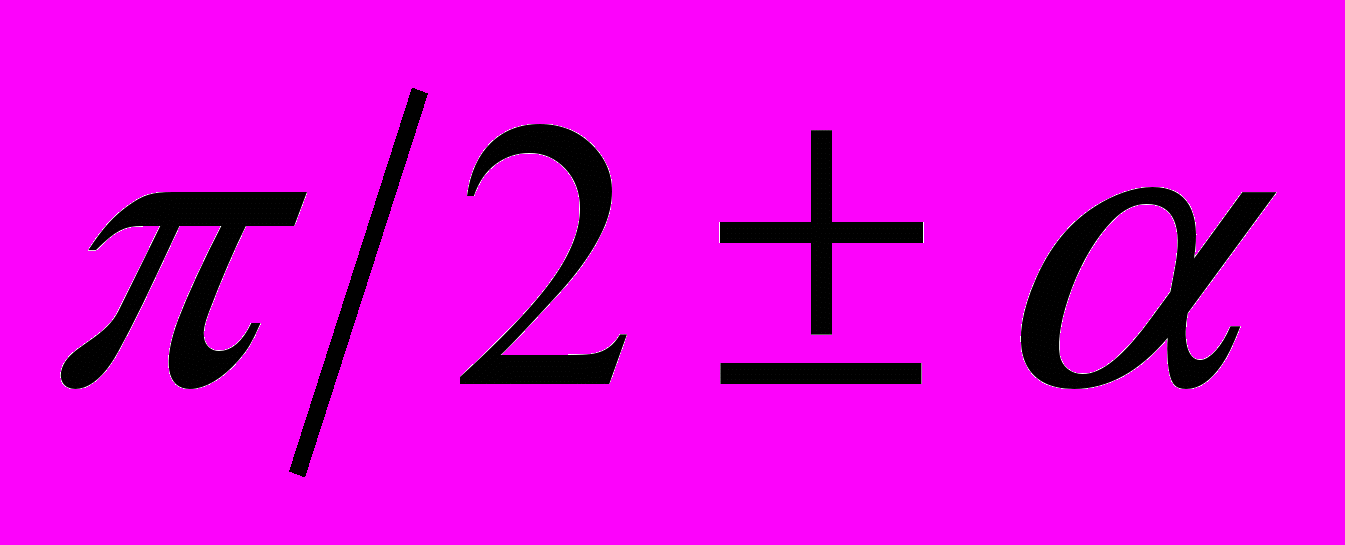и

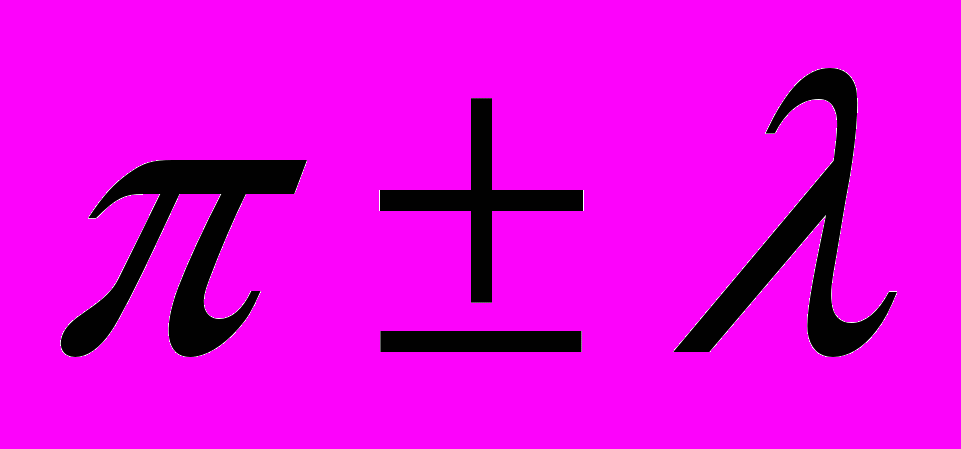
Тригонометрический материал: уравнения, неравенства и их системы и т.д. будет еще изучаться в 10-11 классах. Но в связи с недостаточностью отведенного для изучения этой сложной темы времени, учащимся невозможно в достаточной степени изучить все тонкости материала. Поэтому, с целью облегчения изучения этой темы в 10-11 классах, необходимо ввести этот элективный курс в программу 9-х классов.

В программе этого элективного курса учащиеся впервые знакомятся с доказательствами тригонометрических тождеств. Задания подобраны таким образом, что не требуется находить допустимые значения величин углов, фигурирующих в тождестве. Учащимся, интересующимся математикой, должны быть предложены задачи, условиями которых предусмотрено нахождение допустимых значений величин углов, входящих в тригонометрическое тождество.

Формулы приведения должны быть хорошо усвоены учащимися, так как они найдут дальнейшее применение на уроках геометрии, физики и других смежных дисциплин.

Элективные курсы компенсируют достаточно слабые возможности базовых программ, помогают многим учащимся сделать выбор профиля старшей школы.

Основная цель курса - развитие памяти, логического мышление привитие интереса к математике, используя возможности индивидуальной и коллективной исследовательской работы учащихся.

§ 1. Тригонометрические функции любого угла (4 часа)

1. Определение синуса, косинуса, тангенса и котангенса (2 часа).

2. Свойства синуса, косинуса, тангенса и котангенса (1 час).
   
3. Радианная мера угла (1 час)
   

§2. Основные тригонометрические формулы (6 часов).

1. Соотношения между тригонометрическими функциями одного и того же угла (2 часа).
   
2. Применение основных тригонометрических формул к преобразованию выражений (2 часа).
   
3. Формулы приведения (2 часа).
   

§3. Формулы сложения и их следствия (7часов).

1. Формулы сложения (2 часа).
   
2. Формулы двойного угла (2 часа).
   
3. Формулы суммы и разности тригонометрических функций (3 часа).
   

Основное содержание курса

§1. Тригонометрические функции любого угла.

Определение синуса, косинуса, тангенса и котангенса. Синус, косинус, тангенс и котангенс произвольного угла. Значение синуса, косинуса, тангенса и котангенса для некоторых углов (0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°). Свойства тригонометрических функций в каждой из четвертей, четность и нечетность, сохранение значения при прибавлении к аргументу целого числа оборотов. Переход от радианной меры угла к градусной мере и наоборот. Нахождение значений тригонометрических функций с помощью калькулятора или таблицы В.М. Брадиса.

Понятие синуса и косинуса как координаты точки единичной окружности, полученной в результате поворота точки Р (1;0). Область определения функций синус, косинус, тангенс и котангенс.

§2. Основные тригонометрические формулы.

Основные тригонометрические тождества: sin²x+cos²x=l; ctgx=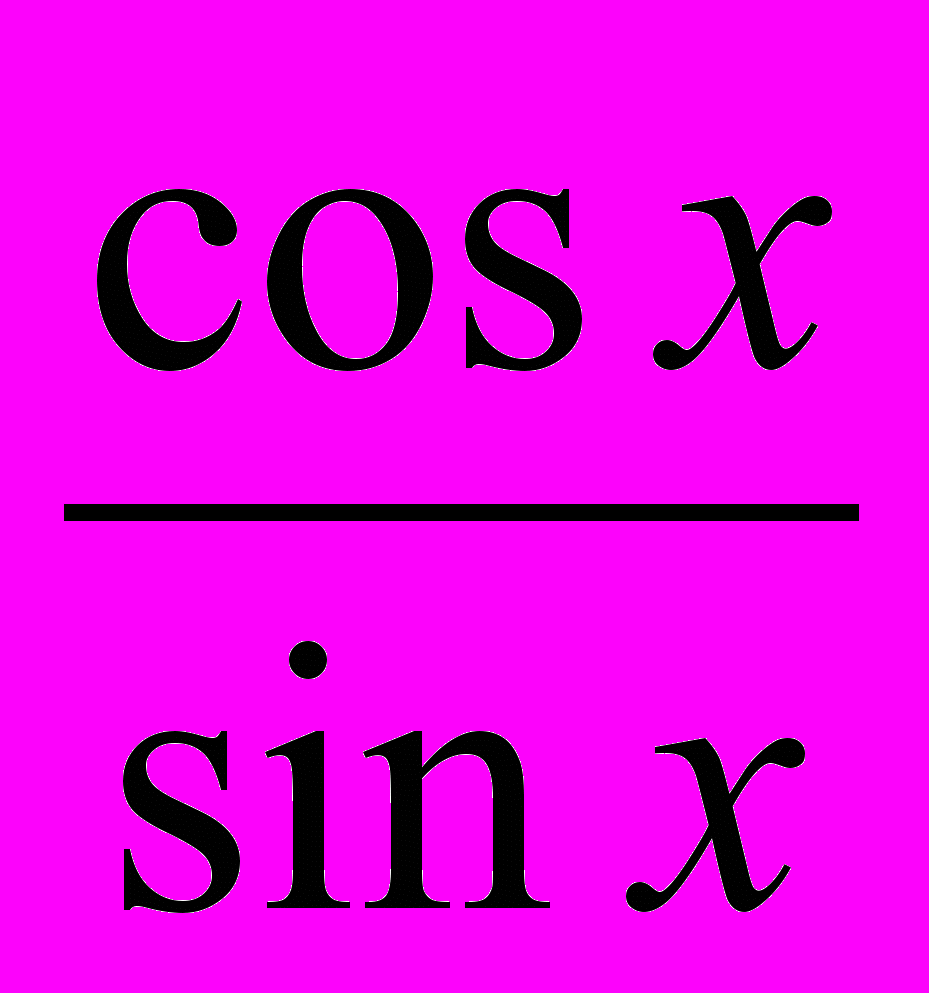; tgx=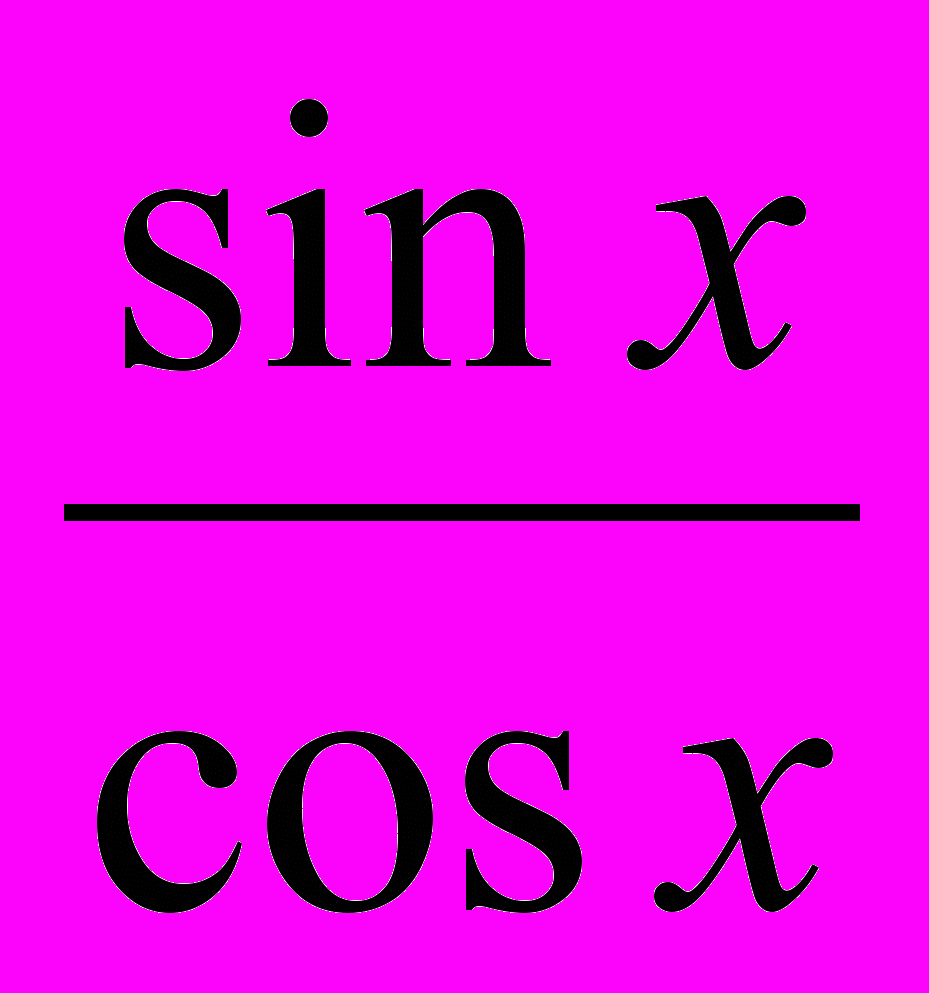; tgx*ctgx=1. Формулы приведения, преобразования тригонометрических функций, доказательство тождеств. Формулы, выражающие соотношения между тригонометрическими функциями одного и того же аргумента. Вычисление по известному значению одной из тригонометрических функций значений остальных тригонометрических функций.

§3. Формулы сложения и их следствия.

Формулы синуса (косинуса, тангенса) суммы и разности углов и следствия их них. Формулы двойного угла синуса, косинуса и тангенса. Формулы преобразования суммы и разности синусов (косинусов) углов в произведение. Ситуации, в которых применимы эти формулы и выполнение преобразований по соответствующему алгоритму. Обоснование формул приведения через формулы синуса (косинуса, тангенса) суммы и разности углов.


Методическое обеспечение

§1.Урок 1 - лекция;

Урок 2, 3 - практические занятия;

Урок 4 - самостоятельная работа №1.

§2. Урок 1 - лекция;

Урок 2, 3, 4, 5 - практические занятия;

Урок 6 - самостоятельная работа №2.

§3. Урок 1 -лекция;

Урок 2, 3, 4, 5 - практические занятия;

Урок 6 - зачет;

Урок 7 - тестовая работа.

Литература

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова СБ. Алгебра. Учебник для 9 класса средней школы. Под ред. С.А. Теляковского. М.: Просвещение, 1992.
   
2. Гусев В.А., Мордкович А.Г. Математика. Справочные материалы. М,: Просвещение, 1990.
   
3. Крамор B.C. Повторяем и систематизируем школьный курс алгебры и начал анализа. М.: Просвещение, 1990.
   
4. Симонов А.Я., Бакаев Д.С., Абрамов А.Л. и др. Система тренировочных задач и упражнений по математике. М.: Просвещение, 1991.
   
5. Гришина И.В., Распарин В.Н. Математика. Подготовка к Государственному централизованному тестированию. 9 класс. Саратов, изд-во «Лицей», 2004.
   
6. Альхова З.Н., Алгебра. Проверочные работы с элементами тестирования. Изд-во «Лицей», 1999.
   
7. Пирютко О.Н., Рачковский Н.Н., Янцевич В.А. Математика. Разноуровневые тесты. 9класс. Минск, «Книжный Дом», 2004.
   
8. Виленкин Н.Я. и др. «Алгебра, 9 класс». Учебное пособие для школ и классов с углубленным изучением математики. М.: Просвещение, 1990.
   
9. Антипов И.Н. и др. Избранные вопросы математики. 9 класс. Факультативный курс. М.: Просвещение, 1979.
   

Самостоятельная работа №1

Вариант 1 Вариант 2

1. Определите значение выражений:



Самостоятельная работа №2



Тест







Рецензия

Элективный курс учителя математики МОУ СОШ - 4 Анфимовой Н. Г. по теме «Тригонометрические выражения и их преобразования» в 9 классе нацелен на подготовку учащихся к изучению глубоко и содержательно этой темы в 10 - 11 классах школы и других учебных заведениях.

Элективный курс включает в себя лекции, практикумы, а также зачетные работы.

Тригонометрический материал: уравнения, неравенства и их системы и т.д. будет еще изучаться в 10 - 11 классах. Но в связи с недостаточностью отведенного для изучения этой сложной темы времени, учащимся невозможно в достаточной степени изучить все тонкости материала. Поэтому, с целью облегчения изучения этой темы в 10 - 11 классах, необходимо ввести этот элективный курс в программу 9-х классов.

В программе этого элективного курса учащиеся впервые знакомятся с доказательствами тригонометрических тождеств. Задания подобраны таким образом, что не требуется находить допустимые значения величин углов, фигурирующих в тождестве. Учащимся, интересующимся математикой, должны быть предложены задачи, условиями которых предусмотрено нахождение допустимых значений величин углов, входящих в тригонометрическое тождество.

Необходимость введения данного элективного курса в школьную программу продиктовано важностью и сложностью этой. А также большим количеством заданий по данной теме на экзаменах 11 класса в форме ЕГЭ.

• Первая глава курса посвящена изучению определений и свойств
  основных тригонометрических функций.
  
• Во второй главе курса рассматриваются основные тригонометрические
  формулы (соотношения между функциями одного и того же угла,
  формулы приведения и применение их к преобразованию
  тригонометрических выражений).
  

• Третья глава курса посвящена формулам сложения и их следствиям.

Формулы приведения должны быть хорошо усвоены учащимися, так как они найдут дальнейшее применение на уроках геометрии, физики и других смежных дисциплин. Элективные курсы компенсируют достаточно слабые возможности базовых программ, помогают многим учащимся сделать выбор профиля старшей школы. Основная цель курса - развитие памяти, логического мышления, привитие интереса к математике, используя возможности индивидуальной и коллективной исследовательской работы учащихся.