Специальная математика
| Вид материала | Конспект |
СодержаниеN - множество натуральных чисел. Z |
- Направления работы семинара, 152.43kb.
- «Математика. Прикладная математика», 366.03kb.
- Программа подраздела «Философские проблемы математики», 94.9kb.
- Рабочая программа по курсу «Специальная педагогика и специальная психология» на 5 курсе, 94.48kb.
- Специальная обработка, 1624.5kb.
- Расшифровка : Математика, 146.94kb.
- Abramson Family Cancer Research Institute University of Pennsylvania (usa) Роль апоптоза, 15.2kb.
- Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
- Пангеометризм и математическая мифология, 956.71kb.
- Строительство. Система производственного контроля. Часть, 84.92kb.
1.9. Мощность множества
Обозначения:
N - множество натуральных чисел.
Z - множество целых чисел.
Q - множество рациональных чисел.
R - множество целых чисел.
С - множество комплексных чисел.
1.9.1. Понятие мощности
Г. Кантор понимал мощность, как двойную абстракцию. Мы абстрагируемся от конкретных элементов множества и от порядка, в котором они расположены. То, что в результате остается и есть мощность. Мощности можно сравнивать на больше, меньше, равно.
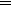
N - мощность множества N.
1.9.2. Аксиоматика Пеано
Наименьшей бесконечной мощностью является счетная мощность - мощность множества натуральных чисел. Это бесконечное множество можно задать с помощью системы аксиом:
1. 0 N
2. n N n’ N
3. n N n’ 0
4. n N, m N, n’ = m’ n = m
}
5
A = N
. 0 A N
n A n’ A
где n’ - элемент, следующий за n .
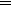
N = 0 (алеф-нуль) - счетная мощность.
1.9.3. Сравнение мощностей
1. Сравним мощность множества N и мощность множества целых четных положительных чисел:
1 2 3 4 5 …
2 4 6 8 10 …
то есть можно между этими множествами установить взаимно-однозначное соответствие. Это будет множество пар вида < n, 2n >.
2. Сравним мощность множества N и множества Z.
1 2 3 4 5 6 …
0 1 -1 2 -2 3 …
Здесь также имееть место взаимно-однозначное соответствие. То есть эти множества равномощны.
3. Сравним мощность множества N и множества Q.
0 1 -1 2 -2 3 -3 ...
1




 1 1 1 1 1 1
1 1 1 1 1 1



0 1 -1 2 -2 3 -3 ... В эту сетку попадут все рациональные числа.
2



 2 2 2 2 2 2
2 2 2 2 2 2


0 1 -1 2 -2 3 -3 ...
3 3 3 3 3 3 3
.
.
.
Мощность Q также равна мощности N.
1.9.4. Мощность множества R.
Теорема Кантора
Аналогом мощности действительных (вещественных) чисел служит множество точек
на отрезке действительной оси или на всей действительной оси.
Равномощность различных отрезков, а также отрезка и всей прямой показаны на рисунках.
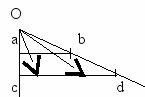
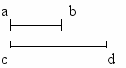
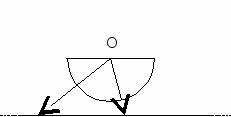
Теорема Кантора.
N < R (0 < 1)
Доказательство.
1. Поскольку множество R имеет такую же мощность, как и любой отрезок R, то будем рассматривать отрезок между 0 и 1. Числа будут представляться в виде бесконечных десятичных дробей. Конечные дроби для однозначности будут заменяться своими бесконечными аналогами. Например, 0.45 = 0.4499999…
Допустим, что каким-то образом установлено взаимно-однозначное соответствие между числами отрезка от 0 до 1 и множеством N.
0, а11, а21, а31 ......
0, а12,а22, а32 ......
0, а13,а23,а33 ...
.
Но здесь отсутствует число 0, b1, b2, b3 ... где a11 b1, b2 a22 ... bn ann
Следовательно, предположение о возможности «пересчитать» множество действительных чисел на отрезке от 0 до 1 неверно. Действительных чисел больше.
Мощность множества действительных чисел 1 называется мощностью континуума.
1.9.5. Арифметика бесконечного
Бесконечных мощностей бесконечно много: 0 < 1 < 2 < 3 < …
0 - самая маленькая бесконечная мощность.

 0 + A = 0 1 - 0 = 1
0 + A = 0 1 - 0 = 10 + 0 = 0 0 - A = 0
1 + 1 = 1 0 - 0 = 0
1 + 1 = 1 0 - 1 = 1
1.9.6. Противопоставление системного и
теоретико-множественного подходов
1. Системы, как и множества, состоят из элементов.
Теория систем исходит из первичности системы, в то время как теоретико-множественный подход считает, что первичен элемент.
2. Естественность системы (в ней нет случайных элементов) и "неразборчивость" множества.
3. Абстракция отождествления для множеств и априорная организация систем.
4. Системам присуща внутренняя организация, множествам - внешняя.
