Курс лекций для студентов заочного факультета самара
| Вид материала | Курс лекций |
- Курс лекций для студентов заочного и очно-заочного образования рпк «Политехник», 941.31kb.
- Курс лекций для студентов очного и заочного отделения специальностей 1-25 01 10 коммерческая, 830.45kb.
- Курс лекций для студентов заочного обучения Бурмистрова Л. А., Финансы предприятий:, 1991.45kb.
- Методические указания для студентов 1 курса заочного отделения исторического факультета, 244.82kb.
- В. С. Юрчук философия права курс лекций, 1556.93kb.
- Планы семинарских занятий на 2011-2012 учебный год (6 часов) по предмету «Экономическая, 205.43kb.
- Курс лекций Санкт-Петербург 2007 удк 342. 9 Ббк 67. 401 Б83 Рецензенты, 6052.89kb.
- Тексты лекций для студентов заочной формы обучения всех специальностей москва 2001, 2466.08kb.
- Краткий конспект лекций по дисциплине «Основы лесоводства и лесной таксации» Для студентов, 923.35kb.
- Лекций для студентов 4 курса педиатрического факультета, переведенных на контролируемую, 18.72kb.
4.2.Особые случаи вещественной арифметики
При реализации операций с вещественными числами возникают внутренние прерывания сопроцессора, называемыми особыми случаями сопроцессора (ОС). Если результат арифметической операции меньше минимального отрицательного числа или больше максимального положительного числа в данном формате, то такое состояние называется переполнением.
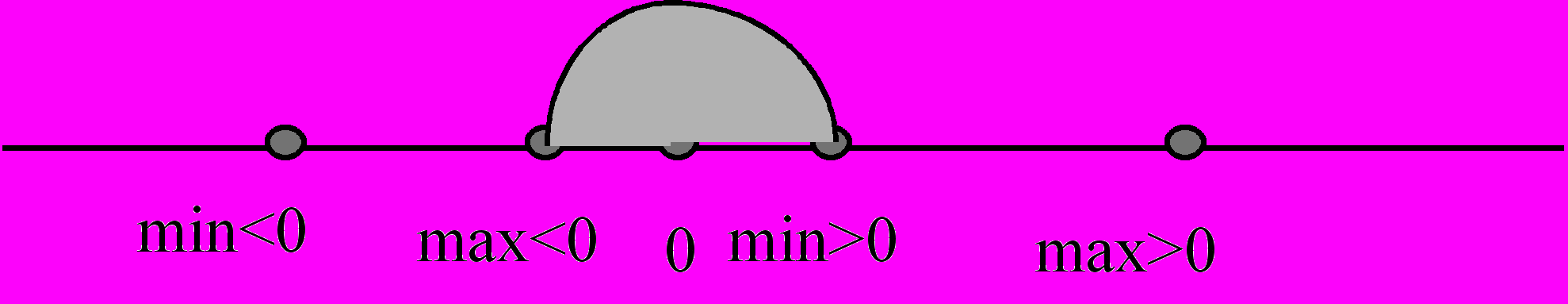
Если результат арифметической операции меньше минимального положительного числа и больше максимального отрицательного числа в данном формате, то такое состояние называется антипереполнением.
Сопроцессор генерирует шесть особых случаев вещественной арифметики:
1. Неточный результат. Возникает, когда результат операции невозможно точно представить в формате приемника. Например, при делении 1 на 3 получается бесконечная дробь;
2. Численное антипереполнение. Ненулевой результат слишком мал по абсолютной величине для представления в формате приемника. Например, при делении 1 на максимальное число с расширенной точностью 1.2*104932 получается очень маленькое число, которое не может быть представлено в формате с расширенной точностью. В данном случае результатом является денормализованное число. Денормализованными называются числа с плавающей точкой, имеющие в поле порядка все нули и нулевой старший бит мантиссы.
3. Денормализованный операнд. Возникает, когда операндом команды оказывается денормализованное число.
4. Деление на ноль. Результатом операции является бесконечность.
5. Численное переполнение. Возникает, когда результат слишком велик по абсолютной величине, чтобы быть представленным в формате приемника. Например, при сложении двух максимальных чисел в формате с расширенной точностью.
6. Недействительная операция. Включает в себя все арифметические операции, при которых нет приемлемого результата. Например, при делении нуля на ноль, при извлечении квадратного корня из отрицательного числа.
Обычная обработка особых случаев заключается в том, чтобы немедленно остановить операцию и передать управление процедуре обработки особого случая (внутреннего прерывания процессора).
Второй подход состоит в том, чтобы заставить операцию возвратить специальное значение особого случая и продолжить вычисления.
Оба подхода применяются в арифметическом сопроцессоре, программист может сам выбрать режим обработки особых случаев вещественной арифметики. При инициализации сопроцессора по умолчанию устанавливается режим формирования специальных значений. Для формирования специальных значений можно использовать числа с минимальными и максимальными значениями порядков в каждом формате, что не сильно сокращает диапазон значений нормализованных чисел. Кроме того, наборы специальных значений выбраны так, что большинство сравнений на равенство или неравенство выполняется правильно (эти сравнения редки для плавающей арифметики). Сделано это для того, чтобы при получении в качестве промежуточных результатов специальных значений, программа имела возможность сформировать правильный окончательный результат.
4.3.Формирование специальных значений в особых случаях
4.3.1. Случай неточного результата.
В качестве специального значения используется приближенное значение числа с плавающей точкой. Существуют четыре режима округления:
в направлении к 0 (обычно для целочисленной арифметики);
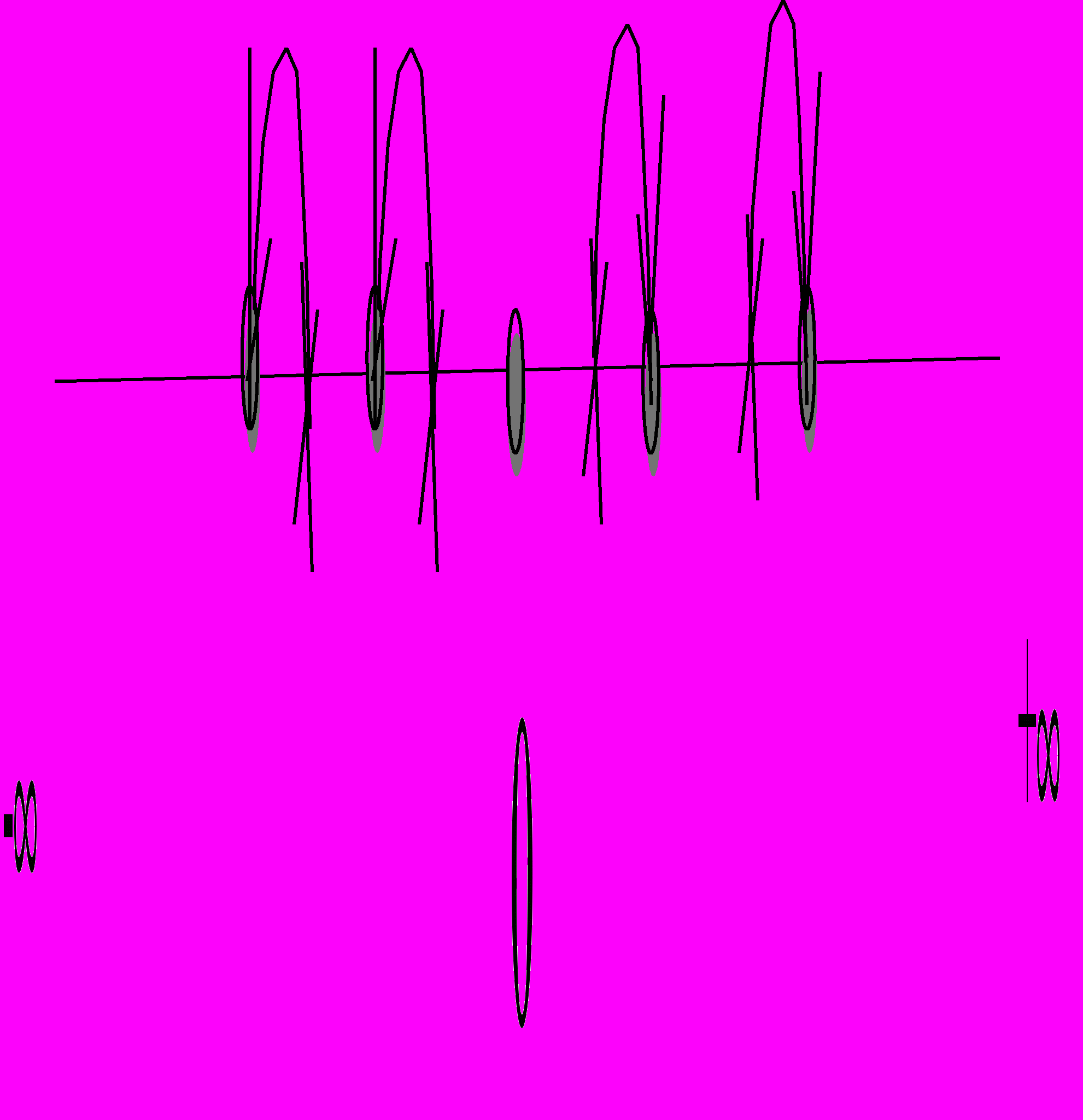
до ближайшего числа (если результат посередине, то выбирается ближайшее четное число).
округление к +
округление к -
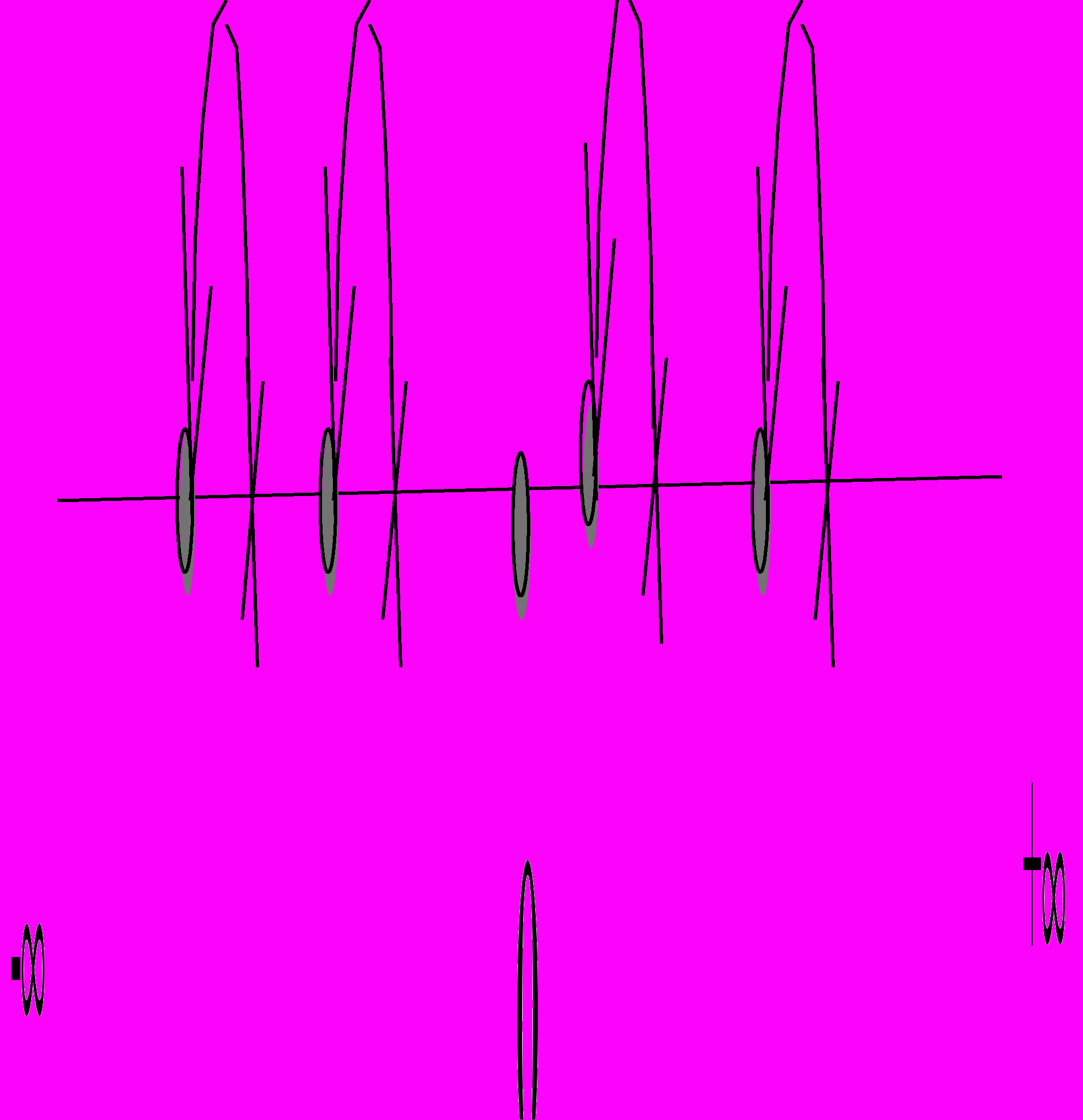
Режимы c) и d) используются для реализации интервальной арифметики : операция выполняется дважды: с округлением к + и с округлением к-. Истинный результат находится между двумя результатами, следовательно не требуется анализ ошибок округления. При инициализации сопроцессора по умолчанию устанавливается режим округления к ближайшему числу, однако программист может его изменить.
4.3.2.Численное антипереполнение.
Принято соглашение, что для денормализованного числа поле порядка 00..00 считается равным 00...01, но старший бит мантиссы равен 0 (а не 1). Для одинарной точности смещение равно 127, следовательно, поле порядка 00000001 соответствует порядку - 126.
Пример :
| Знак | Порядок | Старший бит мантиссы | Мантисса – 23 бита | |
| 0 | 00000001 | 1 | 10...00 | = 1.12*2-126 - норм. |
| 0 | 00000001 | 1 | 00...00 | =1.02*2-126 - норм. |
| 0 | 00000000 | 0 | 10...00 | =0.12*2-126 - денорм. |
| 0 | 00000000 | 0 | 01...00 | =0.12*2-127 - денорм. |
| | ............ | | ................ | ................................. |
| 0 | 00000000 | 0 | 00...01 | =0.12*2-149 – денорм. |
Точность минимального числа равна 1 биту, то есть происходит потеря точности ради расширения диапазона. Специальное значение - денормализованное число, а если результат мал для денормализованого числа, то в качестве результата формируется нуль.
На числовой оси плотность представимых чисел выше у нуля и ниже у максимальных значений.
-
+++++++
++-+++-+++-+
++-++-++-+-+-+-+-+-
+- -+- -+- - -+- - -+
0 Денорм.
Нормализованные числа
4.3.3. Денормализованный операнд.
Для денормализованных операндов выполняются следующие правила формирования результатов операций:
Результат равен 0, если он слишком мал для представления денормализованным числом (например, при умножении двух денормализованных чисел).
Результат - денормализованное число, если он представим в формате денормализованных чисел ( например, при сложении двух денормализованных чисел).
Результат - нормализованное число, если неточность денормализованного числа влияет на результат меньше, чем ошибка округления (например, при сложении денормализованного и большого нормализованного числа).
Результат - ненормализованное число, если результат слишком велик для денормализованного числа, неточный, а приемник имеет расширенную точность (например, при сложении денормализованного и большого нормализованного числа).
Ненормализованным числом называется число с расширенной точностью, имеющее обычное (ненулевое и неединичное) поле порядка и нулевой старший бит мантиссы.
Ненормализованные операнды в операциях подчиняются правилам для денормализованных чисел. Особый вид ненормализованного числа - псевдоноль. Псевдоноль имеет ненулевое поле порядка и нулевую мантиссу. В сравнениях псевдонули считаются нулями. Данный формат чисел поддерживается сопроцессором модели 80287 и не поддерживается моделью 80387 и устройством с плавающей точкой процессора 80486 и последующих моделей, так как уточнился стандарт представления чисел с плавающей точкой.
Результат - особый случай недействительной операции (наример, при делении на денормализированное число или попытке извлечения квадратного корня из денормализованного числа).
4.3.4. Деление на ноль.
Бесконечность - число, имеющее в поле порядка все единицы, а в поле мантиссы - все нули . Единица в старшем разряде хранится явно в расширенном формате. Так как поле знака может быть равным единице или нулю, то существуют положительная и отрицательная бесконечности.
Если x - конечное положительное число, не равное нулю, то разрешены следующие операции с бесконечностью:
1) x : + 0 = +
- x : + 0 = -
x : - 0 = -
- x : - 0 = +
2) x : + = + 0
- x : + = - 0
x : - = - 0
- x : - = +0
3) x *+ = +
- x * + = -
x * - = -
x * - = +
4) + : x = +
+ : - x = -
: x = -
: - x = +
5) + * + = +
+ * - = -
- * + = -
- * - = -
Запрещены следующие операции с бесконечностью (в качестве результата они дают особый случай недействительной операции ):
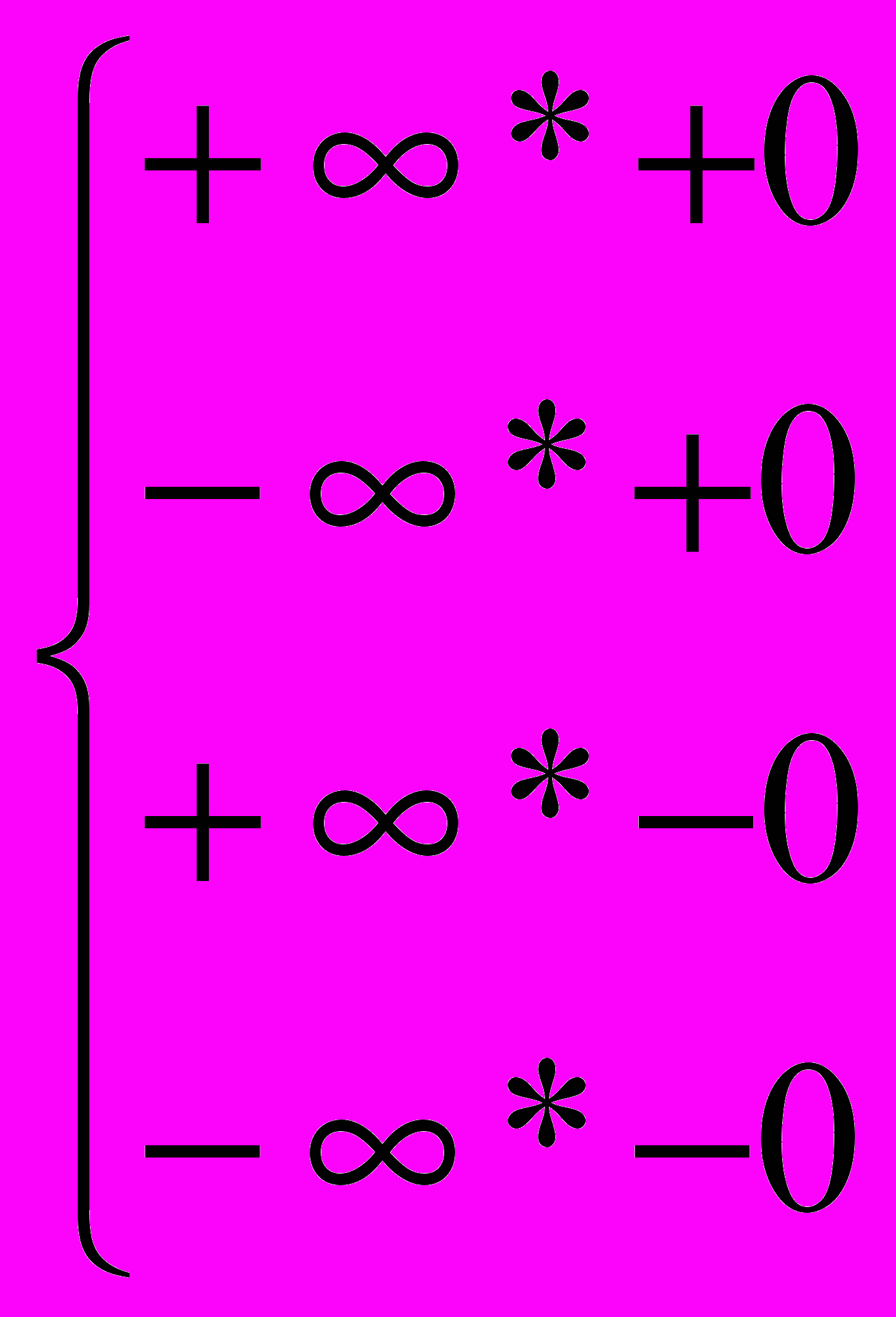
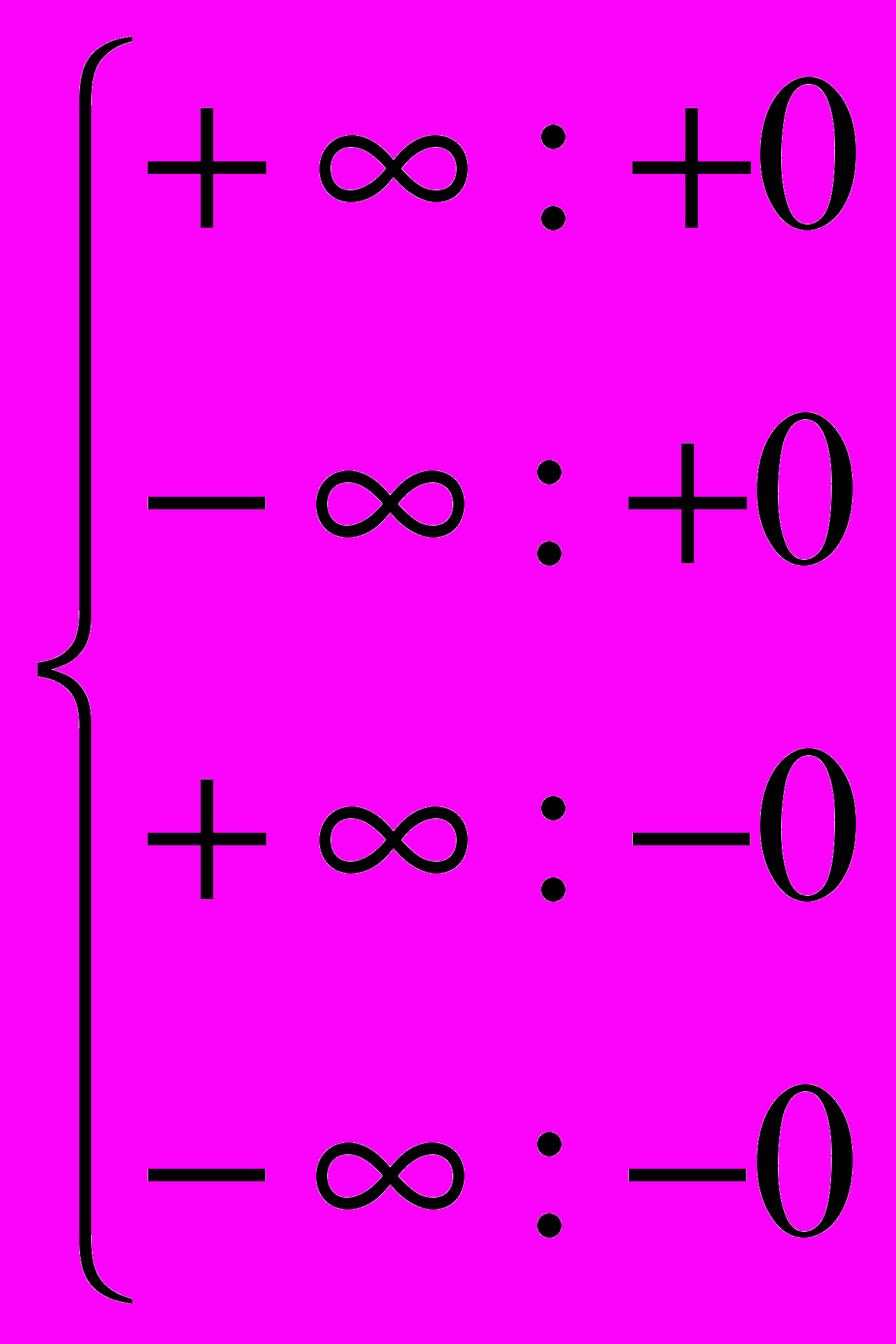
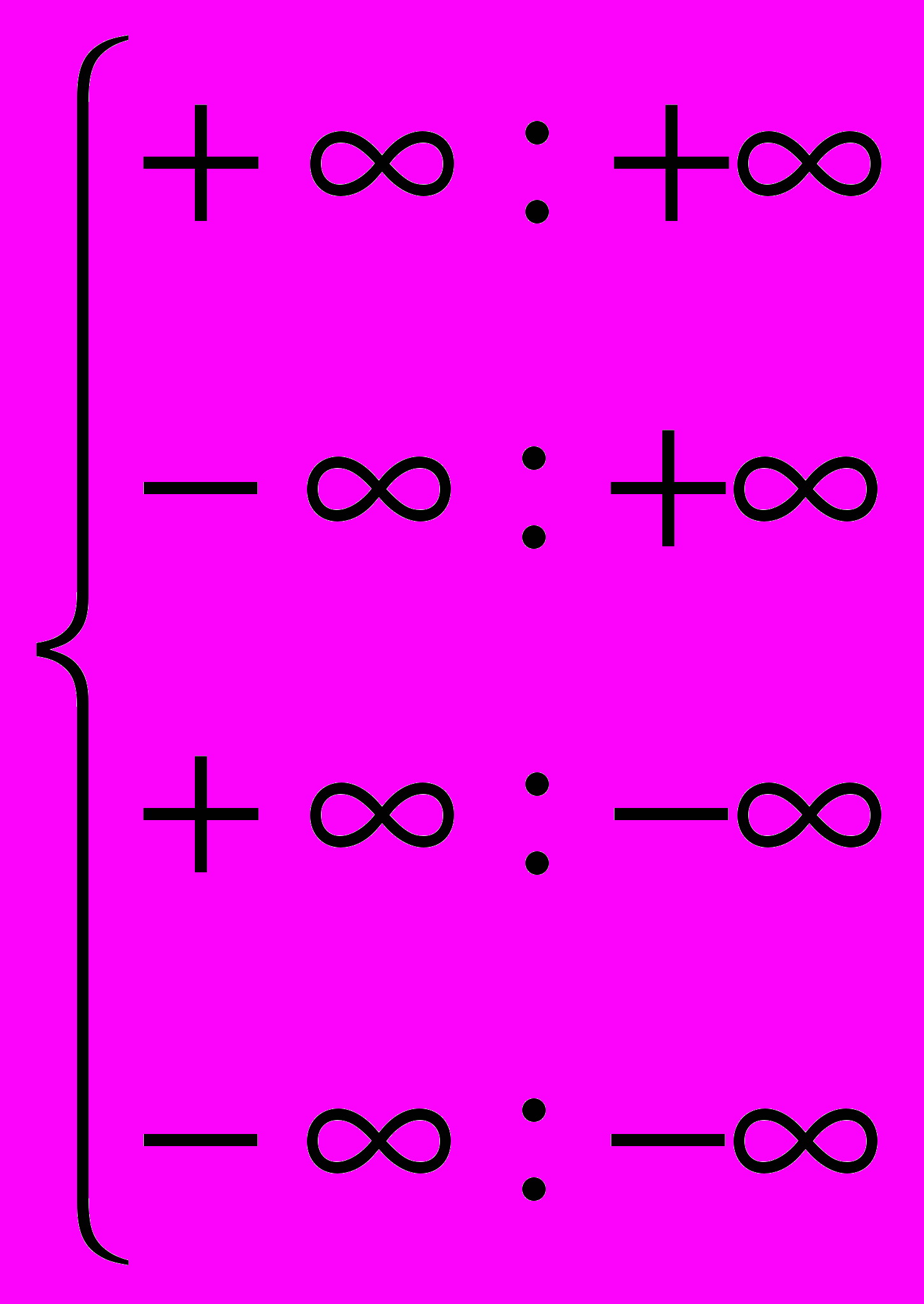
Для операций сложения, вычитания и сравнения бесконечностей появляются трудности. Математический сопроцессор 80287 имеет два режима управления бесконечностью : проективный и аффинный.
В проективном режиме - скрыт факт наличия двух бесконечностей и двух нулей. Сравнение бесконечности с конечным числом в качестве результата вызывает особый случай недействительной операции, сравнение двух бесконечностей дает результат “равны”. Сложение и вычитание бесконечностей дает в результате особый случай недействительной операции. Сложение и вычитание бесконечности и конечного числа дает в результате бесконечность.
В аффинном режиме существуют положительная и отрицательная бесконечности и существуют положительный и отрицательный нули. Этот режим разрешает сложение бесконечностей с одинаковыми знаками и вычитание бесконечностей с разными знаками:
(+ ) + (+ ) = + ;
(- ) - (+ ) = - .
В аффинном режиме также разрешены сложение и вычитание бесконечности и конечного числа, сравнение конечного числа с бесконечностью и сравнение бесконечностей друг с другом.
Проективный режим упразднен, начиная с математического сопроцессора 80387, у него и последующих версий устройства с плавающей точкой существует только аффинный режим управления бесконечностью.
4.3.5.Численное переполнение.
Численное переполнение наступает тогда, когда результат превышает наибольшее конечное число в формате приемника. Переполнение опасно, так как знак может оказаться неверным, а результат будет не бесконечность, а слишком большое для представления число.
Пример: деление большого числа на малое число (близкое к 0). Знак результата будет зависеть от знака малого числа, хотя он может быть неверным в результате ошибки округления.
Специальное значение формируется в зависимости от режима округления, установленного в регистре управления сопроцессора:
1) если установлен режим округления к ближайшему числу - то результат- плюс или минус бесконечность;
2) если установлен режим округления к минус бесконечности, то для положительных чисел результат - максимальное число больше нуля, для отрицательных чисел - минус бесконечность;
3) если установлен режим округления к плюс бесконечности, то для положительных чисел результат – плюс бесконечность, а для отрицательных чисел - максимальное число меньше нуля;
4) если установлен режим округления к нулю, то для положительных чисел результат - максимальное число больше нуля, для отрицательных чисел - максимальное число меньше нуля.
4.3.6.Недействительная операция.
Возникает, когда нет приемлемого результата в арифметической операции, операции сравнения или при стековых операциях (при этом флаг SF в регистре состояния равен единице):
при реализации операций сложения, вычитания, умножения и деления может возникнуть особый случай недействительной операции (например, при запрещенных операциях с бесконечностью);
- при реализации операции сравнения результатом является код условия. Обычно он показывает отношения “<”, “=”, “>”. Если при этом возникает особый случай недействительной операции (например, в проективном режиме при сравнении бесконечности и конечного числа, или при сравнении нечисла и конечного числа), то код условия принимает специальное значение “не сравнимы”. При этом нарушается закон трихотомии арифметики :
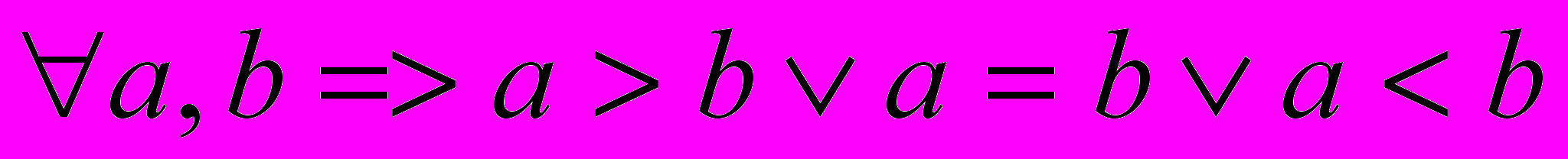. Это вызывает трудности в языках высокого уровня при исполнении оператора IF, так как, например, отрицанием условия больше или равно является не только меньше, но и “не сравнимы”;.особый случай стека: переполнение, то есть попытка включения числа в заполненный стек или антипереполнение, то есть попытка извлечения числа из пустого стека;
Во всех случаях результатом недействительной операции будет нечисло (NAN).
Нечисло – это двоичное вещественное число, у которого в поле порядка все единицы, а в поле мантиссы - все, кроме значения, зарезервированного за бесконечностью, то есть 1.000000...0.
Если один или оба операнда в операции -нечисло - то результатом тоже является нечисло. Таким образом, полученное в промежуточном результате операции нечисло распространяется в вычислениях и выдается как окончательный результат.
Особый случай нечисла - неопределенность. Сопроцессор формирует неопределенность как результат недействительной операции (остальные нечисла формируются программистом).
Для вещественных чисел неопределенность - это нечисло у которого в поле мантиссы две старшие цифры – единицы, а все остальные – нули (1.1...00), а поле порядка одни единицы (11...11). Поле знака также равно единице.
Для формата десятичных чисел неопределенность имеет следующее представление :
| Знак | 1 | 2 | 3 | 4 | мусор |
| 79 | 75 - 78 | 71 - 74 | 67 - 70 | 63 - 66 | 0 - 62 |
| 1 | 1111 | 1111 | 1111 | 1111 | хх...хх |
Десятичную неопределенность нельзя преобразовать в вещественное число, результат при этом - неопределенность.
Для двоичных целых форматов неопределенность представляется максимальным по модулю отрицательным числом, то есть имеет код
| 1 | 0000...00 |
| Знак | |
Целочисленная неопределенность при преобразовании в формат с плавающей точкой дает обычное отрицательное число.
Попытка преобразования нечисла, денормализованного, ненормализованного числа или бесконечности в формат целых чисел вызывает особый случай недействительной операции, результатом которой и является неопределенность.