Принципы и задачи проектирования 1 Уровни, аспекты и этапы проектирования

Вид материала

Документы

Содержание Постановка задачи синтеза маршрутов обработки 1 — возможные варианты; 2 —

Подобный материал:

• Лекция: Организация разработки ис: Каноническое проектирование ис. Стадии и этапы процесса, 312.68kb.
• А. П. Марков Технологические практикум, 91.28kb.
• "Сапр web pack ise. Этапы и технология проектирования устройств на базе плис. Примеры, 449.82kb.
• А. Е. Стешков методология проектирования металлорежущих инструментов, 74.74kb.
• 1 Цели и задачи курсового проектирования, 12.27kb.
• Программа дисциплины Проектирование информационных систем Семестры, 9.14kb.
• С. П. Колотовкин организация курсового проектирования, преддипломной практики и дипломного, 276.32kb.
• Список билетов для экзамена по курсу Моделирование и исследование систем, 99.07kb.
• 05. 13. 12 Системы автоматизации проектирования (по отраслям) Формула специальности, 21.27kb.
• Методы автоматизированного проектирования системы прогнозирования землетрясений 05., 315.41kb.

Постановка задачи синтеза маршрутов обработки

поверхности детали


При построении графа принима­лись во внимание заданные глубины резания на каж­дом переходе, которые могут существенно отличаться от фактических, упругие отжатия, износ инструмента и т. д. Граф, построенный по изложенной методике, формально описывает возможные варианты обработки какой-то детали из определенной заготовки на заранее выбранном оборудовании. Каждому ребру произвольной цепи, построенному для конкретного заданного значе­ния глубины резания ti и подачи Si, будет соответство­вать определенная технологическая себестоимость C_{nep i} при выполнении данного перехода i. Поэтому задача оптимизации структуры плана маршрута многопереход­ной обработки поверхностей деталей формально может быть представлена следующим образом: среди опреде­ленного множества цепей графа, построенного для кон­кретного случая обработки, нужно отыскать цепь, удов­летворяющую ограничениям и дающую минимальное значение целевой функции:



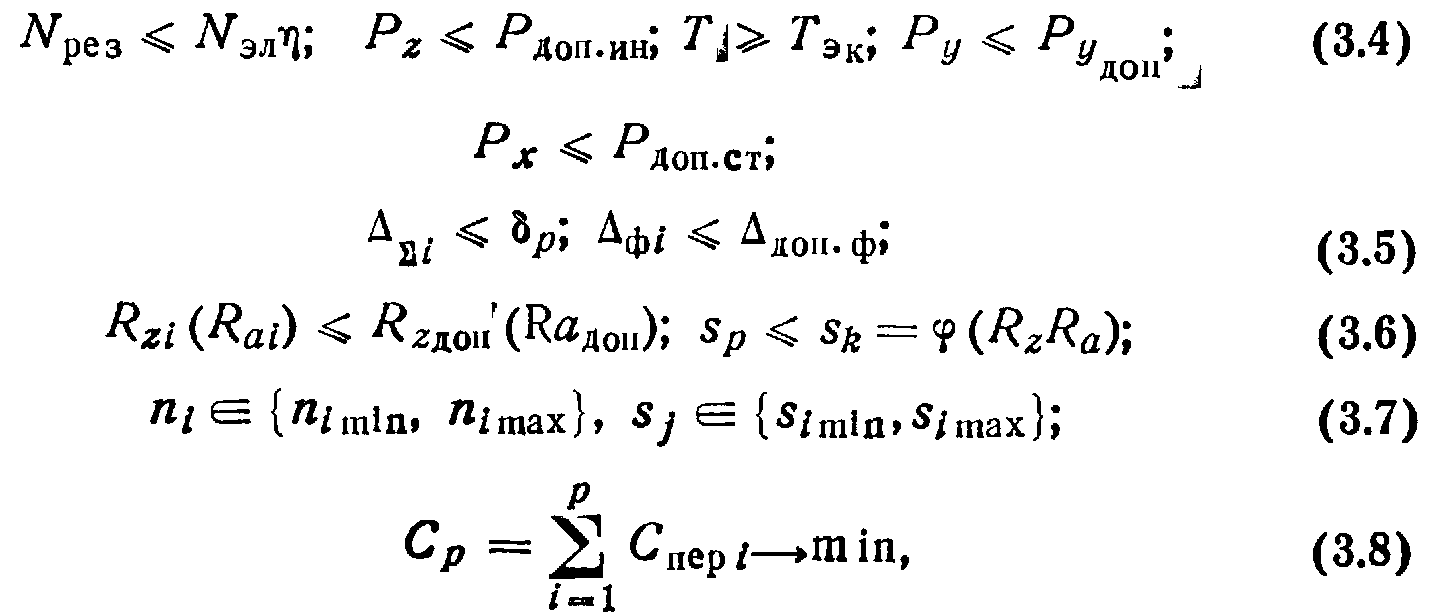
где Nрез—мощность, расходуемая на резание; Рz, Py, P_x—тангенциальная, радиальная и осевая составляю­щие усилий резания; Δ_i—суммарная погрешность об­работки; Δ_фi — отклонение формы; N_элη — мощность привода станка; Р_доп.ин—допускаемая нагрузка на ин­струмент; Т— стойкость инструмента; Тэк—экономиче­ская стойкость инструмента; Р_удоп— допускаемая ра­диальная сила резания; Р_доп.ст—усилие, допускаемое механизмом подачи станка; р—допуск на размер; Δ_доп.ф—допускаемое отклонение формы обрабатывае­мой поверхности; Rz—высота неровности; Р_zдоп—до­пускаемая высота неровности; Р_а —среднее арифмети­ческое отклонение профиля; Р_zдоп —допускаемое сред­нее арифметическое отклонение профиля; Sp—значение подачи при выполнении р-го перехода; Sk—значение подачи, обеспечивающее требуемое значение Р_z или R_a ; n_i и s_i—частота вращения шпинделя и подача на i-м переходе; {n_imin, n_imax} — предельные значения частот вращения шпинделя по паспортным данным станка; {S_imin, S_imax} — предельные значения подач по паспортным данным; С_перi—технологическая себестоимость i-го перехода.

В качестве целевой функции можно принимать себестоимость Ср выполнения р переходов при обработке

поверхности 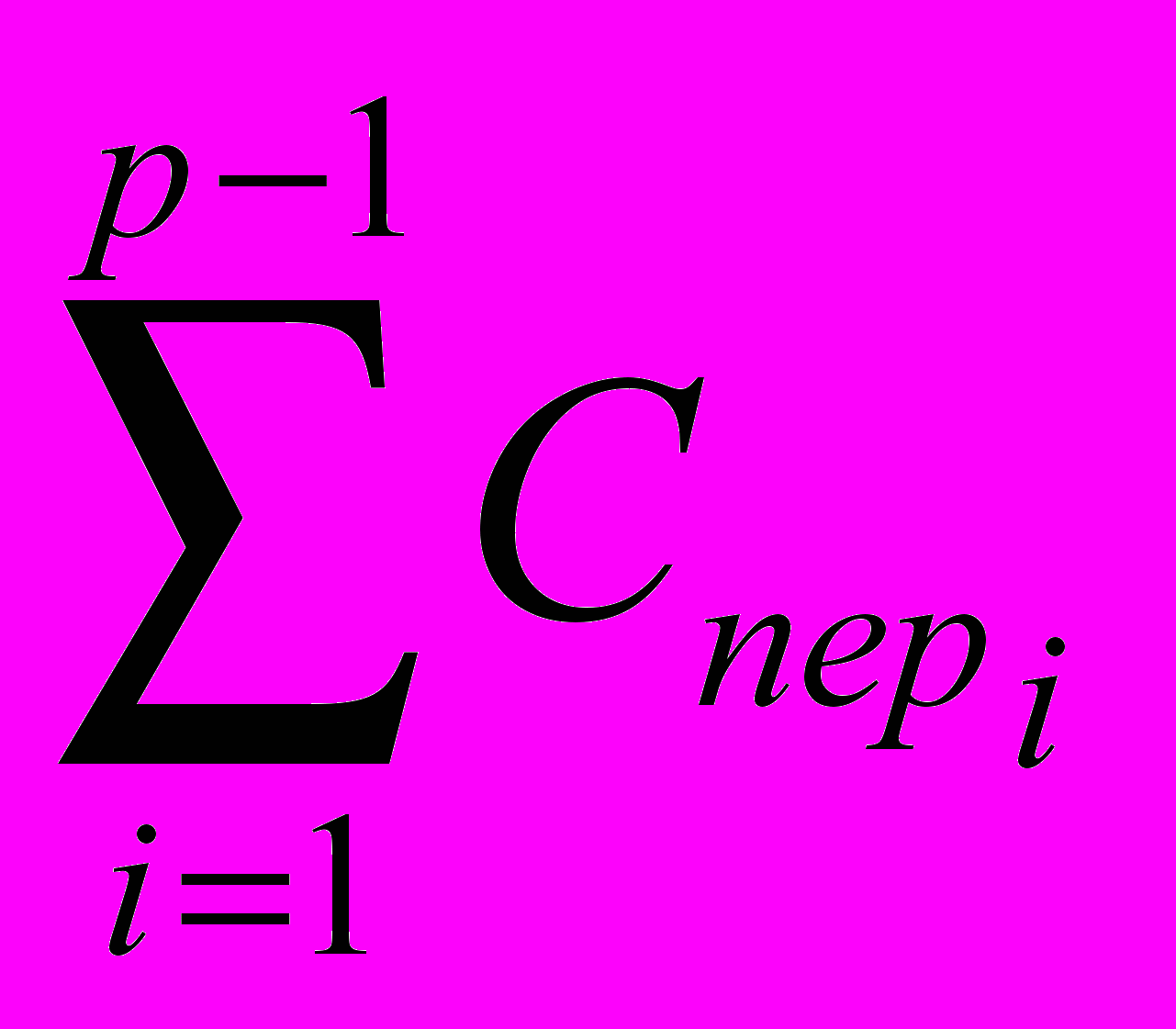, а также неполное время штучное

t’_шт, оперативное t’_on или основное t_o.

Условия (3.4) используют только на черновых пере­ходах. В каждом конкретном случае отдельные ограни­чения можно не учитывать, если они не активны.

Оптимальное решение находится путем определения экстремального значения функции (3.8) для всего под­множества ребер, исходящих из каждой вершины.


3.5.3 Решение задачи синтеза маршрута обработки

поверхности детали


Для поиска оптимального варианта пла­на маршрута обработки поверхностей используют дина­мическое программирование. Общей особенностью моде­лей динамического программирования является сведение задач принятия решений к получению рекуррентного соотношения, которое можно представить как



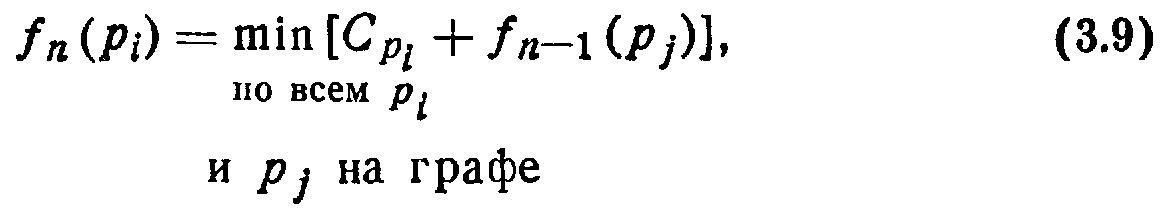
где fn {р_i) — технологическая себестоимость, отвечающая стратегии минимальных затрат для плана обработки от технологического перехода р_i, если до последнего пере­хода остается п шагов; Ср_i — технологическая себестои­мость при выполнении технологического перехода pi, причем переход pi предшествует переходу pj.

Возможные варианты обработки поверхности могут быть представлены в виде сети или графа.

Методика поиска наилучшего варианта маршрута обработки поверхности предусматривает распределение заданного общего минимального припуска Z_{o min} на N этапов. Величина припуска на первом этапе (нумера­ция этапов ведется от поверхности обработанной дета­ли) равна l ₁= t_min, где t_min —наименьшая глубина реза­ния, допускаемая процессом резания. Величина припу­ска на втором этапе l₂ = t_min +, на третьем — l₃ = t_min +2 и т. д. Величина припуска на этапе с номе­ром т равна l_min = t_min +(m-1). Шаг  определяется возможностью станка перемещать режущий инструмент или заготовку на заданный настроечный размер.

Поверхность заготовки в процессе обработки может иметь ряд значений промежуточных технологических до­пусков: ₃, _i, _Д (₃—допуск на размер поверхности заготовки; _i —промежуточный допуск на размер; _Д— допуск на размер поверхности детали).

Выбор оптимального варианта проводится начиная с первого этапа. Этот этап соответствует заключительно­му переходу обработки поверхности и при назначении его необходимо знать параметры предшествующего пе­рехода. Располагая зависимостью суммарной погрешно­сти обработки от управляемых переменных, т. е. _i = f(t, s, v), где t—глубина резания; s—подача; v— скорость резания, для конкретного метода механиче­ской обработки резанием и зная параметры планируемо­го перехода, можно было бы рассчитать ожидаемую по­грешность обработки. Однако, не имея данных о пред­последнем переходе, делают различные предположения о том, какая погрешность обработки может иметь место после его выполнения. Следуя принципу оптимальности динамического программирования, для каждого из этих предположений необходимо выбрать такие переменные, чтобы на заключительном переходе получить оптималь­ное решение. Этот принцип сохраняется при выборе оп­тимального варианта на каждом этапе.

На этапе 1 для уменьшения количе­ства расчетных вариантов перебор возможных допусков _1,i начинают с _1,i = ₃. При этом глубина резания t₁ = t_min +_1,i + _Д. Определяют ожидаемую погрешность обработки. Если _i  _Д то для этого варианта вычисляются значения целевой функции (рекуррентное соот­ношение) :



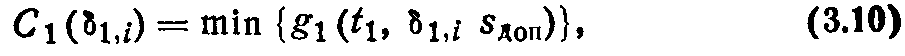
где минимум берется по всем подачам из массива по­дач А^(S).

Подача S_доп в этом случае должна удовлетворять ограничению, связанному с шероховатостью поверхности детали S_доп  S_Rz, где S_Rz — подача, обеспечивающая заданную величину неровности Rz- Значения допусков на отклонение размера поверхности после предшествую­щего перехода на этапе 1, обеспечивающее _Д , образуют массив A₁^().

На этапе 2 - l₂ = t_min + , глубина реза­ния t₂ = (t_min +) + _2,i + _Д, а рекуррентное соотношение

С₂(_2,i ) = min g₂( t₂ , _{2,i Sдоп} , ) (3.11)

Поэтому план нахождения g₂( t₂ , _{2,i Sдоп} , ) обеспечи­вает заданный параметр точности _Д обработанной по­верхности и образует массив А₂^() промежуточных до­пусков.

Однако на этапе 2 возможна обработка поверхности за один переход (р=1) и за два перехода (р=2). При р=2 необходимо обеспечить не только заданный допуск _Д , но и допуск ранее выполненного перехода (этапа) k, принадлежащего массиву допусков А_^(), для которо­го уже имеется план обработки. При этом максимально возможная подача определяется ограниче­ниями по мощности привода станка, прочности и стой­кости режущего лезвия инструмента и т. д.

Глубина резания на этапе r при р==2



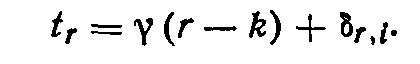
Подставляя значения подач s{s_min, S_max}, допусков А_r^(){А_r^()_min, А_r^()_max }, можно рассчитать ожидаемую погрешность на этапе r, т. е. _{r, i} , и проверить условие_{r, i}  _R . В результате образуются массивы допусков А_r^()и подач А_r^(S). Так как при одном и том же допуске заготовки , _{r ,i} при разных значениях подачи можно по­лучить различные допуски _{r, j} предшествующего этапа, то варианты на этапе r будут отличаться по технологической себестоимости.

Сравнивая возможные однопереходные и двухпере­ходные планы обработки, можно составить вариант с наименьшим значением технологической себестоимости:

С_r=(_{r, i}) = min g_r( t_r , S_r,i , S_доп , ) (3.12)

Возможны планы обработки за один (p=1), два (p=2) и три (p=3) перехода. Величина припуска на этапе будет l_q = t_min +(q-1).

Первый и второй варианты маршрута обработки оп­ределяются расчетом аналогично расчету ранее рассмот­ренного этапа с номером r.

При трехпереходном маршруте обработки p=3, t_q= (q-r)+_{q, i} находят значения _{q, i} и S_{q, i}, которые образуют соответственно массивы допусков А_q^()и подач А_q^(S) на этапе q при условии _{q, i}  _{r, i}. Технологи­ческая себестоимость обработки при р==3 складывается из себестоимости обработки и величины С_г(_{r, i}).

В общем случае для этапа с номером и₁ возможны различные варианты маршрутов обработки поверхности р=1 и p>1. Величина припуска на этапе и будет 1_и= t_min+(u - 1). Тогда рекуррентное соотношение будет иметь вид




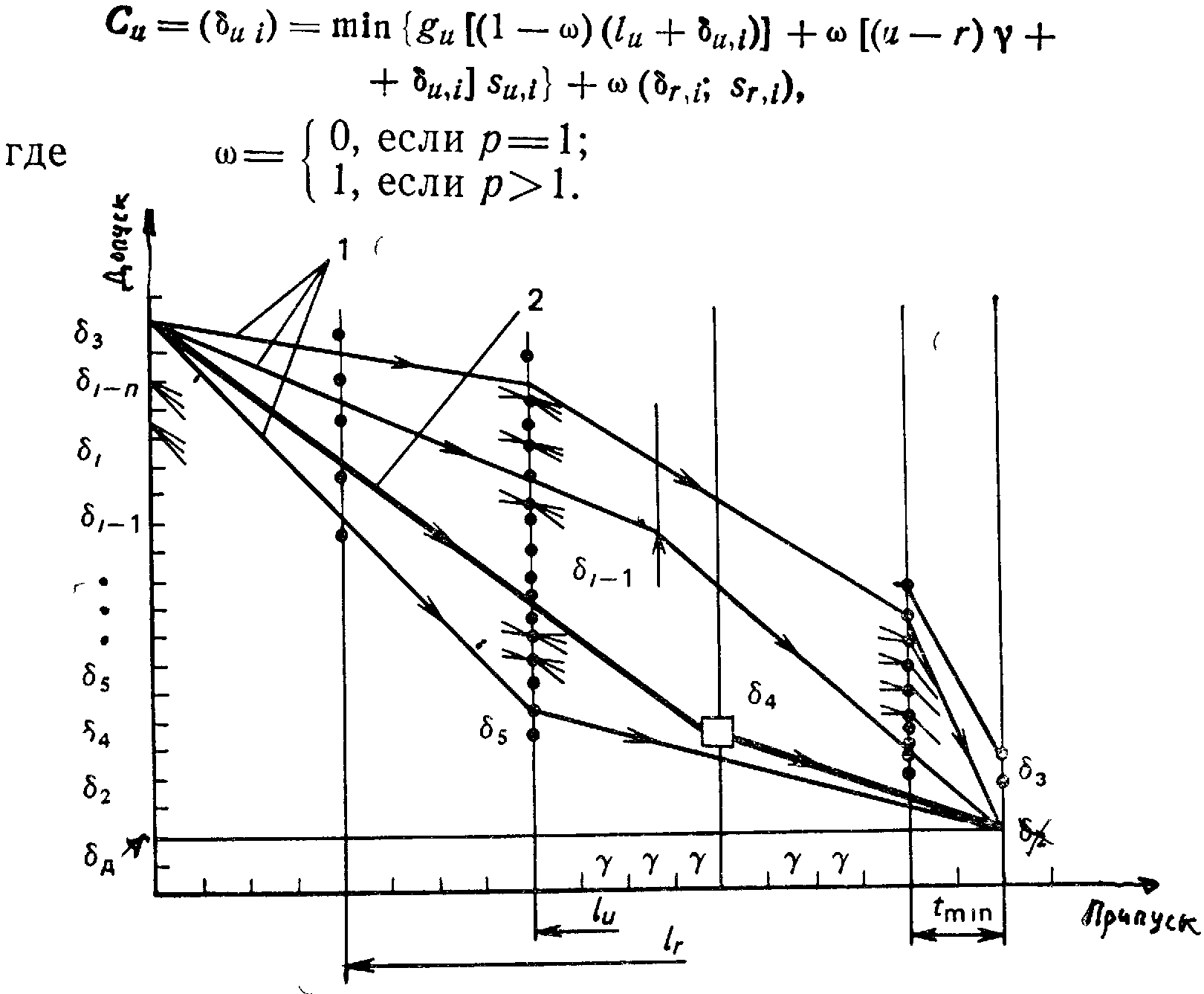
Рисунок 3.9 - Общая схема нахождения оптимального варианта плана маршрута обработки поверхности детали:

1 — возможные варианты; 2 — оптимальный вариант


Это соотношение позволяет из множества сформулированных вариантов выбрать один оптимальный по технологической себестоимости вари­ант с указанием глубин резания, подач и скоро­стей резания по техноло­гическим переходам (рисунок 3.9). В случае многопереходной обработки число вариантов для срав­нения по технологической себестоимости определя­ют от первого перехода

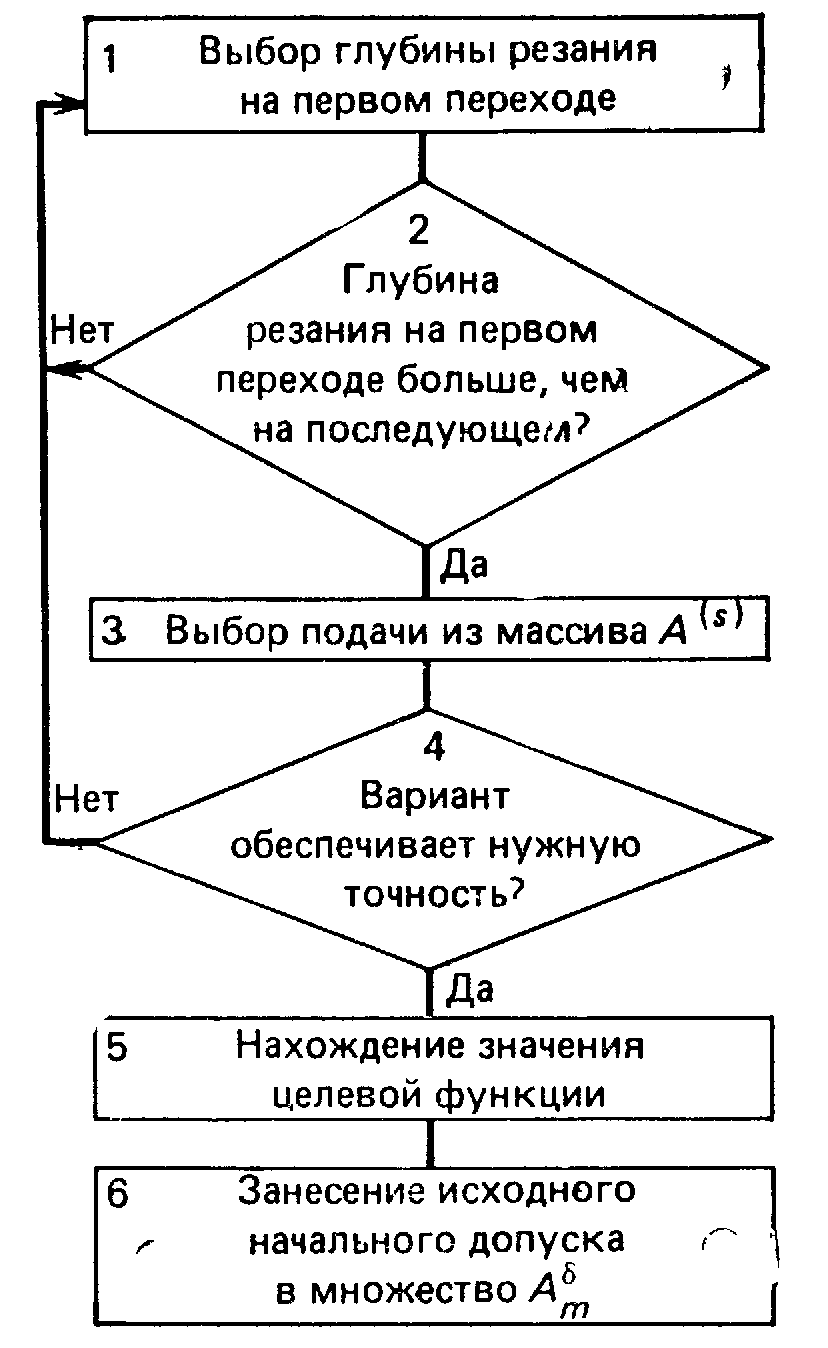
(от заготовки). Для этого предусматривают несколько шагов (рисунок 3.10)


Рисунок 3.10 - Схема алгоритма нахождения варианта плана маршрута обработки поверхно­сти детали с учетом технологи­ческих параметров


3.6 Выводы


Проектирование - процесс, заключающийся в преобразовании исходного описания объекта в окончательное описание. Оно различается на неавтоматизированное, автоматизированное и автоматическое.

Основные принципы проектирования – декомпозиция и иерархичность описания объектов, многоэтапность и итерационность, типизация и унификация проектных решений и средств проектирования.

Стадии, этапы, проектные процедуры и операции являются составными частями процесса проектирования.

Цепочка: синтез - анализ - оценка и модификация параметров или изменение структуры или корректировка технического задания является типичной последовательностью проектных процедур при автоматизации технологического проектирования.

При синтезе технологических маршрутов и операций обработки деталей используют метод структурного синтеза, основанный на использовании типовых решений и относящийся к методам выделения варианта из обобщенной структуры.

Для поиска оптимального варианта плана маршрута обработки поверхностей используют методы направленного перебора, динамического программирования и другие.


Первым аспирантом стал Кунгуров В.В., который до настоящего времени успешно работает в АлтГТУ. Под руководством Т.В. Ершова за период его работы на кафедре было подготовлено 13 кандидатских диссертаций. Большинство выпускников аспирантуры остались работать на кафедре: это кандидаты технических наук, доценты Каменская А.А., Ковалова Р.И., Лукин Л.Н., Гончаров В.Д., Федорова Н.П., Аскалонова Т.А., Лабецкий В.М., Неверов В.И..

Огромная роль в оснащении лабораторий станками, технологической оснасткой, исследовательской аппаратурой принадлежит ветерану кафедры и института Ласкину Виктору Алексеевичу, который заведовал лабораториями более 30 лет. Имея золотые руки мастера и инженерное мышление, он участвовал как соавтор и исполнитель многих научных и инженерных разработок как для исследовательских работ своей кафедры, так и по заказам других кафедр и заводов.

За весь период работы кафедрой "Технология машиностроения" выпущено более 10 тыс. инженеров-технологов. Большинство из них стали ведущими специалистами производства и крупными руководителями предприятий. Мэр г. Барнаула Баварин В.Н. – выпускник кафедры. Генеральным директором ОАО "Барнаульский станкостроительный завод" много лет работал выпускник специальности "Технология машиностроения" герой социалистического труда, почетный гражданин города Барнаула Кулагин П.С., и сейчас этот завод возглавляет выпускник кафедры Яшкин В.А. Главными инженерами предприятий города в 70-е – 80-е годы работали Лунев А.В., Егоров В.Н., Цемахович А.Д., главными технологами – Майданский Я.В., Сорокин Г.П. (Продолжение на стр.165).