Сапр 1 Общие положения

Вид материала

Документы

Содержание Синтез параметрический ТТ может быть формализована и представлена как зада­ча оптимального преобразования ТТ ТТ можно представить как выделение в пространстве УП Задача совмещения Задача центрирования Задача оптимизации параметров без учета сведений об их распределении Задача назначения допусков Основная задача оптимизации параметров и допус­ков Математическая формулировка основной задачи оптимизации параметров и допусков. Хд== {ххп | (х)  о, (х) =0}, (5.146) Разновидности постановок задач параметрического синтеза Задачи назначения допусков Задачи совмещения и центрирования Задачи назначения технических требований Задачи назначения технических требований Задачи идентификации параметров разрабатываемых математических моделей Задачи определения областей адекватности математи­ческих моделей Классификация задач структурного синтеза Выбор основных принципов функционирования объ­екта Выбор технических решений ... Полное содержание

Подобный материал:

• Оренбургский государственный университет вопросы для вступительного экзамена в аспирантуру, 61.82kb.
• Одобрен Советом Федерации 11 июля 2008 года                                 Раздел, 2086.04kb.
• Управление информационным обеспечением телекоммуникационной учебно-исследовательской, 27.98kb.
• 05. 13. 12 Системы автоматизации проектирования (машиностроение), 22.99kb.
• И в срок Для приобретения полной версии работы щелкните по Содержание Общие положения, 36.48kb.
• Принят Государственной Думой 27 сентября 2002 года Одобрен Советом Федерации 16 октября, 3283.83kb.
• Методические рекомендации к разработке рабочих программ учебных дисциплин. Общие положения, 67.97kb.
• 1. Общие положения, 622.12kb.
• 1. Общие положения, 814.49kb.
• Принят Государственной Думой 22 апреля 2011 года Одобрен Советом Федерации 27 апреля, 757.89kb.

Классификация задач пара­метрического синтеза. К задачам параметрического син­теза относится совокупность задач, связанных с определением

СИНТЕЗ ПАРАМЕТРИЧЕСКИЙ





Назначение технических требований

Расчёт параметров элементов

Идентификация математических моделей


при внешнем проектировании

совмещение



центрирование в пространстве ХП



при нисходящем проектировании

расчёт параметров моделей



оптимизация параметров

определение параметров адекватности




назначение допусков





Основная задача оптимизации параметров и допусков





Рисунок 5.13 - Классификация задач параметрического синтеза

требований к параметрам объекта, номинальных значений параметров и их допусков. Классификация за­дач параметрического синтеза показана на рисунке 5.13.

Для пояснения сущности задач параметрического син­теза используют геометрическую интерпретацию, связан­ную с введением n-мерного пространства ХП управляе­мых параметров и (или) m-мерного пространства УП вы­ходных параметров. Здесь п—количество управляемых параметров, т. е. внутренних параметров, значения кото­рых должны быть определены при параметрическом син­тезе, т—количество выходных параметров. Каждой точ­ке пространства ХП (УП) соответствует вектор значений управляемых (выходных) параметров, составляющие этого вектора суть координаты точки.

Группа 1 задач параметрического синтеза связана с назначением технических требований к выходным па­раметрам объекта. На верхнем иерархическом уровне нисходящего проектирования или на каждом иерархиче­ском уровне восходящего проектирования эта задача не может быть полностью формализована. Как правило, исходное ТЗ отражает потребности в новых технических изделиях, их назначение, опыт производства и исполь­зования прототипов и т. п. Это ТЗ формулируется на ос­нове мнений экспертов и требует дальнейшей конкрети­зации и согласования. Существенной частью формируе­мого ТЗ должны стать перечень выходных параметров объекта y_j и значения технических требований TT_j к ним, т. е. условия работоспособности y_j  TT_j. Определе­ние вектора технических требований ТТ—основная за­дача параметрического синтеза, решаемая при внешнем проектировании.

На всех иерархических уровнях нисходящего проек­тирования, кроме самого верхнего, задача назначения ТТ может быть формализована и представлена как зада­ча оптимального преобразования ТТ к выходным пара­метрам объекта на k-м уровне в ТТ к выходным пара­метрам частей объекта на (k+1)-м уровне.

Назначение ТТ можно представить как выделение в пространстве УП области работоспособности УР:

УР={У УП| у_j  ТТ_j, j [1:m]},

где [1 : m] означает множество целых чисел в интерва­ле [1, m ].

Областью работоспособности ХР в пространстве управляемых параметров называют множество точек ХХП, в которых выполняются все заданные условия работоспособности у_j (X)  тт] и дополнительные огра­ничения на управляемые параметры вида

x’_j  x_j x’’_j, (5.13)

называемые прямыми ограничениями и выражающие условия физической или технологической реализуемости параметров, т. е.

ХР = {X  ХП | у_j (X)  ТТ_j, х’_j  x_j < х’’_j ,

j[1:m], i[l:n]}.

Группа 2 задач параметрического синтеза связана с расчетом параметров элементов объекта при заданной структуре объекта. Параметры проектируемых объектов, как правило, являются случайными величинами вследст­вие не поддающихся строгому учету производственных погрешностей изготовления и случайного характера па­раметров исходных материалов. Поэтому в наиболее об­щей постановке определение параметров подразумевает расчет как вектора номинальных значений параметров Х_ном, так и вектора их допусков G. Обычно сведения о характере распределения вектора Х при проектировании весьма приближенные. При этом под номинальным зна­чением x_{ном i} параметра x_i чаще всего понимают его ма­тематическое ожидание, а под допуском gi—половину интервала со значением x_{ном i} в центре и вероятностью попадания в него значений x_i , равной заданной величи­не Р.

Задача определения параметров решается после то­го, как назначены условия работоспособности.

В САПР встречаются следующие разновидности задач определения параметров элементов.

Задача совмещения, решаемая при известной форме (часто и при известных размерах) области XG и сводя­щаяся к такому совмещению областей ХР и XG, при ко­тором вероятность выполнения заданных условий работоспособности максимальная [5].

Задача центрирования, являющаяся наиболее часто встречающимся частным случаем задачи совмещения, когда сведения о предполагаемой корреляции и асиммет­рии распределений параметров отсутствуют. Задача сво­дится к нахождению центра X* области ХР в нормиро­ванном пространстве параметров, этот центр и принима­ется в качестве искомой точки Х_ном [5].

Задача оптимизации параметров без учета сведений об их распределении, сводимая к задаче математическо­го программирования. Для нормирования выходных па­раметров полезно иметь сведения о допусковой области, но не в пространстве ХП управляемых параметров, а в пространстве УП выходных параметров.

Задача назначения допусков, решаемая при заданных векторе Хном и предположениях относительно экономи­чески оправданных соотношений между допусками gi отдельных параметров. Эта задача сводится к выбору приемлемого процента выхода годных изделий при их производстве и вписыванию гиперпараллелепипеда до­пусков в ХР.

Основная задача оптимизации параметров и допус­ков, заключающаяся в определении векторов Хном и G при заданных соотношениях между допусками gi отдель­ных параметров [5].

Группа 3 задач параметрического синтеза связана с определением параметров используемых в САПР мате­матических моделей и определением областей их адек­ватности. Эти процедуры входят составной частью в ме­тодику моделирования.

Математическая формулировка основной задачи оптимизации параметров и допусков. Большинство задач па­раметрического синтеза элементов сводится к решению задач математического программирования.

Задача математического программирования формули­руется следующим образом:

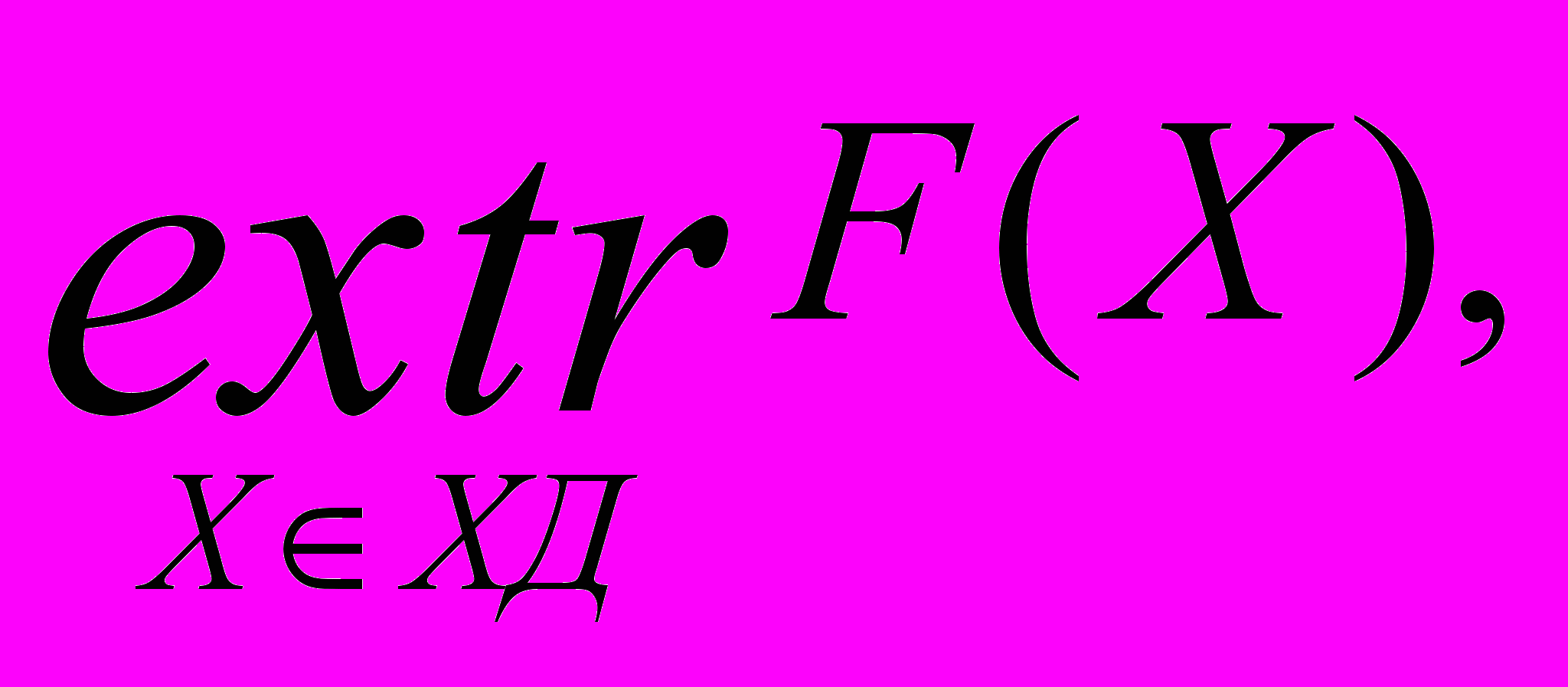(5.14a)

т. е. нужно найти экстремум (максимум или минимум) целевой функции F(X), иначе называемой функцией ка­чества, в пределах допустимой области ХД изменения управляемых параметров X. Область ХД может зада­ваться совокупностью ограничений типа неравенств (Х) 0 и типа равенств (Х) =0, т. е.

ХД== {ХХП | (Х)  О, (Х) =0}, (5.146)

где (Х) и (Х) —вектор-функции.

Основная задача оптимизации парамет­ров и допусков—двухэтапная.

Этап 1 — решение задачи предварительной оптими­зации параметров элементов. Цель решения этой зада­чи—определение некоторой опорной точки Х_э ХР. Воз­можны случаи, когда вектор ТТ задан достаточно жест­ко и область ХР оказывается пустой. В этих случаях ре­зультатом решения является фиксация факта, что ХР=0, с указанием тех конфликтных (противоречивых) выходных параметров, требования к которым не могут быть одновременно удовлетворены. На основании этих данных инженер принимает решение либо об изменении:

структуры объекта, либо об изменении технических тре­бований к конфликтным выходным параметрам.

Основными вопросами, решаемыми при сведении предварительной задачи оптимизации к задаче матема­тического программирования (5.14), являются выбор критерия оптимальности, количественно выражаемого целевой функцией, ограничений и способа нормирова­ния параметров.

Целевая функция и ограничения обычно формируются на основе заданных условий работоспособности. Наибо­лее популярны частный и максиминный критерии опти­мальности. В частном критерии оптимальности в каче­стве целевой функции выбирается один из выходных па­раметров, например y_R, тогда условия работоспособно­сти всех остальных выходных параметров y_j(Х)  TT_j, (jk) входят в ограничения. Система ограничений до­полняется прямыми ограничениями (5.13). Управляемы­ми параметрами являются рассчитываемые параметры элементов объекта. При этом опорная точка Х_э—ре­зультат решения задачи предварительной оптимиза­ции, — как правило, будет найдена на границе области ХР. В большинстве случаев такое положение точки Х_э неблагоприятно для выполнения второго этапа оптими­зации, поэтому чаще используют максиминный критерий оптимальности, при котором точка Х_э размещается внут­ри области ХР на максимальном расстоянии от ближай­шей границы области ХР.

При постановке и решении задач предварительной оптимизации могут присутствовать операции, основанные на сравнении различных параметров, например опреде­ление расстояний. Для их выполнения необходима нор­мализация параметров, сводящаяся к преобразованию исходных параметров, имеющих физические размерно­сти, в безразмерные величины.

Для управляемых параметров X_i в пространстве ХП при решении предварительной задачи оптимизации целе­сообразно использовать логарифмическую нормализацию

U_i=ln x_i/_i (5.15)

где под и_i, и x_i понимаются нормализованный и ненорма­лизованный параметры соответственно; _i —коэффици­ент, равный единице параметра Xi.

Способ (5.15) удобен тем, что приводит к использова­нию относительных приращений параметров в процессе оптимизации, так как du_i=dx_i/x_i.

Для выходных параметров один способ нормализации основан на преобразовании S_j(X) = (ТТ_j—y_j(X )/ТТ_j; другой способ—на понятии запаса работоспособности Zj. Последний способ удобен при наличии некоторых ап­риорных сведений о допусках выходных параметров _j, и заключается в переходе от параметров у_j, к их нормали­зованным запасам работоспособности в виде

Zj = а_j ((ТТ_j – у_j (Х))/_j - 1), (5.16)

где а_j— некоторый весовой коэффициент.

Постановка задачи предварительной оптимизации на основе максиминного критерия обычно производится при выборе в качестве целевой функции минимального запаса среди запасов работоспособности всех выходных параметров, а в качестве ограничений—прямых огра­ничений.

Этап 2 — решение задачи вписывания допусковой области. Задача сводится к взаимному расположению заданной области работоспособности ХР и некоторой допусковой области XG с заданными свойствами в про­странстве ХП. Задача может быть представлена как за­дача математического программирования, в которой в ка­честве управляемых параметров Х фигурируют парамет­ры, задающие форму гиперфигуры XG и ее положение в пространстве ХП, в качестве целевой функции—некото­рая оценка размеров области пересечения ХР∩ХС, а в качестве ограничений—условия малости рассогласова­ния положений областей ХР и XG.

При определении допусков вписываемой фигурой яв­ляется гиперпараллелепипед. Заданные соотношения между допусками g_i и результаты предварительной опти­мизации обычно используют для нормализации парамет­ров х_i на этапе вписывания. Например,

u_i=а_i(x_i - x_эi)/x_эi + 1, (5.17)



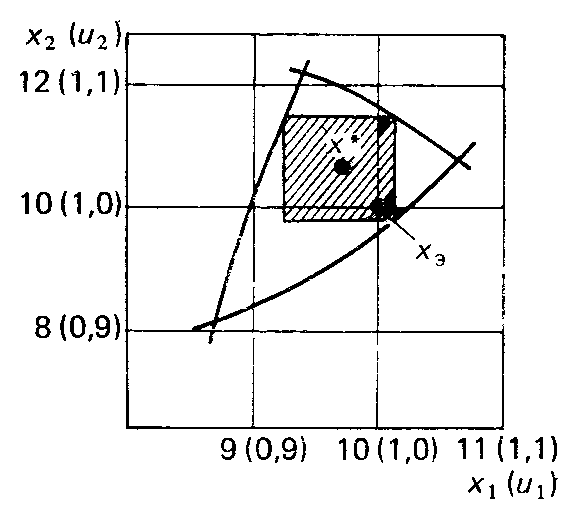
Рисунок 5.14 – Задача вписывания допусковой области

где x и х_эi — ненормализованный i-й параметр и его зна­чение в опорной точке; a_i=gi/gi; Ui—нормализованный i-параметр.

При таком способе нормирования вписываемой фигу­рой должен быть гиперкуб. Рисунок 5.14 поясняет способ (5.17) для случая, когда затраты при производстве на получение допуска g₁=20% эквивалентны затратам на получение допуска g₂=40% и известна опорная точка X_э=(10.10). Процедура вписывания квадрата (на рисунке 5.14 заштрихован) в область работоспособности дает допусковую область.

Разновидности постановок задач параметрического синтеза. Постановки остальных задач параметрического синтеза как задач математического программирования являются теми или иными разновидностями рассмотрен­ных постановок предварительной оптимизации и вписы­вания гиперфигур.

Для решения задач оптимизации параметров доста­точно выполнить этап предварительной оптимизации с использованием максиминного критерия и с нормирова­нием пространства выходных параметров с помощью за­пасов работоспособности (5.16).

Задачи назначения допусков сводятся к выполнению только этапа вписывания гиперфигуры в область рабо­тоспособности. Упрощающим отличием этих задач явля­ется задание положения центра вписываемого гиперкуба.

Задачи совмещения и центрирования, как и основная задача оптимизации,—двухэтапные: этап 1—предварительная оптимизация во всех этих задачах—выполняет­ся аналогично, а этап 2—собственно центрирование— отличается тем, что здесь допуски g_i заданы и нужно только совместить центр области работоспособности с центром допусковой области. Такое совмещение может выполняться аналогично вписыванию гиперкуба в основ­ной задаче, но возможны и другие способы, например центрирование путем вписывания гиперсферы макси­мального радиуса.

Специфической особенностью задач совмещения при заданных сведениях об асимметрии распределений и корреляции параметров является целесообразность осо­бого нормирования пространства управляемых парамет­ров с использованием указанных сведений. Фактически такое нормирование приводит к выполнению процедуры вписывания в пространстве преобразованных параметров Ui, являющихся некоррелированными случайными вели­чинами, распределенными по нормированному нормаль­ному закону. Обратное преобразование из нормирован­ного пространства в пространство исходных параметров элементов дает уточненные оценки процента выхода год­ных, что зачастую позволяет увеличить допуски по срав­нению с решением, полученным в обычной задаче цент­рирования. Эти возможности иллюстрирует рисунке 5.15, где множество отдельных точек соответствует множеству объектов. Задача центрирования, решаемая без учета корреляции, дает точку X* как совмещенную точку цент­ров допусковой области XG и области работоспособно­сти ХР. Однако такое положение точки X* номинальных значений параметров не­оптимально. Из рисунка 5.15 видно, что значительная часть точек, соответству­ющих случайным реали-зациям вектора X, оказы­вается вне пределов ХР и, следовательно, при произ­водстве будет наблюдать­ся повышенный процент брака. Из этого же рисун­ка следует, что если вы­брать центр допусковой области иначе, например совпадающим с точкой А на рисунке 5.15, то точки, характеризующие распределение вектора X, переместятся соответственно вверх направо и вероятность выполнения условий работоспособности заметно повысится. В задаче совмещения в отличие от задачи центрирования будет получена именно точка А, которая и будет принята в ка­честве точки Х_ном.

Задачи назначения технических требований ТТ на промежуточных иерархических уровнях нисходящего проектирования по своему характеру, а следовательно, и способам постановки и решения близки к основной задаче оптимизации параметров и допусков. Но в задачах назначения ТТ результатом решения являются условия работоспособности при проектировании объекта на сле­дующем иерархическом уровне, а не допуски, использу­емые при дальнейшем изготовлении



Х₂




А





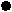
Х


Х₁

Рисунок 5.15 – Задача совмещения и центрирования

деталей. Условия ра­ботоспособности—это обычно односторонние ограниче­ния, а допуски характеризуют двусторонние ограничения. Как следствие, повышается ответственность назначения прямых ограничений, так как без них область ХР часто неограниченна.

Задачи назначения технических требований ТТ на ос­нове мнений экспертов решаются в процессе внешнего проектирования, когда структура будущего объекта от­личается большой неопределенностью. Поэтому первой особенностью этих задач является использование при­ближенных математических моделей, отражающих пред­ставления идеологов разрабатываемой сложной системы о соотношениях между достижимыми параметрами объ­ектов, сроками проектирования, затратами на разработку и изготовление, т. е. учитываются технико-экономические соображения, относящиеся ко всему жизненному циклу объекта. В процессе внешнего проектирования разработ­чик должен иметь возможность оперативного внесения изменений в используемые математические модели, изме­нений целевых функций, ограничений и управляемых параметров. Такая оперативность—вторая особенность реализации задач назначения ТТ при внешнем проекти­ровании.

Задачи идентификации параметров разрабатываемых математических моделей формулируются как задачи ма­тематического программирования, в которых целевая функция—оценка степени совпадения выходных пара­метров, получаемых с помощью испытуемой и эталонной моделей, а управляемые параметры—параметры испы­туемой математической модели.

Задачи определения областей адекватности математи­ческих моделей отличаются от задач назначения допус­ков при заданном векторе номинальных значений тем, что вписывание производится не в пространстве пара­метров элементов, а в пространстве внешних парамет­ров, так как область адекватности должна характеризо­вать диапазоны изменения внешних переменных, в ко­торых математическая модель адекватна.

Решение задач параметрического синтеза в САПР выполняется методами поисковой оптимизации (основана на последовательных приближениях к опти­мальному решению). Каждая итерация представляет со­бой шаг в пространстве управляемых параметров. Ос­новными характеристиками метода оптимизации являют­ся способы определения направления, в котором произво­дится шаг в пространстве ХП, величины этого шага и момента окончания поиска. Эти характеристики наряду с особенностями математических моделей оптимизируе­мых объектов и формулировки задач как задач матема­тического программирования определяют показатели эф­фективности поиска — надежность отыскания экстремаль­ной точки, точность попадания в окрестности этой точки, затраты вычислительных ресурсов на поиск.

Классификация задач структурного синтеза. Про­цедуры структурного синтеза относятся к наиболее трудноформализуемым в процессе проектирования. В то же время дальнейшее повышение степени автоматизации проектирования зависит в первую очередь от успехов в разработке методов и алгоритмов структурного синтеза.

Задачи структурного синтеза классифицируют по ря­ду признаков.

В зависимости от стадии проектирова­ния, на которой производится синтез, различают про­цедуры:

1) выбора основных принципов функционирования бу­дущего объекта (здесь речь может идти о принципах ин­формационных, организационных, физических и т. п.);

в этой группе процедур часто выделяют группу процедур выбора физических принципов действия (ФПД);

2) выбора технического решения в рамках заданных принципов функционирования;

3) оформления технической документации.

Выбор основных принципов функционирования объ­екта выполняется на ранних стадиях проектирования, обычно на стадиях научно-исследовательских работ. При получении ТЗ на разработку нового объекта проектиров­щик пытается решить задачу на основе имеющихся зна­ний и накопленного опыта. При этом ему необходимо учитывать достигнутый глобальный технический уровень, который дает прототипы и ориентиры, существенно помо­гающие при внешнем проектировании. Однако ориента­ция только на накопленный опыт часто сковывает твор­ческую фантазию проектировщика и мешает увидеть принципиально новые решения. Эта особенность выпол­нения процедур синтеза получила название психологи­ческой инерции.

В САПР средства автоматизации процедур синтеза принципиальных решений должны помогать проектиров­щику как в учете накопленного опыта, так и в преодо­лении психологической инерции. Накопленный опыт во­площается в специальных разделах базы данных, напри­мер в разделе типовых решений, использовавшихся ранее, разделе физических эффектов. Получению оригиналь­ных решений способствует наличие раздела, содержаще­го описание эвристических приемов синтеза. Так, в опи­сании физических эффектов для устройств автоматиче­ской печати могут присутствовать описания механическо­го удара по носителю информации через красящую лен­ту, электротермического и фотографического способов получения изображений и др.

Эвристические приемы можно сгруппировать в при­емы изменений в пространстве, во времени, преобразо­ваний формы, материалов, видов движения, модифика­ций добавлением, исключением, заменой и т. и., напри­мер: «заменить ориентацию объекта в пространстве— повернуть низом вверх», «совместить операции во вре­мени», «сделать объект прозрачным», «разделить движу­щийся поток на два или несколько» и т. п. Такие раз­делы могут постоянно пополняться.

Выбор технических решений выполняется на последу­ющих стадиях проектирования и относится к задачам конкретизации ранее выбранных принципов построения и функционирования объекта. Например, механический принцип получения отпечатка на бумаге в печатающих устройствах может быть реализован в конструкциях ры-чажно-литерных, с матричным, сферическим, цилиндриче­ским или дисковым знаконосителями и др. Здесь также полезно использовать биб­лиотеки типовых решений,

В процедурах оформ­ления технической доку­ментации синтезируется не содержание, а форма представления описании проектных решений, Оформление технической документации регламен­тируется правилам:) ЕСКД. Для преобразования описаний с внутрен­него языка ЭВМ в тексто­вую и графическую доку­ментацию, выполняемую на устройствах документиро­вания в соответствии с ЕСКД, нужно осуществить ряд процедур, связанных с трансляцией языковых представ­лений, компоновкой текстовой и графической информа­ции по страницам и листам, размещением фрагментов графических изображений на бумаге, синтезом проек­ций, сечений, простановкой размеров, вспомогательных надписей и т. п.

Специфическая особенность оформления технической документации как процедуры структурного синтеза за­ключается в ее рутинном характере, т. е. в очевидной воз­можности ее формализации. Это обусловливает, с одной стороны, актуальность, а с другой стороны, возможность формализации. Поэтому в существующих САПР, как правило, имеются подсистемы оформления технической документации. Однако принципиальная возможность формализации еще не означает легкости ее практическо­го осуществления. Ограничивающими факторами в авто­матизации изготовления сложных схем и чертежей явля­ются такие недостатки используемых устройств машин­ной графики, как недостаточное удовлетворение требо­ваний точности изображений, скорости вычерчивания, ин­формационной емкости и большие затраты машинного времени на исполнение программ машинной графики.

В зависимости от возможностей формализации задачи синтеза делятся на несколько уров­ней сложности.

К уровню I сложности относят задачи, в которых тре­буется выполнение лишь параметрического синтеза, а структура объекта определена либо спецификой ТЗ, либо результатами про­цедур, выполненных на предыдущих этапах про­ектирования.

К уровню II сложности относят задачи, в которых возможен полный перебор известных решений. Сле­довательно, это комбина­торные задачи, т. е. зада­чи выбора элементов в ко­нечных множествах, при­чем в множествах малой мощности. В этих задачах либо элементы множества структур представляют собой заранее составленные и включенные в базу данных описания структур, либо имеется алгоритм, позволяющий поочередно получать и анализировать все элементы множества за приемлемое время.

К уровню III сложности относят комбинаторные зада­чи, которые при существующих технических и програм­мных средствах не могут быть решены путем полного перебора за приемлемое время. Имеется большое коли­чество практических важных задач синтеза, относящихся к уровню III. Примерами таких задач являются задачи компоновки и размещения заданного оборудования в ограниченных пространствах, проведения трасс, боль­шинство процедур оформления технической документа­ции. К третьему уровню сводятся многие задачи синтеза более высоких уровней при принятии соответствующих ограничений и допущений.

К уровню IV сложности относят задачи поиска вари­антов структур в счетных множествах неизвестной или неограниченной мощности. Формализация именно таких задач представляет наибольшие трудности. Их особен­ностью является возможность получения новых ориги­нальных патентоспособных решений.

К уровню V сложности относят задачи синтеза, реше­ние которых является проблематичным. Если в задачах уровня IV возможности создания структур бесспорны и главная проблема заключается в нахождении среди мно­гих генерируемых структур некоторой, удовлетворяющей определенным количественным требованиям, то в зада­чах уровня V получение решения эквивалентно предложению принципиально новых основ построения целого клас­са технических объектов.

Существуют также и другие признаки классификации задач синтеза. Среди них следует выделить классифика­цию задач по типу синтезируемых струк­тур, порождающую задачи одномерного, схемного и геометрического синтеза.

При одномерном синтезе решаются задачи упорядо­чения элементов структуры в одномерных пространствах (например, задачи составления расписаний, синтеза про­цессов, представляемых в виде упорядоченной последова­тельности элементов).

При схемном синтезе определяется структура объек­та без конкретизации его геометрических форм. Харак­терные примеры — синтез кинематических, электрических, функциональных схем и т. п.

Геометрический синтез заключается в конкретизации геометрических свойств проектируемых объектов и вклю­чает в себя охарактеризованные выше задачи оформле­ния конструкторской документации, а также задачи по­зиционирования и синтеза поверхностей и траекторий. К задачам позиционирования относятся задачи взаимно­го расположения в пространстве деталей заданной гео­метрической формы, например задачи выбора баз для механической обработки деталей сложной формы, син­тез композиций из заданных деталей и т. п. К синтезу поверхностей и траекторий относятся задачи проектиро­вания поверхностей, обтекаемых потоком газа или жид­кости или направляющих такой поток (крыло самолета, корпус автомобиля, лопатка турбины), синтеза траекто­рии движущихся рабочих органов технологических авто­матов, синтеза профилей несущих конструкций и др.




Описание структур проектируемых объектов в виде И-ИЛИ-дерева. Для решения в САПР задач структур­ного синтеза необходимо решить вопрос о способах фор­мального описания структур проектируемых объектов, установить правила преобразования описаний и выбрать стратегию применения этих правил, ведущую от исход­ных описаний в виде ТЗ к описанию структур в виде комплекта конструкторско-технологической документа­ции.

Рассмотрим способы формального описания структур в рамках блочно-иерархического подхода с помощью И-и И-ИЛИ-деревьев. И-дерево удобно применять для опи­сания структуры конкретного объекта. Оно представляет собой множество вершин и связываю­щих их ребер.

Рисунок 5.16 - Фрагмент И-дерева

Вершины разделены на ярусы, каждый ярус относится к одному из иерархических уровней, а вершины отображают состав­ные части проектируемого объекта. Пример И-дерева дан на рисунке 5.16, где единственная вершина нулевого яруса, называемая корневой, отображает проектируемую сложную систему (например, автомобиль ВАЗ-2106). Эта вершина соединена ребрами с вершинами первого яруса, отображающими подсистемы (примеры подсистем — двигатель, ходовая часть, трансмиссия, электрооборудо­вание и т. п. в автомобиле). Вершины n-го яруса, где п—число выделенных иерархических уровней в описа­нии сложной системы, называются листьями и отобража­ют базовые элементы (например, поршень, шатун, винт, коленчатый вал и т. п.).

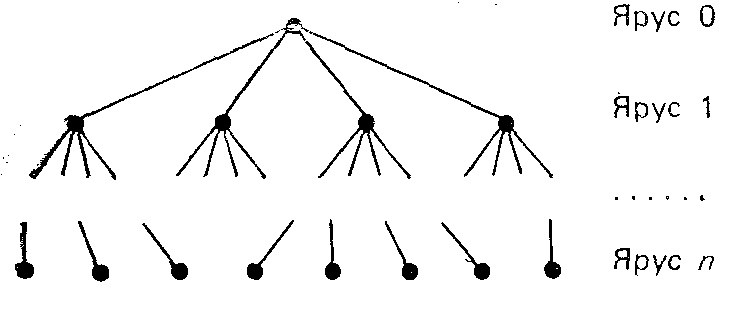
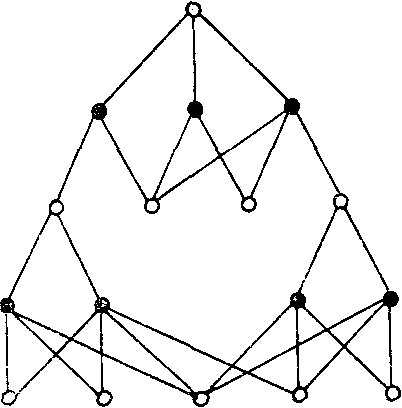
Аналогичное изображение структуры, но не отдель­ной системы, а некоторого класса систем, дается с по­мощью И-ИЛИ-дерева. В И-ИЛИ-дереве каждый ярус состоит либо из вершин ИЛИ, либо из вершин И, при­чем соседние ярусы являются ярусами разнотипных вер­шин. На рисунке 5.17 дан фрагмент И-ИЛИ-дерева, на котором вершины И показаны темными кружками, а вер­шины ИЛИ—светлыми.

В И-ИЛИ-дереве полезно выделять кусты. Кустом типа И называют часть дерева, состоящую из одной вершины И и всех смежных с ней вершин ИЛИ из со­седнего нижнего яруса. Для примера, показанного на рисунке 5.17, некоторые кусты типа И выделены пунктирны­ми контурами. В кусте типа И вершина И отображает определенный вариант (тип) построения объекта, а вер­шины ИЛИ—составные части этого варианта объекта. Если в куст включить одну вершину ИЛИ и все смежные с ней вершины И из соседнего нижнего яруса, то имеем куст типа ИЛИ. В таком кусте вершинами И представ­лены всевозможные взаимоисключающие варианты по­строения объекта, отображаемого вершиной ИЛИ. Эти варианты называют альтернативами, а совокупность вер­шин И в кусте типа ИЛИ — альтернативной линейкой. И-ИЛИ-деревья могут представлять собой как узкие,



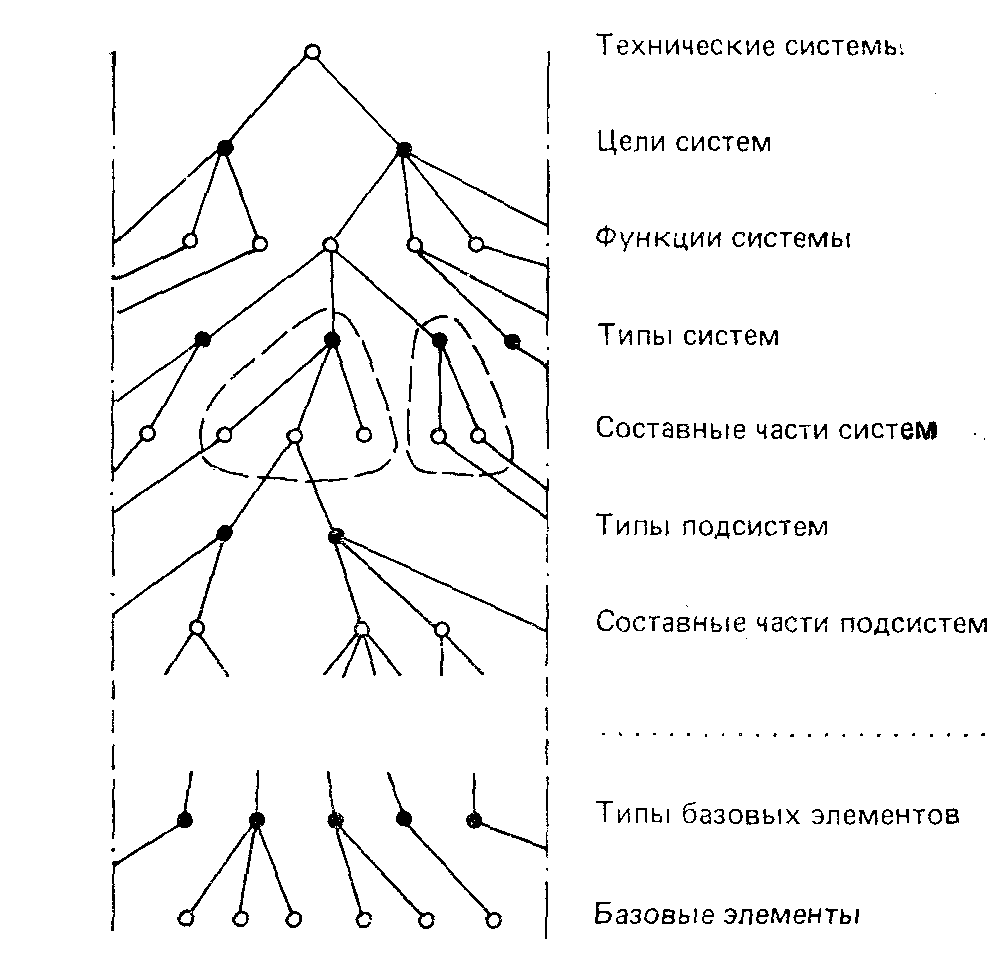
Рисунок 5.17 - Фрагмент И-ИЛИ-дерева


так и обширные классы систем. Например, возмож­но построение И-ИЛИ-дерева только для легковых ав­томобилей ВАЗ или для легковых и грузовых автомо­билей разных марок. Обобщение И-ИЛИ-дерева на все более обширные классы технических систем приводит к появлению в нем дополнительных верхних ярусов вер­шин. В наиболее общем И-ИЛИ-дереве (которое практи­чески может быть представлено только в виде некото­рых своих фрагментов) корневая вершина соответствует множеству разнообразных технических систем. Вершины первого яруса соответствуют различным альтернати­вам—целевым назначениям систем. Каждому целевому назначению соответствуют вершины второго яруса, отоб­ражающие свойства (функции) системы. Вершины по­следующих ярусов служат для отображения блочно-ие-рархической структуры систем, т. е. типов и составных частей систем, подсистем и т. д. вплоть до базовых эле­ментов.

Различным аспектам описаний одной и той же систе­мы соответствует своя иерархия. Аналогично, в И-ИЛИ-деревьях различные аспекты представляются поддеревь­ями, начинающимися в некоторой общей для них вершине одного из верхних ярусов. Поддеревья разных аспек­тов могут иметь ту или иную степень совпадения струк­тур. Например, если каждому элементу функциональной схемы соответствует определенный конструктивный эле­мент на любом из иерархических уровней, то имеется пол­ное совпадение структур деревьев, т. е. структуры функ­ционального и конструкторского аспектов описания изо­морфны. Противоположный пример—оптико-электрон­ная система, в которой структуры оптической и электрон­ной частей полностью различны.

Обычно И-ИЛИ-деревья выражают накопленный опыт в разработке технических систем определенного' класса и получаются объединением описаний нескольких конкретных структур (И-деревьев). Сведения, заключен­ные в И-ИЛИ-дереве, представляют в принятой для дан­ной САПР форме и помещают в базу данных. Каждой вершине при этом соответствует некоторая порция инфор­мации, а всему И-ИЛИ-дереву—совокупность порций. Такая форма представления И-ИЛИ-дерева называется явной, поскольку в ней можно выделить описание каж­дой вершины.

Очевидно, что вид И-ИЛИ-дерева могут иметь све­дения не только о структурах, ранее реализованных, но и о структурах, которые еще не были воплощены в ка­ких-либо проектах, в том числе о структурах хотя и не­известных, но принципиально возможных. Поэтому сре­ди И-ИЛИ-деревьев можно выделять деревья с конеч­ным и бесконечным множествами вершин. Бесконечными могут оказаться множества вершин И в связи с неограни­ченностью множеств аль­тернатив при выборе спо­собов реализации систем.

И
-ИЛИ-деревья с не­ограниченным или просто чрезмерно большим чис­лом вершин уже нельзя представлять в явной фор­ме. Их представляют в ви­де совокупности правил порождения новых вер­шин из ограниченного множества исходных дан­ных. Такая неявная форма перспективна для созда­ния в САПР баз знаний.


Рисунок 5.18 - Фрагмент И-ИЛИ-графа

Следует также отметить, что в общем случае И-ИЛИ-деревья становятся И-ИЛИ-графами, т. е. сетевыми структурами. На рисунке 5.18 представлен фрагмент И-ИЛИ-графа, в котором изображе­ния однотипных элементов, отно­сящихся к разным подсистемам, объединены в общих вершинах. Такое сетевое представление хо­тя и усложняет управление про­цессом синтеза, но снижает тре­бования к емкости памяти ЭВМ.

Рассмотренный способ сжатия И-ИЛИ-дерева мож­но назвать сжатием по горизонтали. Способ сжатия по вертикали заключается в объединении вершин ИЛИ двух соседних иерархических уровней с ликвидацией яруса вершин И между ними. Сжатие по вертикали приводит к тому, что только часть вершин ИЛИ в кустах типа И будут составными частями в конкретных структурах. Следовательно, сжатие по вертикали должно сопровож­даться записью условий включения вершин ИЛИ в кон­кретные структуры.

Подходы к решению задач структурного синтеза. Формализация процедур структурного синтеза на каж­дом иерархическом уровне осуществляется на основе од­ного из следующих основных подходов: 1) перебор;

2) последовательный синтез; 3) трансформация описа­ний разных аспектов.

Классификация алгоритмов структурного синтеза да­на на рисунке 5.19.

Переборные алгоритмы характеризуются возможностями оценки только вариантов готовых закон­ченных структур. Такие структуры либо создаются зара­нее и хранятся в базе данных, либо генерируются по тем или иным правилам из заданного набора элементов. Пол­ный перебор вариантов возможен лишь в простейших случаях. Как правило, перебор должен быть частичным (сокращенным). Переборные алгоритмы включают в се­бя части: 1) выбора или генерации очередного вариан­та; 2) оценки варианта; 3) принятия решения.

Алгоритмы выбора варианта при частичном переборе могут быть основаны на случайной выборке, использо­вании эвристических способностей человека в диалого­вых режимах работы с ЭВМ, установлении корреляции



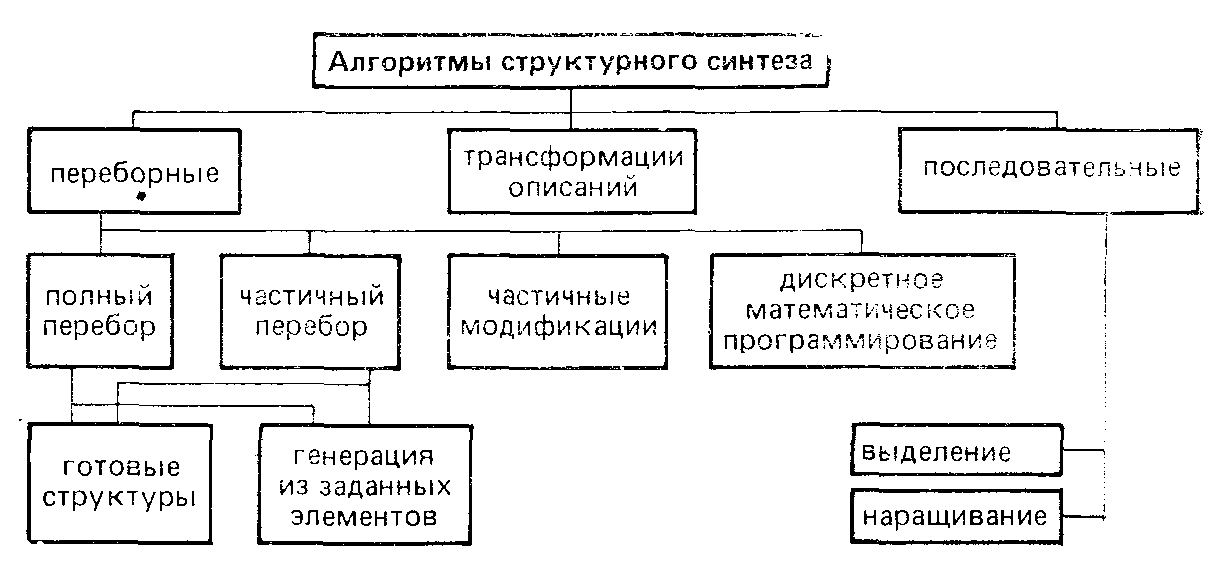
Рисунок 5.19 - Классификация алгоритмов структурного синтеза

некоторых параметров, характеризующих структуру, с заданными требованиями к объекту. Например, типовые структуры могут быть сгруппированы в базе данных по. диапазонам мощностей, частот, скоростей и других по­казателей эффективности проектируемых объектов.

Для задач третьего уровня сложности затруднитель­но, а для задач четвертого уровня уже невозможно по­строение множества законченных структур для хранения в базе данных. В таких случаях вместо законченных структур хранению подлежат описания типовых элемен­тов объектов. Это связано с тем, что, как правило, коли­чество типов элементов существенно меньше количества возможных структур из этих элементов. Автоматизация синтеза при этом основана на алгоритмизации процеду­ры генерации структур из типовых элементов. От успе-ха этой алгоритмизации зависят возможности автомати­зации синтеза и качество синтезируемого объекта. Так как общих алгоритмов генерации, ориентированных на структуры разнообразных технических объектов, не су­ществует, то такие алгоритмы входят в проблемно-ориен­тированное математическое обеспечение.

Частичный перебор чаще всего удается осуществить на основе частичных модификаций некоторых исходных структур. Последние получаются либо из ограниченного множества готовых структур, либо с помощью экономич­ных последовательных алгоритмов. Далее вносятся не­которые модификации. Например, при размещении мик­росхем на печатной плате или оборудования в отсеке ко­рабля такие модификации могут представлять собой парные перестановки—взаимные перемены мест двух элементов оборудования.

Оценка варианта структуры, сгенерированной или выбранной из базы данных, выполняется с помощью про­цедуры параметрического синтеза и анализа. Использо­вание полных математических моделей и процедур па­раметрической оптимизации, как правило, характеризу­ется высокой трудоемкостью, что не позволяет в процессе перебора просмотреть достаточное количество вариан­тов структур. Поэтому переборные алгоритмы применя­ют только в тех случаях, когда для оценки удается при­менить упрощенные математические модели и некоторые косвенные критерии предпочтения вариантов, отличаю­щиеся простотой вычисления. Лишь по отношению к не­большому числу отобранных перспективных вариантов следует применять анализ по полным математическим моделям и оптимизацию параметров.

Принятие решения при переборе основано на сравне­нии результатов оценки очередного варианта структуры с лучшей из ранее просмотренных структур. Для такого сравнения должен быть выбран некоторый скалярный критерий, объединяющий частные показатели в много­критериальных ситуациях.

Особое место в переборных алгоритмах отводится ал­горитмам дискретного математического программирова­ния (ДМП). Эти алгоритмы применяют, если задачу структурного синтеза удается сформулировать как зада­чу ДМП:



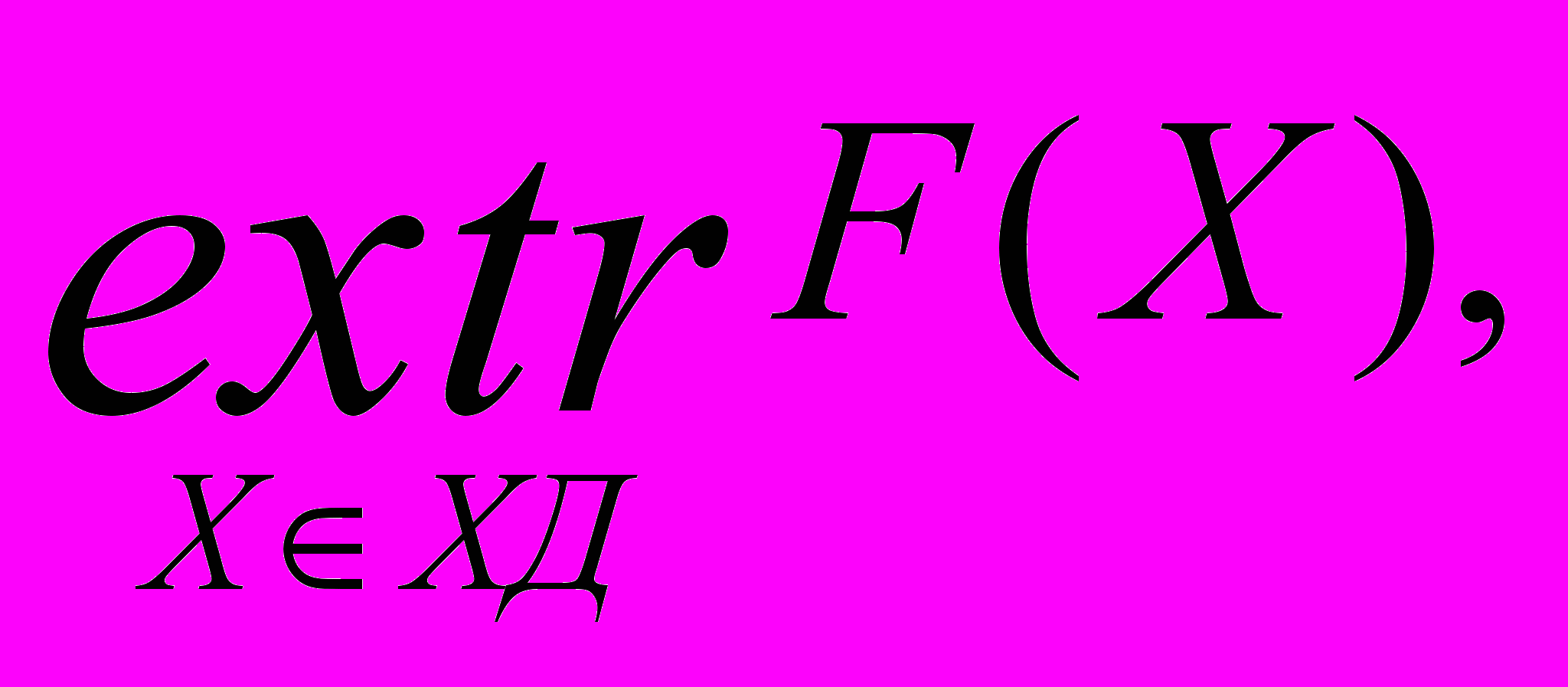
хд= {XD | (X)0, (Х)=о}.

Эта формулировка отличается от формулировки (5.14) тем, что здесь XD, где D—дискретное множест­во. Приведение к задаче ДМП основано на поиске при­знаков структур, выражаемых количественно, и на опре­делении функции этих признаков, которая выражала бы правило предпочтения одних вариантов перед другими. Такие признаки объединяют в вектор X, а формула пред­почтения становится целевой функцией F(X). Примера­ми параметров x_i, входящих в X, могут служить количе­ства элементов некоторого типа в структуре, тогда x_i принадлежит множеству целых чисел; наличие или от­сутствие в структуре некоторого свойства, тогда x_i есть булева величина, принимающая значения из множества {1 (есть), 0 (нет)}, и т. п.

Следует, однако, отметить, что сведение задачи к задаче ДМП еще не гарантирует успеха дальнейшего ре­шения, так как существующие методы ДМП не отлича­ются универсальностью, надежностью и экономичностью.

Последовательные алгоритмы характери­зуются поэтапным решением задачи синтеза с возможно­стями оценки получающихся промежуточных структур. Различают два способа получения законченной структу­ры: 1) наращивание; 2) выделение.

Способ 1—наращивание. При наращивании про­исходит поочередное добавление элементов к некоторой исходной структуре (в частном случае за исходную струк­туру может быть принят какой-либо элемент). Примера­ми алгоритмов наращивания могут служить последова­тельные алгоритмы компоновки и размещения оборудо­вания. Например, при распределении оборудования по конструктивным блокам основой оценок вариантов мо­жет служить количество межблочных связей. Тогда пред­почтение нужно отдавать тем промежуточным вариан­там, при которых большее число связей оказывается сконцентрированным в пределах одного блока.

Способ 2 — выделение. При выделении из некоторой избыточной обобщенной структуры постепенно удаляют­ся лишние элементы. Алгоритмы выделения могут ис­пользоваться, если предварительно составлена обобщен­ная структура для рассматриваемого класса объектов. Примерами таких обобщенных структур могут служить обобщенные технологические маршруты обработки дета­лей некоторых классов на металлообрабатывающих станках. В обобщенный маршрут включают операции, которые могут встретиться при различных сочетаниях конструктивных особенностей в деталях данного класса. Дальнейшее сопоставление чертежа конкретной детали и обобщенного маршрута позволяет убрать лишние опе­рации и сформировать конкретный технологический мар­шрут.

Трансформация описаний разных аспектов формали­зуется с тем большим успехом, чем в большей мере сов­падают структуры И-ИЛИ-деревьев, относящихся к рас­сматриваемым аспектам. Для совпадающих вершин обычно удается установить однозначное соответствие структурных единиц и свести преобразование к поиску совпадений и подстановкам.

Алгоритмы транс­формации описаний разных аспектов широко используются в действующих САПР. Так, на основе соответствий между функциональным и структурным описаниями строятся программы так называемых кремниевых компиляторов в САПР больших интегральных схем. В кремниевом ком­пиляторе каждой функци­ональной ячейке ставится

в соответствие определенная конструктивная ячейка. Трансформация описаний лежит также в основе фор­мального синтеза функциональных схем ЭВМ по задан­ным алгоритмам функционирования. Другим примером является функционирование систем изготовления конст­рукторской документации, в которых формализовано пре­образование результатов конструкторского проектирова­ния в графическое изображение, выполняемое по прави­лам проекционного черчения.

Реальные алгоритмы структурного синтеза обычно являются комбинированными: сочетают в себе черты бо­лее чем одного подхода, например в последовательных алгоритмах наращивания возможен перебор претенден­тов на роль очередного добавляемого элемента.

Ограниченные возможности формализации процедур синтеза привели к широкому использованию в САПР диалоговых систем синтеза, в которых процедуры оцен­ки выполняет ЭВМ, а принятие решения остается за че­ловеком. Что касается непосредственной генерации структур, то здесь ЭВМ и человек могут эффективно вза­имодействовать. Типичное назначение ЭВМ—подсказать типовые варианты и эвристические приемы. Типичная роль человека—реализовать эвристические приемы и модификации структур. Иногда удается формализовать применение эвристических приемов и получить алгорит­мы синтеза, выполняемые без участия человека. Однако наличие эффективных алгоритмов автоматического син­теза скорее исключение, чем правило. Поэтому основной практический подход к решению задач структурного син­теза в современных САПР—это использование эвристических приемов синтеза в диалоговом режиме работы с ЭВМ.

Получают развитие экспертные системы, которые воспринимают от высококвалифицированных специалис­тов знания в соответствующей предметной области, а за­тем используют их при решении задач структурного син­теза. Возможные формы представления знаний в ЭВМ— сематические сети, И-ИЛИ-деревья и т. п. В семанти­ческих сетях вершинам соответствуют понятия, а связям—отношения между понятиями. Программное обеспечение экспертных систем служит для генерации вариантов структуры и для связи пользователя с систе­мой в режиме диалога.