Ы, включают методы обработки данных многих ранее су­ществовавших автоматизированных систем (АС), с другой обладают спецификой в организации и обработке данных

Вид материала

Документы

Содержание 5.3. Особенности моделирования в ГИС Операции преобразования форматов и представлений данных Векторно-растровое преобразование. Проекции и проекционные преобразования Конические проекции (konical projection). Азимутальные проекции (azimuthal projection). Цилиндрические проекции (cylindrical projection). Поликонические проекции Видоизмененная простая полнконнческая проекция. Псевдоцилиндрические проекции. Проекция Гаусса-Крюгера. Х всех точек имеют положительное значение. Координаты Y Геометрический анализ Оверлейные операции Функционально - моделирующие операции Построение буферных зон. Анализ сетей. Поиск путей Цифровое моделирование рельефа.

Подобный материал:

• Методы анализа данных, 17.8kb.
• Методика определения актуальных угроз безопасности персональных данных при их обработке, 175.98kb.
• Понятия о базах данных и системах управления ими. Классификация баз данных. Основные, 222.31kb.
• Анализ и оценка дисциплин обслуживания требований (запросов) с учетом их приоритетов, 20.53kb.
• Программа дисциплины «Методы обработки экспериментальных данных», 318.77kb.
• «Прикладная информатика (по областям)», 1362.72kb.
• Методические указания к курсовому проектированию по курсу "Базы данных" Составитель:, 602.97kb.
• Концепция баз данных уже давно стала определяющим фактором при создании эффективных, 293.58kb.
• Доклад Тема: «Информационные технологии», 58.36kb.
• Рабочей программы дисциплины Структуры и алгоритмы обработки данных по направлению, 21.62kb.

5.3. Особенности моделирования в ГИС

При моделировании в ГИС можно выделить следующие програм­мно-технологические блоки:

• операции преобразования форматов и представлений данных;

• проекционные преобразования;

• геометрический анализ;

• оверлейные операции;

• функционально-моделирующие операции.

Операции преобразования форматов и представлений данных

Операции преобразования форматов и представлений данных при­сутствуют в каждой ГИС, в системах обработки данных дистанционно­го зондирования и САПР, в силу чего имеют важное значение для ГИС как средство обмена данными с другими системами. По набору форма­тов ввода-вывода определяются возможности ГИС использовать данные, получаемые в других технологиях.

Исходные пространственные данные и данные, полученные в про­цессах обработки ГИС, могут иметь различные наборы форматов. Тип формата чаще всего определяется используемыми программными сред­ствами, что особенно характерно при сборе данных по разным техноло­гиям. Преобразование форматов осуществляется с помощью специаль­ных программ - конвертеров.

Векторизация. Данные могут иметь векторное или растровое пред­ставление. Между векторными и растровыми изображениями имеется существенное различие, характерное именно для ГИС. Растровые изображения отображают поля данных, т.е. носят полевой характер. Векторные изображения в ГИС, как правило, отображают геоинформационные объекты, т.е. носят объектный характер.

Операции преобразования данных из растрового представления в векторное (векторизация) - одни из наиболее важных при обработке про­странственно-временных данных в ГИС.

В технологическом плане преобразование от растра к вектору для ГИС означает переход от полевого представления данных к объектному.

Растрово-векторное преобразование применяется при интерпрета­ции сканированных аэрокосмических изображений (выделение и оконтуривание на них однородных областей), в методах дигитализации циф­ровых растровых картографических изображений, при обработке дан­ных, полученных с цифровых фотокамер или от видеосъемки, и т.п.

Векторные изображения вычерченных на бумаге чертежей, карт не­возможно получить с помощью сканера. При сканировании получается только растровая копия оригинала.

Векторные представления по сравнению с растровыми обладают ря­дом преимуществ:

• многие приложения, использующие графику для расчетов, работа­ют только с векторными файлами, так как векторная технология эффек­тивнее;

• при хранении на компьютере векторные файлы занимают меньший (в 100- 1000 раз ) объем памяти, чем растровые оригиналы;

• векторные рисунки легко редактируются, масштабирование и трансформирование векторного изображения происходит без искаже­ний, чего нельзя сказать о преобразовании растровых изображений.

Векторные изображения обычно создаются и редактируются с по­мощью специальных программ - графических редакторов. Такой редак­тор входит в состав всех инструментальных ГИС-систем. Тем не менее существует большое число специализированных программ - векторизаторов.

Векторизация может быть ручной, полуавтоматической и автомати­ческой. В графических редакторах ГИС обычно используется ручная век­торизация, что обусловлено необходимостью решения экспертных за­дач, создания топологии, присвоения идентификаторов графическим объектам и т.д.

Программы-векторизаторы в основном ориентированы на автома­тизацию процесса векторизации растрового изображения. Ручной ре­жим в них вводится для коррекции векторизованного изображения, полученного в автоматическом режиме. Вот некоторые из таких программ-векторизаторов: AUDREO (па), AUTOVECT(рп), AutoVEC (рпа), CADOverlay (р), ColorFast (a), DIGI Map (рпа), EasyTrase (рп), I / EOVEC (рп), I / VEC (a), MapEDIT (рп), POCKBIT (a), Spotlight (рп), TRACK(рпa), Vectory(pa), WinGIS (р), Вектометр (рпа), ИНТЕЛВЕК (рпа), ЦКМ-век-торизатор (рпа).

Буквы в скобках обозначают: р - ручной; п — полуавтоматический; а - автоматический режимы векторизации.

Программы-векторизаторы отличаются друг от друга следующими параметрами:

• видом управляющей операционной системы;

• возможностью векторизации различных видов растра: бинарного, полутонового или цветного;

• требуемым качеством векторизации растра;

• наборами фильтров (тематическими);

• возможностью и методами редактирования исходного растрового изображения;

• видом графической оболочки, посредством которой оператор осу­ществляет управление векторизатором.

Векторизация позволяет преобразовать растровые изображения, хра­нящиеся в растровых файлах, в векторные рисунки и сохранять их в векторных файлах.

Задачей преобразования является не только получение векторного образа, практически идентичного исходному растровому, но и сохране­ние в распознанном векторном объекте геометрических связей растро­вых аналогов при максимальной информативности векторного образа.

С этих позиций векторизация может быть рассмотрена как способ сжа­тия растровых данных с сохранением информативности исходного изобра­жения по заданным критериям выделения. В частности, растровое изобра­жение размерной линии со стрелками должно распознаваться именно как размерная линия, а не как совокупность отдельных линий.

Векторизация может быть грубой (быстрой), например применяет­ся алгоритм для векторизации растровых аналогов линий с углом накло­на, кратным 45°.

Для векторизации ареальных объектов растрового изображения при­меняют известный фильтр типа outline, который векторизует границы в виде контура.

Несмотря на наличие автоматизированных режимов в программах-векторизаторах, автоматизация этого процесса сталкивается с больши­ми трудностями, поэтому эффективность в значительной мере зависит от того, насколько успешно чисто автоматизированные методы вектори­зации сочетаются с интерактивными возможностями пользователя кон­тролировать процесс растрово-векторного преобразования и влиять на него.

Пока трудно поддаются автоматизации процессы фильтрации исход­ного растрового изображения, подавления шумов, индикации и устра­нения разрывов линий, учета изменения толщины линий, сохранения топологических признаков.

При автоматизированной векторизации картографических данных возникают сложности в распознавании ситуаций с большим числом раз­рывных дискретных элементов, распознавании надписей в областях с высокой плотностью нанесения или переносом надписи.

Несмотря на наличие большого числа программных средств, вы­полняющих преобразование растра в вектор, пока наиболее точным и надежным является интерактивный метол преобразования, осно­ванный на эвристическом моделировании. Это обусловлено значи­тельным количеством искажений, производимых программами-пре­образователями.

В основу векторного преобразования положен набор процедур, со­здающих векторный аналог растрового изображения и применяющих свой алгоритм векторизации.

В процессах автоматизированного преобразования растрового изоб­ражения в векторное применяют ряд специальных терминов:

• алгоритм векторизации - алгоритм, который осуществляет авто­матический поиск растровых аналогов векторных объектов заданных типов (примитивов) и создает векторные аналоги найденных фрагмен­тов растрового изображения;

• векторная форма представления изображений - совокупность векторных объектов и векторных файлов;

• векторный объект - графический объект, заданный своим анали­тическим описанием. Описание включает в себя тип векторного объек­та, который определяет его форму (отрезок прямой, окружность, дуга), а также параметры (координаты базовых точек , характерные размеры, ширина, масштаб и т.д.) ;

• векторный рисунок - совокупность векторных объектов,

• векторный файл ~ файл, содержащий информацию о векторном рисунке;

• маска - задаваемая пользователем прямоугольная область растро­вого изображения, которая игнорируется при векторизации;

• параметры векторизации - набор логических и числовых (раз­мерных) параметров, управляющих процессом распознавания;

• примитив - тип векторного объекта, атомарная графическая модель векторизации. Могут использоваться следующие типы векторных моделей: линия, дуга, текст, полилиния, контур и размерная линия;

• рабочая область - прямоугольный фрагмент растрового изобра­жения, который обрабатывается программой, задается пользователем. Основное назначение рабочей области - выделение фрагмента изобра­жения, в котором происходит векторизация;

• растровое изображение (монохромное) - изображение, представ­ляющее собой двухмерный массив точек, каждая из которых имеет чер­ный или белый цвет;

• режим распознавания - поименованный набор всех параметров распознавания, запомненный в дисковом файле, применяется для векто­ризации изображений одинаковых типов (изображения городских пла­нов, карт, электрических схем и т. п.);

• табличная область - задаваемая пользователем прямоугольная область растрового изображения, используется для модификации про­цесса распознавания тех частей растрового изображения, которые со­держат таблицы;

• текстовая область - задаваемая пользователем прямоугольная область растрового изображения, предназначена для модификации про­цесса распознавания фрагмента растрового изображения, содержащего тексты. Растровое изображение в текстовой области может быть векто­ризовано полилиниями или контурами. В некоторых программах-векто­ризаторах текстовые области на изображении могут быть найдены авто­матически;

• файл параметров - уникальный для каждого растрового файла файл. Содержит: все параметры распознавания; информацию о распо­ложении рабочей области, текстовых, табличных областей и масок на изображении; значение разрешения растрового изображения (в точках на дюйм); текущие единицы - точки, миллиметры или дюймы;

• текущий алгоритм фильтрации;

• фильтр - алгоритм, используемый в процедуре фильтрации;

• фильтрация - процедура, применяемая для повышения качества растрового изображения. При фильтрации программа анализирует ин­формацию о цвете растровых точек, расположенных в окрестности каж­дой точки, и меняет или оставляет без изменения цвет этой точки со­гласно одному из алгоритмов фильтрации (фильтра).

Показ векторного изображения в любом масштабе происходит без искажений, поскольку при отображении на экране программа, исполь­зуя математическое описание каждого векторного объекта, всегда мо­жет вычислить расположение и цвет пикселей экрана так, чтобы опти­мальным образом передать изображение. Возможными становятся и такие режимы показа векторного изображения, которые не имеют ана­логов при управлении видом растрового изображения. Например, показ векторных объектов в каркасном (проволочном) представлении, что дает возможность найти ошибки в построении картографической информа­ции (увидеть, какие линии не соединяются в концевых точках), и делает векторное изображение легко читаемым.

При создании векторного объекта пользователь выбирает необходи­мый ему тип векторного объекта и задает параметры, описывающие гео­метрические размеры этого объекта. При редактировании векторного изображения применяются простые алгоритмы, с помощью которых можно легко выбирать и изменять векторные объекты. При этом можно использовать геометрические отношения между объектами, оперируя точными математическими терминами.

Режим ортогональности позволяет строить линии вертикально и го­ризонтально, с помощью специальных опций проводить их перпенди­кулярно или параллельно другим.

Растровые изображения обрабатывают, добавляя или стирая части бинаризованного изображения на экране компьютера.

Процесс распознавания становится эффективнее за счет примене­ния системы фильтров. Это дает возможность векторизовать растровые изображения различной структуры: машиностроительные чертежи, ар­хитектурные планы, карты, схемы, рисунки.

Некоторые программы-векторизаторы позволяют производить рас­познавание наборов растровых файлов в пакетном режиме.

Как правило, программы-векторизаторы обрабатывают бинарные изображения, представленные двухмерным массивом точек, каждая из которых имеет черный или белый цвет. Эти точки называются растро­выми точками. Бинарные растровые изображения создаются с помощью конвертеров или специальных программ обработки изображений. При­мером такой программы может служить широко известный редактор PhotoFinish.

Когда растровое изображение выводится на монитор компьютера, каждый пиксель экрана соответствует определенному количеству рас­тровых точек изображения. Цвет пикселя будет черным или белым в зависимости от того, каких растровых точек - черных или белых - в нем больше. Черные пиксели, сливаясь между собой, образуют пятна и по­лосы, которые передают изображение чертежа или рисунка.

При векторизации можно управлять режимом показа растрового изображения, используя команды управления экраном. Например, ус­тановка режима просмотра "один в один" означает, что программа отобразит каждую точку растрового изображения одним пикселем экрана.

При увеличении в два раза для изображения каждой растровой точки будет использовано четыре пикселя. Такая простая операция приводит к искажению вида растрового изображения - неровности контуров, незаметные при прежнем масштабе, вырастают пропорци­онально степени увеличения. Все это происходит потому, что рас­тровые модели при компьютерной обработке данных имеют суще­ственный недостаток: информация об изображении представляется в виде набора точек и поэтому не содержит в явном виде данных о гео­метрии и размерах отображаемых объектов.

Поэтому программы, которые используют компьютерную графику для расчетов (интегрированные системы, программы по созданию объем­ной мультипликации и др.), работают не с растровыми изображениями, а с векторными.

Анализ растра почти всегда позволяет определять, какая его часть изображает линию или дугу, контур или ареал. Это достигается на осно­ве использования векторных аналогов.

Действие программ-векторизаторов основано на поиске связи меж­ду формой растровой линии и векторным объектом определенного типа. При этом используется понятие растрового аналога векторного прими­тива. Это означает, что существует векторный объект данного типа та­кой, что его растровая модель будет практически идентична изображе­нию фрагмента растра на экране компьютера.

Полоса растра может быть тонкой линией, линией с шириной или контуром. Ее можно показать с помощью векторных объектов трех ти­пов. Очевидно, что без дополнительной информации эта задача автома­тически не решается.

Распознавание векторных объектов на растровых (векторизация) представляет собой автоматическую процедуру поиска растровых ана­логов заданного набора векторных примитивов с последующим преоб­разованием их в векторные объекты.

При векторизации ставится задача не только получить векторный рисунок, практически идентичный исходному растровому, но, кроме того, уменьшить количество создаваемых объектов с тем, чтобы с изображе­нием впоследствии было удобно работать. Например, пересекающиеся линии на чертеже должны быть представлены именно как две линии, а не как четыре отрезка, окружность, пересекаемая прямой, - как целая окружность, а не как совокупность отдельных дуг.

При распознавании необходимо сохранить в векторном рисунке гео­метрические связи растровых аналогов: если растровые аналоги двух линий образуют угол, то векторные линии должны пересекаться в вер­шине этого угла.

Растровое изображение может иметь дефекты, получающиеся при сканировании (разрывы линий, смаз изображения и т. д.), на нем могут быть линии, которые были неправильно проведены на исходном чертеже или искажены при сканировании оригинала (например, из-за перекоса на­рушены горизонтальность и вертикальность).

Исправление подобных дефектов растрового изображения в процессе векторизации достигается применением фильтров и установкой режи­мов (степень ортогонализации прямых).

Следует подчеркнуть, что основой большинства программ-век­торизаторов служат бинарные изображения. Это ограничивает эф­фективность автоматизированной векторизации и требует больших затрат времени при обработке полутоновых изображений в интерак­тивных режимах.

В настоящее время применяется комплексный подход, включающий сканирование, частичную автоматизированную векторизацию, визуаль­ный контроль преобразования, интерактивное редактирование данных; унификацию и преобразование данных для хранения в базе данных.

Векторно-растровое преобразование. Его можно использовать для генерализации изображения. При этом существенное значение имеет разрешающая способность создаваемой (электронной ) карты. Преоб­разование типа вектор-растр - более простая задача. Оно осуществля­ется при выводе векторных данных на устройства печати, при визуали­зации графики на растровых видемониторах, построении электронных карт или карт-подложек.

К этой же группе операций относят сжатие или развертку растро­вых данных, основанных на алгоритмах кодирования и компрессии, раз­биения на слои, фрагментации или дефрагментации слоев.

Примером системы, осуществляющей преобразование в растровый формат, может служить продукт фирмы ESRI ArePress. Это програм­мный растеризатор, преобразующий векторную, растровую или смешан­ную векторно-растровую графику в формат растрового устройства вывода, растр заданного разрешения и размера. Он обеспечивает быструю распечатку карт и изображений на растровых устройствах вывода, та­ких, как струйные и электростатические плоттеры.

В качестве входных данных он может использовать как графичес­кие метафайлы в стандартах ESRI, так и файлы других систем в форма­тах CGM, PostScript (Level 1, Level 2). На выходе ArePress могут быть получены растровые форматы для направления на устройство вывода и для экспорта в другие форматы, использующиеся для обмена (TIFF, РВМ, PCX BW, BMP, BIT).

ArePress выполняет программную растеризацию непосредственно на рабочей станции, используя ее ресурсы памяти. Это позволяет обой­тись без добавления памяти в плоттер стандартной конфигурации (осо­бенно при выводе на большие форматы), одновременно распечатывать один файл и растеризовать другие, исключить ограничения на размер файла для устройства вывода.

Проекции и проекционные преобразования

Координаты точек пространственных объектов используют для ука­зания местоположения объектов на земной поверхности. Поверхность Земли имеет сложную форму. При составлении карт пространственное положение точек отображается в плоском (двухмерном) представлении. Для отображения положения точек поверхности на плоскости применя­ют различные математические модели поверхности, задающие различ­ные картографические проекции.

Группа математических процедур ГИС, осуществляющая переход от одной картографической проекции к другой или от пространствен­ной системы к картографической проекции, носит название проекци­онных преобразований. Эта группа реализуется методами моделиро­вания, образуя единый блок. В этот блок входят и различные процедуры обработки пространственных данных для получения новых проекций на основе исходных. Эти процедуры включают и простые операции пе­ресчета координат пространственных объектов (поворота, смещения, масштабирования и т. п.), более сложные (связанные, например, с "ук­ладкой" объектов в систему опорных точек) и самую сложную подгруп­пу операций (трансформация картографических проекций).

Число проекционных преобразований в блоках моделирования ГИС различно: в системе ER Mapper их свыше 700, в ГеоГраф - около трех десятков, а в некоторых настольных системах (DeskTop GIS) их нет вообще.

Рассмотрим наиболее общие классы проекционных преобразований [2] для решения задач в ГИС.

Преобразования картографических проекций применяют для перехода от исходной (хранимой в базе данных) картографической композиции к за­даваемой пользователем. В частности, когда цифровая карта (слой), выпол­ненная в известной проекции и соответствующая ее теоретическим коор­динатам, должна быть преобразована в географические координаты либо в другую картографическую проекцию.

Достоинством моделирования в ГИС является возможность трансформирования космического (или аэро-) снимка непосредственно в картографическую проекцию, минуя построение фотограмметрической модели или традиционное фотограмметрическое трансформирование сним­ков. Эта возможность предоставляется в пакетах ГИС, в первую очередь связанных с обработкой данных дистанционного зондирования.

Выделение подгруппы преобразования проекций связано с необхо­димостью интеграции данных из различных картографических источ­ников с разнородной математической основой. Карты могут отличаться моделью Земли, примененной при создании карты; картографической проекцией; системой координат, привязанной к используемой модели Земли.

Технологически для проекционных преобразований в ГИС необхо­димо создать файл описания картографической проекции и выбрать ис­ходный файл. Из набора типов преобразований выбирают необходимое, задают требуемые параметры, и проекционное преобразование осуще­ствляется автоматически путем создания новой картографической про­екции в заданном слое и соответствующем файле.

Проекционные преобразования требуют рассмотрения различных классов проекций, применяемых для создания карт[2]. Картографичес­кие проекции классифицируют по различным признакам, например в зависимости от характера и размера искажений.

Равноугольные проекции (conformai projection) сохраняют без иска­жений углы и формы малых объектов, но в них резко деформируются длины и площади объектов. В математике такие преобразования назы­вают конформными.

Равновеликие проекции (equivalente projection) не искажают пло­щадей, но в них искажены углы и формы объектов. Первый вид проек­ций приемлем для прокладки маршрутов транспортных средств, второй - для определения площадей и землепользования.

Произвольные проекции (arbitrary projection) имеют искажения углов, площадей и длин, но эти искажения распределены по карте, например, так, что минимальные искажения имеются в центральной части и возрастают к краям. Среди произвольных проекций выделяют равнопромежуточные (equidistant projection), в которых искажения длин отсутствуют по одному из направлений: вдоль меридиана или вдоль параллели.

Конические проекции (konical projection). По характеру искажений конические проекции могут быть различными. Наибольшее распростране­ние получили равноугольные и равнопромежуточные проекции.

Образование конических проекций можно представить как проек­тирование земной поверхности на боковую поверхность конуса, опре­деленным образом ориентированного относительно земного шара (эл­липсоида) (рис. 5.1, а). В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий.

После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость (рис. 5.1, б). При проектировании по методу линейной перспективы получаются перспек­тивные конические проекции, обладающие только промежуточными свойствами по характеру искажений.

Другой метод образования конических проекций - аналитический. В его основу положены уравнения проекций, вытекающие из их опреде­ления и формулы общей теории искажений. В конических проекциях имеются две постоянные проекции ее и с. Постоянная а равняется синусу широты стандартной параллели или, что то же самое, синусу угла при вершине конуса.

В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохра­няются длины без искажений. Одна параллель (касательная) принима­ется при небольшом протяжении по широте; две параллели (секущие) – при большом протяжении для уменьшения уклонений масштабов от еди­ницы. В литературе их называют стандартными параллелями.

Коническая проекция данной группы вполне определяется, если за­даны постоянные проекции или любые величины, с ними связанные. Это могут быть широты стандартных или крайних параллелей. В после­днем случае, например, может быть дополнено условие, чтобы масшта­бы на крайних параллелях и на параллели с наименьшим масштабом были равны по абсолютной величине.

Азимутальные проекции (azimuthal projection). В них параллели (альмукантараты) изображаются концентрическими окружностями, а меридианы (вертикалы) - пучком прямых, исходящих из центра (рис. 5.2, а).






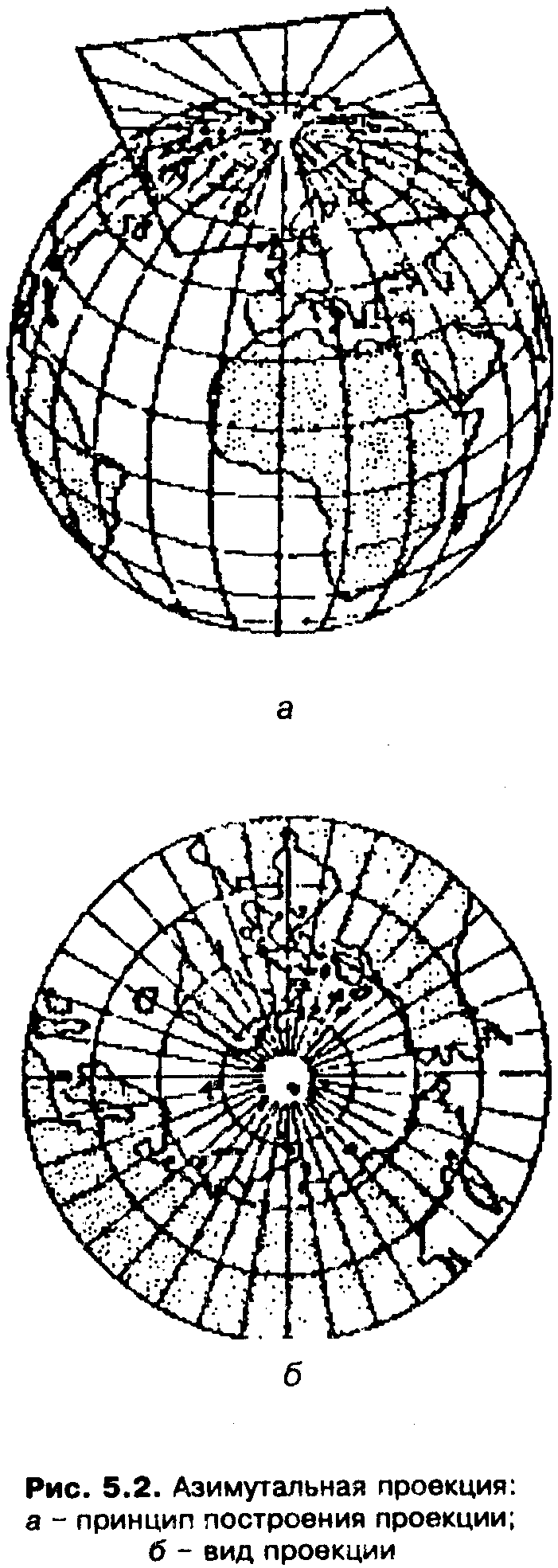
Рис. 5.1. Коническая проекция: а – принцип построения проекции; б – вид проекции

Рис. 5.2. Азимутальная проекция: а – принцип построения проекции; б – вид проекции







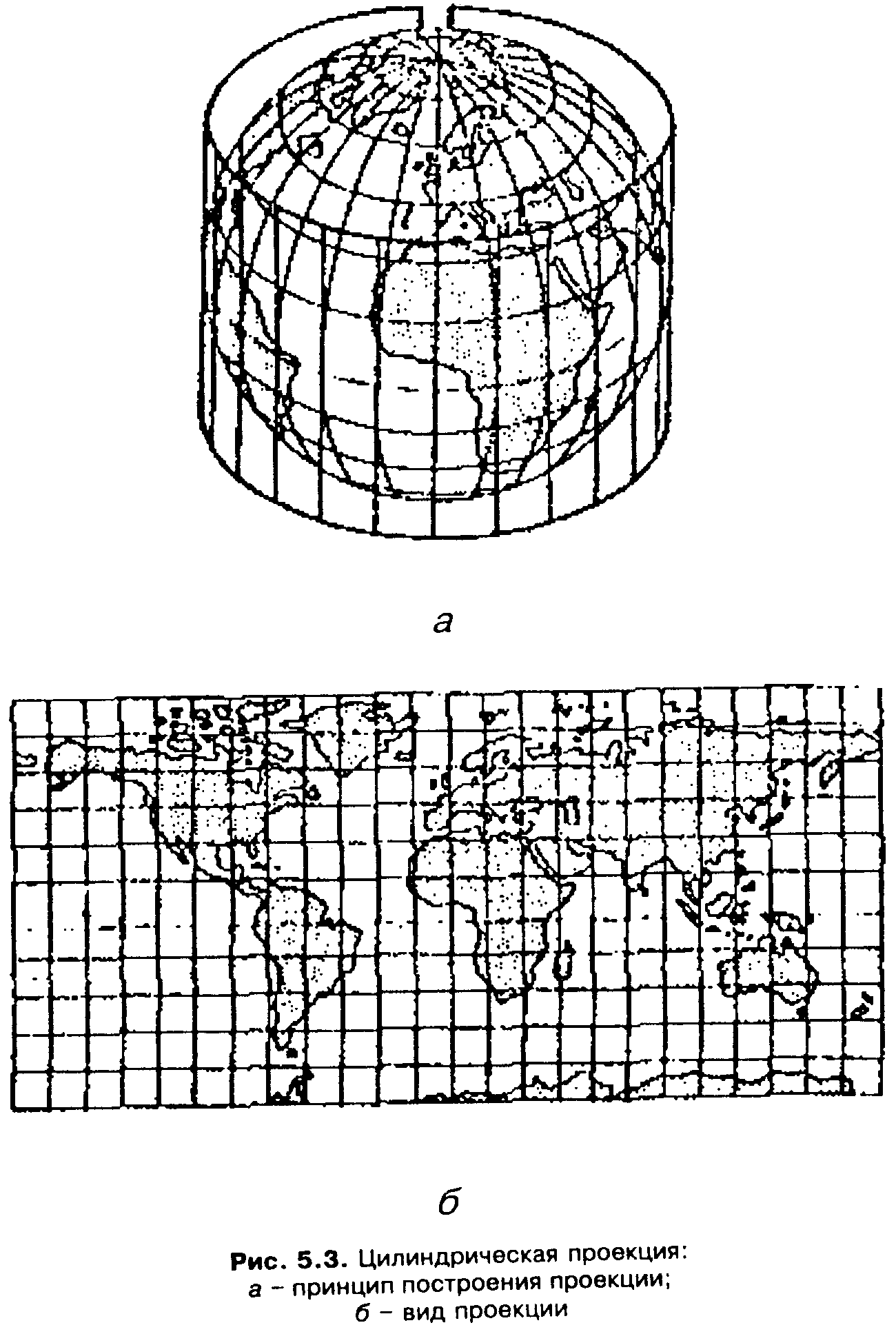
Рис. 5.3. Цилиндрическая проекция: а – принцип построения проекции; б – вид проекции



Углы между меридианами проекции равны соответствующим раз­ностям долгот. Промежутки между параллелями определяются при­нятым характером изображения (равноугольным или другим) или спо­собом проектирования точек земной поверхности на картинную плос­кость.

Нормальная сетка азимутальных проекций ортогональна. Их мож­но рассматривать как частный случай конических проекций, в кото­рых a=1 (альфа=1).

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор кото­рой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.

В зависимости от искажений азимутальные проекции подразделя­ются на равноугольные, равновеликие и с промежуточными свойства­ми. В проекции масштаб длин может сохраняться в точке или вдоль од­ной из параллелей (вдоль альмукантарата). В первом случае предпола­гается касательная картинная плоскость, во втором - секущая. В пря­мых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных - только для поверхности шара (рис.5.2, б).

Цилиндрические проекции (cylindrical projection). В прямых ци­линдрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг дру­гу. Таким образом задается прямоугольная сетка цилиндрических про­екций (рис. 5.3, а).

Промежутки между параллелями пропорциональны разностям дол­гот. Промежутки между меридианами определяются принятым характе­ром изображения или способом проектирования точек земной поверх­ности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна. Цилинд­рические проекции можно рассматривать как частный случай коничес­ких при (х=0 (вершина конуса в бесконечности).

По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и попе­речные цилиндрические проекции в зависимости от расположения изоб­ражаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Существуют разные способы образования цилиндрических проек­ций. Наглядным представляется проектирование земной поверхности на боковую поверхность цилиндра (рис. 5.3, а), которая затем разверты­вается на плоскости [2] (рис.5.3, б). Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору, во втором - по двум стандартным параллелям, симметрич­ным относительно экватора.

Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов - от общегеографических до специаль­ных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равно­угольных проекциях (на шаре).

В прямых цилиндрических проекциях одинаково изображаются одни и те же участки земной поверхности вдоль линии разреза - по восточ­ной и западной рамкам карты (дублируемые участки карты) и обеспечи­вается удобство чтения по широтным поясам (например, на картах рас­тительности, осадков) или по меридианальным зонам (например, на кар­тах часовых поясов).

Косые цилиндрические проекции при широте полюса косой сис­темы, близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшени­ем широты полюса кривизна параллелей увеличивается, а их протя­жение уменьшается, поэтому уменьшаются и искажения (эффект сфе­ричности).

В прямых проекциях полюс показывается прямой линией, по дли­не, равной экватору, но в некоторых из них (проекции Меркатора, Уэтча) полюс изобразить невозможно. Полюс представляется точкой в косых и поперечных проекциях. При ширине полосы до 4,5° можно использовать касательный цилиндр, при увеличении ширины поло­сы следует применять секущий цилиндр, т.е. вводить редукционный коэффициент.

Поликонические проекции (policonic projection). В них паралле­ли изображаются дугами эксцентрических окружностей с центрами на среднем (прямолинейном) меридиане или его продолжении, а меридиа­ны - кривыми, симметричными относительно среднего меридиана (рис. 5.4).



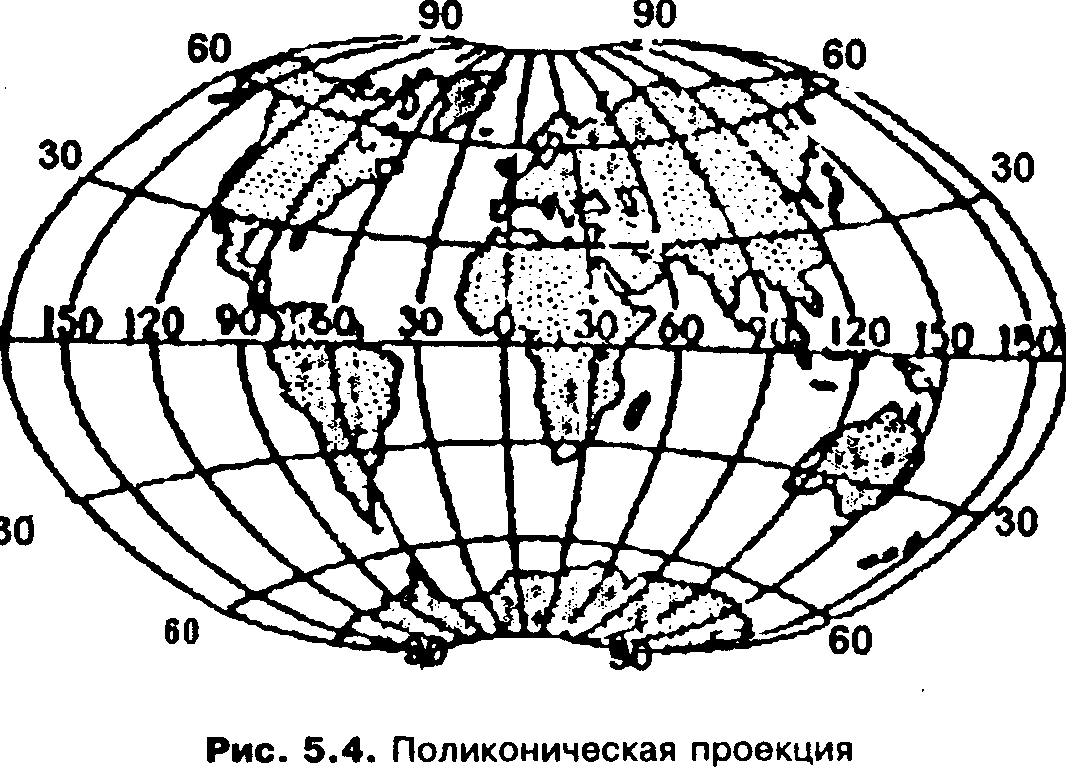
Рис. 5.4. Поликоническая проекция

Частным случаем поликонических проекций являются собственно поликонические проекции, для которых принимаются дополнительные условия, и круговые проекции с меридианами в виде дуг эксцентричес­ких окружностей.

К поликоническим проекциям в широком понимании относятся про­екция Таича (определялась аналитически) и проекции Гинзбурга (полу­чены численными методами).

Видоизмененная простая полнконнческая проекция. Она при­меняется как многогранная. Земная поверхность, принимаемая за по­верхность эллипсоида вращения, делится линиями меридианов и парал­лелей на трапеции.

При рассмотрении данной проекции учтем особенности ее приме­нения при создании карты масштаба 1:1 000 000.

Трапеции изображаются на отдельных листах в одной и той же про­екции (для карты масштаба 1:1 000 000 - в видоизмененной простой поликонической).

Листы международной карты мира масштаба 1:1 000 000 имеют определенные размеры сторон трапеций: по меридианам -4°, по парал­лелям - 6°; на широте от 60 до 76° листы сдваивают, они имеют размеры по параллелям 12°; выше 76° листы счетверяют, их протяжение по па­раллелям - 24°.

Применение проекции как многогранной определяет необходимость введения номенклатуры - системы обозначения отдельных листов.

Для карты масштаба 1:1 000 000 установлено обозначение трапеций по широтным поясам в направлении от экватора к полюсам буквами латинского алфавита (А, В, С, D и т.д.) и по колоннам - арабскими циф­рами (1, 2, 3, 4 и т.д.), которые считают от меридиана с долготой 180° (по Гринвичу) против часовой стрелки.

Номенклатура сдвоенных и счетверенных листов карты складыва­ется из обозначений широтного пояса и соответственно двух или четы­рех колонн.

Отметим особенности видоизмененной простой поликониче'кой проекции и распределение искажений б пределах отдельных листов карты масштаба 1:1 000 000.

Меридианы изображаются прямыми линиями. Длина двух мериди­анов, отстоящих от среднего на ±2° по долготе (на ±4° на сдвоенных листах и на ±8° на счетверенных), искажений не имеет.

Крайние параллели каждого листа (северная и южная) являются ду­гами окружностей, центры этих параллелей находятся на среднем мери­диане, длина их не искажается.

Для построения внутренних параллелей используют способ Хинкса, т. е. проводят эти параллели через точки, полученные путем деления всех меридианов на четыре равные части.

Картографическая сетка строится через 1 ° по широте и по долготе, на сдвоенных листах - по долготе через 2°, на счетверенных - через 4°. Таким образом, все листы карты масштаба 1:1 000 000 имеют пять па­раллелей и семь меридианов.

Криволинейные меридианы простой поликонической проекции заменяются в видоизмененной поликонической проекции прямыми, соединяющими соответствующие точки крайних параллелей, поэто­му масштабы на внутренних параллелях будут меньше единицы.

Минимальный масштаб получают на средней параллели каждого листа карты. Для карты масштаба 1 : 1 000 000 искажение длины сред­ней параллели каждого листа Vn-0,06%.

Масштабы по меридианам и параллелям для этой карты могут быть приняты за экстремальные (а и Ь), так как сетка проекции практически ортогональна. На каждом листе имеются четыре точки, в которых от­сутствуют искажения всех видов; эти точки находятся на пересечении крайних параллелей листа с меридианами, удаленными от среднего на 2° к западу и востоку.

Максимальное искажение площади Vp находится в середине листа, оно имеет знак минус и может достигать -0,14 %. Изоколы нулевых искажений площади имеют вид кривых, проходящих через точки, в которых отсутствуют искажения, и вытянутых вдоль крайних меридианов.

Достоинством видоизмененной простой поликонической проекции, применяемой как многогранная, является небольшая величи­на искажений. Анализ в пределах листа карты показал, что искажения длин не превышают 0,10 %, площади -0,15 %, углов - 5' и являются практически неощутимыми. Недостаток этой проекции - появле­ние разрывов при соединении листов по меридианам и параллелям.

Псевдоцилиндрические проекции. В прямых псевдоцилиндрических проекциях параллели изображаются в виде прямых параллельных линий, меридианы - в виде кривых (дуг, синусоид, гипербол, парабол, эллипсов и т.д.) , симметричных относительно среднего прямолиней­ного меридиана (рис.5.5).



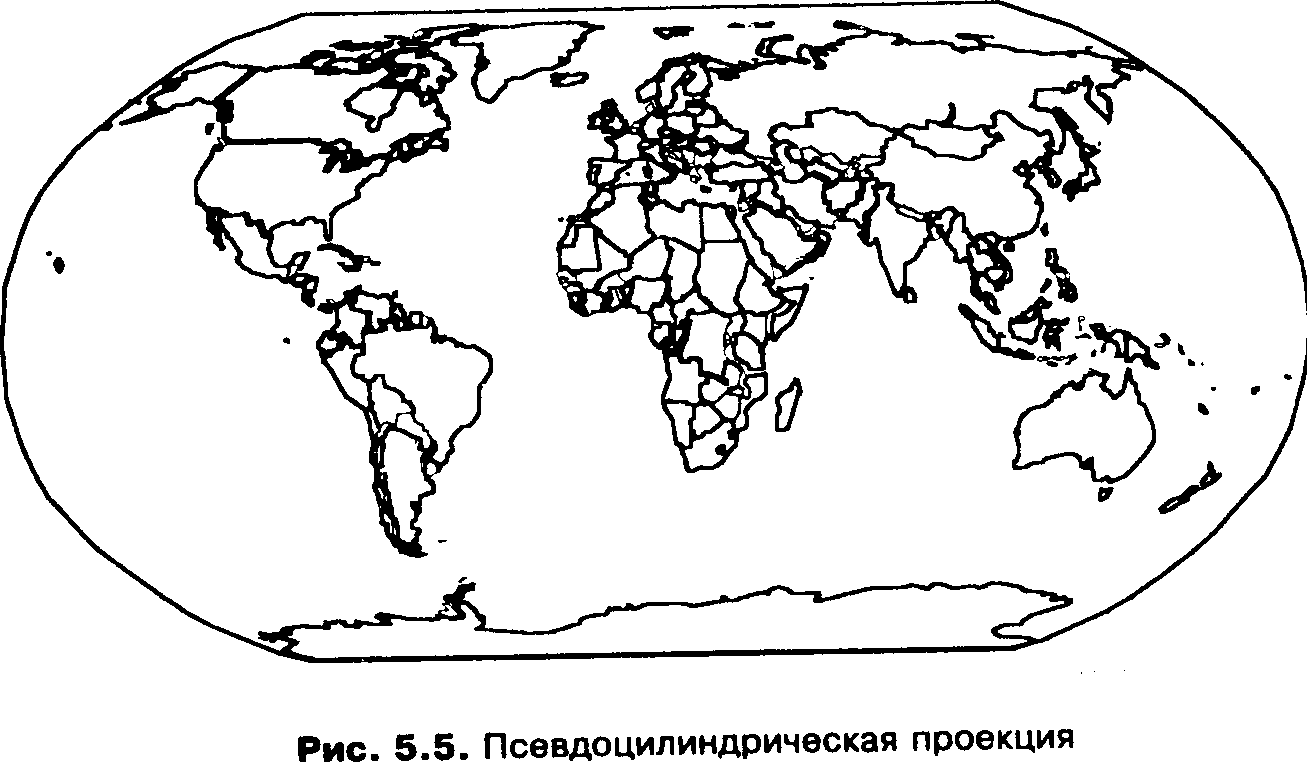
Рис. 5.5. Псевдоцилиндрическая проекция

Промежутки между параллелями определяются принятым законом изображения земной поверхности на плоскости. Промежутки между меридианами в равновеликих проекциях пропорциональны разностям долгот, в других проекциях они могут убывать или, значительно реже, воз­растать от среднего меридиана к востоку и западу.

Полюс в псевдоцилиндрических проекциях изображается точкой или полярной линией, длина которой устанавливается или получается из зада­ния. Поэтому сетка меридианов и параллелей не ортогональна, в силу чего эти проекции не могут быть равноугольными.

При рассмотрении цилиндрических проекций как частного случая псевдоцилиндрических проекций, когда меридианы изображаются пря­мыми параллельными линиями, ортогональными к параллелям, цилин­дрическую равноугольную проекцию Меркатора можно считать равно­угольной псевдоцилиндрической проекцией.

Из-за неортогональности сетки экстремальные масштабы не совпа­дают с направлением меридианов и параллелей, за исключением сред­него меридиана и экватора.

Псевдоцилиндрические проекции в основном применяются для изображения всей земной поверхности или значительных ее частей в мелких масштабах, поэтому земная поверхность принимается за по­верхность шара с радиусом R. Эти проекции имеют две оси симмет­рии - экватор и средний меридиан нормальной сетки. Косые и попе­речные псевдоцилиндрические проекции используются крайне редко.

Проекция Гаусса-Крюгера. К.Ф. Гаусс в 1820 - 1830 гг. разра­ботал "двойную" равноугольную проекцию, сохраняющую длины на среднем меридиане. Л.Крюгер в 1912и 1919 гг. предложил способ непосредственного отображения эллипсоида взамен определения, указанного двойной проекцией, и эту проекцию стали называть про­екцией Гаусса-Крюгера (Gauss - Kruger projection). Она была приня­та в СССР ( на эллипсоиде Бесселя) в 1928 г. для всех геодезических и топографических работ. В ней создавали топографические карты масштабов крупнее 1:500 000, а с 1939 г. проекция Гаусса-Крюгера стала применяться и для карты масштаба 1:500 000.

В апреле 1946 г. постановлением правительства были утверждены размеры референц-эллипсоида Красовского и новые исходные даты, характеризующие систему координат 1942 г.

Проекция Гаусса-Крюгера не является строго равноугольной, так как при ее получении использовано разложение в такой ряд, для которо­го выполняется только одно из условий Коши-Римана.

При введении в уравнение проекции еще одного дополнительного члена ряда начинает выполняться второе условие, а первое, которое со­хранялось ранее, не выполняется.

Проекция при сохранении в ее формулах достаточного количества (7-8) членов является практически равноугольной, поэтому можно счи­тать, что в ней соблюдаются условия ортогональности сетки и равен­ства масштабов.

В проекции Гаусса-Крюгера поверхность эллипсоида на плоскости отображается по меридианным зонам, ширина которых равна 6° (для карт масштабов 1:500000-1:10 000) и 3° (для карт масштабов 1:5 000 -1: 2 000) (рис. 5.6, a).

Меридианы и параллели изображаются кривыми, симметричными относительно осевого меридиана зоны и экватора, однако их кривизна настолько мала, что западная и восточная рамки карты показаны пря­мыми линиями.

Параллели, совпадающие с северной и южной рамками карт, изоб­ражаются прямыми на картах крупных масштабов (1:2 000 - 1:50 000), на картах мелких масштабов - кривыми. Начало прямоугольных коор­динат каждой зоны находится в точке пересечения осевого меридиана зоны с экватором (рис. 5.6, б).

В России принята нумерация зон, отличающаяся от нумерации колонн карты масштаба 1:1 000 000 на тридцать единиц, т. е. крайняя западная зона с долготой осевого меридиана 1=21° имеет номер 4, к востоку номера зон возрастают. Номер зоны N и долгота осевого меридиана 1° в градусах свя­заны между собой равенством L°= 6N-3.

Территория России находится в северном полушарии, поэтому ко­ординаты Х всех точек имеют положительное значение. Координаты Y имеют отрицательные значения левее осевого меридиана и положитель­ные правее его (рис. 5.6, б ). Чтобы исключить из обращения отрица­тельные координаты и облегчить пользование прямоугольными коорди­натами на топографических картах, ко всем координатам Y добавляют постоянное число 500 000 м (см. рис. 5.6, б). Для указания зоны, к кото­рой относятся координаты, к значению Y слева приписывают номер зоны. Например, запись координаты Y" 30 786 543м означает, что точка нахо­дится в 30-й зоне, ее реальная координата равна 786 000 - 500 000 = 286 543 м, т.е она расположена правее осевого меридиана 30-й зоны. Запись координаты Y= 8 397 720 м означает, что точка находится в 8-й зоне, ее реальная координата равна 397 720 - 500 000 = 102 280 м, она расположена левее осевого меридиана 8-й зоны.

Изоколы в проекции Гаусса-Крюгера имеют вид овалов, вытянутых вдоль осевого меридиана; в пределах отдельных листов карт они имеют вид прямых. Максимальные искажения в каждой зоне будут при значе­ниях широт 0° и ±3°, в этих точках они достигают пи»=0,14 %.

На расстоянии около 200 км по обе стороны от осевого меридиа­на и параллельно ему находятся две изоколы с нулевыми иска­жениями длин. При дальнейшем удалении от осевого меридиана масштаб длин становится больше единицы и достигает максиму­ма на пересечении крайних меридианов зоны с экватором (Vmax = +0,05 %).






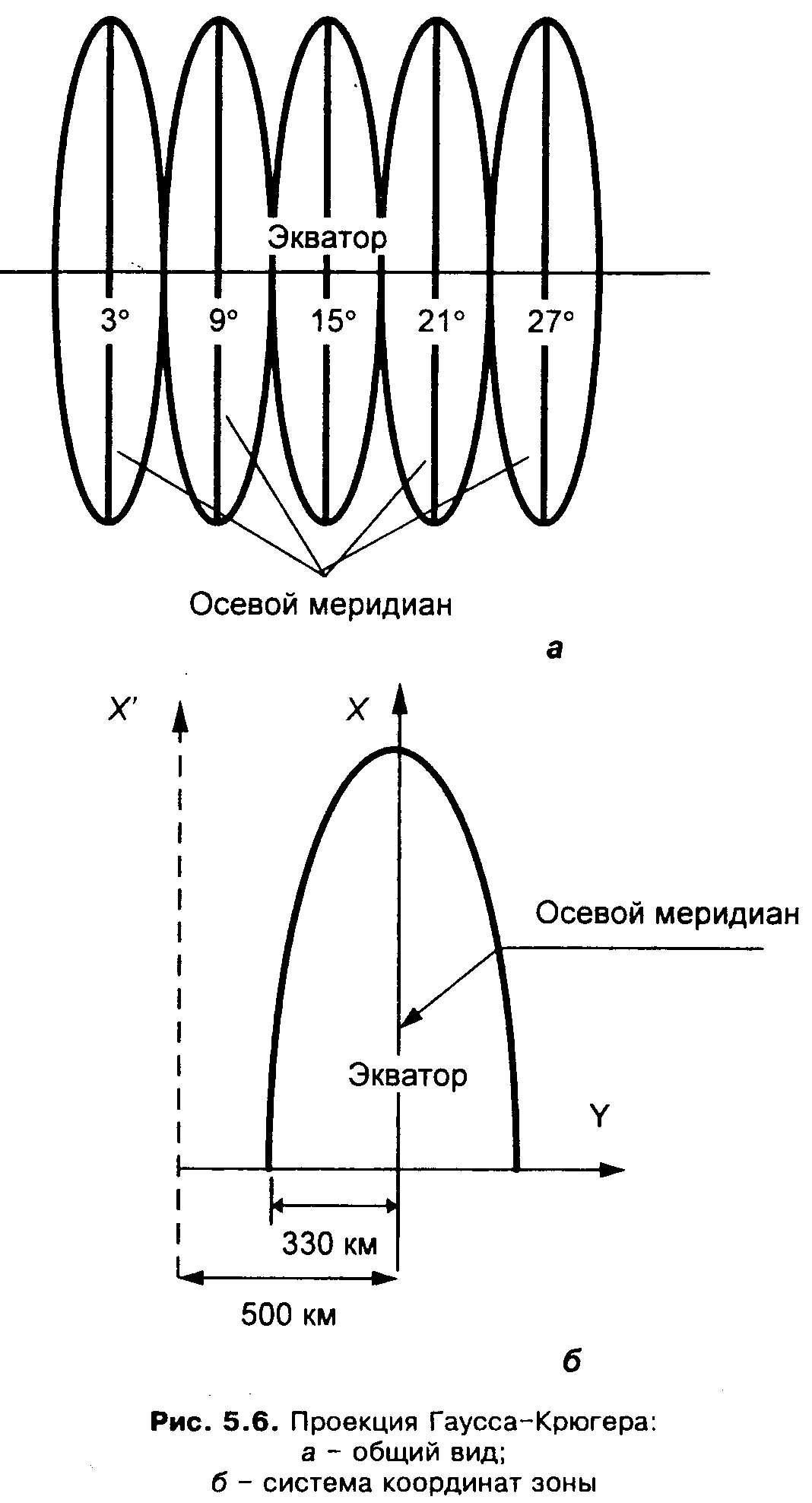
Рис. 5.6. Проекция Гаусса – Крюгера: а – общий вид; б – система координат зоны



Осевые меридианы трехградусных зон совпадают попеременно то с осевыми меридианами шестиградусных зон, то с крайними меридиана­ми этих зон.

Во многих странах применяют для составления топографичес­ких карт универсальную поперечно-цилиндрическую проекцию Меркатора (UTM) в шестиградусных зонах. Эта проекция близка по сво­им свойствам и распределению искажений к проекции Гаусса-Крюгера, но на осевом меридиане каждой зоны масштаб М=0,9996, а не единица. Проекция UTM получается двойным проектированием: эллипсоида на шар, а затем шара - на плоскость в проекции Меркатора.

Достаточно полное описание перечня проекций приведено в [2] . Важно отметить, что существует различие между проекцией, с которой работает пользователь, и проекцией исходной карты. Для мелкомасш­табных карт существенно различие картографических проекций. Про­цесс трансформации картографических данных из одной проекции в другую требует знания параметров проекции источника и производной проекции, известных из курсов математической картографии и теории картографических проекций и справочных изданий.

Пересчет координат может быть представлен как решение обратной задачи математической картографии, т.е. преобразования прямоуголь­ных координат в географические, а вслед за нею - прямой задачи с ис­пользованием уравнения производной проекции либо непосредствен­ного пересчета данных из проекции в проекцию, минуя приведение к системе географических координат.

При неизвестных функциональных зависимостях, определяющих соответствие географических и условных координат, можно воспользо­ваться методами трансформации по сети опорных точек с известными координатами. В этом случае возникает проблема оптимального выбора аппроксимирующей функции. Наличие координатной основы - обяза­тельное требование трансформационных преобразований.

Программные средства ГИС содержат различные блоки преобразо­вания, включающие различные проекции: равновеликую коническую Алберса, азимутальную равнопромежуточную, коническую равнопромежуточную, гномоническую, равновеликую азимутальную Ламберта, кони­ческую равноугольную Ламберта, Меркатора, цилиндрическую Милле­ра, косую Меркатора (Hotine), ортографическую, полярную стереогра­фическую, поликоническую, синусоидальную, стереографическую, поперечную Меркатора, универсальную поперечную Меркатора (UTM), Гринтена.

На практике использование модулей трансформации проекций может быть осложнено отсутствием параметров проекции карты-источника.

При определении проекций исходной карты рекомендуют пользо­ваться атласом для отечественных карт [4] и для зарубежных [17].

Для топографических карт в отличие от мелкомасштабных нет тако­го разнообразия проекций, однако имеется разнообразие моделей Зем­ли и географических систем координат.

Специфика российского рынка геоинформационных технологий определяет проблемы проекционных преобразований в России. Одна из серьезных проблем связана с использованием отечественной картогра­фической информации, имеющей значительные отличия от аналогич­ной иностранной. Как правило, иностранные программные средства не поддерживают напрямую распространенные в нашей стране проекции, а информацию о типе проекции и ее параметрах получить довольно сложно.

Другая проблема состоит в том, что широко распространенные в России разнообразные методы работы с пространственными данными не получили признания или не имеют аналогов за рубежом и нуждаются в анализе и классификации.

Геометрический анализ

Программные средства ГИС позволяют выполнять ряд операций геометрического анализа для векторных и растровых моделей. Для век­торных моделей такими операциями являются: определение расстояний, длин ломаных линий, координат центроидов полигонов, расчет площа­дей векторных объектов, трансформирование точек объекта. Особо сле­дует отметить процедуры поиска точек пересечения линий.

Для растровых моделей технологии ГИС обеспечивают выполнение следующих операций геометрического анализа: идентификацию зон, вы­числение площадей зон, расчет периметров зон, определение рассто­яния от границы зоны, определение формы зоны, трансформирование растрового слоя.

Для векторных моделей, каждая из которых отображает отдельный объект, процедуры геометрического анализа во многом используют тра­диционную геометрию и выполняются без каких-либо предварительных преобразований как алгоритмы прямого счета. Кроме того, например, площадь и периметр элемента могут входить в число обязательных ат­рибутов полигонов.

Для растровых моделей, которые создаются не по объектным при­знакам, проведению практически любой геометрической процедуры должны предшествовать анализ и выделение необходимого объекта (рас­познавание образа).

В ГИС эти процедуры упрощаются заданием исчерпывающей ин­формации в атрибутах модели. Но даже при таких условиях простая операция типа вычисления площади для растрового объекта существен­но отличается от аналогичной для векторного. Например, чтобы изме­рить по карте площадь объекта (зоны) признака А, необходимо обойти дерево иерархической структуры модели и сложить все листья, содер­жащие признак А, с учетом веса площади на уровне данного листа.

Более сложные алгоритмы основаны на развитии методов САПР, машинной графики, распознавания и анализа сцен. К таким алгоритмам принадлежат:

• задача построения полигонов Тиссена, которые представляют собой гео­метрические конструкции, образуемые относительно множества точек таким образом, что границы полигонов являются отрезками перпендикуляров, восста­навливаемых к линиям, соединяющим две ближайшие точки;

• расчет площадей трехмерных объектов;

• определение принадлежности точки внутренней области выпукло­го или невыпуклого полигона;

• описание геометрических и топологических отношений, линейных и полигональных объектов двух разноименных слоев при их наложении (оверлее).

В связи с возможными погрешностями, локализованными в плано­вых координатах объектов, применяемых для территорий глобального, семиглобального и регионального уровней, целесообразно использовать равновеликие проекции.

При наличии значительных площадных искажений возможно при­менение трансформации проекции исходных слоев.

Оверлейные операции

Особенностью цифровой карты является возможность ее организации в виде множества слоев (покрытий или карт-подложек).

Сущность оверлейных операций состоит в наложении разноимен­ных слоев (двух или более) с генерацией производных объектов, возни­кающих при их геометрическом наслоении, и наследованием их атрибу­тов. Наиболее распространены операции оверлея двух полигональных слоев.

Площадь и периметр элемента могут входить в число атрибутов поли­гонов. Их значения используются в операциях удаления границ полигонов, принадлежащих к одинаковым классам, и в оверлейных операциях.

Для растровых форматов данных такие расчеты достаточно просты. Для векторных представлений используют алгоритмы, основанные на формулах аналитической геометрии.

Практические трудности реализации оверлейных процедур связаны с большими затратами машинного времени на поиск координат всех пересе­чений, образующих полигоны линейных сегментов (возрастающих экспо­ненциально при росте числа полигонов); определение топологии получен­ной производной полигональной сети при так называемом топологическом оверлее, переприсвоение атрибутов производной сети различными метода­ми наследования атрибутов качественного (символьного, типового) или ко­личественного (числового, знакового) характера.

В алгоритмах операций наложения широко применяются методы математической логики и структурного анализа.

В настоящее время оверлейные процедуры ГИС обеспечивают высокопрофессиональные средства анализа и использования географичес­кой информации, включая взаимоналожение полигональных, точечных и линейных покрытий, создание буферных зон, объединение полигонов и ряд других функций, основывающихся на пространственной и топо­логической взаимосвязи данных.

В качестве примера рассмотрим подсистему Overlay широко извес­тной инструментальной системы Arcinfo, которая предоставляет доста­точно разнообразные средства обработки и анализа географической информации.

Шесть оверлейных команд, каждая из которых выполняет опреде­ленную функцию, обеспечивают максимальную гибкость пространствен­ного анализа. Это команды CLIP, ERASE, IDENTITY, INTERSECT, UNION и UPDATE.

При наложении картографических покрытий в результате пересече­ний границ полигонов образуется новый набор объектов покрытия. Ха­рактеристики новых полигонов определяются характеристиками исход­ных, что создает новые пространственные и признаковые взаимосвязи данных.

При табличном анализе данных, полученных с использованием фун­кций подсистемы Overlay, можно использовать dBASE-совместимую систему хранения и анализа данных. В частности, можно классифици­ровать участки территории для выбора оптимальных мест строитель­ства объектов жилых домов, основываясь на таких критериях, как ха­рактеристики грунтов, уклоны, близость к зонам затопления и т.п.

Оверлейные процедуры позволяют соединять сетку административ­ных районов, коммуникационные линии, зоны затопления, статистику преступности и другую информацию о городской среде для ежедневно­го анализа различных аспектов жизни большого города.

В подсистеме Overlay содержится команда BUFFER для создания буферных зон, т.е. зон, границы которых удалены на известное рас­стояние от любого объекта на карте. Буферные зоны различной ши­рины могут быть созданы вокруг выбранных объектов на базе таблиц сопряженных характеристик. Например, ширина лесных защитных полос вдоль дорог или водотоков может автоматически задаваться в соответствии с классом дорог или расходом водотока. Подсистема Overlay позволяет автоматически объединять друг с другом буфер­ные зоны, удаляя лишние внутренние границы. Она обеспечивает пользователя профессиональными средствами обработки разноплановых источников информации. В частности, в ней содержатся ко­манды MAPJOIN для соединения смежных листов карты в единое картографическое покрытие и команда SPLIT для разбиения боль­шого покрытия на более мелкие.

Команды DISSOLVE и ELIMINATE позволяют объединять выбран­ные полигоны в одном картографическом покрытии для создания новых полигональных объектов.

Команда RESELECT позволяет выбирать объекты картографичес­ких покрытий в соответствии с пространственными или логическими критериями, заданными пользователем новых полигональных объектов.

Команда INTERSECT соединяет две карты , оставляя только общие для обеих карт участки.

Команда CLIP удаляет все объекты, которые оказываются за предела­ми указанных пользователем границ. Команда SPLIT разбивает картогра­фические покрытия на покрытия меньшего размера.

Функционально - моделирующие операции

В ГИС используются различные аналитические операции:

• расчет и построение буферных зон - областей, ограниченных эквидистантными линиями, построенными относительно множества то­чечных, линейных и площадных объектов;

• анализ сетей;

• генерализация;

• цифровое моделирование рельефа.

Построение буферных зон. Буферная зона может создаваться вок­руг точки, линии или ареала. В результате образуется новый ареал, вклю­чающий исходный объект,

Операции построения буферной зоны применяются в транспортных системах, лесном хозяйстве, при создании охранных зон вокруг озер и вдоль водотоков, при определении зон загрязнения вдоль дорог, зоны влияния существующей или проектируемой сети транспортных коммуникаций, свя­занной с изменением экологической обстановки, и т.д.

В векторных моделях отсутствуют некоторые возможности растро­вых систем, например моделирования слоя "трения", поэтому построе­ние буферных зон на основе векторных моделей ГИС более трудоемко. При использовании буферных зон растровых моделей используют ап­робированные методы лексического анализа.

Методология создания буферных зон использует общие принципы пространственного анализа ГИС, в частности набор операций ГИС, при которых из уже имеющихся пространственных объектов формируются новые. Новые объекты могут иметь атрибуты старых, из которых они образованы.

Этот подход взят за основу при формировании буферных зон. Иногда ширину буферной зоны можно определить исходя из признака объекта. Ширина (радиус для точечных объектов) зоны может быть постоянной или зависеть от значения соответствующего атрибута объекта. В последнем слу­чае имеет место буферизация со "взвешиванием".

Анализ сетей. Операции анализа сетей позволяют решать оптими­зационные задачи на сетях. Они основаны на использовании векторных моделей, на координатном и атрибутивном представлении линейных пространственных структур и на введении в них топологических харак­теристик (моделей).

Координатные векторные пространственные объекты ( точки, ли­нии, полигоны, ареалы ) определены в векторных моделях наборами упорядоченных пар координат х, у:

• точка: (х, у),

• линия: (x1, y1), (x2, у2), ... , (xn, yn);

• полигон: (x1, y1), (х2, у2),..., (хn, уn).

Это обеспечивает идентичность цифрового представления указан­ных трех пространственных объектов, позволяя использовать группо­вые процедуры пространственного анализа.

Для построения линии или ареала нужно соединить каждую после­дующую пару точек прямой линией. Точки не всегда должны соединяться прямыми линиями. Особенности соединения и вида линий могут быть описаны в атрибутивных данных. Атрибуты объектов хранятся в таблицах.

Общая структура векторных моделей, применяемых для анализа сетей, состоит обычно из двух частей: координат к атрибутов.

Координаты хранятся в одном файле, каждая группа координат оп­ределяет один объект, обозначенный индивидуальным идентификато­ром (индексом ID);

Атрибуты содержатся в таблице с одним атрибутом, идентифициру­ющим объект, к которому привязаны все остальные.

В инструментальных ГИС используются различные термины наи­менования для этих взаимосвязанных понятий;

• атрибуты - дескрипторный набор данных, файл описаний данных, таблица атрибутов полигонов,

• координаты - геометрия, наборы данных изображения, данные о положении, география.

Основу анализа сетей определяет исследование связей между объек­тами, что задается топологией, или топологическими свойствами век­торной модели.

Топологические свойства выражают множество возможных отно­шений между объектами, например "ближайший к", "пересекает", "со­единен с". Этими выражениями пользуются для установления связей между двумя объектами.

Каждому объекту можно присвоить признак, который представляет собой идентификатор ближайшего к нему объекта того же класса; таким образом кодируются связи между парами объектов.

Следует выделить два особых типа связей: связи в сетях и связи меж­ду полигонами.

Связи в сетях определяются взаимодействием основных объектов сетей: линий, также известных как дуги, звенья, грани, ребра, и узлов, известных еще как пересечения, соединения, вершины.

Простейший способ кодирования связей между дугами и узлами -присвоение каждой дуге двух дополнительных атрибутов - идентифи­каторов узлов на каждом конце (входной узел и выходной узел). В этом случае будут иметь место два типа записей:

1) координаты дуг: (х1,y1), (х2, y2), ... , (хn, yn);

2) атрибуты дуг: входной узел, выходной узел, длина, вспомогатель­ные атрибуты.

Используя эти записи, можно двигаться от дуги к дуге, отыскивая те из них, у которых перекрываются номера узлов.

Таким образом, механизм анализа сетей основан на особой органи­зации структур данных и кодировании связей. Собственно анализ про­исходит с использованием информационной основы моделей сети.

Методы анализа географических сетей являются мощным аналити­ческим средством для моделирования реальных сетей (улицы, водото­ки, телефонные линии и линии электросвязи) для поиска объектов по его адресу (например, привязка табличных данных к географическим объектам с использованием файлов формата TIGER).

В системе ArcInfo имеется для этой цели специальная программная подсистема Network. Она обеспечивает выполнение двух основных фун­кций: анализ географических сетей и поиск объекта по его адресу (ад­ресное геокодирование).

Подсистема Network позволяет рассчитывать оптимальные марш­руты движения транспорта, места размещения объектов, оптимизиро­вать районирование. Точность моделирования реальных сетей при ис­пользовании этой подсистемы высока, так как различная информация типа направления и стоимости передвижения или перемещения грузов может храниться в таблицах сопряженных характеристик для каждой линии в сети.

Анализ сетей включает в себя три функции: поиск путей, аллока­цию и районирование.

Поиск путей обеспечивает оптимизацию перемещения ресур­сов по сети, например выбор альтернативных маршрутов движения ма­шин аварийных служб во время максимальной загруженности транспор­тных магистралей.

Аллокация позволяет отыскать ближайшие центры (минималь­ную стоимость перемещения) для каждой точки сети в целях оптимиза­ции функционирования последней. Например, аллокация может исполь­зоваться при поиске ближайшей станции пожарной охраны для каждой улицы или ближайшей школы для каждого конкретного школьника.

Районирование включает в себя группировку участков, ограничен­ных элементами сети, например городских кварталов, ограниченных ули­цами. Это средство ценно при планировании. Районирование может исполь­зоваться, например, для определения границ участков доставки газет.

Если организация использует информацию, содержащую уличную адресацию, то применение средств Network позволяет определить ха­рактеристики объекта по его адресу. Система геокодирования дает возможность соединить табличные данные адресных файлов с гео­графическим положением объектов в форматах ЕТАК, TIGER или ArcInfo.

При использовании покрытий с адресацией все данные могут ана­лизироваться и наноситься на карту любым набором программных средств Arcinfo.

Подсистема Network полностью поддерживает выполнение таких при­кладных задач, как маркетинговые исследования, оптимизация размеще­ния сервисных центров по адресам клиентов, компоновка списков расселе­ния, распределение детей по школам, направление машин аварийных служб, картографирование мест совершения преступлений и др.

Успешный анализ сетей возможен только при наличии качествен­ных обобщенных моделей сетей и движения потоков по ним. Структура данных Arcinfo, средства анализа и отображения, содержащиеся в под­системе Network, обеспечивают такую возможность.

Генерализация. Генерализация в ГИС - это набор процедур клас­сификации и обобщения, предназначенных для отбора и отображения картографических объектов соответственно масштабу, содержанию и тематической направленности создаваемой цифровой карты.

Относительно информационного моделирования генерализация может быть рассмотрена как группа методов, позволяющих сохранить объем информации даже при уменьшении объема данных. Например, при сокращении числа точек на линии остающиеся должны быть выб­раны так, чтобы внешний вид линии не изменился. При генерализации происходит геометрическое манипулирование с цепочками координат­ных пар (х, у).

Рассмотрим методику генерализации линий. Более общая задача включает, например, генерализацию ареалов до уровня точки.

Генерализация как группа методов включает в себя следующие про­цедуры:

• упрощение - набор алгоритмов, которые позволяют убрать лиш­ние или ненужные координатные пары, исходя из определенного гео­метрического критерия (например, расстояние между точками, смеще­ние от центральной линии);

• сглаживание - комплекс методов и алгоритмов, которые позволя­ют переместить или сдвинуть координатные пары с целью устранить мелкие нарушения и выделить только наиболее значимые тенденции изменения линии;

• перемещение объектов - процедуры сдвига двух объектов, про­водимые во избежание их слияния или наложения при уменьшении мас­штаба. Большинство алгоритмов перемещения объектов в векторном формате ориентировано на интеллектуальный интерактивный режим, когда векторы начального перемещения задаются специалистом-картографом. В иных случаях для регулирования процесса перемещения ис­пользуется уменьшенная копия объекта;

• слияние - объединение двух параллельных объектов при умень­шении масштаба. Например, берега реки или обочины дороги в мелком масштабе сливаются, остров превращается в точку;

• корректировка (текстурирование) - набор эвристических про­цедур, которые позволяют в уже упрощенный набор данных снова ввес­ти некоторые детали. Например, сглаженная линия может потерять сход­ство с оригиналом, тогда для улучшения ее вида будет проведено текстурирование в случайных точках.

Один из методов генерализации предполагает расчленение линии путем введения дополнительных точек и придания большего сходства с оригиналом.

Цифровое моделирование рельефа. Оно заключается в построе­нии модели базы данных, которая бы наилучшим образом отображала рельеф исследуемой местности. Эти процессы связаны с трехмерным моделированием и с задачами пространственного анализа.

Говоря терминами моделирования, происходит переход от аналоговой модели непрерывной поверхности к дискретной модели набора точек, оп­тимально отображающей форму этой поверхности.

Координаты точек цифровой модели рельефа (ЦМР) расположены на земной поверхности, имеющей сложную форму. Для подробного отобра­жения такой поверхности требуется очень большое число точек, поэтому в ЦМР используют различные математические модели поверхности.

В свою очередь, это определяет проблему выбора оптимального ана­литического описания или набора функций для отображения рельефа местности. При этом может возникнуть задача учета возможных картог­рафических представлений и проекций.

В зависимости от характера рельефа местность подразделяют на равнинную, всхолмленную и горную. Вводят понятие пяти основных форм рельефа; гора, котловина или впадина, хребет, лощина, седловина

Отображают рельеф разными способами: цветом, штриховкой, го­ризонталями, отметками характерных точек с подписями и т.п.

Одним из наиболее распространенных методов построения релье­фа является метод горизонталей. Горизонталью называют геометричес­кое место точек (линия) с равными отметками (одинаковая высота над уровнем моря).

Метод горизонталей наиболее приемлем для ГИС. Он открывает большие перспективы для моделирования горизонталей на основе трех­мерных моделей, вписывается в послойное представление векторных данных ГИС (оверлей), что создает возможность применения ряда стан­дартных математических алгоритмов, входящих в состав ГИС. Наконец, этот метод позволяет использовать ряд процедур пространственного анализа данных линейных объектов, т.е. применять процедуры анализа 20-объектов для объектов, относящихся к классу 3D.

Цифровое моделирование будет подробно рассмотрено в разд. б. Здесь отметим лишь различие между цифровой моделью рельефа и циф­ровой моделью картографического отображения рельефа. В первом слу­чае речь идет об информационной структуре базы данных, во втором -об информационной структуре, предназначенной для визуального ото­бражения цифровых данных с помощью дисплея или плоттера.

Выводы

Отечественная картографическая информация имеет значитель­ные отличия от аналогичной иностранной. Как правило, иностранные программные средства не поддерживают напрямую распространен­ные в нашей стране проекции, а информацию о типе проекции и ее па­раметрах получить довольно сложно. Это определяет преимущество отечественных разработок ГИС, содержащих наборы нужных проек­ционных преобразований.

Моделирование в ГИС охватывает ряд областей, ранее не объеди­нявшихся для совместной обработки информации. Оно включает по­строение проекта карты на основе методологии САПР, проекционные преобразования, цифровое моделирование, автоматизацию процедур генерализации, анализ сетей, преобразование форм представления дан­ных и др.

Интеграция данных в ГИС создает возможности для качественно­го совершенствования моделирования (трехмерных объектов или прост­ранственных сетей) с целью использования результатов моделирова­ния в управлении, планировании, бизнесе.