Автоматизация системы экспертного оценивания качества технологических процессов в непрерывном производственном цикле промышленных предприятий

Специальность 05.13.06 – Автоматизация и управление технологическими процессами и производствами (промышленность)

Автореферат

диссертации на соискание ученой степени

кандидата технических наук

Москва - 2008

Работа выполнена в Московском автомобильно-дорожном институте (государственном техническом университете)

Научный руководитель	Заслуженный деятель науки РФ, доктор технических наук, профессор Николаев Андрей Борисович, профессор МАДИ(ГТУ)
Официальные оппоненты	Доктор технических наук, профессор Строганов Виктор Юрьевич, профессор МГТУ им.Н.Э.Баумана
	Кандидат технических наук, Лукащук Петр Иванович Генеральный директор ООО «Спецстройбетон-200», г.Москва

Ведущая организация: Российский научно-исследовательский институт информационных технологий и систем автоматизированного проектирования (Рос НИИ ИТ и АП), г.Москва.

Защита состоится 2 июля 2008г. в 10 часов на заседании диссертационного совета Д.212.126.05 при Московском автомобильно-дорожном институте (государственном техническом университете) по адресу:

125319, ГСП А-47, Москва, Ленинградский пр., д.64.

С диссертацией можно ознакомиться в библиотеке МАДИ(ГТУ)

Текст автореферата размещен на сайте Московского автомобильно-дорожного института (государственного технического университета): www.madi.ru

Автореферат разослан 2 июня 2008г.

Отзыв на автореферат в одном экземпляре, заверенный печатью, просим направлять в адрес совета института.

Ученый секретарь

диссертационного совета,

кандидат технических наук,

доцент

Михайлова Н.В.

Общая характеристика работы

Актуальность проблемы

В настоящее время большое внимание уделяется разработке систем поддержки принятия решений в оценке качества промышленной продукции. При этом качество продукции напрямую связано с качеством технологических процессов. Применение статистических методов - весьма действенный путь разработки технологий контроля качества. Многие ведущие фирмы стремятся к их активному использованию, и некоторые из них тратят более ста часов ежегодно на обучение этим методам, осуществляемое в рамках самой фирмы. Знание методов - часть нормы образования инженеров по контролю качества, но само знание еще не означает умения применить его. Дать разумную интерпретацию события с математической точки зрения, важнее, чем знание самих методов. Кроме того, надо уметь идентифицировать недостатки и возникшие затруднения в плане изменения самого технологического процесса. Важно не столько знание самих методов, сколько сознательное желание их использовать.

Производственный процесс должен быть управляемым. Иными словами, если средние значения последовательных выборок оценок допусков сильно флуктуируют или явно находятся вне заданного допуска, то вначале нужно решить проблемы качества. Следовательно, первый шаг к организации высококачественного процесса производства состоит в том, чтобы сделать процесс управляемым, в том числе с помощью методов, основанных на картах контроля качества. Если процесс управляем, то можно ставить вопрос о его пригодности.

Цель и основные задачи исследования

Целью настоящей работы является повышение эффективности оценки качества технологических процессов в непрерывном производственном цикле за счет автоматизации процедур экспертного оценивания на основе карт контроля качества.

В соответствии с поставленной целью в диссертации решаются следующие задачи:

анализ методов и моделей оценки качества технологических процессов в непрерывном производственном цикле;
разработка и параметризация планов контроля качества технологических процессов;
разработка методов и моделей классификации качества технологических процессов и формирование обобщенных критериев качества;
анализ и разработка системы экспертного оценивания показателей технологических процессов;
разработка программно-моделирующего комплекса системы управления контролем качества продукции.

Объект исследования

Объектом исследования является технологический процесс в непрерывном производственном цикле промышленных предприятий.

Методы исследования

Теоретической основой диссертационной работы являются общая теория систем, методы оптимизации, случайные процессы, имитационное моделирование, исследование операций, регрессионный анализ, дисперсионный анализ, карты контроля качества и другие.

Научная новизна

Научную новизну работы составляют методы, модели и методики, обеспечивающие автоматизацию экспертного оценивания качества технологических процессов в непрерывном производственном цикле промышленных предприятий.

На защиту выносятся:

методы агрегирования показателей карт контроля качества;
классификация показателей качества технологического процесса в условиях коррелированности показателей качества промышленных изделий;
модели латентно-структурного анализа в системе экспертного оценивания качества
программно-моделирующий комплекс оценки качества технологических процессов.

Достоверность научных положений, рекомендаций и выводов

Обоснованность научных положений, рекомендаций и выводов, изложенных в работе, определяется корректным использованием современных математических методов, согласованным сравнительным анализом аналитических и экспериментальных зависимостей. Достоверность положений и выводов диссертации подтверждена положительными результатами внедрения разработок в ряде предприятий.

Практическая ценность и реализация результатов работы

Научные результаты, полученные в диссертации, доведены до практического использования. Разработан программно-моделирующий комплекс, позволяющий в интерактивном режиме формировать и корректировать экспертные оценки качества продукции. Разработанные методы и алгоритмы прошли апробацию и внедрены для практического применения в ЗАО НПВФ «СВАРКА» и ЗАО «ФИРМА ПРОМСТРОЙМОНТАЖ».

Результаты внедрения и эксплуатации подтвердили работоспособность и эффективность разработанных методов.

Апробация работы

Содержание разделов диссертации докладывалось и получило одобрение:

на республиканских и межрегиональных научно-технических конференциях, симпозиумах и семинарах (2005-2008 г.г.);
на заседании кафедры «Автоматизированные системы управления» МАДИ(ГТУ).

Содержание работы

Структура работы соответствует списку перечисленных задач и содержит описание разработанных методов, моделей и алгоритмов.

Во введении обосновывается актуальность работы. Ставятся цели и задачи исследований. Приводится краткое содержание глав диссертации.

В первой главе диссертации проведен анализ и показано, что существует два обстоятельства, наиболее сильно влияющих на качество продукции: отклонения от плановых спецификаций и слишком высокая изменчивость реальных характеристик изделий (относительно плановых спецификаций). На ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества часто используются методы планирования эксперимента. Изменчивость или вариабельность - причина дефектов. Что будет, если изготавливать изделия из материалов одинакового качества на одинаковых станках, с помощью одних и тех же методов и проверять эти изделия совершенно одинаковым образом? Вне зависимости от того, сколько изделий будет изготовлено, все они должны быть идентичными, пока идентичны упомянутые условия, т.е. либо все изделия будут соответствовать требованиям, либо не будут им соответствовать. Все изделия окажутся дефектными, если материалы, станки, методы изготовления или контроля будут ненадлежащими. В этом случае неизбежно появление одинаковых дефектных изделий. Если же никаких отклонений в перечисленных условиях производства не будет, то все изделия должны быть "идентичными" - бездефектными.

В работе проведен анализ и классификация типов контрольных карт, которые используются для отслеживания характеристик качества изделий. Функционал основных контрольных карт для оценки изменчивости производственного процесса представлен в табл.1.

При этом все виды карт контроля качества дают информацию, необходимую для принятия решений по переналадке технологического процесса. При этом каждая карта рассматривается как некоторый показатель оценки качества, однако интерпретация всех показателей для решения вопроса об изменении технических характеристик (переналадке, замене, установке новых агрегатов и др.) формулируется как задача экспертного оценивания качества в условиях многокритериальности.

Таблица

Функционал карт контроля качества

Карта	Функционал
X-bar	Контроль отклонений от среднего значения непрерывной переменной.
X	Кроме выборок, состоящих из нескольких наблюдений, X-карты могут быть построены для отдельных наблюдений, полученных в ходе производственного процесса.
MА	Контрольная карта экспоненциально взвешенного скользящего среднего.
CUSUM	Вместо отдельных наблюдений фиксируется накопленная сумма отклонений отдельных измерений от центральной линии или спецификации для обнаружения малых постоянных сдвигов производственного процесса.
R	Контроль за степенью изменчивости непрерывной величины (в контрольной карте этого типа наносятся значения размахов выборок).
MR	В паре с картами X и CuSum используется для контроля за изменчивостью переменной.
S	Рассматриваются значения выборочных стандартных отклонений.
S2	Контроль изменчивости выборочных дисперсий.
C	В предположении, что дефекты контролируемой характеристики встречаются сравнительно редко, контрольные пределы рассчитываются на основе свойств Распределения Пуассона.
U	Не требуется постоянство числа единиц проверяемых изделий, поэтому ее можно использовать при анализе партий различного объема. Строится график относительной частоты дефектов.
Np	Контрольные пределы рассчитываются на основе биномиального распределения, а не распределения редких событий. Строится график для числа дефектов.
P	Контрольные пределы находятся на основе биномиального распределения. Строится график процента обнаруженных дефектных изделий.

Для приведенных карт контроля качества стандартное отклонение для совокупности измерений определяется как:

=( r₁ / d₂ + ... + r_k / d₂ ) / k

(1)

для каждой из k выборок с объемом n больше 1, где r₁ ... r_k - размахи для каждой из k выборок и d₂ - постоянная для данного объема выборок. Стандартная ошибка среднего, _ср., рассчитывается как:

_ср. =  / ( ( n₁ + ... + n_k) / k ) ^½_.

(2)

а стандартная ошибка размаха, _разм, определяется на основе выражения:

_разм. = ( d3 ( Ср. N ) ),

(3)

где d3 - постоянная для данного объема выборки, а Ср. N - округленный средний объем выборок. Верхний контрольный предел (ВКП) и нижний контрольный предел (НКП) для каждой j-той выборки карты рассчитываются по формулам:

НКП_j = M - ( ( q * ) / n_j^1/2), ВКП_j = M + ( ( q * ) / n_j^1/2),

(4)

где M - взвешенное среднее выборочных средних, а q - эмпирический множитель.

Моделирование динамики принятия решений связано с процессами старения компонентов технологического оборудования, что может сказаться на выборе режимов работы для устранения причин выпуска дефектных изделий. В диссертации проведен анализ методов и моделей экспертного оценивания текущего состояния технологического процесса и сравнительный анализ степени соответствия принимаемых решений по управлению технологическими режимами, которые основаны на определении оценок качества в некоторой шкале качества. Так, существует множество различных видов шкал, которые группируются в три группы: номинальные, порядковые и количественные.

При проведении экспертного оценивания количественных показателей по заранее разработанному алгоритму необходимо произвести обработку полученной от экспертов информации и найти результирующую оценку из множества допустимых оценок (МДО) , являющуюся решением исходной задачи оценивания. Если полученное решение не устраивает, то возможно предоставление экспертам дополнительной информации, т.е. необходимо организовать обратную связь, после чего пользователи вновь решают соответствующие задачи выбора. Для формализованного описания самой экспертизы используются следующие компоненты:  - исходное МДО; _Э – МДО для экспертов; L – взаимодействие между экспертами; Q – обратная связь для представления экспертам интегрированной оценки;  - аналитическая обработка результатов (отображение ^N_Э  ).

Во второй главе диссертации разработаны формальные методы и модели контроля качества промышленной продукции. Ставится и решается задача формализации моделей контроля качества на основе карт контроля качества (глава 1) и принципов их включения в систему поддержки принятия решений по управлению технологическими процессами.

Для преобразования количества обнаруженных в каждой выборке дефектов при построении кратких C-карт будем использовать соотношение:

c'_j_,_k=(c_j_,_k - t_k)/t_k^1/2.

(5)

Для каждой выборки j и группы данных k, точки графика краткой C-карты (c'_j,k) находятся путем стандартизации отклонений наблюдаемых пуассоновских интенсивностей для числа дефектов от планового значения частоты t_k. По умолчанию t_k равна средней пуассоновской частоте для каждой из групп данных.

Для преобразования частоты дефектов, обнаруженных в выборках, при построении кратких U-карт будем использовать соотношение:

u'_j,k=u_j,k - t_k/(t_k/n_j)^1/2.

(6)

Для каждой выборки j и группы данных k, точки графика краткой U-карты (u'_j,k) находятся путем стандартизации отклонений наблюдаемых относительных пуассоновских частот от планового значения относительной частоты t_k. По умолчанию t_k равна средней пуассоновской частоте для каждой из групп данных k.

Для преобразования биномиальных интенсивностей случаев обнаружения брака, обнаруженных в выборках, при построении кратких Np-карт будем использовать соотношение:

np'_j,k=np_j,k - n_j*t_k/(n_j * t_k (1 - t_k))^1/2.

(7)

Для каждой выборки j и группы данных k, точки графика краткой Np-карты (np'_j,k) находятся путем стандартизации отклонений наблюдаемых биномиальных интенсивностей (np'_j,k) от планового значения биномиальной интенсивности n_jt_k. По умолчанию биномиальная интенсивность t_k равна средней биномиальной интенсивности для каждой из групп данных k.

Для преобразования биномиальных долей, обнаруженных в выборках, при построении кратких P-карт будем использовать соотношение:

p'_j,k=p_j,k - t_k /(t_k * (1 - t_k )/n_j)^1/2.

(8)

Для каждой выборки j и группы данных k, точки графика краткой P-карты (p'_j,k) находятся путем стандартизации отклонений наблюдаемых биномиальных долей от планового значения биномиальной доли t_k. По умолчанию t_k равна средней биномиальной доле для каждой из групп данных k.

Потенциальная пригодность (C_p) технологического процесса определяется как отношение размаха допуска к размаху процесса и при использовании границ ± 3 сигма данный показатель можно выразить в виде:

C_p = (ВГД-НГД)/(6*).

(9)

где: ВГД – верхняя граница диапазона, НГД – нижняя граница диапазона.

Данное отношение выражает долю размаха кривой нормального распределения, попадающую в границы допуска.

Обычное качество технологических процессов по производству железобетонных плит составляет примерно C_p=.67. В идеале, конечно, было бы хорошо, если бы этот показатель превышал 1, т.е. хотелось бы достигнуть такого уровня пригодности процесса, чтобы никакое (или почти никакое) изделие не выходило за границы допуска.

Показатель отношения пригодности (C_r) почти эквивалентен C_p; а именно, он вычисляется как 1/C_p (величина, обратная C_p).

Нижняя/верхняя потенциальная пригодность: C_pl, C_pu. Недостаток показателя C_p (и C_r) состоит в том, что он может дать неверную информацию о технологическом процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован. При этом сначала можно вычислить верхний и нижний показатели пригодности, чтобы отразить отклонение наблюдаемого среднего процесса от НГД и ВГД. Приняв в качестве размаха процесса границы ± 3 сигма можно вычислить показатели:

C_pl = (M - НГД)/3* и C_pu = (ВГД - M)/3*,

(10)

где M – среднее значение по выборке. Ясно, что если эти значения не совпадают, то процесс не центрирован.

Поправка на нецентрированность (K) дает возможность скорректировать индекс C_p, чтобы учесть смещение. А именно:

K=abs(Номинал - M)/(1/2*(ВГД - НГД))

(11)

где Номинал = (ВГД+НГД)/2. Этот поправочный множитель выражает отношение нецентрированности (номинал минус среднее) к допуску.

Показатель подтвержденного качества (C_pk) используется для корректировки C_p, внеся поправку на нецентрированность посредством вычисления:

C_pk = (1-k)*C_p.

(12)

Если процесс идеально центрирован, то k равно нулю и C_pk равно C_p. Однако когда процесс смещается от номинального значения, k увеличивается, и C_pk становится меньше C_p.

Показатель потенциальной пригодности: C_pm является модификацией показателя C_p, и направлен на уточнение оценки сигмы с целью учесть влияние случайной нецентрированности.

Вся совокупность критериев, полученных на основании анализа карт контроля качества приводит к необходмости многоритериальной задачи оценки качества технологического процесса, причем показатели качества естественным образом корелируют. При этом возникает необходимость решения задачи классификации, в которой предполагается, что группа испытуемых образцов характеризуется многомерным нормальным распределением W_k~N(m_k,D_k), где m_k=(m_k1, m_k2,…,m_kp) - математическое ожидание W_k. а

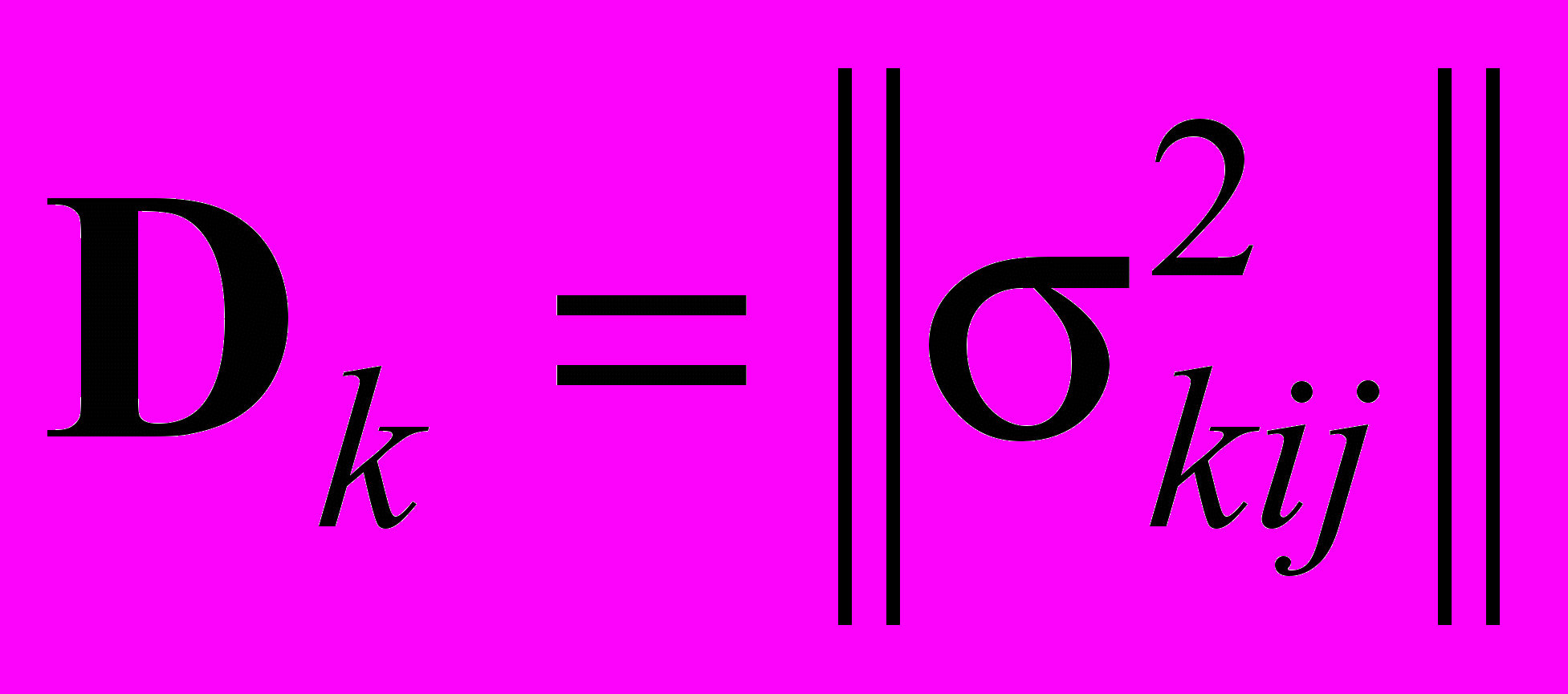- дисперсионная матрица W_k.

Предполагается, что дискриминантная функция z представляет линейную комбинацию результатов экспертного оценивания показателей качества:

z=₁x₁ + ₂x₂ + ... + _nx_n,

(13)

где _i - набор постоянных весовых коэффициентов.

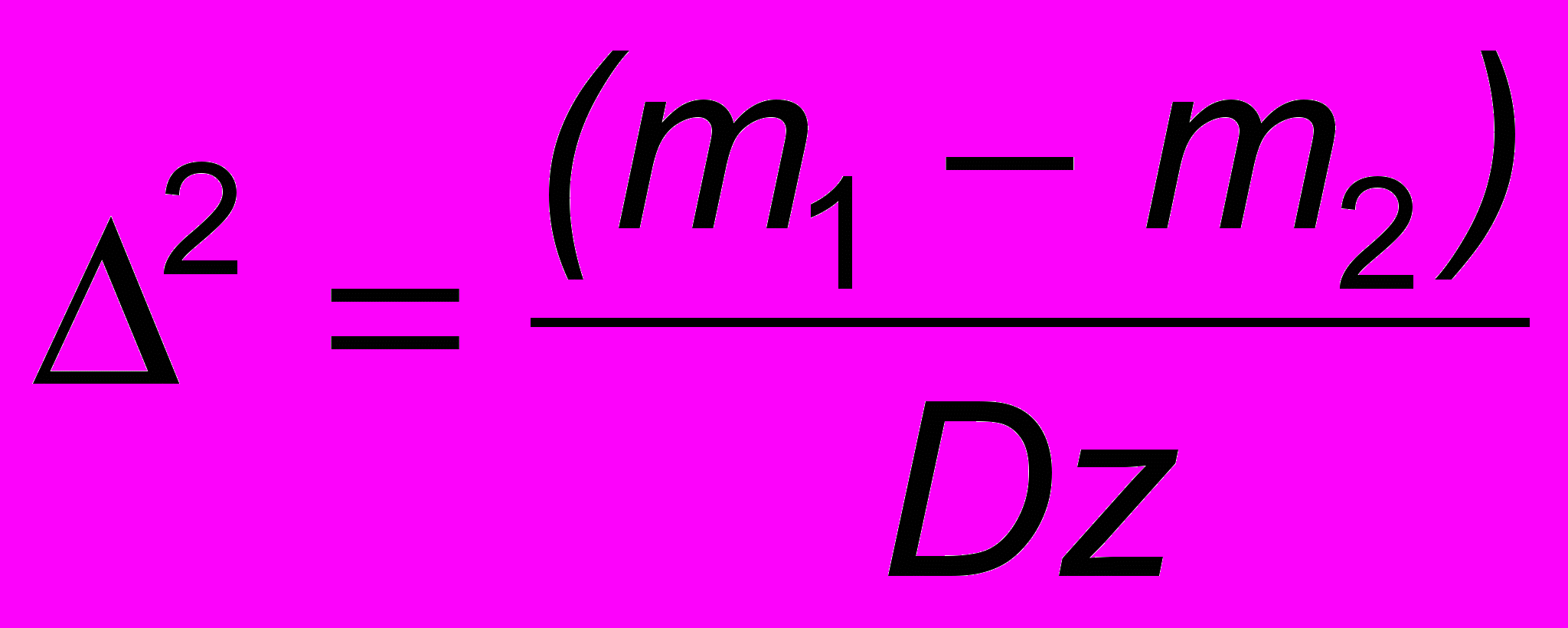Процедура классификации заключается в подборе константы с и отнесении X к W₁(качественный), если zc; и к W₂(некачественный), если z для которых вероятность ошибочной классификации минимальна. В общем случае эта задача является двухкритериальной оптимизационной. Ищется значение, которое максимизирует разность математических ожиданий и одновременно минимизирует дисперсию разности:

max.

(14)

На основании введенного критерия, двухкритериальная задача переходит в обычную задачу оптимизации, т.е. выбора значений _i, минимизирующих значение функции ². После определения _i наблюдаемому вектору X ставится в соответствие значение дискриминантной функции z.

Константа с выбирается из соображений минимизации вероятности ошибочной классификации. Сумма вероятностей ошибочных классификаций P(2|1)+P(1|2) минимальна при выборе константы .

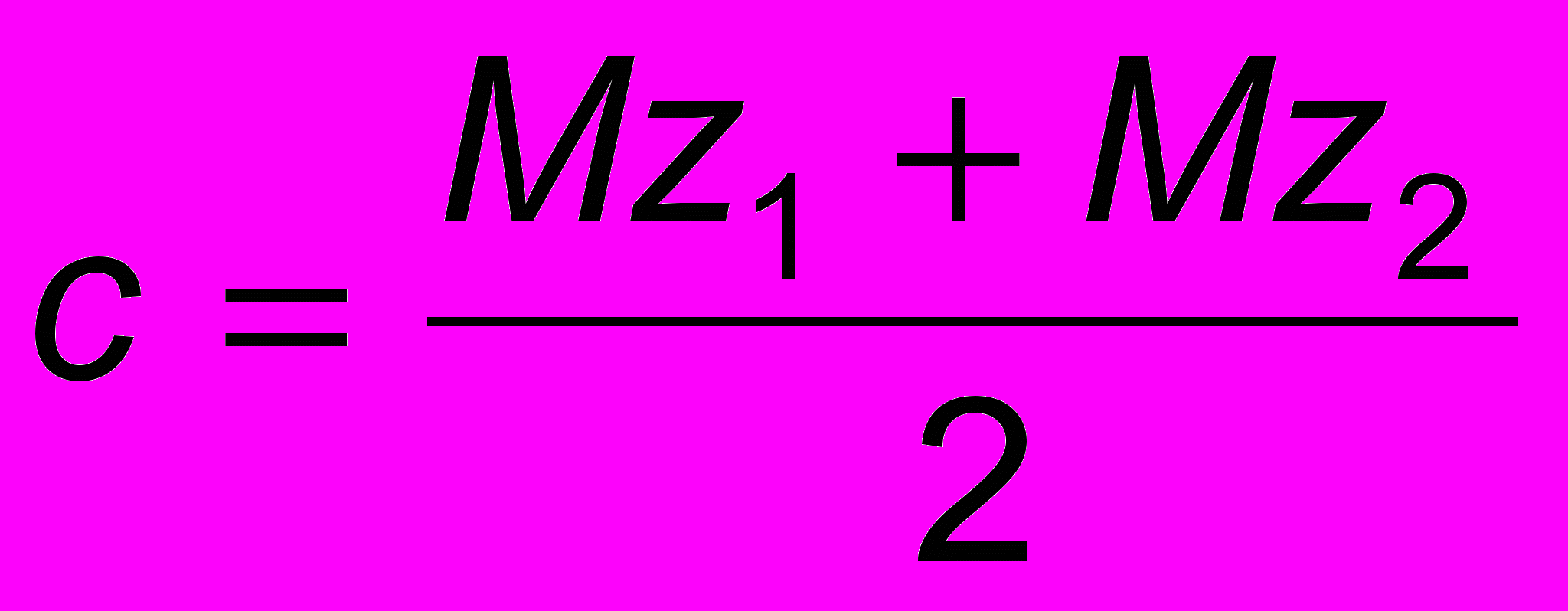В качестве оценки влияния коррелированности результатов рассмотрим пример для четырех показателей качества. Пусть разность математических ожиданий для двух групп по каждому уровню равна M=(1, 1, 1, 1) и корреляции между результатами оценки также отсутствует, тогда для весов заданий справедливо
=(1, 1, 1, 1).

Если же сделать предположение о наличии даже небольших корреляций (₂₃,=0.2), то в этом случае решение уравнений для весов будет =(1, 0,83, 0,83, 1). В данном случае видно существенное снижение весов для коррелированных оценок. Таким образом, показано, что корреляция и распределение оценок существенно влияют на параметры алгоритма классификации. Имея статистические данные по результатам оценки качества можно вычислить все корреляции и в процедуре классификации заменить дисперсионную матрицу ее оценкой, что повысит эффективность процедур классификации с точки зрения вероятности ошибочной классификации.

В случае непригодного технологического процесса необходимо решение задачи разработки мер по реорганизации процесса, которая также является результатом обработки мнений экспертов. Для решения этой задачи в диссертации предлагается использовать попарные сравнения. В этом случае эксперт дает не численное значение оценки, а предпочтение одних мер другим. Хотя это более трудоемкая процедура экспертного оценивания, она позволяет повысить адекватность принятых мер по устранению недостатков. То есть каждая опросная карта каждого эксперта представляет бинарное отношение. Таким образом, по результатам анализа всех экспертов составляется обобщенная матрица 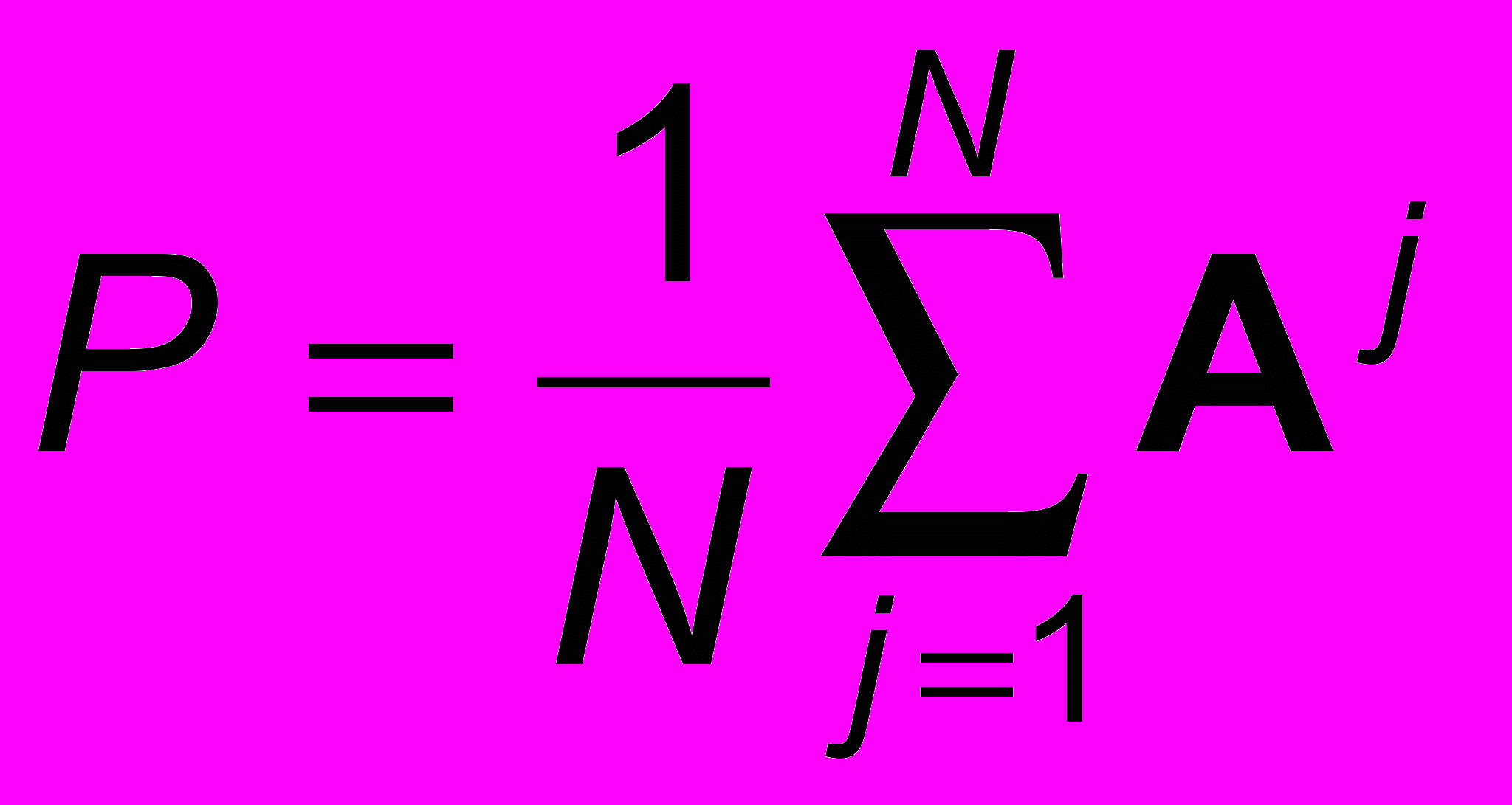, где A^j - ранжировка j-го эксперта, P=||p_ij||- матрица вероятностей предпочтения качества i-го и j-го варианта модернизации технологического процесса.

Следующим этапом является переход от матрицы попарных сравнений к перестановке =E_n _Э по уровню качества, которая определяется числовым значением. Числовая мера различия из вероятности предпочтения реализуется на основании поиска Z_ij,:

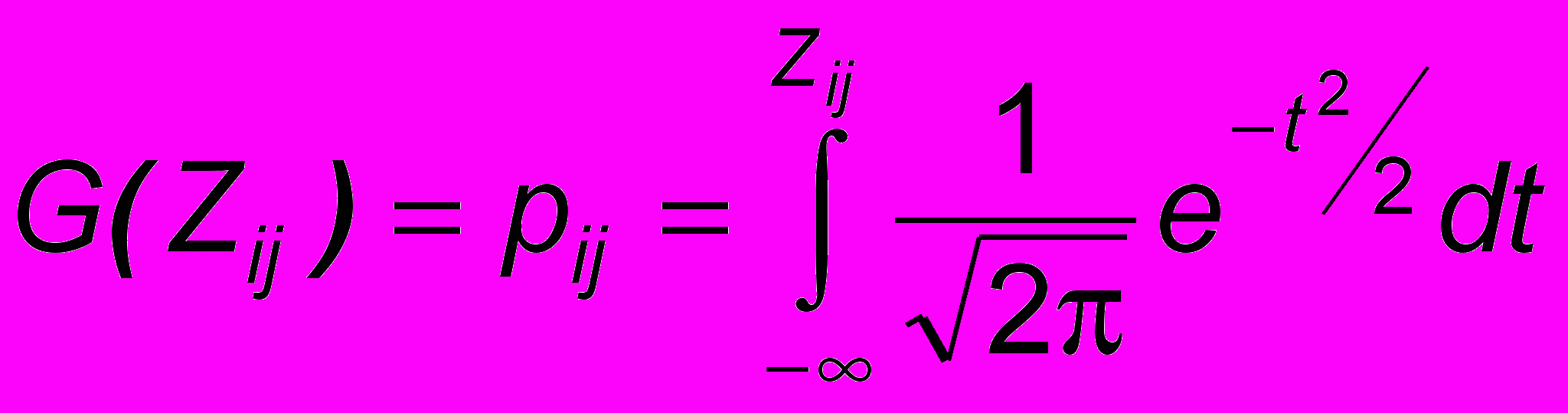(15)

где Z_ij - определено в единицах стандартного отклонения.

Все попарные различия сводятся в матрицу Z=||Z_ij|| и вычисляется сумма каждой строки 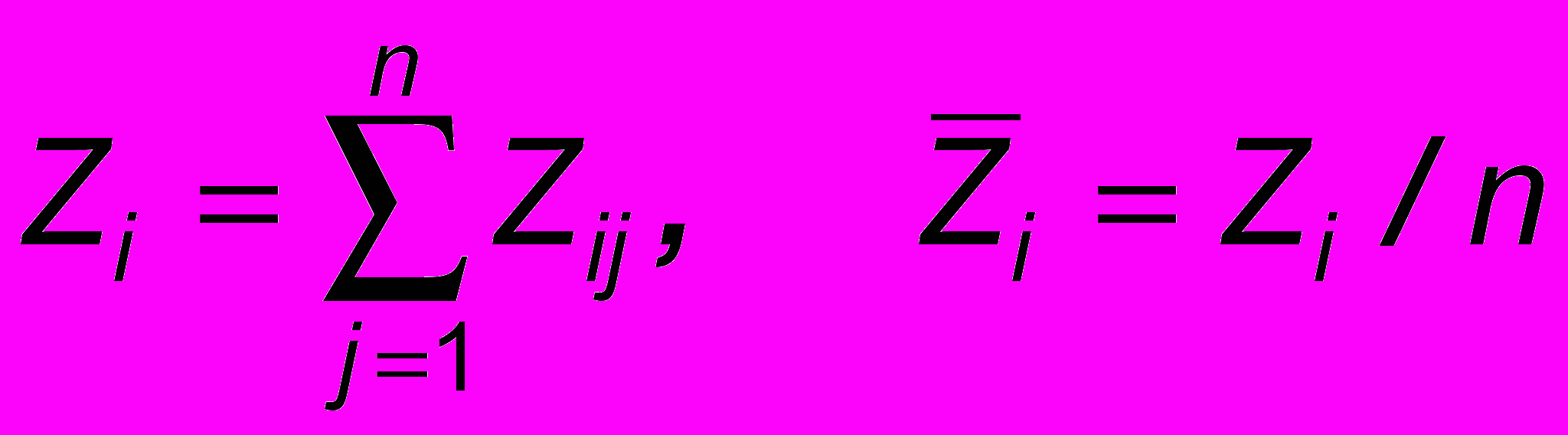. В результате Z_i принимается за оценку качества соответствующей альтернативы.

Затем выполняется проверка на непротиворечивость, которая основывается на сравнении исходных вероятностей предпочтения и вероятностей, полученных в результате вторичного вычисления исходя из числовых оценок качества каждого варианта 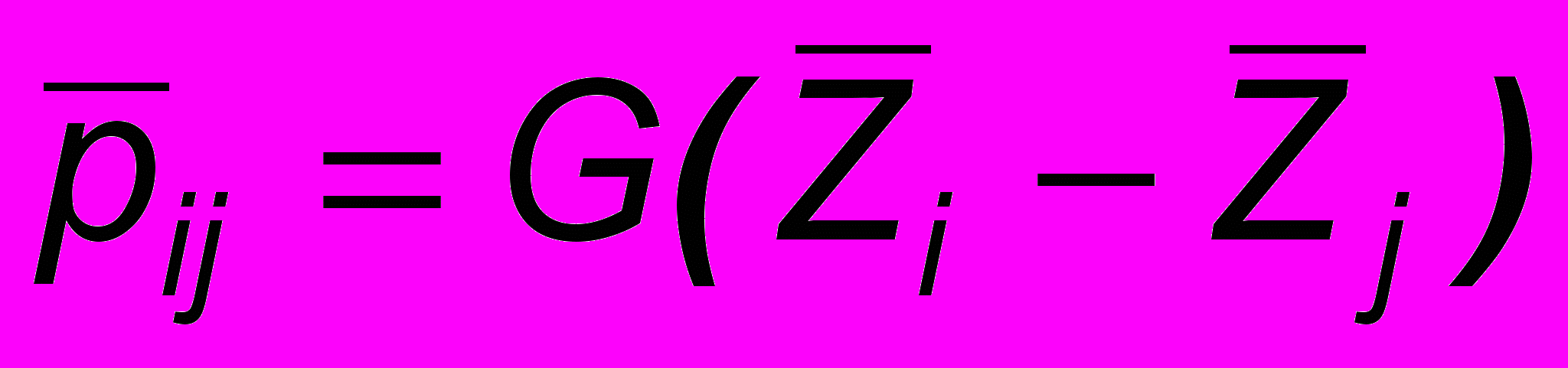. Сумма разностей 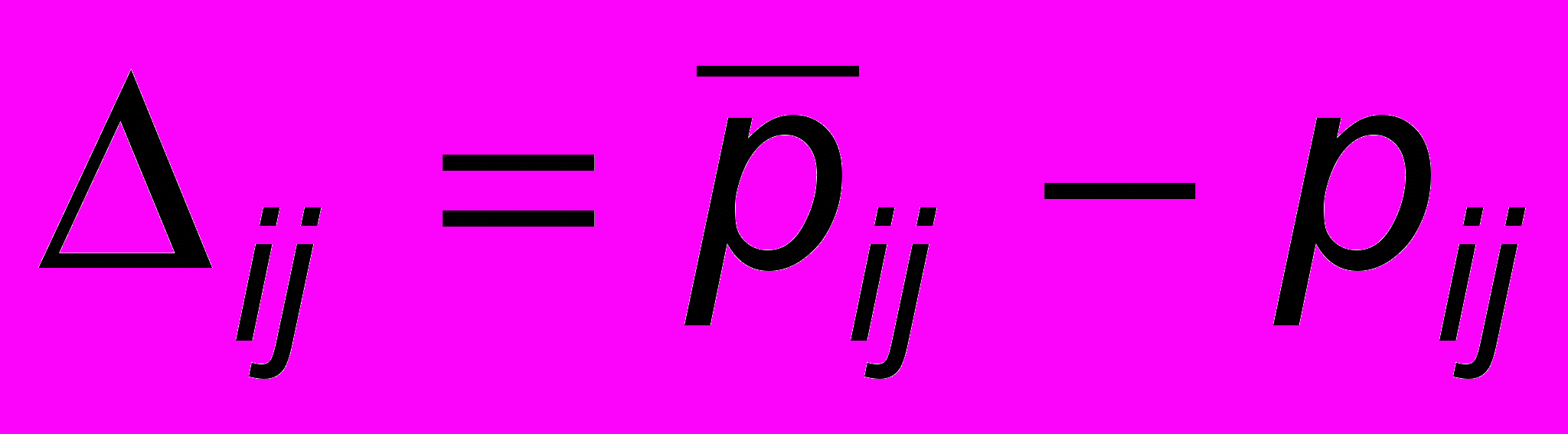дает оценку согласия исходного и вторичного предпочтения:

.

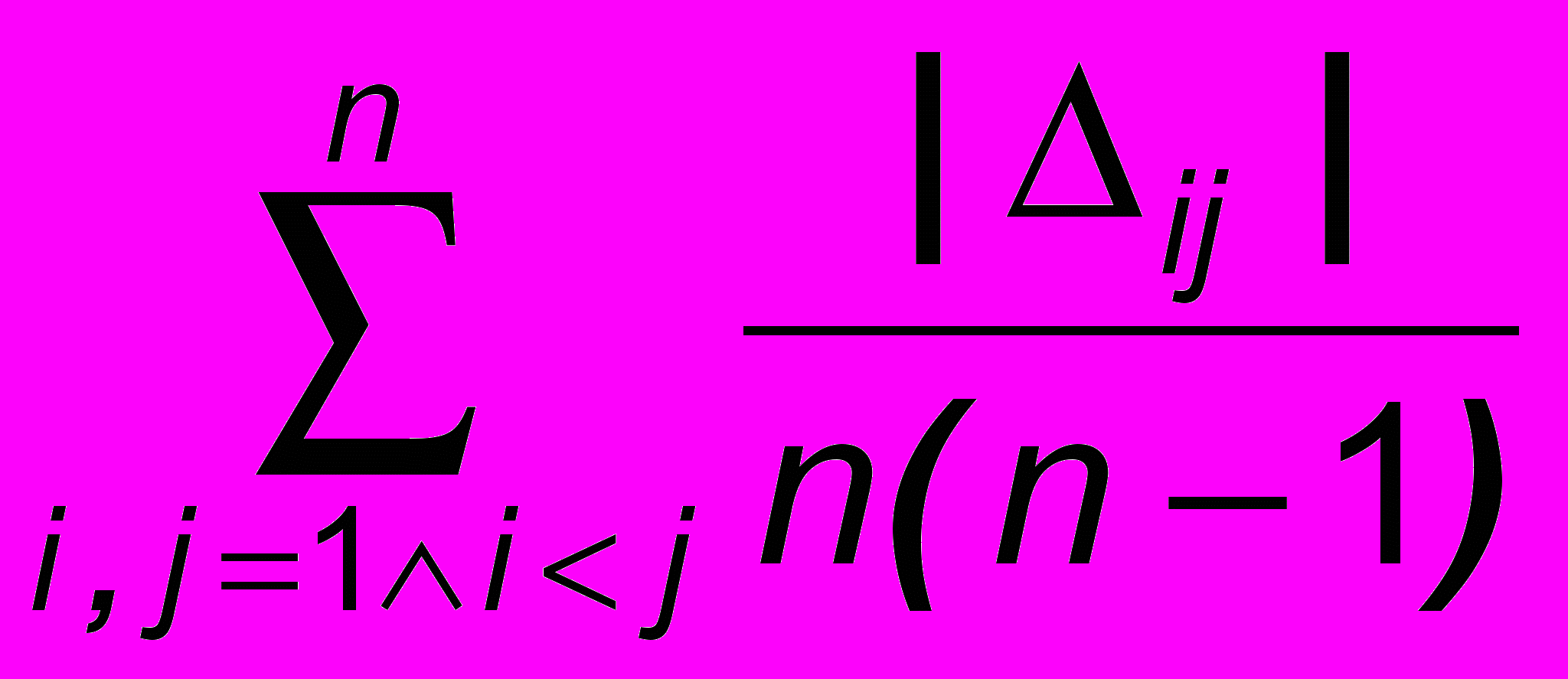(16)

Далее задаваясь порогом точности, на основании сравнения вычисленной суммы разностей решается задача о соответствии оценки качества.

Для организации сбора экспертной информации по оценке контроля качества предлагается методика, основанная на формализованном описании информационных потоков. С теоретико-множественных позиций описываются и документы и сообщения как элементы информационного потока. Каждый документ (экспертное заключение) есть множество лексических единиц. В данном случае целесообразно введение универсального словаря D. Таким образом, k l_kD, где l_k - некоторое сообщение. При этом l_k является элементом некоторого потока L={l₁,…,l_k,…,l_n}.

Подобно универсальному словарю, содержащему все термины (тезаурус) вводится универсальный массив L₀, содержащий все сообщения L₀={l₁,…,l_k,…,l_n}. Прообразами L₀ могут явится поисковый массив ИПС, отраслевой справочно-информационный фонд, массив библиотеки и др. Такое представление документа не противоречит современным тенденциям развития систем документооборота и ИПС

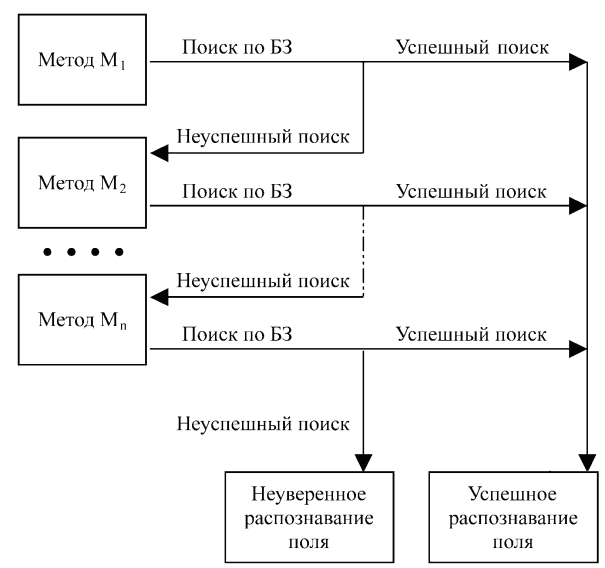
При реализации системы документооборота в диссертации разработан метод распознавания рукопечатных форм заполнения карт экспертного опроса.

Структура многоуровневой системы распознавания рукопечатных форм

Рис.

1.

В процессе распознавания полей формы на вход системы подаются рукопечатные символы. На первом уровне с помощью самого быстрого (и соответственно самого простого) алгоритма М₁определяется принадлежность входных символов к одному из известных классов. Затем по определенным классам выполняют поиск по соответствующему альтернативному ключевому полю в БД. Если удается найти уникальную запись, то результатом распознавания принимается значение точного поля, и на этом процесс распознавания прекращается. В противном случае, когда не удается найти уникальную запись или найдется несколько записей, то результаты распознавания передаются на второй уровень. Здесь с помощью более «тонких» методов и алгоритмов делается попытка точно определить символы внутри класса и, как и в предыдущем уровне, выполняется поиск в БД по распознанным символам, но по другому альтернативному ключевому полю, соответствующему этому уровню. Если опять не удается найти нужную запись, то результаты распознавания передаются на следующие уровни более глубокой обработки и т.д.

В последнем уровне, если поиск не дает результатов, то поле формы отмечается как нераспознанное и нуждающееся в ручной проверке со стороны оператора, а процесс распознавания прекращается (рис.1.). Очевидно, что эффективность всей системы РРФ будет существенно зависеть от полноты БД, которая может пополняться для конкретной предметной области.

Алгоритм построения скелета или алгоритм «утоньшения» представляет собой итеративный процесс. На каждой итерации последовательно просматриваются все точки изображения, и те из них, которые принадлежат границе области черных точек, удаляются, т.е. помечаются как 0 (рис. 3). Исключение составляют точки, нарушающие 8-связность области черных точек и концы линий толщиной в одну точку. Процесс заканчивается, если на некоторой итерации не удалось удалить ни одной точки.

Решение об удалении той или иной точки принимается на основе значений соседних точек, т.е. изображение сканируется окном 3×3. Существует несколько вариаций критерия удаления точки p; здесь мы рассмотрим один из наиболее используемых критериев. Пронумеруем соседние точки, как показано в табл.2., и обозначим множество всех соседей x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈ как N(p). Количество черных точек в N(p) обозначим как b(p).

Таблица

2.

Сканированное окно

X₆

X₇

X₈

X₅

P

X₁

X₄

X₃

X₂

Для удаления точки необходимо выполнение следующих условий.

Точка принадлежит границе области единичных точек, что равносильно условию – среди 4-связных соседей есть белые точки. Данное условие можно записать как x₁x₃x₅x₇ = 0 .

Удаление точки не нарушает 8-связность области, что равносильно условию – количество 8-связных областей черных точек в N(p) равно 1.

Точка не является концом линии черных точек. Данное условие можно записать как b(p)>1.

Для предотвращения «разрушения» области черных точек белыми точками необходимо также условие b(p)<7.

В третьей главе диссертации ставится и решается задача формализации моделей экспертного опроса и оценки качества экспертизы с учетом оценки компетентности самих экспертов.

Подбор экспертов необходимо проводить из соображений:

много экспертов - плохо, так как больше вероятность привлечения некомпетентных специалистов;

мало - тоже плохо, так не будет достаточной статистики согласования мнений экспертов.

При этом необходимо учитывать основные показатели качества эксперта, а именно, профессиональные качества (компетентность), способность решать задачи, метод решения которых полностью или частично неизвестен (креативность), способность выявлять неочевидные проблемы (эвристичность), способность угадывать решение без его обоснования (интуиция), способность предсказать будущее решение (предикатность), способность противостоять большинству (независимость), способность видеть проблему с разных точек зрения (всесторонность).

Кроме того, должны быть разработаны формальные оценки качества экспертиз и механизмов выбора рациональных решений, основанные на предположениях 1-7.

1. Условие наследования (H):

X’X  C(X’)C(X)X’.

(17)

Если рассмотреть выбор из произвольного множества и выбор из некоторого его подмножества, то все альтернативы, которые были выбраны из исходного множества и вошли в рассматриваемое подмножество будет выбраны также из этого подмножества.

2. Условие независимости от отвергнутых альтернатив (О):

C(X)X’X  C(X’)=C(X).

(18)

Если рассмотреть произвольное подмножество X’ , содержащее все альтернативы, выбранные из X , то выбор из X’ будет совпадать с выбором из исходного множества, в частности C(C(X))=(X).

3. Условие согласия (С):

.

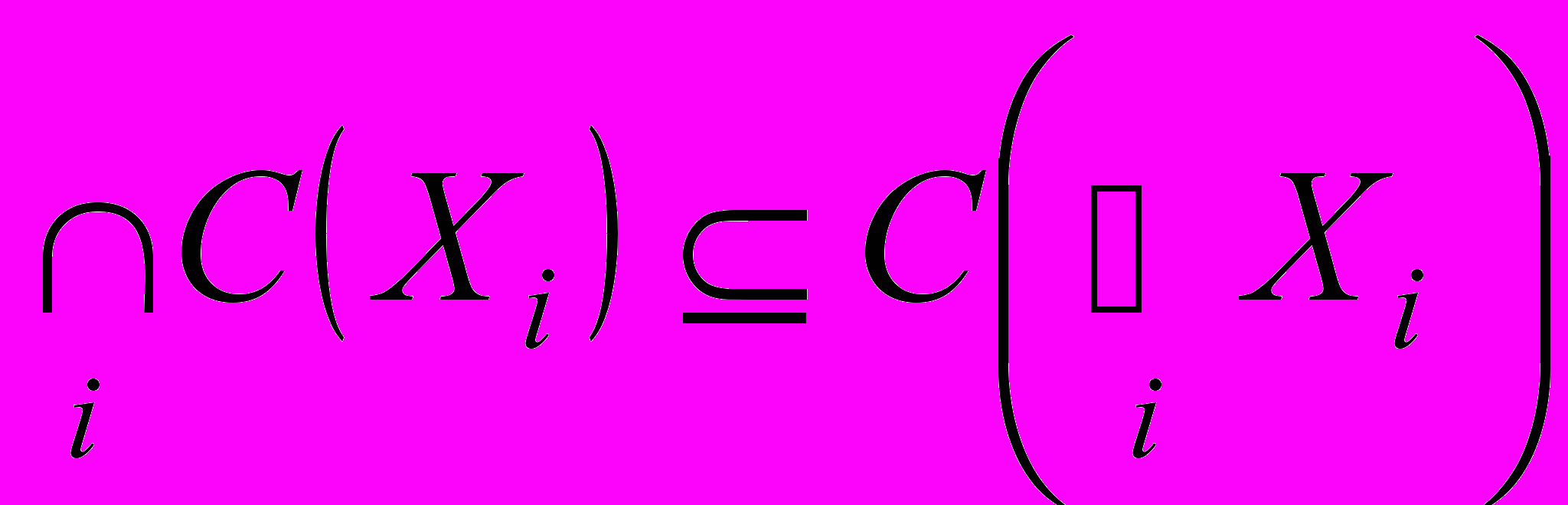(19)

Альтернативы, которые были выбранные из каждого X_i, будут выбраны и из их объединения.

4. Условие Плотта (квазисумматорности)– независимость выбора от пути (KC):

C(X₁X₂)=С(C(X₁)C(X₂)).

(20)

Условие Плотта требует, чтобы выбор из объединения множеств совпадал с выбором из объединения выборов, сделанного из каждого в отдельности.

5. Условие сумматорности (СМ):

C(X₁X₂)=C(X₁)C(X₂).

(21)

Условие сумматорности предполагает, что выбор из объединения множеств равен объединению выборов из каждого множества в отдельности.

6. Условие мультипликаторности (МП):

C(X₁X₂)=C(X₁)C(X₂).

(22)

7. Условие монотонности

X₁X₂  C(X₁) C(X₂).

(23)

Смысл условия заключается в том, что выбор из более широкого подмножества будет более широкий.

В ряде случаев при подборе экспертов используются некоторые численные оценки, характеризующие их квалификацию. Такие статистические оценки носят экспертный характер, и их применение возможно только тогда, когда эксперт достаточно часто привлекался для решения задач экспертизы одного типа. Примером может служить определение экспертами качества продукции в отделе технического контроля. Численные оценки могут быть использованы для улучшения состава экспертной группы и повышения достоверности результирующей оценки.

Целью анализа является получение весов экспертов _i. Пусть после многократного оценивая набрана статистика относительно ошибок i-го эксперта в j-ой экспертизе. Значения ошибок вычисляются на основании соотношения:

,

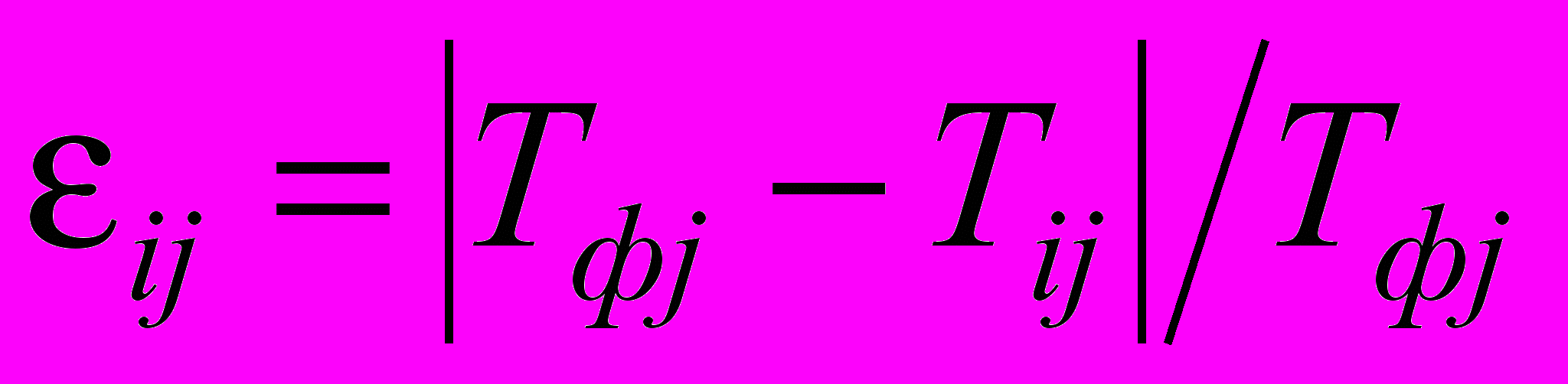(24)

где T_фj – фактическое значение, полученное после реализации проекта;

T_ij – оценка, данная i-ым экспертом.

Тогда веса формируются на основании соотношения:

,

(25)

где k_j – количество оценок, которые дал i-ый эксперт.

Для повышения точности классификации экспертов и идентификации ситуаций по показателям технологического процесса в диссертации разработана модель кластеризации на основе методов латентно-структурного анализа, в которой предполагается, что каждый латентный класс является однородным относительно любых оценочных величин. Требуется, чтобы каждый латентный класс был достаточно однородным по отношении к любой латентной величине, так чтобы все единичные высказывания внутри класса были статистически независимы. Эта независимость внутри классов выражается следующими уравнениями:

p_ljk = p_lkp_lj, p_2jk = p_2kp_2j, … , p_qjk = p_qkp_qj,

p_ljkl = p_lkp_ljp_ll, p_2jkl = p_2kp_2jp_2l, …, p_qjkl = p_qkp_qjp_ql,

(26)

Преобразование уравнений в соответствии с требованиями однородности групп приводит к системе уравнений:

n=n₁+ n₂+…+ n_q

n_j=n₁p_1j+ n₂p_2j +…+ n_qp_qj

n_jk=n₁p_lkp_lj+ n₂p_2kp_2j +…+ n_qp_qkp_qj

n_jkl=n₁ p_2kp_2jp_2l + n₂ p_2kp_2jp_2l +…+ n_q p_qkp_qjp_ql

и т.д.

(27)

Все наблюдаемые совместные частоты выражаются через (q+sq) латентных параметров, q объемов классов и q латентных вероятностей (p_1j, p_2j, … , p_qj) для каждого из s признаков анкеты экспертной карты. Последовательные ступени эмпирических частот насчитывают соответственно 1, s, s(s-1)/2 и т.д. членов, являющихся коэффициентами бинома (а+b)^s. Складывая их, получаем 2^s уравнений, связывающих наблюдаемые и латентные величины в этой модели.

Задача, как и в факторном анализе, заключается в решении основных уравнений относительно неизвестных латентных параметров. Большинство из известных решений не используют совместные частоты с повторяющимися индексами (n_jj, n_jjk, n_jjj, n_jjkl и т. д.). В анализе латентной структуры (рис.2.) они рассматриваются как аналоги общих факторных дисперсий факторного анализа, которые нам неизвестны. В диссертации доказано, что представление их в виде эквивалентов, соответствующих смешанным частотам более низкой ступени без повторяющихся индексов (то есть n_jj=n_j, n_jjk=n_jk, и т. д.) дает аналог использования равных единиц корреляций в факторном анализе.

Гипотетическая диаграмма рассеяния

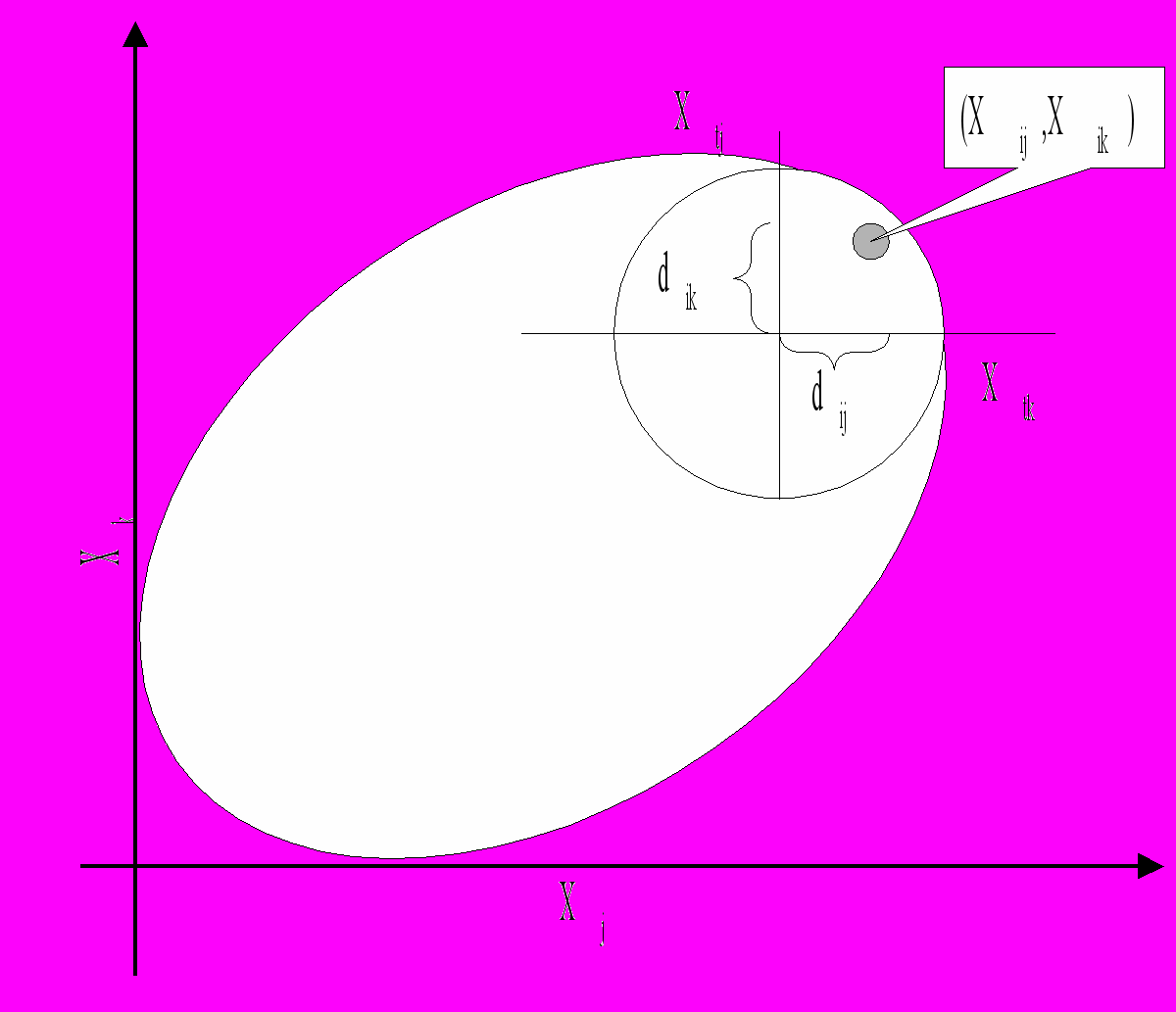
Рис.

2.

В работе предполагается, что имеется набор s количественных измерений, таких, как баллы карт экспертизы в выборке из п экспертов. По некоторому правилу каждый член этой выборки приписывается одной, и только одной, из q подгрупп. Тогда размер выборки, суммы баллов и суммы произведений баллов для всей выборки выражаются через соответствующие статистики для подгрупп следующим образом:

n=n₁+ n₂+…+ n_q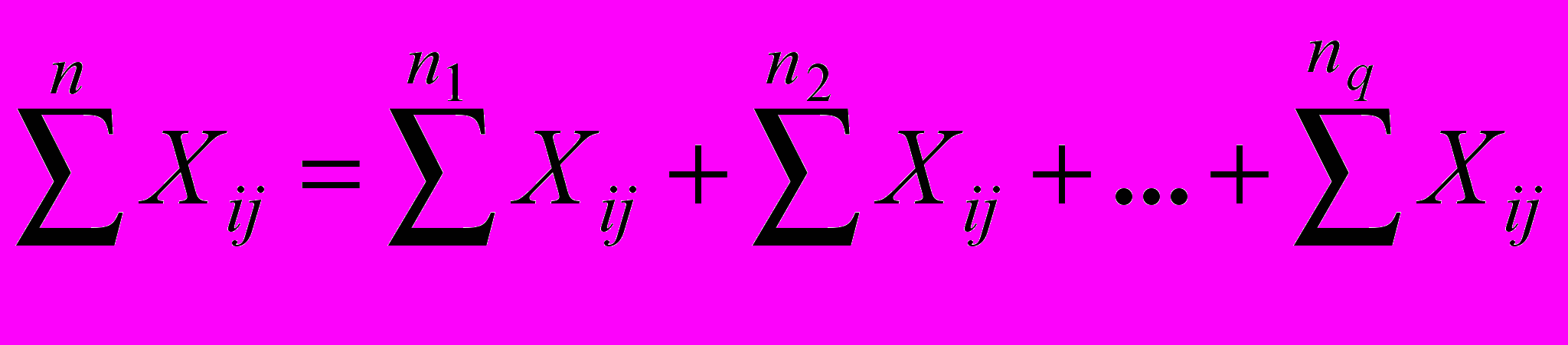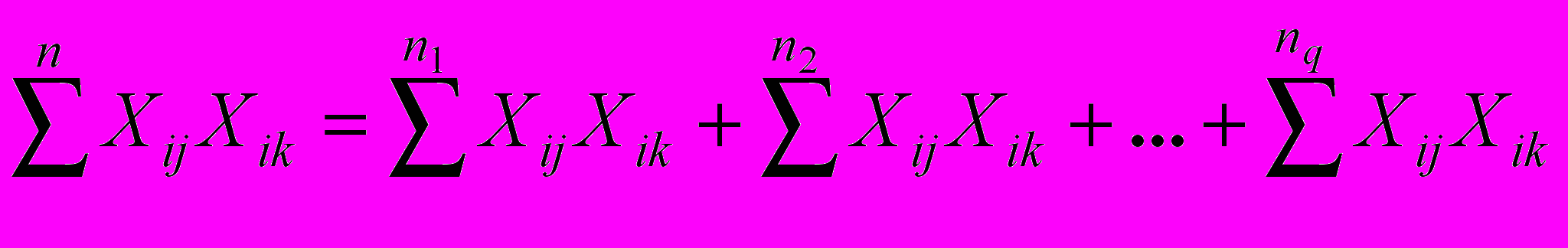

и т.д.

(28)

Все суммирования в (26) проводятся по экспертам. Суммирования слева проводятся по всей выборке, а справа — по экспертам различных подгрупп; величина Х_ij есть балл эксперта i по экспертизе j, и она может быть дана в единицах стандартного отклонения или в каких-либо других единицах. То же самое относится и к Х_ik, Х_il и т. д.

Проведена апробация процедуры экспертного оценивания и классификации ситуаций, возникающих в ходе технологического процесса.

Таблица

3.

Решение латентного профиля

для гипотетического примера трех классов

Номер карты

Латентный класс

I

II

III

Средние по классам

1

-1,50

0,50

0,50

2

-1,50

0,50

0,50

3

-1,00

0,00

1,00

4

-0,50

-0,50

1,50

5

-0,50

-0,50

1,50

Размеры класса

0,25

0,50

0,25

Линия регрессии тестов на латентном континууме

для гипотетического случая двух классов

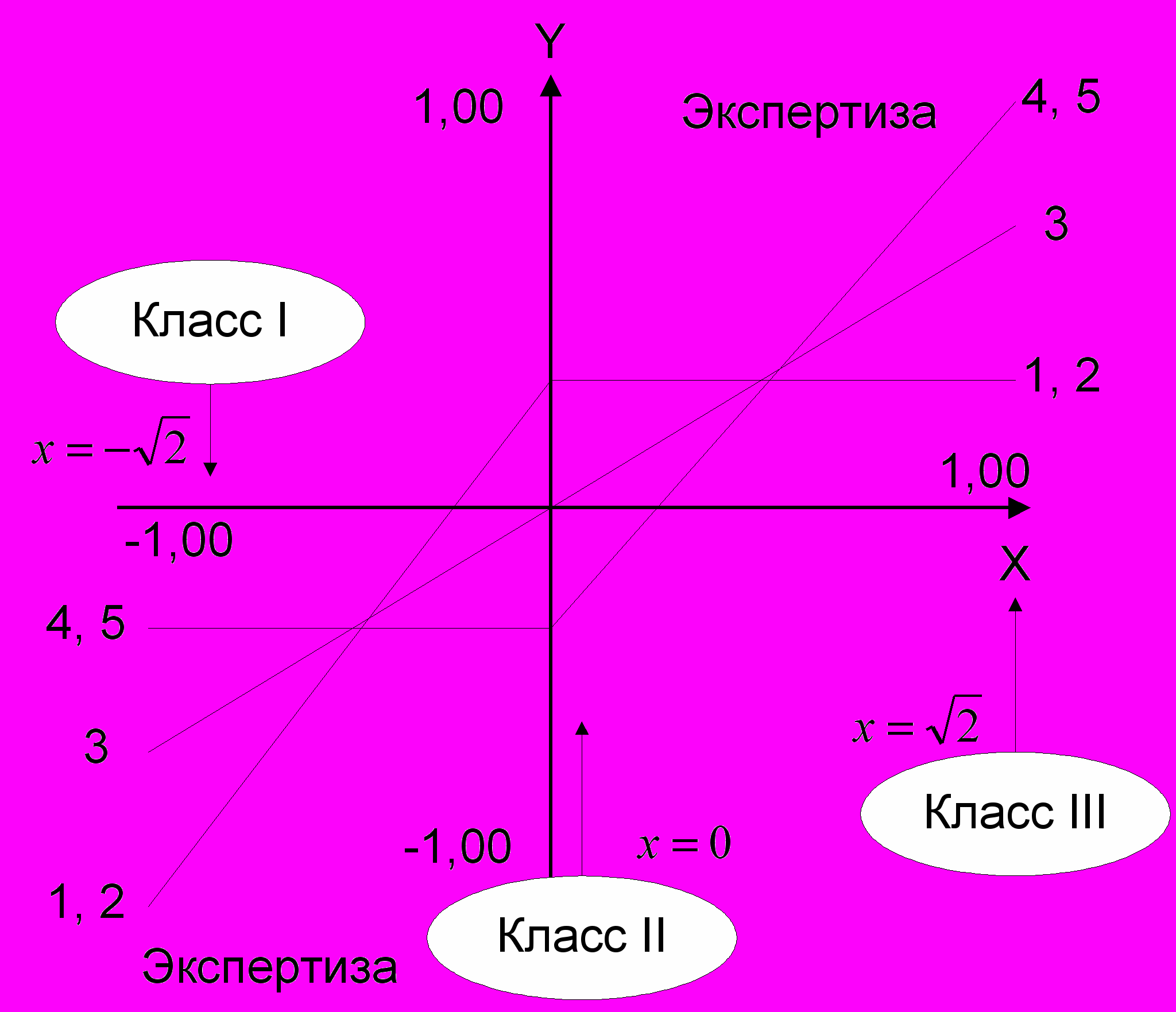
Рис.

3.

Вид различных регрессий на рис.3. такой, как следовало ожидать в предположении от относительной сложности опросной карты. Простые карты (1 и 2) являются различающими на нижнем конце латентного континуума. Сложные карты (4 и 5) – на верхнем. Карта (3) средней сложности – на всем континууме. В таб.3. приведены полученные характеристики трех латентных классов.

В четвертой главе проведена апробация методики оценки контроля качества на примере анализа технологических процессов производства железобетонных плит.

При производстве бетонных плит ширина и длина являются важными характеристиками качества, так как плита по размерам должна точно подходить предусмотренному для нее месту. Для контроля ширины сначала используются X-bar и R карты. Затем строится контрольная карта для длины. Ниже иллюстрация методики дается в предположении, что всего имеется 20 выборок по 3 наблюдения в каждой. Эти данные могли быть получены как непосредственно с измерительного устройства, так и из базы данных.

Следующим этапом строится составной график, в котором в верхней части находится X-bar карта (для контроля за средним процесса), а в нижней - R карта (для контроля за изменчивостью процесса). Для обеих карт выдаются гистограммы (рис.4.), которые показывают распределение характеристик качества (средних и размахов в выборках, соответственно).

Карта размахов и формирования показателей пригодности

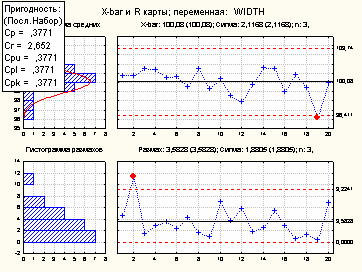
Рис.

4.

Перед тем, как сказать, верно ли идет производственный процесс, нужно убедиться в том, что изменчивость процесса находится под контролем. Поэтому сначала исследуется контрольная карта изменчивости процесса (в данном случае - R карта). В данном случае вторая выборка свидетельствует о разладе процесса, так как размах для нее превышает верхний контрольный предел.

Далее проводится анализ X-bar карты. Из рисунка видно, что выборка 19 также может говорить о разладе процесса, так как среднее для нее находится ниже нижнего контрольного предела.

Чтобы убедиться в случайности выборок, проверяются критерии серий. Отображаются две таблицы (одна для X-bar карты, другая для R карты).

Если известны допустимые отклонения от спецификаций для ширины изделия, мы можем изучить пригодность процесса и отобразить на графике индексы пригодности процесса. При этом задается Номинал+-дельта, для которого отображаются две таблицы с индексами пригодности и индексами производительности процесса. Изучив индексы пригодности данного процесса, делаем вывод, что процесс можно считать пригодным и центрированным (хотя у нас есть выборки за контрольными пределами).

На следующем этапе проводится анализ индексов пригодности Cp, Cr, Cpl, Cpu, и Cpk (на рис. 4. левый верхний угол).

Формирование отметок на карте

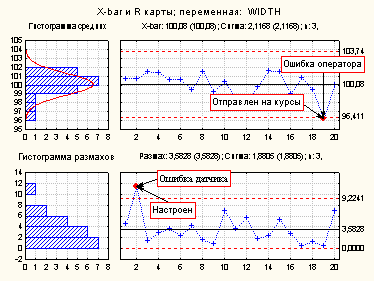
Рис.

5.

Предположим известно, что повлияло на выброс во 2 и 19 выборках. Выброс в выборке 2 был вызван ошибкой измерения из-за внешнего временного воздействия на датчик. Выборка 19 была получена новым, еще необученным оператором, которого затем отправили на обучающие курсы. Эту информацию также целесообразно хранить в БД с возможностью отображения на карте контроля качества (рис.5.). Так как выборка 2 выходит за контрольные пределы только R карты, используется опция R или S (MR/MS) карты для описания причины для второй выборки - "Ошибка датчика". Аналогично можно присвоить причину для выборки 19.

Коды для различных причин и действий хранятся в выбранных для них переменных.

Предположим, что достоверно известно, что для первых десяти выборок процесс находится под контролем. Начиная с выборки 11, станок заменили на новый. Следовательно, нужно задать два набора выборок и провести вычисления параметров карты для каждого набора отдельно (и определить, сместился ли процесс). Первый набор содержит выборки 1 - 10, второй - 11 - 20.

Изучив X-bar карту, можно сделать вывод, что после установки нового станка процесс действительно сместился. Тем не менее, процесс для каждого набора выборок находится под контролем (т.е., на карте нет выбросов).

Разделение исследуемой выборки на составляющие

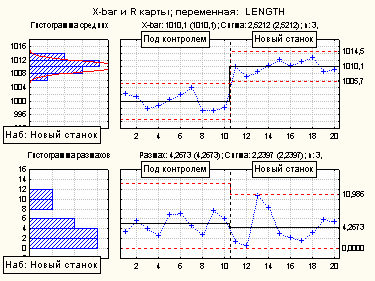
Рис.

6.

Карта скользящего среднего необходима для определения малых систематических сдвигов (трендов) среднего или дисперсии процесса от спецификаций. Предполагаем, что рассматриваем сдвиг процесса, который приводит к увеличению средней толщины плиты. Мы бы хотели определить этот сдвиг как можно раньше, чтобы эта ситуация не привела к большому числу бракованных изделий. В этом случае для контроля изменчивости используются MA X-bar и R карты и задается количество смежных выборок, используемых для вычисления скользящего среднего, выводимое на карте.

Анализируя карту скользящего среднего можно сделать вывод, что хотя нет точек, пересекающих контрольные пределы - остается два вопроса. Несмотря на то, что скользящие средние уменьшаться от начала к выборке 9, данные после этого начинают возрастать. Также наблюдается нарушение критерия серий (2 из 3 выборок в Зоне A или ниже) для стандартных установок критериев серий. Это также свидетельствует о том, что что-то не в порядке в производственном процессе. Возможно, что на ранней стадии разладки карты со скользящими размахами нет тренда или каких-либо других заметных проблем. Следовательно, изменчивость ("ширина") процесса будет постоянной с течением времени.

Карта скользящего среднего для выявления тренда изменчивости

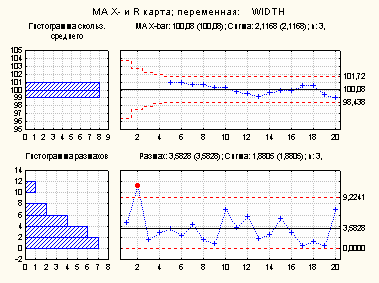
Рис.

7.

Можно было бы найти причины тренда в первых 9 выборках, устранить эту причину изменчивости, тем самым настроить процесс. Другими словами решения о настройке процесса не должны опираться только на поиск причин разладок (выход процесса за контрольные пределы) или нарушения критериев серий карт контроля, а также и на знаниях технических аспектов самого процесса.

В заключении представлены основные результаты работы.

Приложение содержит документы об использовании результатов работы.

Публикации. По результатам выполненных исследований опубликовано 6 печатных работ, которые приведены в списке публикаций.

Основные выводы и результаты работы

Проведен анализ методов и моделей оценки качества технологических процессов в непрерывном производственном цикле.

Выполнен анализ системы экспертного оценивания контроля качества технологических процессов.

На основе статистических карт контроля качества разработаны методы и модели классификации качества промышленных изделий.

Сформированы обобщенные критерии качества и пригодности технологических процессов.

Сформирован набор требований к методике проведения экспертизы оценки качества и разработана латентно-структурная модель оценки квалификации экспертов.

Разработана методика формирования и анализа карт контроля качества в системе экспертного оценивания.

Разработан программно-моделирующий комплекс системы экспертного оценивания качества железобетонных изделий.

Проведен анализ программных технологий, направленных на оперативную программную реализацию методик оценки контроля качества, и разработан программно-моделирующий комплекс, реализующий предложенные методы и алгоритмы. Комплекс внедрен для практического применения в ЗАО НПВФ «СВАРКА» и ЗАО «ФИРМА ПРОМСТРОЙМОНТАЖ».

Публикации по теме диссертационной работы

Паршин, Д.А. Антикризисный менеджмент складских технологий / Д.А. Паршин, А.М. Ивахненко, К.И. Атаев // Методы прикладной информатики в автомобильно-дорожном комплексе: сб. науч. тр. / МАДИ(ГТУ). М., 2007. -С.71-74.

Паршин, Д.А. Определение факторов спроса на складские товары / Д.А. Паршин, К.И. Атаев, И.В. Захватошина // Организационно-управляющие системы на транспорте и в промышленности: сб. науч. тр. / МАДИ(ГТУ). – М., 2007. –С.124-134.

Паршин, Д.А. Автоматизация документооборота на промышленном предприятии / Д.А. Паршин, А.А. Шарков, Н.Г. Куфтинова // Вопросы теории и практики автоматизации в промышленности: сб. науч. тр. / МАДИ(ГТУ). – М., 2008. –С.146-153.

Паршин, Д.А. Система поддержки принятия решений оценки состояния технологических процессов в непрерывном производственном цикле промышленных предприятий // Д.А. Паршин // Инновационные модели и методы автоматизации технологических процессов и производств: сб. науч. тр. / МАДИ(ГТУ). – М., 2008. –С.14-21.

Паршин, Д.А. Модели и методы контроля качества промышленной продукции / Д.А. Паршин // Инновационные модели и методы автоматизации технологических процессов и производств: сб. науч. тр. / МАДИ(ГТУ). – М., 2008. –С.22-32.

Подход к построению системы распознавания печатных форм / Д.А. Паршин, А.Ч. Ахохов, А.М. Ивахненко, Ла Суан Тханг // Вестник / МАДИ (ГТУ). -2008. -Вып. 1(12). – С. 81-87.

	Номер карты	Латентный класс
	Номер карты	I	II	III
Средние по классам	1	-1,50	0,50	0,50
	2	-1,50	0,50	0,50
	3	-1,00	0,00	1,00
	4	-0,50	-0,50	1,50
	5	-0,50	-0,50	1,50
Размеры класса		0,25	0,50	0,25

Blog

Автоматизация системы экспертного оценивания качества технологических процессов в непрерывном производственном цикле промышленных предприятий

Содержание