Разработка моделей и алгоритмов оптимизации процедур диагностирования на граф-моделях технических систем

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Актуальность проблемы.

Стремительные темпы развития и внедрение во все сферы деятельности современных технических систем, непрерывный рост их структурной сложности и размерности, специализированные условия применения и требования к безотказности выполняемых аппаратурой функций определяют актуальность проблемы надежности, качества и безопасности эксплуатации технических объектов. Большое значение в успешном решении этих задач принадлежит методам и средствам контроля и диагностики технических систем и программного обеспечения.

При проектировании сложных объектов следует учитывать требования технического контроля - своевременно определять действительное состояние объекта (исправное, допустимое, предаварийное, аварийное), и, в случае неисправности, эффективно обнаруживать и устранять возникшие дефекты.

Инженерная практика все чаще сталкивается с проблемой решения задач диагностики сложных технических систем с большим числом возможных дефектов, требующих быстрой локализации для предотвращения серьезных аварийных последствий. Решение этих задач требует разработки математических моделей, методов и алгоритмов эффективного обнаружения дефектов, применимых не только в конкретной прикладной области, но обладающих свойством общности для большого класса технических систем.

Проблема оптимизации стратегии диагностирования с целью оперативной локализации и устранения дефектов существенно обостряется, учитывая требования надежности опасных производственных объектов. Решение этой задачи принимает первостепенное значение для систем, качество функционирования которых существенно влияет на экологическую обстановку, и несвоевременное обнаружение дефектов может привести к необратимым катастрофическим последствиям. Оптимизация управленческих решений, обеспечение оперативного контроля и диагностирования технического состояния таких структурно-сложных систем является актуальной, требующей особого внимания проблемой.

Основоположниками теории диагностирования дискретных и непрерывных технических систем являются отечественные и зарубежные ученые П.П. Пархоменко, Е.С. Согомонян, В.В. Карибский, А.В. Мозгалевский, Я.Я. Осис, В.А. Гуляев, Д. Маеда, С. Рамомурти. Дальнейшее развитие теория синтеза контролепригодных объектов получила в работах П.В. Глущенко, В.И. Сагунова, С.И. Беляевой, Л.С. Ломакиной, где в качестве моделей объектов диагностирования используются логические модели и графы причинно-следственных связей, анализ которых позволяет назначить оптимальные совокупности точек контроля для снятия диагностической информации, а процедуры диагностирования реализуются в соответствии с матрицей проверок. Разработка автоматизированных методов построения матрицы проверок и анализ результатов ее обработки позволили эффективно решить задачу своевременного обнаружения дефектов в объектах невысокой сложности, в которых число возможных состояний, обусловленных дефектами, сравнительно невелико. Рост размерности и структурной сложности технических устройств опережает возможности активно используемых методов поддержания их в работоспособном состоянии своевременным обнаружением дефектов. Необходима разработка новых эффективных моделей для решения задач диагностики объектов, состоящих из нескольких сотен и даже тысяч единиц, автоматизация процедур построения оптимальных стратегий диагностирования технического состояния и прогнозирования поведения сложных современных технических систем.

Диссертационная работа выполнена по межвузовской научно-технической программе «Диагностические и информационно-поисковые системы».


Цель работы

Разработка и исследование моделей и методов оптимизации процедур обработки диагностической информации на граф-моделях восстанавливаемых объектов с большим числом состояний при реализации допусковых методов контроля. Автоматизация разработанных алгоритмов для их практического применения.


Методы исследования

Для теоретических исследований в диссертационной работе использовались методы теории графов, методы оптимизации, комбинаторный анализ, теория множеств, численное моделирование, генетические алгоритмы.


Объекты исследования

Объектами исследования являются восстанавливаемые технические объекты, представимые логическими моделями или графами причинно-следчтвенных связей, число возможных состояний, обусловленных возникновением дефектов, в которых достигает сотен и тысяч единиц.


Научная новизна диссертационной работы

1. Разработана модель классов эквивалентности диагностических пар (МКЭДП), компактно представляющая все множество отображений «вход-выход» многовходовых граф-моделей диагностирования, построенных на большом числе вершин, соответствующих состояниям технического объекта.
   
2. Разработан метод построения оптимальных процедур диагностирования дефектов в объектах высокой сложности на базе МКЭДП по числу элементарных проверок на заданной глубине поиска дефектов.
   
3. Предложена символьная модель кодирования допустимых решений для использования методов эволюционного моделирования при решении задач синтеза контролепригодных объектов.
   
4. Разработан алгоритм построения и визуализации граф-модели объекта с заданными свойствами, характеризуемыми коэффициентом достижимости, для моделирования процесса построения диагностических процедур.
   
5. Выполнена аналитическая оценка переборных методов в задачах построения оптимальных процедур диагностирования объектов высокой структурной сложности и показана невозможность их практической реализации.
   
6. Предложены критерии оценки эффективности методов построения процедур диагностирования. Проведен анализ вычислительной трудоемкости разработанных методов построения оптимальных процедур диагностирования по критерию объема обрабатываемой диагностической информации.
   

Практическая значимость работы

Применение разработанной модели классов эквивалентности диагностических пар позволяет генерировать эффективные алгоритмы построения процедур диагностирования технических систем на граф-моделях с большим числом возможных состояний – дефектов. Оптимизация объема обрабатываемой диагностической информации обеспечивает своевременность принятия управленческих решений с целью предотвращения аварийных ситуаций. Автоматизация построения оптимальных процедур диагностирования дефектов позволяет существенно повысить эффективность проектирования контролепригодных систем.


Реализация результатов работы

Разработанные математические модели, методы и алгоритмы

- реализованы в среде Borland С++ с использованием MFC (Microsoft Foundation Classes) и библиотеки Gdiplus.dll. Получено свидетельство об официальной регистрации программы для ЭВМ № 2007610902 “Модуль исследования контролепригодности системы (Defectoscopy)”;

- используются в учебном процессе в виде фрагмента лекций в рамках курса «Надежность, эргономика и качество АСОиУ» для студентов, обучающихся по специальности 22.02.00 «Автоматизированные системы обработки информации и управления» в ГОУ ВПО Нижегородский Государственный Технический Университет.


Апробация работы

Основные результаты диссертационной работы докладывались и обсуждались на Всероссийских научно-технических конференциях “Информационные системы и технологии” ИСТ-2003, ИСТ-2004, ИСТ-2005, на Международной научно-технической конференции “Информационные системы и технологии” ИСТ-2006, на V Международной конференции «Идентификация систем и задачи управления» SICPRO '06, на 11-й Нижегородской сессии молодых ученых (технические науки).


Публикации

По результатам диссертационной работы опубликовано 13 работ в печатных изданиях, в том числе 1 работа в издании, рекомендованном ВАК.


Структура и объём работы

Диссертационная работа изложена на 147 печатных листах, включает 33 рисунка и 18 таблиц, состоит из введения, 4 глав, заключения, списка литературы и 3 приложений.


СОДЕРЖАНИЕ РАБОТЫ


Во введении обосновывается актуальность диссертационной работы, формулируются цели исследования, раскрывается научная новизна и практическая ценность полученных результатов, определяются выносимые на защиту положения.

В первой главе исследуется состояние проблемы синтеза структурно-сложных контролепригодных систем, приводится обзор литературных источников по проблеме обеспечения контролепригодности и диагностирования технических систем, анализируются основные результаты, полученные в этой области за последнее время.

Повышение конструктивной сложности систем при прочих равных условиях неизбежно ведет к снижению их надежности и эффективности выполнения ими заданных функций. Противоречие между ростом сложности технических систем и снижением их надежности приводит к необходимости разработки эффективных методов контроля и диагностики их состояния. Реализация мероприятий по повышению надежности за счет обеспечения контролепригодности и диагностируемости связана с дополнительными затратами, в этой связи актуальна задача оптимизации ресурсов по критериям максимума показателей надежности. Анализ причин и характеристик дефектов позволил выполнить их классификацию по основным признакам, т.к. успешность применения методов диагностирования определяется точностью построения модели причинно-следственных связей дефектов.

Обзор работ в области диагностики технических средств показал отсутствие общего подхода к построению эффективных моделей и алгоритмов диагностирования причин возникновения отказов и анализа предаварийных ситуаций в объектах на граф-моделях с числом дефектов до нескольких сотен единиц. В результате формулируются постановки задач исследования – разработка моделей и алгоритмов синтеза процедур диагностирования структурно-сложных объектов, оптимизирующих объем обрабатываемой диагностической информации с целью принятия решений по управлению объектом.

Во второй главе приводится классификация диагностических моделей, и описываются их свойства. Показано, что большой класс объектов различной физической природы можно представить логическими моделями или графами причинно-следственных связей (ГПСС), построенными в пространстве их свойств. Граф-модель объекта диагностирования хорошо приспособлена к решению задач обнаружения дефектов, описывает все множество возможных состояний объекта, вызванных дефектами, на качественном и структурном уровне определяя причины их возникновения и следствия их проявления. Свойства граф-моделей привели к их широкому применению в задачах технической диагностики.

Для целей диагностирования восстанавливаемые структурно-сложные объекты представляются граф-моделями с множеством входов X=(x₁, x₂, …, x_n) и выходов Z=(z₁, z₂, …, z_m), где n и m достаточно большие величины (до 100 и более единиц) (рисунок 1). Вершины графа представляют возможные состояния объекта, вызванные дефектами – отказом структурных элементов, выходом за пределы допуска параметров, событиями или явлениями, вызывающими неисправности в объекте, а дуги отражают соответствующие причинно-следственные связи. Граф упорядочивается так, что направление дуги в графе соответствует перемещению от причины дефекта к следствию и отражает направление распространения или обнаружения дефекта.



Пусть G=(V, A) – ориентированный упорядоченный граф без контуров и петель, где V=(v₁, v₂, …,v_N) – множество вершин графа, соответствующих возможным дефектам, A=(a₁, a₂, …,a_k)={(v_i, v_j), i, j=1,…,N} – множество дуг графа, отражающих причинно-следственные связи между дефектами. Эквивалентная матричная модель - матрица смежности вершин графа.

Обозначим X=(x₁, x₂, …,x_n) – множество входных вершин графа  G, соответствующих функциональным входам исследуемого объекта, или входам, на которые возможна подача тестовых воздействий (в ГПСС – это дефекты, которые не являются следствием проявления других дефектов); Z=(z₁, z₂, …,z_m) – множество выходных вершин графа, соответствующих диагностическим параметрам, снимаемым в точках контроля.

Матрицей проверок называется матрица B, составленная из N-мерных векторов проверок b_r(x_i, z_j)= (b_1r, b_2r, …,b_Nr), b_rB, компоненты которых b_kr=1, если k-я вершина  (k=1, . . . , N) принадлежит хотя бы одному пути от x_i к z_j, и b_kr=0 в противном случае.

Стратегия диагностирования и поиска дефектов заключается в подаче тестовых воздействий на входы x_i , снятии результатов на выходах z_j и обработке результатов логическим перемножением строк матрицы проверок, для которых результат проверки равен 0 (параметр не в допуске) и инверсий строк проверок с единичным результатом (параметр в допуске).

Исследования многовходовых объектов, процесс диагностирования которых осуществляется поочередной подачей тестовых воздействий на входы объекта, показали, что число назначаемых контрольных точек для локализации дефектов значительно меньше, чем в случае одновременной подачи сигналов на все входы. Кроме того, тестовый режим большинства классов объектов предполагает возможность только поочередной подачи тестов для поиска дефектов. Полная матрица проверок, построенная на множестве назначенных контрольных точек для многовходовых моделей, избыточна. Проведенные исследования показали, что ее размер (число элементарных проверок) можно сократить в несколько раз при сохранении заданной глубины диагностирования дефектов, определяемой критерием различимости столбцов матрицы проверок.

В работе решается задача минимизации числа реализуемых проверок, т.е. построения процедур диагностирования, оптимальных по критерию объема обрабатываемой диагностической информации. Показано, что переборные методы для сложных объектов с большим числом состояний, вызванных дефектами, нереализуемы. Приведена оценка сложности переборного метода, определяемая количеством элементарных операций сравнения элементов в столбцах матрицы проверок при реализации процедуры поиска ее совпадающих столбцов. Рассмотрен наихудший случай реализации вычислений в предположении достижимости каждой выходной вершины от каждого входа в граф-модели объекта.

Пусть n и m – количество входных и выходных вершин графа, тогда общее число строк в матрице B будет равно n·m. При построении оптимальной стратегии диагностирования по критерию минимального количества проверок, удовлетворяющих заданному критерию глубины поиска дефекта, в процессе работы алгоритма будут строиться матрицы проверок, содержащие 1, 2, …, n·m проверок. Количество всех возможных матриц, содержащих по i проверок из возможных n·m, вычисляется с помощью формулы сочетаний: .

Среднее количество строк матрицы проверок, определяющее вычислительную сложность алгоритма, будет равно 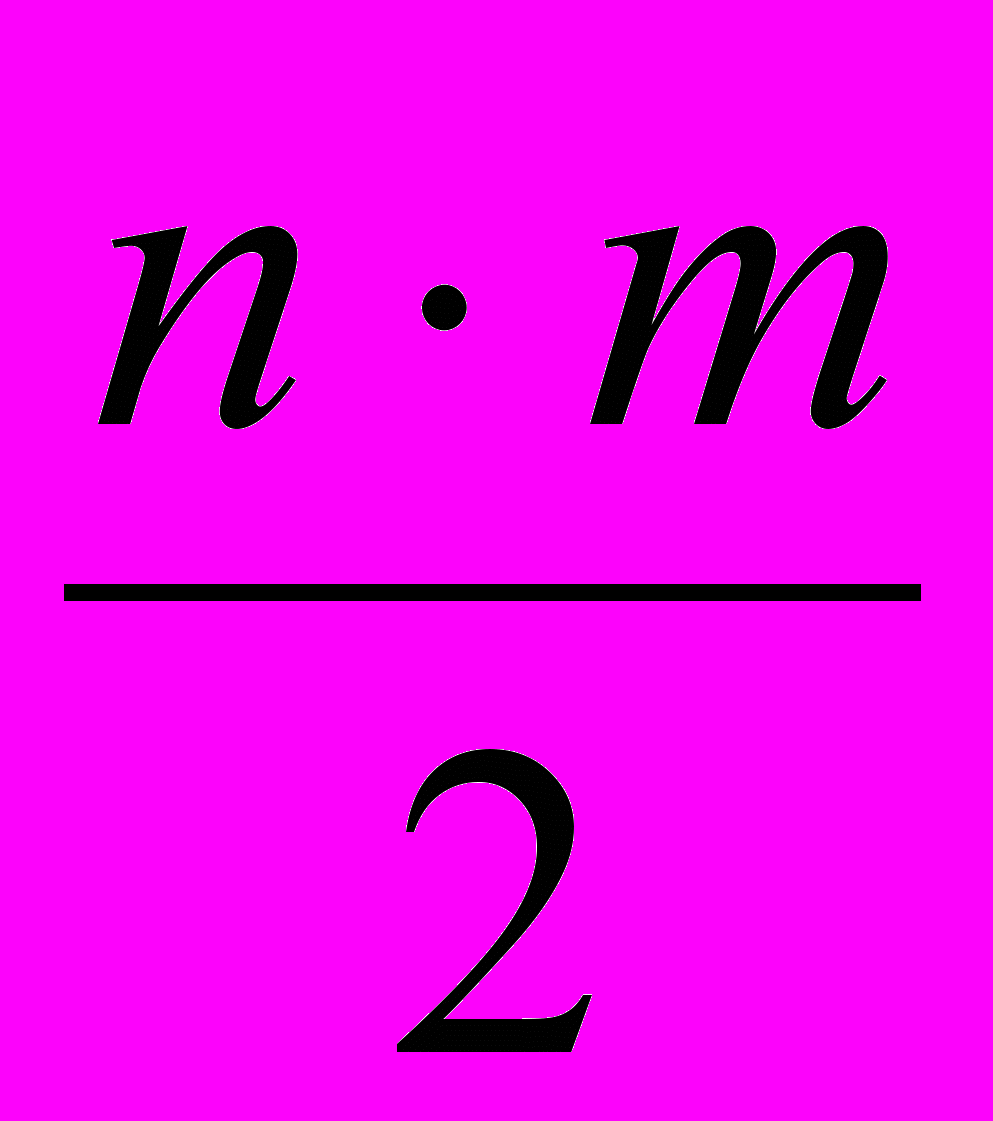. Общее число матриц проверок B, построенных в процессе работы алгоритма, соответственно равно: .

Количество возможных проверок зависит от степени связности вершин графа. Учитывая коэффициент достижимости К_Д, характеризующий степень связности исследуемых графов и определяющий долю заполнения матрицы ненулевыми элементами: , ( N – размерность матрицы достижимости D; – общее число элементов в матрице достижимости D; k - число ненулевых элементов в матрице достижимости D выше главной диагонали), получим общее число диагностических пар во всех построенных матрицах проверок для заданного графа с учетом его топологии: .

Число столбцов в матрице проверок B равно числу вершин в графе (N). Поэлементное сравнение между собой всех возможных пар столбцов, количество которых , определяется выражением:

.

Так как количество строк в полной матрице проверок составляет значение n·m·К_Д, выражение для общего количества элементарных операций сравнения элементов столбцов в полной матрице проверок В имеет вид:

.

Суммируя значения l₁ и l₂, получим аналитическое выражение для определения общего количества элементарных операций сравнения  элементов столбцов матрицы проверок:



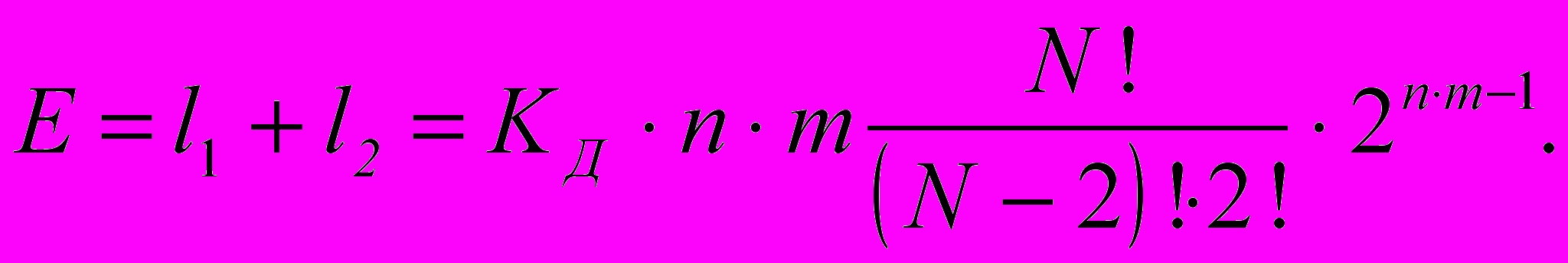
Согласно полученному аналитическому выражению, даже для небольшого объекта, граф-модель которого имеет n=10 входов и m=10 выходов при общем числе вершин N=100 и значении К_Д = 0,2, количество операций сравнения пар элементов столбцов матрицы проверок будет составлять порядка 6,27×10³⁴. И если ЭВМ обрабатывает, например, 3×10⁸ подобных операций в секунду, то потребуется 6,63×10¹⁸ лет на обработку данных для решения поставленной задачи методом полного перебора.

Анализ работы методов направленного поиска показал их значительную погрешность в определении квазиоптимального решения, т.к. поиск оптимальных решений происходит не во всём пространстве допустимых решений.

Таким образом, возникла необходимость разработки простой и удобной модели представления области допустимых решений в задачах диагностирования сложных объектов с большим числом состояний, представимых граф-моделями. Решение, определяющее минимальный вид матрицы проверок, соответствует оптимальной комбинационной процедуре диагностирования технического состояния объектов.

Для разработки алгоритма построения оптимальных процедур поиска дефектов была предложена модель классов эквивалентности диагностических пар (МКЭДП) (рисунок 2), позволяющая эффективно решать поставленную задачу.

Диагностической парой (x_i ,z_j) назовем пару вершин x_i и z_j в графе G, если результат тестового воздействия, поданного на вход элемента x_i, может быть снят на выходе элемента z_j. При этом сигнал, снимаемый в точке контроля z_j, является диагностическим параметром объекта.

Эквивалентными диагностическими парами (принадлежащими одному классу эквивалентности) назовем диагностические пары b = (x_i, z_j), имеющие одинаковые значения выходов z_j.

Все множество диагностических пар единственным образом разбивается на непересекающиеся классы эквивалентности.



Модель классов эквивалентности диагностических пар объединяет в себе две части: входы и выходы граф-модели объекта. Поскольку каждый из m выходов (z₁, z₂, … , z_m) графа достижим от определенного числа его входов (x₁, x₂, … , x_n), все множество входов X в соответствии с критерием достижимости от них m выходов разбивается на совокупность множеств X₁, X₂, …, X_m. Множество X₁ включает все входы, от которых достижим выход z₁, множество X₂ включает все входы, от которых достижим выход z₂, и т.д. Так как от одного и того же входа могут быть достижимы несколько различных выходов (например, z_i и z_j), то данные множества в общем случае пересекаются (X_i  X_j ≠ , i, j =1, ... , m, i  j).

Входы в модели МКЭДП кодируются номерами, соответствующими номерам входов граф-модели объекта, выходы кодируются номерами, соответствующими номерам точек контроля, используемых для диагностирования технического состояния объекта.

Каждый массив входов представляется некоторой лентой LX_i, состоящей из совокупности кадров одинаковой длины по количеству входов r_i , от которых достижим выход i (i=1, ... , m). Длина кадра для каждой ленты LX_i различна, так как каждый выход достижим от различного числа входов.

Вычислим наименьшее общее кратное L для мощностей множеств входов |X₁|=r₁, … , |X_m|=r_m. Введем шкалу длины L, разбитую на единичные интервалы. Поместим шкалу под лентами множеств входов так, чтобы их границы совпали (рисунок 2).

Вертикальное сечение лент входов LX_j (j=1, ... , m) определяет частное решение задачи.

Назовем частным решением П_i совокупность, состоящую из m диагностических пар , образующих очередную процедуру диагностирования, заключающуюся в подаче диагностических воздействий на соответствующие входы и снятие реакций в соответствующих точках контроля (выходах граф-модели).

Очевидно, что каждое частное решение определяет некоторое значение целевой функции, соответствующее числу диагностических пар, и удовлетворяет (или не удовлетворяет) заданному ограничению на глубину поиска дефекта. Таким образом, двигаясь по шкале с шагом, равным масштабной единице, можно анализировать каждое возможное частное решение.

В третьей главе разрабатываются методы оптимизации процедур диагностирования технического состояния объекта по числу диагностических пар. Приводятся постановки задач диагностирования с максимальной глубиной поиска дефектов на заданном множестве точек контроля при наличии ограничений, связанных с реализацией процедур диагностирования, и разрабатываются алгоритмы их решения.

В качестве модели, обрабатываемой алгоритмом, используется МКЭДП, эффективно кодирующая все множество возможных решений.

Разработано и приведено описание алгоритма построения процедуры диагностирования объекта (рисунок 3) для следующей постановки задачи.

Задача 3.1. Минимизировать число диагностических пар, построенных на множестве точек контроля, обеспечивающих глубину диагностирования дефекта, равную единице, при поочередной подаче тестовых воздействий на диагностические входы:



где В_П - полная матрица проверок на назначенной совокупности точек контроля; 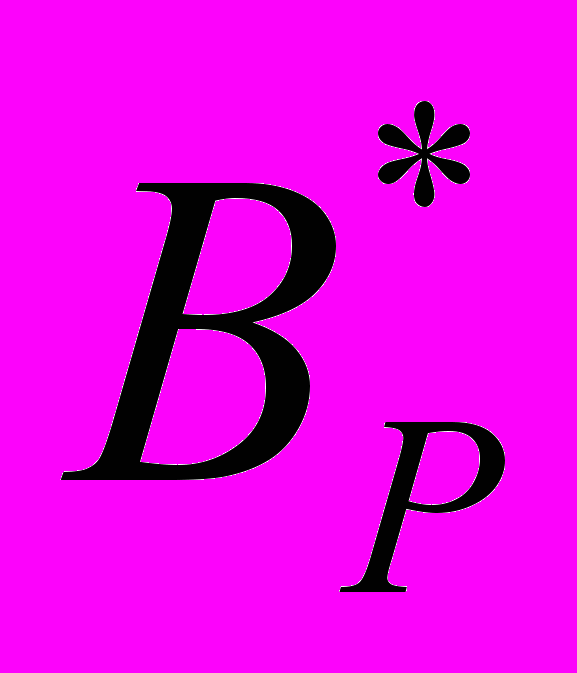- матрицы проверок, обеспечивающие одноразличимость дефектов; 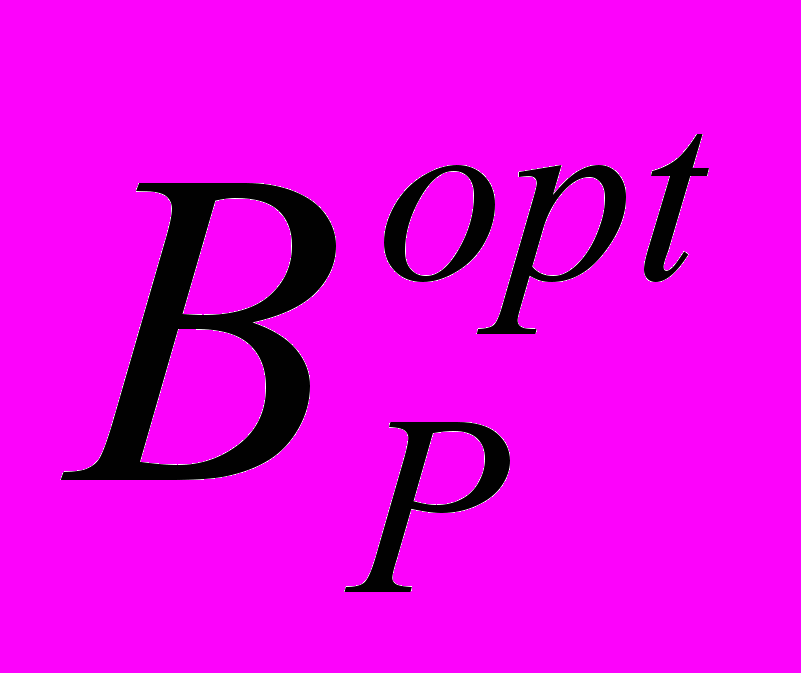- матрица проверок, включающая минимальное число диагностических пар и сохраняющая одноразличимость дефектов; К_ГП - коэффициент глубины поиска дефекта, являющийся мерой контролепригодности, определяющий долю однозначно различимых дефектов. Значение коэффициента глубины поиска дефекта определяется по матрице проверок В в соответствии с выражением:

,

где T(z) - число совпадающих столбцов в матрице проверок В, определяющих число неразличимых дефектов; p - общее число столбцов матрицы В.



Для объекта, представленного граф-моделью, следует заполнить модель классов эквивалентности диагностических пар (МКЭДП) и выполнить алгоритм оптимизации процедуры диагностирования по числу диагностических пар, обеспечивающих одноразличимость дефектов (рисунок 3). Процедура интерпретации графической модели в множество решений задачи построения процедуры диагностирования, включенная в алгоритм, позволяет определить координаты границ частных решений в координатах шкалы L.

Назначение и обслуживание точек съема диагностической информации может требовать определенных, в том числе и дифференцированных, затрат. Процедуры диагностирования, включающие в себя различные подмножества диагностических пар, различаются, в том числе, вычислительной сложностью (например, при анализе результатов диагностирования за счет обработки аналитических зависимостей преобразования сигналов выход-вход, если в граф-модели объекта они имеют различную физическую природу). В связи с этим поставлены и решены следующие задачи:

где – затраты на организацию диагностических проверок; С*- заданное значение ограничений на затраты.

Приведены алгоритмы решения задач 3.2 и 3.3, где в качестве показателя контролепригодности используется коэффициент глубины поиска дефекта K_ГП. Для решения задачи 3.2 необходимо реализовать обход путей дерева решений в направлении сверху вниз и слева направо, проанализировать соответствующие матрицы проверок, и вычислить затраты на организацию диагностических проверок . При этом, если в процессе выполнения алгоритма возникает нарушение ограничения по стоимости (текущее значение затрат на реализацию диагностических пар больше минимального С_min), то обход дерева в данном направлении не продолжается. Решая задачу 3.3, необходимо произвести обход путей дерева решений в направлении сверху вниз и слева направо, отсекая ветви, для которых в процессе выполнения алгоритма нарушаются ограничения по стоимости (текущее значение затрат на реализацию диагностических пар больше заданного С^*). Как и при решении задачи 3.2, следует производить обход l-го пути полного дерева решений в направлении от начальной вершины к висячей и подсчитывать суммарные затраты на организацию точек съема диагностической информации С(l) построенного частного решения, сравнивая ее с порогом С^*.

В работе рассмотрены возможности применения эволюционного подхода к решению задач построения процедур диагностирования на базе МКЭДП для дальнейшего увеличения эффективности разработанных методов.

Для граф-модели объекта диагностирования строится модель классов эквивалентности диагностических пар и выполняется ее анализ следующим образом.

Вычислить сумму V мощностей множеств входов X₁,…,X_m :



В результате вычислений возможны два случая:

1. Полученное значение V не превышает размерности шкалы L: V ≤ L.

2. Полученное значение V > L.

Для вычисления V используется матрица достижимости D исходного графа, в которой следует проанализировать подматрицу размерности n×m, расположенную в правом верхнем углу, т.е. рассмотреть строки, соответствующие входам x₁, ... , x_n, и столбцы, соответствующие выходам z₁, ... , z_m исходной граф-модели.

Очевидно, что количество единиц в каждом столбце, соответствующем выходу z_i (i=1, ... , m), равно мощности множеств входов X_i (i=1, ... , m), а сумма всех единиц в рассматриваемой подматрице будет равна V.

Результат закодирован в виде символьной модели, используемой в генетических алгоритмах, следующим образом. В первом случае формируется символьная модель, представляющая собой двоичный вектор длины V, содержащий единицы в тех битах, которые соответствуют диагностическим парам, образующим допустимое решение задачи.

Во втором случае строится символьная модель, соответствующая двоичному вектору длины W:

W=2*counter+2,

где counter – общее число различных частных решений, полученных для исходного вида модели классов эквивалентности диагностических пар. Пример такого вектора приведен на рисунке 4.



В предложенной символьной модели выделено три функциональных участка (А, Б и О).

Первый и второй участки (А, Б) двоичного вектора W соответствуют отрезкам [1, counter] и [counter+1, 2*counter] длины counter. Они содержат единицы в битах, соответствующих частным решениям, которые будут участвовать в построении допустимого решения задачи.

Третий участок (О) вектора W соответствует отрезку [2*counter+1, 2*counter+2]. Этот участок символьной модели несет информацию о том, какая операция будет выполнена над множествами B_А и B_Б, соответствующими множествам диагностических пар, построенным по отрезкам А и Б, соответственно:

- 00 – разность множеств B_А и B_Б: B_А \ B_Б,. Из общего числа диагностических пар, построенных по участку А, исключаются те пары, которые одновременно принадлежат и отрезку А, и отрезку Б (B_А \ B_Б = B_А \ B_А&B_Б) вектора W;

- 01 – разность множеств B_Б и B_А: B_Б \ B_А;

- 10 – объединение множеств B_А и B_Б: B_А  B_Б. К диагностическим парам, построенным по участку А, добавляются пары, соответствующие участку Б;

- 11 – пересечение множеств B_А и B_Б: B_А & B_Б. Учитываем только те диагностические пары, которые одновременно принадлежат и отрезку А, и отрезку Б символьной модели (рисунок 5).

Такой метод кодировки дает возможность наряду с полными частными решениями выделять еще и их части, что существенно увеличивает диапазон охватываемых решений, а значит, и повышает скорость и вероятность приближения к оптимальному решению задачи.

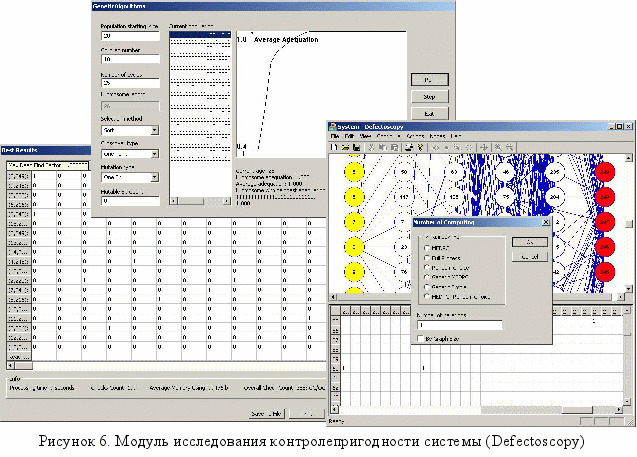
В четвёртой главе приведено краткое описание разработанного программного продукта «Модуль исследования контролепригодности системы Defectoscopy» (рисунок 6) для решения задач построения процедур диагностирования восстанавливаемых объектов, использующих допусковые методы контроля, представленных граф-моделями, построенными в пространстве конструктивных свойств или взаимосвязей их параметров.

Для исследования эффективности разработанных методов в программное приложение включены перечисленные ниже методы построения минимальной по числу проверок диагностической процедуры:

- метод на базе разработанной МКЭДП;

- метод полного перебора решений;

- метод случайного выбора строки, удаляемой из полной матрицы проверок, при выполнении критерия различимости столбцов;

- комбинации методов на базе МКЭДП и метода случайного выбора удаляемой строки;

- генетический алгоритм поиска решения.

Оценена эффективность разработанных методов.

Исследования, проведенные для графов различной топологии (обработано ~ 700 графов) показали, что метод построения оптимальной процедуры диагностирования, основанный на анализе МКЭДП, требует по сравнению с методами случайного выбора и комбинированного метода (МКЭДП+ случайный выбор) меньших временных затрат, и с увеличением размерности обрабатываемого графа выигрыш во времени растет (рисунок 7).

Например, для графов с количеством вершин N=450 время построения оптимальной процедуры диагностирования при использовании метода на основе МКЭДП составило в среднем 35 секунд, метод случайного выбора потребовал 176 секунд, а при использовании комбинации методов: сначала метода на базе МКЭДП, а затем метода случайного выбора временные затраты составили 91секунду.

В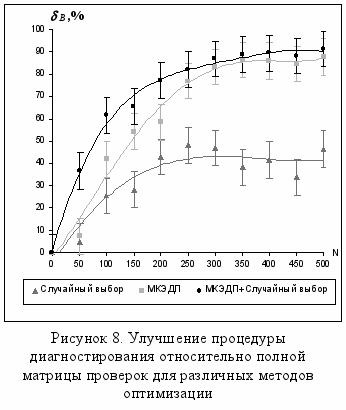веден показатель относительного улучшения процедуры диагностирования _B, характеризующий степень улучшения процедуры диагностирования относительно полной матрицы проверок, вычисляемый по формуле:

,

где |B_opt| – мощность матрицы проверок, полученной в результате оптимизации процедуры диагностирования, |B_full| – мощность полной матрицы проверок.

Экспериментально получено, что комбинация метода на основе МКЭДП с методом случайного выбора, а также метод, построенный на базе МКЭДП, дают лучшие решения по критерию относительного улучшения процедуры диагностирования (рисунок 8). Например, для графов с количеством вершин N=450 использование метода на основе МКЭДП позволило сократить процедуру диагностирования в среднем на 86,41%, метод случайного выбора – на 38,25%, а при использовании комбинации методов: сначала метода на базе МКЭДП, а затем метода случайного выбора процедура диагностирования сократилась на 88,71%.

Приведены результаты применения разработанных моделей и алгоритмов к диагностированию участка газотранспортной сети (ГГТС) между двумя компрессорными станциями Заволжской и Сеченовской Ужгородского коридора, модель которого представлена графом причинно-следственных связей, содержащим 531 вершину, 319 входных вершин, 98 назначенных точек контроля. Метод оптимизации процедуры поиска с использованием МКЭДП позволил в 12 раз (на 91,69%) сократить количество обрабатываемой диагностической информации, т.е. размер матрицы проверок уменьшился в 12 раз при условии одноразличимости дефектов. Комбинированный метод в 18 раз (на 94,43%) сократил матрицу проверок.

Если по факту контроля установлено наличие дефектов типа утечек среды, то необходимо выполнить перекрытие вентилей для локализации диагностируемого участка. Решена задача минимизации множества перекрытий вентилей для диагностирования утечек транспортируемой среды.

В заключении формулируются основные результаты, полученные в диссертационной работе.


ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

1. Предложена новая модель классов эквивалентности диагностических пар, позволяющая эффективно решать задачу синтеза оптимальных процедур диагностирования по числу элементарных проверок для объектов с большим числом состояний, вызванных наличием дефектов.
   
2. Разработан алгоритм построения диагностических процедур на базе модели классов эквивалентности диагностических пар и алгоритм интерпретации графической модели в множество решений задачи построения эффективных процедур диагностирования.
   
3. Проведен анализ и показана эффективность применения эволюционного моделирования к решению задач синтеза диагностических процедур. Разработаны механизмы кодирования допустимого решения в виде битовой строки с применением генетических алгоритмов.
   
4. Реализован алгоритм автоматизированного проектирования граф-модели объекта с заданной топологией, определяемой коэффициентом достижимости, и требуемым коэффициентом глубины поиска дефекта с целью моделирования и апробации разработанных моделей и алгоритмов.
   
5. Проведена оценка вычислительной трудоемкости решения задач построения оптимальных по числу проверок процедур диагностирования методами полного перебора, случайного и направленного поиска решений и их модификаций. Экспериментально показана эффективность использования в составе исследуемых методов разработанной модели классов эквивалентности диагностических пар.
   
6. Выполнена апробация разработанных алгоритмов для диагностирования участка газотранспортной сети между компрессорными станциями Заволжской и Сеченовской Ужгородского коридора. В результате сокращен объём хранимой в базе данных информации для оценки качества функционирования газотранспортной сети.
   

Список публикаций по теме диссертации

1. Степаненко, М.А. Контролепригодность обьекта диагностирования с одиночными дефектами / М.А. Степаненко // Информационные системы и технологии (ИСТ-2003): тез. докл. всеросс. науч.-техн. конф., Нижегород. гос. техн. ун-т. - Н.Новгород, 2003. C.132-133.
   
2. Степаненко, М.А. Решение задачи распределения коэффициента глубины диагностирования в сложной системе / М.А. Степаненко // Системы обработки информации и управления: Труды Нижегород. гос. тех. ун-та / НГТУ.- Н.Новгород, 2003. Т.37. В.10. С. 83-92.
   
3. Соколова, Э.С. Об основных принципах тестирования программ/ Э.С. Соколова, М.А. Степаненко// Информационные системы и технологии (ИСТ-2004): тез. докл. всеросс. науч.-техн. конф., Нижегород. гос. техн. ун-т. - Н.Новгород, 2004. C.109-110.
   
4. Соколова, Э.С. Формализованный подход к тестированию кратных ошибок в программных модулях / Э.С. Соколова, М.А. Степаненко // Системы обработки информации и управления: Труды Нижегород. гос. тех. ун-та / НГТУ.- Н.Новгород, 2004. Т.47. В.11. С. 90-93.
   
5. Соколова, Э.С. Построение процедур диагностирования технического состояния объектов / Э.С. Соколова, М.А. Степаненко, О.Е. Гущин // Информационные системы и технологии (ИСТ-2005): тез. докл. всеросс. науч.-техн. конф., Нижегород. гос. техн. ун-т. - Н.Новгород, 2005. С. 136-137.
   
6. Гущин, О.Н. Разработка нового подхода к построению процедур диагностирования технических объектов / О.Н. Гущин, С.Н. Капранов, М.А. Степаненко // Системы обработки информации и управления: Труды Нижегород. гос. тех. ун-та / НГТУ.- Н.Новгород, 2005.Т.54. В.12. С.54-57.
   
7. Гущин, О.Н. Оптимизация процедур диагностирования технического состояния объекта / О.Н. Гущин, С.Н. Капранов, М.А. Степаненко // Системы обработки информации и управления: Труды Нижегород. гос. тех. ун-та / НГТУ.- Н.Новгород, 2005.Т.54. В.12. С. 58-61.
   
8. Степаненко, М.А. Метод построения процедур диагностирования технического состояния объектов с использованием символьной модели / М.А. Степаненко, Э.С. Соколова, С.Н. Капранов // Программа (с аннотациями докладов) V Международной конференции «Идентификация систем и задачи управления» SICPRO '06 Москва 30 января – 2 февраля 2006г., Институт проблем управления им. В.А.Трапезникова РАН.  М. 2006.
   
9. Степаненко, М.А. Метод построения процедур диагностирования технического состояния объектов с использованием символьной модели / М.А. Степаненко, Э.С. Соколова, С.Н. Капранов // Труды V Международной конференции «Идентификация систем и задачи управления» SICPRO '06 Москва, 30 января – 2 февраля 2006 г., Институт проблем управления им. В.А.Трапезникова РАН.  М. : 2006. C. 1254-1266.
   
10. Акатьев, Н.Д. Алгоритм оптимизации программы поиска дефектов / Н.Д. Акатьев, М.И. Минеев, М.А. Степаненко // Информационные системы и технологии (ИСТ-2006): тез. докл. международ. науч.-техн. конф., Нижегород. гос. техн. ун-т. Н.Новгород, 2006. С. 183-184.
    
11. Степаненко, М.А. Оптимизация автоматического метода синтеза ацикличного однонаправленного графа / М.А. Степаненко // XI Нижегородская сессия молодых ученых. Технические науки “Татинец”, 12-16 февраля 2006г., Н.Новгород. С. 29-30.
    
12. Соколова Э.С. Разработка алгоритма локализации дефектов на назначенной совокупности контрольных точек / Э.С. Соколова, М.А. Степаненко // Журн. Контроль. Диагностика. – 2006. №9. C. 41-44.
    
13. Акатьев, Н.Д. Алгоритм оптимизации назначения контрольных точек / Н.Д. Акатьев, М.И. Минеев, М.А. Степаненко // Информационные системы и технологии (ИСТ-2007): тез. докл. международ. науч.-техн. конф., Нижегород. гос. техн. ун-т. Н.Новгород, 2007. С. 138-139.