В. Е. Латов Тульский государственный университет mibo@klax tula ru Эволюционное моделирование в задача

Вид материала

Задача

Содержание Эволюционные вычисления

Подобный материал:

• "Философские науки", 789.13kb.
• Центр содействия занятости молодёжи и трудоустройству выпускников техникума: десять, 75.01kb.
• П. П. Порешин московский инженерно-физический институт (государственный университет), 23.75kb.
• В. В. Шахов Московский инженерно физический институт (государственный университет), 28.32kb.
• Бюджетный процесс в Российской Федерации: эволюционное развитие и качество управления, 595.53kb.
• -, 304.96kb.
• Отчёт о деятельности виртуального филиала 2009, 107.01kb.
• Московский государственный университет коммерции Тульский филиал, 227.84kb.
• Дискурсивные особенности текста современной англоязычной пародии, 375.74kb.
• Информационное письмо, 46.52kb.

М. Ю. Богатырев,

В. Е. Латов

Тульский государственный университет

mibo@klax.tula.ru

Эволюционное моделирование
в задачах оптимизации

Термин «эволюционное моделирование» известен достаточно давно []. Первоначально эволюционное моделирование применялось исключительно для исследования биологических моделей, например, моделей эволюции. Далее этот метод в общей форме стал применяться в задачах оптимизации. Здесь необходимо отметить работы Л. А. Растригина о «бионическом» подходе к оптимизации [], предвосхитившие появление генетических алгоритмов [] — наиболее популярных представителей эволюционных алгоритмов.

В настоящее время эволюционное моделирование представляет собой направление в математическом моделировании, объединяющее компьютерные методы моделирования биологических процессов эволюции, а также другие, идеологически близкие направления в математическом программировании, использующие эвристические методы и эволюционный принцип, рассматриваемый ниже. Инструментами эволюционного моделирования являются генетические алгоритмы, эволюционные стратегии, эволюционное программирование, а также искусственные нейронные сети, нечеткая логика.


Принцип эволюционного моделирования


Принцип эволюционного моделирования основан на эволюционных вычислениях. Эволюционные вычисления — это термин, относящийся к нескольким методам оптимизации, объединенных тем, что все они используют понятие эволюции объектов, входящих в систему. С точки зрения теории систем эволюция представляет собой процесс адаптации системы через изменение ее параметров под воздействием внешних условий. Поэтому эволюционные вычисления можно трактовать как развитие методов теории адаптивных систем.

Суть эволюционного подхода в общем виде сводится к следующему.

Фиксируется множество объектов X, обладающих некоторыми параметрами и связанных друг с другом посредством определенной структуры. Среди этих объектов необходимо выбрать наилучшие в смысле некоторого критерия. Критерий оптимальности формируется на основе свойств объектов и не обязательно существует в виде аналитических выражений. Важно, что существует отображение

F: X → R (R — множество действительных чисел) и каждому объекту x  X из множества X сопоставлено значение критерия F(x).

Природа исследуемого множества объектов произвольна, поэтому необходимо построить представление исходного множества объектов в другом, конечном множестве, обладающем структурой, например, векторного пространства. Такое представление φ: X → S описывает связь между исследуемыми объектами, которые выступают в качестве потенциальных решений задачи поиска экстремума, и объектами, управлением и манипулированием которых занимается поисковый алгоритм. Существует обратное представление φ^-1: S → X и каждому вновь сгенерированному элементу представления s  S соответствует элемент в множестве X.

Процесс оптимизации состоит в построении множества объектов — решений x^* X ^*, для которых выполняются условия:

x^* = argmax F [φ^-1(s)]

s  S.

В процессе оптимизации исходное множество X развивается или эволюционирует к оптимальному состоянию, изменяя свой состав и параметры входящих в него объектов.

Способ построения множества объектов s  S определяется эволюционным алгоритмом, который и реализует метод оптимизации.

Особенностью всех эволюционных алгоритмов является то, что в качестве множества S строится так называемое кодовое пространство — множество представлений объектов x в виде кодов.

Эволюция множества 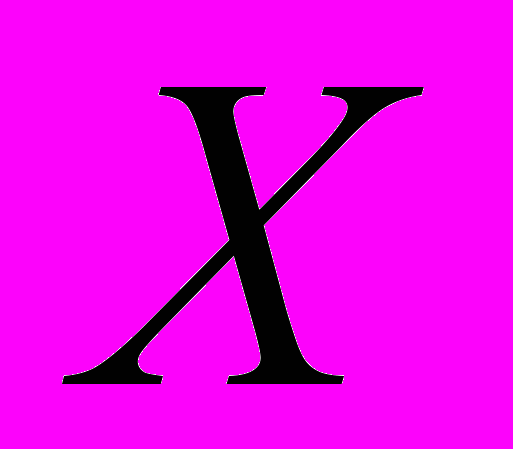задается эволюцией представления 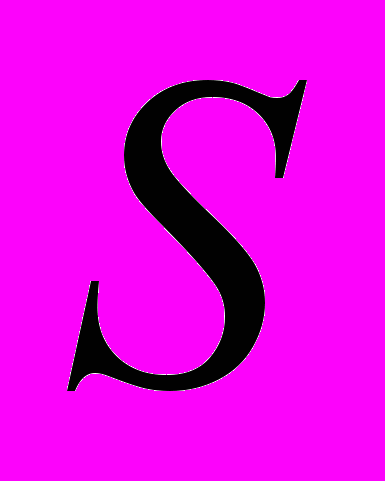. На множестве 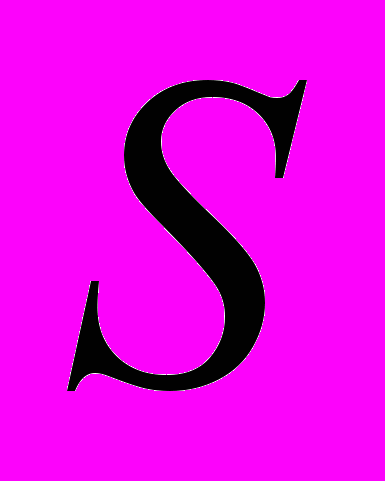определяется подмножество 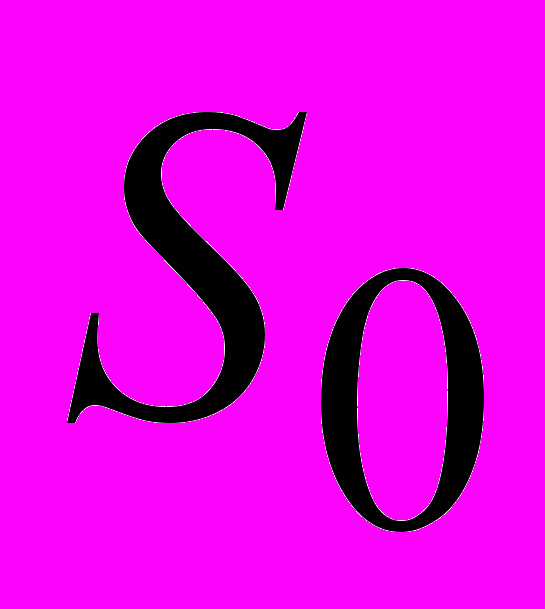— начальная популяция, состав которой определяется либо случайным образом, либо задается.

Решение на каждом шаге эволюции определяется разностной схемой

,

где — эволюционный оператор, в котором выделены эвристическая составляющая в виде оператора (отбор решений) и регулярная составляющая в виде операторов , – знак композиции. Критерий оптимальности вычисляется на каждом шаге вместе с критерием отбора решений, реализуемым в операторе .

Применение данного принципа в моделировании имеет две особенности.

1. Эволюционное моделирование представляет собой «экспериментальный» способ решения задач оптимизации, в которых связь оптимизируемых объектов с управляемыми и наблюдаемыми объектами сложна и не может быть выражена аналитически. Примером служат задачи поиска оптимальных значений параметров систем, описываемых моделями в виде нелинейных уравнений [].

2. Применение эволюционного моделирования эффективно в задачах, где необходимо получить всю историю поведения системы, ее эволюцию. Заметим, что эволюционное моделирование первоначально как раз и возникло как метод моделирования эволюционных процессов в целом.

Технология эволюционного моделирования

Рассмотрим вариант реализации системы эволюционного моделирования, который применим к широкому кругу задач моделирования. Это вариант опирается на описанный выше принцип, согласно которому эволюционный метод оптимизации работает не в исходном множестве решений, а в его представлении в кодовом пространстве.

Система эволюционного моделирования представляет собой систему с обратной связью, как показано на рис. 1, в которой оптимизируемая модель и эволюционный алгоритм разделены. В данном случае математическая природа модели не имеет значения. Модель получает от алгоритма очередной набор значений параметров (x₁,x₂,…,x_m) и выдает соответствующее значение функции качества F. Данное значение используется алгоритмом при отборе и формировании новых решений. Процесс останавливается, когда текущий набор значений параметров удовлетворяет заданному критерию, то есть найдено оптимальное решение (x₁^opt,x₂^opt,…,x_m^opt).

Внешне простая схема на рис. 1 требует ряда принципиальных решений при ее реализации.



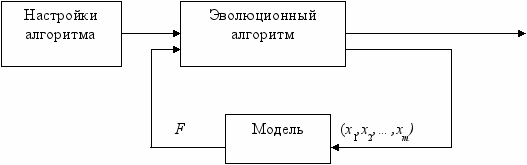
(x1opt, x2opt, …, xmopt)


Рис. 1. Структура системы эволюционного моделирования


1. Независимая реализация модели и оптимизационного алгоритма требует, тем не менее, единой инструментальной среды программирования, в которой реализуется вся система. Такой средой выбрана система Java. В данном случае система не накладывает ограничений на средство создания модели, что дает возможность оптимизировать модели, написанные на разных языках программирования. Модель может представлять из себя либо исполняемый модуль (файл с расширением .ехе), либо динамическую библиотеку (.dll), загружаемую другими приложениями.

2. Из самой природы эволюционных алгоритмов следует, что они не отличаются быстродействием. Необходимость генерации сразу нескольких решений, образующих популяцию, а также случайный характер поиска обусловливают наличие множества операций, снижающих быстродействие системы моделирования. Поэтому декомпозиция в системах эволюционного моделирования, относящаяся как к самой модели, так и к схеме вычислений, имеет принципиальное значение. Одно из направлений декомпозиции систем эволюционного моделирования основано на анализе симметрий оптимизируемых моделей и симметрий, присущих самим эволюционным алгоритмам [].

На рис. 2 показаны результаты эволюционного моделирования поведения системы координатно-параметрического управления [], в которой определенные сочетания параметров обусловливают как приемлемые (монотонные), так и неприемлемые (колебательные) с точки зрения эксплуатации системы переходные процессы в ней. На рис. 2. изображены все переходные процессы, которые проверил генетический алгоритм, выполняя эволюцию параметров настройки регулятора системы. Среди множества процессов, показанных на рисунке, мы видим процессы всех известных в теории управления типов, в том числе и искомые монотонные процессы.




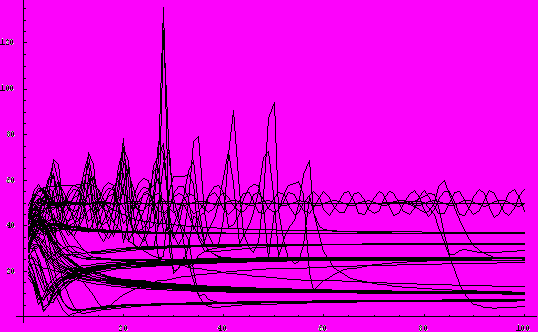
Рис. 2. Эволюция популяций переходных процессов

в системе координатно-параметрического управления


Характерные процессы с пиковыми значениями регулируемой величины соответствуют аварийному режиму системы. В данном случае эволюционное моделирование позволило исследовать все возможные процессы в установке в заданных диапазонах настроек регулятора и определить конкретные настройки, обеспечивающие заданное качество процессов регулирования.


Список литературы

1. Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. — М.: Мир, 1969.
   
2. Растригин Л. А. Адаптация сложных систем. — Рига: Зинатне, 1981.
   
3. Holland J. H. Adaptation in Natural and Artificial Systems, Ann Arbor: The University of Michigan Press. Reprinted by MIT, 1992.
   
4. Bogatyrev M. Modelling Systems With Symmetry // Proceedings of the 4 th International IMACS Symposium of Mathematical Modelling. — ARGESIM-Verlag, Vienna, 2003.
   
5. Богатырев М. Ю. Эволюционный подход к многокритериальной оптимизации в системах координатно-параметрического управления // Изв. ТулГУ. Сер. Математика. Механика. Информатика. Т. 8. Вып. 3 . Информатика. — Тула, 2002.