Методические указания по выполнению лабораторной работы Для самостоятельной работы студентов III курса специальности

Вид материала

Методические указания

Содержание Численность страховых агентов (чел.) Пробег (тыс. км) Привлеченные средства (млн. руб.) Собственные средства Темп инфляции (%) Примерный график изучения дисциплины Эконометрика Тема 1. Введение. Эконометрика и эконометрическое моделирование. Тема 2. Корреляция. Парная регрессия. Тема 2. Корреляция. Парная регрессия. Тема 3. Множественная регрессия. Тема 3. Множественная регрессия. Тема 4. Временные ряды. Основная литература Методические указания Электронные материалы (Web-сайт ВЗФЭИ станмчка кафедры, сервер ВЗФЭИ)

Подобный материал:

• Методические указания по выполнению контрольных работ для самостоятельной работы студентов, 868.03kb.
• Методические указания по выполнению лабораторной работы на пэвм для самостоятельной, 1165.71kb.
• Методические указания по выполнению контрольной работы для самостоятельной работы студентов, 164.27kb.
• Методические указания к выполнению лабораторной работы №10 для студентов очной формы, 240.19kb.
• Методические указания по выполнению лабораторной работы №6 для студентов 1-го курса, 124.2kb.
• Методические указания по выполнению контрольной работы с использованием компьютерных, 1010.76kb.
• Методические указания по проведению лабораторной работы для студентов Vкурса специальности, 364.3kb.
• Методические указания по выполнению контрольной работы для самостоятельной работы студентов, 371.12kb.
• Методические указания по выполнению лабораторной работы №14 для студентов специальности, 187.8kb.
• Методические указания по выполнению лабораторной работы №12 для студентов специальности, 141.78kb.

Задача 5. Исследуется взаимосвязь курса доллара США с курсами евро, японской иены и английского фунта стерлингов. Имеются данные об официальных курсах валют, установленных Центральным Банком России, за двенадцать дней:

День	Доллар США (руб./долл.)	Евро (руб./евро)	Японская иена (руб./100 иен)	Английский фунт (руб./фунт)
1	28,12	36,13	26,97	52,63
2	28,18	35,97	26,80	52,32
3	28,13	35,97	26,77	52,26
4	28,08	36,00	26,63	52,28
5	28,06	36,13	26,53	52,43
6	28,03	36,28	26,70	52,58
7	28,02	36,34	26,67	52,90
8	28,00	36,47	26,63	52,99
9	27,99	36,54	26,60	52,81
10	27,93	36,50	26,50	52,89
11	27,95	36,52	26,55	52,62
12	27,97	36,54	26,52	52,67

Требуется:

1. Построить линейную регрессионную модель курса доллара США, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Значимо ли статистически уравнение регрессии?
   
3. Изменение курсов каких валют существенно влияет на изменение курса доллара США?
   
4. Спрогнозировать курс доллара, если предполагается, что курсы евро, иены и фунта составят соответственно: 36,38 руб./евро; 26,65 руб./100 иен и 52,73 руб./фунт.
   

Задача 6. По заводу безалкогольных напитков изучается зависимость месячного объема реализованной продукции от затрат в предыдущем месяце на теле-, радио-, газетную и наружную рекламу. Имеются данные за двенадцать месяцев:

Месяц	Объем реализации (тыс. руб.)	Затраты на рекламу (тыс. руб.)
		телерекламу	радиорекламу	газетную рекламу	наружную рекламу
1	15304	133	35	38	27
2	17554	152	40	32	29
3	16876	130	48	35	28
4	16435	165	40	44	25
5	15229	125	42	48	18
6	16986	158	37	37	32
7	17914	165	50	43	38
8	16817	149	37	38	29
9	16579	169	33	28	27
10	15330	137	31	39	22
11	16781	178	42	42	18
12	17008	147	49	37	19

Требуется:

1. Построить линейную регрессионную модель объема реализованной продукции, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Присутствует ли в остатках регрессии автокорреляция первого порядка?
   
3. Как влияет на изменение объема реализованной продукции изменение затрат на каждый вид рекламы?
   
4. Изменение затрат на какой вид рекламы сильнее всего влияет на изменение объема реализованной продукции?
   
5. Спрогнозировать значение объема реализованной продукции, если прогнозные значения факторов на 35 % превышают свои средние значения.
   

Задача 7. По хлебобулочному предприятию исследуется зависимость месячного объема реализованной продукции от затрат в предыдущем месяце на теле-, радио-, газетную и наружную рекламу. Имеются данные за двенадцать месяцев:

Месяц	Объем реализованной продукции (тыс. руб.)	Затраты на рекламу (тыс. руб.)
		телерекламу	радиорекламу	газетную рекламу	наружную рекламу
1	14050	240	42	42	34
2	16310	263	47	44	36
3	15632	241	55	45	35
4	15126	276	47	42	32
5	13972	236	49	47	25
6	15753	272	44	45	39
7	16661	276	57	55	45
8	15584	260	46	47	36
9	15326	280	40	35	34
10	14077	248	38	38	29
11	15528	289	49	45	25
12	15755	258	56	52	26

Требуется:

1. Построить линейную регрессионную модель объема реализованной продукции, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Какая доля вариации объема реализованной продукции объясняется вариацией факторов, включенных в модель регрессии?
   
3. Присутствует ли в остатках регрессии автокорреляция первого порядка?
   
4. Приемлема ли точность регрессионной модели?
   
5. Спрогнозировать значение объема реализованной продукции, если прогнозные значения факторов на 25 % превышают свои средние значения.
   

Задача 8. По четырнадцати страховым компаниям исследуется зависимость месячной прибыли от численности страховых агентов, затрат на рекламу и расположения офиса компании (центральный или периферийный районы города):

№ компании	Прибыль (тыс. руб.)	Численность страховых агентов (чел.)	Затраты на рекламу (тыс. руб.)	Район расположения
1	726	14	75	периферийный
2	550	8	36	центральный
3	429	4	55	периферийный
4	439	4	45	периферийный
5	646	10	79	периферийный
6	507	10	53	периферийный
7	834	13	69	центральный
8	579	9	47	периферийный
9	701	16	45	центральный
10	532	14	49	периферийный
11	281	7	53	периферийный
12	349	5	45	периферийный
13	625	10	68	периферийный
14	533	11	38	центральный

Требуется:

1. Построить линейную регрессионную модель прибыли страховой компании, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Значимо ли статистически уравнение регрессии?
   
3. Существенна ли разница в прибыли компаний, офисы которых расположены в центральном и периферийных районах города?
   
4. Спрогнозировать месячную прибыль страховой компании, если прогнозные значения факторов равны своим средним значениям, а офис расположен: а) в центре города; б) на окраине.
   

Задача 9. Строится модель цены автомобиля на вторичном рынке в зависимости от пробега, срока эксплуатации и объема двигателя. Имеются данные по пятнадцати автомобилям одной и той же модели:

№ автомобиля	Цена автомобиля (долл. США)	Пробег (тыс. км)	Срок эксплуатации (лет)	Объем двигателя (л)
1	12500	130	12	2,3
2	13700	120	10	1,9
3	9200	300	15	1,8
4	11400	180	13	2,1
5	15800	150	14	2,6
6	12300	80	8	1,7
7	16300	170	10	2,4
8	10200	210	11	1,9
9	11000	250	7	1,9
10	12700	150	9	1,7
11	15000	90	4	2,2
12	10500	230	13	2,4
13	17200	120	8	2,3
14	16000	110	9	2,5
15	17100	120	6	2,6

Требуется:

1. Построить линейную регрессионную модель цены автомобиля, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Построить модель множественной линейной регрессии со статистически значимыми факторами
   
3. Существенно ли влияние пробега, срока эксплуатации и объема двигателя на изменение цены автомобиля?
   
4. Что сильнее влияет на изменение цены автомобиля — изменение пробега или срока эксплуатации?
   
5. Спрогнозировать цену автомобиля с пробегом 150 тыс. км, сроком эксплуатации 10 лет и объемом двигателя 2 л. Пункты 4 и 5 выполнить, используя вторую модель.
   

Задача 10. По тринадцати коммерческим банкам имеются данные, характеризующие зависимость годовой прибыли от размера собственного капитала, общей суммы привлеченных средств и среднегодовых ставок по рублевым депозитам и краткосрочным кредитам:

№ банка	Прибыль (млн. руб.)	Собственный капитал (млн. руб.)	Привлеченные средства (млн. руб.)	Депозитная ставка (% годовых)	Кредитная ставка (% годовых)
1	115	4428	3278	12,5	17,7
2	80	3756	5696	11,7	18,2
3	97	2970	2210	11,2	19,1
4	92	6231	5823	9,7	15,2
5	129	3960	4569	13,5	18,5
6	223	7354	2896	10,8	18,6
7	251	4662	3526	12,1	15,7
8	267	4760	2259	11,7	16,6
9	137	4569	4596	13,7	17,3
10	163	5274	3271	12,5	19,3
11	225	5418	4596	12,8	17,8
12	278	5359	3256	11,2	14,5
13	367	8254	5189	10,4	13,7

Требуется:

1. Построить линейную регрессионную модель годовой прибыли банка с полным набором факторов. Оценить параметры модели.
   
2. Построить линейную регрессионную модель годовой прибыли банка только с существенно влияющими на ее изменение факторами. Оценить параметры модели.
   
3. Значимо ли статистически уравнение регрессии второй модели?
   
4. Имеют ли остатки второй регрессии одинаковую дисперсию?
   
5. Используя вторую модель, сравнить силу влияния факторов на годовую прибыль банка.
   

Задача 11. По четырнадцати страховым компаниям имеются данные, характеризующие зависимость чистой годовой прибыли от годовых размеров собственных средств, страховых резервов, страховых премий и страховых выплат (все в тыс. руб.):

№ компании	Годовая прибыль	Собственные средства	Страховые резервы	Страховые премии	Страховые выплаты
1	92	3444	9563	11456	1659
2	42	2658	6354	5249	2625
3	186	9723	10245	12968	4489
4	48	4526	6398	7589	6896
5	38	5369	5692	7256	5698
6	74	2248	6359	4963	4321
7	48	5671	6892	7259	6692
8	82	4312	7256	6935	756
9	45	2226	8256	2693	5532
10	46	3654	5982	6324	3235
11	65	2635	6359	7853	5325
12	29	2463	7532	8253	6862
13	34	3265	5632	7564	6325
14	66	7546	7625	9638	4569

Требуется:

1. Построить линейную регрессионную модель годовой прибыли страховой компании, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Значимы ли статистически уравнение регрессии и его коэффициенты?
   
3. Имеют ли остатки регрессии одинаковую дисперсию?
   
4. Приемлема ли точность регрессионной модели?
   
5. Дать экономическую интерпретацию коэффициентам уравнения регрессии.
   

Задача 12 . По литейному предприятию исследуется влияние объемов производства алюминия, меди и олова на технологические затраты электроэнергии. Имеются данные за одиннадцать месяцев:

Месяц	Затраты электроэнергии (тыс. кВтч)	Объем производства (тонн)
		алюминия	меди	олова
1	286	68	42	7
2	374	45	32	27
3	308	59	36	14
4	319	62	43	18
5	616	72	59	26
6	495	128	63	48
7	825	78	42	23
8	253	42	34	7
9	495	52	26	27
10	1056	96	75	36
11	902	122	56	43

Требуется:

1. Построить линейную регрессионную модель энергозатрат, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Проверить статистическую значимость уравнения регрессии и их отдельных коэффициентов.
   
3. Оценить точность модели.
   
4. На сколько в среднем изменяются технологические энергозатраты при увеличении производства каждого из металлов:
   

1. на одну тонну;
   
2. на один процент?
   

Задача 13. Исследуется зависимость цены акции компании «Атон» от цен акций смежных компаний «Бридж», «Вортекс» и «Радон». Имеются данные о результатах биржевых торгов за пятнадцать дней:

День	Цена акции (руб.)
	«Атон»	«Бридж»	«Вортекс»	«Радон»
1	67	30	59	75
2	63	27	55	68
3	58	22	52	78
4	66	27	55	60
5	63	18	78	72
6	67	33	68	73
7	70	32	72	71
8	63	24	75	78
9	60	29	56	72
10	64	27	79	65
11	56	32	62	82
12	68	32	79	71
13	71	56	75	72
14	62	40	72	78
15	64	37	68	75

Требуется:

1. Построить трехфакторную и три однофакторные линейные регрессионные модели цены акции «Атона». Оценить параметры моделей.
   
2. Проверить статистическую значимость всех уравнений регрессии и их коэффициентов.
   
3. Используя трехфакторную модель, сравнить силу влияния факторов на изменение цены акции «Атона».
   
4. Используя трехфакторную и однофакторные модели, спрогнозировать среднюю цену акции «Атона», если предполагается, что цены акций «Бриджа», «Вортекса» и «Радона» составят соответственно 40; 70 и 80 руб. Сравнить результаты расчетов по трехфакторной и однофакторным моделям.
   

Задача 14. По хладокомбинату изучается зависимость месячного объема реализации мороженного от средней цены выпускаемой продукции, затрат на рекламу, среднемесячной температуры воздуха и месячного темпа инфляции. Имеются данные за двенадцать месяцев:

Месяц	Объем реализации (тыс. руб.)	Цена (руб.)	Затраты на рекламу (тыс. руб.)	Температура воздуха (С)	Темп инфляции (%)
1	185	8,3	6	2	0,3
2	162	8,3	7	4	0,4
3	182	8,9	5	7	0,3
4	195	10,6	5	10	0,2
5	226	10,7	7	13	0,7
6	279	10,8	22	18	0,9
7	312	12,2	12	22	0,9
8	286	14,2	17	24	0,4
9	212	14,5	22	17	0,1
10	178	13,7	26	13	0,1
11	182	13,3	8	8	0,5
12	173	12,1	4	5	0,9

Требуется:

1. Построить линейную регрессионную модель объема реализации мороженного, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Значимо ли статистически уравнение регрессии и его коэффициенты?
   
3. Присутствует ли в остатках регрессии автокорреляция первого порядка?
   
4. Приемлема ли точность регрессионной модели?
   
5. Изменение какого из факторов сильнее всего влияет на изменение объема реализации мороженного?
   

Задача 15.

По тринадцати супермаркетам исследуется зависимость квартального торгового оборота от размера торговых площадей, района расположения (центральный или периферийные) и формы собственности (муниципальный или частный). Имеются следующие данные:

№ магазина	Торговый оборот (млн. руб.)	Торговые площади (м2)	Район расположения	Форма собственности
1	59	2500	периферийный	муниципальный
2	85	2172	периферийный	частный
3	127	2928	центральный	муниципальный
4	178	3943	центральный	муниципальный
5	156	2819	центральный	частный
6	122	4902	периферийный	муниципальный
7	89	4236	центральный	муниципальный
8	159	5486	периферийный	муниципальный
9	256	7186	центральный	частный
10	156	4501	центральный	частный
11	149	3495	центральный	муниципальный
12	122	4562	периферийный	частный
13	178	2706	центральный	частный

Требуется:

1. Построить линейную регрессионную модель торгового оборота магазина, не содержащую коллинеарных факторов. Оценить параметры модели.
   
2. Существенна ли разница в торговом обороте магазинов: а) расположенных в центральном и периферийных районах города; б) частных и муниципальных?
   
3. Соответствуют ли остатки регрессии нормальному закону распределения?
   
4. Спрогнозировать значение торгового оборота муниципального магазина с торговой площадью 4000 м², расположенного в центральном районе города
   

Примерный график изучения дисциплины Эконометрика

№ лекции/ количество часов	Тема	Самостоятельная работа – теоретические вопросы, изучаемые после лекции	Самостоятельная работа - задания, выполняемые после лекции
1/2 часа	Тема 1. Введение. Эконометрика и эконометрическое моделирование.	1.Основные понятия и особенности эконометрического метода. 2.Типы экономических данных, используемых в эконометрических исследованиях: пространственные данные и временные ряды. 3.Специфика экономических данных. 4.Классификация эконометрических моделей. 5.Основные этапы построения эконометрических моделей.
1/2 часа	Тема 2. Корреляция. Парная регрессия.	1.Функциональные и стохастические типы связей. Ковариация, корреляция. 2.Анализ линейной статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции, проверка значимости. 3.Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции. 4.Понятия регрессионного анализа: зависимые и независимые переменные. 5.Предпосылки применения метода наименьших квадратов (МНК). 6.Свойства оценок метода наименьших квадратов (МНК). 7.Линейная модель парной регрессии. Оценка параметров модели с помощью метода наименьших квадратов (МНК).	Задача 1. Решение пунктов 1-2.
2/2 часа	Тема 2. Корреляция. Парная регрессия.	8.Показатели качества модели парной регрессии. 9. Анализ статистической значимости параметров модели парной регрессии. 10.Интервальная оценка параметров модели парной регрессии. 11.Проверка выполнения предпосылок МНК. 12.Интервалы прогноза по линейному уравнению парной регрессии.(Прогнозирование с применением уравнения регрессии). 13.Понятие и причины гетероскедастичности. Последствия гетероскедастичности. Обнаружение гетероскедастичности. 15.Нелинейная регрессия. Нелинейные модели и их линеаризация.	Задача 1. Решение пунктов 3-5.
2/2 часа	Тема 3. Множественная регрессия.	1.Модель множественной регрессии. Построение системы показателей (факторов). 2.Мультиколлинеарность. Последствия мультиколлинеарности. Способы обнаружения мультиколлинеарности. Способы избавления от мультиколлинеарности. 3.Отбор факторов при построении множественной регрессии. Процедура пошагового отбора переменных.
3/4 часа	Тема 3. Множественная регрессия.	4..Модель множественной регрессии. Выбор вида модели и оценка ее параметров. 5.Оценка параметров множественной регрессии методом наименьших квадратов (МНК). Свойства оценок МНК. 6.Понятие и причины автокорреляции остатков. Последствия автокорреляции остатков. Обнаружение автокорреляции остатков. 7.Проверка качества многофакторных регрессионных моделей. Оценка качества всего уравнения регрессии. 8.Проверка качества многофакторных регрессионных моделей. Коэффициент детерминации 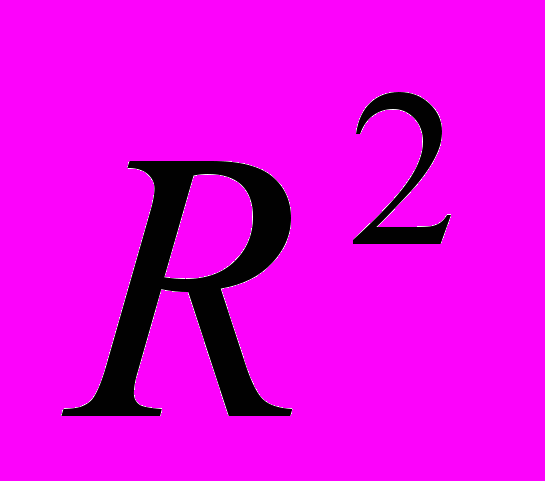. Скорректированный . 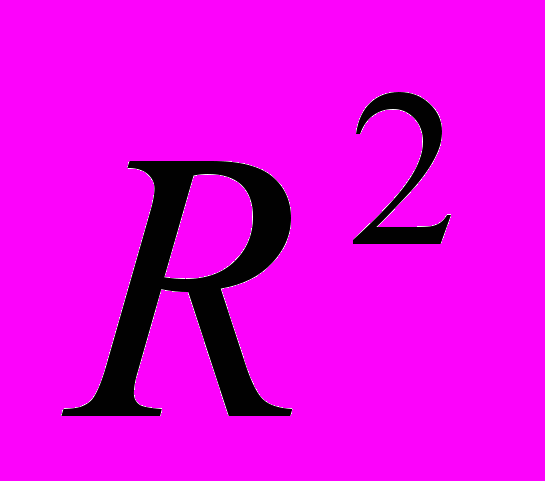Проверка гипотез с помощью t-статистик и F-статистик. 9.Оценка существенности параметров линейной регрессии. 10.Оценка влияния факторов на зависимую переменную (коэффициенты эластичности, бета коэффициенты). 11.Анализ экономических объектов и прогнозирование с помощью модели множественной регрессии. 12.Регрессионные модели с переменной структурой (фиктивные переменные).	Задача 1. Решение пунктов 6-7.
4/4 часа	Тема 4. Временные ряды.	Структура временных рядов экономических показателей. Требования, предъявляемые к исходной информации при моделировании экономических процессов на основе временных рядов. Основные этапы построения моделей экономического прогнозирования. Выявление и устранение аномальных наблюдений во временных рядах. Предварительный анализ временных рядов. Проверка наличия тренда. Предварительный анализ временных рядов. Сглаживание временных рядов. Предварительный анализ временных рядов. Вычисление количественных характеристик развития экономических процессов. Построение моделей кривых роста. Оценка параметров кривых роста с помощью метода наименьших квадратов (МНК). Проверка адекватности и оценка качества моделей прогнозирования. 10.Построение моделей. Адаптивны модели прогнозирования.	Задача 2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
Итого:
4 лекции/ 16 часов		Практические занятия на ПЭВМ – 4 часа	Контрольная работа – две задачи.
		Лабораторная работа – одна задача на ПЭВМ - 4 часа

Литература

Основная литература:

1. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. пособие – М.: Вузовский учебник, 2007-365 стр.
   
2. Орлова И.В. , Концевая Н. В., Филонова Е. С., Уродовских В. Н. Многомерный статистический анализ в экономических задачах: компьютерное моделирование в SPSS. (в электронном виде).
   
3. Методические указания по выполнению контрольной работы для самостоятельной работы студентов III курса специальности 080109 (060500) «Бухгалтерский учет, анализ и аудит», 060400 «Финансы и кредит» (второе высшее образование). - М.: ИНФРА-М; Вузовский учебник, 2007-72 стр.
   

Дополнительная литература:

1. Практикум по эконометрике: Учебное пособие / Под ред. Елисеевой И.И. - М.: Финансы и статистика, 2001,2002,2003,2004. - 192с

2. Орлова И.В.   Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL: Практикум: Учебное пособие / И. В. Орлова; ВЗФЭИ. - М.: Финстатинформ, 2000. - 136с.
   
3. Орлова И.В.   Экономико-математическое моделирование. Практическое пособие по решению задач / И. В. Орлова; ВЗФЭИ. - М.: Вузовский учебник, 2004. - 144с.
   
4. Малашенко В.М., Кокунов В.А., Трубников С.В. Эконометрическое моделирование: Учебное пособие. — Брянск: БГУ, 2007. — 158 с.
   
5. Сошникова Л.А., Тамашевич В.Н., Уебе Г., Шефер М. Многомерный статистический анализ в экономике: Учеб. Пособие для вузов/Под ред. проф. В.Н. Тамашевича.- М.: ЮНИТИ-ДАНА, 1999.-558 с.
   

Компьютерные обучающие программы (Web-сайт ВЗФЭИ)


КОПР3- Компьютерные обучающие программы для студентов 3-го курса:

- Эконометрика

Электронные материалы (Web-сайт ВЗФЭИ станмчка кафедры, сервер ВЗФЭИ)

Образцы решения типовых задач.