Задание Построение модели множественной регрессии для пространственных данных

Вид материала

Документы

Содержание Множественная регрессия

Подобный материал:

• Рабочая программа учебной дисциплины ф тпу 1- 21/01 «утверждаю», 156.29kb.
• Приближается время экзаменов в школе. Последние недели наиболее тревожное время у ученика, 761.34kb.
• Эконометрика, 104.66kb.
• Техническое задание на разработку, 373.09kb.
• К индекс ригидности эритроцитов, рассчитанный по уравнению Quemada, 167.24kb.
• Оптимальное распределение ресурсов на основе модели линейной временной регрессии, 27.03kb.
• «Построение сечений тетраэдра и параллелепипеда», 77kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.
• Проектирование базы данных, 642.58kb.
• Использование материалов радиолокационной космической съемки для иформационнного обеспечения, 147.26kb.

Задание 1. Построение модели множественной регрессии для пространственных данных.


Для этого задания каждый студент выбирает из предложенного файла не менее 50 наблюдений для построения моделей. В файле Квартиры.sta представлены данные о квартирах на вторичном рынке жилья в г. Минске за июль 2006 года. Названия и описания переменных приведены в таблице 1.

Таблица 1

Имя переменной	Описание
raion	Район расположения квартиры
komnat NKomnat	Число комнат(в том числе не смежных)
Var3	Адрес
Cena	Цена
PlOb	Общая площадь
PlochadZ	Площадь жилая
PlochadKukh	Площадь кухни
Etaz	Этаж расположения квартиры/число этажей
Type	Тип дома
GodPostr	Год постройки

Для выбранных данных необходимо построить модель зависимости стоимости жилья от ряда факторов, число и состав которых определяется студентом самостоятельно.

Обязательным является проверка качества построенной модели, заключающаяся в следующем:

• Проверка значимости коэффициентов регрессии;
  
• Проверка общего качества уравнения регрессии;
  
• Проверка остатков модели на наличие гетероскедастичности и автокорреляции;
  
• Проверка соответствия остатков нормальному распределению.
  

Решение.

Используем пакет Statistica 6.0, модуль Множественная регрессия.

Создадим новый документ с данными, введем число переменных – 3 и число регистров – 60. Введем наименования переменных и исходные данные.

В качестве зависимой переменной Cena выберем стоимость квартиры, в качестве независимых переменных возьмем: переменная PlochadZ – площадь жилья; переменная PlochadKukh – площадь кухни; NKomnat – число комнат.

Вызовем модуль Множественная регрессия. (Команда СтатистикаМножественная регрессия). Выберем переменные (кнопка (Variables). Зависимая (Dependent) – Cena; независимые (Independent) – PlochadZ, PlochadKukh, NKomnat.

Нажмем кнопку ОК в правом углу стартовой панели.

Появится окно результатов множественной регрессии.

Результаты множественной регрессии в численном виде представлены в табл. 1.2. и 1.3.

Таблица 1.2.




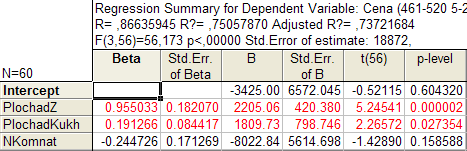
Таблица 1.3.




В первом столбце таблицы 1.2. даны значения коэффициентов beta — стандартизованные коэффициенты регрессионного уравнения, во втором — стандартные ошибки beta, в третьем – В – точечные оценки параметров модели.

Далее, стандартные ошибки для коэффициентов модели В, значения статистик t-критерия и т.д.

Из таблицы 1.2. мы видим, что оцененная модель имеет вид:

Cena = -3425 + 2205∙ Pl_Z + 1810∙ Pl_Kukh – 8023∙N_Kom (1.1)

(t) (-0,521) (5,245) (2,266) (-1,429)

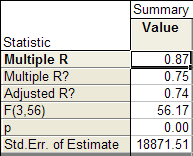
В верхней части таблицы 1.2. и в таблице 1.3. (а также в информационном окне) приведены следующие данные:

Коэффициент множественной корреляции Multiple R = 0,87;

Коэффициент детерминации R-square = 0,75;

Скорректированный на поте­рю степеней свободы коэффициент множественной детерминации Adjusted R² = 0,74;

Критерий Фишера F = 56,2;

Уровень значимости модели р < 0,000;

Стандартная ошибка оценки Std. Error of estimate = 18872.

Проанализируем данные множественной регрессии.

Табличное значение критерия Стьюдента, соответствующее доверительной вероятности  = 0,95 и числу степеней свободы v = n – m – 1 = 56; t_кр. = t_0,025;56 = 2,3.

Сравнивая расчетную t-статистику коэффициентов уравнения с табличным значением, заключаем, что будут значимые коэффициенты регрессии при переменных жилая площадь и площадь кухни. Коэффициент регрессии при переменной число комнат значимым не будет, так же не будет значима постоянная в уравнении регрессии.

Уравнение (1.2.) выражает зависимость стоимости квартиры Cena от площади жилья PlochadZ, площади кухни PlochadKukh, числа комнат Nkomnat. Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других.

Множественный коэффициент корреляции построенной модели (Multiple R) R = 0,87 высок, что говорит о сильной связи между исследуемыми факторами.

Коэффициент детерминации (R Square) R² = 0,75, что говорит о том, что 75% вариации переменной Cena объясняется вариацией переменных PlochadZ и PlochadKukh, Nkomnat, а на 25% приходятся на долю других неучтенных факторов.

Критическое (табличное) значение критерия Фишера для доверительной вероятности  = 0,95 и числа степеней свободы v₁ = 3 и v₂ = 56: F_кр. = F_0,05;3;56 = 2,769.

Расчетное значение критерия Фишера F = 56,17 превышает табличное значение критерия F_табл. = 2,769, что говорит о адекватности модели экспериментальным данным. Уровень значимости p = 0,000 показывает, что построенная регрессия значима при 0,000% уровне значимости.

Исследуем степень корреляционной зависимости между переменными. Для этого построим корреляционную матрицу. Чтобы корреляционная матрица была построена при множественной регрессии, нужно установить флажок в строке Review descriptive statistics, correlations matrix в окне Multiple Regressions.

Корреляционная матрица приведена в таблице 1.4.

Таблица 1.4.




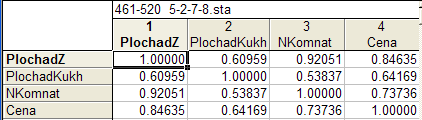
Из корреляционной матрицы видно, что наибольшее значение коэффициента корреляции наблюдается между переменными NKomnat и PlochadZ, но данные переменные являются объясняющими. Такая тесная связь между объясняющими переменными может свидетельствовать о мультиколлениорности.

Проведем анализ остатков от регрессии.

Остатки представляют собой разности между наблюдаемыми значениями и модельными, то есть значениями, подсчитанными по модели с оцененными параметрами.

Проверим остатки на наличие автокорреляции. Для этого вычислим статистику Дарбина-Уотсона (Darbin-Watson Stat). Результаты вычисления статистики Дарбина-Уотсона приведены в табл. 1.5.

Таблица 1.5.




Из табл. 1.5 определяем наблюдаемое значение критерия Дарбина-Уотсона:

DW = 1,552.

По таблице приложения 4 [1] определяем значащие точки d_L и d_U для 5% уровня значимости.

Для m = 3 и n = 60 d_L = 1,48; d_U = 1,689.

Так как d_L < DW < d_U (1,48 < 1,552 < 1,689), то мы можем не утверждать, что в модели отсутствует автокорреляция остатков, но и не можем утверждать присутствие автокорреляции, так как значения DW попали в зону неопределенности критерия.

Для проверки наличия гетероскедастичности воспользуемся тестом Уайта. Стоим модель регрессии между квадратами остатков модели и квадратами значений объясняющих переменных:

Е² =a+ b₁∙ Pl_Z + b₁₁∙ Pl_Z ² + b₂∙ Pl_K + b₂₂∙ Pl_K ² + b₃∙ N_Kom + b₃₃∙ N_Kom ²


Результаты множественной регрессии в численном виде представлены в табл. 1.6. и табл. 1.7.

Таблица 1.6.



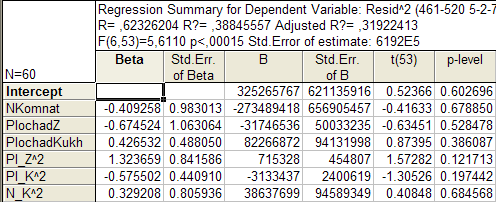
Таблица 1.7.



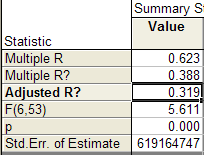
Расчетное значение критерия Фишера F = 5,611 превышает табличное значение критерия F_табл. = 2,275, что говорит о присутствии в модели гетероскедастичности.

Проверим соответствие остатков нормальному распределению, для этого строим гистограмму остатков.




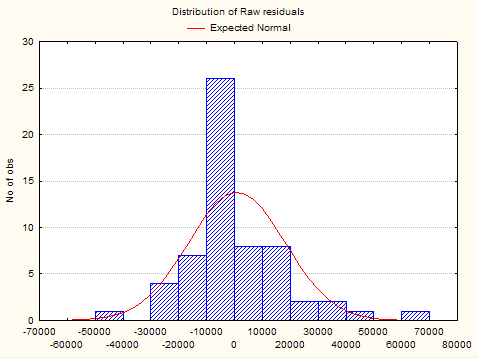
Рис. 1.1. Гистограмма остатков.


Как видно из рисунка вид гистограммы практически повторяет кривую нормального распределения, что позволяет предположить нормальность остатков случайных отклонений.

Вывод:

Построенное уравнении регрессии (1.1) не может быть использовано в практических целях, так как оно имеет следующие недостатки: в модели присутствует гетероскедастичность, не все коэффициенты регрессии статистически значимы.

Перечисленные недостатки могут привести к ненадежности оценок, выводы по t- и F- статистикам, определяющим значимость коэффициентов регрессии и детерминации, возможно, неверны.