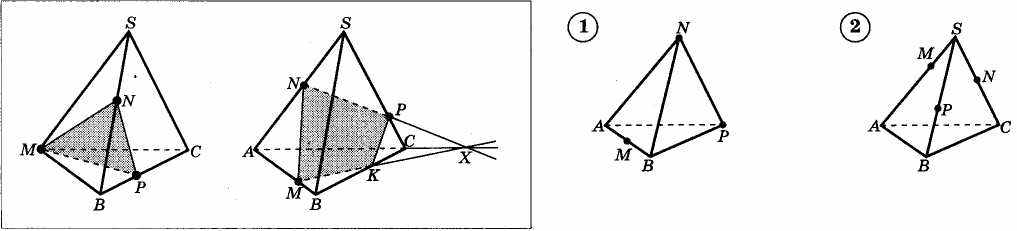
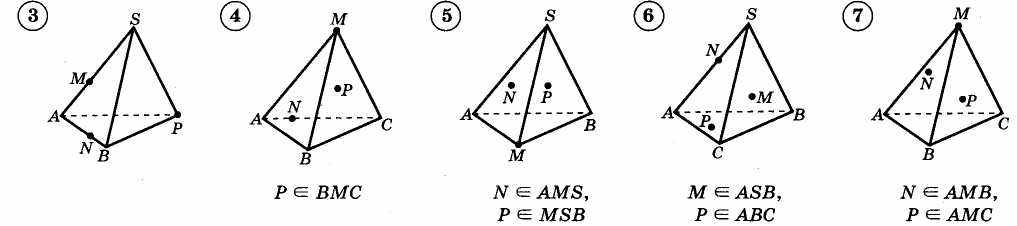
«Построение сечений тетраэдра и параллелепипеда»

Вид материала

Урок

Содержание Техническое обеспечение Структура урока. 1)Приветствие. Организационный момент. 4) Актуализация опорных знаний. 5) Практическая работа на построение сечений с последующей взаимопроверкой. 6) Взаимопроверка. 7) Домашнее задание. 8) Рефлексия. 9) Итог урока.

Подобный материал:

• 2 Гл. I. Построение сечений многогранников на основе системы аксиом стереометрии, 248.63kb.
• «Решение задач на построение сечений многоугольников», 72.88kb.
• Кольцов Михаил Петрович Государственное учреждение средняя школа №41 города Астаны, 51.47kb.
• Лебедева Татьяна Владимировна, учитель истории и обществознания моу новогоркинская, 20.69kb.
• «Объем прямоугольного параллелепипеда» в ходе, 67.71kb.
• Лектор: доц. Педиков, 76.4kb.
• Лектор: доц. Педиков, 63.98kb.
• Шейчекова Марина Евгеньевна, 10А класс Научный Кулигина Анна Леонидовна, учитель информатики, 18.75kb.
• Антонова Ирина Игоревна, 233.92kb.
• И в срок Содержание Введение Глава Одномерный полюсный метод Ньютона Построение метода, 188.07kb.

Урок

Тема: « Построение сечений тетраэдра и параллелепипеда».


Предмет: геометрия

Класс: 10

Используемые педагогические технологии:

технология проектного обучения, информационные технологии.

Тема урока: Построение сечений тетраэдра и параллелепипеда

Тип урока: урок закрепления и развития знаний.

Формы работы на уроке: фронтальная, индивидуальная

Список используемых источников и программно-педагогических средств:

1. Л.С. Атанасян. Геометрия. 10-11 классы,- М: Просвещение, 2006г.
   
2. В. Н. Литвиненко. Задачи на развитие пространственных представлений. Книга для учителя. - М.: Просвещение, 1991.
   
3. Г. Прокопенко. Методы решения задач на построение сечений многогранников. 10 класс. ЧПГУ, г. Челябинск. Еженедельная учебно-методическая газета "Математика" 31/2001.
   
4. А. Мордкович. Семинар девятый. Тема: Построение сечений многогранников (позиционные задачи). Еженедельное приложение к газете "Первое сентября". Математика. 3/94.
   
5. Мультимедийный интерактивный курс "Открытая математика. Стереометрия." Физикон
   
6. «Живая геометрия»
   

Цели:

Образовательные:

Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед).

Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат.

Отработать навыки решения задач на построение сечений многогранников.

Развивать графическую культуру и математическую речь.

Формировать навыки использования компьютерных технологий на уроках геометрии.


Развивающие:

Развивать познавательный интерес учащихся.

Формировать и развивать у учащихся пространственное воображение.


Воспитательные:

Воспитывать самостоятельность, аккуратность, трудолюбие.

Воспитывать умения работать индивидуально над задачей.

Воспитывать волю и настойчивость для достижения конечных результатов.


Техническое обеспечение:

Компьютер с установленными программами «Живая геометрия», Power Point, мультимедиапроектор.


Раздаточный материал:

Бланки-карточки с заданиями для практической работы, бланки-карточки с ответами для взаимопроверки, опоры – памятки, презентация по теме «Аксиомы стереометрии, следствия из них», презентация ученика «Построение сечений параллелепипеда», цветные карандаши.


Структура урока.

1.	Приветствие. Организационный момент.	1 мин
2.	Постановка цели и задачи урока.	2 мин
3.	Повторение изученного материала с использованием презентации.	5 мин
4.	Актуализация опорных знаний.	12мин
5.	Практическая работа на построение сечений.	15мин
6.	Взаимопроверка.	5 мин
7.	Домашнее задание	2 мин
8.	Рефлексия.	2 мин
9.	Итоги	1 мин

Ход урока:

1)Приветствие. Организационный момент.


2) Постановка цели и задачи урока.

- Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений являет­ся основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью.

На предыдущих уроках мы с вами познакомились с аксиомами стереометрии, следствиями из аксиом и с теоремами о параллельности прямых и плоскостей в пространстве. Мы рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами повторим геометрические утверждения, позволяющие сформулировать правила построения сечений. А также научимся применять эти знания при решении задачи на построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани.

3) Повторение изученного материала с использованием презентации.

- Давайте повторим некоторые вопросы теории.

• Что такое секущая плоскость?
  
• Как можно задать секущую плоскость?
  
• Что такое сечение тетраэдра (параллелепипеда)?
  
• Какие многоугольники мы получали при построении сечений тетраэдра?
  
• А какие многоугольники мы можем получить при построении сечений параллелепипеда?
  
• Давайте повторим аксиомы стереометрии, следствия из них и способы задания плоскости (презентация 1, слайды 1-10)
  

4) Актуализация опорных знаний.

Презентация ученика «Построение сечений параллелепипеда».


- Теперь давайте вспомним алгоритм построения сечения тетраэдра на примере двух задач (презентация 1, слайды 11-12). (построение комментируется пошагово учителем).

- Пащенко Алексей с помощью своей презентации напомнит нам об алгоритмах построения сечений параллелепипеда (презентация 2, слайды 1-5) (ученик демонстрирует слайды, комментируя последовательность построения)

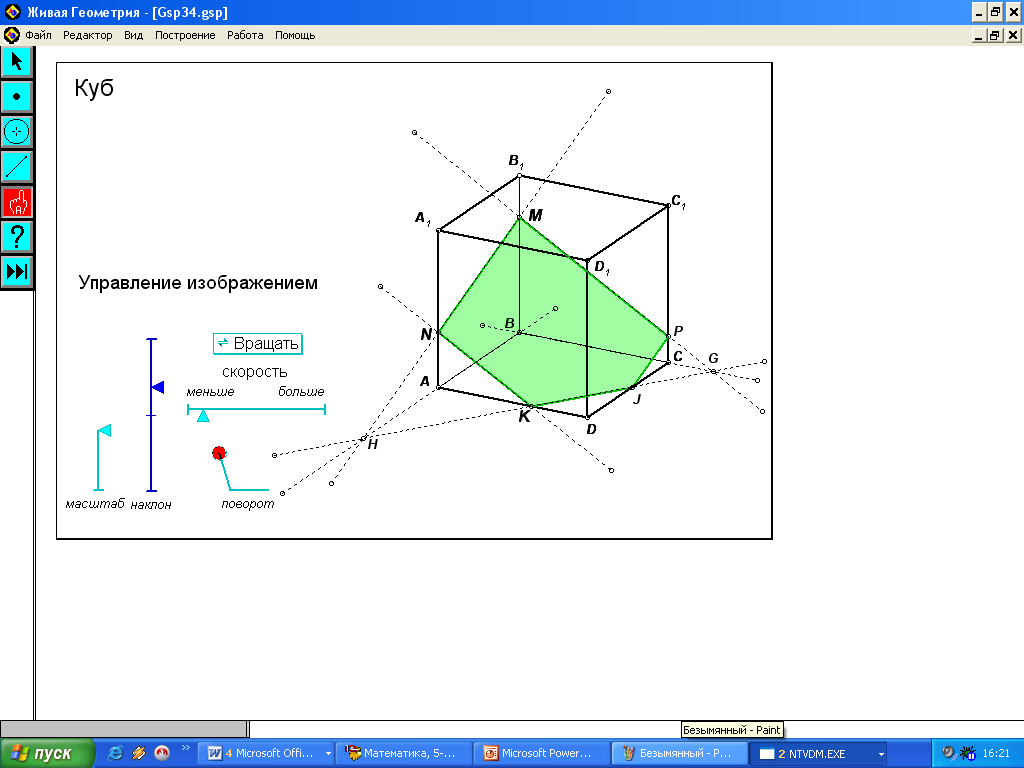- А сейчас с помощью программы «Живая геометрия» мы «оживим» пространство на примере сечения куба. Программа позволяет вращать многогранник, что позволит вам увидеть сечение со всех сторон.


5) Практическая работа на построение сечений с последующей взаимопроверкой.


Ученики получают бланки-карточки для практической работы (приложение 1) Малая наполняемость класса (5 человек), достаточно большое количество посадочных мест, а также последующая взаимопроверка позволяет выполнение работы одного варианта.

На бланках также расположено несколько различных примеров построения сечений. У каждого ученика на парте опора-памятка (приложение 2).

Практическая работа состоит из 12 заданий разного уровня сложности. 5-7 правильно выполненных заданий – оценка «3», 8-10 заданий - оценка «4», 11-12 заданий - оценка «5»

6) Взаимопроверка.


Ученики меняются листами с практической работой, получают для проверки бланки с ответами (приложение 3). Проверяют работы друг друга, отмечая правильно построенные сечения.


7) Домашнее задание.

- В качестве домашнего задания я попрошу вас решить задачи, аналогичные задачам в практической работе, но на построение сечений тетраэдра. Каждому предлагается выполнить по 4 задания (приложение 4) Задания имеют три уровня сложности.


8) Рефлексия.


- Итак, подведем итог, чему мы научились сегодня на уроке?

- Какие теоретические положения нам часто приходилось использовать?

- Какие ошибки были допущены при решении задач? Как вы их устранили?

- Кому приходилось возвращаться к задаче несколько раз?

- Где в практической деятельности вам пригодится сегодняшний урок?

На этапе рефлексии деятельности учащиеся анализируют, где и почему были допущены ошибки, каким способом они были исправлены, повторяют алгоритмы, вызвавшие затруднения, оценивают свою деятельность на уроке.


9) Итог урока.


В завершение урока учащиеся с помощью учителя фиксируют степень соответствия поставленной цели и результатов деятельности. Выставляются оценки.






















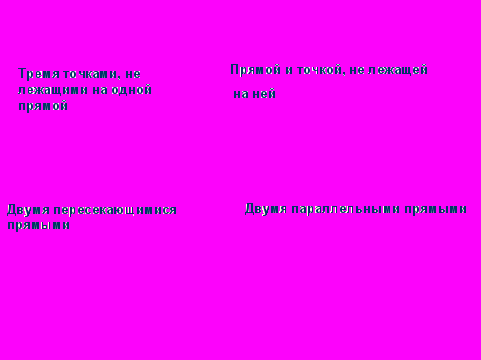
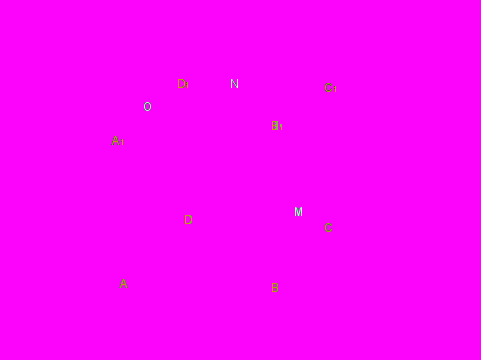
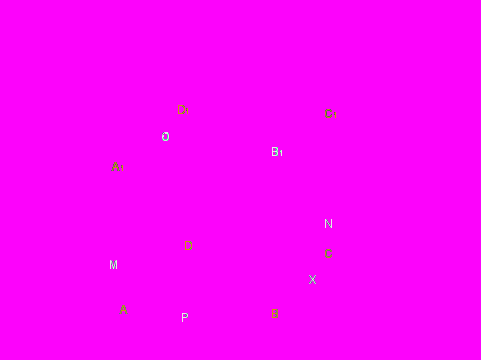
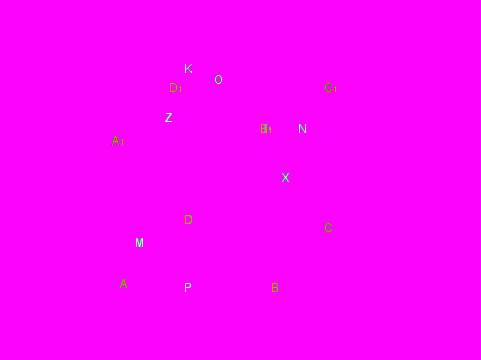
Практическая работа по построению сечений параллелепипеда. Приложение 1










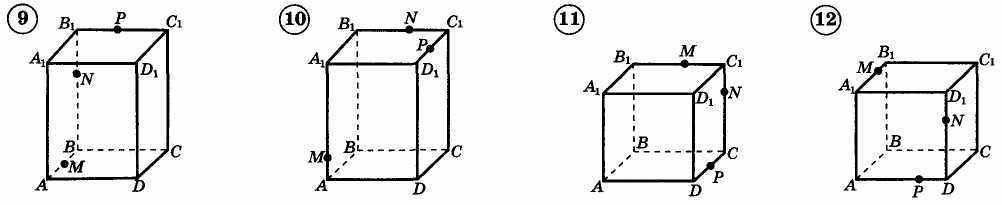
Приложение 2

Опора-памятка

• Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и причем только одна.
  
• Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
  
• Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
  

Следствия из аксиом:

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
   
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
   

Способы задания плоскости:

           


       


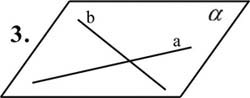
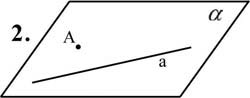
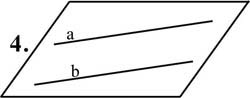
Приложение 3

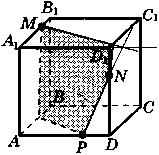
Ответы к практической работе.





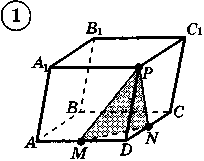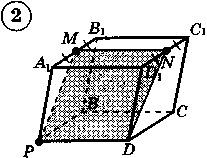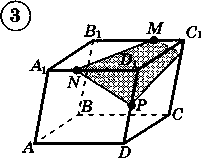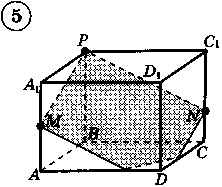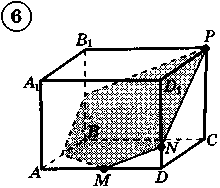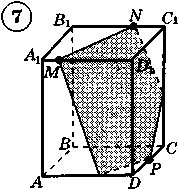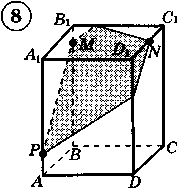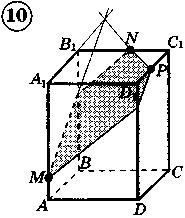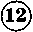Приложение 4