Выбор кривой роста для прогнозирования

Вид материала

Лабораторная работа

Содержание Исходные данные=трендсезонностьцикличностьнерегулярность Скользящее среднее=трендцикличность

Подобный материал:

• Альтернативные подходы к измерению бедности в регионах России, 36.92kb.
• Чем цифровое представление сигналов отличается от аналогового?, 443.31kb.
• Каждая точка нашей кривой сравнивается с такой же точкой эмпирической кривой, 32.66kb.
• Международная научно-практическая конференция «Выбор пути: совместная ответственность, 103.12kb.
• Нейронные сети как механизм представления лексико-семантической информации, 376.06kb.
• Парадигма экономического роста в условиях открытой экономики аннотация, 124.15kb.
• Методики прогнозирования потребности в рабочей силе для региона, 171.64kb.
• Морское наслаждение … Болгария!!!, 948.86kb.
• Программа дисциплины ''Полюса и зоны роста мировой экономики'' для направления 080100., 62.74kb.
• Курс «Методы прогнозирования и оценки мпи» (для гин) Лекция, 100.16kb.

Лабораторная работа №4:

Выбор кривой роста для прогнозирования


Используя данные из лабораторной работы №3, необходимо выбрать такое математическое уравнение зависимости объёмов продаж автомобилей от фактора времени, которое бы наиболее точно характеризовало развитие данного показателя.

Для построения линии тренда необходимо выделить на диаграмме временной ряд и выбрать в контекстном меню (вызывается щелчком правой клавиши мыши) команду Добавить линию тренда. Будет вызвано диалоговое окно Линия тренда, содержащее вкладку Тип, на которой задаётся тип тренда: 1) линейный, 2) логарифмический, 3) полиномиальный (от 2-ой до 6-ой степени включительно), 4) степенной, 5) экспоненциальный, 6) скользящее среднее (с указанием периода сглаживания от 2 до 15).





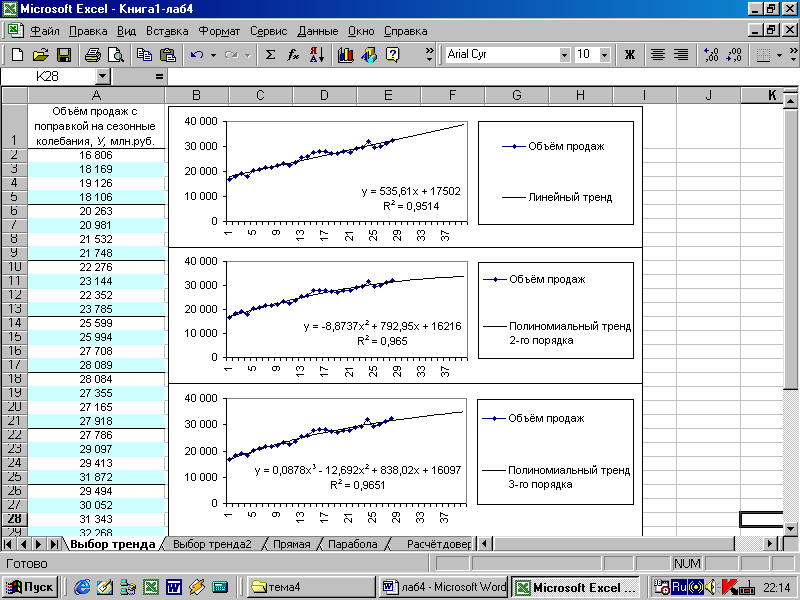
Рисунок 1 - Линейный, полиномиальные тренды 2-го и 3-го порядка хорошо описывают развитие объёма продаж автомобилей, поэтому могут использоваться при прогнозировании


Вкладка Параметры предназначена для задания параметров тренда:

1. имя тренда - можно выбрать автоматическое (Excel именует линию тренда, основываясь на выбранном типе тренда и ряде динамики, с которым она ассоциирована) или другое (вводится уникальное имя тренда);
   
2. прогноз вперед на – указывается количество периодов, на которое линия тренда экстраполируется в будущее, в данном случае следует ввести число 12;
   
3. показывать уравнение на диаграмме – чтобы появилось уравнение регрессии, необходимо поставить флажок;
   
4. поместить на диаграмму величину достоверности аппроксимации (R2) – чтобы появилось значение коэффициента детерминации, необходимо поставить флажок.
   

Критерием выбора линии тренда является величина коэффициента детерминации R² – чем она ближе к 1, тем лучше выбранная зависимость сглаживает эмпирические данные.





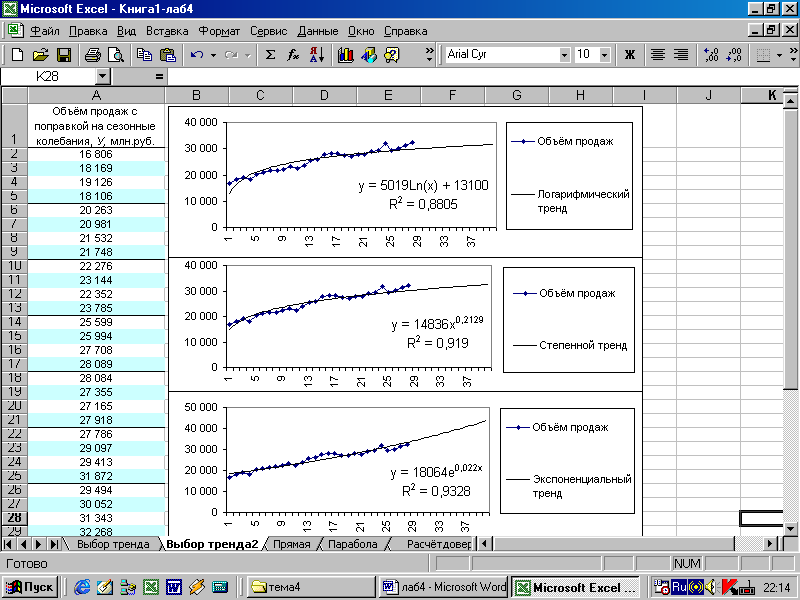
Рисунок 2 - Логарифмический, степенной и экспоненциальные тренды также могут использоваться при прогнозировании, но, судя по критерию R², они менее точно описывают объемы продаж автомобилей, чем линейный и полиномиальные тренды на рисунке 1.

На рисунке 2 отражены логарифмический, степенной и экспоненциальный тренды. Они менее точно описывают динамику изменения эмпирических (фактических) данных об объёмах продаж автомобилей, поэтому не будут использоваться при прогнозировании.

Чтобы выбрать для прогнозирования один из трёх оставшихся трендов (линейного, полиномиальных 2-го и 3-го порядка) необходимо более детально проанализировать исходный динамический ряд.

Общая зависимость между компонентами временного ряда может быть представлена следующей мультипликативной моделью:

Исходные данные=трендсезонностьцикличностьнерегулярность

Ранее были выделены такие компоненты временного ряда, как тренд и сезонные колебания. Остались без анализа циклическая и нерегулярная (случайная) компоненты. Циклическую компоненту можно выделить, выразив её из следующей зависимости:

Скользящее среднее=трендцикличность

Циклическая компонента находится делением скользящих средних на значения, рассчитанные по уравнению тренда.

Столбцы А, В и С можно взять из предыдущей лабораторной работы. В диапазон ячеек D2:D29 введите формулу:


=ТЕНДЕНЦИЯ(В2:В29;А2:А29).


Ячейку Е4 рассчитаем по формуле:


=С4/D4 (Результат: 0,9657)


и скопируем в остальные ячейки столбца Е кроме E2, Е3, Е28, Е29. В ячейки E2, Е3, Е28, Е29 введём число 1, так как отсутствуют соответствующие значения в столбце С.

Исключение цикличности в столбце F осуществляется следующим образом.

В ячейку F2 введём:


=В2/Е2 (Результат: 16806)


В остальные ячейки столбца F формулу можно скопировать.

После того, как из исходных данных удалены сезонная и циклическая компоненты, в ряду остаются тренд и нерегулярная (случайная) компонента. На диаграмме справа (рисунок 3) для построения нового тренда использовался столбец F.

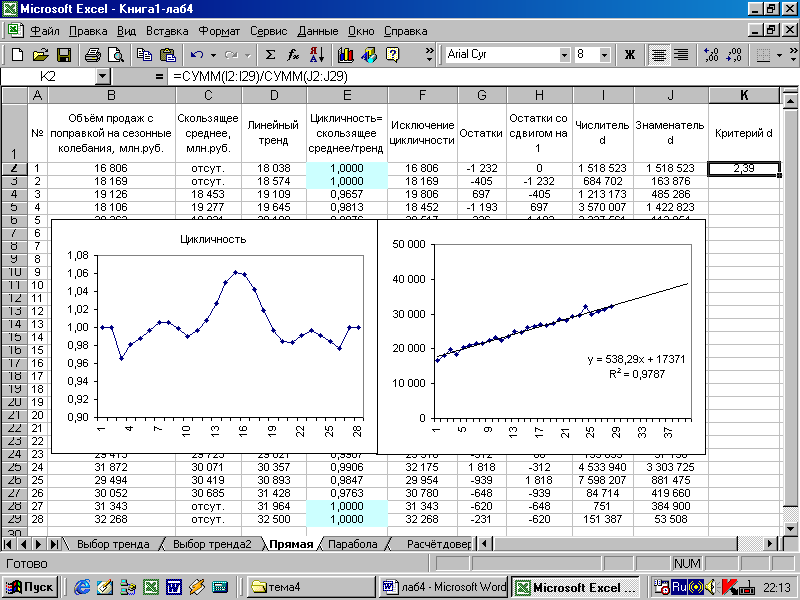
Рисунок 3 - После исключения из исходного динамического ряда циклической компоненты (диаграмма слева) линейный тренд более точно стал описывать ряд (оцените изменение критерия R² на диаграмме справа и на рисунке 1). Адекватность тренда, сезонной и циклической компонент характеризуется критерием d (Дарбина-Уотсона)

В столбце G содержатся остатки, то есть нерегулярная компонента. Исключим из ряда тренд, введя следующую формулу в ячейку G2:


=F2-D2 (Результат: -1232)


Остальные ячейки столбца G скопируем.

Аналогичные расчёты проведём и для полиномиального тренда 2-го порядка (параболы). При расчёте столбца D будем использовать формулу, полученную при построении линии тренда (левая диаграмма на рисунке 4).





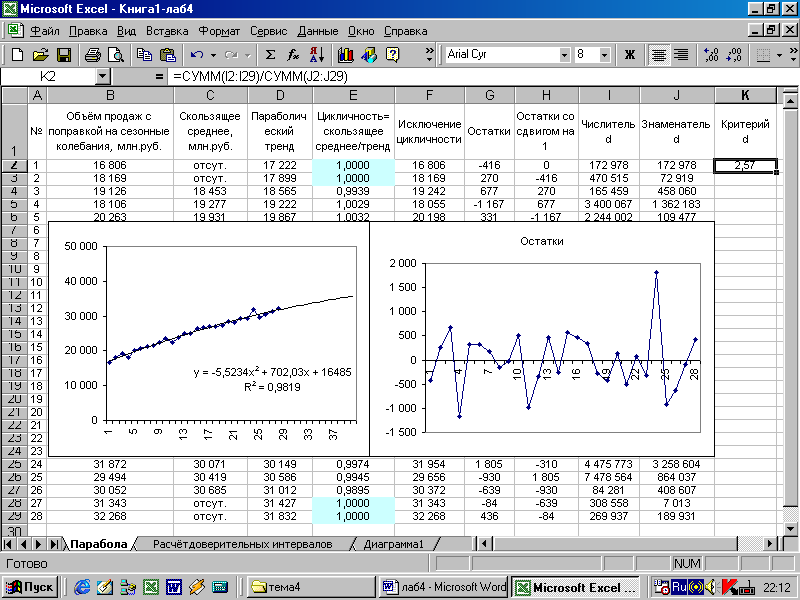
Рисунок 4 - После исключения из исходного динамического ряда циклической компоненты параболический тренд более точно стал описывать ряд (оцените изменение критерия R² на диаграмме слева и рисунке 1). Диаграмма справа характеризует случайность остатков.


В ячейку D2 введём формулу:


=16534+692,83*А2-5,2307*А22 (Результат 17312).


Остальные ячейки столбца D скопируем. Обратите внимание, что при расчёте параболического тренда используются округлённые значения параметров, что может вызвать несоответствие ваших расчётов с теми, которые приведены на рисунке 4.

Модель временного ряда адекватна описываемому процессу, ес­ли значения остаточной компоненты удовлетворяют свойствам случайно­сти, независимости, а также случайная компонента подчиняется нормаль­ному закону распределения.

При правильном выборе вида тренда отклонения от него будут но­сить случайный характер. Это означает, что изменение остаточной случай­ной величины не связано с изменением времени. Таким образом, про­веряется гипотеза о зависимости последовательности значений остатков от време­ни, или, что то же самое, о наличии тенденции в ее изменении.

Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок. Наи­более распространенным критерием проверки на наличие или отсутствие в остатках автокорреляции является критерий d (Дарбина-Уотсона), который определяется по фор­муле:



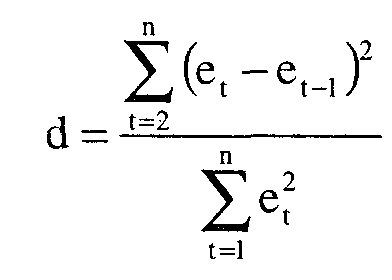
Если в значениях e_t (остатках в период t) имеется силь­ная положительная автокорреляция, то величина d=0, в случае силь­ной отрицательной автокорреляции d=4. При отсутствии автокорре­ляции d=2.

На рисунках 3 и 4 в столбцах G-K производится расчёт критерия Дарбина –Уотсона.

Столбец Н содержит те же значения, что и столбец G, но со сдвигом на одну ячейку вниз. Введём следующие формулы в ячейку I2:


=(G2-H2)2 (Результат для линейного тренда: 1 518 523),

(Результат для параболического тренда: 256 238);


в ячейку J2:


=G22 (Результат для линейного тренда: 1 518 523), (Результат для параболического тренда: 256 238);


Остальные ячейки столбцов I и J скопируем.

Ячейка К2 рассчитывается по формуле:


=СУММ(I2:I29)/СУММ(J2:J29) (Результат для линейного тренда: 2,39),

(Результат для параболического тренда: 2,58).


Полученные значения необходимо сравнить с табличными при 95% уровне вероятности и сделать вывод о наличии или отсутствии в остатках автокорреляции. В нашем случае при линейном тренде d=2,39 (автокорреляция отсутствует), а при параболическом d=2,58 (автокорреляция присутствует). Поэтому, нельзя использовать параболу для прогнозирования - она не адекватна реальному ходу развития анализируемого процесса.

Другой не менее важной проблемой прогнозирования является расчёт доверительных интервалов точечного прогноза. На рисунке 5 представлен расчёт доверительных интервалов для прогнозируемого периода (периода упреждения), составившего 12 кварталов 2003-2005 гг.





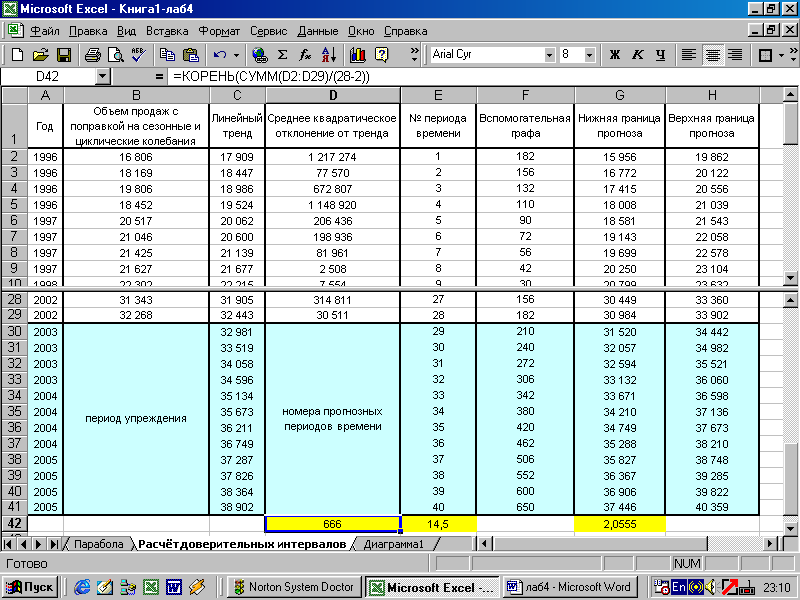
Рисунок 5 - Ширина доверительного интервала при прогнозировании по линейному тренду зависит от среднего квадратического отклонения эмпирических данных от тренда, t-критерия Стьюдента, длины временного ряда и периода упреждения


Из столбца F (исключение цикличности) рисунке 3 скопируем значения объёма продаж с поправкой на сезонные и циклические колебания в рисунок 5. Для этого воспользуемся следующим приёмом:

1. выделим диапазон F2:F29 в рабочем листе «Прямая» (рисунок 3);
   
2. в контекстном меню (правая клавиша мыши) выберем КопироватьСпециальная вставкаЗначения;
   
3. перейдём на лист «Расчёт доверительных интервалов» (рисунок 5) и вставим скопированные значения в диапазон ячеек В2:В29.
   

Новые значения столбца С (ячейки С30:С41) рассчитываются с помощью функции:


=ТЕНДЕНЦИЯ(B2:B29;E2:E29;E30:E41).


Ячейка D2 рассчитывается по формуле:


=(B2-C2)2 (Результат: 1 217 274),


и копируется в оставшийся диапазон D3:D29.

Среднее квадратическое отклонение от тренда, характеризующее колеблемость индивидуальных значений ряда от тренда, вычисляется в ячейке D42 по формуле:


=КОРЕНЬ(СУММ(D2:D29)/(28-2)) (Результат: 666).


В ячейке Е42 находится среднее значение номера временного периода по формуле:


=СРЗНАЧ(E2:E29) (Результат: 14,5).


Ячейка F2 рассчитывается по формуле:


=(E2-$E$42)2 (Результат: 182),


и копируется в диапазон F3:F41.


В ячейке G42 содержится формула:


=СТЬЮДРАСПОБР(0,05;26) (Результат: 2,0555),


по которой рассчитывается t-критерий Стьюдента при 5% уровне значимости (95% уровне вероятности) и 26 (28-2=26) степенях свободы. Две степени свободы были потеряны из-за того, что в уравнении прямой содержится 2 параметра.

Нижняя граница прогноза рассчитывается в ячейке G2 по формуле:


=C2-$D$42*$G$42*КОРЕНЬ(1+1/28+((E2-$E$42)2)/СУММ($F$2:F2))

(Результат: 15956).


Верхняя граница прогноза рассчитывается в ячейке H2по формуле:


=C2+$D$42*$G$42*КОРЕНЬ(1+1/28+((E2-$E$42)2)/СУММ($F$2:F2))

(Результат: 19862).


Оставшиеся ячейки в столбцах G и H копируются.

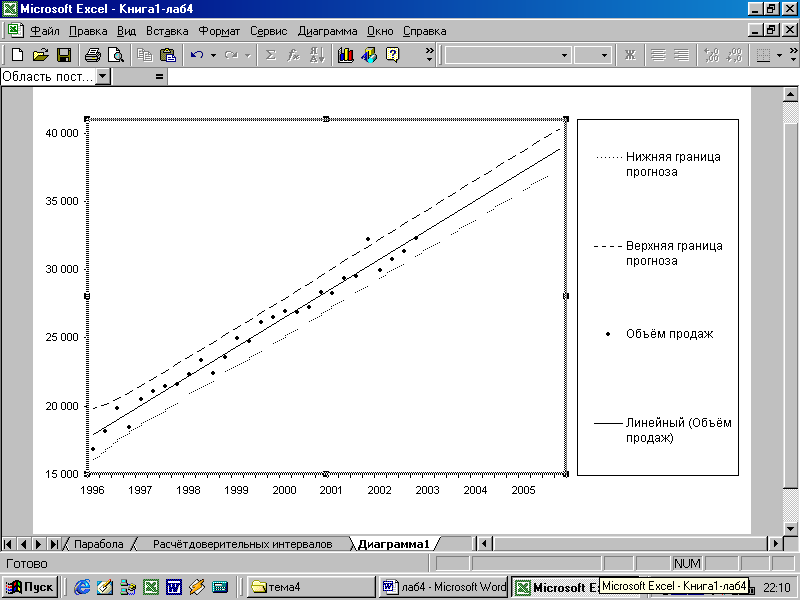
Рисунок 6 - Прогнозируемые значения объёма продаж автомобилей с 95% уровнем вероятности будут сосредоточены между верхней и нижней границами прогноза. Одна из точек фактического объёма продаж находится выше верхней границы прогноза, что подчёркивает вероятностный характер прогнозирования

На рисунке 6 отражены верхняя и нижняя границы прогнозов, линия тренда и ряд объёмов продаж автомобилей с поправкой на сезонные и циклические колебания.