Лекция №7
| Вид материала | Лекция |
- «Социальная стратификация и социальная мобильность», 46.19kb.
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
- Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
- Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
- Тема Лекция, 34.13kb.
- Лекция посвящена определению термина «транскриптом», 219.05kb.
- А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
Лекция № 7
Определение динамических характеристик промышленных объектов по результатам пассивного эксперимента
Пассивные методы экспериментального определения динамических характеристик промышленных объектов основаны на теории случайных процессов и заключаются в определении и обработке статистических характеристик сигналов на входе и выходе объекта. В общем случае задача определения динамических характеристик объектов по результатам пассивного эксперимента решается в два этапа:
- на первом этапе определяются статистические характеристики случайных процессов, действующих на объект;
- на втором этапе по полученным характеристикам рассчитываются динамические характеристики исследуемого объекта.
Большинство пассивных методов экспериментального исследования динамических характеристик объектов (систем) основано на предположении, что входные и выходные сигналы в них являются стационарными эргодическими стохастическими процессами, а сами объекты (системы) - линейными. Данное предположение позволяет определить статистические характеристики входных и выходных сигналов по достаточно длинной их реализации за некоторый промежуток времени T.
Случайным (стохастическим) процессом называется функция времени одной или нескольких физических величин, изменяющихся случайным образом.
Свойство стационарности случайного процесса означает, что его статистические характеристики не изменяются во времени, то есть:
- его математическое ожидание постоянно во времени -
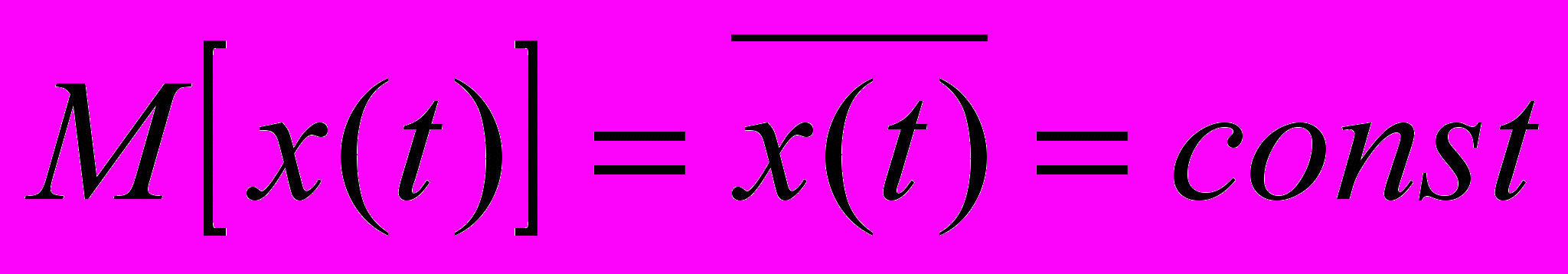 ,
, - корреляционная функция, определяющая зависимость между значениями случайного процесса, разнесенными во времени на некоторое
 , (называемая также автокорреляционной функцией) зависит только от
, (называемая также автокорреляционной функцией) зависит только от  и не зависит от самих сравниваемых моментов времени t1 и t2 -
и не зависит от самих сравниваемых моментов времени t1 и t2 - 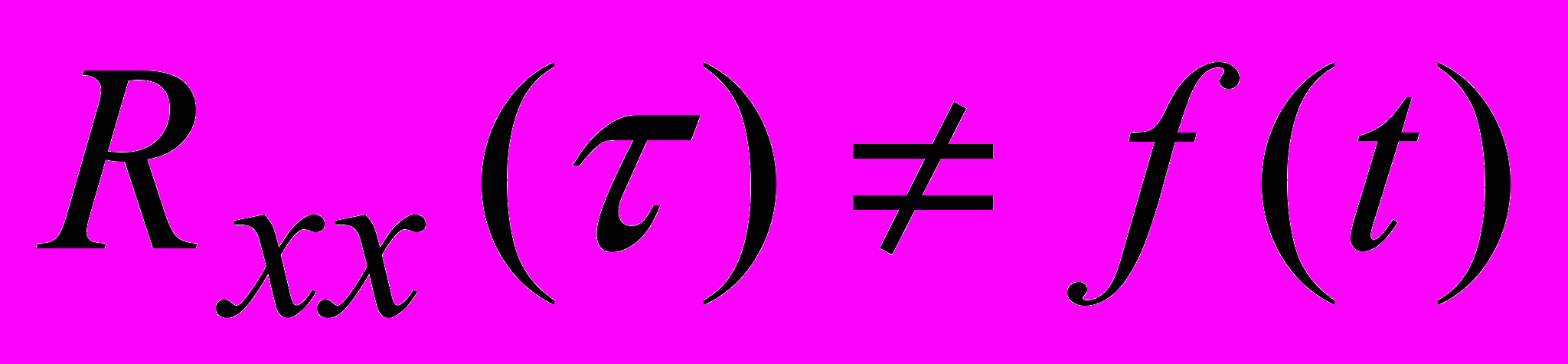 .
.Эргодическая гипотеза состоит в предположении, что у стационарного случайного процесса средние по времени такие же, как и средние по ансамблю. То есть статистические свойства ансамбля случайных процессов от идентичных источников, поступающих на входы n различных объектов, идентичны статистическим свойствам ансамбля случайных процессов от идентичных источников, поступающих на вход одного объекта в течении некоторых следующих друг за другом периодов времени. Следствием этой гипотезы является возможность определения статистических характеристик объекта как путем обработки одной достаточно длинной во времени реализации случайного процесса, так и путем обработки множества независимых реализаций случайного процесса для фиксированного момента времени. Необходимым и достаточным условием эргодичности стационарного случайного процесса практически является -
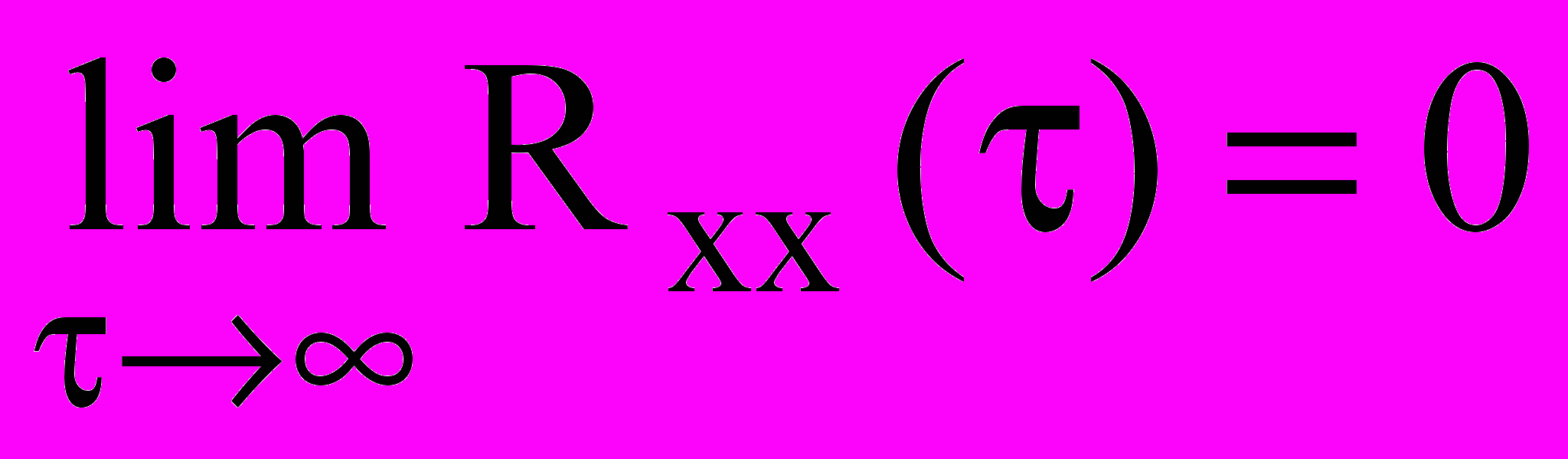 .
.Исходя из приведенных положений, применительно к исследованию динамических характеристик промышленных объектов (систем) корреляционную функцию входного воздействия можно описать выражением:
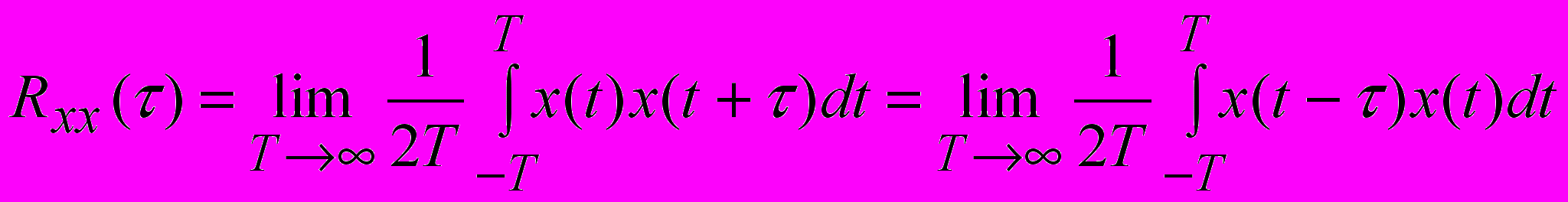 , (1)
, (1)где 2Т – интервал времени, на котором производится усреднение произведения
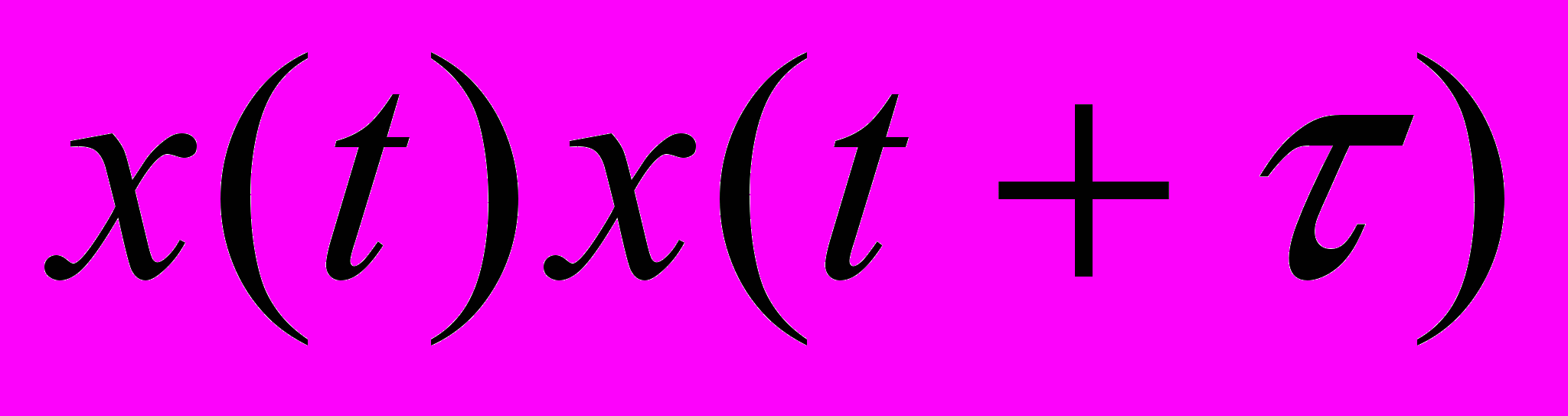 ;
; - величина сдвига между перемножаемыми значениями входного сигнала.
- величина сдвига между перемножаемыми значениями входного сигнала.Из выражения (1) следуют основные свойства корреляционной функции стационарного эргодического случайного процесса:
-
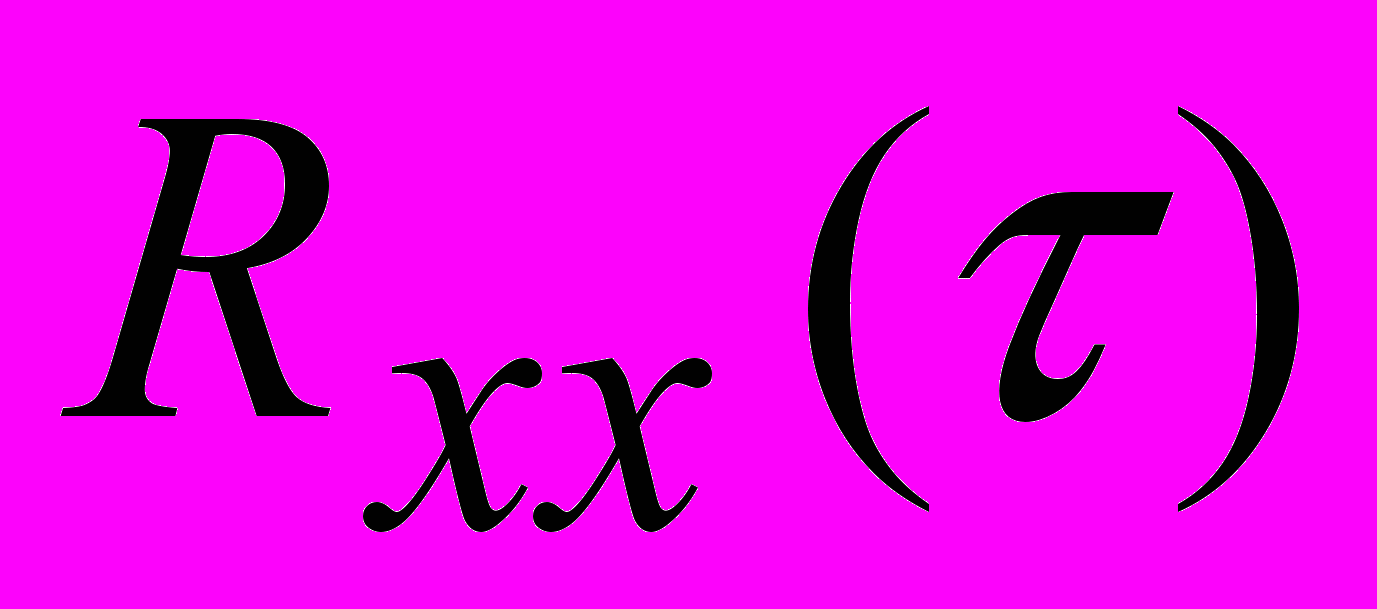 является четной функцией -
является четной функцией - 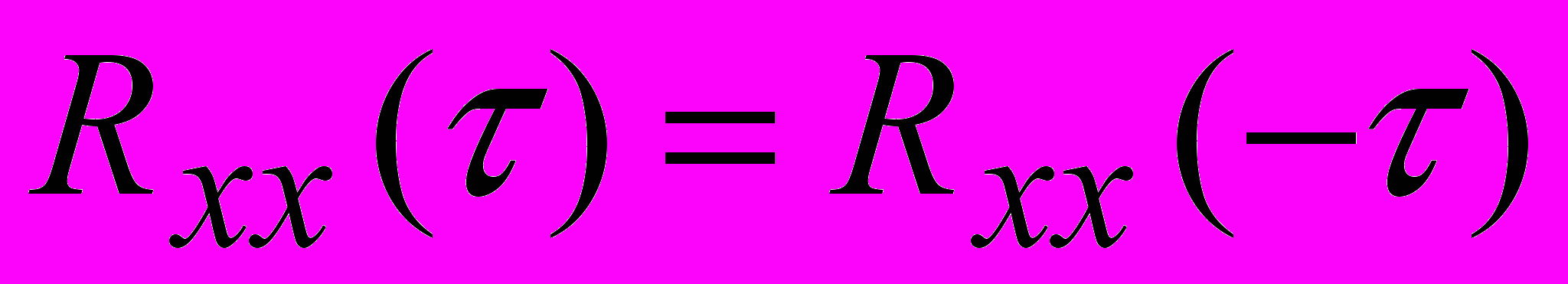 ;
;- наибольшие значения функция
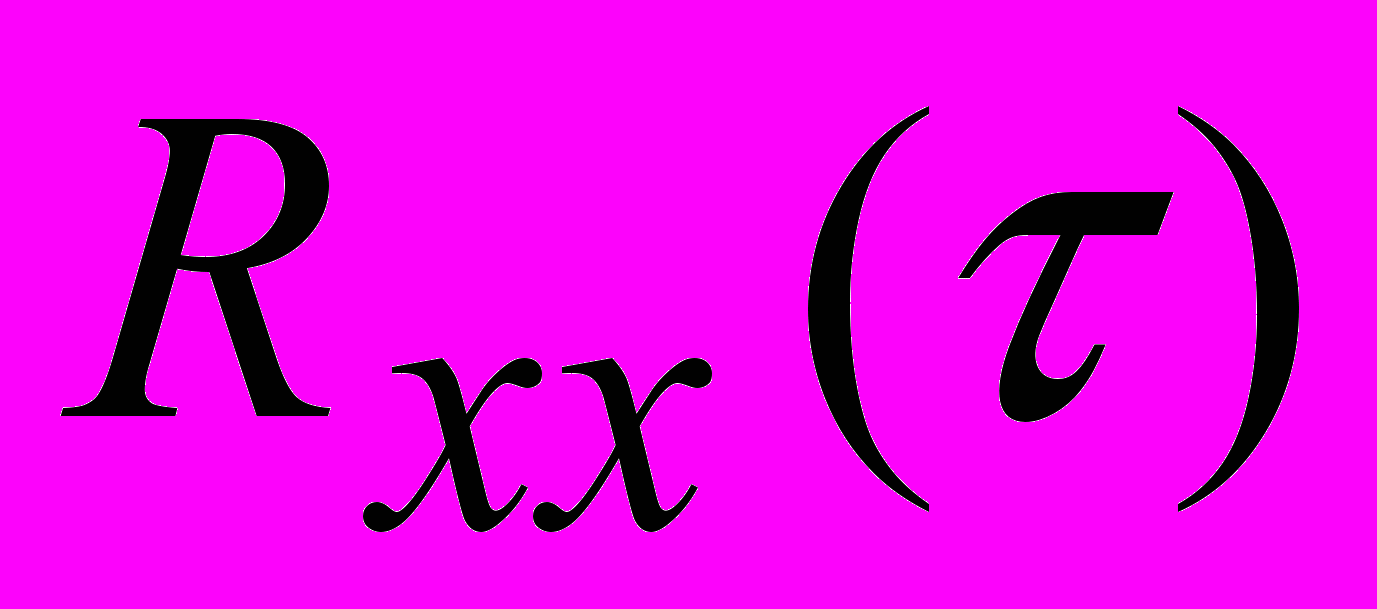 имеет при малых
имеет при малых  . В частности, при
. В частности, при 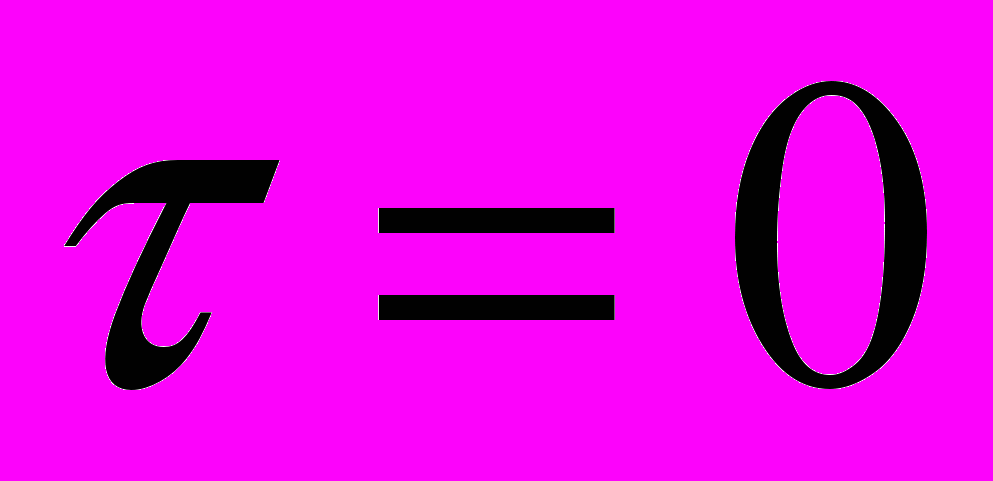 , корреляционная функция имеет максимум, равный дисперсии x(t) (среднему значению квадрата отклонения случайного процесса от его математического ожидания);
, корреляционная функция имеет максимум, равный дисперсии x(t) (среднему значению квадрата отклонения случайного процесса от его математического ожидания);- при
 корреляционная функция, если сигнал не содержит неслучайных составляющих, стремиться к нулю.
корреляционная функция, если сигнал не содержит неслучайных составляющих, стремиться к нулю. Взаимная корреляционная функция эргодического стационарного процесса, которая в нашем случае устанавливает среднюю величину связи между входным воздействием и реакцией объекта, разделенными интервалом времени
 , также может быть найдена усреднением по времени:
, также может быть найдена усреднением по времени: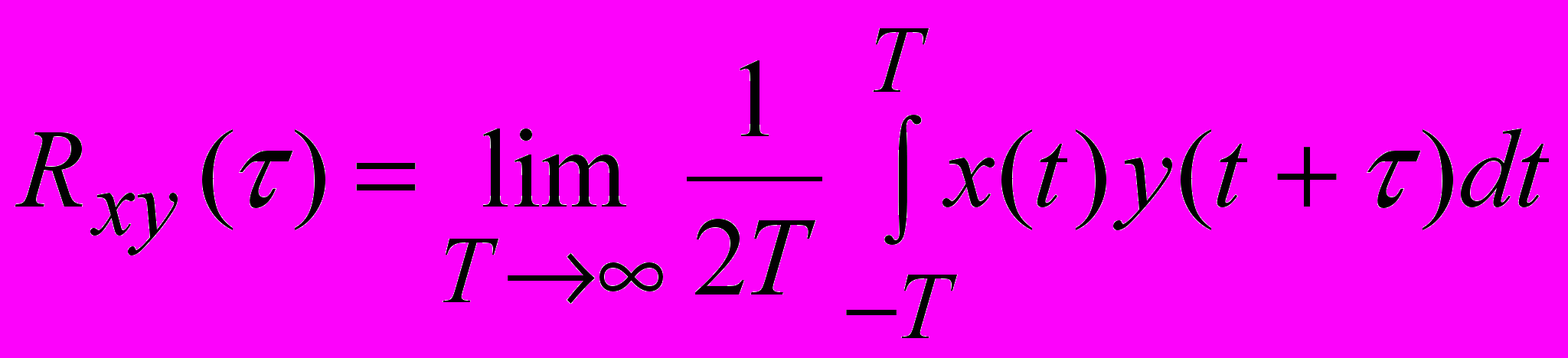 (2).
(2).Основными свойствами взаимной корреляционной функции являются:
-
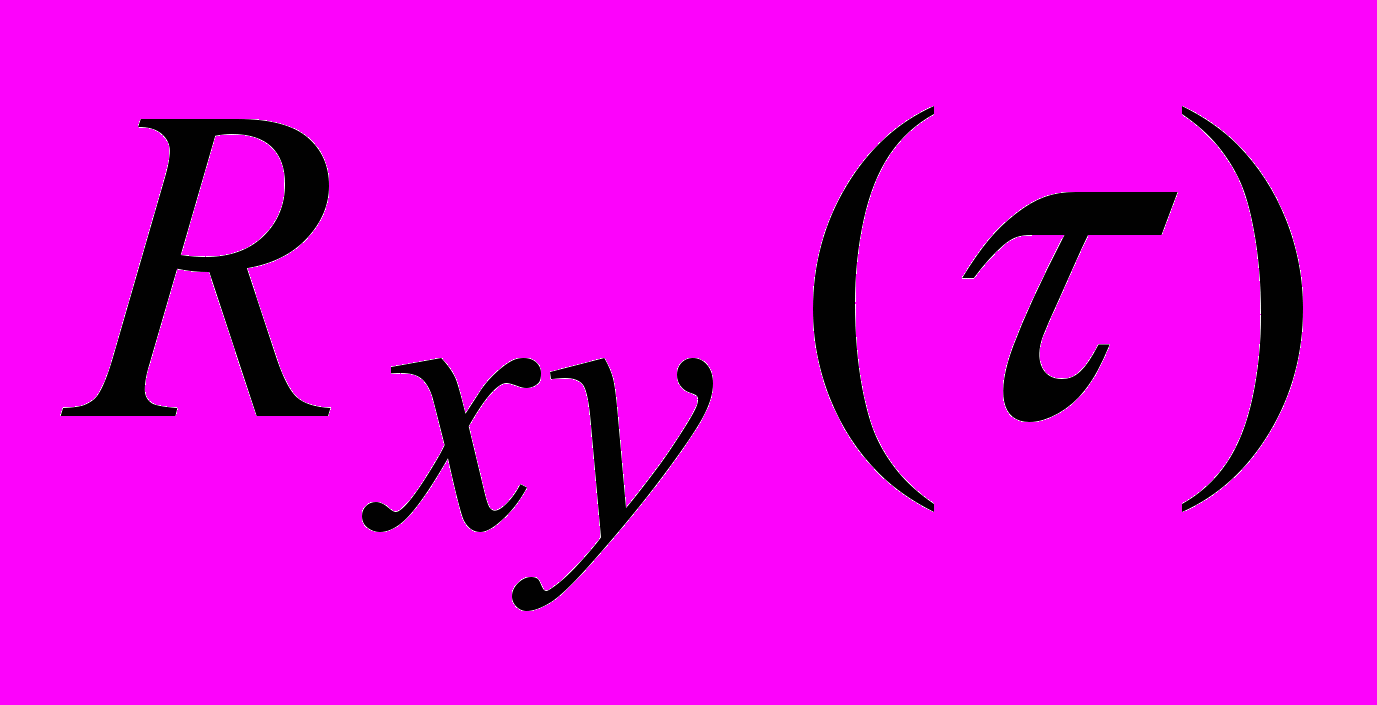 в отличие от
в отличие от 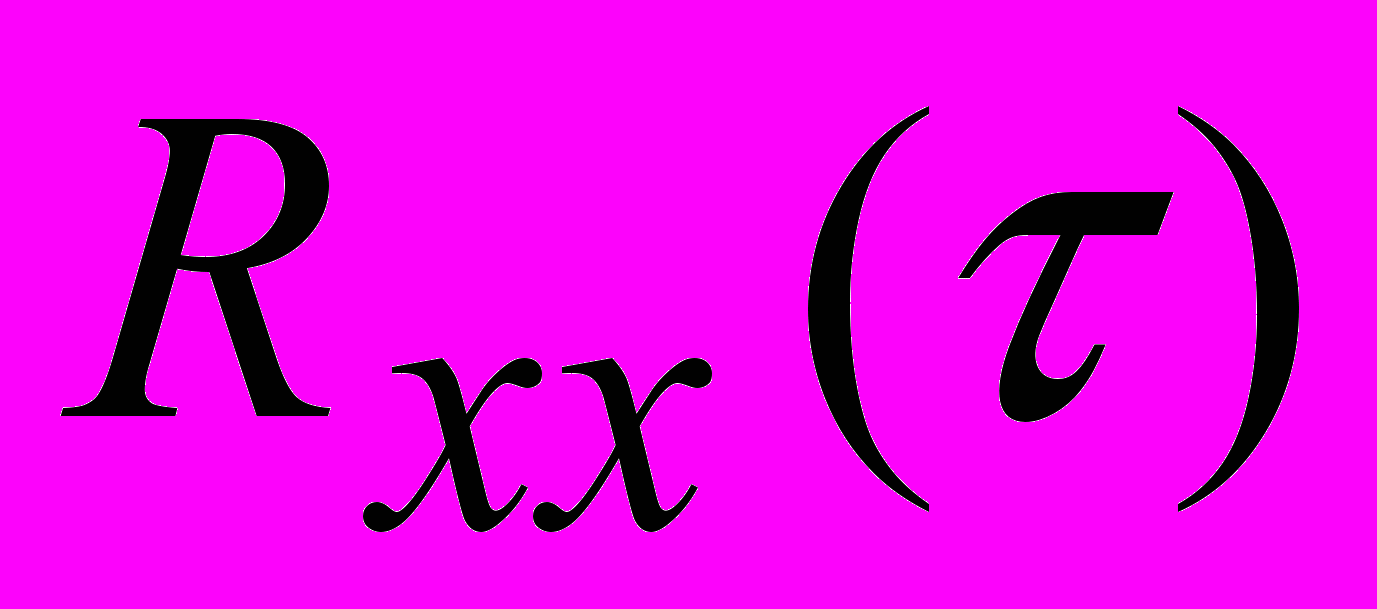 не является четной и не обладает симметрией относительно оси ординат
не является четной и не обладает симметрией относительно оси ординат 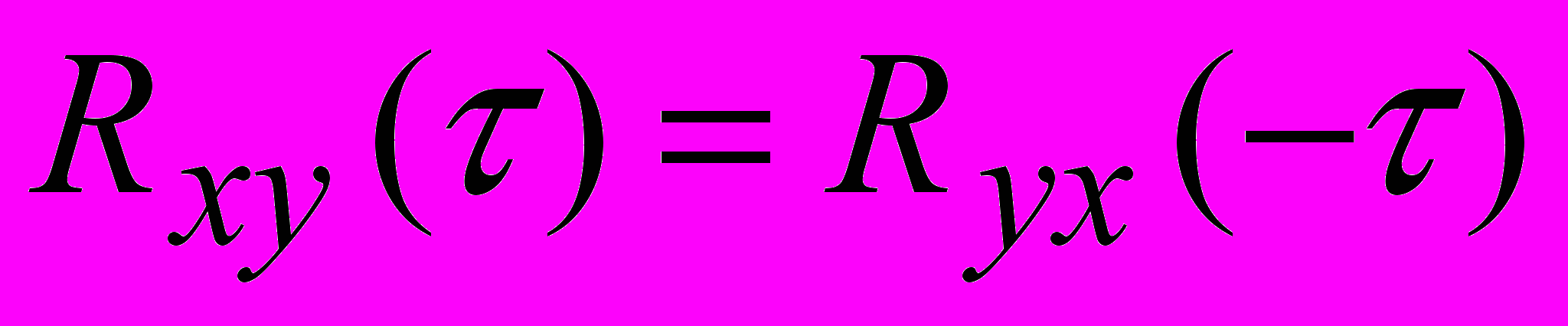 ;
;- при

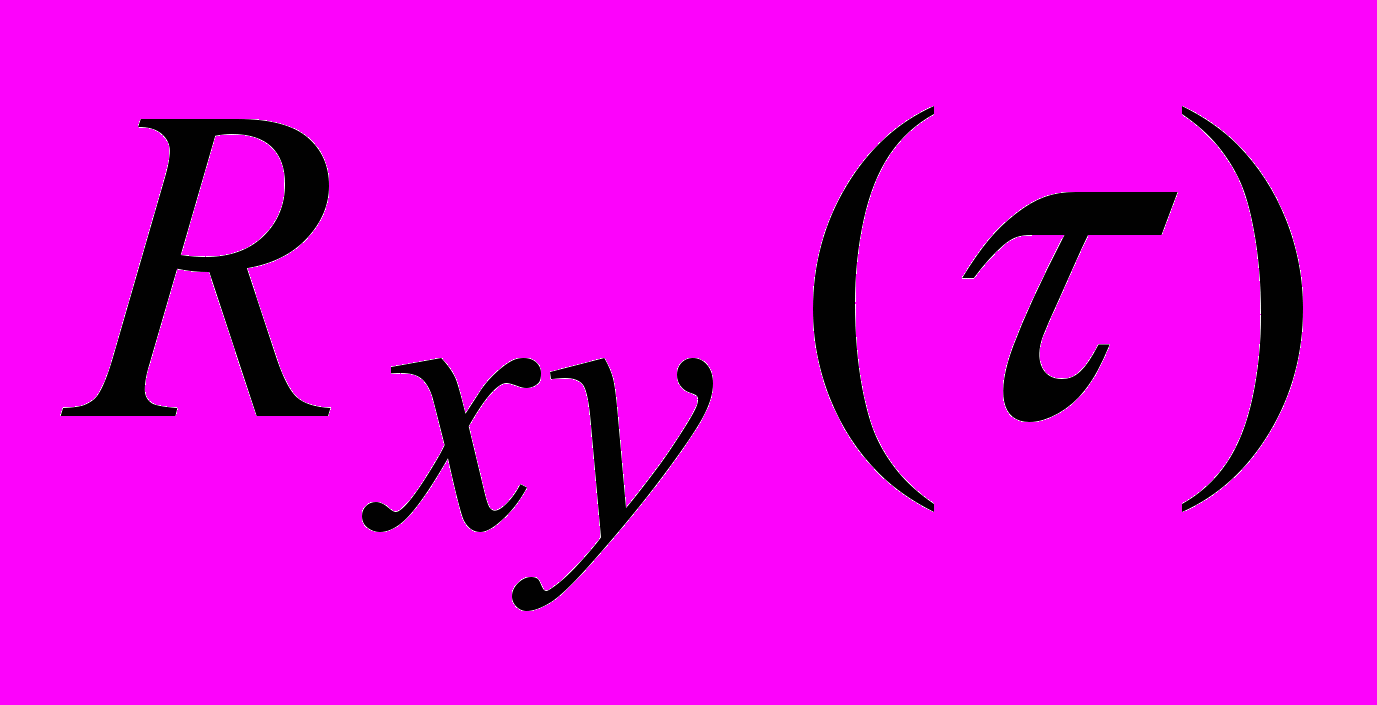 стремиться к нулю.
стремиться к нулю. Другой важной характеристикой стационарного случайного процесса является его спектральная плотность, которая математически определяется как преобразование Фурье от корреляционной функции:
 (3)
(3)Физически величина спектральной плотности для частоты
 показывает, какая доля мощности случайного процесса приходится на эту частоту.
показывает, какая доля мощности случайного процесса приходится на эту частоту.  является четной функцией и для любой частоты
является четной функцией и для любой частоты  .
.Преобразование Фурье взаимной корреляционной функции называется взаимной спектральной плотностью:
 (4)
(4)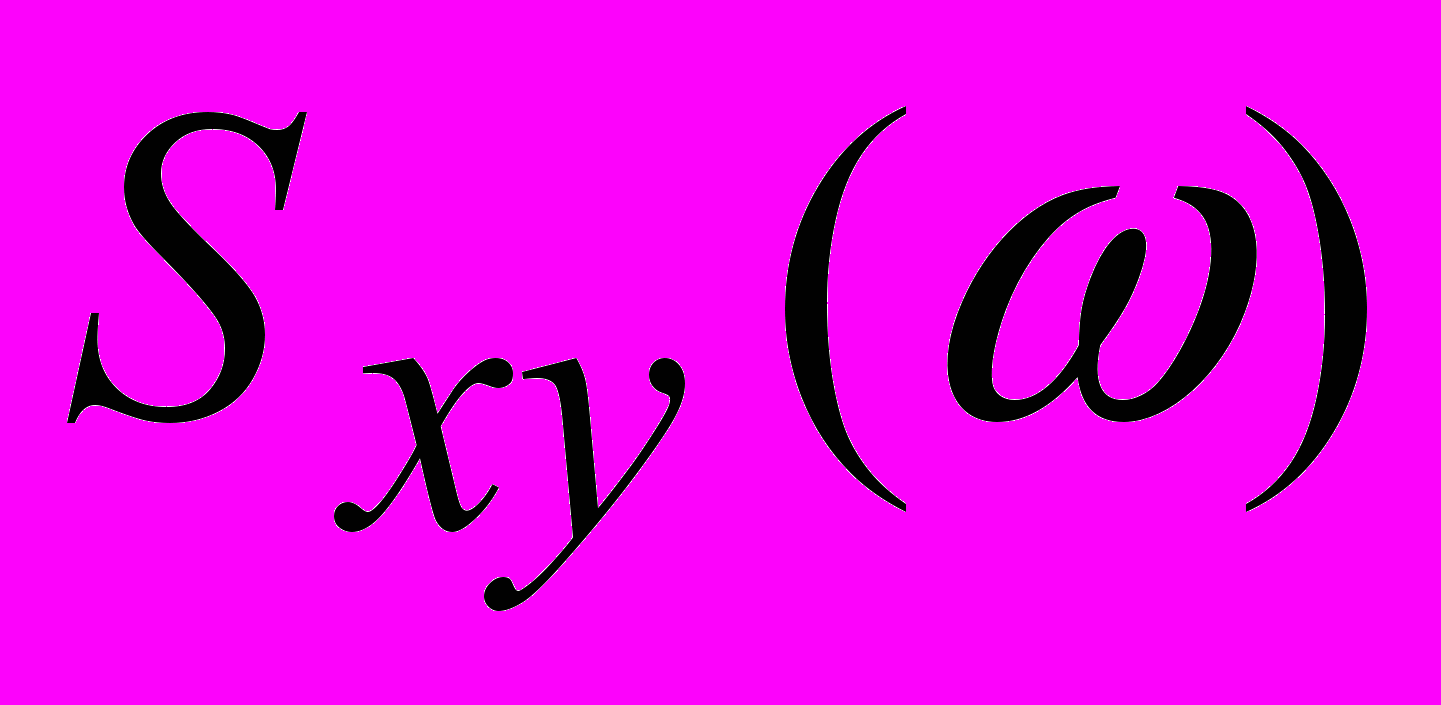 не является четной функцией частоты и обладает свойством
не является четной функцией частоты и обладает свойством 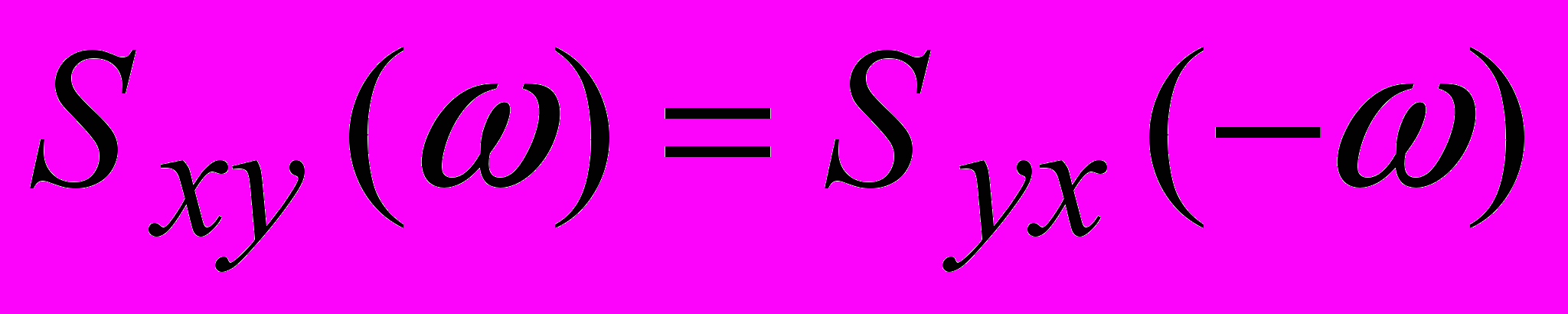 .
.При прохождении случайного сигнала через линейную систему его характеристики изменяются. Известно, что выходной сигнал
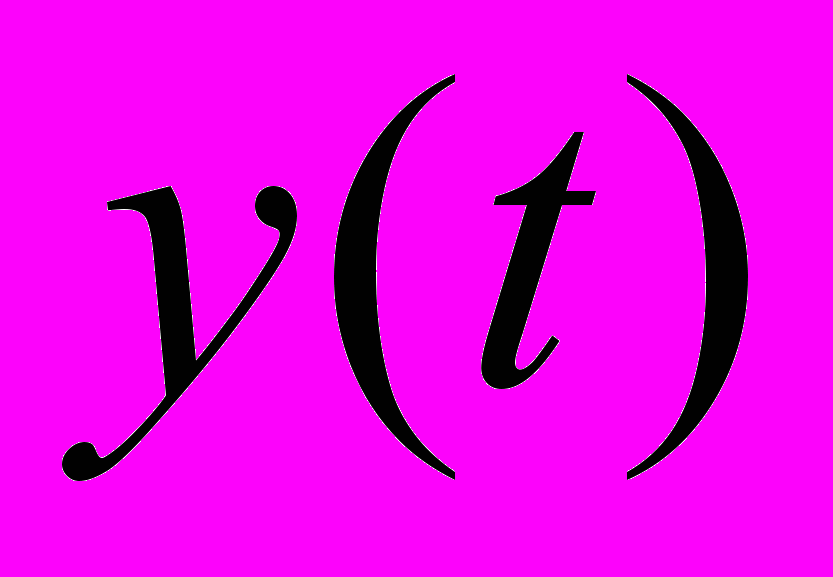 линейной динамической системы может быть выражен через входной сигнал
линейной динамической системы может быть выражен через входной сигнал 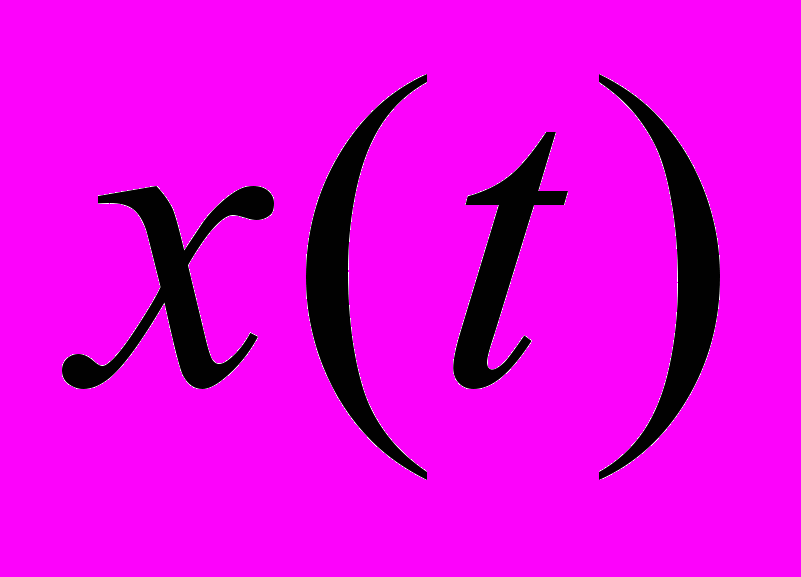 и импульсную характеристику
и импульсную характеристику 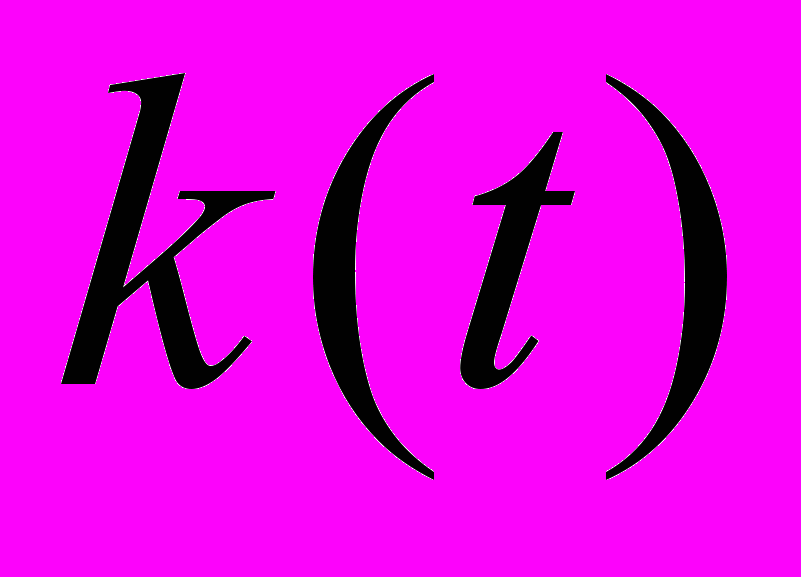 этой системы –
этой системы – 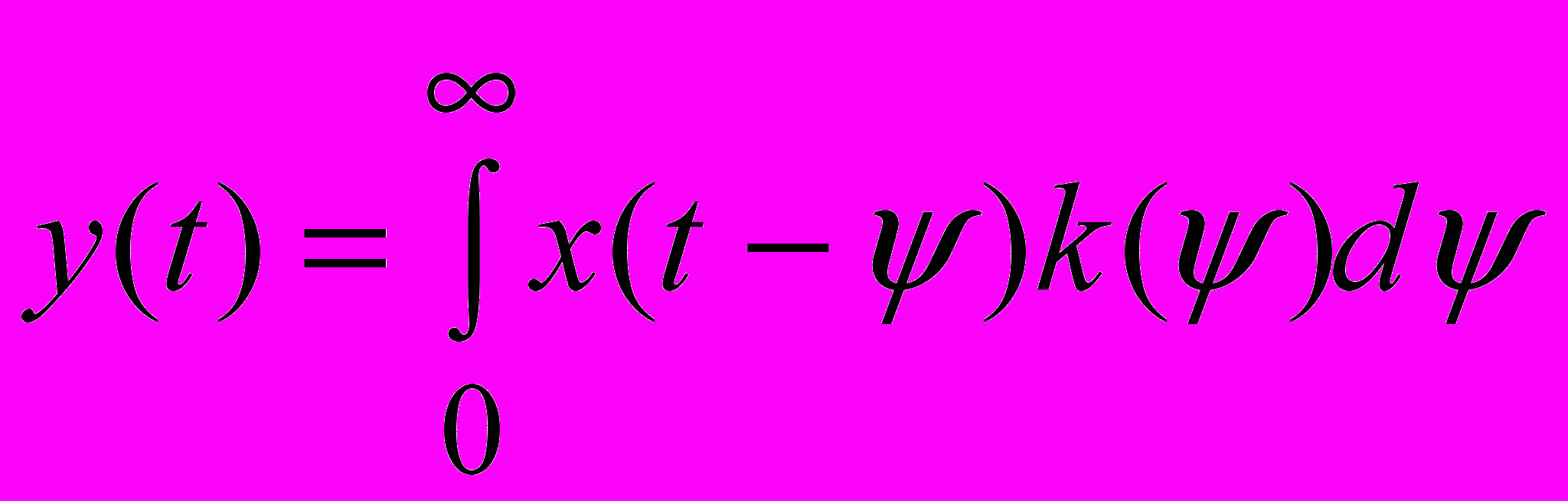 , (5)
, (5)где
 - вспомогательное время интегрирования.
- вспомогательное время интегрирования.Используя (2) и его свойства нетрудно получить так называемое уравнение Винера-Хинчина, на котором основано большинство методов определения динамических характеристик объектов по данным пассивного эксперимента -
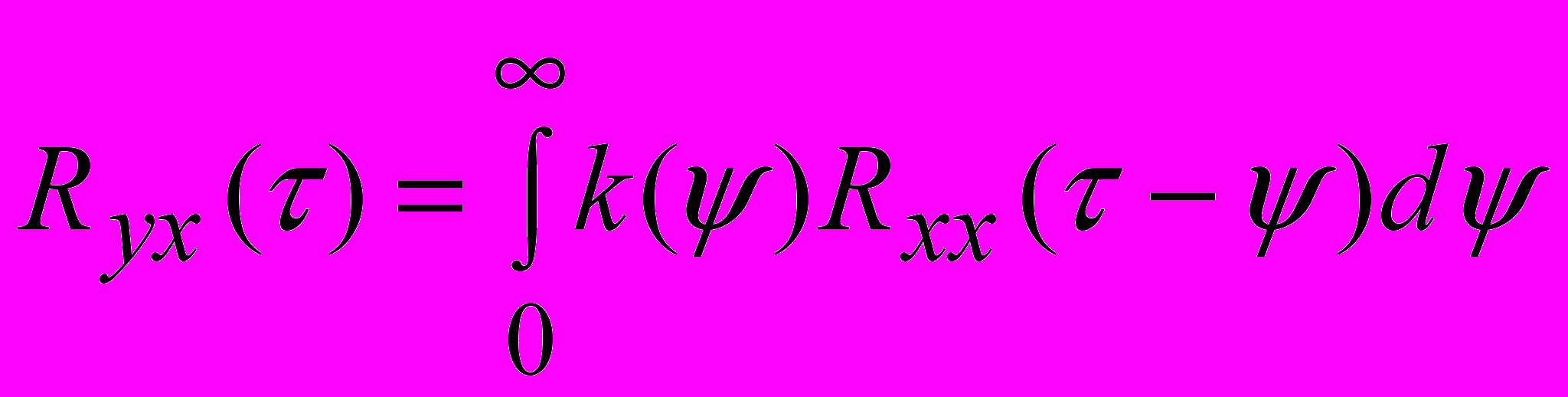 . (6)
. (6)Постановка эксперимента по определению характеристик случайных процессов
Очевидно, что прямое использование выражений (1)-(4) не представляется возможным ввиду необходимости получения бесконечно большой выборки исходных данных. Поэтому на практике используется информация, соответствующая конечной выборке на интервале времени Т. Величина интервала Т, во-первых, должна быть значительно больше реальной длительности переходного процесса в исследуемой системе, а во-вторых – соответствовать заданным требованиям к определению характеристик случайных процессов. Современная аппаратура позволяет без труда осуществлять измерение и автоматическое вычисление корреляционных функций и спектральных плотностей.
Метод определения передаточной функции объекта на основе моментов импульсной характеристики (метод моментов)
Данный метод основан на следующих соображениях. Передаточная функция объекта может быть представлена через импульсную характеристику при помощи следующего выражения:
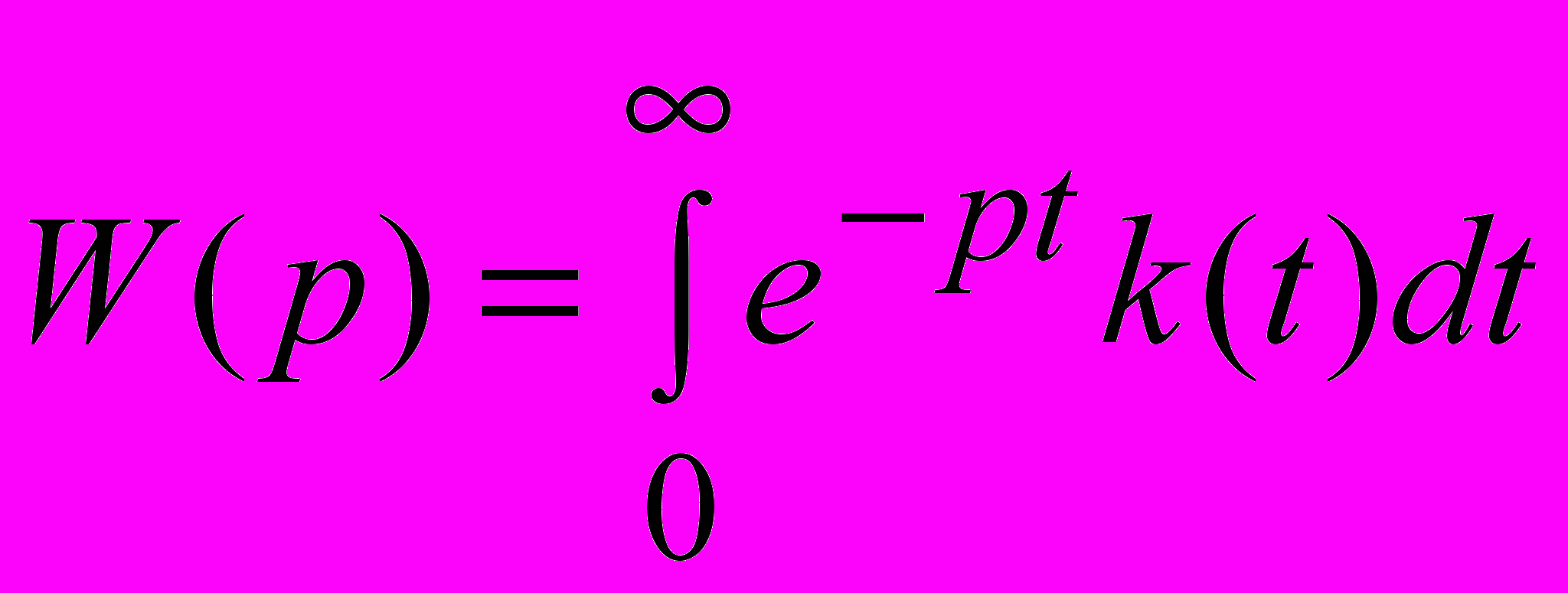 . (7)
. (7)Функция
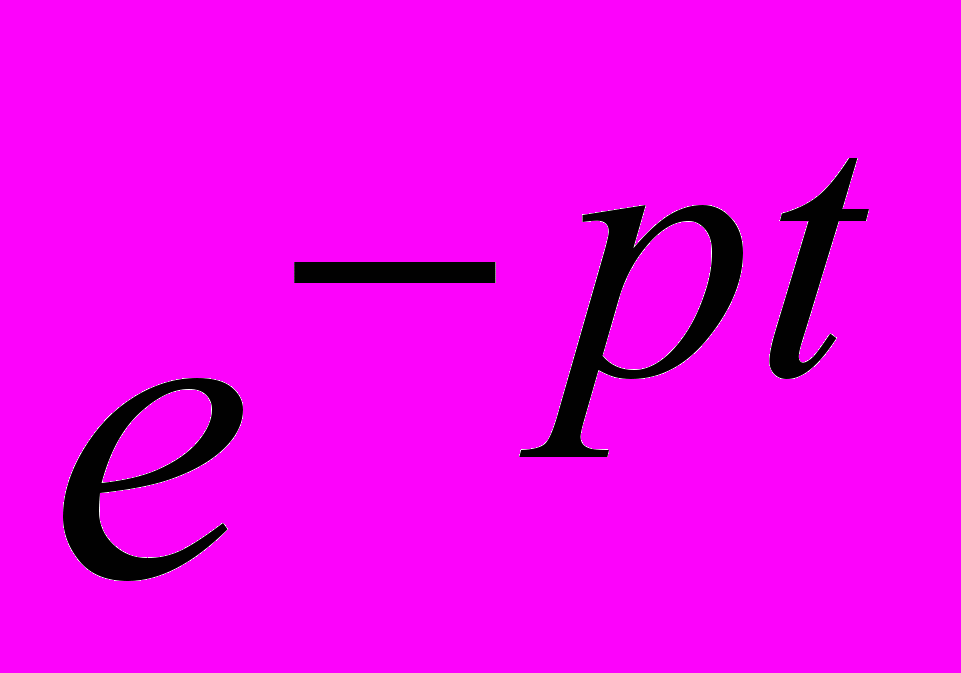 может быть представлена в виде степенного ряда Маклорена
может быть представлена в виде степенного ряда Маклорена(
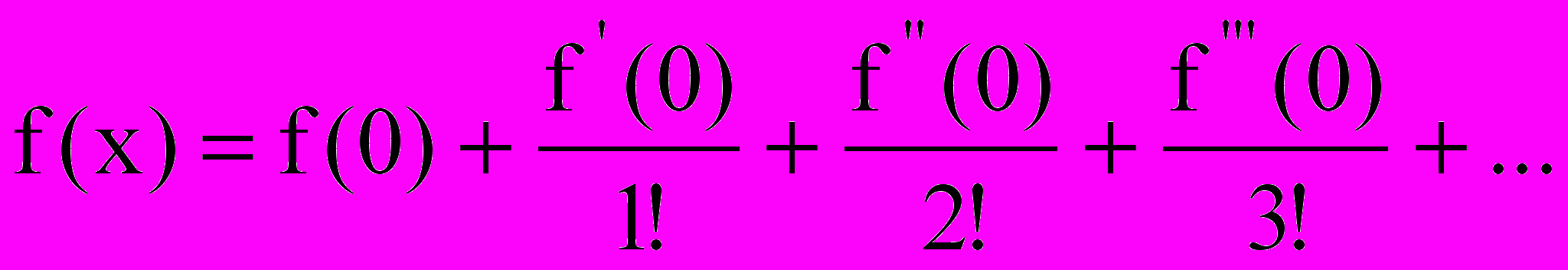 ):
):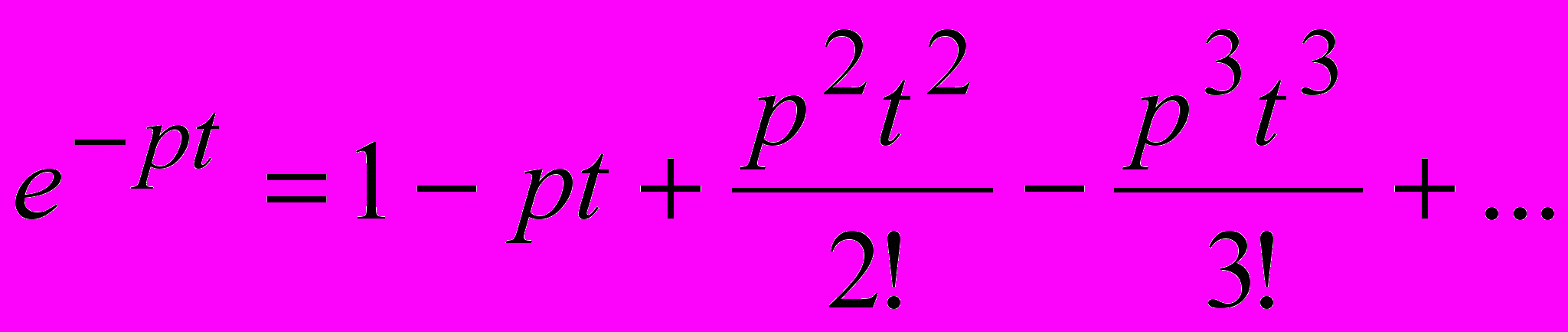 (8)
(8)Подставляя (8) в (7) получим:
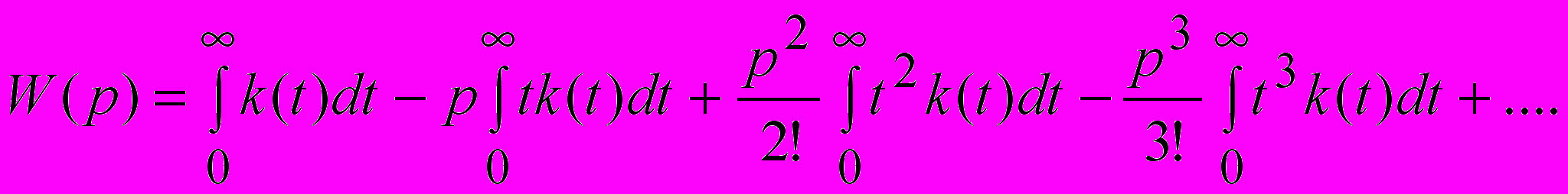 , (9)
, (9)где функция
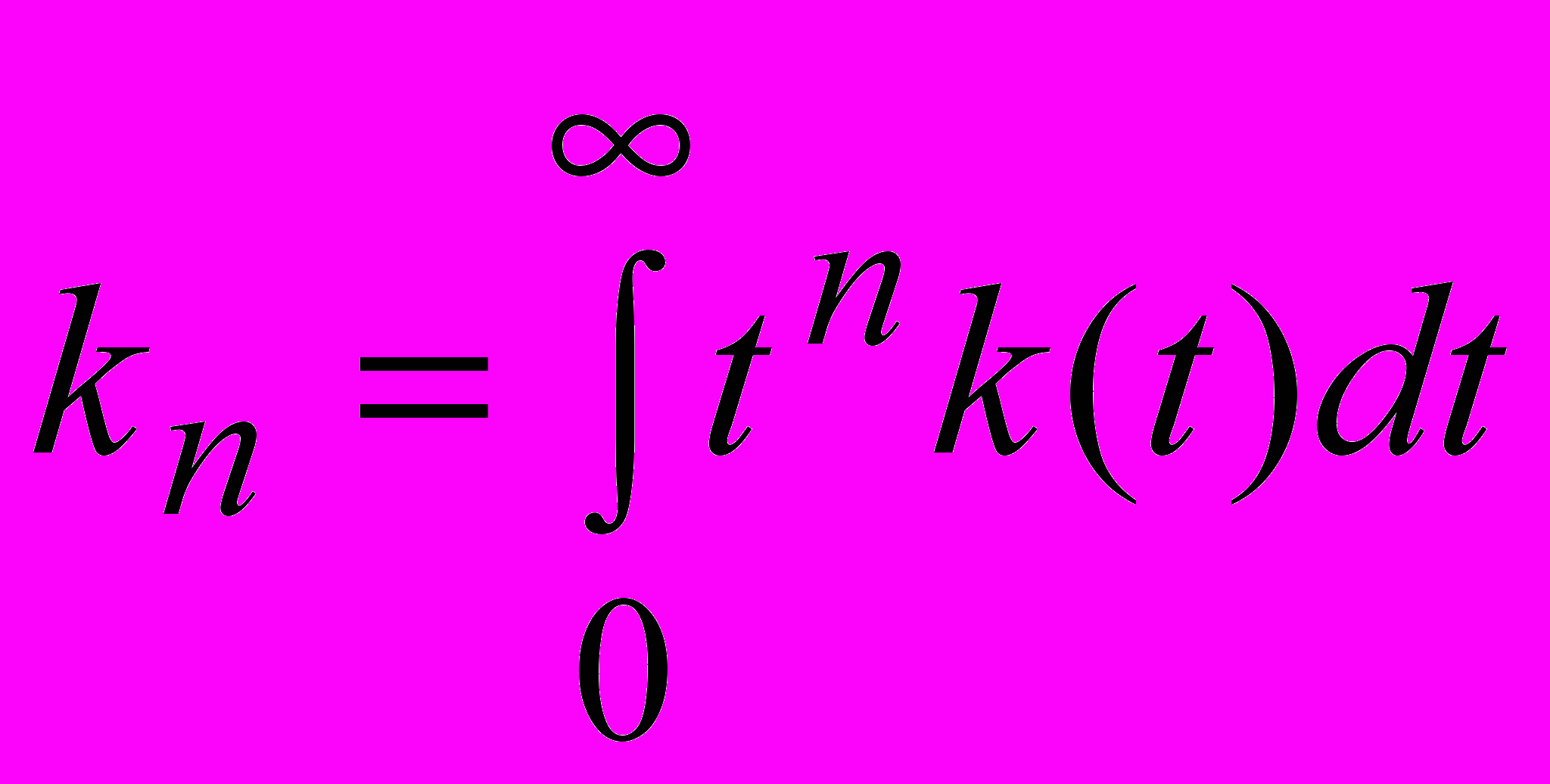 - называется моментом n-го порядка импульсной характеристики объекта.
- называется моментом n-го порядка импульсной характеристики объекта.Таким образом, выражение для передаточной функции может быть получено на основе известных моментов импульсной характеристики:
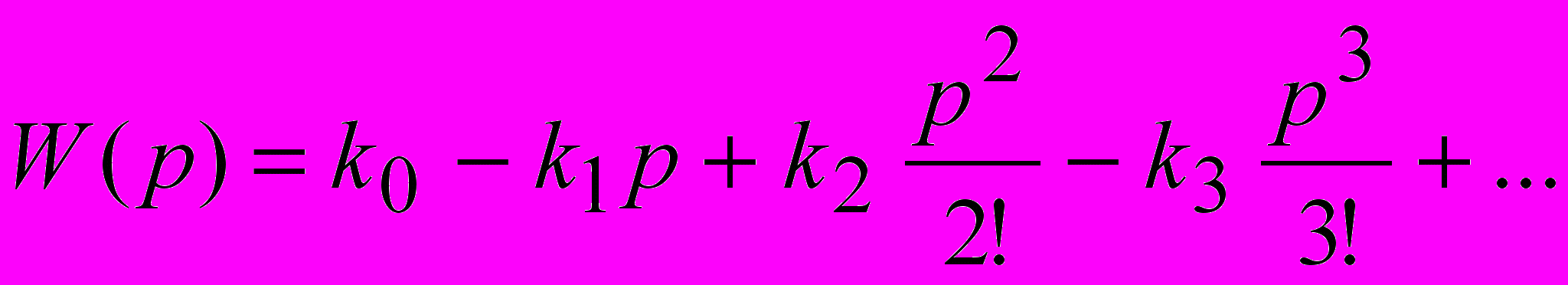 (10).
(10).Моменты импульсной характеристики могут быть вычислены по корреляционным функциям следующим образом.
Моментом n-го порядка корреляционной функции называется –
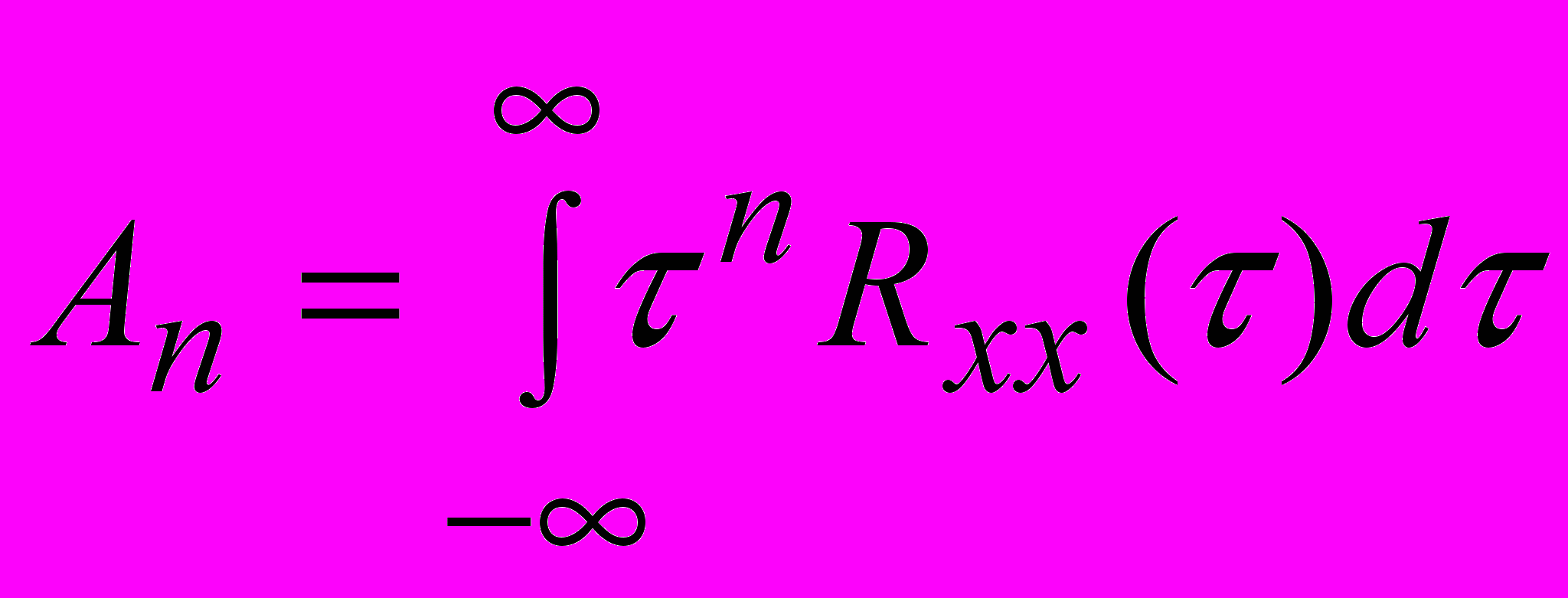 (11).
(11).Подобно этому моментом n-го порядка взаимной корреляционной функции будет -
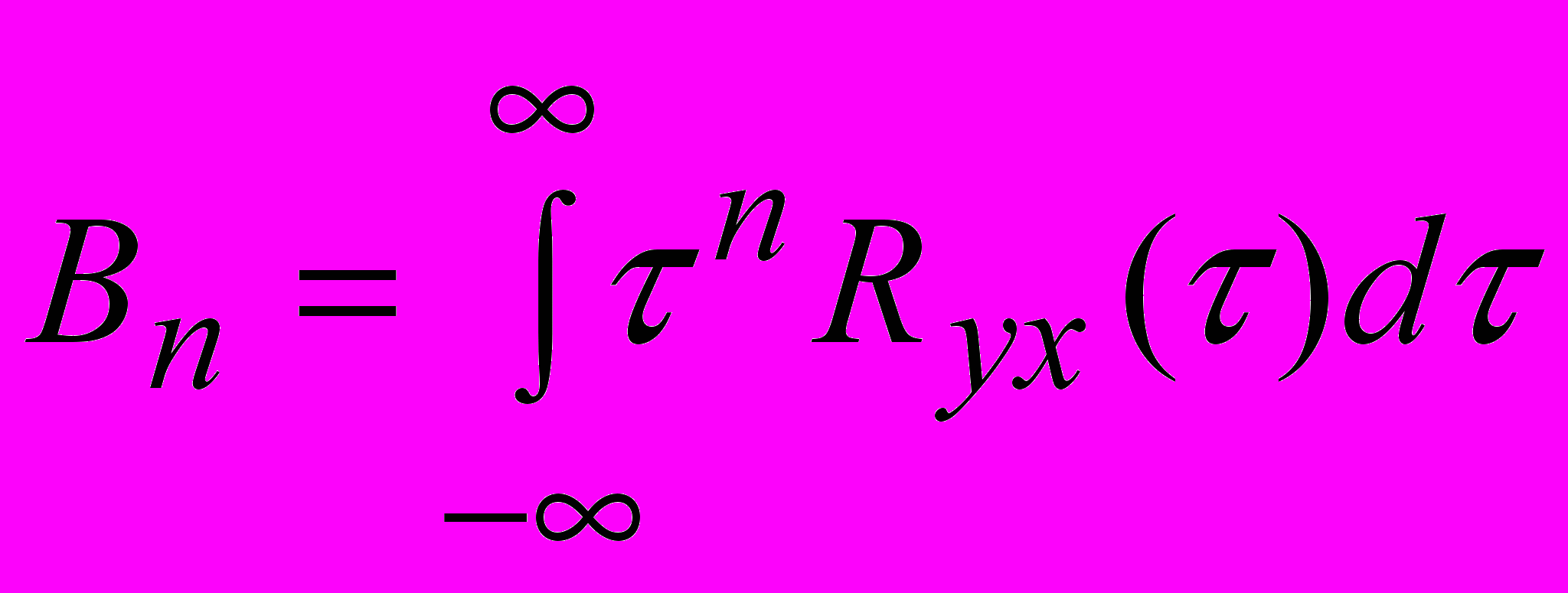 (12).
(12).Очевидно, что интегралы (11) и (12) могут сходиться только в том случае, если подынтегральные корреляционные функции не содержат постоянной или периодической составляющих. А так как при практических вычислениях приходиться ограничиваться конечными значениями
 , то необходимым условием сходимости интегралов (11) и (12) является также достаточно быстрое уменьшение корреляционной функции до нуля при возрастании
, то необходимым условием сходимости интегралов (11) и (12) является также достаточно быстрое уменьшение корреляционной функции до нуля при возрастании  . В этих условиях интегралы (11) и (12) приближенно могут быть заменены следующими:
. В этих условиях интегралы (11) и (12) приближенно могут быть заменены следующими: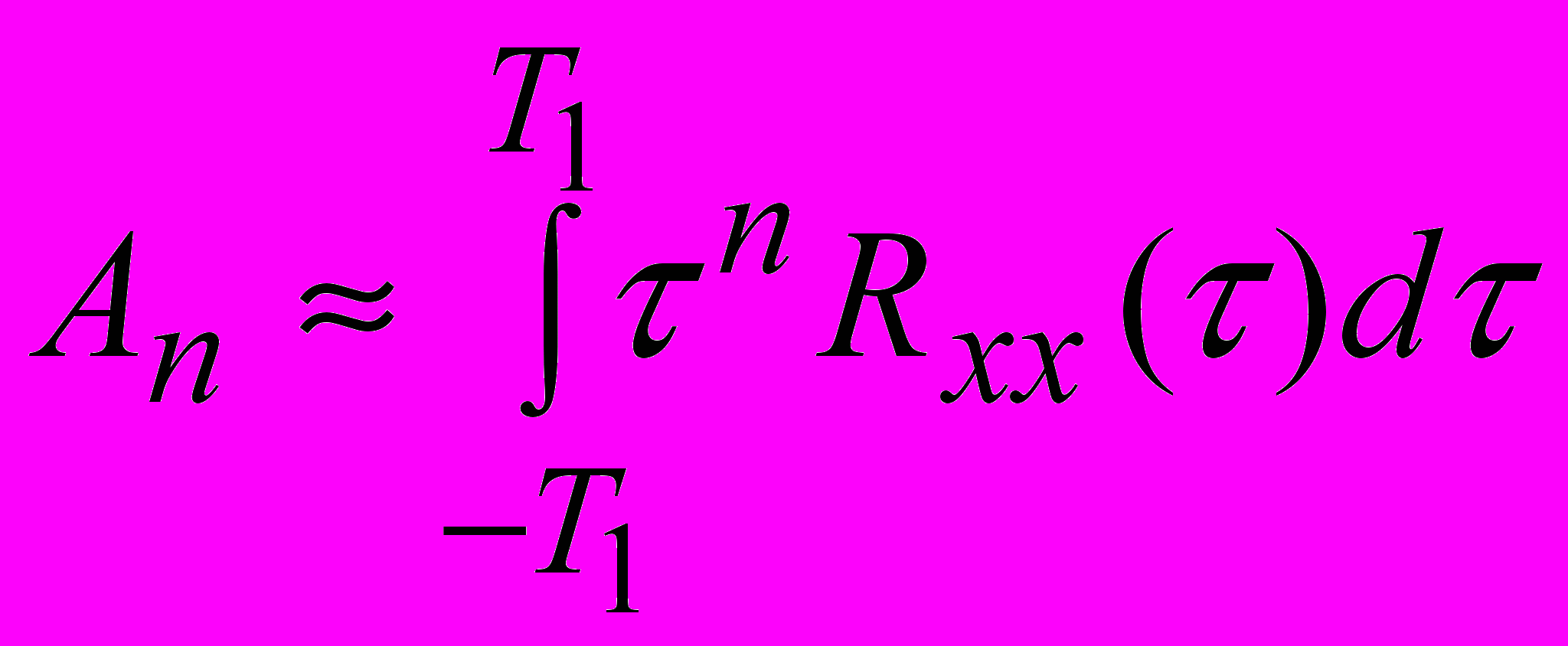 (13)
(13)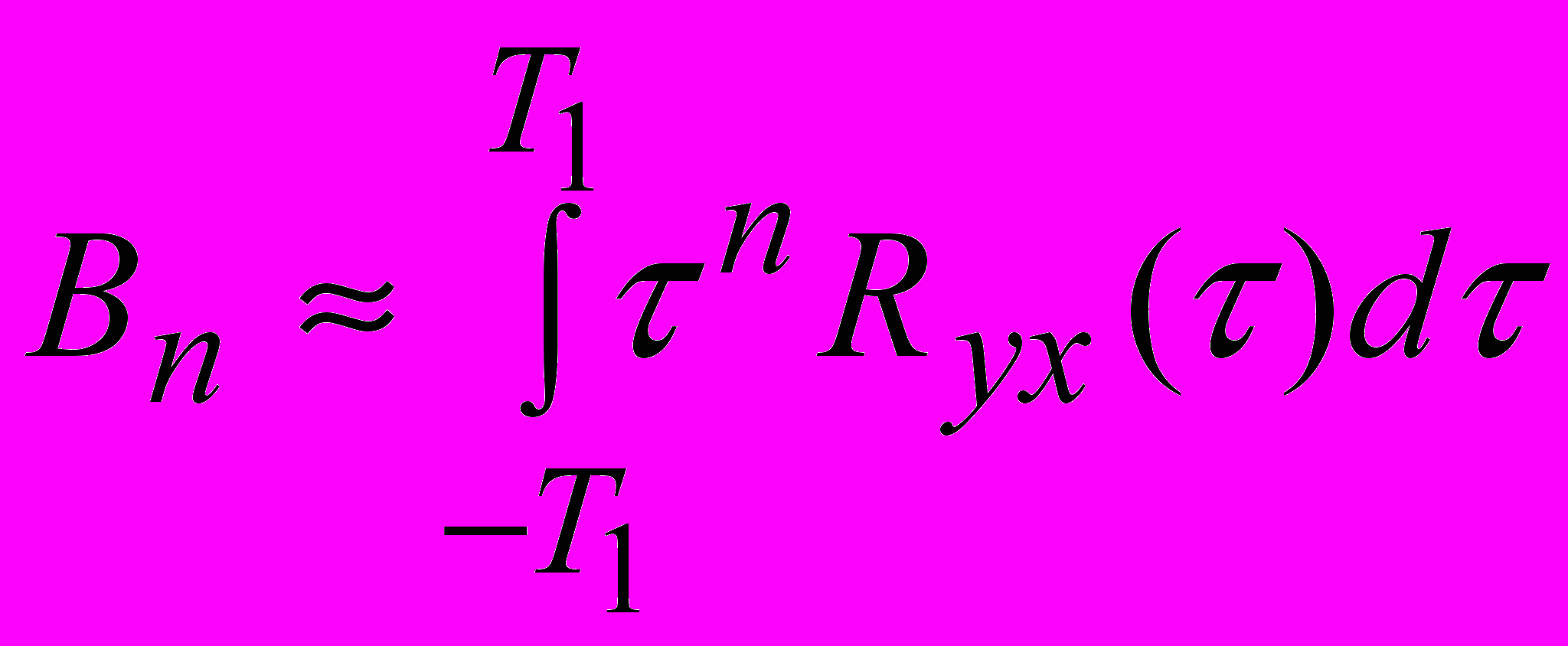 , (14)
, (14)где Т1 – значение
 , выбранное так, что при
, выбранное так, что при 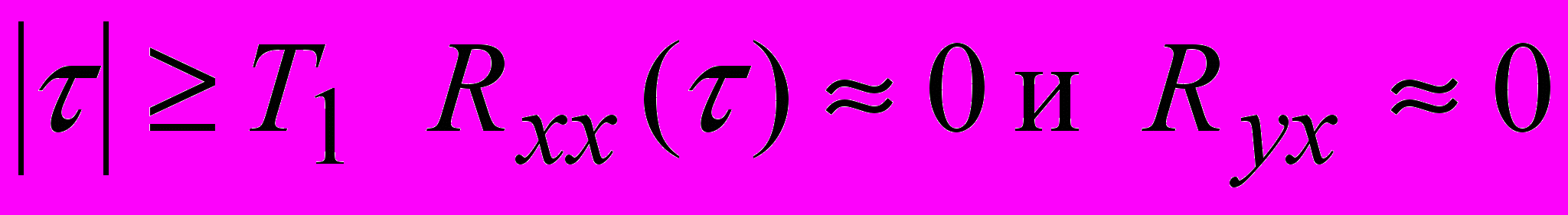 .
.Разбив интервал [-T1,T1] на 2m равных интервалов
 (m- четное число), получим ординаты корреляционных функций в точках -T1, -T1+
(m- четное число), получим ординаты корреляционных функций в точках -T1, -T1+ , -T1+2
, -T1+2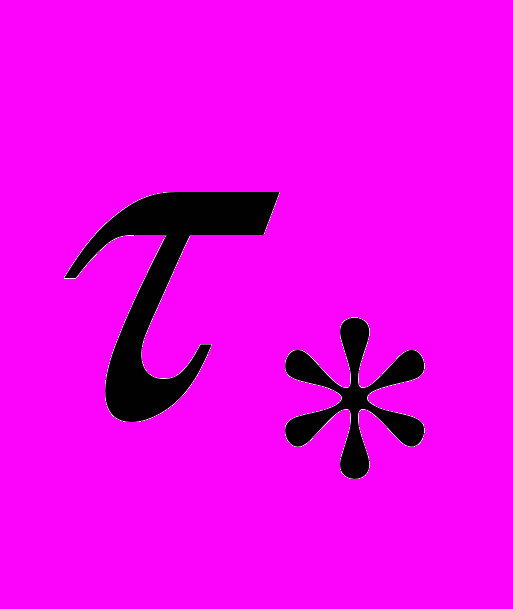 , …, -2
, …, -2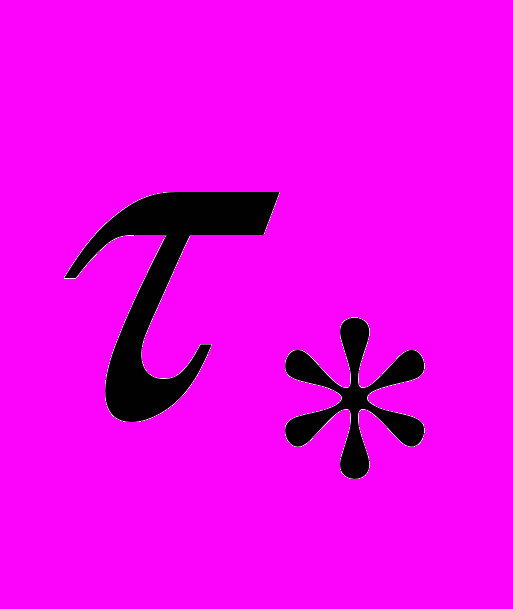 , -
, - 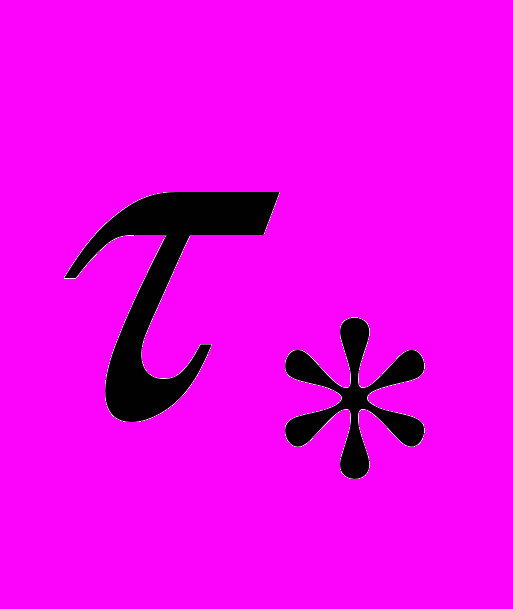 , 0,
, 0, 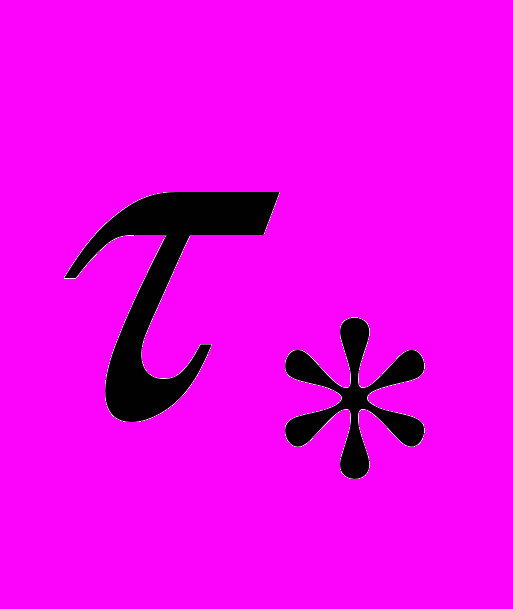 , 2
, 2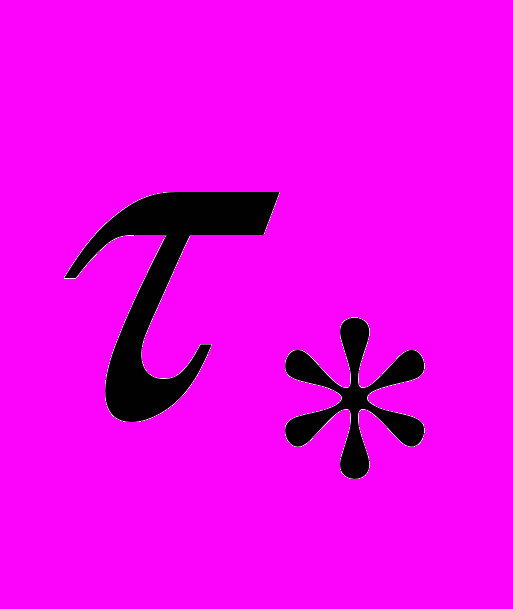 , …, T1-
, …, T1-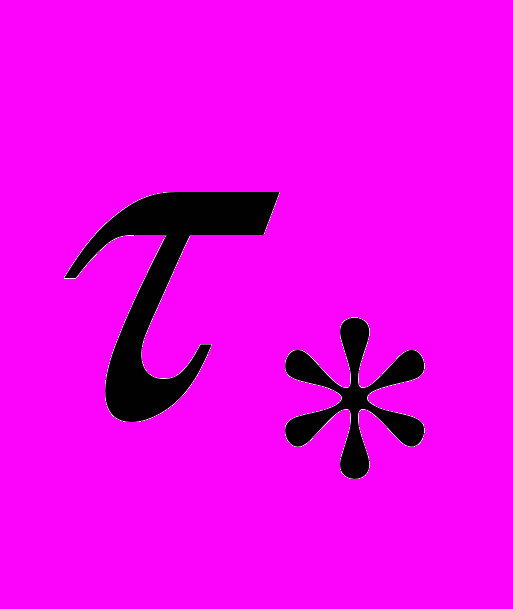 , T1 (рис.2). Тогда интеграл (13) на основании формулы приближенного интегрирования Симпсона [
, T1 (рис.2). Тогда интеграл (13) на основании формулы приближенного интегрирования Симпсона [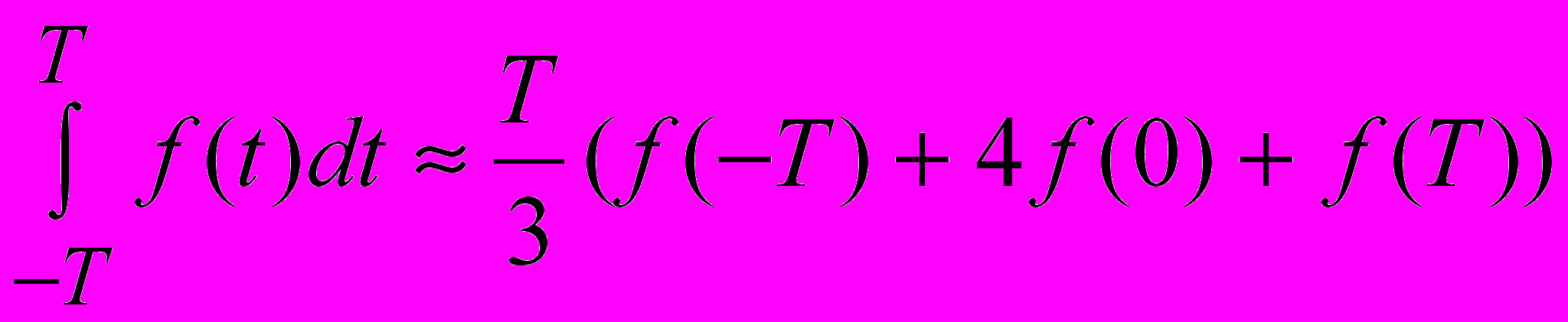 ] может быть представлен в виде суммы:
] может быть представлен в виде суммы: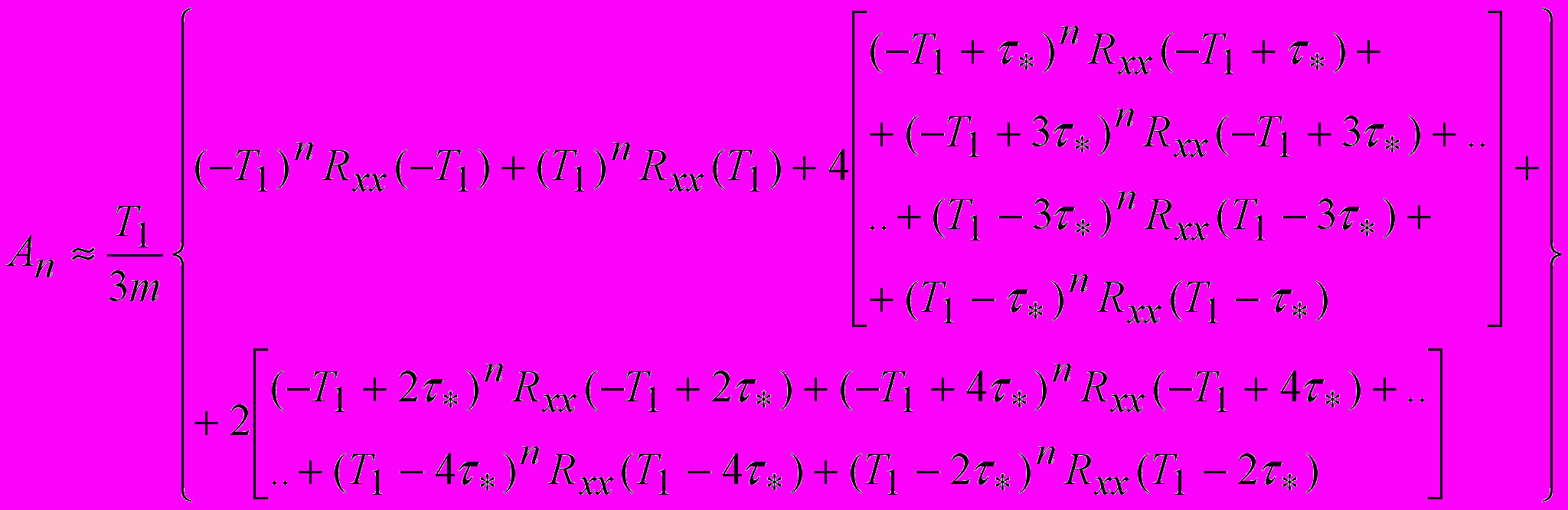 (15)
(15)Если учесть основные свойства
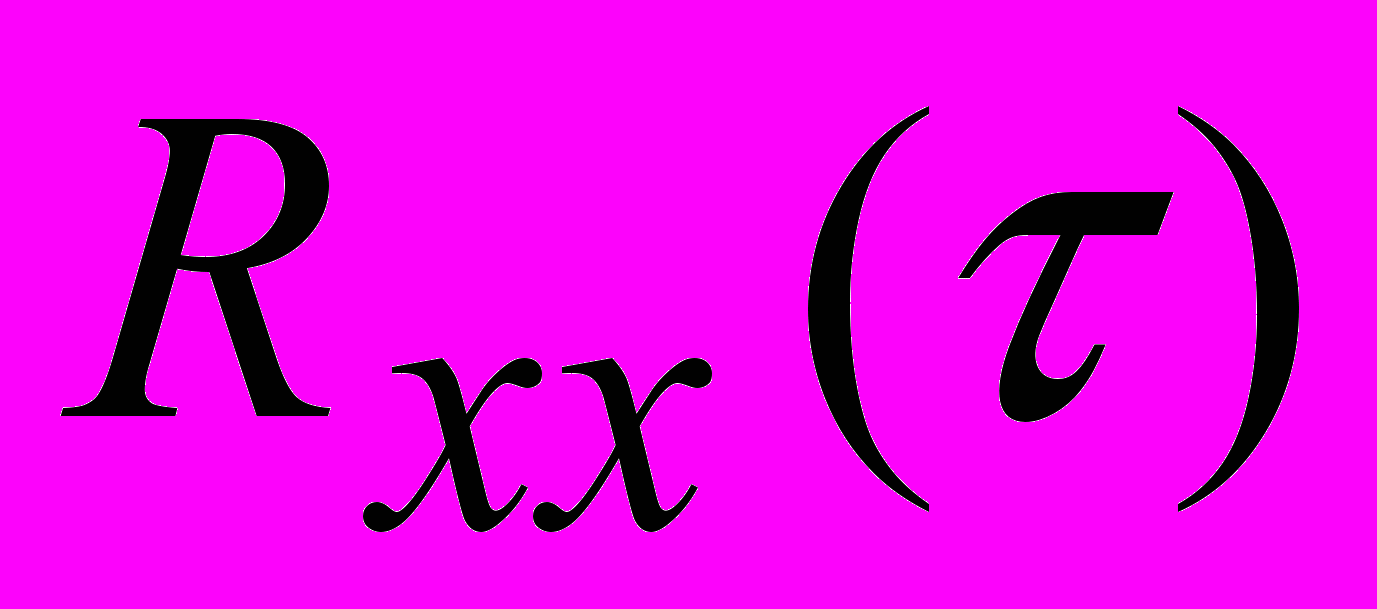 , а именно:
, а именно:- при
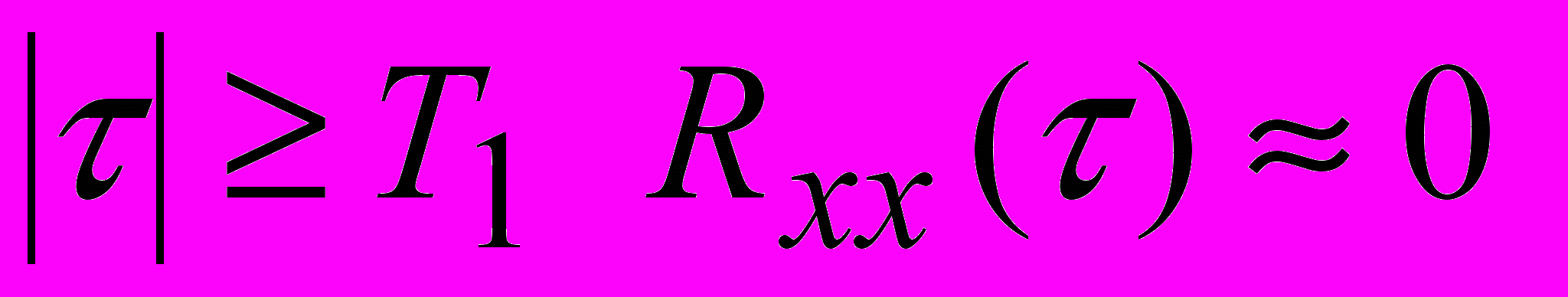 ;
;
- при
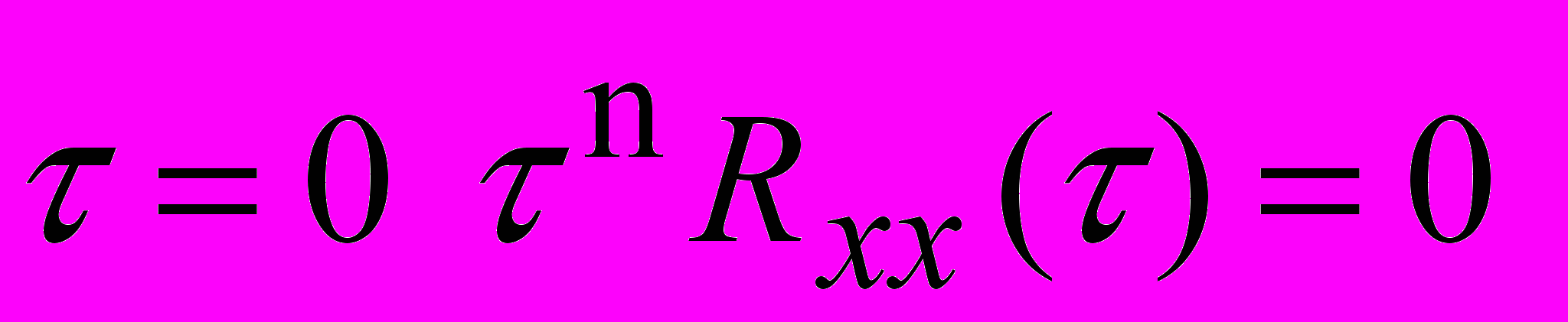 ;
;
- если n – нечетное, то
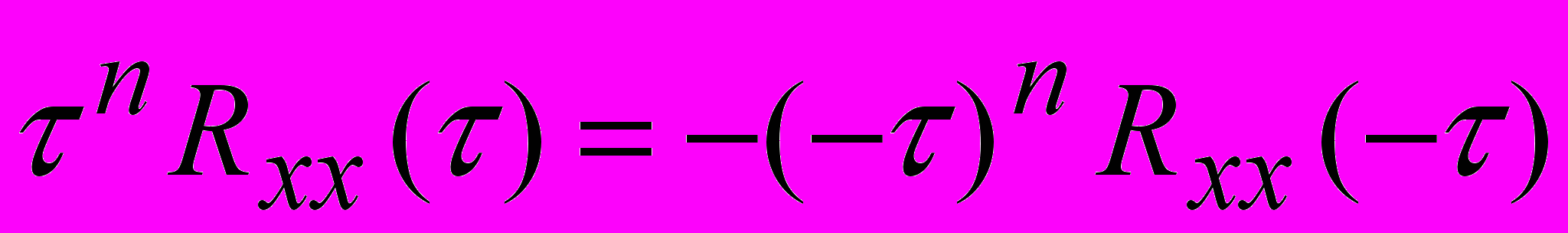 ;
;
- если n – четное, то
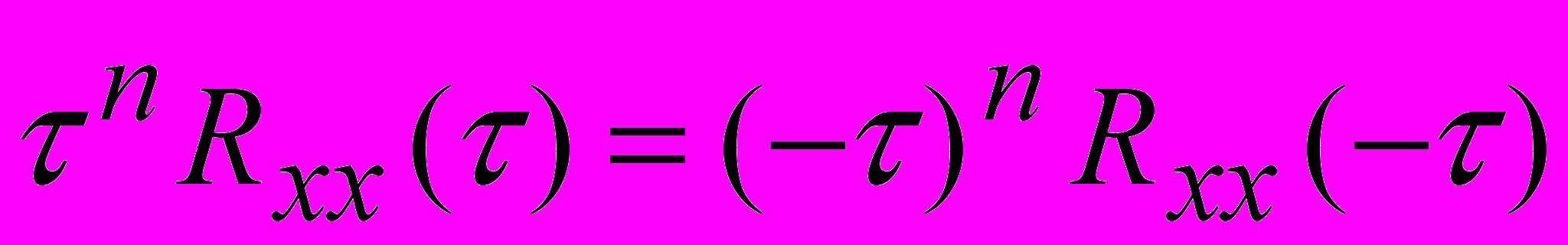 ,
,
то выражение (15) можно упростить –
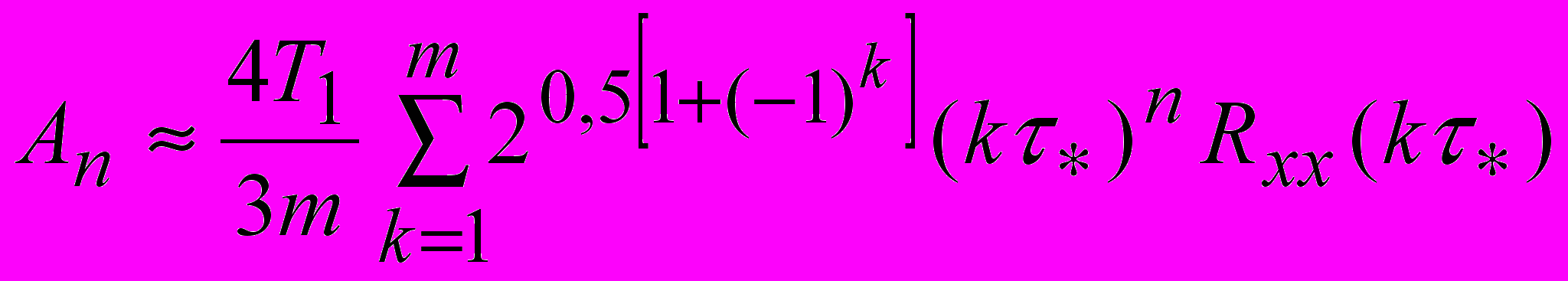 (16).
(16).Формула для вычисления
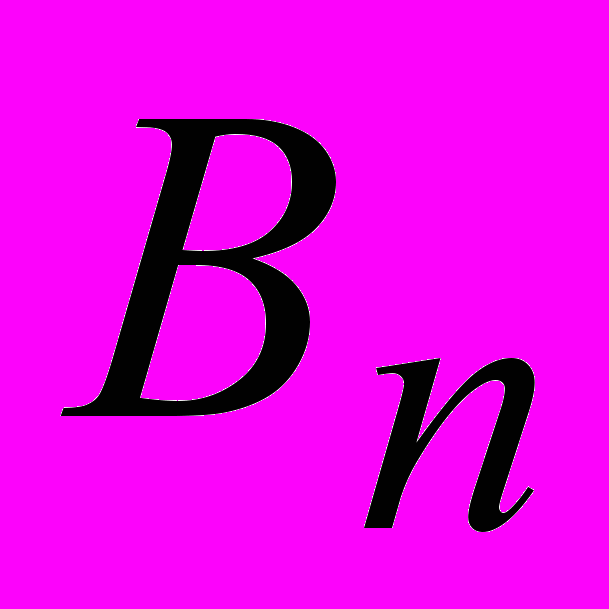 имеет тот же вид, что и (15). Однако, так как взаимно корреляционная функция не обладает симметрией относительно оси ординат второе и третье свойства корреляционной функции для нее несправедливы. Поэтому упрощенное выражение для расчета
имеет тот же вид, что и (15). Однако, так как взаимно корреляционная функция не обладает симметрией относительно оси ординат второе и третье свойства корреляционной функции для нее несправедливы. Поэтому упрощенное выражение для расчета 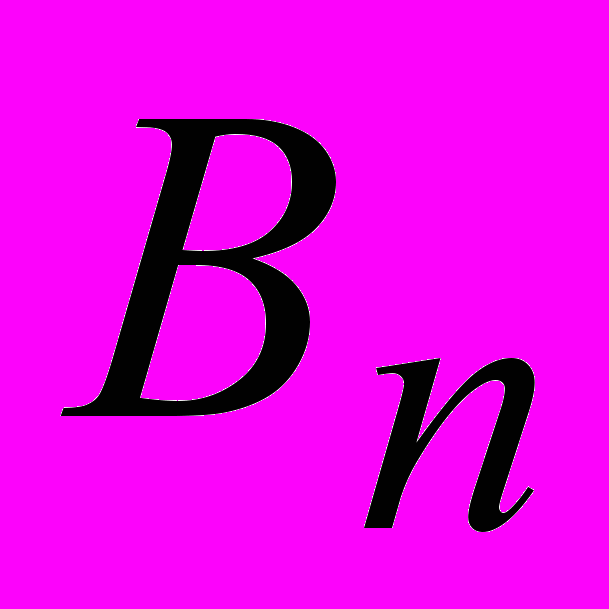 имеет вид:
имеет вид: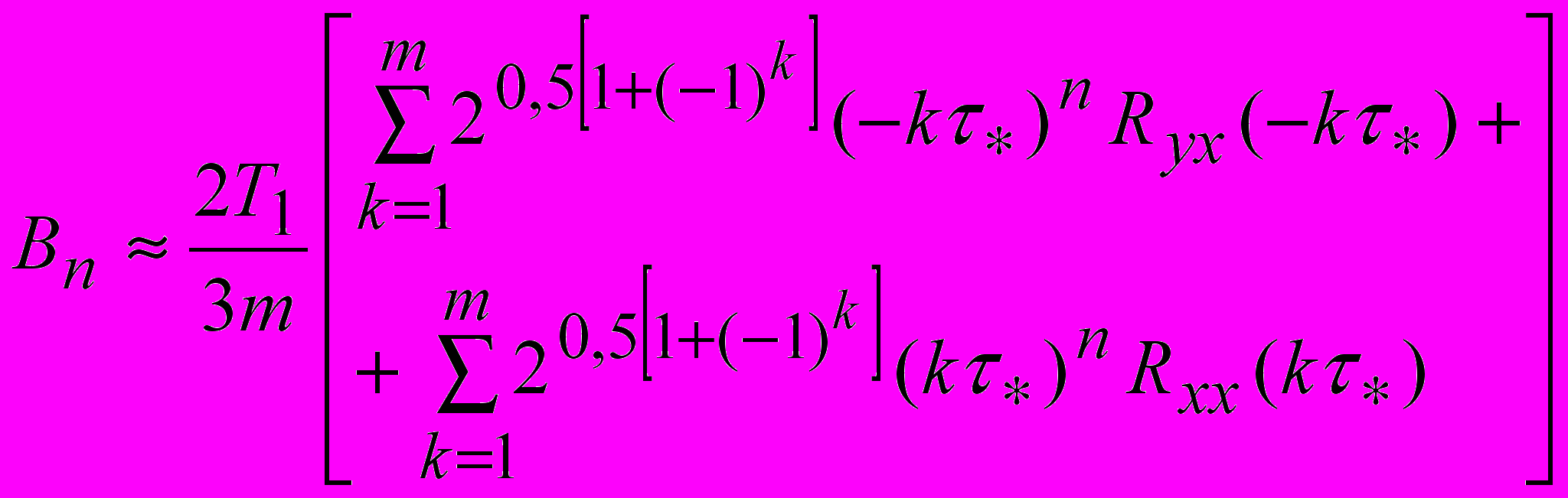 (17).
(17).Зависимость взаимной корреляционной функции от корреляционной функции определяется формулой Винера-Хинчина (6). Структура выражения (6) аналогична выражению, определяющему импульсную характеристику последовательного соединения двух динамических систем, которому соответствует операторное выражение передаточной функции последовательного соединения двух систем (
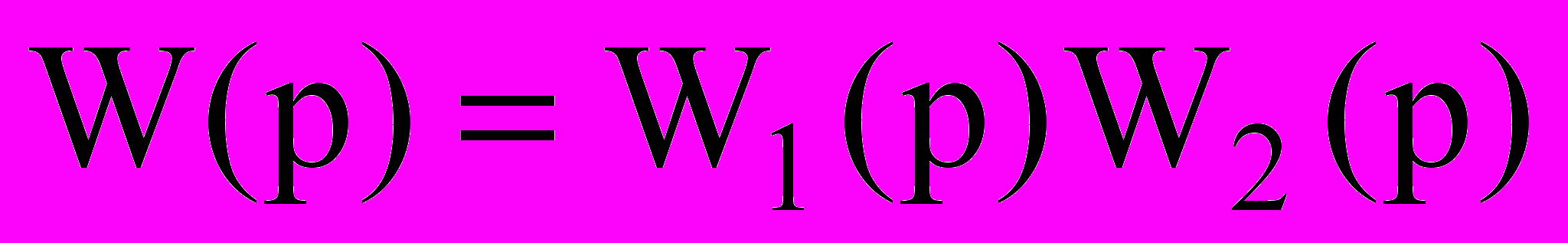 ). Воспользовавшись этой аналогией можно получить операторное выражение, соответствующее формуле (6):
). Воспользовавшись этой аналогией можно получить операторное выражение, соответствующее формуле (6):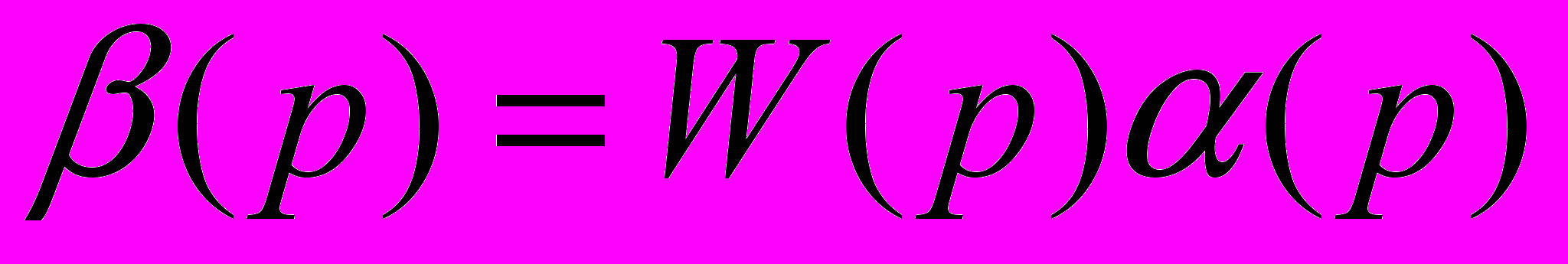 , (18)
, (18)где
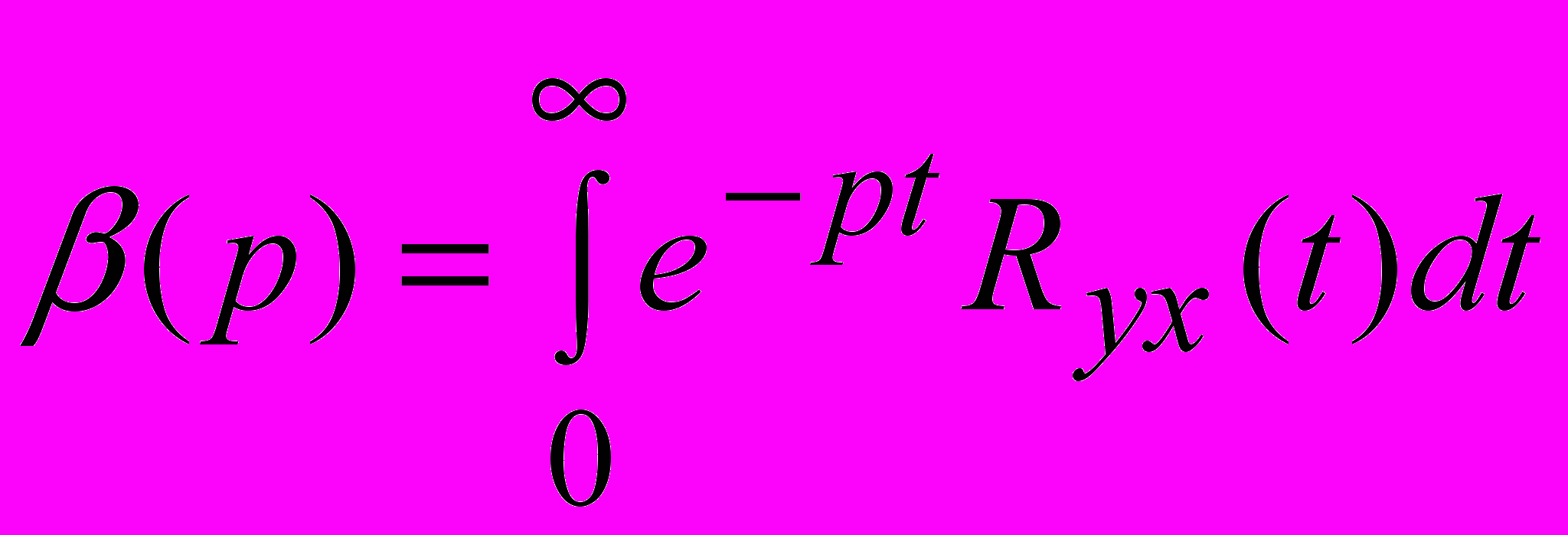 ,
, 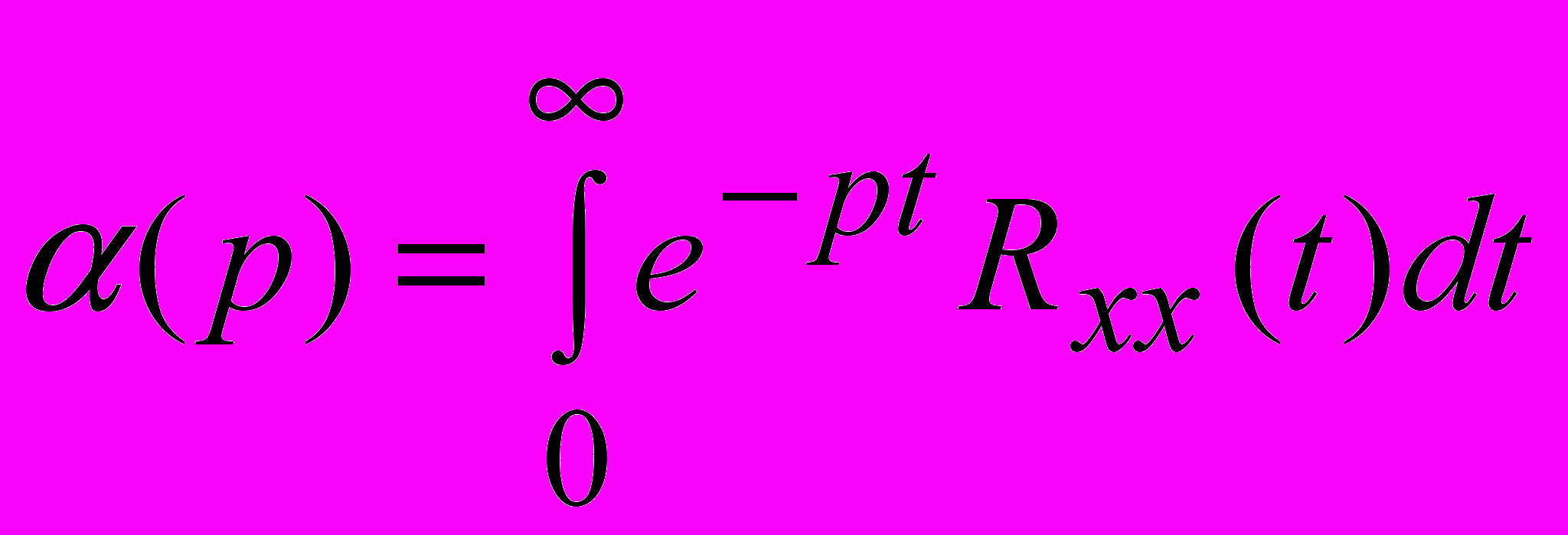 ,
, 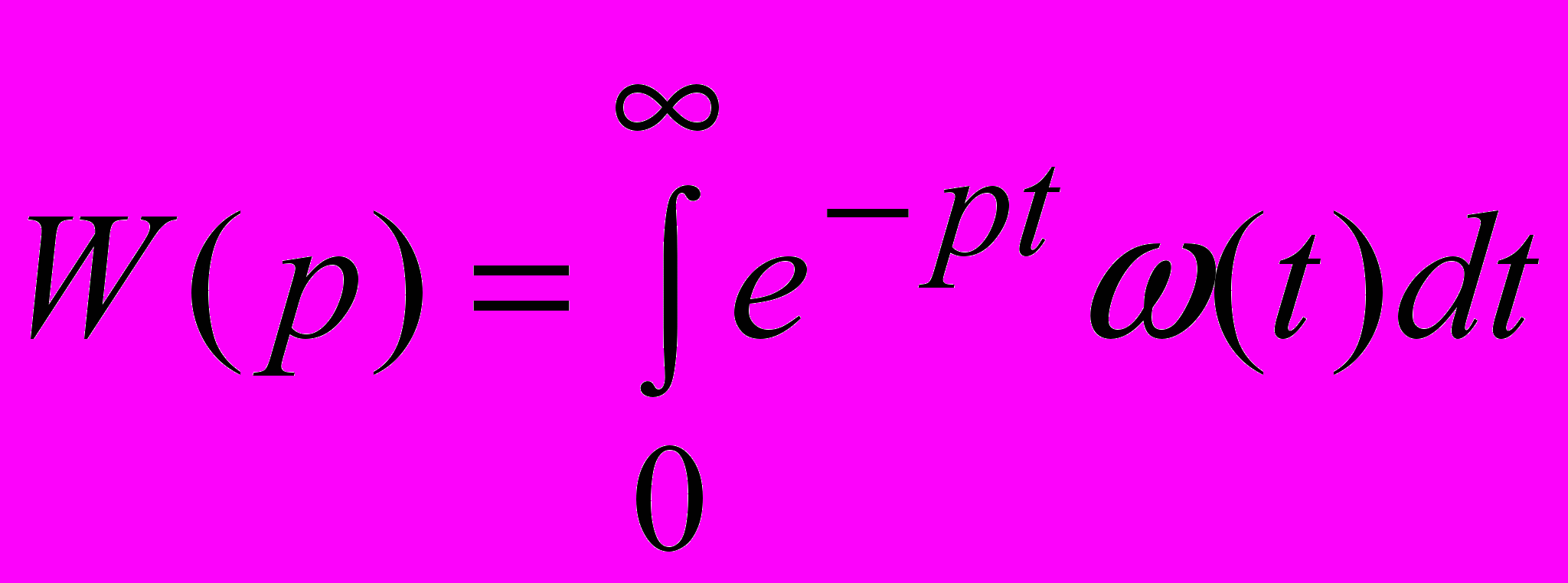 .
.(Интегральное преобразование Лапласа -
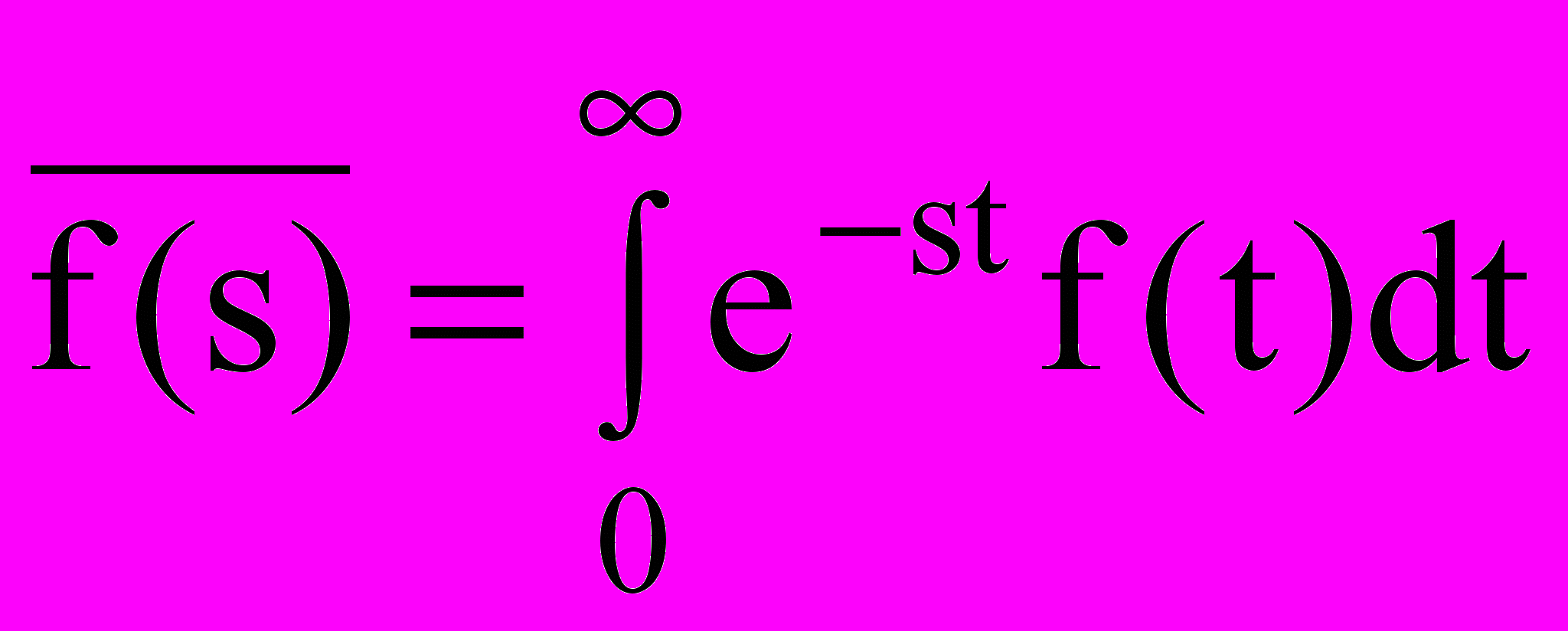 )
)Используя формулу (8) выражение (18) можно преобразовать в следующий вид:
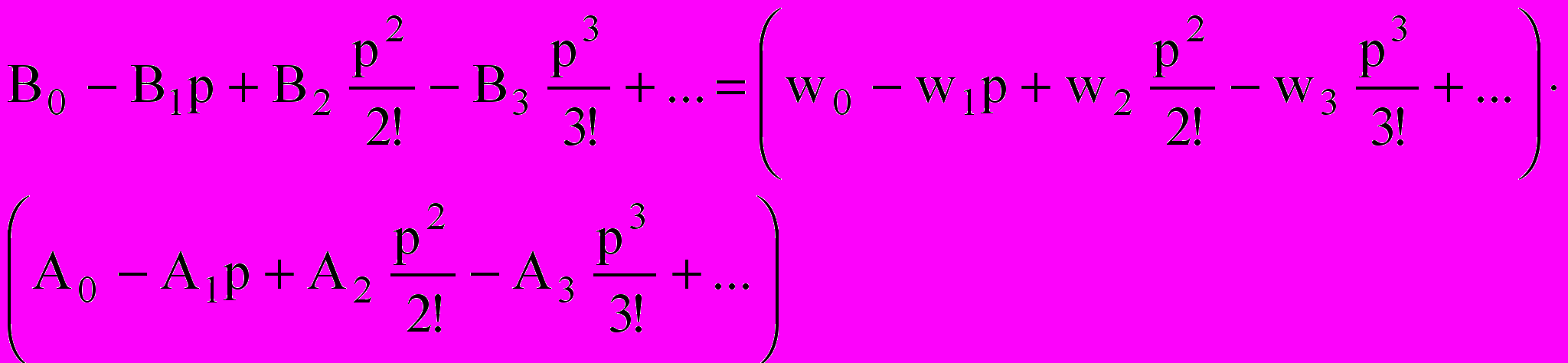 (19).
(19).Приравняв в уравнении (19) члены, стоящие при одинаковых степенях, можно получить зависимости моментов импульсной характеристики от моментов корреляционной функции и взаимно корреляционной функции:
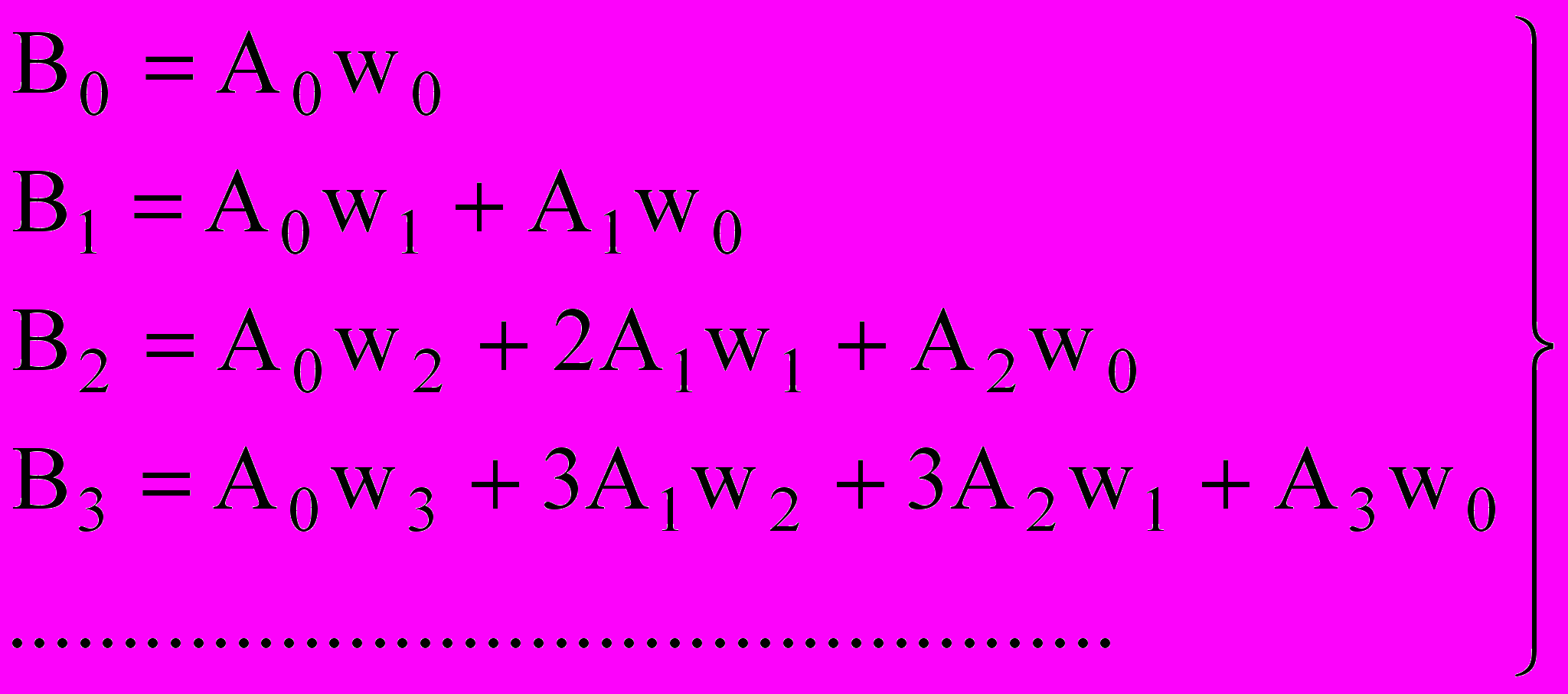 (20)
(20)Отсюда, если известны моменты корреляционной и взаимно корреляционной функций, можно вычислить моменты импульсной характеристики:
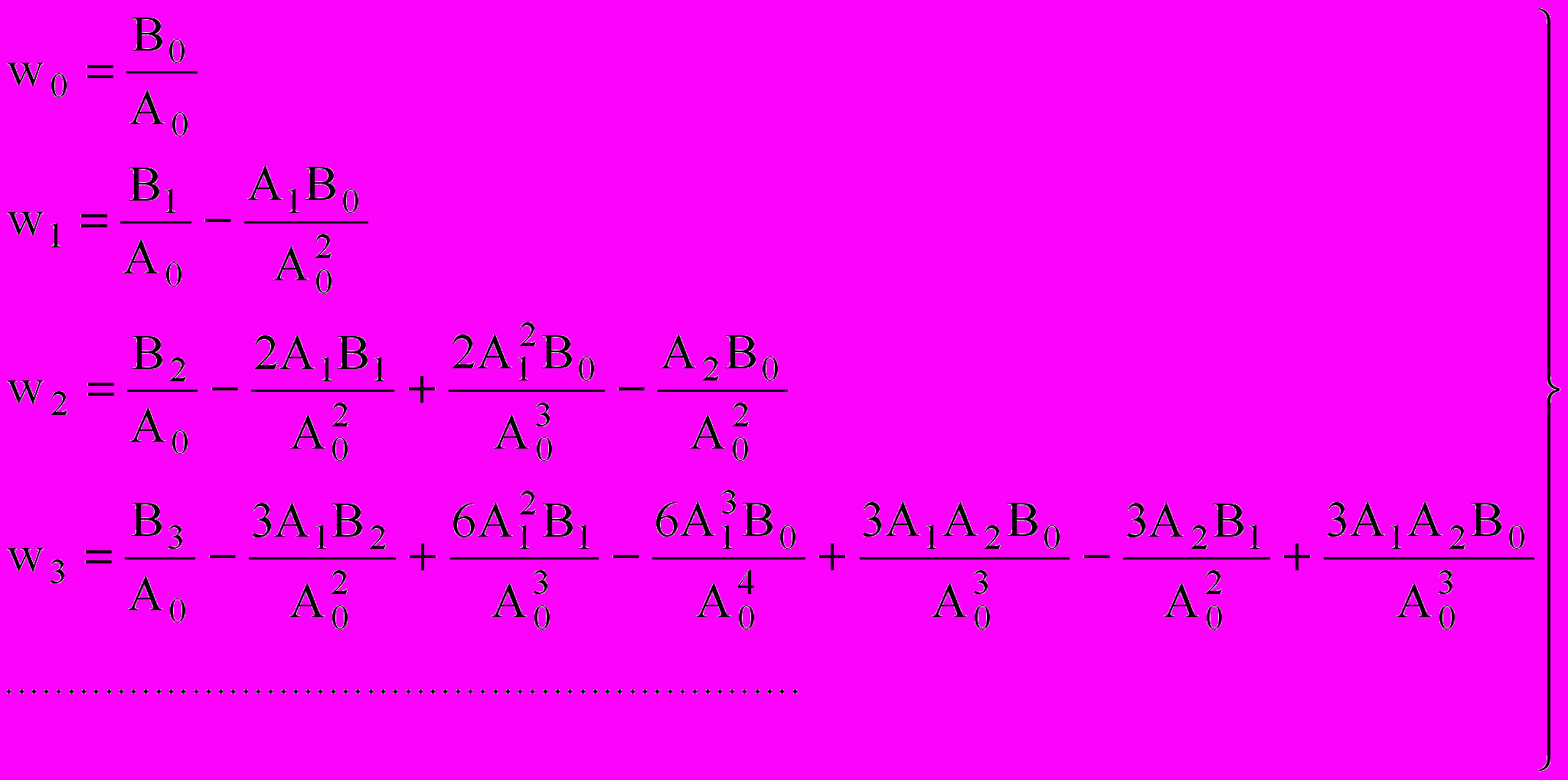 (21)
(21)Учитывая принятые допущения о стационарности и эргодичности случайного процесса на входе динамической системы, можно утверждать, что все моменты нечетного порядка корреляционной функции равны нулю -
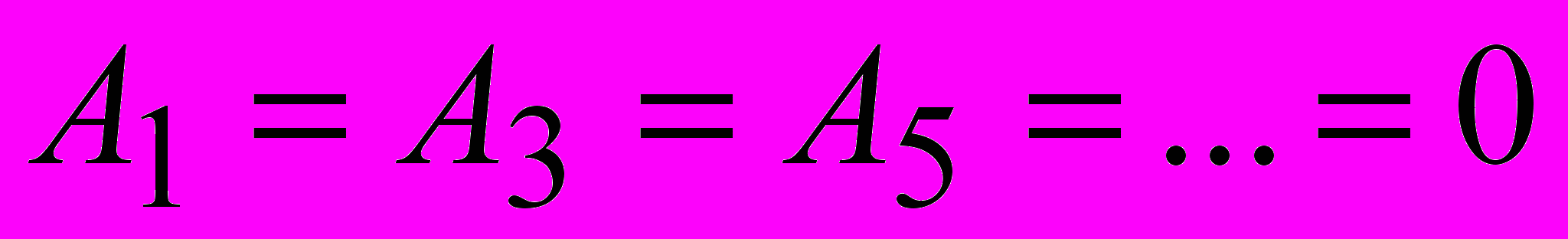 .
.Тогда формулы (21) примут достаточно простой вид:
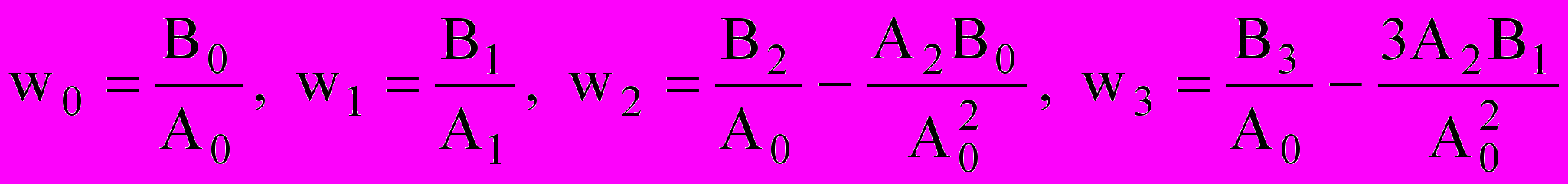 (22).
(22).На практике представление передаточной функции в виде ряда ограничивает возможности ее использования в математических моделях. Поэтому целесообразно применять метод моментов для объектов и систем, в качестве математического описания динамики которых можно ограничиться первыми членами ряда (12).
Метод определения частотных характеристик по спектральным
плотностям
Данный метод основан на следующих соображениях. Связь стохастического процесса на входе динамической системы x(t) со стохастическим процессом на ее выходе y(t) описывается обыкновенным линейным дифференциальным уравнением:
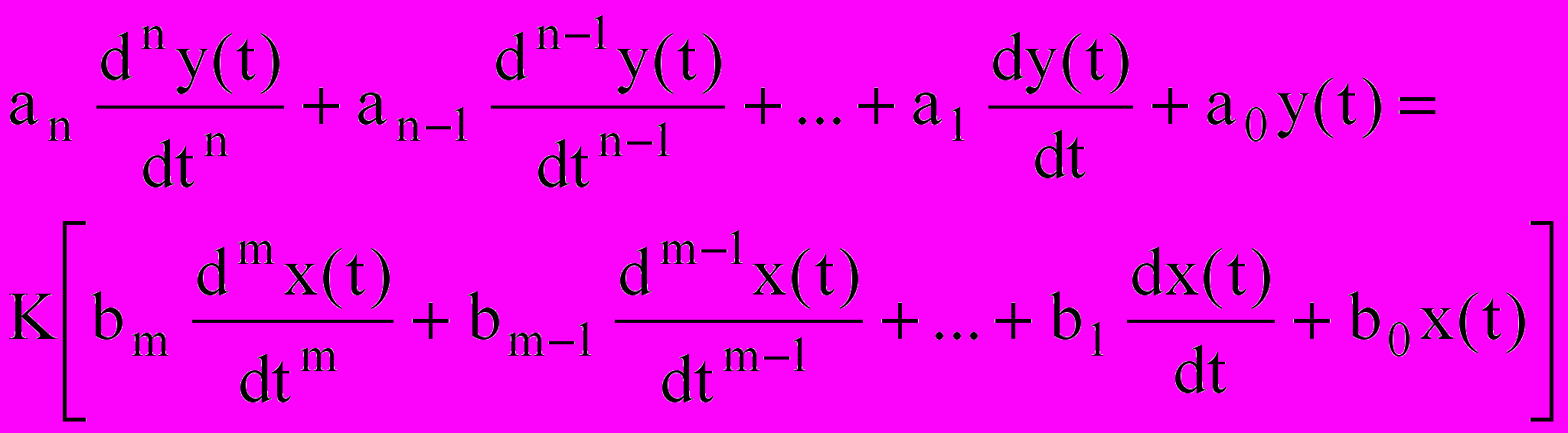 (23)
(23)Однако если было бы возможно на вход той же системы подать сигнал, совпадающий по форме с корреляционной функцией
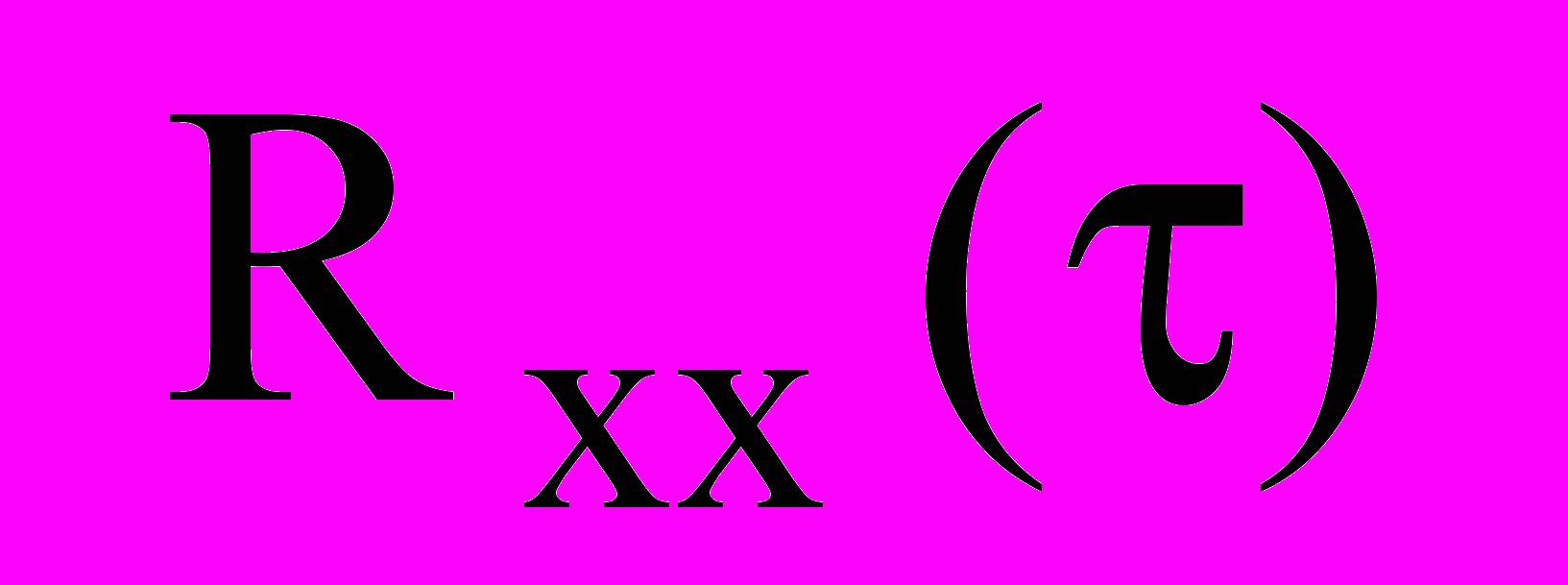 , то в соответствие с выражением (6) он вызвал бы переходный процесс, совпадающий по форме со взаимно корреляционной функцией
, то в соответствие с выражением (6) он вызвал бы переходный процесс, совпадающий по форме со взаимно корреляционной функцией 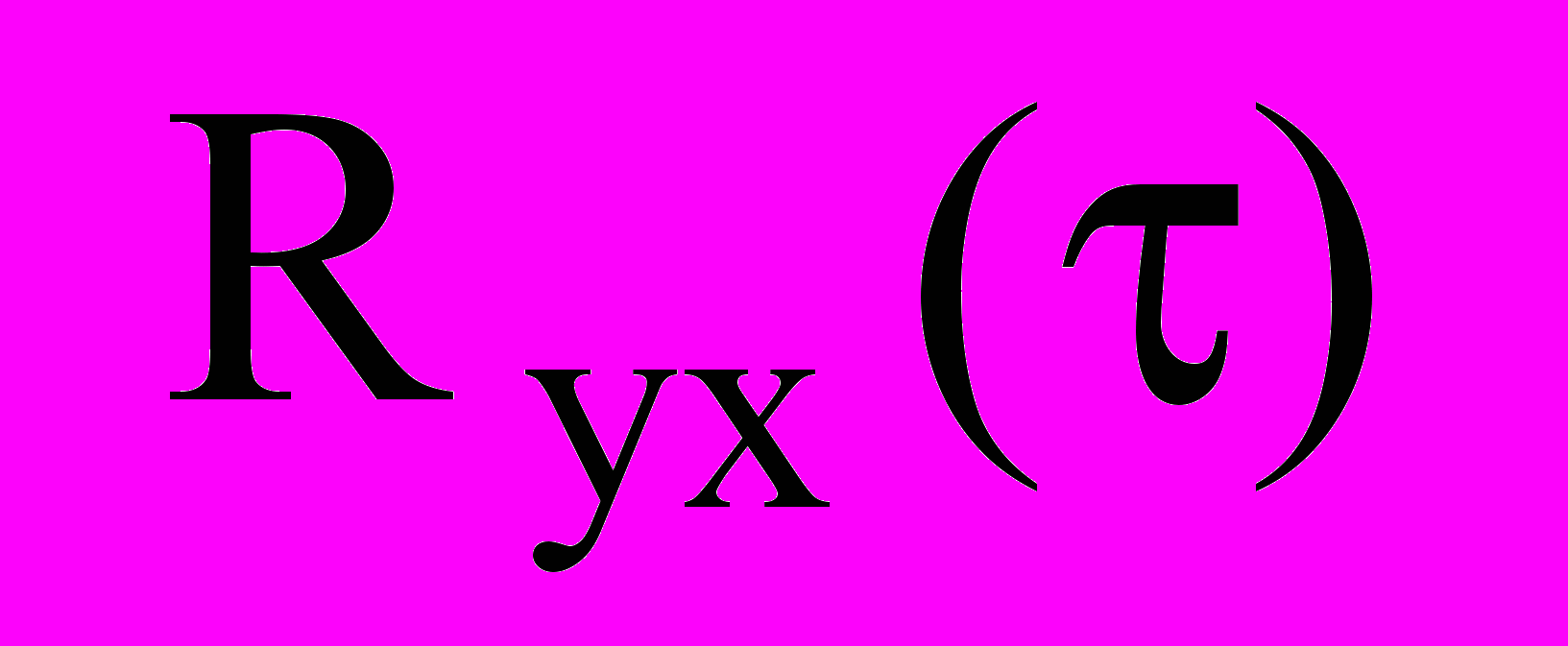 . Осуществив данные подстановки в выражении (23) получим следующее уравнение:
. Осуществив данные подстановки в выражении (23) получим следующее уравнение: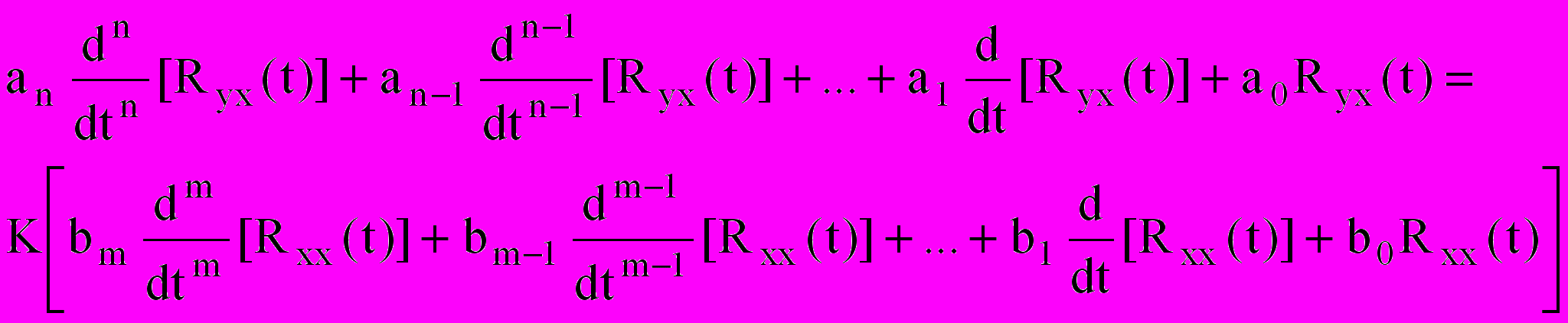 (24)
(24)С учетом того, что при n-кратном дифференцировании корреляционной функции спектральная плотность умножается на
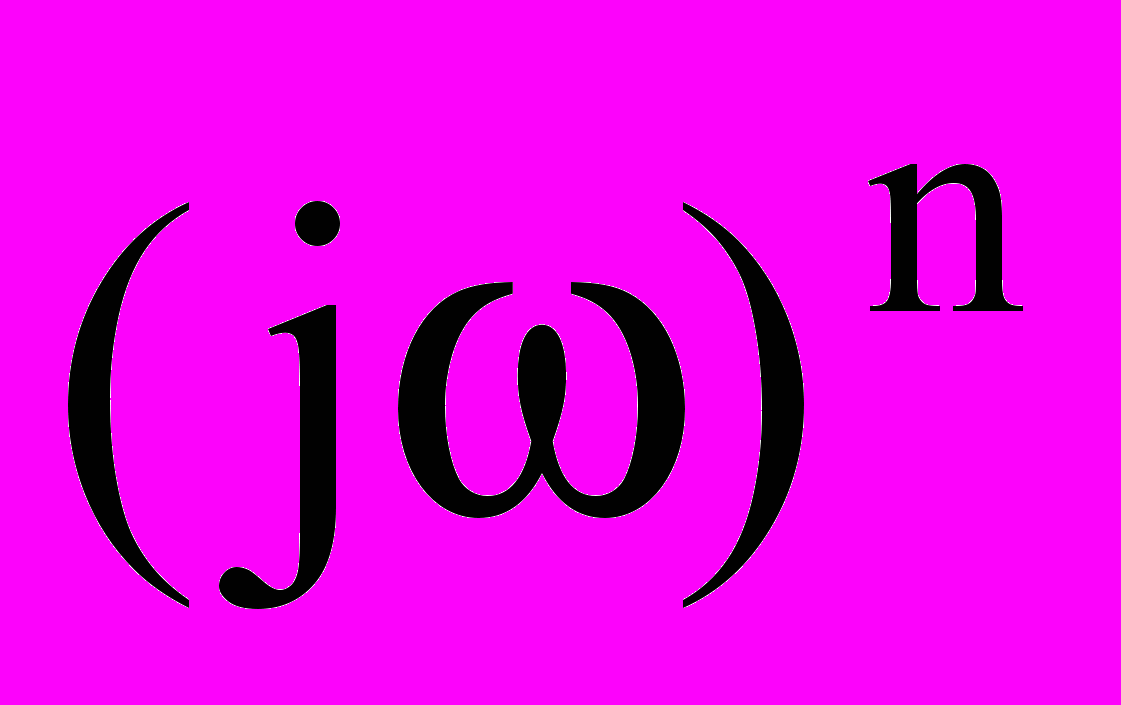 и применив преобразование Фурье к левой и правой частям уравнения (24) получаем следующее выражение:
и применив преобразование Фурье к левой и правой частям уравнения (24) получаем следующее выражение: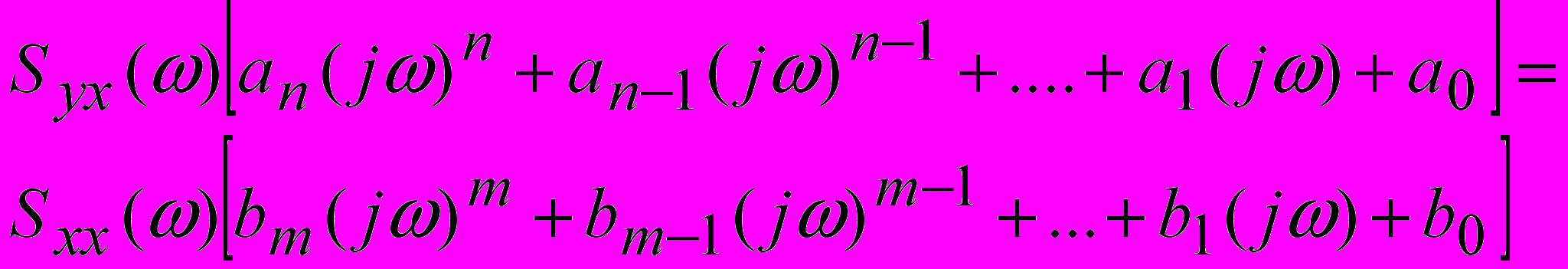 , (25)
, (25)Используя известное представление АФХ в виде отношений двух полиномов выражение (25) нетрудно привести к виду:
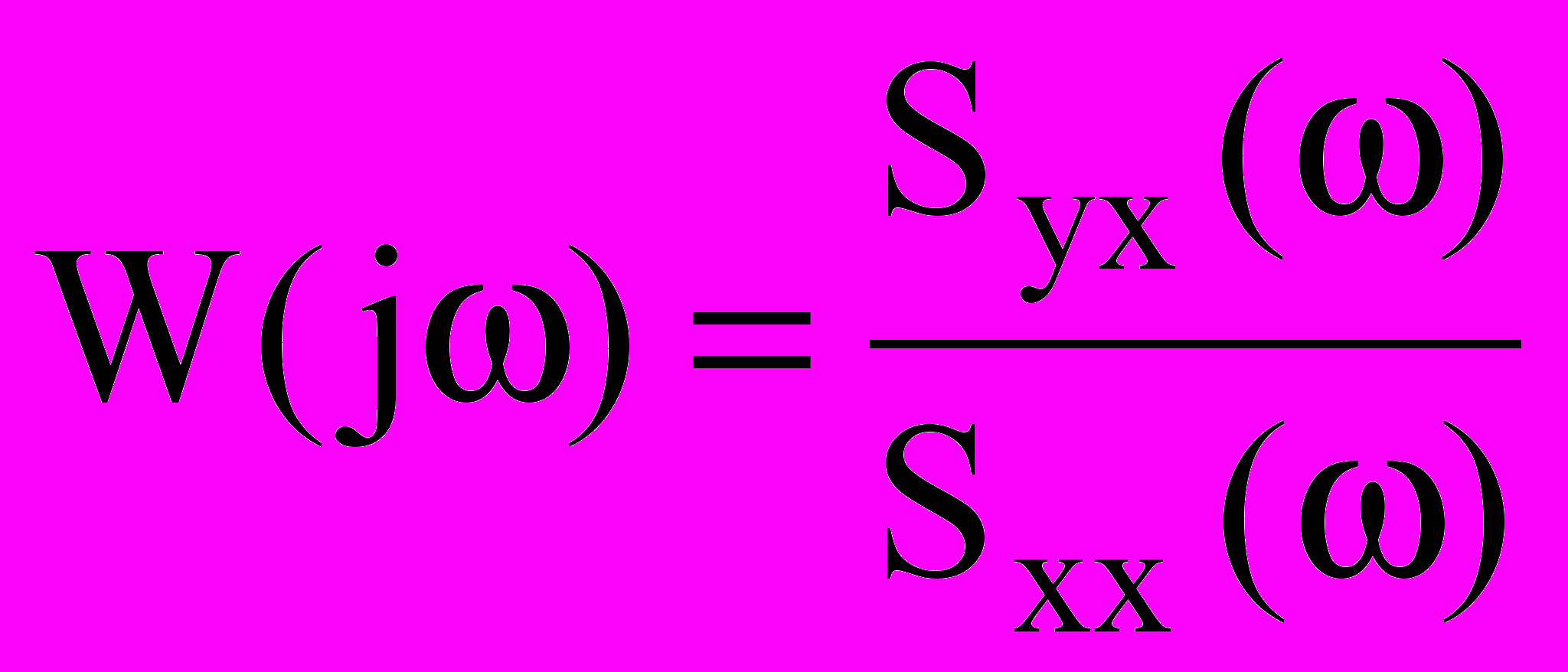 , (26)
, (26)где
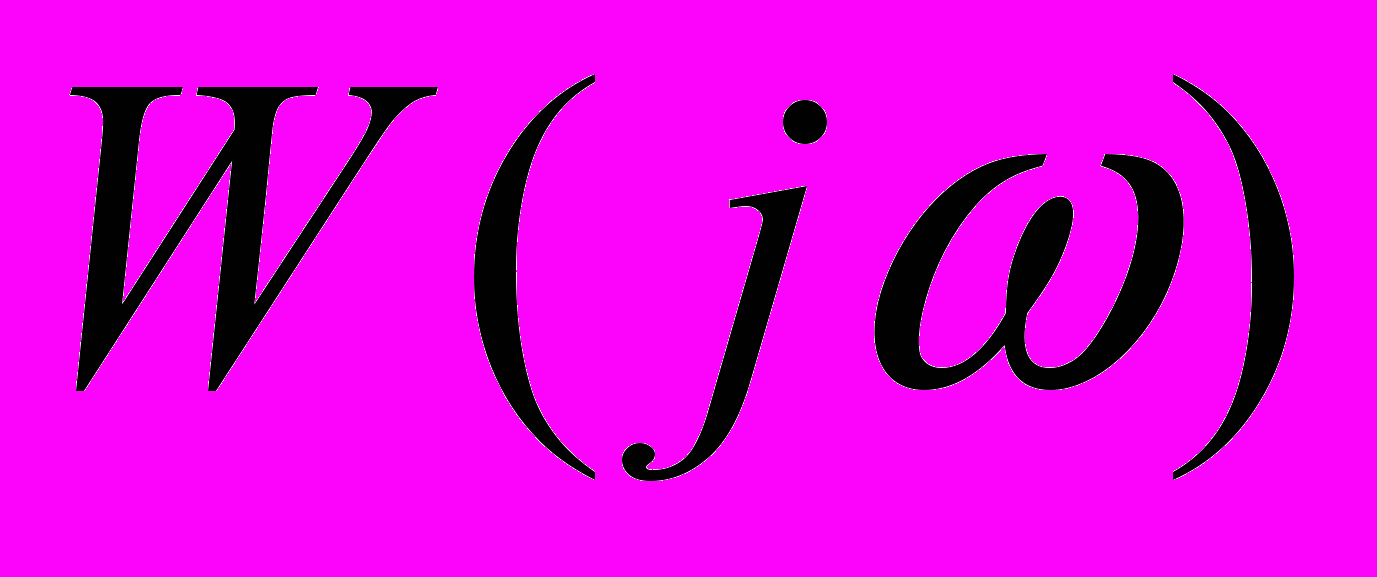 - АФХ.
- АФХ.Таким образом, имея спектральную плотность входного сигнала и взаимную спектральную плотность входного и выходного сигналов можно определить АФХ исследуемого объекта.
Автоматическое определение динамических характеристик на моделирующей установке
Известно (см. прошлые лекции), что довольно часто технологические объекты могут быть описаны передаточной функцией относительно несложного вида, например:
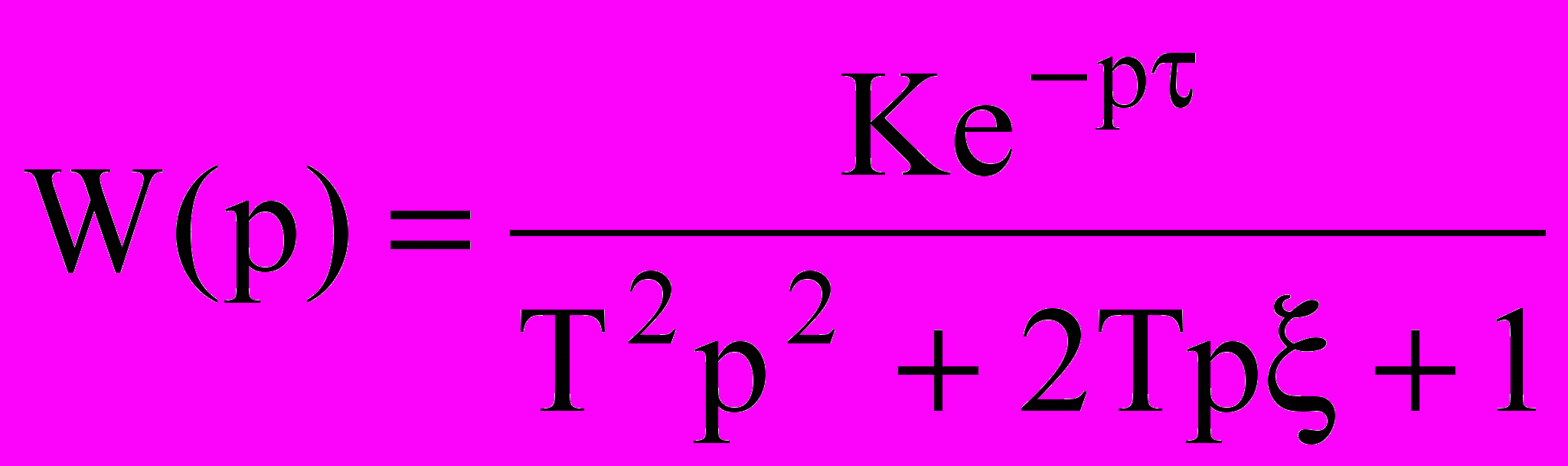 ;
; 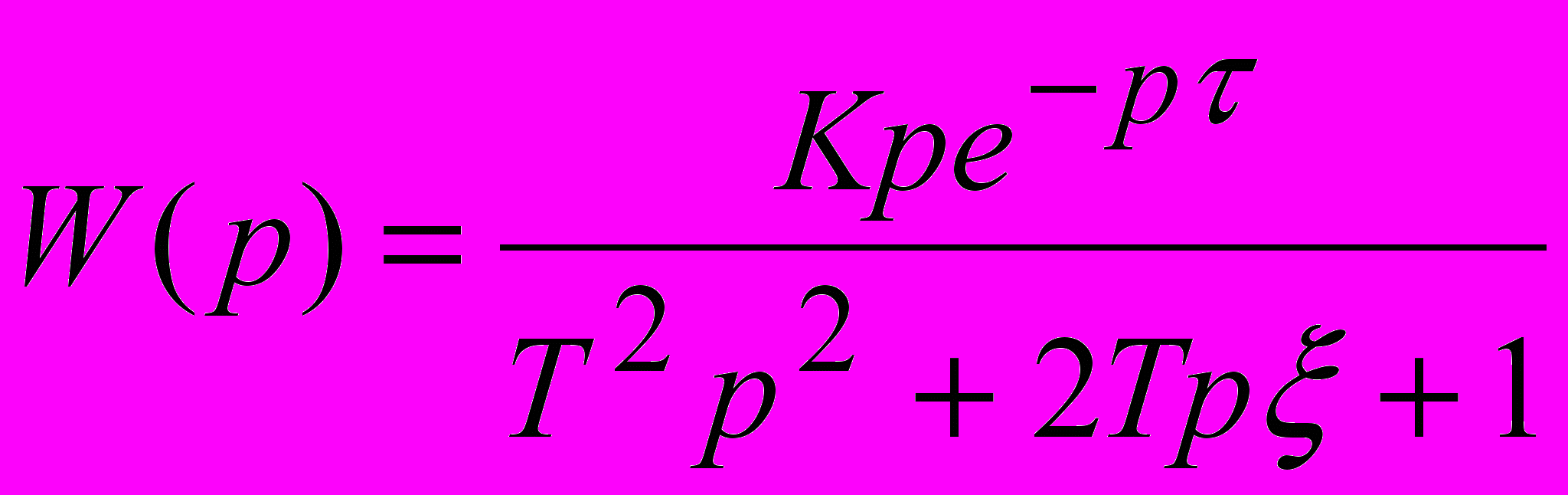 и др.
и др.В одних случаях, можно определить приблизительный вид аппроксимации некоторых свойств объекта на основе имеющегося опыта, в других – актуальным является уточнение численных значений коэффициентов известного уравнения динамики объекта. Одним из путей получения необходимых математических зависимостей является автоматический подбор соответствующих объекту значений коэффициентов на специальной установке, изображенной на рис. 3.
Суть ее работы заключается в следующем. В ЭВМ непрерывно поступают входной и выходной сигнал исследуемого объекта. ЭВМ накапливает информацию за время Т и затем приступает к настройке выбранной модели. На вход модели подается снятый с объекта сигнал x(t), а с ее выхода снимается сигнал, который сравнивается с записанным выходным сигналом объекта путем расчета среднеквадратичной ошибки. Настройка параметров модели (изменение коэффициентов передаточной функции) осуществляется методом последовательной оптимизации на основе критерия минимума вычисляемой среднеквадратичной ошибки. Фактически все описанные блоки составляют единый программный модуль, работа которого организуется человеком-оператором путем выбора вида соответствующей передаточной функции и алгоритма оптимизации ее коэффициентов. В целях повышения универсальности таких моделирующих установок в рабочую программу ЭВМ закладывают множество возможных вариантов передаточных функций, а также используют передаточную функцию в виде -
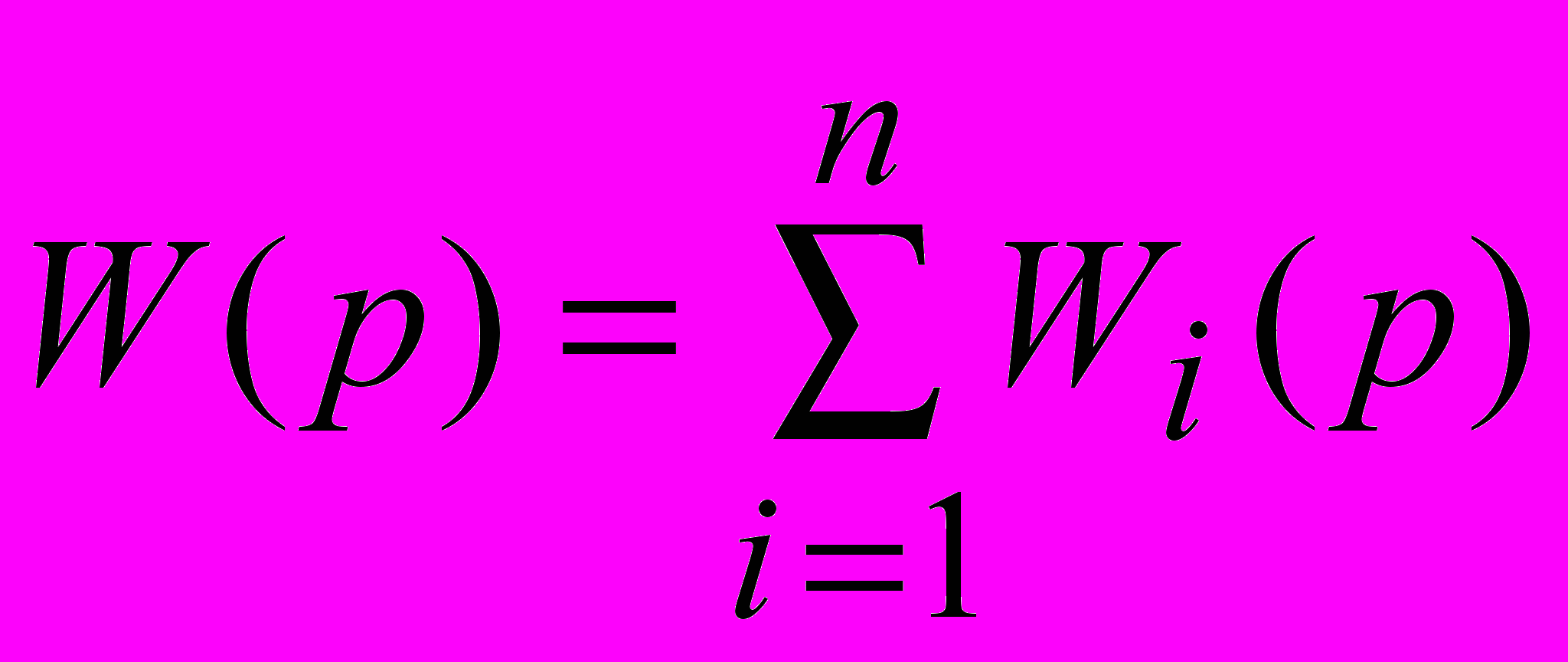 , где
, где 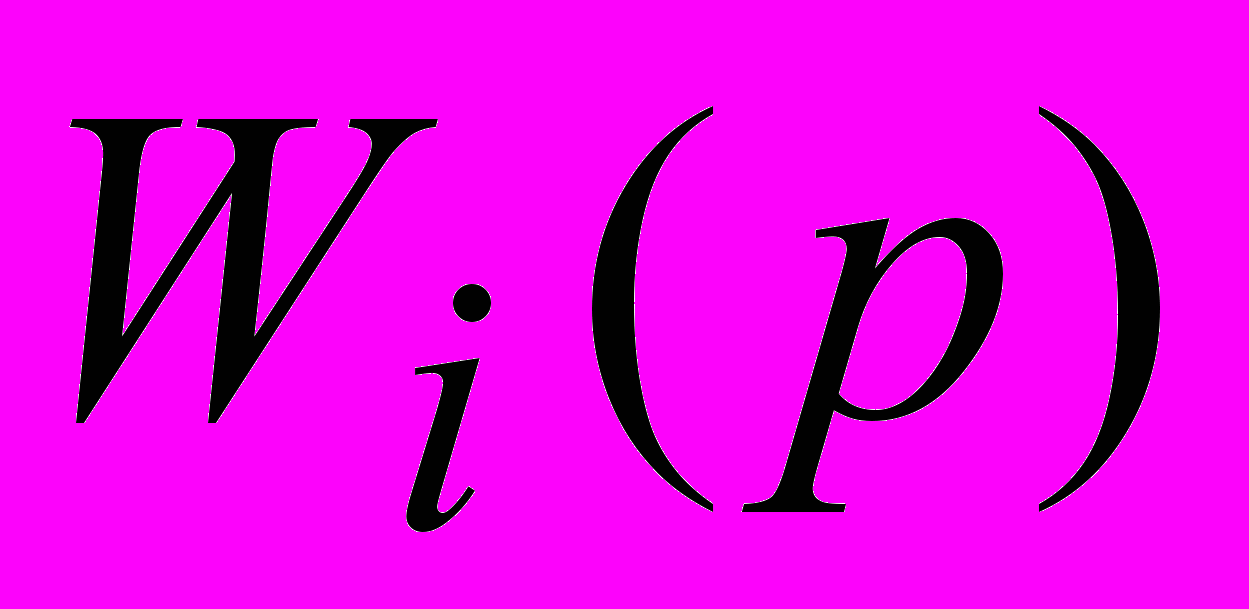 - типовые передаточные функции, соответствующие различным динамическим звеньям малых порядков.
- типовые передаточные функции, соответствующие различным динамическим звеньям малых порядков.Метод определения коэффициентов дифференциального уравнения на основе модулирующих функций
Данный метод предназначен для определения дифференциальных уравнений динамической системы при случайных воздействиях, совокупность которых является ограниченной стационарной случайной функцией с математическим ожиданием, равным нулю.
Рассмотрим суть метода на примере. Для практического использования метода задаются видом дифференциального уравнения на основании предварительно имеющейся информации об объекте. В частном случае динамическая связь "вход-выход" может быть записана в виде дифференциального уравнения:
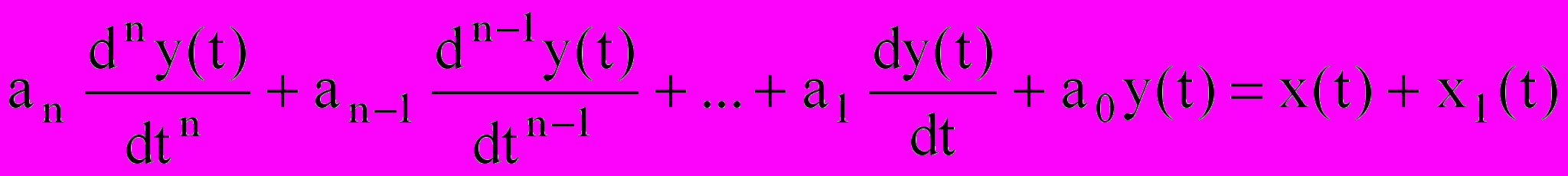 , (27)
, (27)где a0, a1, …, an – неизвестные коэффициенты, подлежащие определению;
x1(t) – случайный процесс на входе системы.
Далее производится подбор модулирующей функции
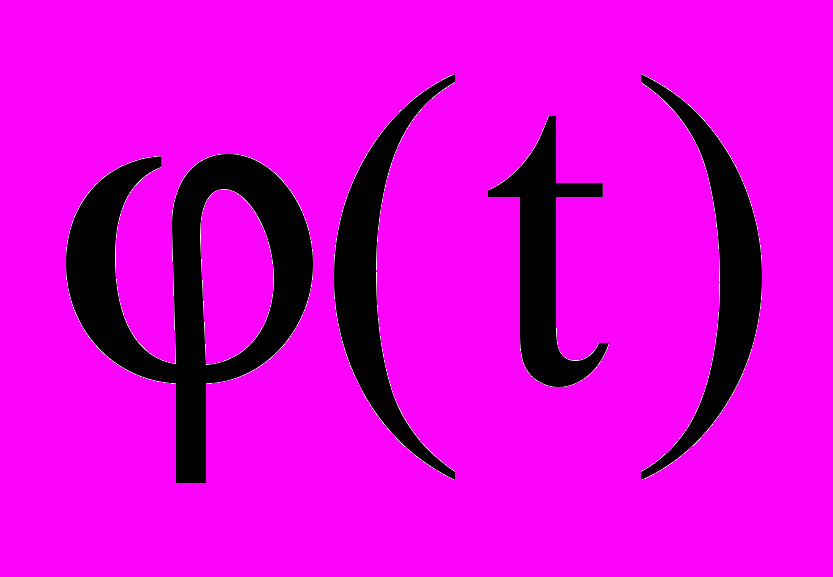 . К этой функции предъявляются следующие требования – она должна быть ограниченной, непрерывной и дифференцируемой, а также в моменты времени t=0 и t=T модулирующая функция и все ее производные до (n-1)-й включительно должны обращаться в ноль.
. К этой функции предъявляются следующие требования – она должна быть ограниченной, непрерывной и дифференцируемой, а также в моменты времени t=0 и t=T модулирующая функция и все ее производные до (n-1)-й включительно должны обращаться в ноль.В качестве модулирующих функций для исследуемого интервала времени [0,T] можно воспользоваться функциями вида:
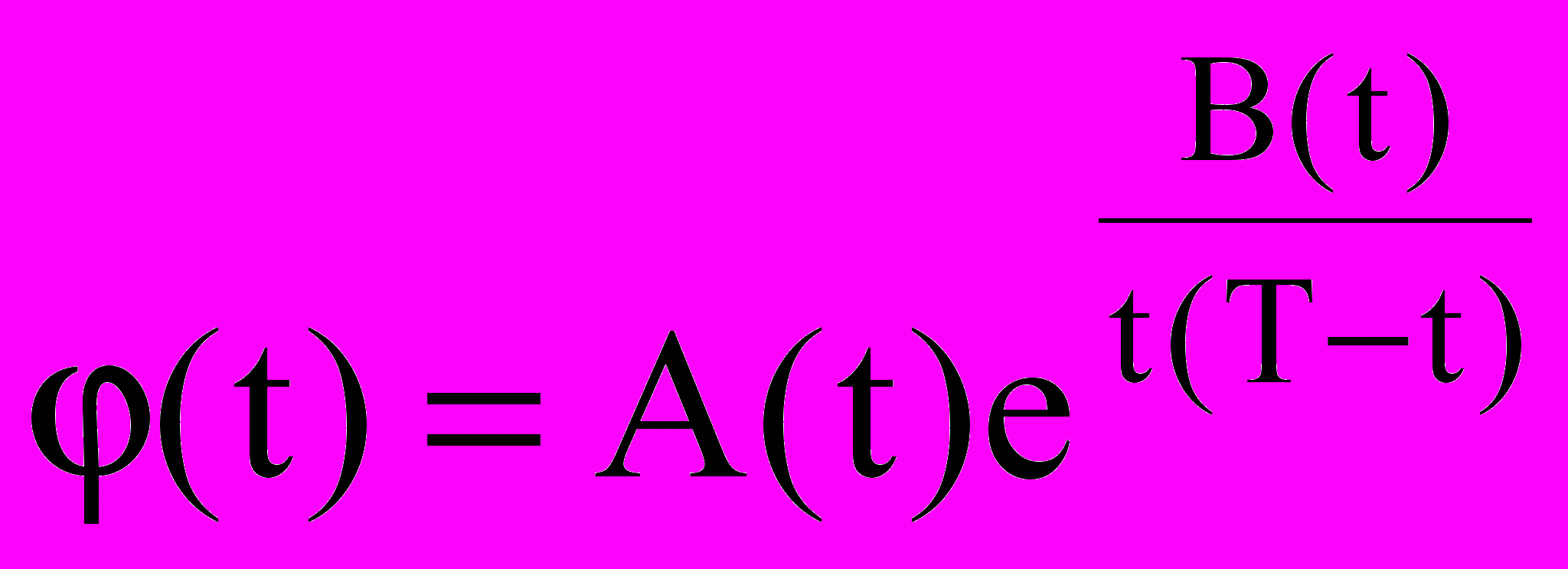 или
или 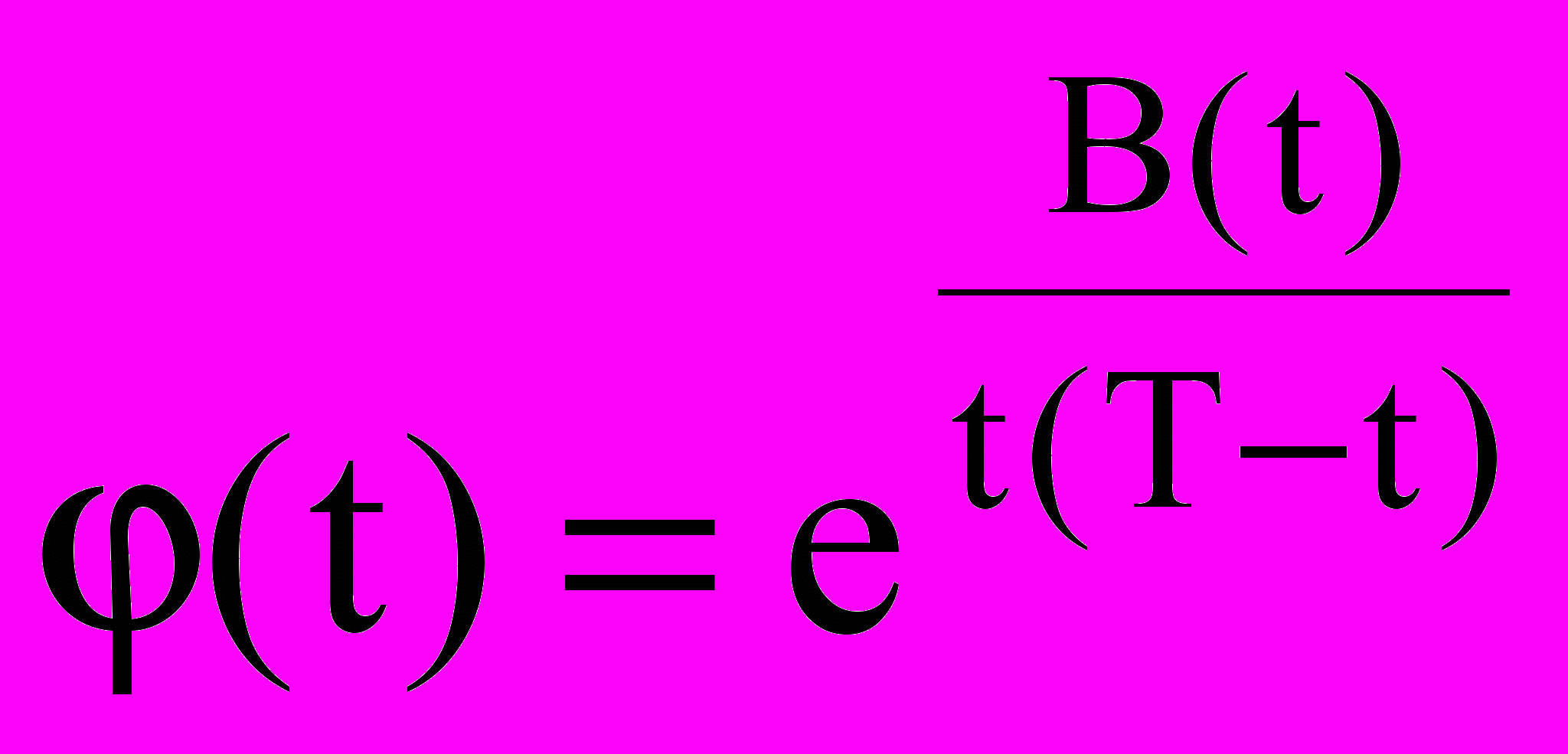 .
.Уравнение (27) умножается на модулирующую функцию, а потом интегрируется:
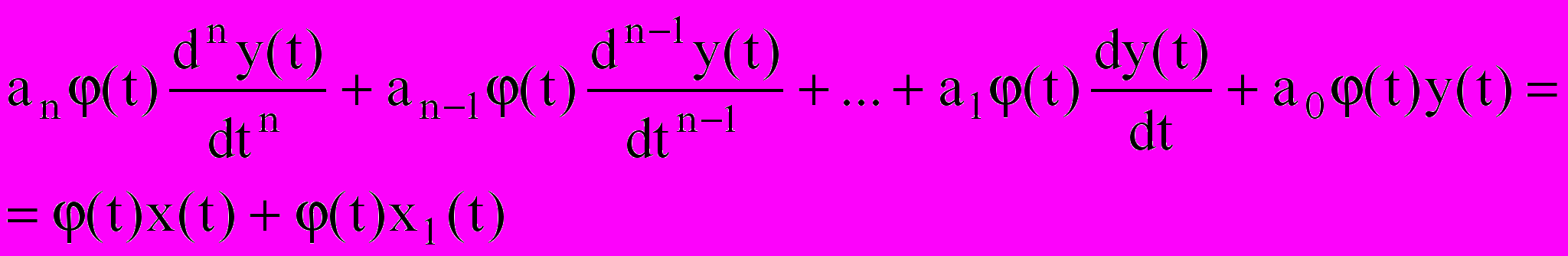
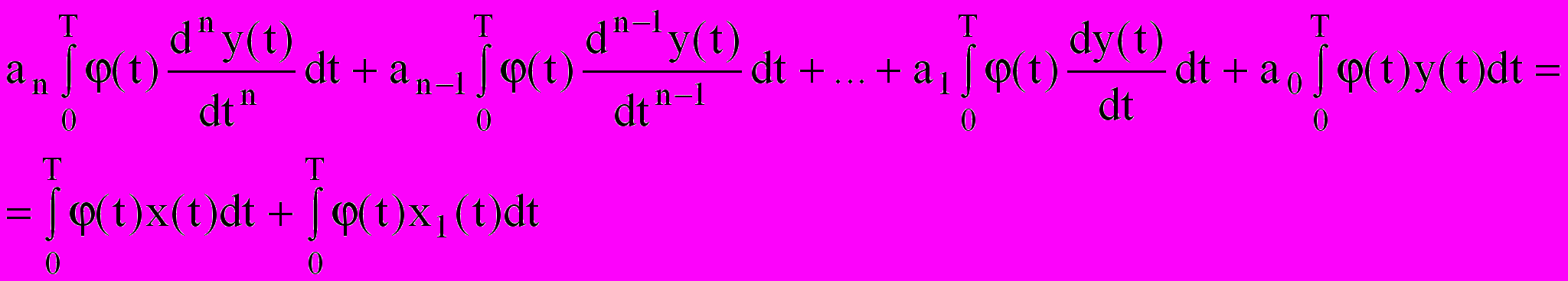 (28)
(28)Если каждый из членов полученного уравнения проинтегрировать по частям число раз, равное порядку производной величины y(t), стоящей под знаком интеграла, а затем исключить из полученного выражения составляющие, обращающиеся в ноль вследствие предъявленных в функции
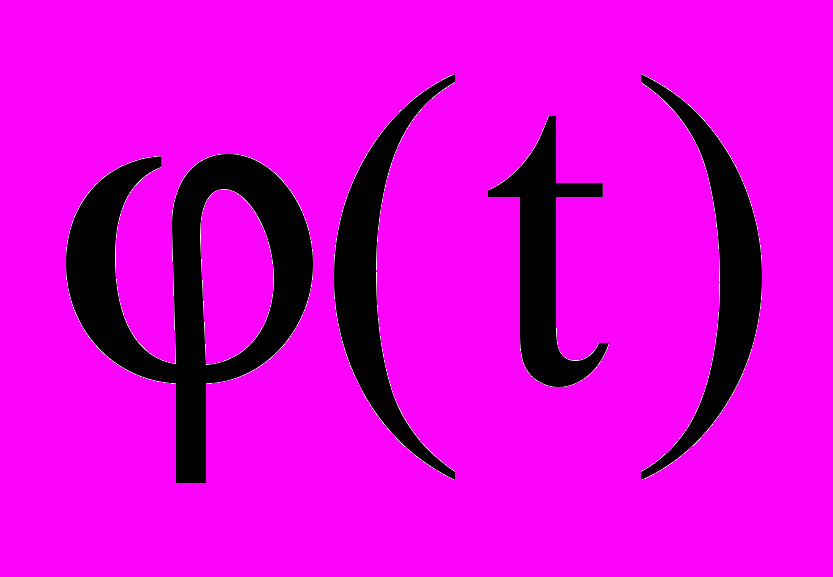 требований, а также пренебречь интегралом от случайного процесса ввиду принятого допущения о равенстве нулю его математического ожидания, то выражение (28) примет следующий вид:
требований, а также пренебречь интегралом от случайного процесса ввиду принятого допущения о равенстве нулю его математического ожидания, то выражение (28) примет следующий вид: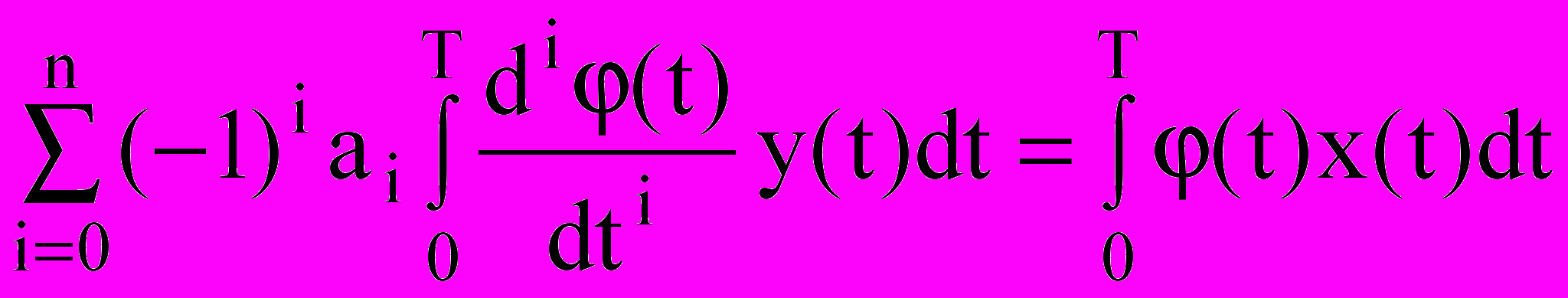 (29).
(29).Уравнение (29) имеет (n+1) неизвестный. Для того, чтобы их определить необходимо располагать по крайней мере (n+1) реализацией величины y(t) и соответствующими по времени реализациями величины x(t). Подставляя их значения в выражение (29), получаем систему из (n+1) уравнения с (n+1) неизвестными, которая может быть решена известными математическими методами. Для уменьшения погрешности определения коэффициентов аi при наличии достаточного количества реализаций составляется и решается избыточное количество уравнений. Для решения такой системы можно воспользоваться методом наименьших квадратов.
Балакирев В.С. и др. Экспериментальное определение динамических характеристик промышленных объектов управления. М. Энергия , 1967, 232 с.
Ордынцев В.М. Математическое описание объектов автоматизации. М. Машиностроение, 1965, 360 с.
