Удк 51-77 компьютерная реализация математической модели рынка труда1

Вид материала

Документы

Подобный материал:

• Информатика, вычислительная техника и инженерное образование 2011, №1(3) эволюционное, 635.81kb.
• Реализация и исследование устойчивости модели распределения ресурсов, 26.84kb.
• С. Н. Трапезников московский инженерно-физический институт (государственный университет), 22.46kb.
• Построение математической модели эмоций, 109.31kb.
• Лекции по математической логике и теории алгоритмов для студентов 2 курса специальности, 769.24kb.
• Шкаберин В. А. Определение математической модели. Преимущества математического моделирования., 66.58kb.
• И бурно развивающихся направлений научных исследований сегодня является компьютерная, 61.81kb.
• Списо к научных трудов Сатаева, 51.11kb.
• Создание матричных математических моделей для компьютерных лабораторных работ в mathcad, 41.98kb.
• Программа по курсу «Дифференциальные уравнения», 41.77kb.

УДК 51-77

КОМПЬЮТЕРНАЯ РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЫНКА ТРУДА¹

О.И. Скворцова,

И.В. Зайцева

Ставропольский государственный университет


Приведем алгоритм исследования на устойчивость математической модели самоорганизации рынка труда представленной для двух отраслей экономики в работе [1] и в работе [2] для нескольких отраслей экономики, которая в матричном виде записывается следующим образом:

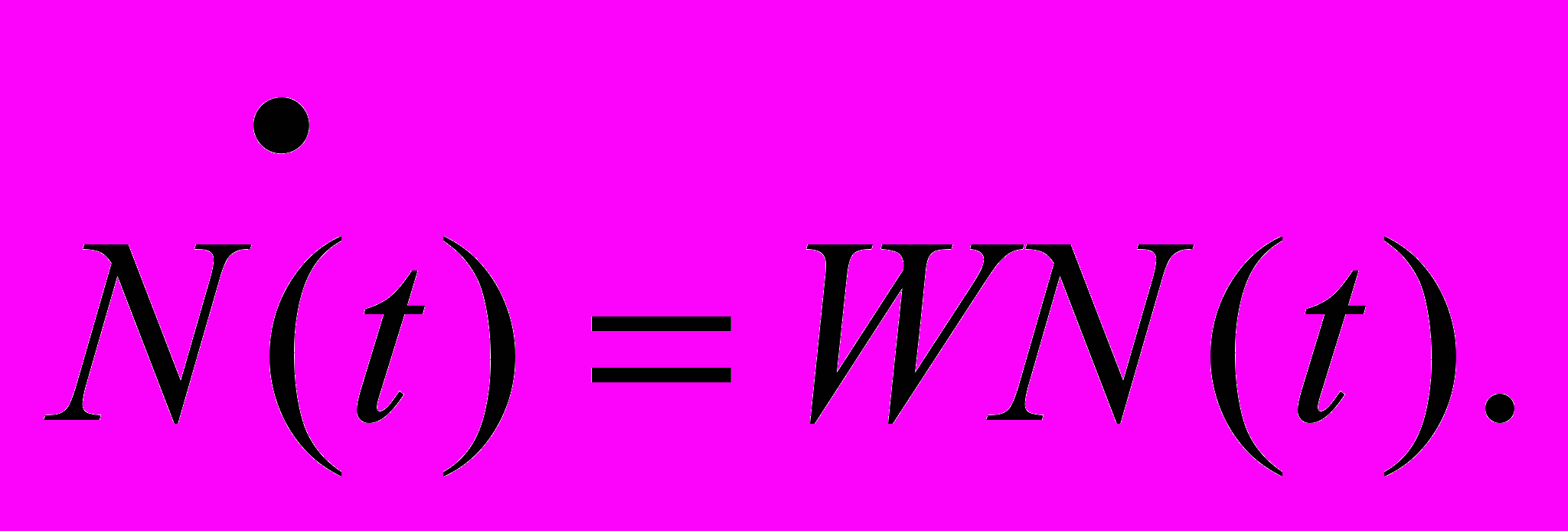(1)

Для исследования на устойчивость системы дифференциальных уравнений, описывающей динамику перераспределения рабочей силы в n различных отраслях экономики, необходимо:

1. записать систему дифференциальных уравнений, описывающую динамику перераспределения рабочей силы для нескольких различных отраслей экономики;
   
2. составить матрицу W коэффициентов системы дифференциальных уравнений, введя конкретные значения вероятностей 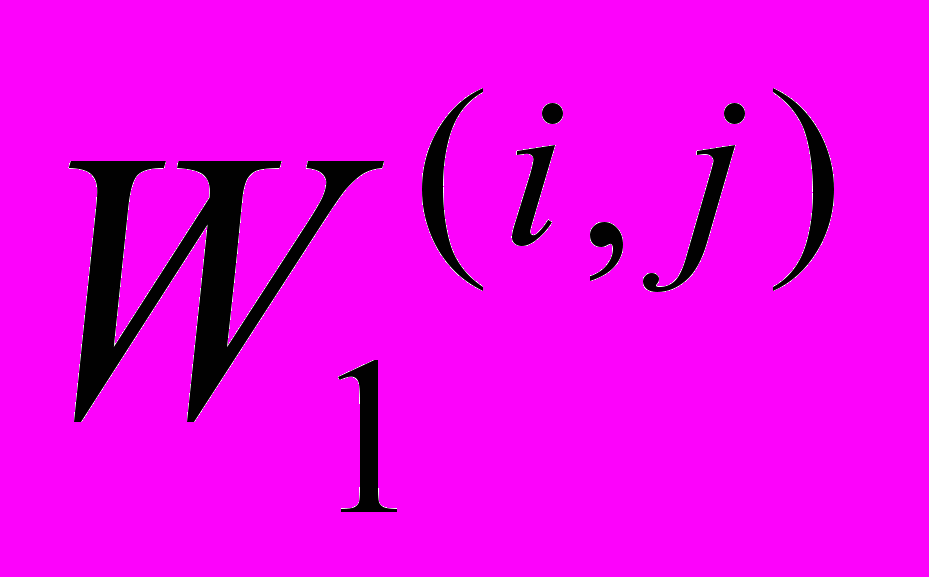, , 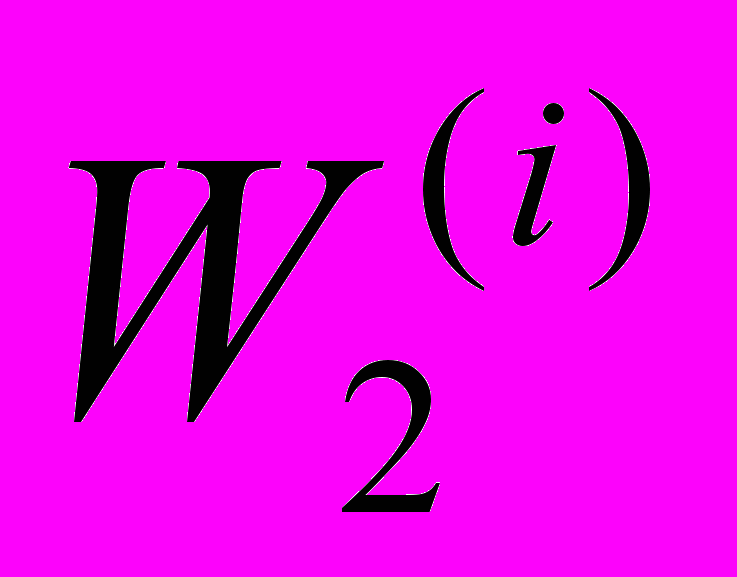i, j=1,…,n;
   
3. составить характеристическое уравнение det (W–I) = 0 для полученной матрицы коэффициентов W;
   
4. составить матрицу Гурвица для характеристического уравнения матрицы коэффициентов W;
   
5. вычислить диагональные миноры для полученной матрицы Гурвица;
   
6. сделать вывод об устойчивости системы дифференциальных уравнений.
   

Указанная методика реализована в виде программного продукта (с использованием пакета прикладных программ MathCad).

На основании полученных сведений об устойчивости системы дифференциальных уравнений можно судить о состоянии рынка труда.

Список литературы

1. Семенчин Е.А., Зайцева И.В. Математическая модель самоорганизации рынка труда для двух отраслей экономики. // Экономика и математические методы, 40(2), 2004. – С. 137-139.
   
2. Семенчин Е.А., Зайцева И.В. Математическая модель самоорганизации рынка труда для нескольких отраслей. //Обозрение прикладной и промышленной математики, 10(3), 2003. – С. 740-741.