Предисловие к русскому изданию постижение через сопряжение

Вид материала

Документы

Содержание Таблица 1.2. Перекрестная классификация данных табл. 1.1 45 и моложе 1.3. Выборки, совокупности и случайные отклонения Таблица 1.5. Результаты второй команды 1.4. Нормальное распределение 1.5. Распределение хи-квадрат Y имеет распределение ? с d

Подобный материал:

• Содержание: Предисловие к русскому изданию, 4891.77kb.
• Предисловие к русскому изданию, 304.63kb.
• Предисловие к русскому изданию, 2977.53kb.
• Хейне П. Предисловие к русскому изданию, 9465.34kb.
• Предисловие к русскому изданию, 23302.08kb.
• Предисловие к русскому изданию, 3882.25kb.
• Предисловие к русскому изданию, 7003.78kb.
• За пределами мозга предисловие к русскому изданию, 6134.84kb.
• Предисловие к новому изданию, 3293.79kb.
• Электронная библиотека студента Православного Гуманитарного Университета, 3857.93kb.

Таблица 1.2. Перекрестная классификация данных табл. 1.1

Предпочтение	Мужчины			Женщины
	старше 45 лет	45 лет и моложе	всего	старше 45 лет	45 лет и моложе	всего
Крикет Теннис	58 24	74 38	132 62	12 86	13 95	25 181
Всего	82	112	194	98	108	206

Мы можем рассматривать две части табл. 1.2 как две подтаблицы. Каждая из них учитывает два критерия - пол и предпочтение. Поэтому мы называем такую таблицу таблицей с двумя входами. С другой стороны, поскольку подтаблица легко располагается на плоскости и образует массив чисел, мы можем говорить о ней и как о двумерном массиве или двумерной таблице. Причем полную таблицу можно было бы легко представить на плоскости только после разбиения, показанного в табл. 1.2. Правда, в основу разбиения в табл. 1.2 положен такой признак, как пол, а мы могли бы с равным успехом разделить, скажем, по возрасту, что показано в табл. 1.3.

Табл. 1.2 и 1.3 - это фактически два альтернативных двумерных представления трехмерной таблицы, показанной на табл. 1.4. В табл. 1.4 выявляется симметричность структуры табл. 1.1, которая затушевана во всех других способах представления данных. В этом смысле представления в табл. 1.2 и 1.3, может быть, были бы лучше, но это, конечно, не метод записи данных, который был бы удобен на практике.

Таблица 1.3. Альтернативное представление табл. 1.1

Предпочтение	Старше 45			45 и моложе
	мужчины	женщины	всего	мужчины	женщины	всего
Крикет Теннис	58 24	12 86	70 110	74 38	13 95	87 133
Всего	82	98	180	112	108	220

[8]


Таблица 1.4.

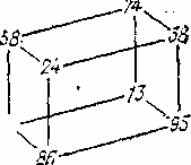Трехмерное

представление табл. 1.2

 

Позже мы выясним, как вести анализ трехмерных данных, вроде тех, что представлены в табл. 1.1, а заодно исследуем и методы, которые с равным успехом можно приложить и к n-мерным данным при n>3.

1.3. ВЫБОРКИ, СОВОКУПНОСТИ И СЛУЧАЙНЫЕ ОТКЛОНЕНИЯ

В табл. 1.1 мы привели гипотетическое множество результатов обследования. Теперь нам стоит проследить за историей этих результатов от исходного набора предписаний, данных коллективу обследователей (<команде>). В общем можно предположить, что эти предписания звучали приблизительно так: <Пойдите и опросите 400 взрослых людей, классифицируя опрашиваемых по следующим правилам...> Если правила выборки сформулированы, то результаты образуют выборку, от которой можно ожидать, что она станет зеркалом совокупности, из которой ее извлекли. Выходит, что сама совокупность оказывается в зависимости от правил выборки. Так, если все опрашиваемые въезжали в Большой Лондон между 10 и 11 часами утра в пятницу 22 июля 1977 г., то результаты, строго говоря, образуют выборку из совокупности людей, доступных для интервьюирования именно в этом месте и в это время. Если эта совокупность совсем такая же (с точки зрения таких признаков, как пол, возраст и крикет/теннис-предпочтение), как и прочее население Великобритании, то тогда и только тогда имело бы смысл извлекать эту выборку из всего населения страны. Огромные трудности выбора из неоднородных совокупностей и детали соответствующих методов мы оставим за границами нашей книги. Заинтересованные читатели могут обратиться к работе [Сосhran W. G., 1963].

Таблица 1.5. Результаты второй команды

Предпочтение	Старше 45			45 и моложе
	мужчины	женщины	всего	мужчины	женщины	всего
Крикет Теннис	53 25	20 76	73 101	68 36	11 111	79 147
Всего	78	96	174	104	122	226

[9]

Мы, конечно, не должны ожидать, что выборочными характеристиками будут всякий раз в точности одни и те же числа. Если, например, другая команда повторит обследование, пользуясь теми же самыми методами, что и первая, то интервьюированию подвергнется другая выборка и результаты могут получиться вроде тех, что представлены в табл. 1.5. Хотя эти результаты разительно отличаются от данных табл. 1.3, все же остаются в силе окончательные суждения о предпочтениях крикета для мужчин и тенниса для женщин. Важный момент состоит в том, что сами изменения надо рассматривать как выборочные различия. Назовем их случайными выборочными различиями (отклонениями). Отсюда само собой следует, что у нас нет оснований верить в точное отражение в выборке свойств совокупности.

1.4. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Есть в статистике очень важная теорема, называемая центральной предельной теоремой. Она, между прочим, утверждает, что любые величины, которые в основном состоят из множества аналогичных отдельных значений, должны иметь приближенное нормальное распределение. А поскольку мы очень часто вынуждены иметь дело с суммами, нормальное распределение играет в статистике важную роль. Особенно важно так называемое единичное (нормированное) нормальное распределение - частный случай нормального со средним 0 и дисперсией 1.

Если X - случайная величина с единичным нормальным распределением, то мы определим

Р [X ? х] = Ф (х), (1.1)

где выражение в левой части уравнения (1.1) читается так: <вероятность того, что случайная величина X примет значение, меньшее или равное x>. Поскольку единичное нормальное распределение симметрично относительно среднего, равного 0, справедливо тождество

Ф(-х) = 1-Ф(х). (1.2)

В приложении 1 приведены краткие таблицы значения Ф (х) для положительных х. А для отрицательных значений х можно воспользоваться соотношением (1.2).

Пример 1.1

Известно, что случайная величина X имеет единичное нормальное распределение. Пусть нас интересуют следующие вопросы:

а. Чему равна вероятность того, что X превышает 0,4?

б. Будет ли значение - 1,8 необычайно малым?

Обратимся к приложению 1. Для х = 0,4 находим Ф(0,4) = 0,655. Это вероятность того, что X меньше, чем 0,4, следовательно, требуемая вероятность равна: 1 - 0,655 = 0,345.

Для х = 1,8 находим Ф(1,8) = 0,964. Нас же интересует вероятность Р [X ? - 1,8], которая в силу симметрии равна Р[X?1,8], и, следовательно, составляет 1 - 0,964 = 0,036, или 3,6%. Мы можем почувствовать, что - 1,8 это действительно довольно малое значение.

[10]

1.5. РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ

Следующее распределение вероятностей, имеющее первостепенное значение при анализе таблиц сопряженности, это распределение хи-квадрат (?²), которое следующим образом соотносится с нормальным распределением. Если X имеет единичное нормальное распределение, то X² имеет распределение ?² с параметром 1. Существует целое семейство распределений ?², зависящих от параметра, называемого <числом степеней свободы>.

Если случайная величина Y имеет распределение ?² с d степенями свободы, то мы пишем, что Y имеет -распределение.

В приложении 2 для разных значений d приводятся значения у, соответствующие вероятностям Р [Y >у] = 0,10; 0,05; 0,01 и 0,001. Ниже показано на примерах, как пользоваться этими таблицами.

У ?²-распределения много интересных и полезных свойств. Так, если Y и Z - независимые случайные величины с распределениями ? - и ?- соответственно, то (У + Z) имеет распределение ?-- А вот еще узелок на память: среднее распределения ?- равно d.

Дальнейшие подробности относительно ?² и нормального распре-делений можно найти в более простых учебниках статистики, см., например, книгу [Yeomans К. А., 1968]. А более подробные таблицы обоих распределений содержатся во многих сборниках статистических таблиц*, например в [Lindley D. V., Miller J. C.P., 1952].