Джеймс трефил

Вид материала

Закон

Содержание Зависимость количества видов от площади экосистемы Оптимального фуражирования Альберт Эйнштейн у доски с формулами специальной теории относительности. Теория относительности и кван Равновесие в природе Зеленая революция

Подобный материал:

• Джеймс А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон, 42.79kb.
• Джеймс блиш города в полете 1-4 триумф времени вернись домой, землянин жизнь ради звезд, 10495.38kb.
• Джеймс Н. Фрей. Как написать гениальный роман, 2872.12kb.
• Мюриел Джеймс, Дороти Джонгвард, 4810.7kb.
• Кен Арнольд Джеймс Гослинг, 5058.04kb.
• Джеймс Джодж Бойл. Секты-убийцы (Главы из книги) Перевод с английского Н. Усовой, 844.92kb.
• Джеймс Хэрриот, 3697.74kb.
• В. К. Мершавки Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 1972.4kb.
• В. К. Мершавки   Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 5237.48kb.
• Джеймс Боллард, 2244.23kb.

теорема

о маргинальных

значениях


Многое в поведении животных можно описать с помощью математических методов (см., например, теория оптимального фуражирования). Один из таких аспектов поведения можно выразить простым вопросом: как долго животному имеет смысл добывать корм на одном участке и когда ему уже пора перейти в другое место? Какая стратегия позволяет максимально увеличить его общее энергопотребление?

Это типичная задача для теории игр — раздела математики, в котором для выработки стратегий, позволяющих максимально повысить шансы выигрыша в игре, используется метод вероятностного рассуждения. Эта теория применима и к обычным азартным играм вроде покера, и к таким «играм», как военная стратегия, расположение торговых представительств и размещение рекламы. Эти же методы применяются и для изучения стратегии фуражирования.

Когда животное приходит на новый участок, оно начинает потреблять ресурсы, которые оно там нашло. Представьте лошадь, которая зашла на лужайку с высокой травой, или лисицу, которая оказалась в местности, изобилующей грызунами. Приступив к потреблению этих ресурсов, животное начинает получать энергию. Вначале количество получаемой энергии будет резко расти, поскольку потребление энергии животным подскакивает от нуля (во время поиска энергоресурсов) до того количества, которое оно получает на этом новом участке. Однако по мере того, как животное потребляет эти ресурсы, общее количество полученной энергии достигает определенного стабильного уровня. Когда все ресурсы будут исчерпаны, энергопотребление вновь упадет до нуля и общая энергия, получаемая на данном участке, будет оставаться на постоянном уровне. Вопрос заключается в следующем: когда наступает наилучший момент для животного, чтобы двинуться дальше, оставив некоторое количество неиспользованных ресурсов, и идти вперед, чтобы найти новую ресурсную базу? Ответ на этот вопрос дает теорема о маргинальных значениях, предложенная в 1966 году американским экологом Эриком Л. Чарновом (Eric L. Charnov, р. 1947).

Теорема учитывает время, затраченное на переход от одной ресурсной базы к другой, — назовем его временем перемещения. Время, в течение которого животное остается в определенной ресурсной области, назовем временем пребывания. Оптимальная стратегия — та, которая позволяет максимально увеличить общее потребление энергии с течением времени. Если животное получает энергию E за данное время пребывания, то общая скорость энергопотребления за все время t (включающее время перемещения плюс время пребывания) будет равна E, деленному на t.

Давайте начнем с предположения, что ресурсы на всех участках одинаковые — например, что все лужайки с травой одинаково

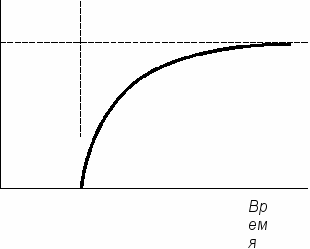Животное, нашедшее новый пищевой ресурс, вначале получает большое количество энергии, но по мере того, как ресурс истощается, лучшей стратегией для животного будет идти вперед в поисках нового ресурса. Вертикальная пунктирная линия — начало потребления животным пищевого ресурса, горизонтальная пунктирная линия — максимальный уровень энергопотребления


зеленые. Математическая теория игр утверждает, что животное максимально увеличит общее получение энергии во времени, если оно будет покидать каждый участок, как только скорость получения энергии в ней достигнет максимума. Иными словами, время идти дальше наступает именно тогда, когда все идет наилучшим образом. Если животное останется на месте, это позволит ему действительно получить больше энергии от известного источника, но общее количество энергии, которое оно приобретет, будет меньшим, чем оно получило бы, если бы ушло на другой участок немедленно.

Что же происходит в реальной ситуации, когда участки различаются по количеству ресурсов? Теорема утверждает, что лучшая стратегия для животного — покидать каждую область, независимо от ее богатства, как только скорость получения энергии упадет до максимума, который может дать средний участок. Таким образом, оптимальный момент для оставления участка наступает тогда, когда маргинальное (предельное) значение скорости получения энергии достигает этой средней скорости потребления (отсюда и название теоремы).

Теорема прогнозирует, что потребители питательных веществ будут проводить меньше времени на лужайках, где меньше пищи. Далее следует, что эти потребители будут уходить с таких лужаек быстрее, если лужайки расположены близко друг к другу, чем когда они находятся далеко друг от друга. Потребители также будут покидать такие лужайки быстрее, если они расположены в местности, изобилующей кормами, чем если этот участок небогат кормом.

По поводу такого подхода к объяснению поведения животных необходимо сделать одно замечание. Никто не предполагает, конечно, что животное садится с калькулятором и высчитывает скорость своего энергопотребления. Если рассуждать с позиций теории эволюции, то теорема о маргинальных значениях говорит нам, что если животное случайно найдет оптимальную стратегию, то оно будет иметь больше шансов передать свои гены следующему поколению. В конце концов через какое-то время животные придут к своей оптимальной стратегии, даже ни разу не задумавшись о ней.

В этом смысле эволюция во многом похожа на «невидимую руку» в теории экономических рынков шотландского экономиста


Адама Смита, бытовавшую в XVIII веке. Действуя за сценой, она способствует такому поведению, которое приносит максимальную выгоду. Классический «экономический человек», согласно этой теории, действует абсолютно рациональным образом с полным знанием рынка и не имеет никакого сходства с реальным человеком, чье поведение будет предпочтительным и в итоге — преобладающим. Аналогичным образом животные, которые не перемещаются из одной области в другую в соответствии с теоремой о маргинальных значениях, будут в среднем менее удачливыми, чем те, которые перемещаются. В конечном счете всегда побеждает стремление к действию.


Теория молекулярных орбиталей

Связывание атомов в молекулах определяется тем, как перекрываются их волновые функции


1919 • ПРАВИЛО ОКТЕТА


1926 • УРАВНЕНИЕ ШРЁДИНГЕРА


кон. • теория 1920-х МОлЕКулЯРНЫХ

орбиталей


1930-е • ХИМИЧЕСКИЕ СВЯЗИ


Атомы объединяются в молекулы благодаря химическим связям. Причем участвуют в образовании этих связей электроны, находящиеся во внешнем слое этих атомов. существует несколько теорий, описьтающих процесс связывания. Одна из них — теория валентных связей, в соответствии с которой связи между атомами образуются, когда атомы обмениваются электронными парами из перекрывающихся орбиталей. Другая — теория молекулярных орбиталей.

Такого рода приблизительные теории полезны, поскольку мы получаем простой, интуитивно понятный способ представления физических процессов. С другой стороны, современные компьютеры дают нам возможность с высокой точностью вычислить энергии связи, однако такие вычисления ничуть не приближают нас к пониманию того, что же происходит, когда атомы соединяются. Роль теорий как раз в том и состоит, чтобы дать нам это понимание.

В основе теории молекулярных орбиталей лежит представление о том, что электронная орбиталь в атоме описывается волновой функцией (см. уравнение шрёдингера). Теория объясняет, как при протекании химической реакции атомные орбитали преобразуются в молекулярные. Подобно большинству известных нам типов волн, волновые функции электронов в орбиталях претерпевают интерференцию. Оказывается, орбитали в молекулах можно, с хорошим приближением, представить как результат интерференции волновых функций атомов.

например, рассмотрим, что происходит при взаимодействии двух атомных орбиталей соседних атомов. Если в области перекрывания орбиталей волновые функции претерпевают конструктивную интерференцию, электроны большую часть времени проводят между ядрами, притягивая атомы друг к другу. С другой стороны, если интерференция в области перекрывания деструктивная, электронная плотность между ядрами равна нулю и между атомами возникает результирующая сила отталкивания. Таким образом, две атомные орбитали объединяются с образованием двух молекулярных орбиталей: одна стремится связать атомы (связывающая молекулярная орбиталь), а другая — оттолкнуть их (разрыхляющая молекулярная орбиталь). и их взаимодействие определяет, будет ли образована стабильная молекула.

Чтобы понять, как работает эта модель, попробуем разобраться, почему водород образует молекулу из двух атомов, а гелий — из одного. В образовании связи между двумя атомами водорода участвуют по одному электрону от каждого атома, а на низшей (связывающей) молекулярной орбитали как раз есть место для двух электронов. Электроны основное время находятся между ядрами, значит, атомы притягиваются и молекула водорода может образоваться. У гелия же в образовании связи между двумя атомами участвуют четыре электрона, поэтому заняты как связывающая, так и разрыхляющая атомные орбитали. Численные вычисления показывают, что в этом случае будет преобладать эффект отталкивания, и даже если молекулы гелия образуются, они будут крайне нестабильны. Поэтому молекула газа гелия состоит из одного атома.

ок. 1900
Теория оптимального фуражирования

Выбор хищником жертвы зависит от того, сколько времени занимает поиск добычи, и от того, сколько времени требуется, чтобы поймать и употребить ее в пищу


•

ЗАВИСИМОСТЬ КОЛИЧЕСТВА ВИДОВ ОТ ПЛОЩАДИ ЭКОСИСТЕМЫ


ТЕРРИТОРИАЛЬНОСТЬ У ЖИВОТНЫХ


1926

1934

ОТНОШЕНИЯ ХИЩНИК—ЖЕРТВА


ПРИНЦИП

КОНКУРЕНТНОГО


1966
ИСКЛЮЧЕНИЯ


ТЕОРИЯ


1970-е
ОПТИМАЛЬНОГО ФУРАЖИРОВАНИЯ


ДИФФЕРЕНЦИАЛЬНОЕ


1976
ИСПОЛЬЗОВАНИЕ РЕСУРСОВ


ТЕОРЕМА

О МАРГИНАЛЬНЫХ

ЗНАЧЕНИЯХ


Иногда чистая математика переплетается с явлениями реального мира довольно неожиданным образом. Теория оптимального фуражирования, которую разработали Роберт Макартур (см. теория равновесия макартура—уилсона) и Эрик Пианка в 1966 году, — типичный тому пример. Многие животные на самом деле могут употреблять в пищу гораздо больше разнообразных видов добычи, чем они реально употребляют. Тогда каковы принципы, которыми руководствуются животные при выборе добычи? С такого рода проблемами имеет дело раздел математики под названием теория игр.

Для начала надо сказать, что каждый тип добычи может обеспечить хищника определенным количеством энергии — назовем ее Е. Чтобы получить эту энергию, хищник должен потратить какое-то время на выполнение двух задач: он должен сначала найти добычу, а затем поймать и съесть ее — экологи называют это временем обработки добычи. Скорость потребления энергии хищником будет равна энергии Е, деленной на сумму времени поиска и обработки добычи. Согласно теории оптимального фуражирования, поведение животных будет развиваться в направлении выработки такой стратегии, которая обеспечит самую высокую скорость потребления энергии.

Из этого положения вытекает несколько выводов. В частности, если на поиск и обработку нового вида добычи животное затрачивает больше энергии, чем на поиск и обработку добычи, уже существующей в его рационе, животное ограничит разнообразие своей диеты. Вот почему животные имеют узкий рацион питания.

Теория также предсказывает, как будут вести себя животные в определенных ситуациях. Например, время поиска может быть долгим, а время обработки коротким — представьте себе птицу, скачущую вокруг дерева в поисках насекомых, или медведя, бредущего по лесу и переворачивающего стволы деревьев в поисках муравьев. Как только добыча найдена, на ее потребление уйдет совсем небольшая часть общего затраченного времени — основное время ушло на поиск. Животные в такой ситуации становятся универсалами, употребляя в пищу самую разнообразную добычу.

Если же, наоборот, время поиска мало, а время обработки велико, можно ожидать различные типы поведения. Например, лев на равнинах африканского национального парка Серенгети живет в пределах прямой видимости антилопьих стад, так что его время поиска добычи практически равно нулю, однако поимка антилопы может потребовать значительных затрат времени и энергии. В этом случае выбор добычи будет узким. Лев будет нападать на старых, хромых или совсем молодых животных, чтобы свести к минимуму время обработки.

Животные могут быть вынуждены отказаться от своей стратегии оптимального фуражирования. Для тех, кто не находится наверху пищевой цепи, существует постоянная угроза со стороны хищников. Перед лицом этой угрозы животное скорее перейдет на менее энергетическую пищу в безопасном месте, нежели будет следовать тому, что в отсутствие хищников было бы для него стратегией оптимального фуражирования. В противном случае оно может закончить свою жизнь в качестве Е в чьем-то еще уравнении.


Теория относительности


•

1604, 1609
Законы природы не зависят от систем отсчета

уравнения

равноускоренного


•

1687
движения


1687

закон всемирного тяготения ньютона


законы механики


1891
ньютона


принцип


1905, 1916
эквивалентности


ТЕОРИЯ

ОТНОСИТЕЛЬНОСТИ


Говорят, что прозрение пришло к Альберту Эйнштейну в одно мгновение. Ученый якобы ехал на трамвае по Берну (Швейцария), взглянул на уличные часы и внезапно осознал, что если бы трамвай сейчас разогнался до скорости света, то в его восприятии эти часы остановились бы — и времени бы вокруг не стало. Это и привело его к формулировке одного из центральных постулатов относительности — что различные наблюдатели по-разному воспринимают действительность, включая столь фундаментальные величины, как расстояние и время.

Говоря научным языком, в тот день Эйнштейн осознал, что описание любого физического события или явления зависит от системы отсчета, в которой находится наблюдатель (см. эффект корио-ли са ). Если пассажирка трамвая, например, уронит очки, то для нее они упадут вертикально вниз, а для пешехода, стоящего на улице, очки будут падать по параболе, поскольку трамвай движется, в то время как очки падают. У каждого своя система отсчета.

Но хотя описания событий при переходе из одной системы отсчета в другую меняются, есть и универсальные вещи, остающиеся неизменными. Если вместо описания падения очков задаться вопросом о законе природы, вызывающем их падение, то ответ на него будет один и тот же и для наблюдателя в неподвижной системе координат, и для наблюдателя в движущейся системе координат. Закон распределенного движения в равной мере действует и на улице, и в трамвае. Иными словами, в то время как описание событий зависит от наблюдателя, законы природы от него не зависят, то есть, как принято говорить на научном языке, являются инвариантными. В этом и заключается принцип относительности.

Как любую гипотезу, принцип относительности нужно было проверить путем соотнесения его с реальными природными явлениями. Из принципа относительности Эйнштейн вывел две отдельные (хотя и родственные) теории. Специальная, или частная, теория относительности исходит из положения, что законы природы одни и те же для всех систем отсчета, движущихся с постоянной скоростью. Общая теория относительности распространяет этот принцип на любые системы отсчета, включая те, что движутся с ускорением. Специальная теория относительности была опубликована в 1905 году, а более сложная с точки зрения математического аппарата общая теория относительности была завершена Эйнштейном к 1916 году.


Специальная теория относительности

Большинство парадоксальных и противоречащих интуитивным представлениям о мире эффектов, возникающих при движении со скоростью, близкой к скорости света, предсказывается именно специальной теорией относительности. Самый известный из них — эффект замедления хода часов, или эффект замедления времени. Часы, движущиеся относительно наблюдателя, идут для него медленнее, чем точно такие же часы у него в руках.

Время в системе координат, движущейся со скоростями, близкими к скорости света, относительно наблюдателя растягивается, а пространственная протяженность (длина) объектов вдоль оси направления движения — напротив, сжимается. Этот эффект, известный как сокращение Лоренца—Фицджеральда, был описан в 1889 году ирландским физиком Джорджем Фицджеральдом (George Fitzgerald, 1851-1901) и дополнен в 1892 году нидерландцем Хендриком Лоренцем (Hendrick Lorentz, 1853-1928). Сокращение Лоренца— Фицджеральда объясняет, почему опыт майкельсона—морли по определению скорости движения Земли в космическом пространстве посредством замеров «эфирного ветра» дал отрицательный результат. Позже Эйнштейн включил эти уравнения в специальную теорию относительности и дополнил их аналогичной формулой преобразования для массы, согласно которой масса тела также увеличивается по мере приближения скорости тела к скорости света. Так, при скорости 260 000 км/с (87% от скорости света) масса объекта, с точки зрения наблюдателя, находящегося в покоящейся системе отсчета, удвоится.

Со времени Эйнштейна все эти предсказания, сколь бы противоречащими здравому смыслу они ни казались, находят полное и прямое экспериментальное подтверждение. В одном из самых показательных опытов ученые Мичиганского университета поместили сверхточные атомные часы на борт авиалайнера, совершавшего регулярные трансатлантические рейсы, и после каждого его возвращения в аэропорт приписки сверяли их показания с контрольными часами. Выяснилось, что часы на самолете постепенно отставали от контрольных все больше и больше (если так можно выразиться, когда речь идет о долях секунды). Последние полвека ученые исследуют элементарные частицы на огромных аппаратных комплексах, которые называются ускорителями. В них пучки заряженных субатомных частиц (таких как протоны и электроны) разгоняются до скоростей, близких к скорости света, затем ими обстреливаются различные ядерные мишени. В таких опытах на ускорителях приходится учитывать увеличение массы разгоняемых частиц — иначе результаты эксперимента попросту не будут поддаваться разумной интерпретации. И в этом смысле специ-









Альберт Эйнштейн у доски с формулами специальной теории относительности. Теория относительности и кван -

товая механика две

революционные теоретические концепции, приведшие в ХХ веке к настоящему перевороту в физике..


альная теория относительности давно перешла из разряда гипотетических теорий в область инструментов прикладной инженерии, где используется наравне с законами механики ньютона.

Возвращаясь к законам Ньютона, я хотел бы особо отметить, что специальная теория относительности, хотя она внешне и противоречит законам классической ньютоновской механики, на самом деле практически в точности воспроизводит все обычные уравнения законов Ньютона, если ее применить для описания тел, движущихся со скоростью значительно меньшей, чем скорость света. То есть специальная теория относительности не отменяет ньютоновской физики, а расширяет и дополняет ее (подробнее эта мысль рассматривается во введении).

Принцип относительности помогает также понять, почему именно скорость света, а не какая-нибудь другая играет столь важную роль в этой модели строения мира — этот вопрос задают многие из тех, кто впервые столкнулся с теорией относительности. Скорость света выделяется и играет особую роль универсальной константы, потому что она определена естественнонаучным законом (см. уравнения максвелла). В силу принципа относительности скорость света в вакууме с одинакова в любой системе отсчета. Это, казалось бы, противоречит здравому смыслу, поскольку получается, что свет от движущегося источника (с какой бы скоростью он ни двигался) и от неподвижного доходит до наблюдателя одновременно. Однако это так.

Благодаря своей особой роли в законах природы скорость света занимает центральное место и в общей теории относительности.


Общая теория относительности

Общая теория относительности применяется уже ко всем системам отсчета (а не только к движущимися с постоянной скоростью друг относительно друга) и выглядит математически гораздо сложнее, чем специальная (чем и объясняется разрыв в одиннадцать лет между их публикацией). Она включает в себя как частный случай специальную теорию относительности (и, следовательно, законы Ньютона). При этом общая теория относительности идет значительно дальше всех своих предшественниц. В частности, она дает новую интерпретацию гравитации.

Общая теория относительности делает мир четырехмерным: к трем пространственным измерениям добавляется время. Все четыре измерения неразрывны, поэтому речь идет уже не о пространственном расстоянии между двумя объектами, как это имеет место в трехмерном мире, а о пространственно-временных интервалах между событиями, которые объединяет их удаленность друг от друга — как по времени, так и в пространстве. То есть пространство и время рассматриваются как четырехмерный пространственно-временной континуум или, попросту пространство-время. В этом континууме наблюдатели, движущиеся друг относительно друга, могут расходиться даже во мнении о том, произошли ли два события одновременно или одно предшествовало другому. К счастью для нашего бедного разума, до нарушения причинно-следственных связей дело не доходит — то есть существования систем координат, в которых два события происходят не одновременно и в разной последовательности, даже общая теория относительности не допускает.

закон всемирного тяготения ньютона говорит нам, что между любыми двумя телами во Вселенной существует сила взаимного притяжения. С этой точки зрения Земля вращается вокруг солнца, поскольку между ними действуют силы взаимного притяжения. Общая теория относительности, однако, заставляет нас взглянуть на это явление иначе. согласно этой теории, гравитация — это следствие деформации («искривления») упругой ткани пространства-времени под воздействием массы (при этом чем тяжелее тело, например солнце, тем сильнее пространство-время «прогибается» под ним и тем, соответственно, сильнее его гравитационное поле). Представьте себе туго натянутое полотно (своего рода батут), на которое помещен массивный шар. Полотно деформируется под тяжестью шара, и вокруг него образуется впадина в форме воронки. Согласно общей теории относительности, Земля обращается вокруг солнца подобно маленькому шарику, пущенному кататься вокруг конуса воронки, образованной в результате «продавливания» пространства-времени тяжелым шаром — Солнцем. А то, что нам кажется силой тяжести, на самом деле является по сути чисто внешнем проявлением искривления пространства-времени, а вовсе не силой в ньютоновском понимании. На сегодняшний день лучшего объяснения природы гравитации, чем дает нам общая теория относительности, не найдено.

Проверить общую теорию относительности трудно, поскольку в обычных лабораторных условиях ее результаты практически полностью совпадают с тем, что предсказывает закон всемирного тяготения Ньютона. Тем не менее несколько важных экспериментов были проведены, и их результаты позволяют считать теорию подтвержденной. Кроме того, общая теория относительности помогает объяснить явления, которые мы наблюдаем в космосе, — например, незначительные отклонения Меркурия от стационарной орбиты, необъяснимые с точки зрения классической механики Ньютона, или искривление электромагнитного излучения далеких звезд при его прохождении в непосредственной близости от Солнца.

На самом деле результаты, которые предсказывает общая теория относительности, заметно отличаются от результатов, предсказанных законами Ньютона, только при наличии сверхсильных гравитационных полей. Это значит, что для полноценной проверки общей теории относительности нужны либо сверхточные измерения массивных объектов, либо черные дыры, к которым никакие наши привычные интуитивные представления неприменимы. Так что разработка новых экспериментальных методов проверки теории относительности остается одной из важнейших задач экспериментальной физики.


Теория равновесия Макартура— Уилсона


нач. XVIII
Число видов в изолированной экосистеме будет постоянным, когда скорость вымирания видов будет равна скорости заселения новыми видами


РАВНОВЕСИЕ В ПРИРОДЕ


1798 ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ


ок. 1900

ЭКОЛОГИЧЕСКАЯ СУКЦЕССИЯ


1950-е

1954

ЗЕЛЕНАЯ РЕВОЛЮЦИЯ


МАКСИМАЛЬНАЯ

УСТОЙЧИВАЯ

ДОБЫЧА


1967