1. Предмет и задачи статистики

Вид материала

Документы

Содержание Форма выражения относительных величин Виды относительных величин 6. Виды средних величин Принципы при расчете средних величин Виды средних Вариация и ее показатели. 7. Средняя арифметическая и правила ее вычисления 8. Использование средней геометрической в статистике Формулы для расчета средней квадратической Средняя кубическая взвешенная 9. Применение средней хронологической 10. Изучение динамики социальных явлений (ряды динамики) 11. Показатели рядов динамики 1-Абсолютный прирост( 2- Коэффициент роста( Кр) -базисный=Уi :У0 ; цепной = Уi -Уi-1 4-абсолютное значение 1% прироста (А%) 12. Статистические таблицы Требования к составлению таблиц 13. Сводка и группировка материалов статистических наблюдений Статистическая группировка ... Полное содержание

Подобный материал:

• План Статистика як наука. Предмет, метод І задачі статистики Предмет статистики, 83.56kb.
• Задачи современной статистики. Статистика и ее роль в познании общественных явлений, 408.08kb.
• Курс. Предмет статистики. Изучение количественной стороны общественных явлений и процессов, 14.22kb.
• 1. Общее понятие статистики. Предмет статистики, 437.86kb.
• Методические указания к контрольной работе по курсу: «Статистика», для студентов очно-заочного, 76.42kb.
• Понятие, значение и задачи статистики. Основные понятия и категории статистики, 38.18kb.
• Задачи статистики рынка Система показателей статистики рынка Информационная база статистики, 1574.49kb.
• Общая теория статистики, 25.3kb.
• 1. Предмет и метод статистики Тема Статистическое наблюдение, 86.97kb.
• Вопросы к экзамену по курсу «Статистика», 36.85kb.

Основное условие правильного расчета относительной величины—сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Т.о, по способу получения относительные показатели — всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т. п.

- Знаменатель (основание сравнения, база) – это величина, с которой производится сравнение.

- Сравниваемая (отчетная, текущая) величина – это величина, которая сравнивается.

Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случае относительная величина показывает, сколько единиц одной величины приходится на единицу другой.

Важное свойство – относительная величина абстрагирует различия абсолютных величин и позволяет сравнивать такие явления, абсолютные размеры которых непосредственно несопоставимы.

Форма выражения относительных величин:

-В результате сопоставления одноименных абсолютных величин получают неименованные относительные величины. Они могут выражаться в виде долей, кратных соотношений, процентных соотношений, в виде промилле и т.д.

- Результатом сопоставления разноименных величин являются именованные относительные величины. Их название образуется сочетанием сравниваемой и базисной абсолютных величин.

Виды относительных величин

- Относительная величина динамики- Достигнутый показатель / базисный показатель.

- Относительная величина планового задания- Плановый показатель / базисный показатель.

- Относительная величина выполнения плана- Достигнутый показатель / плановый показатель.

- Относительная величина структуры- Отношение частей и целого.

- Относительная величина координации- Соотношение частей целого между собой.

- Относительная величина интенсивности- Характеризует распределение явления в определенной среде (насыщенность каким-либо явлением). Это всегда соотношение разноименных величин.

- Относительная величина уровня социально-экономического явления- Характеризует размеры производства различных видов продукции на душу населения.

- Относительная величина сравнения- Представляет собой отношение одноименных величин, относящихся к различным объектам.


6. Виды средних величин

Большое распространение в статистике имеют средние величины. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

Средняя величина - это обобщающий показатель, кот характеризует типический уровень явления, т.е. выражает величину признака отнесенной к единице совокупности.

Вычисление среднего- это один из распространенных приемов обобщения (с одной стороны отриц, а с др – игнорирует).и рассчитывается с учетом:

Принципы при расчете средних величин:

1. Средняя должна определятся для совокупности из качественно однородных единиц;
   
2. Средняя должна исчисляться для совокупности достаточно большого числа единиц;
   
3. - для совок единиц, кот находятся в нормальном естественном состоянии;
   
4. – с учетом естеств эконимического содержания исследуемого показателя.
   

Виды средних:

1- Степенные средние – ср. гармоническая (m-показатель степени)-если m= -1;ср. геометрические – m ­- >о; ср. арифметические – m=1; ср квадратические- m=2; ср кубические- m=3 (Хгарм <=хгеометрич <=Х арифметич <=Х квадрати <=Хкубич )

Ф-ла степенной средней – Х = m Хi m /n, где Х- степенная средняя, Хi –варианта (т.е.значение усредняемого признака), m – показатель степени средней; n- число варианта.

Степенные средние в завис от от представления исходных данных м.б.:

-простыми – (пример со студентами : группа из 20 студентов разного возраста-18;18;19;20;19;и т.д. = 18+18+19+20+19+т.д./20 студентов всего=19,4)

- взвешенными –(эти же студенты, но 2чел по 18 лет; 11 по19 лет; 5-по 20 лет; 1-по 21 г; 1-по22= 18*2+19*11+20*5+21*1+22*1/(2+11+5+1+1)=19.4 -

2- Структурные – мода и медиана

Мода – это наиболее часто встречающаяся(повторяющаяся) величина признака данной совокупностью. Мединой называется значение варьирующего признака, которое находится в середине вариационного ряда, все варианты которого расположены в порядке возрастания или убывания значений признака (для нечетного количества 2,3,4,4,5,6,8,7,9_); для четного - медианой будет среднее, взятое как полусумма значений 2-х центральных значений (0,1,1,2,3,4,5,6)= (2- медиана четного значения+3)/2=2,5 (используется для средних годовых фондов, для ранжирования) .

Мода и медиана в дискретном ряду распределения определяются следующим образом:

Мода принимает самое часто повторяющееся значение признака, т.е. (Х).

Медиана вычисляется по двум способам:

1. Для четного числа единиц совокупности – берутся 2 средних, показателя, чтобы с одной и со второй стороны оставалось равное количество единиц.
   
2. Для начетного числа единиц совокупности медиана принимает одно центральное значение, все варианты которого в одинаковом количестве с одной и со второй стороны будут охватывать данную варианту. Для определения медианы в дискретном ряду для четного числа чисел недостаточно показать 2 серединных значения, а необходимо их суммировать и разделить на 2.
   

И мода и медиана показывают отклонение от средних значений + дисперсное отклонение.


Вариация и ее показатели.

Вариация - это колеблемость признака около средней величины. Основными показ-ми вариации являются: размах вариации (R); среднее линейное отклонение (dcp); дисперсия (G2); среднее квадратическое отклонение (G); коэффициент вариации (V). Размах вариации (R) — есть разность между наибольшим (Xmax) и наи­меньшим (Xmin) значениями признака в ряду распределения: R = Xmax – Xmin. По величине размаха вариации можно судить о различии между передо­выми и отстающими. Однако этот пок-ль имеет тот сущ-й недостаток, что он полностью зависит от отдельных случаев, оказавшиеся на обоих полюсах ранжированного ряда. Между тем, отдельные случаи не всегда достаточ­но характерны, и опора на них может дать превратное предст-е о характере колеблимости. Поэтому возникает необход-ть в другом по­казателе, кот-й опирался бы не на одни только крайние значения, а и на значения опред-го признака в данной совок-ти. Среднее линейное отклонение (dcp) представляет собой среднюю величину отклонений значений признака от их средней величины. При его расче­те все отклонения берутся со знаком плюс. Бывает простое: dcp =  (x – xcp) / n и взвешенное: dcp =  (x – xcp)f / f. Дисперсия, или средний квадрат отклонений вариантов признака от их средней величины (G2), вычисляется по формулам: простая G2 =  (x – xcp)2 / n; взвешенная G2 = ( (x – xcp)2 * f ) / f. Затем возвращаясь к линейному измерению, надо из величины дис­персии извлечь квадратный корень и мы получим наиболее точный пока­затель - среднее квадратическое отклонение: простое G =  (x – xcp)2 / n и взвешенное G2 = ( (x – xcp)2 * f ) / f. В отличие от среднего линейного и среднего квадратического откло-нения коэффициент вариации является мерой относительной колебле­мости признака около средней величины и характеризует степень одно­родности признака в изучаемой совокупности. Он определяется по формуле: V = G / xcp * 100%. Если коэффициент вариации > 33,3 %, исследуемая совокупность счи­тается неоднородной и должна быть разгруппирована. По величине коэффициента вариации можно судить о степени вариа­ции признаков совокупностей. Чем больше его величина, тем больше раз­брос значений признаков вокруг средней, тем менее однородна совокуп­ность по своему составу и тем менее представительна средняя


7. Средняя арифметическая и правила ее вычисления

Средняя арифметическая величина представляет собой са­мый распространенный вид средней величины. Когда речь идет о средней величине без указания ее вида, подразумевается имен­но средняя арифметическая. Формула простой средней арифме­тической имеет вид: где X — средняя величина;

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают через х (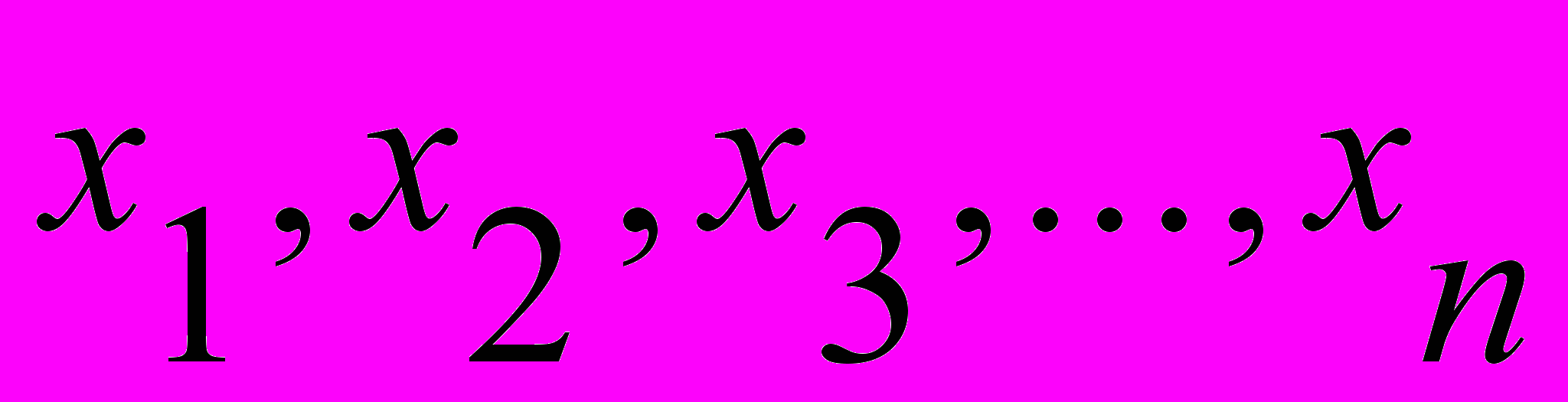); число единиц совокупности обозначают через n, среднее значение признака - через 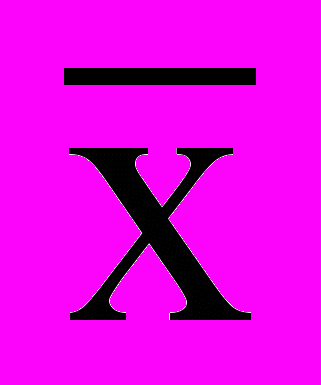. Следовательно, средняя арифметическая простая равна: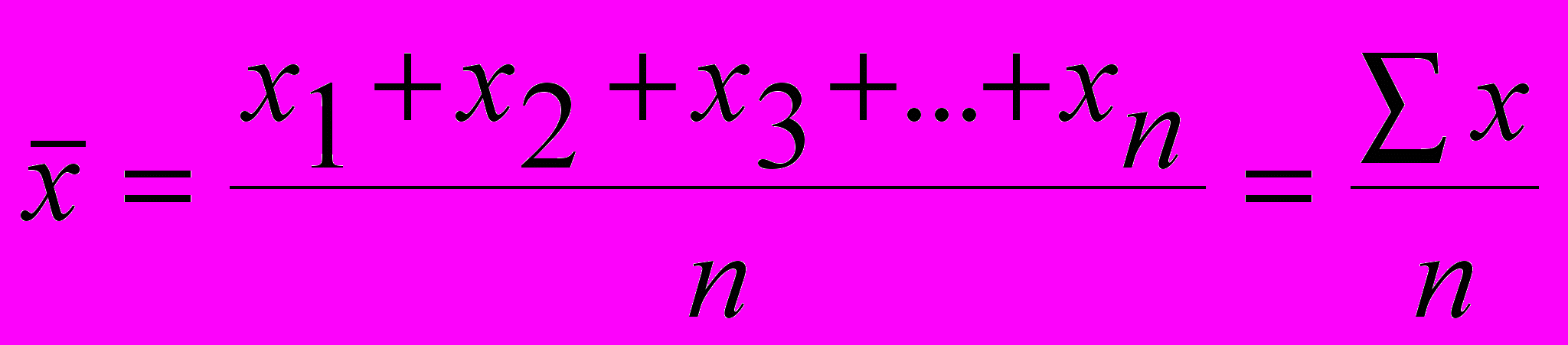



По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта х встречается в совокупности 2 раза, а варианта х-16 раз и т.д.

Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается символом n.

Вычислим среднюю заработную плату одного рабочего 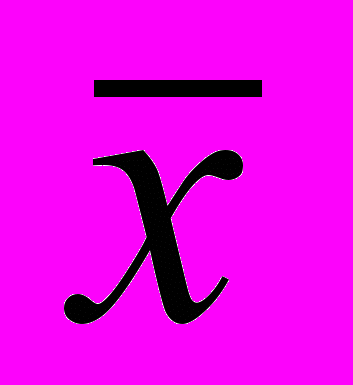в руб.: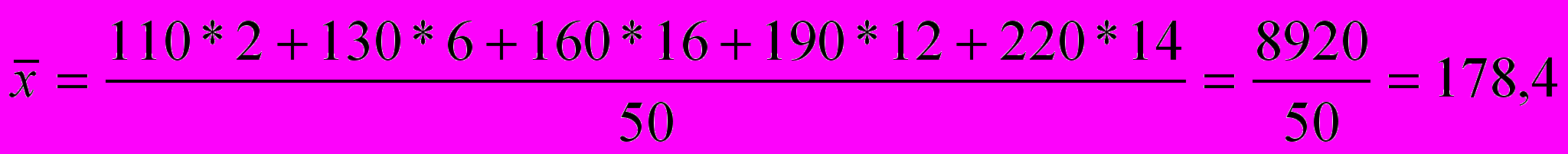



Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих.

В соответствии с этим, расчеты можно представить в общем виде:





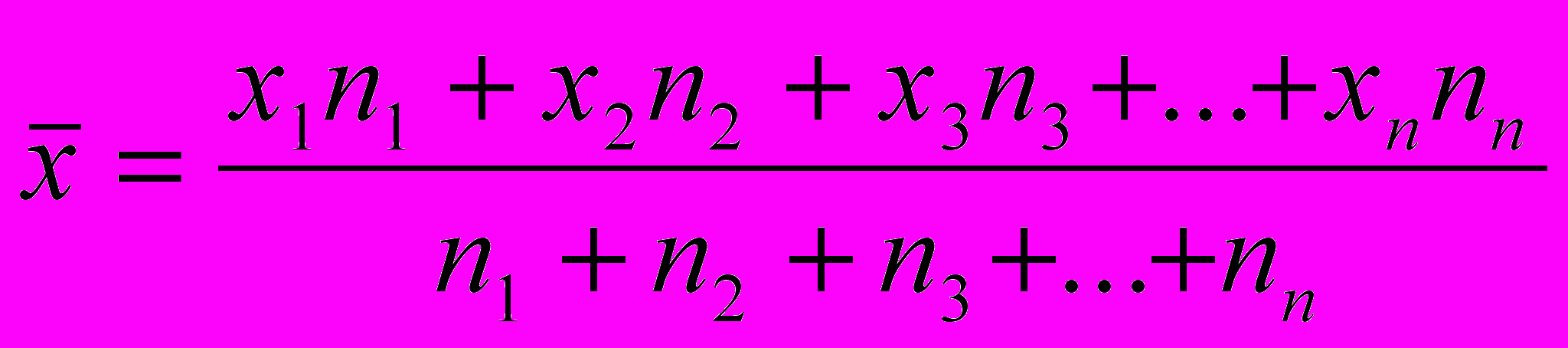
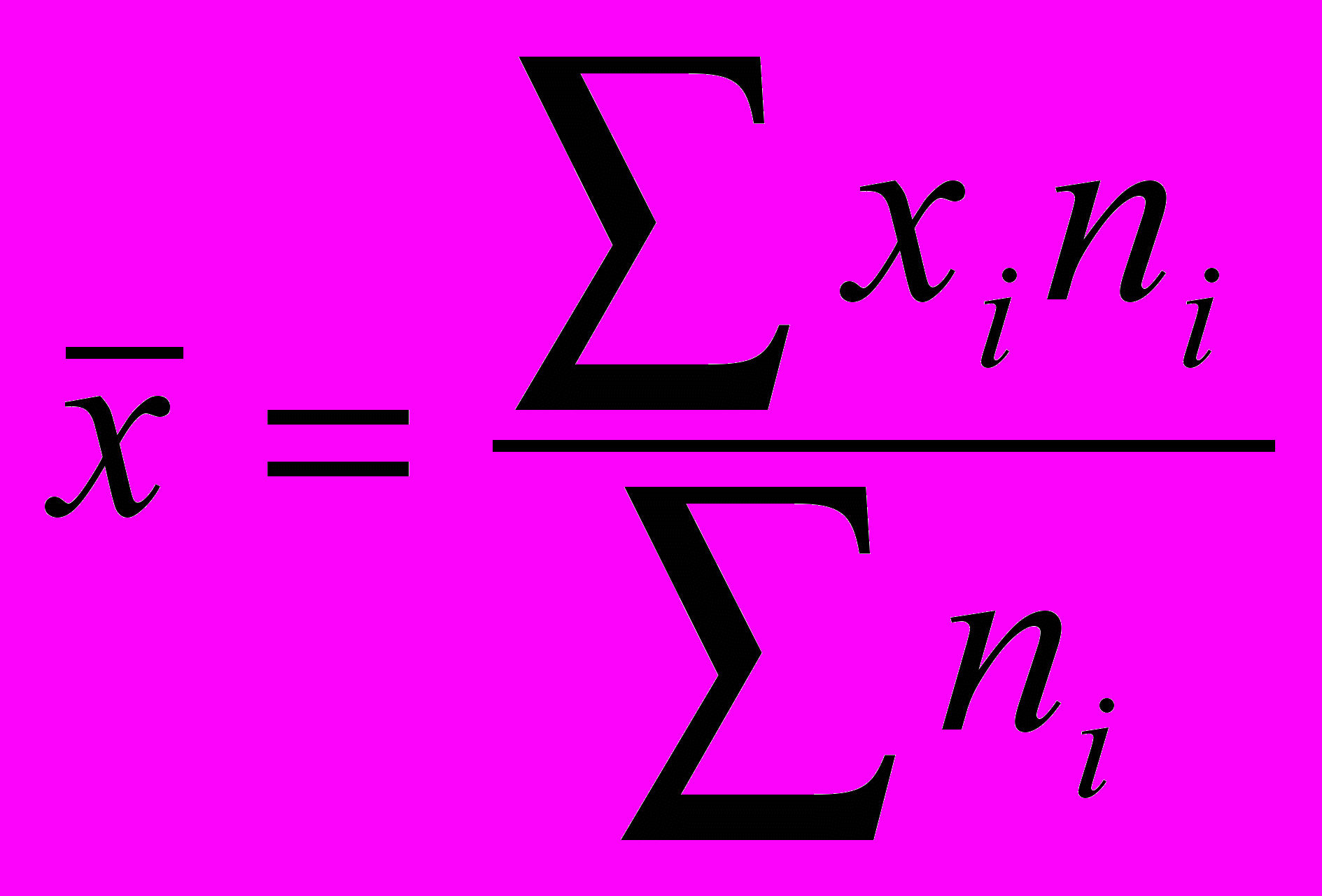
Полученная формула называется средней арифметической взвешенной. Средняя арифметическая взвешенная Эта формула широко используется при расчете среднего бал­ла успеваемости студентов, для расчета фондового индекса «Стен-дард энд пурз-500», в расчетах экономических показателей.

Основные свойства средней арифметической.

1. От уменьшения или увеличения частот каждого значения признака х в п раз величина средней арифметической не изменится.

Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.

2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:



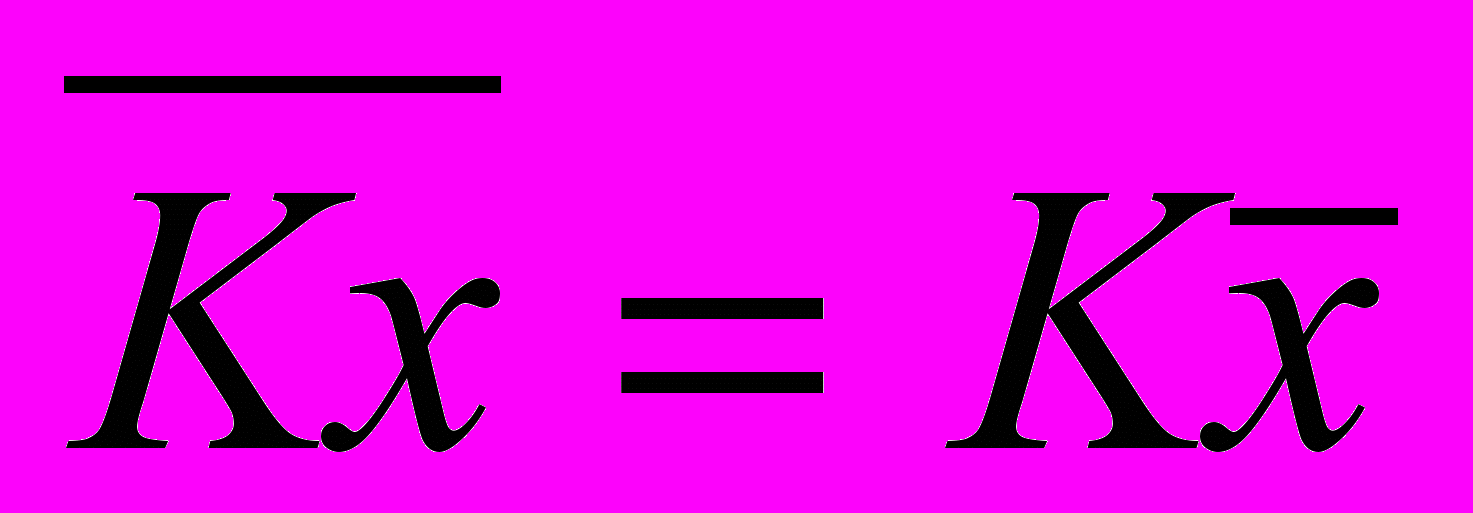
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:



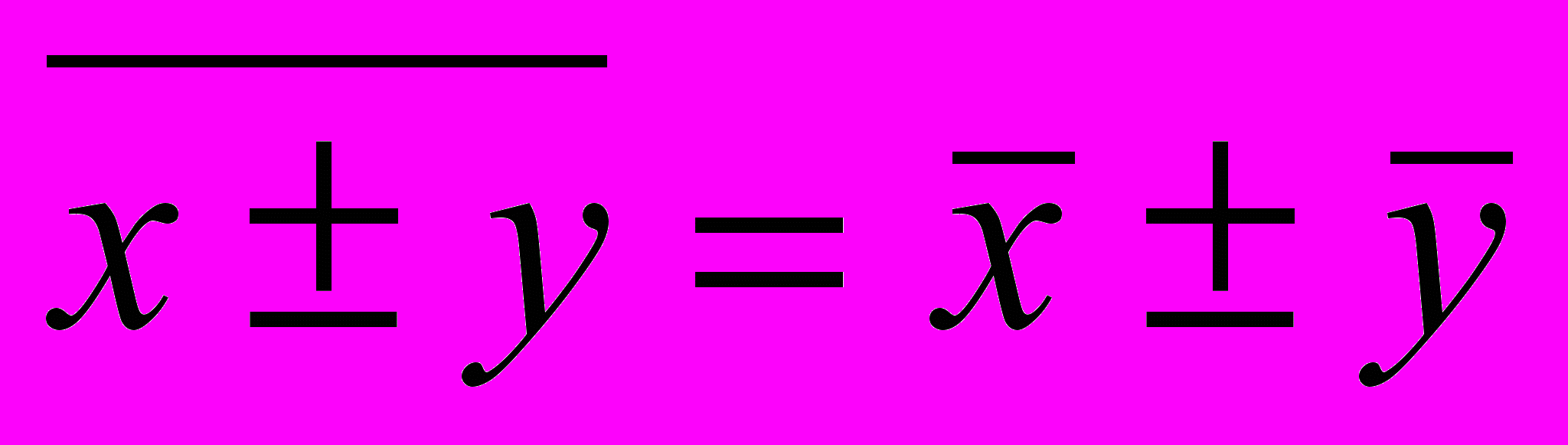
4. Если х = с, где с - постоянная величина, то .

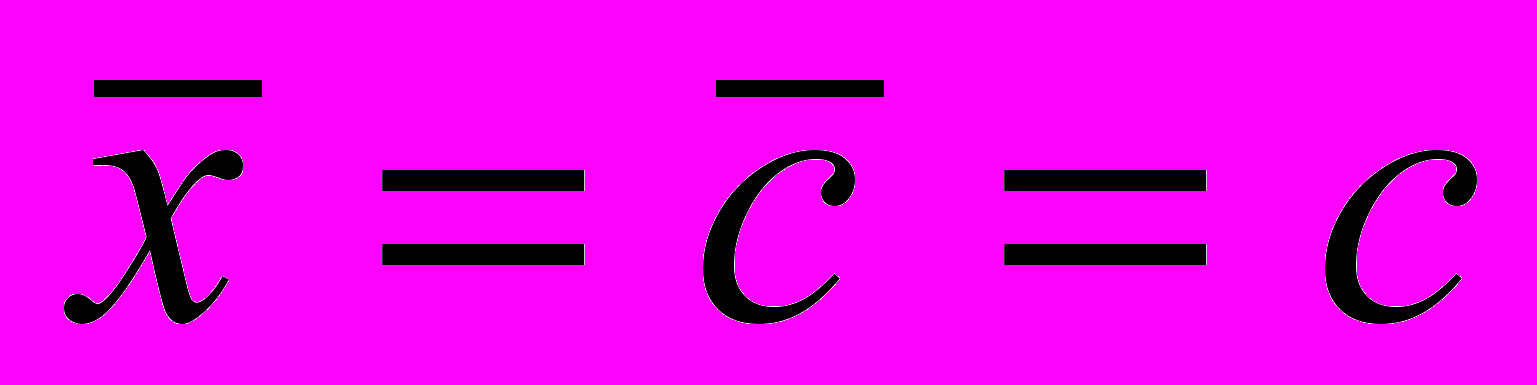5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:



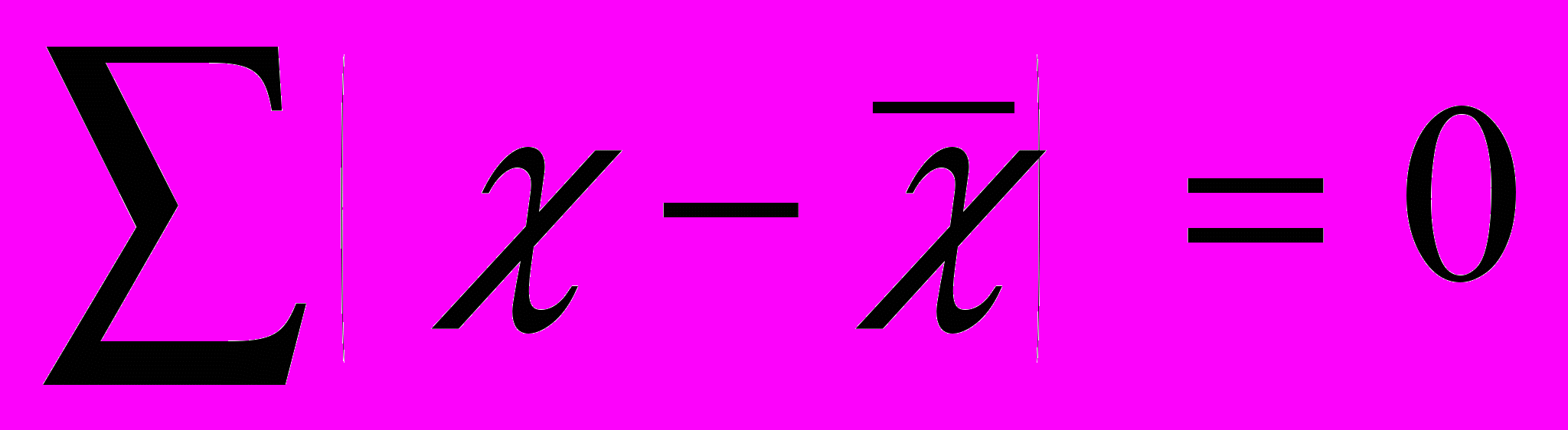
Простая средняя арифметическая используется в расчете фон­дового индекса Доу-Джонса, для определения среднего остатка оборотных средств по балансу, среднегодовой численности насе­ления и др.


8. Использование средней геометрической в статистике

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста. Средняя геометрическая исчисляется извлечением корня степени п из произведений отдельных значений — вариантов признака х.

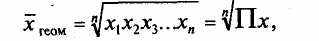
где n - число вариантов; П - знак произведения.

Наиболее широкое применение средняя геом-ая по­лучила для определения средних темпов изменения в рядах ди­намики, а также в рядах распределения.

средняя квадратическая и средняя кубическая. В ряде случаев в экономической практике возникает по­требность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда при­меняется средняя квадратическая (например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (напри­мер, при определении средней длины стороны л кубов).

Формулы для расчета средней квадратической:

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных зна­чений признака на их число:



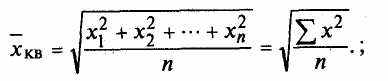
Средняя квадратическая взвешенная

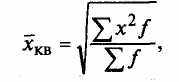где f - веса.

Формулы для расчета средней кубической:

Средняя кубическая простая



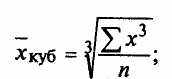
Средняя кубическая взвешенная



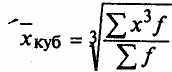
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется стати­стика средней квадр-ой, но не из самих вариантов х, и из их отклонений от средней при расчете показателей ва­риации. Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней мо­жет быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже средних индивидуальных).


9. Применение средней хронологической

Одной из важнейших задач ст. является изучение анализируемых показателей во времени, их динамика. Эта задача решается с помощью рядов динамики.

Ряд динамики представляет собой ряд расположенных в хронологическом порядке показателей, которые характеризуют время. Средние из рядов динамики называются средними хронологическими, т.к. они характеризуют показатели во времени. В расчетах средних хронологических различают начальный уровень ряда x1 и конечный уровень ряда x n. Рассмотрим два вида средних хронологических:

1-Средняя хронологическая из моментного ряда динамики

2-Средняя хронологическая из интервального ряда динамики.

Средняя хронологическая из моментного ряда динамики равна сумме показателей уровней, деленных на (n-1), причем начальный и конечный уровни ряда берутся в половинном значении, где n – число показателей (уровней) ряда.



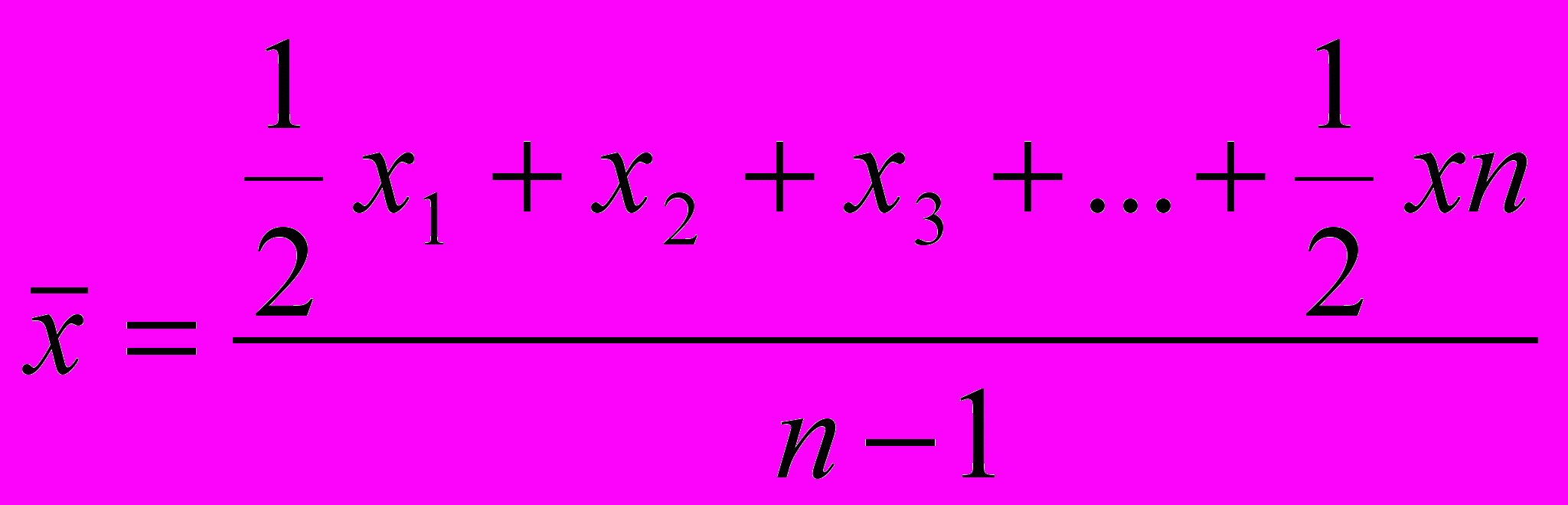
Средняя хронологическая из интервального ряда динамики равна сумме показателей уровней деленных на число уровней (ср. арифметическая простая)




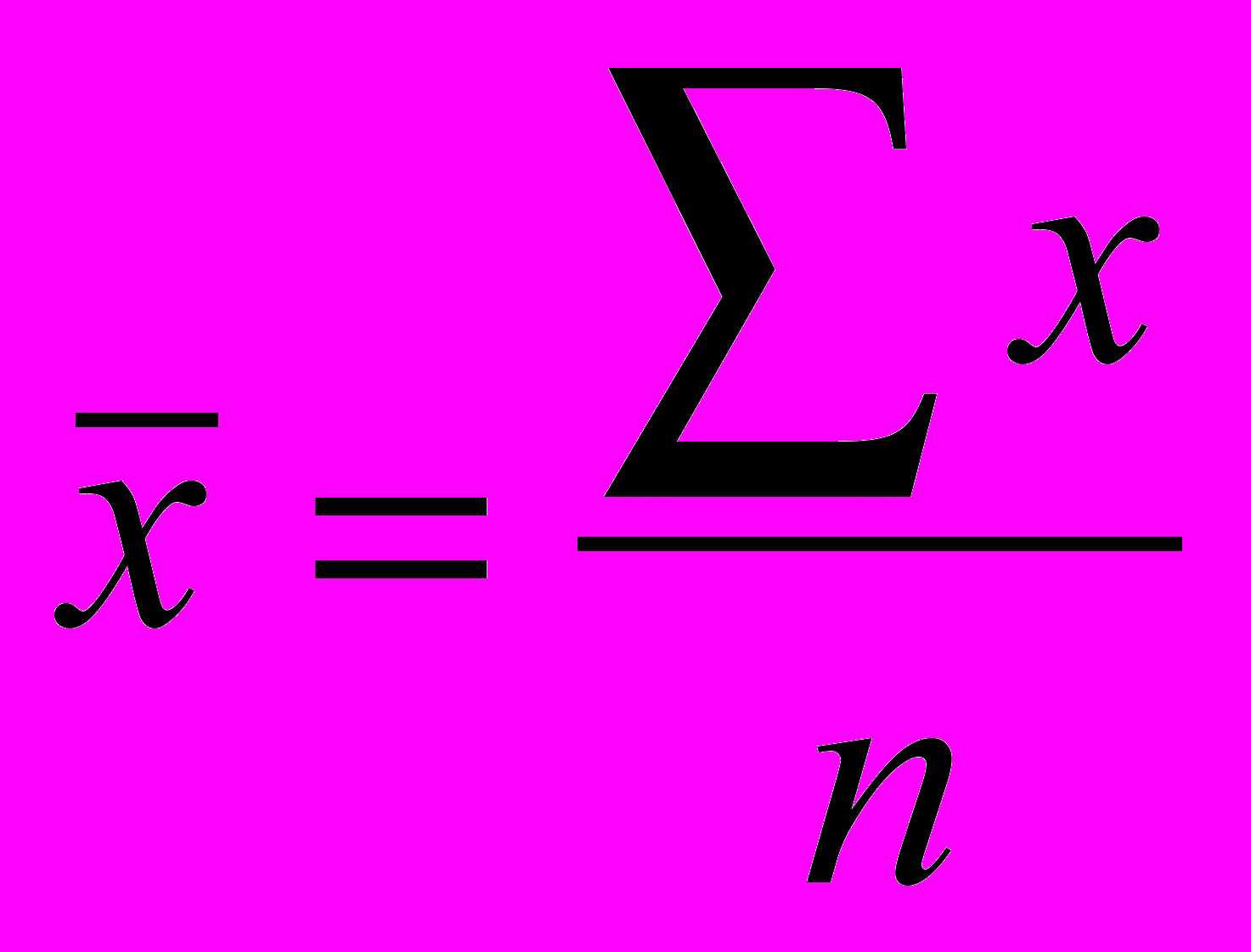
10. Изучение динамики социальных явлений (ряды динамики)

Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.

Ряд динамики – хронологический ряд, совок упорядоченных во времени числовых показателей характеризующих уровень развития изучаемого явления. Или числовые показатели, представленные в виде стат-го ряда, характеризующего изменение соц-экономич-их и др явлений в движении, времени, пространстве.

Числовые значения того или иного стат показателя, составляющие динамический ряд, называются уровнями ряда.

Ряды динамики различают по следующим признакам:

1. по времени-
   

- моментальные – (на определенный момент времени)т.е. если уровень ряда показывает фактическое наличие изучаемого явления на конкретный момент времени, то совок уровней образует –моментальный ряд динамики (числ населения на нач года; величина запаса на нач периода);

- интервальный ряд – (за период времени)это последовательность в кот уровень является относительным к явлению принадлеж к результату накопленному или вновь произведенному за определенный период (интервал времени) –ряды показателей объема продаж по месяцам года; кол-во отработанных чел/дней по периодам.

Отличие м/д интервальными и моментальными рядами: сумма уровней интервального ряда дает вполне реальный показатель (общий выпуск продукции за год; общие затраты раб времени и т.д.), а сумма уровней моментального ряда подсчитывается, но реального содержания не имеет.

2. по форме представления уровней –или в зависимости от типа данных, характеризующих явление, уровня ряда могут быть представлены: абсолютными, относительными и средними величинами.
   

- ряды абсолютных величин – объем продаж $ США на междунар валютной бирже (на10.01.91 – 126,7; на 11.01.94 – 124,3);

- ряды средних величин – потребление прод питания на 1 чел, члена семьи кг/год (молочн прод в год; мясных и т.д.);

- ряды относительных величин – индекс инфляции в… году (на конец года в % к году предыдущему)- в январе индекс инфл составил – 126%; в феврале – 152%.

Чтобы о развитии явления можно было получить представление при помощи числовых уровней, при составлении ряда динамики, сам ряд должен с чем-то сопоставляться, т.е. стат данные д.б. сопоставимыми:

-по территории;

-по кругу охватываемых объектов;

-единицами измерения;

-по времени регистрации;

-по ценам;

-по методологии расчетов

Ряды динамики могут быть полными и неполными.

Полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.

Неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени.


11. Показатели рядов динамики

Показателями изменения уровней ряда динамики (анализа динамич рядов) являются:

1-абсолютный прирост

2-темпы роста

3-темпы прироста;

4-абсол значение 1% прироста

1-Абсолютный прирост(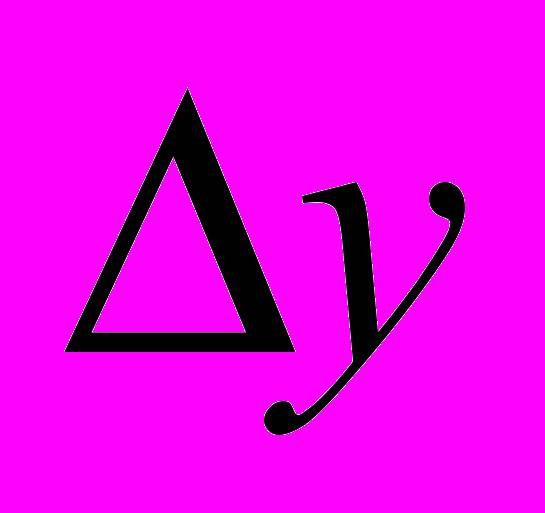) — показатель, показывающий ско­рость роста. Он определяется как разность между двумя сравни­ваемыми уровнями и показывает, на сколько один уровень больше (меньше) по сравнению с другим. Может рассчитываться дву­мя способами: цепным и базисным.

Цепные показатели получают, если каждый последующий уровень сравнивают с предыдущим.

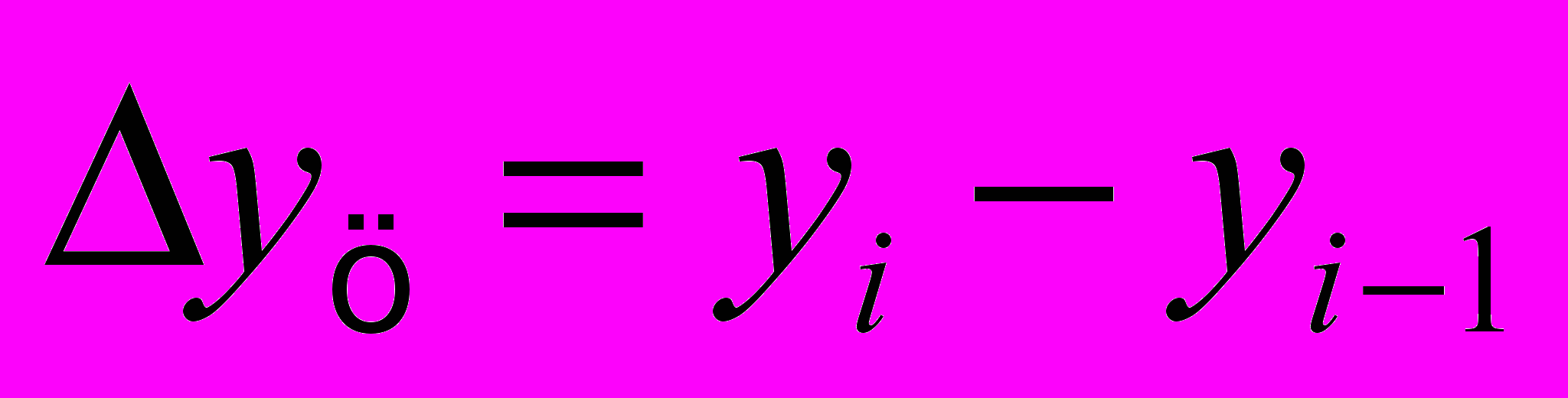
Базисные показатели получают, если каждый последующий уровень сравнивают с первоначальным, принятым за базу срав­нения.

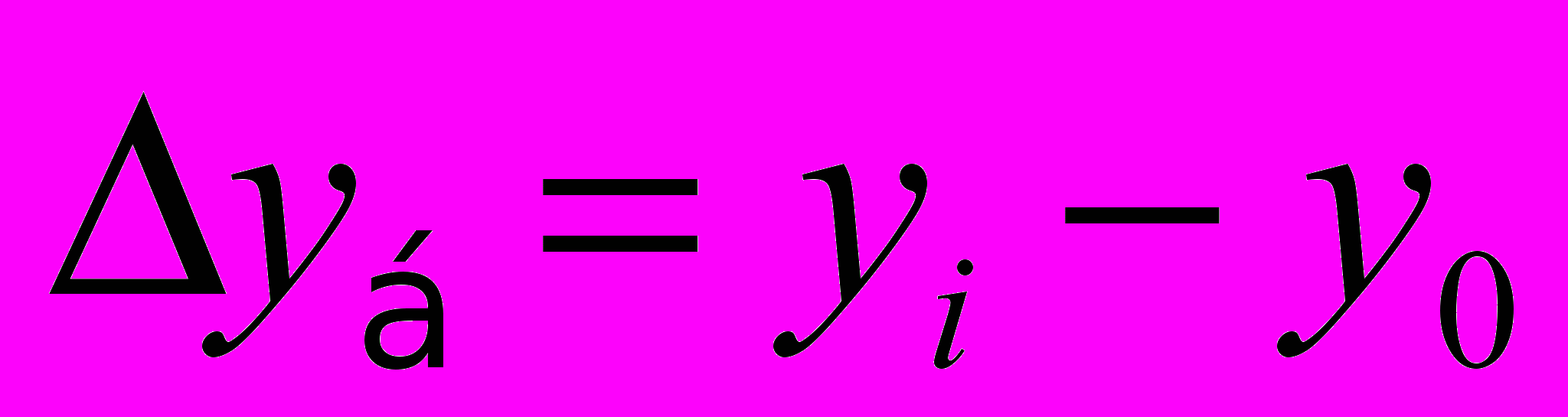
2- Коэффициент роста( Кр) -базисный=Уi :У0 ; цепной = Уi -Уi-1 - определяется как отношение двух сравниваемых уровней и показывает, во сколько раз один уро­вень больше (меньше) по отношению со сравниваемым Темп роста(Тр) - это отношение уровней ряда динамики между собой, когда в качестве базы сравнения принимается уро­вень для предшествующего периода, выражаемое в коэффициен­тах или процентах:

Тр=Крх100%.получающийся в результате деления двух уровней одного ряда друг на друга. базисный=(Уi :У0)х100 ; цепной = (Уi - Уi-1)х100 ;

Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: 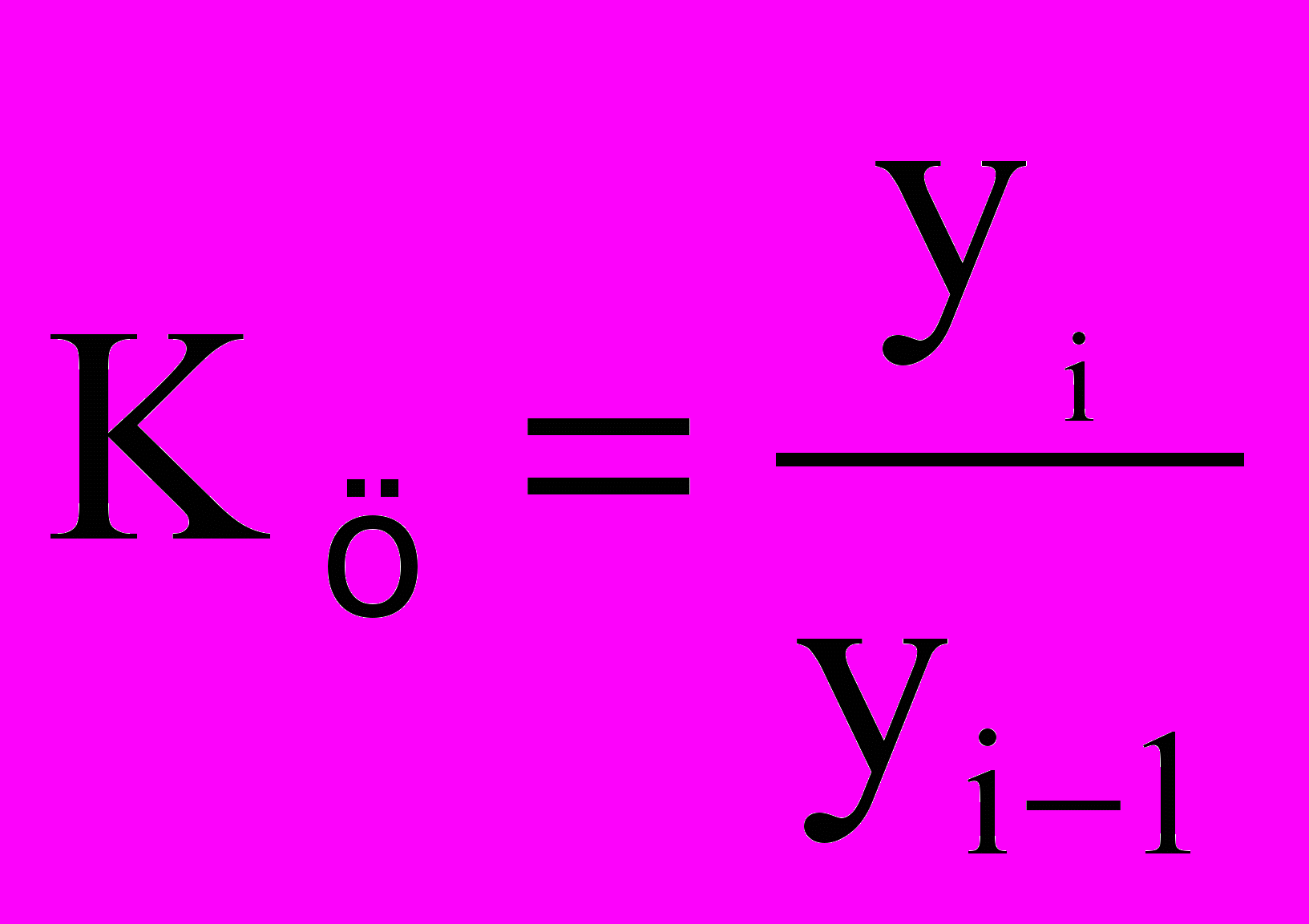х100,

либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем 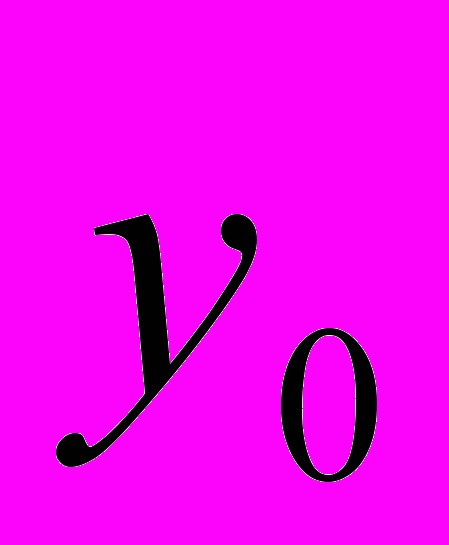, выбранным за базу сравнения: 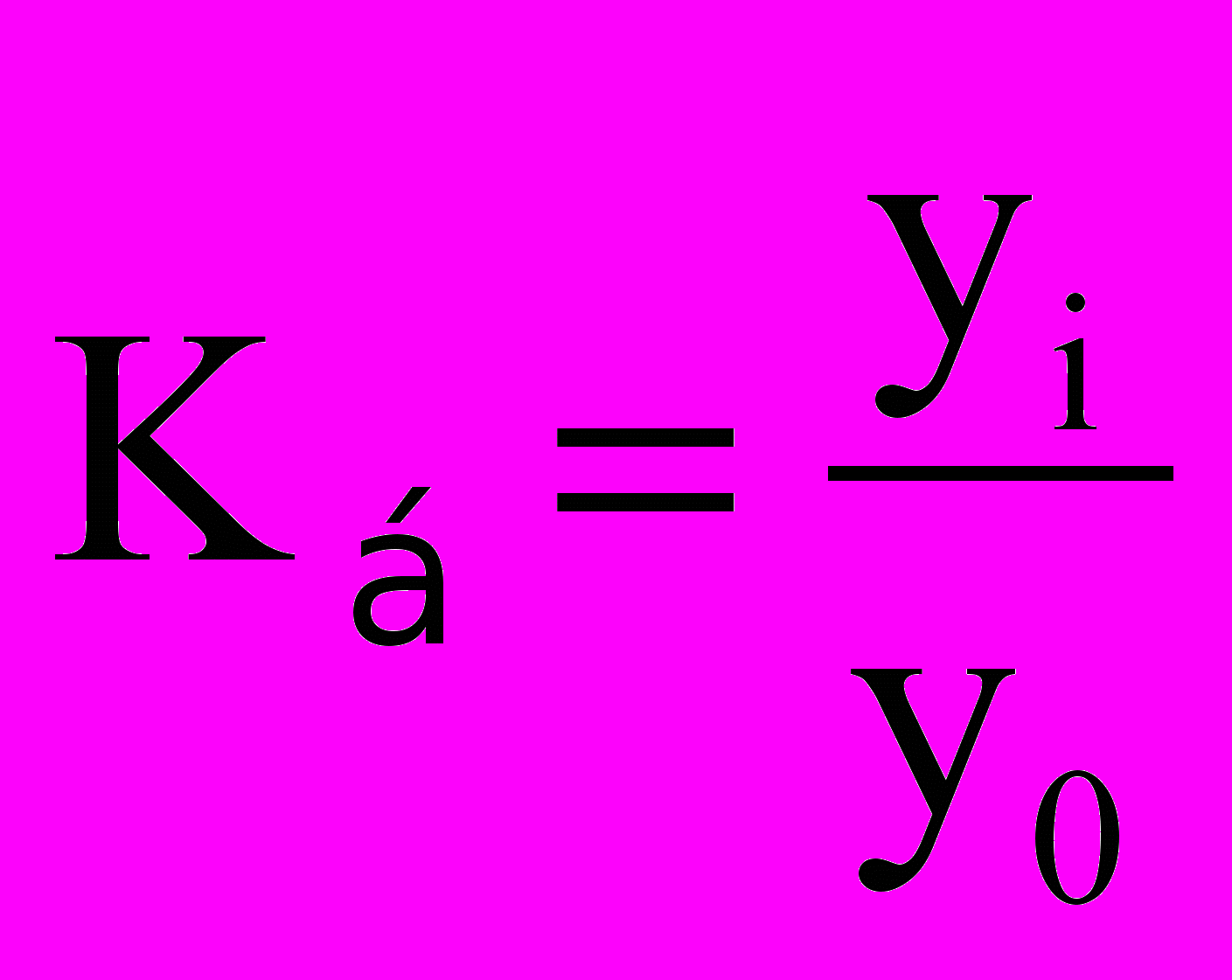х100.

3-Коэффициент прироста( Кпр) -базисный=Кр-1;( Уi :У0)/ У0 ; 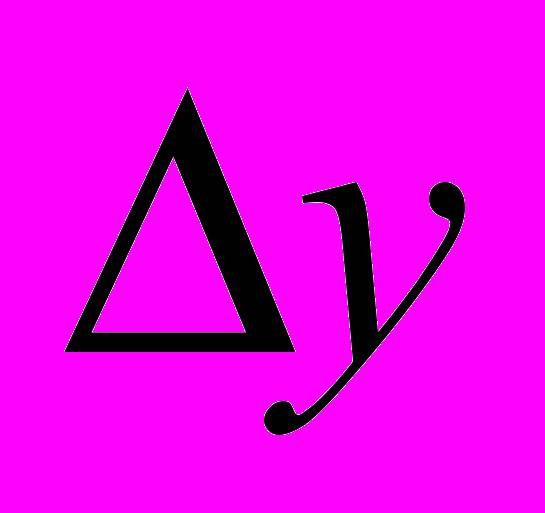базисное/ У0 ; цепной = Кр-1;(Уi - Уi-1)/ Уi-1; 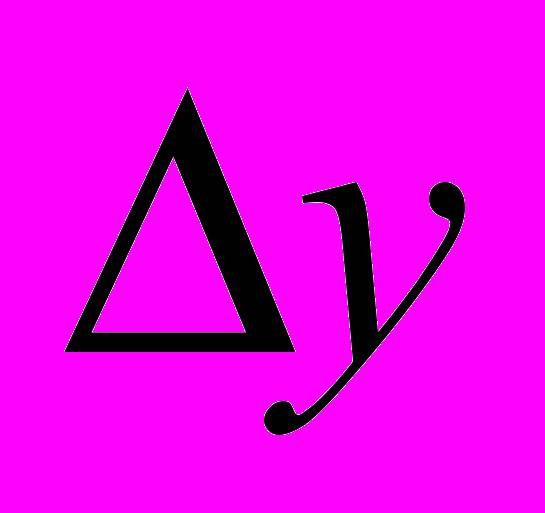цепное/ Уi-1

Темп прироста показывает, на сколько процентов увели­чился (уменьшился) текущий уровень по сравнению с базисным, принятым за 100%. Его можно рассчитать по данным о темпе роста, для чего следует из темпа роста вычесть 100 или из коэф­фициента роста — единицу, тогда получим коэффициент приро­ста:

Тпр = ТР – 100%

Темп прироста(Тпр или Кпр) - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.

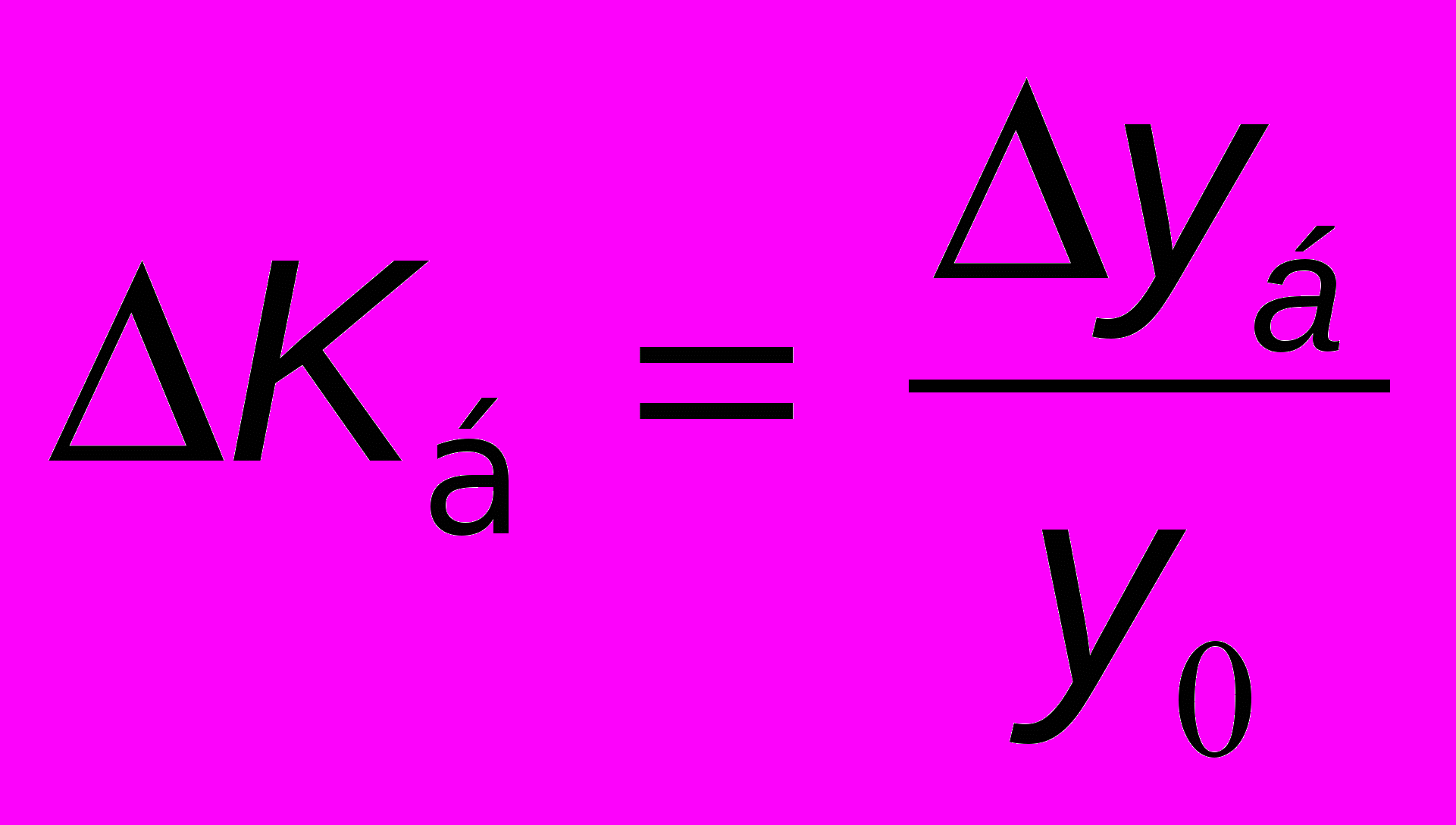
Базисные темпы прироста: ; Кпрх100; Тр-100

Цепные темпы прироста: 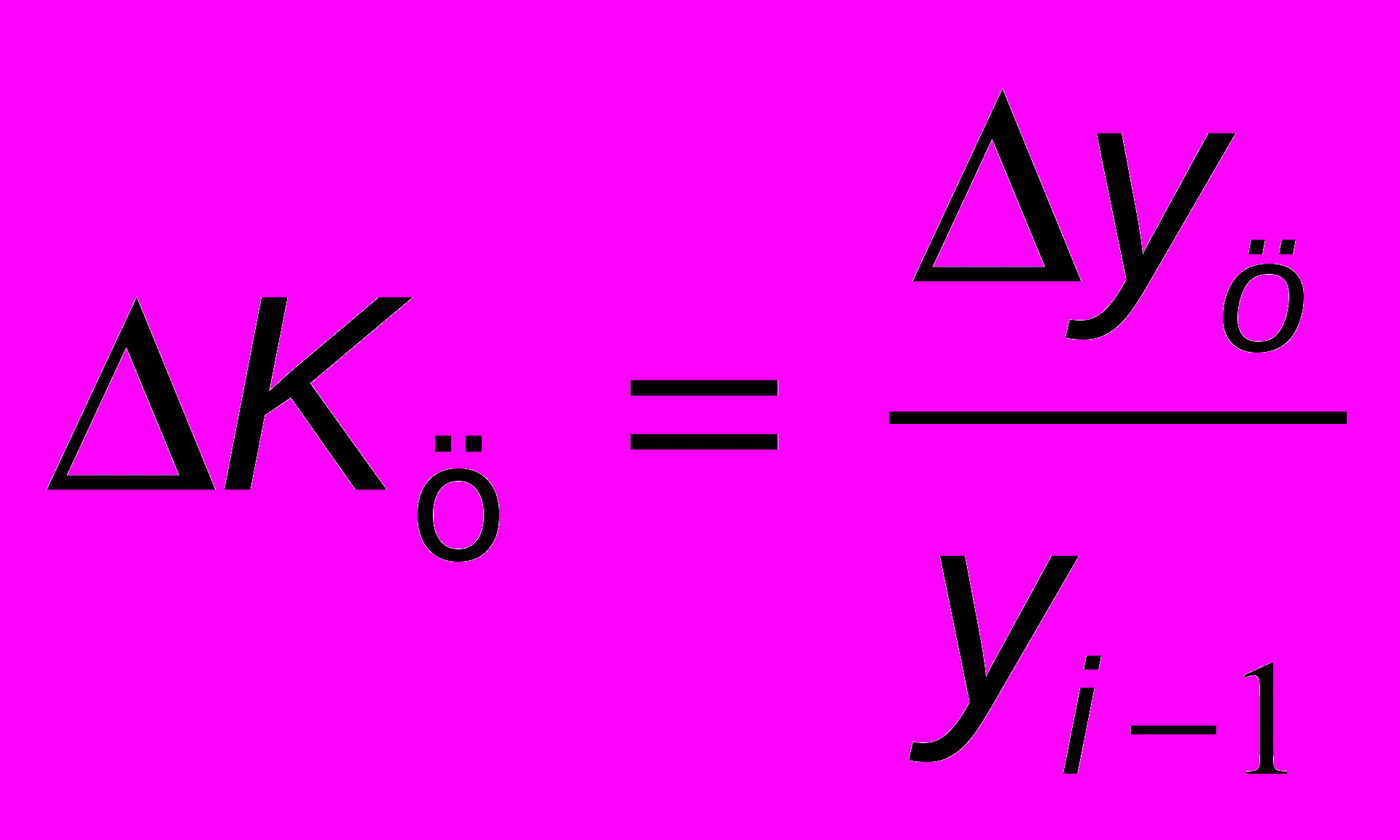; Кпрх100; Тр-100

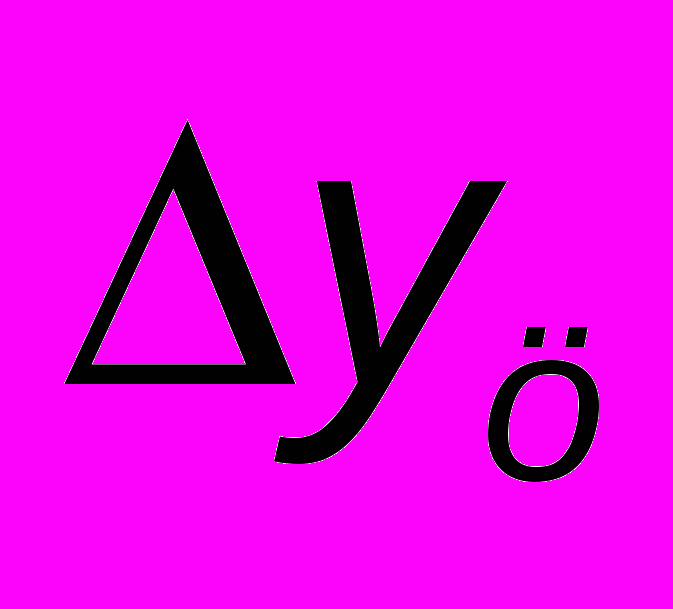и - абсолютный базисный или цепной прирост;

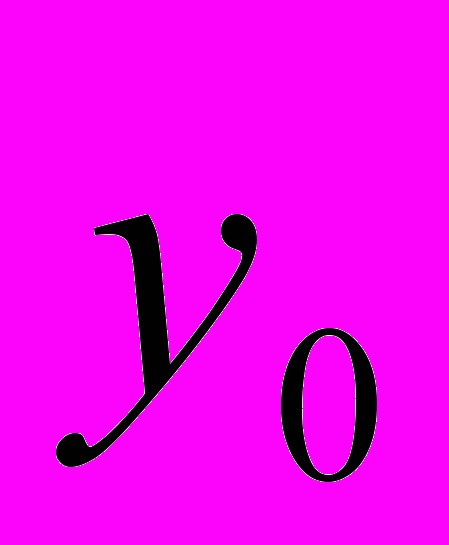- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;

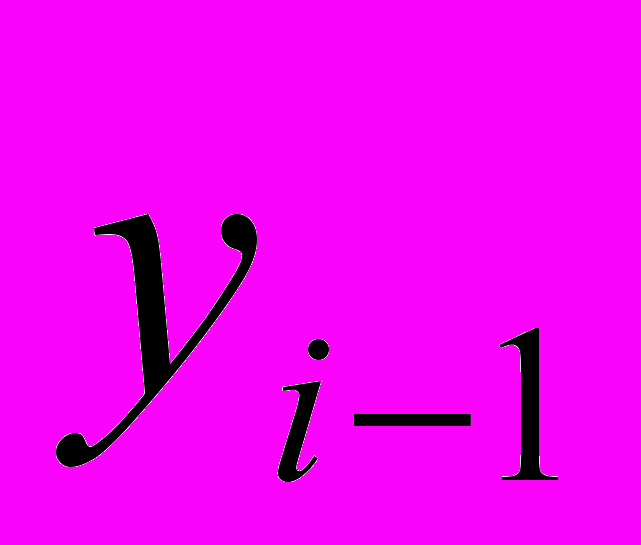- уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.

Существует связь между темпами роста и прироста:

К = К - 1 или К = К - 100 % (если темпы роста определены в процентах).

4-абсолютное значение 1% прироста (А%)-

1.1)-Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый -: .

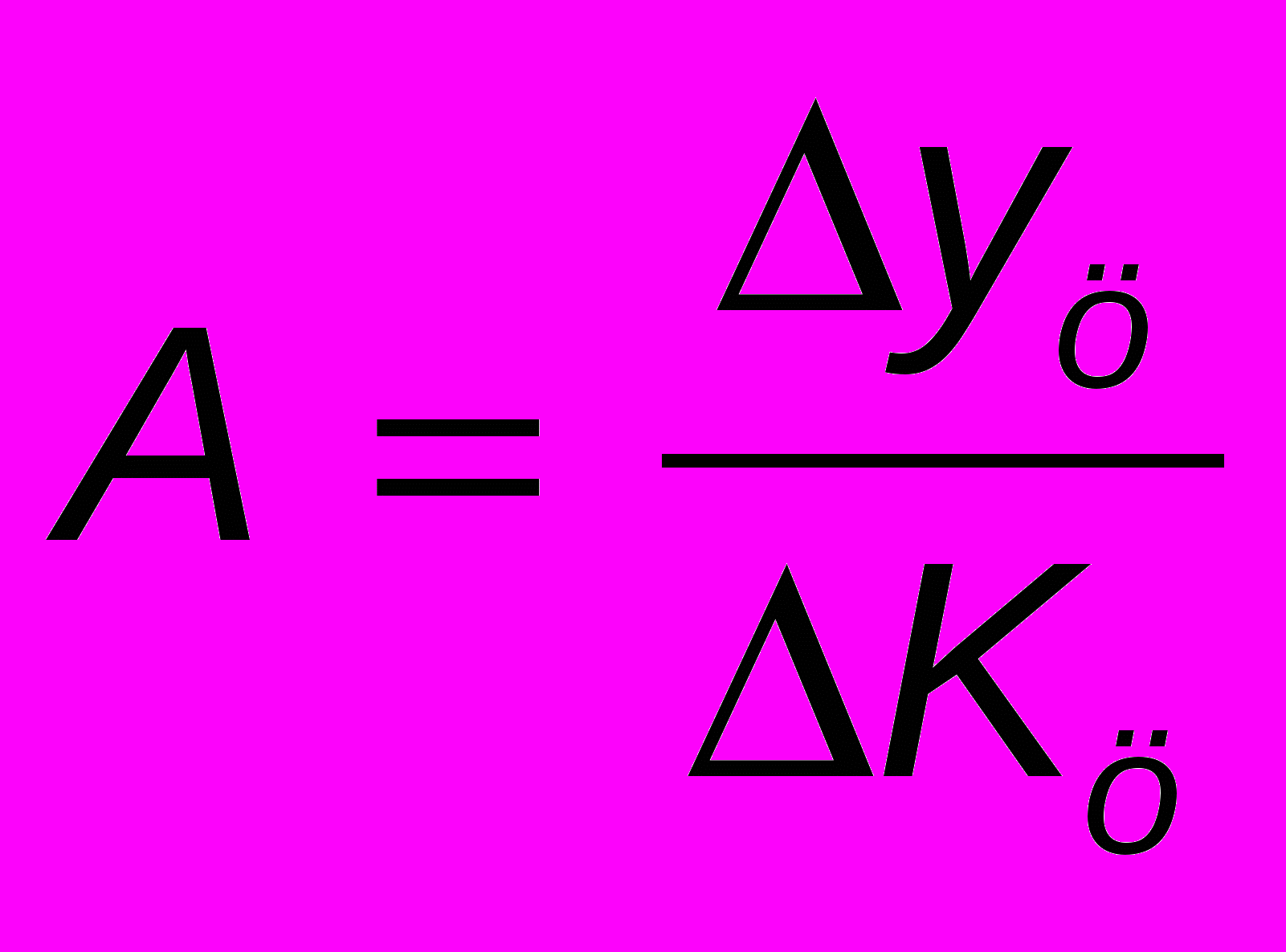1.2) если разделить (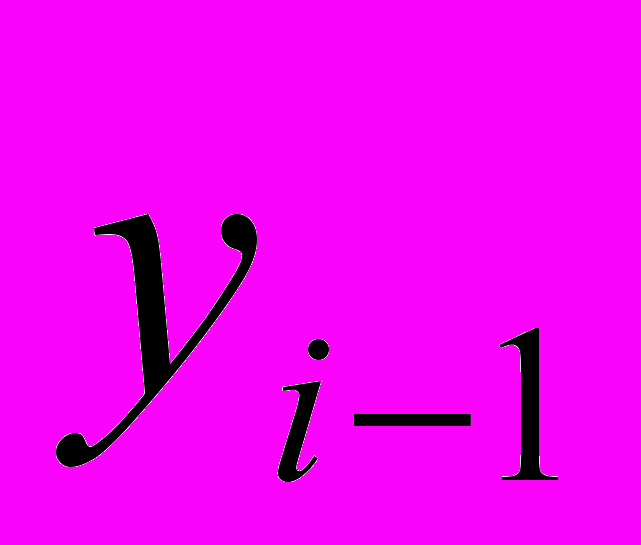) - уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста на 100%:

1.3) абсолютный цепной прирост разделить на (Тр-100)

2)Базисные- Если разделить абсолютный прирост (базисный) на 100%=1%

При изучении явлений во времени необходимо описывать интенсивность изменения и расчета СРЕДНИХ ПОКАЗАТЕЛЕЙ ДИНАМИКИ.

По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.


12. Статистические таблицы

-являются средством наглядного выражения результатов исследования

Таблица — это компактное изображение собранного мате­риала в виде системы строк и столбцов, на пересечении которых приводятся данные, характеризующие изучаемое явление.

Требования к составлению таблиц:

1-должна быть краткой;

2- должна иметь название из кот должно быть известно: какой круг вопросов излагает; -каковы географические границы представленной стат совокупности; -за какой период времени и к которому онии относятся; -каковы ед измерения (если они один для всех табл данных), а если не один, то в верхних или боковых заголовках следует указывать единицы в кот приводятся стат данные.(тонн,шт,руб,кг и т.д.)

3-таблица может сопровожд примечаниями, в кот указыв источники данных, а также более подробно раскрывается содержание показателей, даются и др пояснения, а также оговорки, если табл построена на основе вычислений.

4- при оформл таблиц обычно применяются такие условные обозначения как в случае отсутствия данных ставится «...» или пишется «нет сведений», а в случае отсутствия типа явления ста­вится «—»); Х-не имеет осмысленного содержания; если свед имеются, то числовое значение выражается дробным числом – 0,0; округленные числа приводятся с одинаковой степенью точности (до 0,1; 0,01); если в табл приводятся % роста, то во многих случ целесообразно % от 300% и более – их необходимо заменить соотношениями в разах (1000% = 10 раз)

Все таблицы можно разделить на три группы:

1. Таблицы простые, или перечневые, в которых содержатся сводные показатели или перечень отдельных объектов без расчленения совокупности на группы.
   
2. Групповые таблицы, в которых статистическая совокупность расчленена на отдельные группы и каждая из этих групп охарактеризована рядом показателей.Комбинационные таблицы, в которых статистическая сово­купность разбита на группы по нескольким признакам (та­ким образом, в таблице получается комбинация групп).Статистическая таблица состоит из следующих элементов: общий заголовок — отражает суть всей таблицы, содержит указание на характеризуемый признак объекта исследования, вре­мя, место наблюдения (иногда единицы измерения признака);
   

подлежащее — характеризуемый в таблице объект исследо­вания (находится в левой части таблицы по строкам);

сказуемое — показатели, характеризующие подлежащее (рас­полагается в верхней части по графам);

итоговая строка — может находиться в начале (тогда со­провождается нижеследующей строкой «в том числе») или в конце подлежащего. В тех графах итоговой строки, в которых по смыслу не могут быть подсчитаны результаты, ставится «X»;

цифровые данные — количественная характеристика иссле­дуемого объекта (в случае отсутствия данных ставится «...» или пишется «нет сведений», а в случае отсутствия типа явления ста­вится «—»);

сетка — пересечение горизонтальных и вертикальных ли­ний.

По построению сказуемого различают простые и комбини­рованные таблицы. При простой разработке каждая графа сказу­емого отдельно друг от друга характеризует подлежащее. При
комбинированной таблице показатели сказуемого разрабатыва­ются в сочетании друг с другом.


13. Сводка и группировка материалов статистических наблюдений

Статистическая сводка – это научно организованная обработка материалов наблюдения ( по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин).

Сводка явл 2-ым этапом стат исследования. Различают простую сводку (подсчет только общих итогов) и статистическую группировку.

Целью сводки является получение на основе сведенных материалов обобщающих стат показателей, отражающих сущность соц-экономич-их явлений и определенные стат закономерности.

Предварительно составляется программа.(определяются: группы и подгруппы; системы показателей; виды таблиц) и план сводки – содержит организационные вопросы.

Статистическая группировка – это разбиение совокупности на группы, однородные по к-л признаку, а с т.зр. отдельных единиц совокупности группировка – это объединение от дед совок в группы, однородные по к-л признаку.

Устойчивое разграничение объектов выражается классификацией –это как бы стандарт, в кот каждая атрибутивная запись может быть отнесена лишь к одной группе или подгруппе- т.о. -это узаконенная, общепринятая, нормативная группировка.

Метод группировки основыв на 2-х категориях:

1- группировочном признаке;

2- интервале группировки (конкретном числе групп)