Методические указания и контрольные задания по дисциплине «статистика» для студентов заочного отделения специальности «Экономика, бухгалтерский учет и контроль» новочеркасск, 2005
| Вид материала | Методические указания |
- Методические указания и контрольные задания для студентов заочного отделения Специальность, 415.41kb.
- Методические указания по написанию курсовой работы по дисциплине «Экономика организации, 177.96kb.
- Методические указания и контрольные задания для студентов-заочников образовательного, 250.46kb.
- Методические указания по написанию курсовой работы по дисциплине «Анализ хозяйственной, 350.44kb.
- Методические указания и контрольные задания по выполнению контрольных работ №№1,2 для, 473.31kb.
- Методические указания и контрольные задания по выполнению домашней контрольной работы, 1577.88kb.
- Программа, методические указания и контрольные задания для студентов 5 курса заочного, 439.54kb.
- Программа, методические указания и контрольные задания для студентов 5 курса заочного, 2134.85kb.
- Методические указания и контрольные задания для студентов экстерната, заочной формы, 892kb.
- Методические указания и контрольные задания по английскому языку орёл 2009, 222.99kb.
Каждый вариант домашнего задания состоит из 6 задач по наиболее важным разделам курса. Каждый раздел курса имеет свою нумерацию.
7
| Раздел | Вариант задания —————————,——————————п————'———————————————.——————————.—————————————( | |||||
I | II | Ш | IY | V | YI | |
| номер задач | ||||||
| Средние величины | №1 | №2 | №3 | №4 | №5 | №6 |
| Показатели вариации и выборочное наблюдение | №1 | №2 | №3 | №4 | №5 | №6 |
| Ряды динамики и прогнозирование | №1, №7 | №2, №8 | №3, №9 | №4, №10 | №5, №11 | №6, №12 |
Индексы | №1 | №2 | №3 | №4 | №5 | №6 |
| Корреляционный метод изучения связи | №1 | №2 | №3 | №4 | №5 | №6 |
Раздел: «Средние величины».
В задачах 1— 6 внимательно подойдите к выбору видов средней. Помните, что форма и вид средней должны отражать экономическое содержание определяемых показателей. Например, средняя себестоимость единицы изделия определяется отношением общих затрат на производство к количеству выпускаемых изделий. Если в условии задачи по цехам (бригадам и т. п.) имеются данные о себестоимости единицы изделия и количестве изделий, то исходя из экономического содержания показателя, для расчета средней себестоимости применяется средняя арифметическая взвешенная:
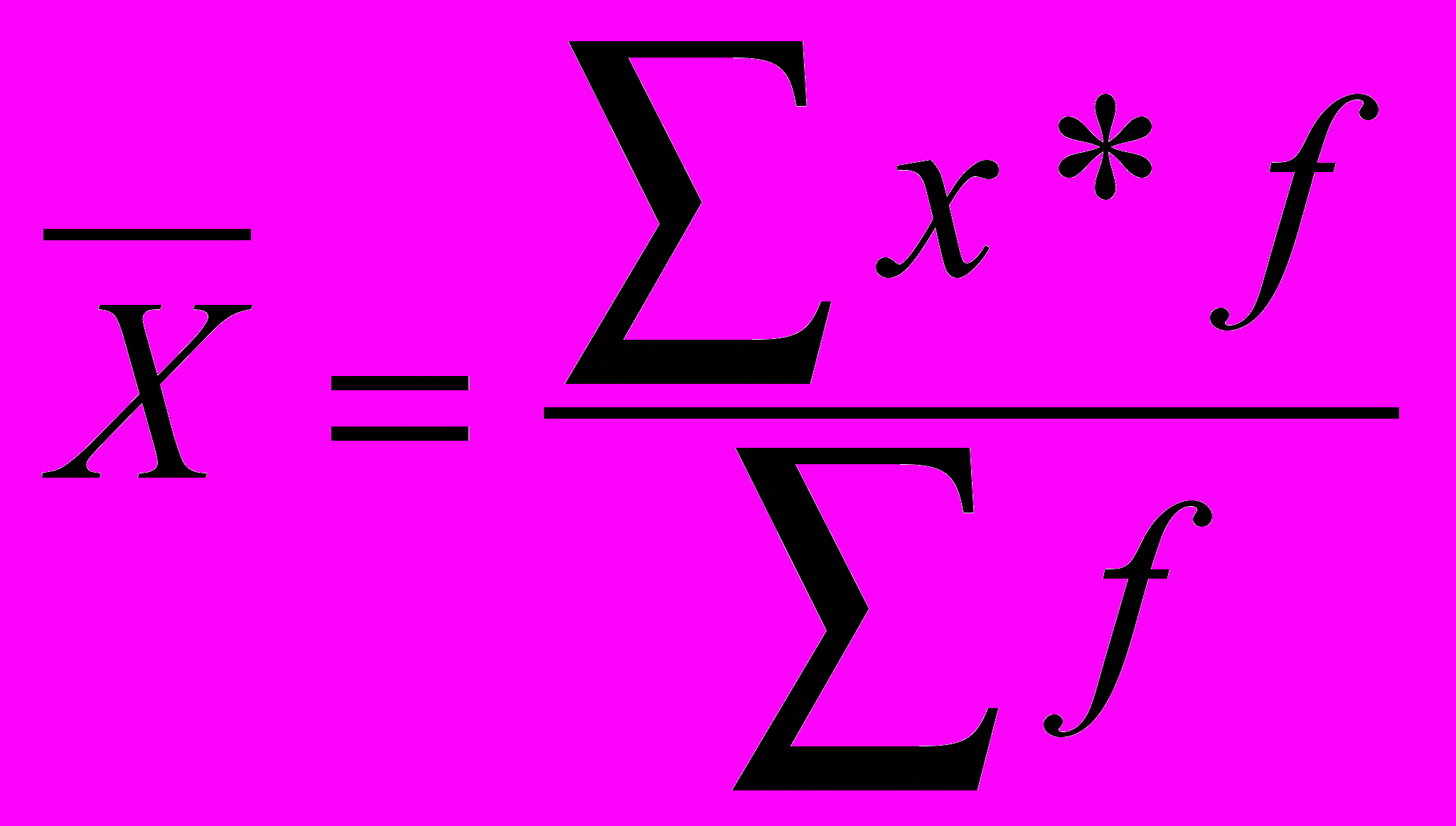 ,
,где х – себестоимость единицы изделия,
f – количество изделий.
Если в условии даны показатели о себестоимости единицы изделия и издержки производства, то для расчета среднего показателя применяется средняя гармоническая взвешенная:
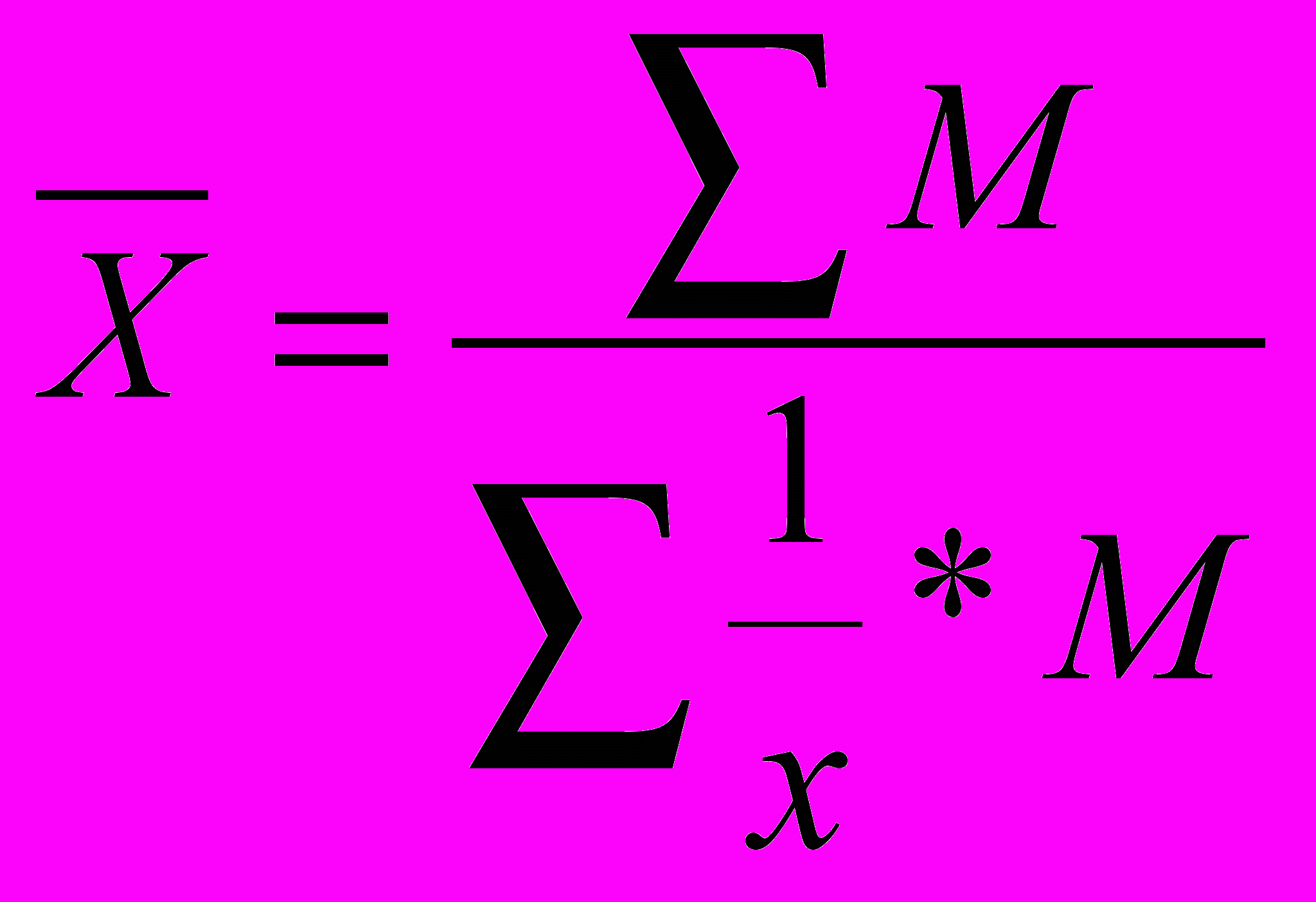 ,
,где х – себестоимость единицы изделия,
М – издержки производства.
8
По разделам «Показатели вариации» и «Выборочное наблюдение» составлены задачи 1—6. Вначале для решения задач необходимо вычислить среднюю арифметическую взвешенную по данным интервального ряда, затем показатели вариации: дисперсию, среднее квадратическое отклонение и коэффициент вариации. Показатель дисперсии (2) необходим для расчета ошибки выборки, а среднее квадратическое отклонение ( =
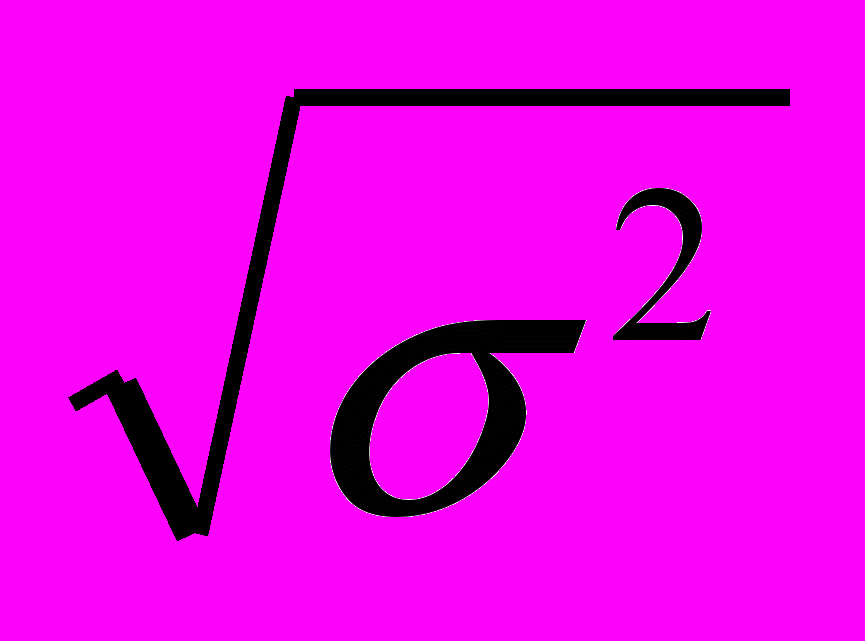 ) - для расчета коэффициента вариации.
) - для расчета коэффициента вариации.Вторая часть задачи выполняется по теме «Выборочное наблюдение». Необходимо разобраться в понятии повторный и бесповторный отбор, вычислении предельной ошибки для среднего значения признака:
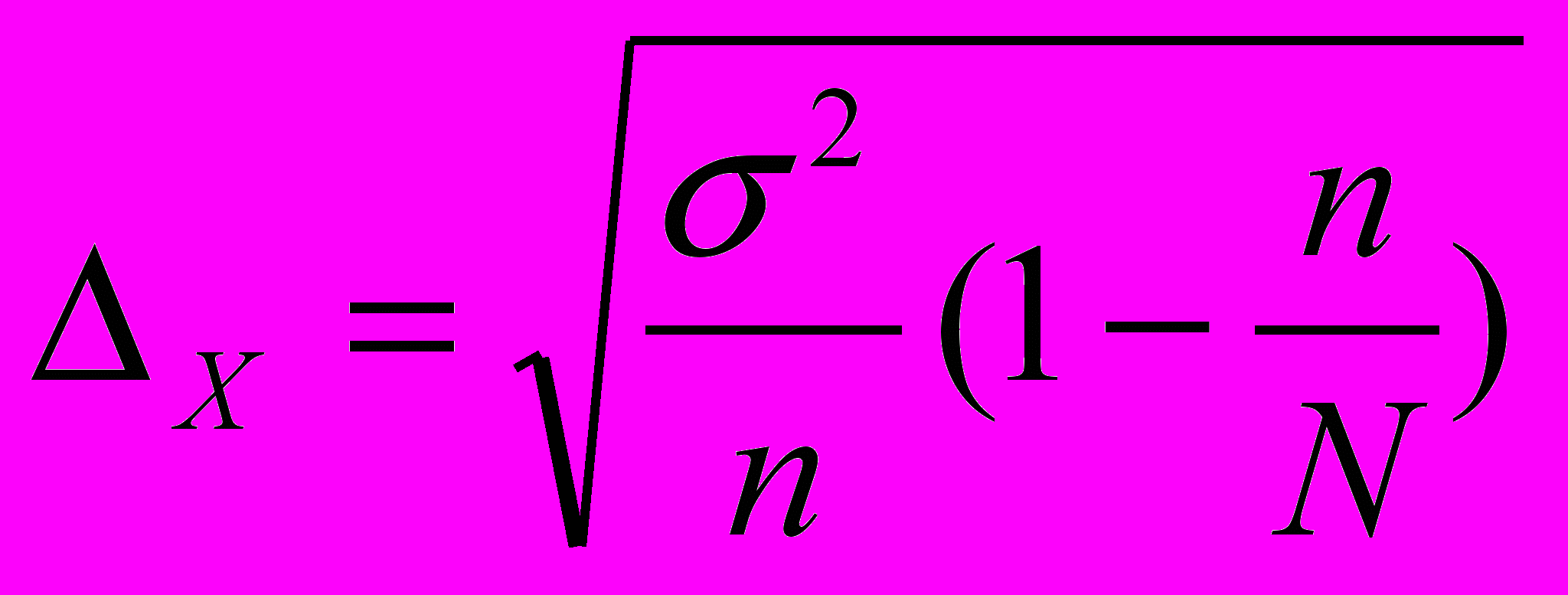
(бесповторный отбор) для доли признака:
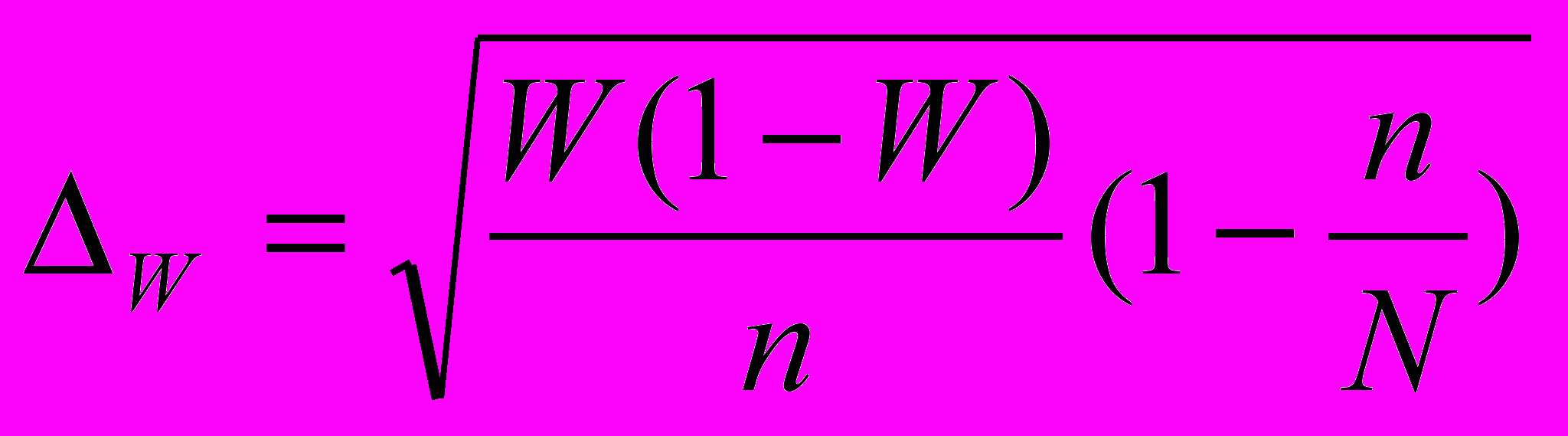
(бесповторный отбор).
Доверительный интервал для генеральной средней может быть рассчитан следующим образом:
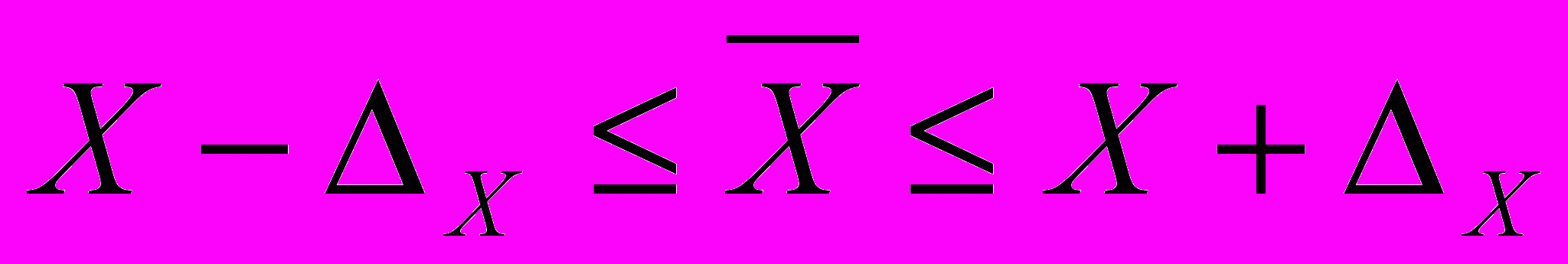
Доверительный интервал для доли признака равен:
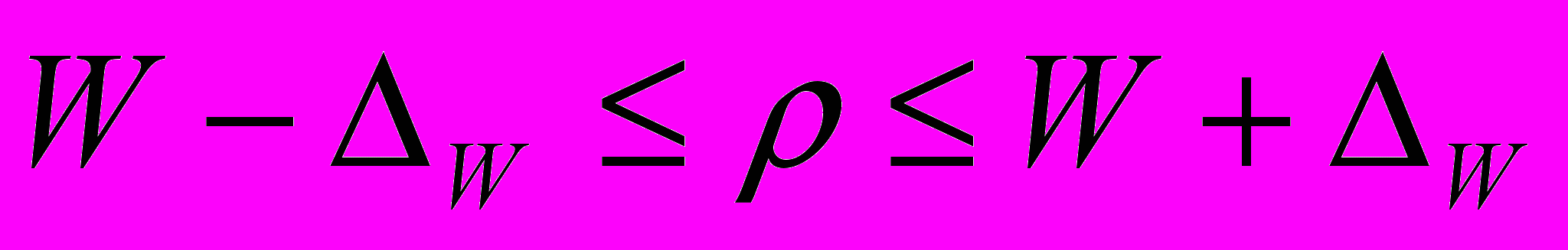
Раздел: «Ряды динамики и прогнозирование».
Эта тема представлена задачами 1—12.
В задачах 1— 6 требуется определить аналитические показатели ряда динамики. Особое внимание следует уделить расчету средних показателей ряда динамики.
Средний уровень ряда в задачах 1—6 вычисляется по формуле;
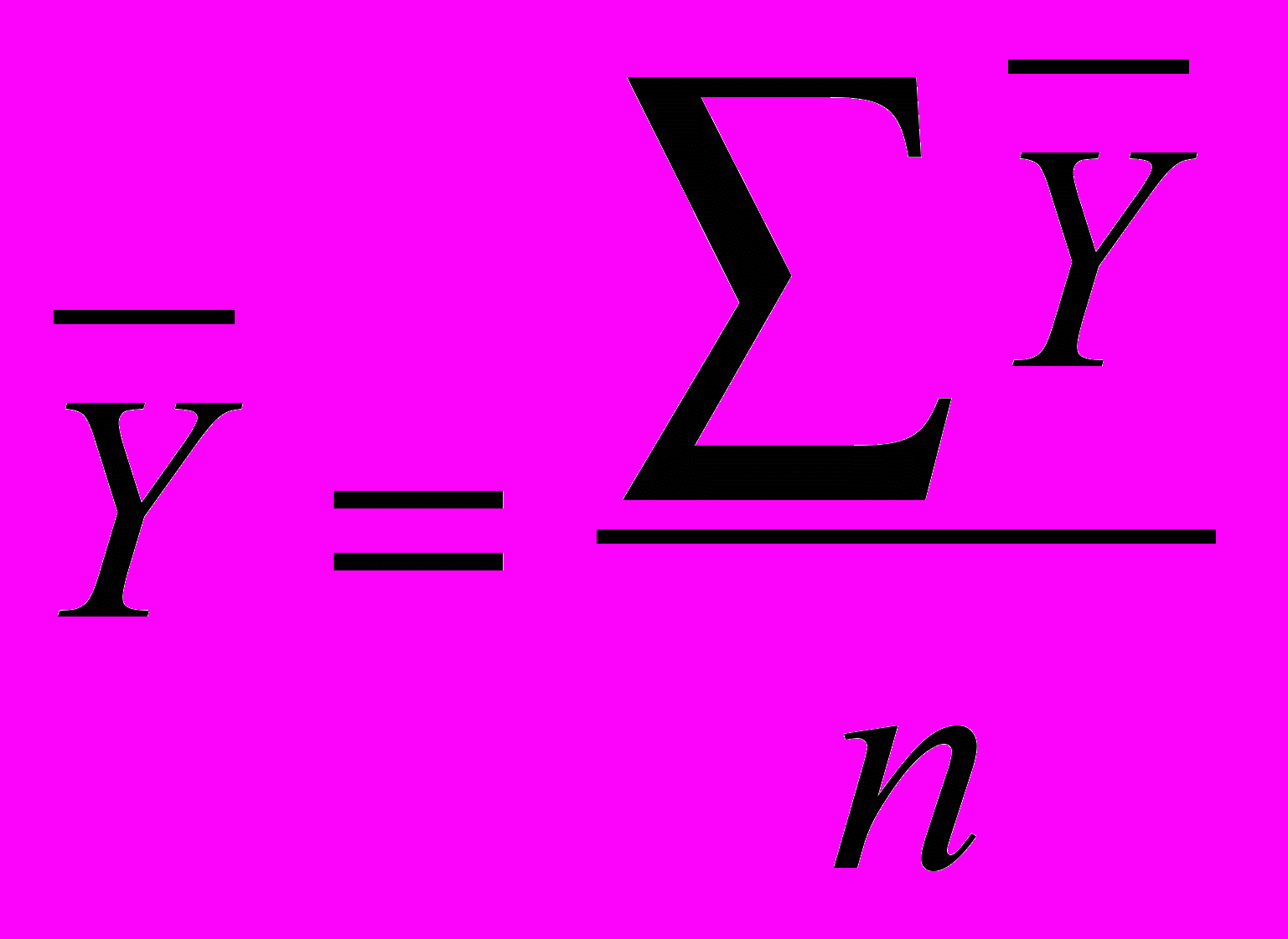
Средний абсолютный прирост исчисляется двумя способами:
а) как средняя арифметическая простая цепных приростов
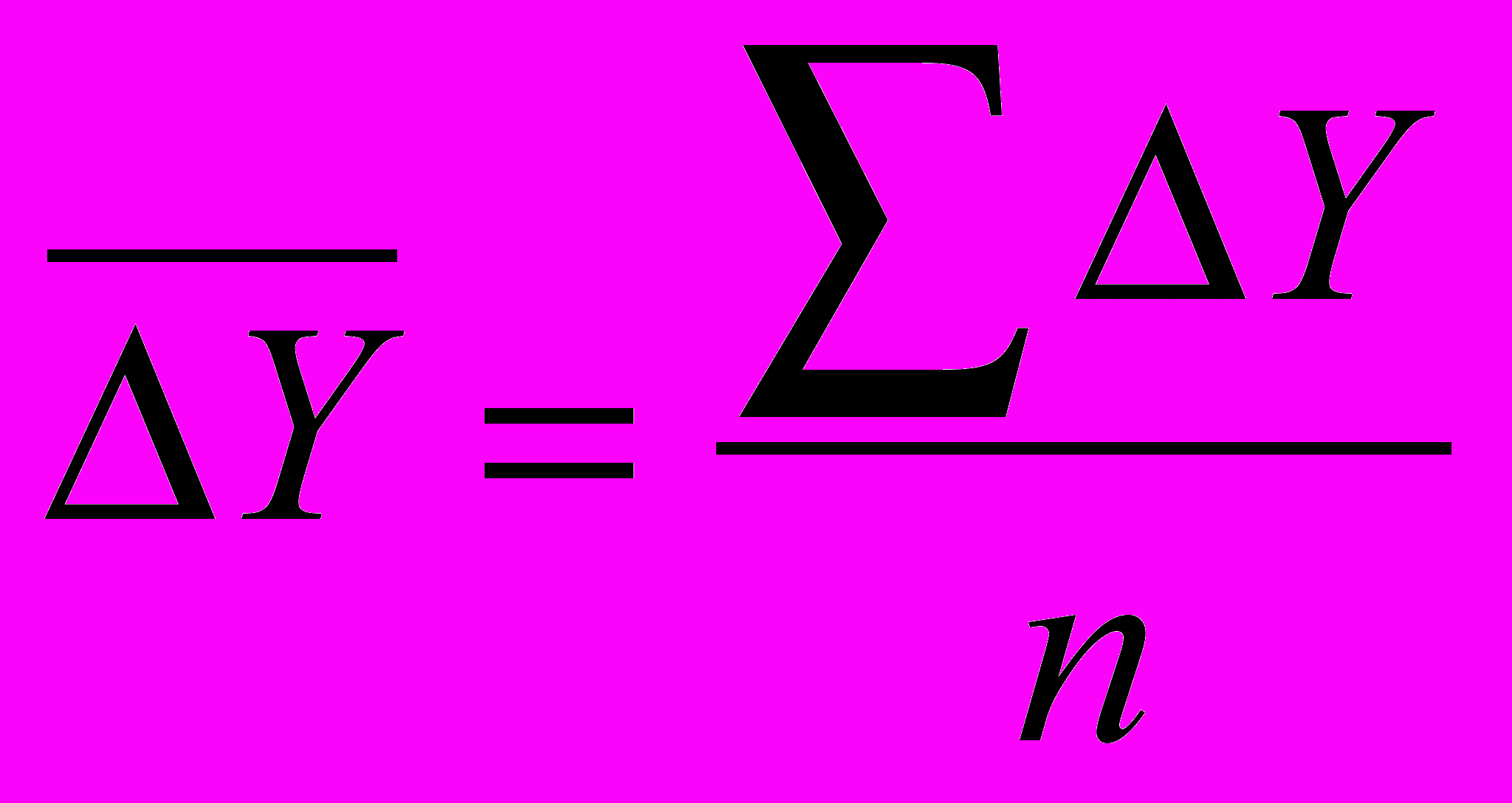 , где Y=Yi – Yi-1;
, где Y=Yi – Yi-1;9
б) делением базисного прироста на число периодов:
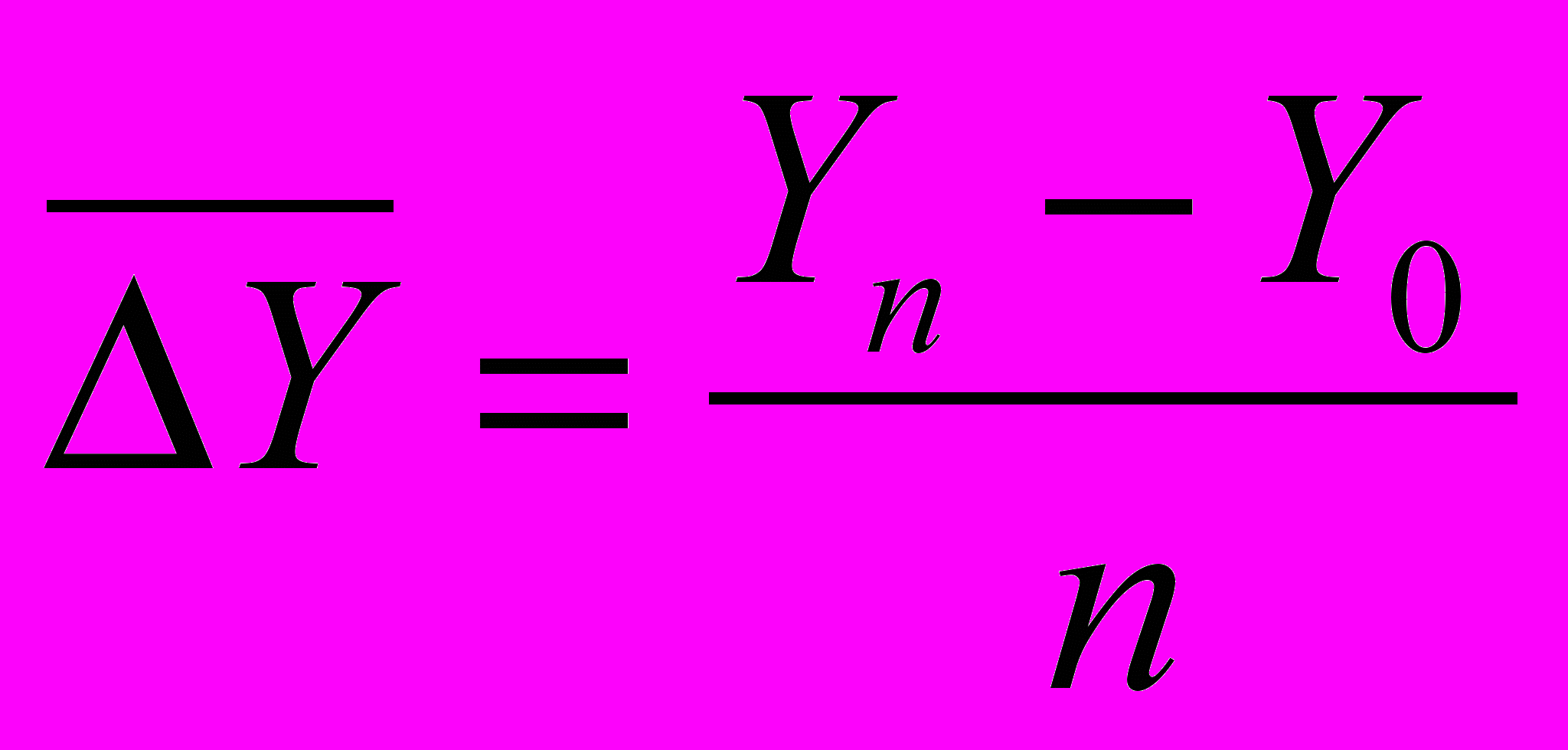 .
.В рядах динамики приняты следующие обозначения:
У0 — начальный уровень ряда;
Уi — каждый последующий уровень, начиная со второго;
Уn — конечный уровень ряда.
Темпы динамики (роста или снижения) вычисляются по формулам:
цепные - Т=
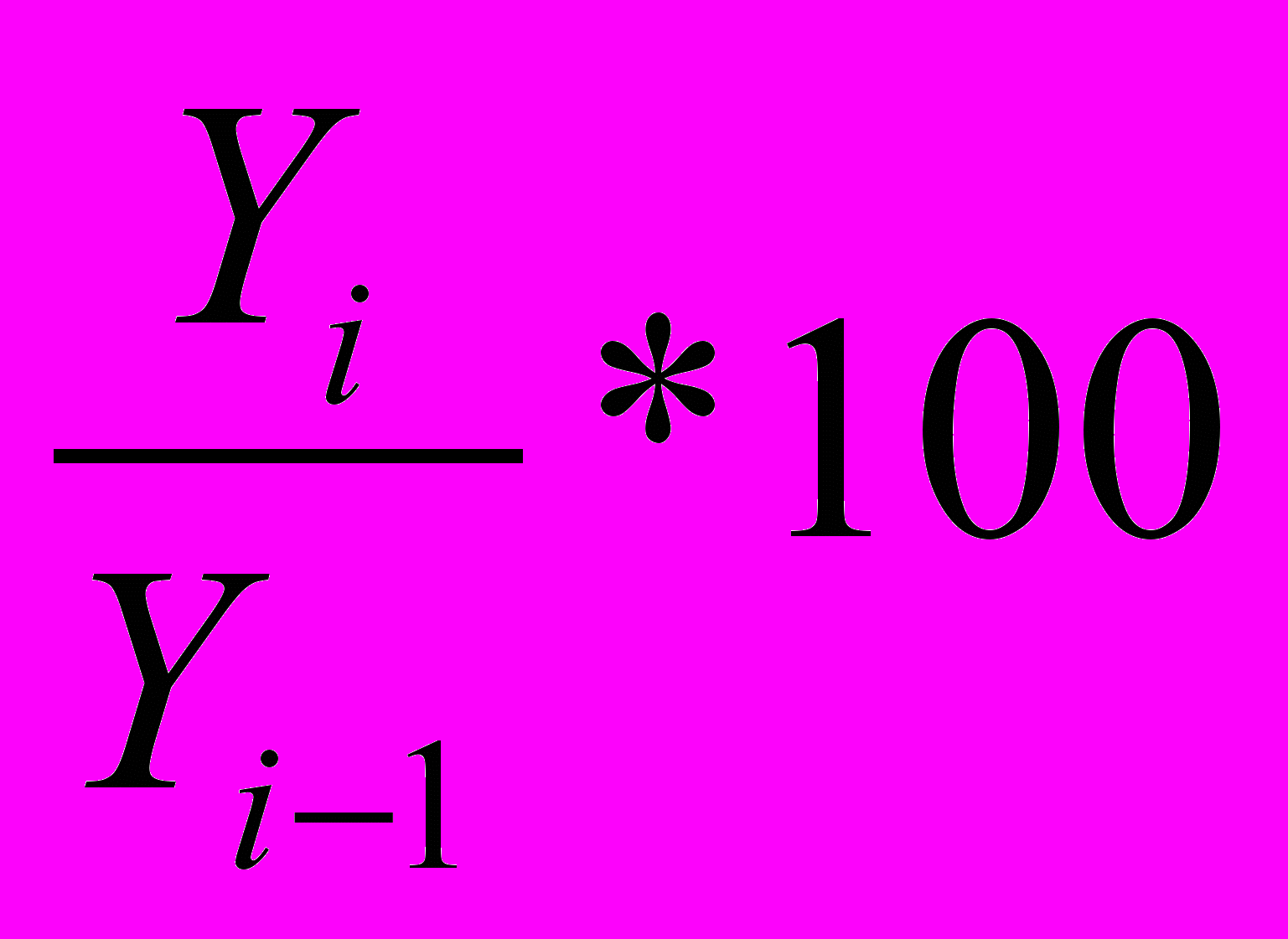
базисные -Т=
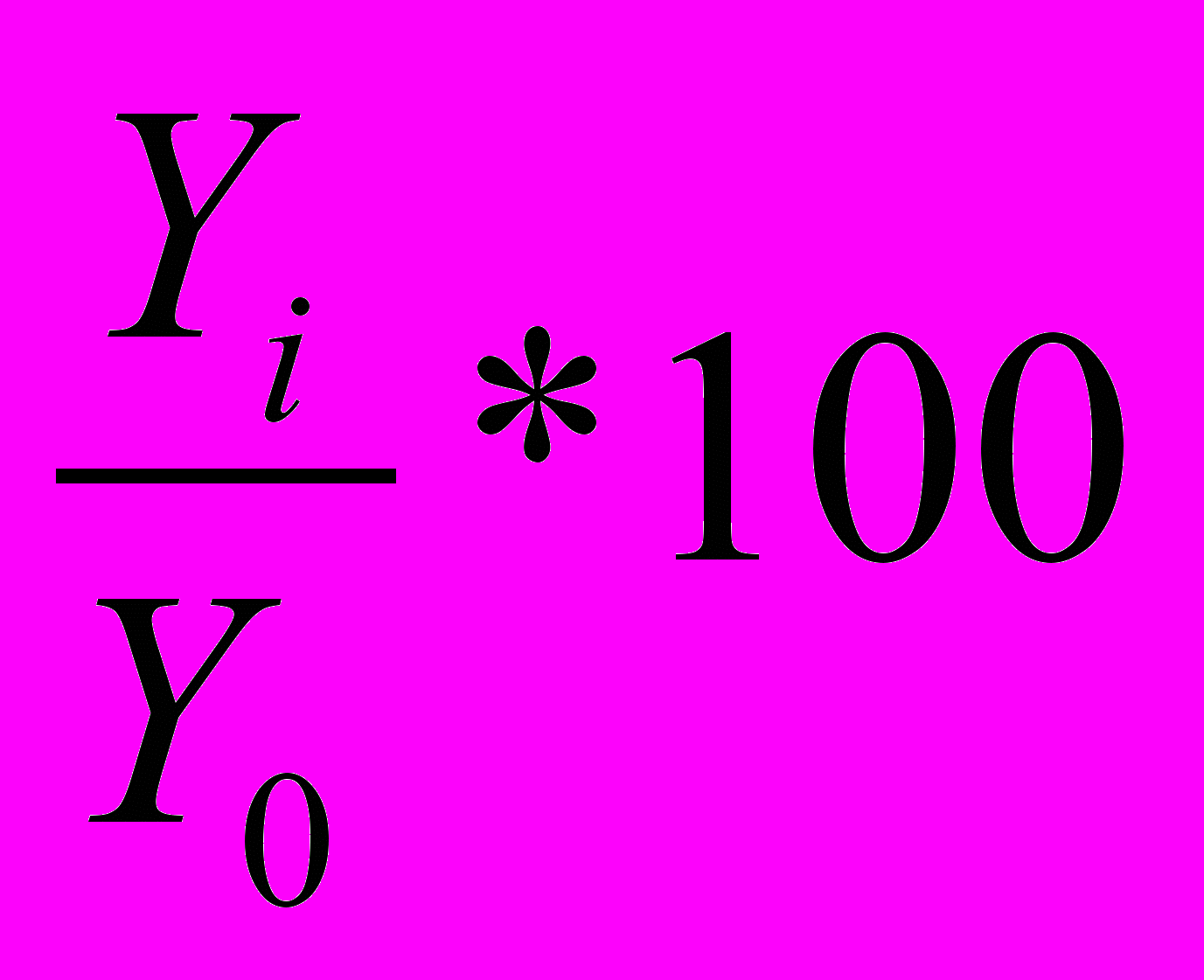
Среднегодовой темп динамики (роста или снижения) исчисляется по
формуле средней геометрической двумя способами:
-
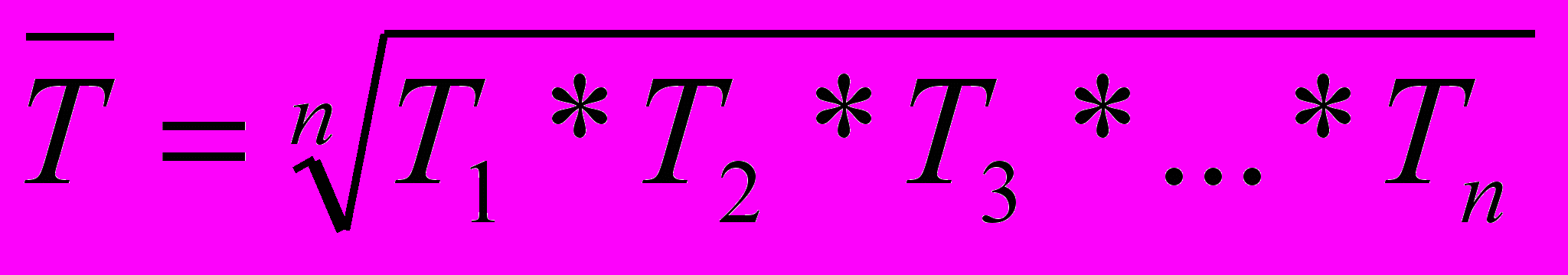 или
или 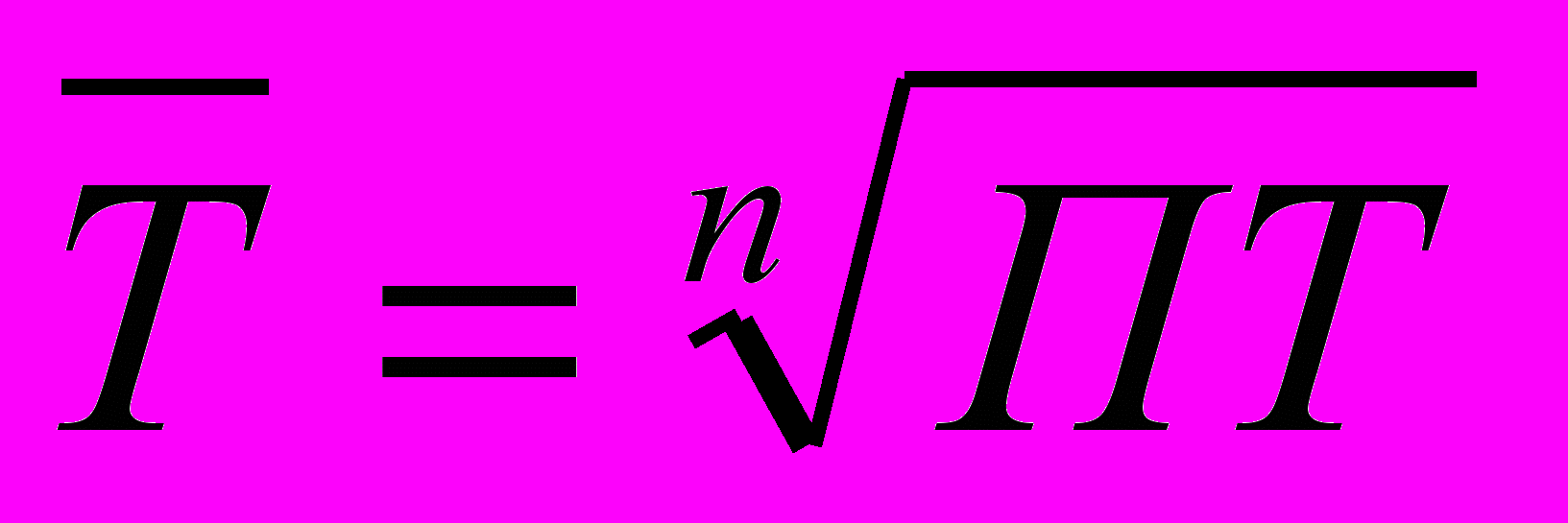 ,
,
где T1; Т2…Tn - цепные темпы роста или снижения;
n - число темпов;
П - знак произведения;
ПТ - произведение цепных темпов роста или снижения.
2.
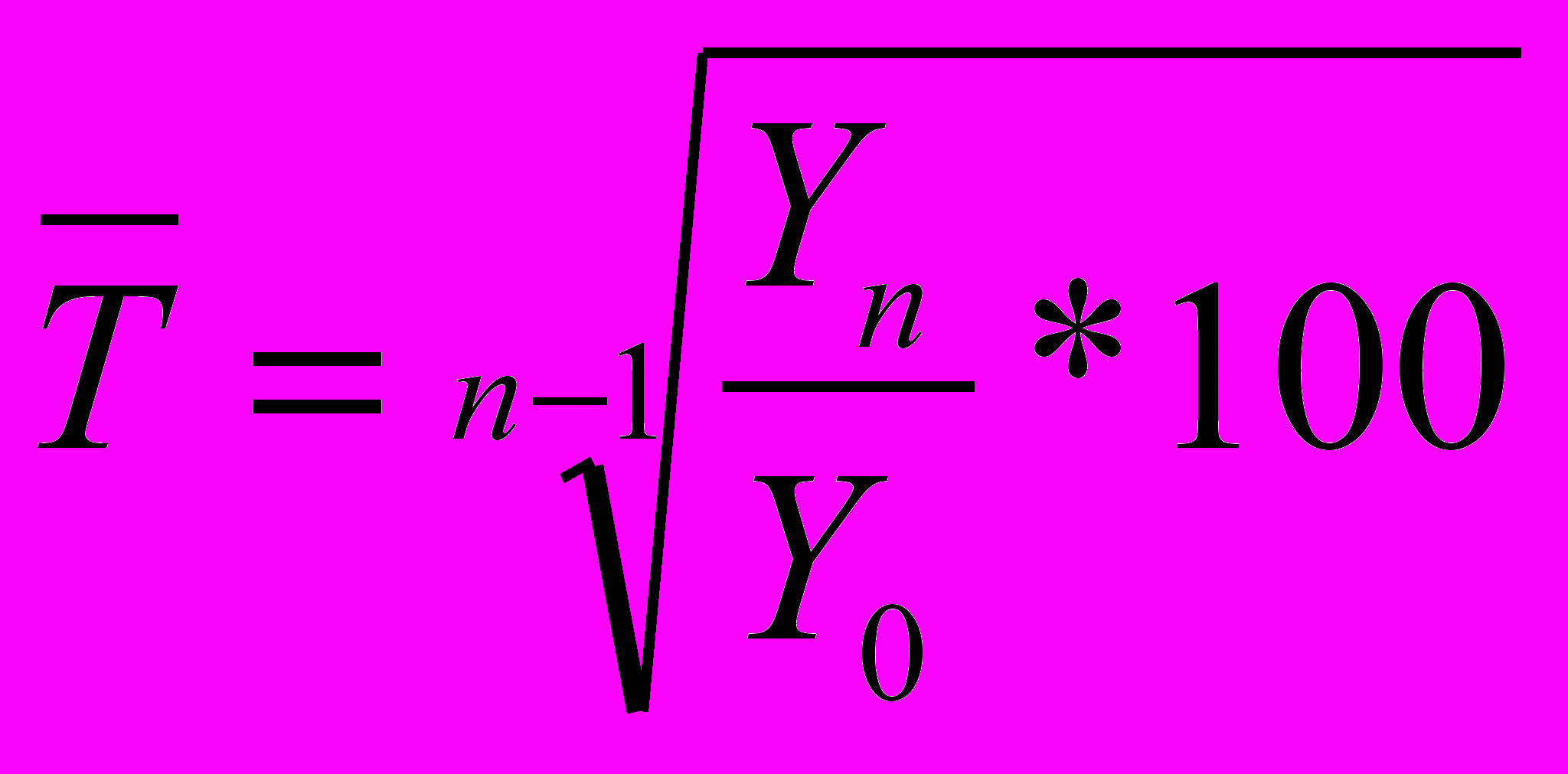
 ,
,где У0 - начальный уровень;
Уn - конечный уровень;
n - число уровней ряда динамики в изучаемом периоде.
Задачи 7-12 составлены на расчет среднего уровня моментного ряда динамики.
Средний уровень моментного ряда динамики с равными интервалами определяется по формуле средней хронологической:
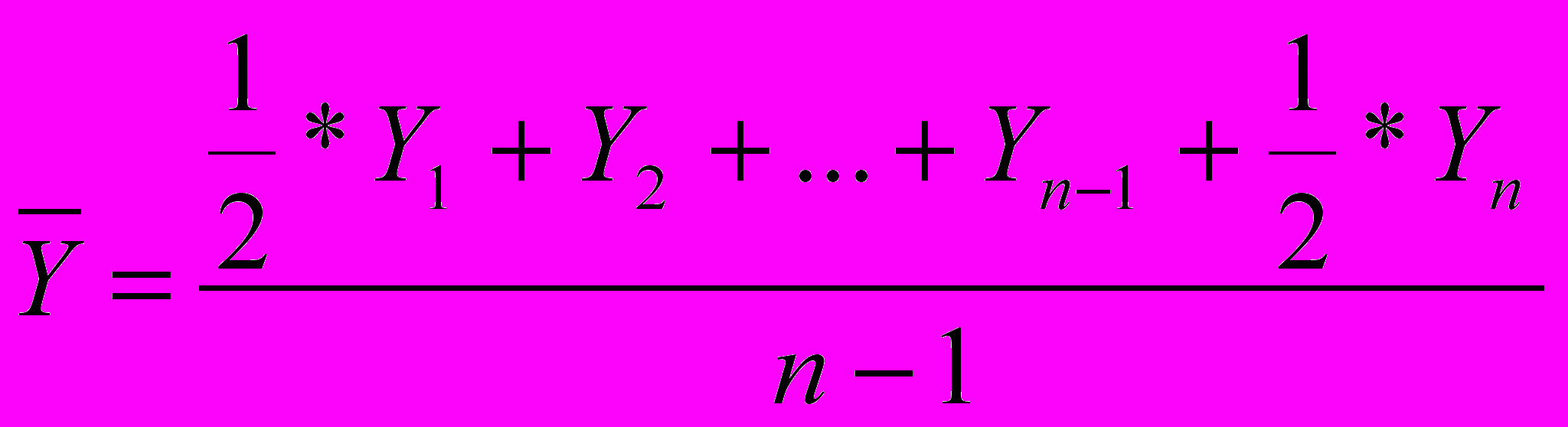 ,
,где n — число уровней ряда.
Средний уровень моментного ряда динамики с неравными интервалами определяется по формуле:
10
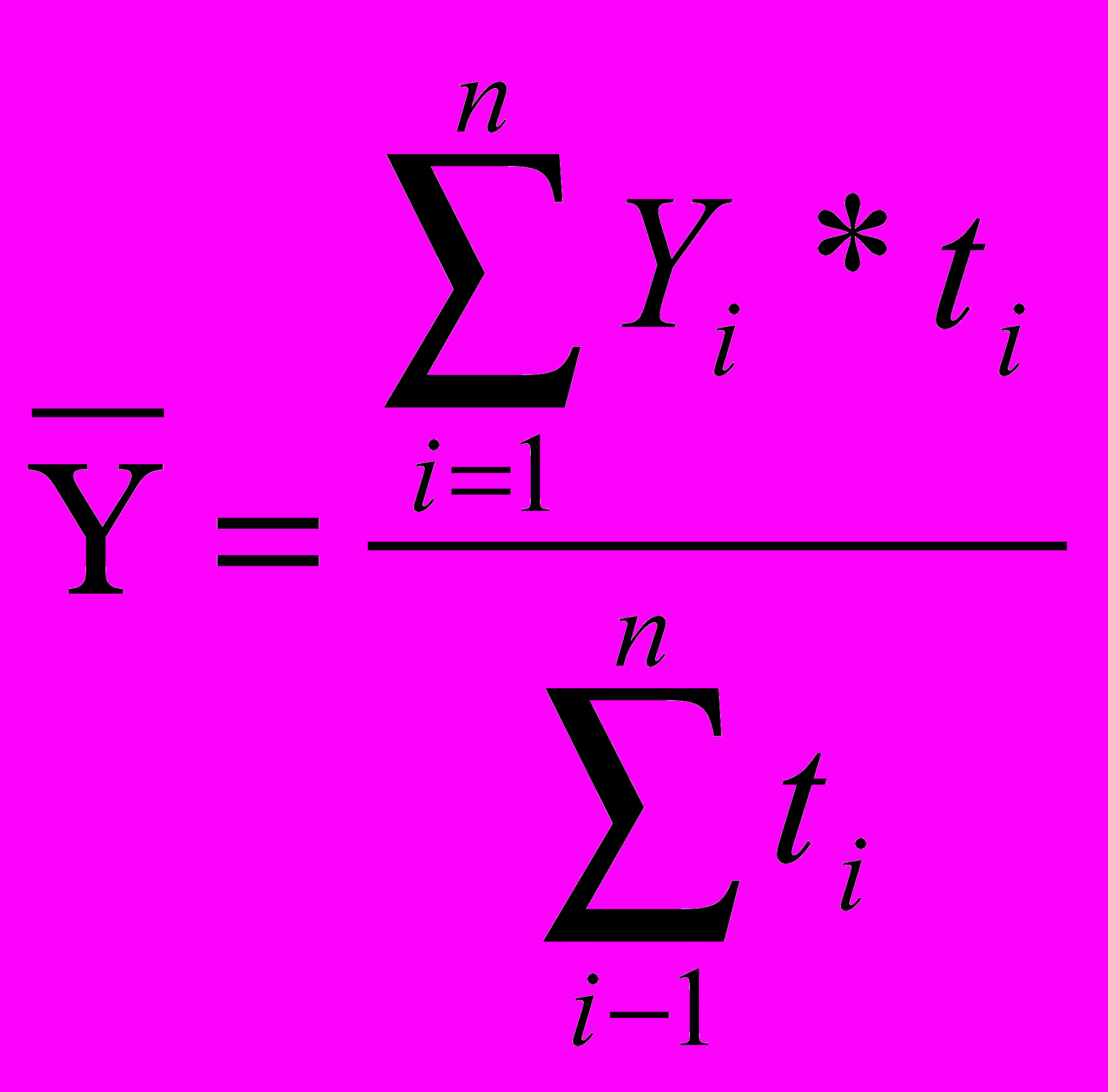 ,
,где n — число уровней ряда.
ti — продолжительность периода, в течение которого уровень не изменялся.
Раздел: «Индексы».
По теме «Индексы» составлены задачи 1—6. Задачи решаются по агрегатной форме индекса.
Агрегатный индекс физического объема продукции:
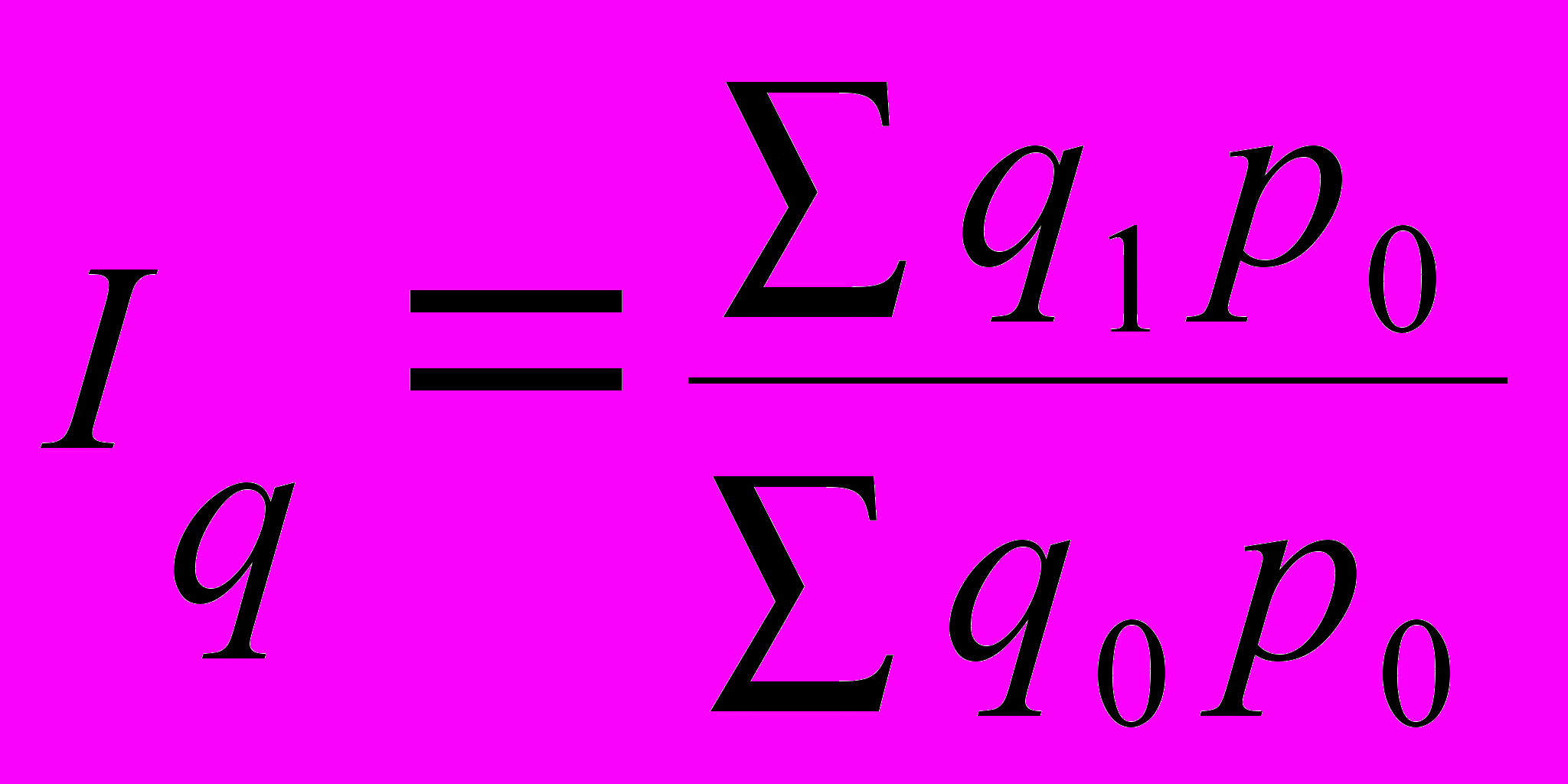 ,
,где q1 и q0 — количество выработанных единиц отдельных видов продукции
соответственно в отчетном и базисном периодах;
p0 — цена единицы отдельного вида продукции в базисном периоде.
Индекс физического объема продукции показывает во сколько раз изменился физический объем продукции или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.
В агрегатном индексе физического объема продукции индексируемой величиной является количество продукции (q); цена (p) служит коэффициентом соизмерения (соизмерителем).
qqp = q1p0 - q0p0,
где qqp абсолютное изменение общей стоимости продукции за счет изменения выпуска
продукции.
В качестве коэффициента соизмерения можно также использовать цены отчетного периода (p1) или сопоставимые (фиксированные – p0).
Агрегатный индекс стоимости продукции или товарооборота:
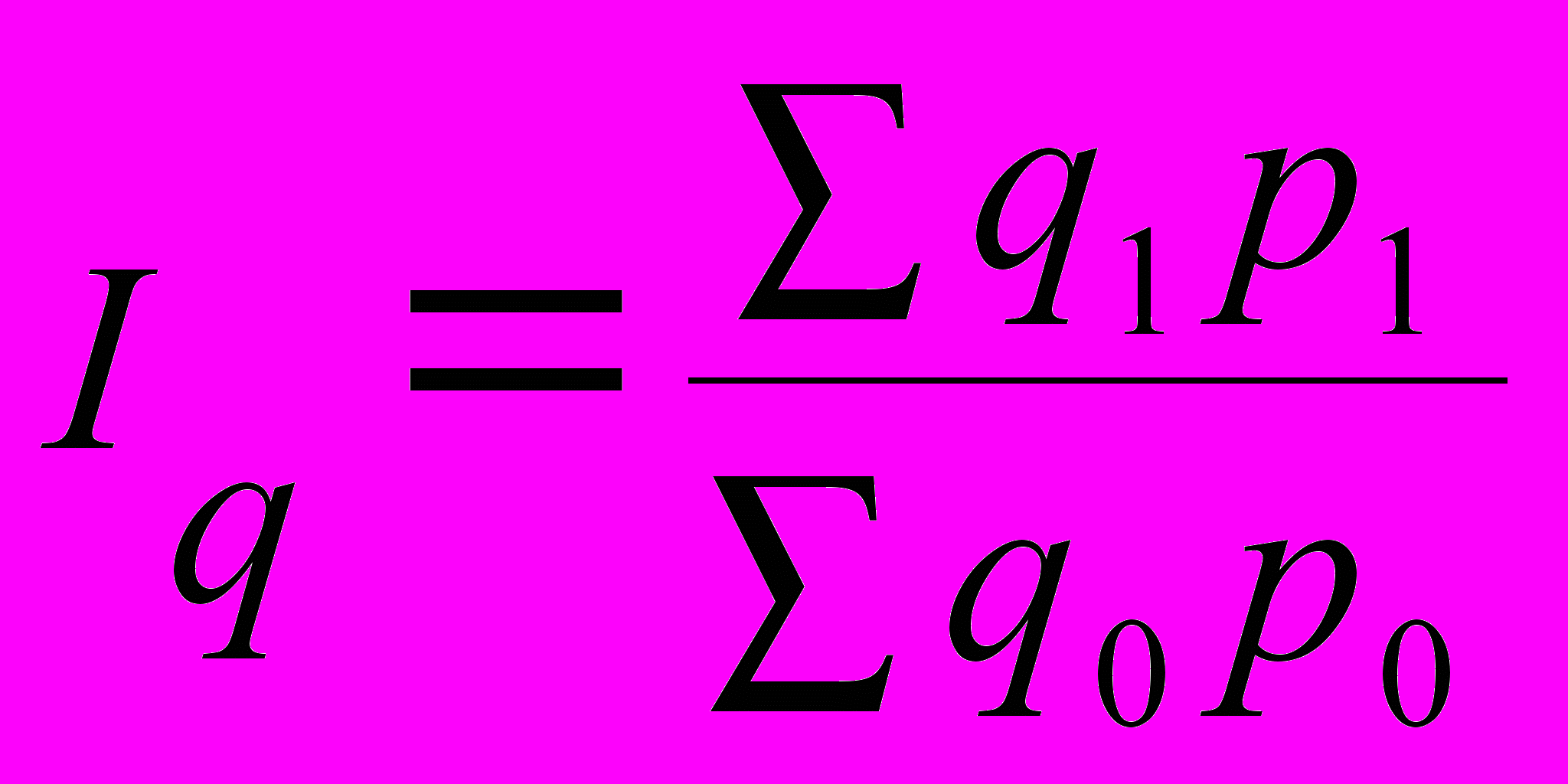 .
.Этот индекс показывает во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.
Кроме того, в качестве соизмерителей могут быть использованы себестоимость единицы продукции, а также затраты рабочего времени на единицу продукции. В этом случае агрегатный индекс физического объема определяется по формулам:
11
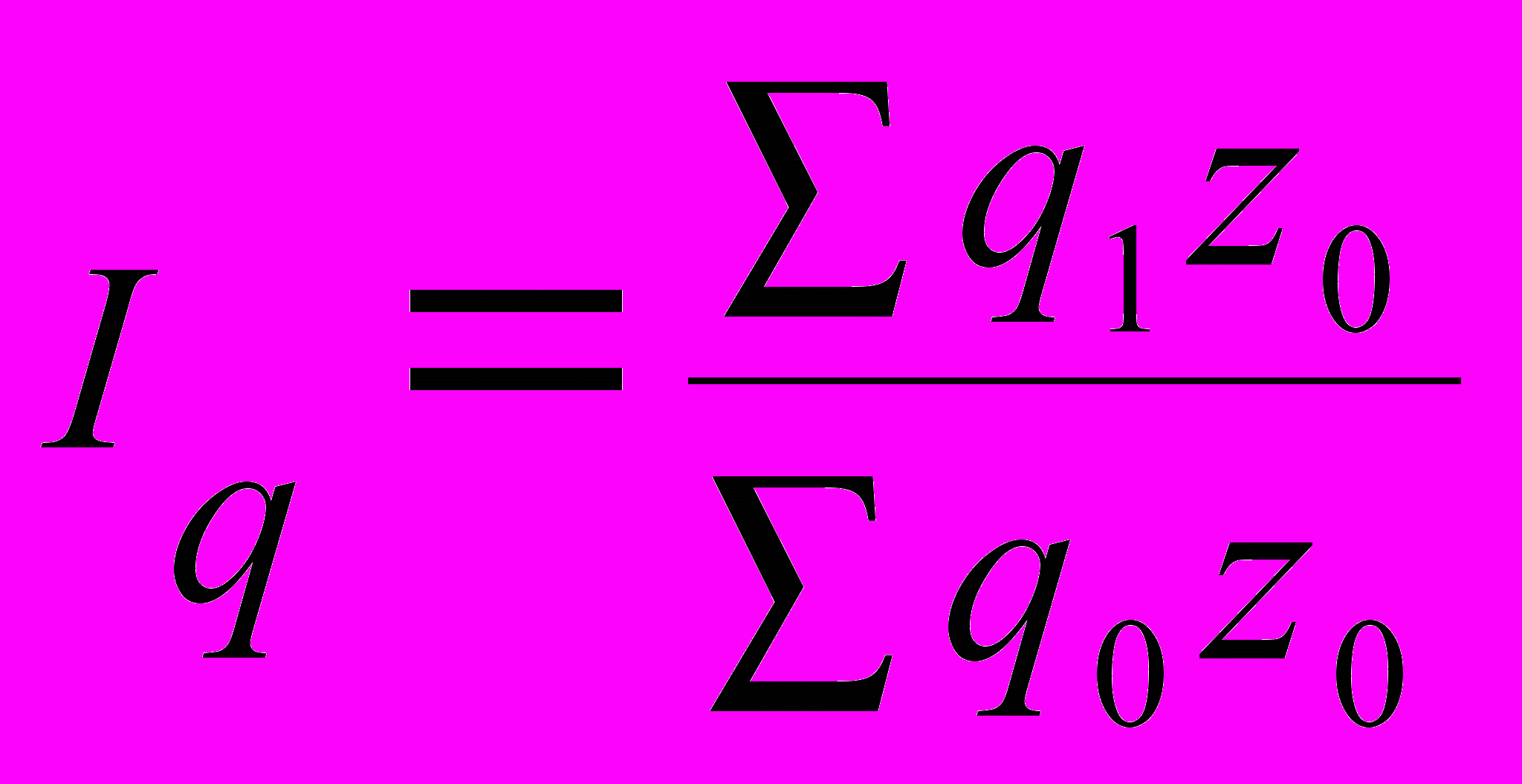 ,
, 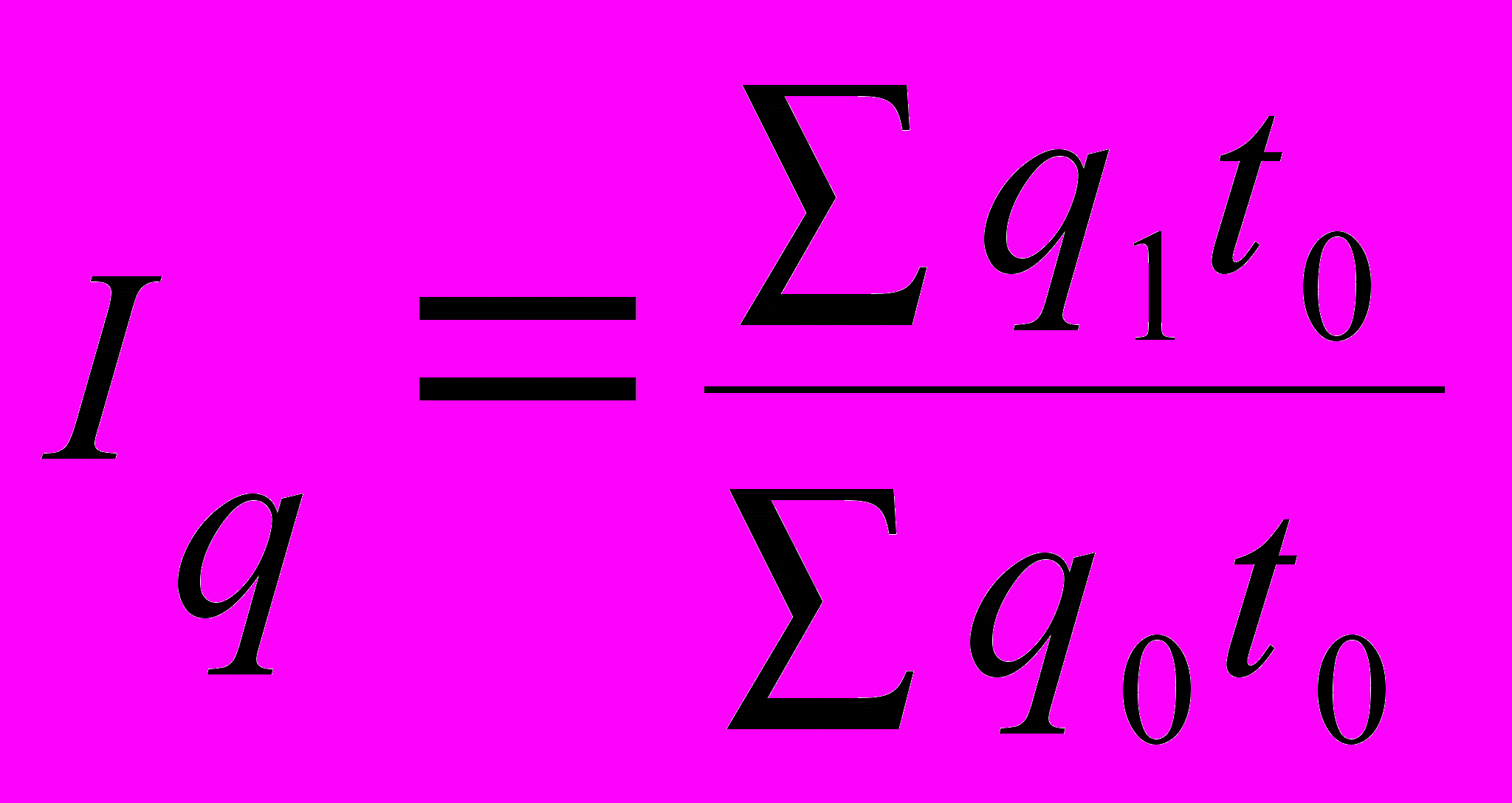 ,
,где z0 — себестоимость единицы продукции каждого вида в базисном периоде;
t0 — затраты рабочего времени на производство единицы продукции каждого вида в
базисном периоде.
Раздел: «Корреляционный метод изучения связи".
Тема «Корреляционный метод изучения связи" представлена задачами
1—6, в которых требуется вычислить линейное уравнение связи и коэффициенты тесноты связи между заданными признаками. Для их решения необходимо внимательно изучить соответствующий материал по учебникам.
Уравнение связи в общем виде:
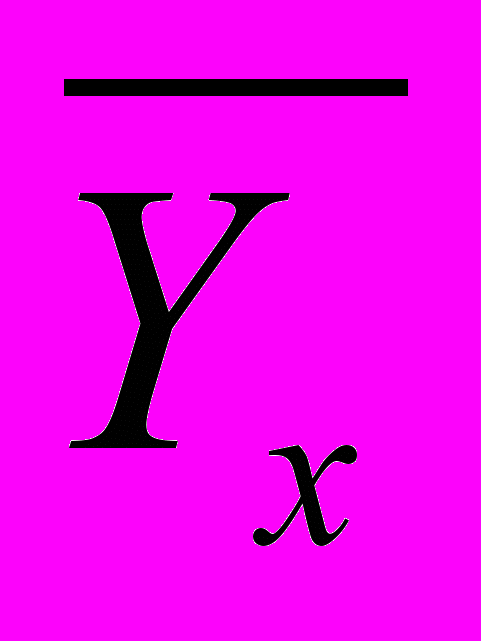 = а0 + a1x.
= а0 + a1x. Параметры уравнения связи а0 и a1 могут быть определены различными способами. Линейный коэффициент корреляции (коэффициент тесноты связи) также имеет несколько способов расчета. Студент может выбрать любой из них.
ПРИ ВЫПОЛНЕНИИ ДОМАШНЕГО ЗАДАНИЯ СЛЕДУЕТ РУКОВОДСТВОВАТЬСЯ СЛЕДУЮЩИМИ ТРЕБОВАНИЯМИ:
1) домашнее задание необходимо выполнять и представлять в
установленный срок;
2) домашнее задание должно выполняться в той последовательности, в
которой указаны номера задач по вариантам;
3) перед решением необходимо полностью привести условия задач;
4) решение задач следует сопровождать формулами, расчетами, краткими
пояснениями, выводами. Задачи, в которых даны только ответы без
расчетов, будут считаться нерешенными;
5) работа должна быть оформлена аккуратно, написана разборчиво, чисто,
без помарок, зачеркиваний, страницы необходимо пронумеровать и
оставить поля для замечаний преподавателя;
6) в конце работы надо указать перечень использованной литературы.
Студенты должны в межсессионный период решить самостоятельно прилагаемые ниже задачи, согласно своему варианту. В установленный срок до начала сессии студенты представляют преподавателю решенные задачи. Студенты, у которых будут зачтены контрольные работы, допускаются к сдаче зачета по курсу «Статистика».
Если в процессе самостоятельной работы над учебным материалом возникнут затруднения, следует обратиться за консультацией к преподавателю.
12
ЗАДАЧИ ПО ОСНОВНЫМ ТЕМАМ КУРСА:
Раздел: "Средние величины".
ЗАДАЧА № 1
Имеются следующие данные по трем заводам, вырабатывающим одноименную продукцию:
| Номер завода | Базисный период | Отчетный период | ||
| затраты времени на единицу продукции,час. | изготовлено продукции, тыс. шт. | затраты времени на единицу продукции, час. | затраты времени на всю продукцию, час. | |
| 1 | 0.40 | 63.0 | 0.35 | 21000 |
| 2 | 0.45 | 56.0 | 0.40 | 25600 |
| 3 | 0.50 | 34.0 | 0.45 | 86200 |
Вычислите средние затраты времени на продукцию по трем заводам в базисном и отчетном периодах. Сравните полученные результаты и сделайте выводы. Укажите, какие виды средних необходимо применить.
ЗАДАЧА № 2
Выработка суровых тканей по цехам фабрики характеризуется следующими показателями:
| Цех | МАРТ | АПРЕЛЬ | ||
| численность рабочих | средняя выработка ткани за смену одним рабочим, м | средняя выработка ткани за смену одним рабочим, м | выработано ткани, всего, м | |
| 1 | 50 | 80 | 83 | 4565 |
| 2 | 70 | 82 | 83 | 5810 |
| 3 | 80 | 85 | 86 | 7740 |
Вычислите выработку ткани на одного рабочего в среднем по фабрике:
а) за март; б) за апрель.
В каком месяце и на сколько средняя выработка была выше? Укажите,
какие виды средних применяли.
13
ЗАДАЧА № 3
Имеются следующие данные по предприятиям:
| Номер пред приятия | 1 квартал | 2 квартал | ||
| себестоимость единицы прдукции, тыс.руб. | количество изделий, тыс. шт. | себестоимость всей продукции (затраты на продукцию), млн. руб. | себестоимость единицы продукции, тыс. руб. | |
| 1 | 10 | 11 | 108 | 9 |
| 2 | 12 | 16 | 200 | 10 |
| 3 | 9 | 18 | 162 | 9 |
Вычислите среднюю себестоимость продукции:
а) за 1 квартал; б) за 2 квартал.
Сравните полученные показатели. Укажите, какие виды средних необходимо применить.
ЗАДАЧА № 4
По трем предприятиям имеются следующие данные о заработной плате работников:
| Предприятие | Базисный период | Отчетный период | ||
| Средняя заработная плата, тыс. руб. | Количество работников | Средняя заработная плата, тыс. руб. | Фонд заработной платы, млн. руб. | |
| 1 | 725 | 400 | 810 | 28000,0 |
| 2 | 740 | 200 | 780 | 186000 |
| 3 | 770 | 300 | 800 | 350000 |
Вычислите среднемесячную заработную плату по трем предприятиям вместе: а) за базисный период; б) за отчетный период.
В каком периоде и на сколько средняя заработная плата была выше? Укажите, какие виды средних необходимо применить.
14
ЗАДАЧА № 5
Имеются следующие данные фирм об объеме экспорта некоторых товаров:
| Наименование товара | Фирмы Ростовской области | Фирмы Краснодарского края | ||
| Средняя стоимость, долл. | Количество продукции, единиц | Средняя стоимость, долл. | Общий объем экспорта, тыс.долл. | |
| 1 | 89.3 | 960 | 97.5 | 19.5 |
| 2 | 162.0 | 3000 | 150.5 | 951.5 |
| 3 | 21.6 | 25000 | 22.9 | 459.0 |
Вычислите среднюю стоимость экспортируемых продовольственных товаров:
а)по фирмам Ростовской области;
б) по фирмам Краснодарского края.
Сравните данные. Укажите, какие виды средних необходимо применить.
ЗАДАЧА № 6
Имеются следующие данные о расходе материалов на строительство хозяйственного комплекса:
| Бригада | Май | Июнь | ||
| Расход материала на 1м2, кг | Количество, кг | Расход материала на 1м2, кг | Общий расход материала на строительство, т | |
| №1 | 700 | 10 | 1100 | 19 |
| №2 | 1000 | 15 | 1650 | 26 |
Определить средний расход материала на один квадратный метр строительных работ:
а) в мае;
б) в июне.
15
Разделы: "Показатели вариации" и "Выборочное наблюдение".
ЗАДАЧА № 1
В результате 4%-го выборочного обследования коммерческих банков о размере прибыли за год получено следующее распределение:
-
Размер прибыли, млрд.руб.
Число банков
4.7 - 5.6
3
5.6 - 6.5
2
6.5 - 7.4
4
7.4 - 8.3
5
свыше 8.3
6
Итого
20
По данным выборочного наблюдения определите:
1) средний размер прибыли банка, дисперсию и среднее квадратическое отклонение;
2) коэффициент вариации;
3) с вероятностью 0.997 возможные пределы, в которых ожидается средний размер прибыли банка;
4) с вероятностью 0.997 возможные пределы удельного веса банков с размером прибыли свыше 7.4 млрд.рублей.
ЗАДАЧА № 2
Проведено 5%-ое выборочное обследование коммерческих фирм по затратам на рекламу в газету "Имидж", результаты которого представлены в следующей таблице:
| Группы фирм по затратам на рекламу, усл.ден.ед. | Количество фирм |
| до 15 | 5 |
| 15-20 | 8 |
| 20-25 | 15 |
| 25-30 | 10 |
| 30 и более | 2 |
| ИТОГО | 40 |
16
По данным выборочного обследования вычислите:
- средний размер затрат на рекламу фирмой, дисперсию и среднее квадратическое отклонение;
- коэффициент вариации;
3) с вероятностью 0.997 возможные границы, в которых находится
средний размер затрат на рекламу фирмой;
4) с вероятностью 0.954 возможные границы,, в которых находится
удельный вес фирм, размер затрат на рекламу которых не превышает 20 усл.ден.единиц.
ЗАДАЧА №3
Для изучения длительности пользования кредитом проведено 2% -ное выборочное обследование предприятий по методу cлучайного бесповторного отбора.
Результаты обследования показали следующее распределение предприятий по длительности пользования кредитом:
| Группа предприятий по длительности пользования кредитом; дн. | Число предприятий | |
| до 35 | 4 | |
| 35 - 40 | 7 | |
| 40 - 45 | 10 | |
| 45 - 50 | 16 | |
| свыше 50 дней | 13 | |
| ИТОГО | 50 | |
По данным выборочного наблюдения определите:
1) среднюю длительность пользования кредитом, дисперсию и среднее квадратическое отклонение;
2) коэффициент вариации;
3) с вероятностью 0.997 возможные пределы, в которых ожидается средняя длительность пользования кредитом;
4) с вероятностью 0.954 возможные пределы удельного веса предприятий, пользующихся кредитом длительностью свыше 45 дней.
17
ЗАДАЧА № 4
Для определения средней суммы вклада в сбербанках района, имеющего 9000 вкладчиков, проведена 10-процентная механическая выборка, результаты которой представлены в следующей таблице:
-
Группа вкладов по размеру, млн.руб.
Число вкладчиков
до 2
80
2 – 4
100
4 – 6
200
6 – 8
370
8 и более
150
ИТОГО
900
По данным выборочного обследования вычислите:
1) среднюю величину вклада, дисперсию и среднее квадратическое
отклонение вклада;
2) коэффициент вариации;
3) с вероятностью 0.954 возможные границы, в которых находится
средняя сумма вклада в сбербанках района;
4) с вероятностью 0.997 возможные границы, в которых находится
удельный вес вкладчиков, вклад которых не превышает 4 млн.руб.
ЗАДАЧА № 5
Для изучения возрастной структуры рабочих завода по состоянию на
1 июля было проведено 5%-ное выборочное обследование по методу случайного бесповторного отбора.
Результаты обследования показали следующее распределение рабочих по возрасту:
-
Группы рабочих по возрасту, лет
Число рабочих
До 20
40
20 – 30
100
30—40
150
40—50
70
50 лет и старше
40
Итого
400
18
На основании данных выборочного обследования вычислите:
1) средний возраст рабочего, дисперсию и среднее квадратическое
отклонение;
2) коэффициент вариации;
3) с вероятностью 0.997 возможные пределы среднего возраста рабочих в
генеральной совокупности;
4) с вероятностью 0.954 определить для всего завода возможные пределы удельного веса рабочих в возрасте от 30 до 40 лет.
ЗАДАЧА № 6
Для изучения норм выработки рабочих-станочников на заводе было проведено 10%-ное выборочное наблюдение.
В механическом порядке обследовано 400 рабочих, показавших
следующие затраты времени на обработку детали:
-
Затраты времени на одну деталь, мин.
Число рабочих
До 14
40
14—16
100
16—18
150
18—20
70
20 и выше
40
Итого
400
По данным выборочного наблюдения определите:
1) Средние затраты времени на обработку одной детали, дисперсию и
среднее квадратическое отклонение.
2) Коэффициент вариации.
3) С вероятностью 0.997 возможные пределы, в которых ожидаются
средние затраты времени на обработку одной детали рабочими завода.
4) С вероятностью 0.954 возможные пределы удельного веса рабочих,
затрачивающих на обработку одной детали свыше 20 минут.
19
Раздел: "Ряды динамики и прогнозирование".
ЗАДАЧА № 1
Производство кожаной обуви в области характеризуется следующими данными:
-
ГОД
Обувь кожаная, тыс. пар
1991
357
1992
362
1993
366
1994
376
1995
387
1996
400
Для анализа ряда динамики исчислите:
1) абсолютные приросты, темпы роста, темпы прироста — базисные и
цепные, абсолютное содержание одного процента прироста, полученные
данные представьте в таблице;
2) среднегодовое производство кожаной обуви;
3) среднегодовой темп роста и прироста;
4) изобразите динамику производства кожаной обуви в области на графике.
Сделайте краткие выводы.
ЗАДАЧА № 2
Производство продукции предприятия характеризуется следующими данными:
-
ГОД
Производство продукции, млн. руб.
1991
600
1992
630
1993
660
1994
680
1995
690
1996
720
Для анализа ряда динамики производства продукции исчислите:
1) абсолютные приросты, темпы роста, темпы прироста - цепные и
базисные; содержание одного процента прироста; полученные
показатели представьте в таблице;
20
2) среднегодовое производство продукции;
3) среднегодовой темп роста и прироста;
4) изобразите динамику производства продукции предприятием на графике. Сделайте краткие выводы.
ЗАДАЧА № 3
Внешнеторговый оборот Волгоградской области характеризуется следующими данными:
-
Год
Внешнеторговый оборот, млн. руб.
1991
878.6
1992
981.4
1993
1065.8
1994
1167.0
1995
1215.5
1996
1040.1
Для анализа ряда динамики исчислите:
1) абсолютные приросты, темпы роста, темпы прироста - базисные и
цепные, абсолютное содержание одного процента прироста, полученные
данные представьте в таблице;
2) среднегодовой внешнеторговый оборот;
3) среднегодовой темп роста и прироста;
4) изобразите динамику внешнеторгового оборота области на графике. Сделайте краткие выводы.
ЗАДАЧА № 4
Имеются следующие данные Госкомстата РФ о количестве россиян,
отдыхающих за рубежом в период 1993-1997 гг. (тыс.чел.):
1993-1577;
1994-2522;
1995- 2555;
1996-3422;
997-3540 (прогноз).
Для анализа ряда динамики исчислите:
1) абсолютные приросты, темпы роста, темпы прироста - базисные и
цепные, абсолютное содержание 1% прироста. Полученные данные
представьте в таблице;
21
2) среднегодовое количество россиян, отдыхающих за рубежом;
3) среднегодовой абсолютный прирост;
4) среднегодовой темп роста и прироста;
5) изобразите динамику отдыхающих россиян за рубежом на графике. Сделайте краткие выводы.
ЗАДАЧА № 5
Динамика объема экспорта Ростовской области за 1992-1997 гг. характеризуется следующими данными (млн.долл.):
1992 - 263,7 1995 - 731,9
1993 - 395,9 1996 - 725,2
1994 - 526,0 1997 - 705,0 (прогноз)
Для анализа ряда динамики исчислите:
1) абсолютные приросты, темпы роста, темпы прироста - базисные и
цепные, абсолютное содержание 1% прироста.
Полученные показатели представьте в виде таблицы.
2) среднегодовой объем экспорта области;
3) среднегодовой абсолютный прирост;
4) базисные темпы роста с помощью взаимосвязи цепных темпов
роста;
5) среднегодовой темп роста и прироста;
6) изобразите динамику объема экспорта Ростовской области на графике. Сделайте выводы.
ЗАДАЧА №6
Динамика средних экспортных цен на медь, поставляемой из России
на мировой рынок в 1996 году, характеризуется следующими данными (долл. США за тонну):
январь — 2614 апрель — 2492
февраль — 2603 май — 2456
март — 2521 июнь — 2427
Для анализа ряда динамики исчислите:
- абсолютные приросты, темпы роста, темпы прироста - базисные и цепные, абсолютное содержание 1% прироста.
Полученные данные представьте в таблице;
22
2) среднее изменение экспортных цен на медь за полугодие;
3) средний абсолютный прирост (снижение) экспортных цен на
медь;
4) базисные темпы снижения с помощью взаимосвязи цепных темпов
снижения;
5) среднеполугодовой темп снижения;
6) изобразите динамику экспортных цен на медь на графике. Сделайте выводы.
ЗАДАЧА № 7
Остатки готовой продукции на складе на начало месяца составили
(млн. руб.):
1 января — 80,2 1 мая — 105.0
1 февраля — 85,4 1 июня — 94,2
1 марта — 100,6 1 июля — 96,0
1 апреля — 90,0
Вычислите среднемесячные остатки готовой продукции на складе:
1) за 1 квартал;
2) за II квартал;
3) за полугодие.
Поясните, почему методы расчета средних уровней рядов динамики в задачах № 1 и № 7 различны.
ЗАДАЧА №8
Имеются следующие данные о численности рабочих пo участкам
цеха:
-
Номер участка, цеха
Число рабочих, чел.
на 1 января
на 1 февраля
на 1 марта
на 1 апреля
1
60
63
65
62
2
82
80
84
88
Вычислите среднесписочное число рабочих за 1 квартал по каждому участку и по цеху в целом.
23
ЗАДАЧА № 9
Остатки вкладов в сберегательных банках района одной из областей за первое полугодие характеризуются следующими данными, млрд. руб.
на 1 января — 10.3 на 1 мая — 11.3
на 1 февраля — 10.5 на 1 июня — 11.6
на 1 марта — 10.9 на 1 июля — 11.8
на 1 апреля — 10.8
Вычислите средний остаток вкладов:
1) за I квартал;
2) за II квартал;
3) за полугодие.
ЗАДАЧА № 10
Получены следующие данные об остатках незавершенного производства фирмы на дату (тыс.руб.):
-
1 января
1 апреля
1 июля
1 октября
1 января
10180
12422
11317
10230
8795
Определите:
1) вид ряда динамики;
2) среднеквартальный остаток незавершенного производства.
ЗАДАЧА № 11
Имеются следующие данные о стоимости основных фондов производственной фирмы (тыс.руб.) на начало месяца:
1 января - 14842 1 июля - 21690
1 февраля - 16911 1 августа - 21690
1 марта - 16210 1 сентября - 21690
1 апреля - 12362 1 октября - 24570
1 мая - 10720 1 ноября - 20216
1 июня - 10720 1 декабря - 19870
1 января - 27980 (след.года)
24
Определите:
1) среднегодовую стоимость основных фондов фирмы;
2) среднемесячные уровни ряда в первом и втором полугодиях;
3) изменение стоимости основных фондов фирмы во втором полугодии по сравнению с первым.
ЗАДАЧА № 12
Имеются следующие данные об остатках дебиторской задолженности фирмы "Сатурн" на начало месяца (тыс.руб.):
-
1 января
1 февраля
1 марта
1 апреля
1 мая
1 июня
1 июля
394.0
312.8
372.6
356.3
390.4
402.8
413.0
Определите:
1) вид ряда динамики;
2) среднемесячные уровни остатка дебиторской задолженности за
1 и 2 кварталы;
3) изменение остатка дебиторской задолженности во 2 квартале по сравнению с 1 кварталом.
Раздел: "ИНДЕКСЫ".
ЗАДАЧА №1
Имеются следующие данные о реализации товаров на колхозном рынке:
| Наименование товара | Единица измерения | Цена единицы товара, тыс. руб. | Количество проданного товара, тыс.единиц | ||
| 1 квартал | 2 квартал | 1 квартал | 2 квартал | ||
| картофель | кг | 1.8 | 2.5 | 25.0 | 20.0 |
| молоко | л | 2.3 | 2.1 | 15.0 | 25.0 |
Определите:
1) общий индекс цен;
2) общий индекс физического объема товарооборота;
3) на основании исчисленных индексов (1,2) - индекс товарооборота
в фактических ценах.
Сделайте краткие выводы.
25
ЗАДАЧА № 2
Имеются следующие данные импортных поставок продукции из Северной Дакоты в г.Краснодар:
| Вид продукции | Количество | Цена за единицу, долл. | ||
| квартал | квартал | |||
| 3 | 4 | 3 | 4 | |
| Краска ДТМ, т | 200 | 250 | 97.5 | 94.5 |
| Гидравлическое масло, 50 фут. | 4 | 6 | 16.5 | 17.4 |
| Насадки для распылителя, шт. | 10 | 18 | 22.95 | 20.5 |
Определите:
1) общий индекс цен;
2) общий индекс стоимости товаров;
- общий индекс физического объема стоимости товаров.
Сделайте выводы.
ЗАДАЧА № 3
Объем произведенной продукции и ее себестоимость характеризуется следующими данными:
Изделия | Себестоимость единицы, тыс. руб. | Выработано продукций, тыс. единиц | ||
| квартал | квартал | |||
| 1 | 2 | 1 | 2 | |
| А | 140.0 | 120.0 | 5.0 | 2 |
| Б | 90.0 | 80.0 | 4,0 | 4.5 |
Определите:
1) общий индекс себестоимости продукции;
2) общий индекс физического объема продукции;
3) общий индекс затрат на производство продукции. Покажите взаимосвязь между исчисленными индексами. Сделайте выводы.
26
ЗАДАЧА № 4
Имеются следующие данные:
| Наименование компании | Курс акций, долл. | Количество выпущенных акций, млн. долл. | ||
| Базисный период | Текущий период | Базисный период | Текущий период | |
| Конагра | 30 | 34 | 17 | 19 |
| Сатур | 50 | 46 | 12 | 10 |
| Чияим | 91 | 98 | 4 | 7 |
| ИТОГО | | | 33 | 36 |
