Geum.ru

Перечень примерных контрольных вопросов по модулю 2

Вид материалаДокументы

Содержание


Примерный вариант тестов по модулю 2
Перечень примерных контрольных вопросов по модулю 3
Задание для самостоятельной работы по модулям 2 и 3
Примерный вариант тестов по модулю 3
Примерный перечень вопросов к зачету (экзамену) по курсу «Общая теория статистики»
Подобный материал:

Перечень примерных контрольных вопросов по модулю 2

  1. Дайте определение статистики как науки.
  2. Что такое совокупность, единица совокупности? Понятие вариации и признака.
  3. Перечислите специфические методы, присущие статистическому исследованию.
  4. Почему статистика изучает явление общественной жизни в движении, изменении и развитии?
  5. Перечислите основные этапы статистического исследования.
  6. Дайте определение предмета статистики.
  7. Что такое статистическое наблюдение?
  8. Перечислите основные этапы статистического наблюдения.
  9. Что понимается под программой наблюдения?
  10. Дайте определение форм, видов и способов наблюдения.
  11. Какие бывают ошибки наблюдения?
  12. В чем заключается суть сводки статистических материалов?
  13. Какие существуют виды сводки?
  14. Какие задачи решаются в статистике при помощи метода группировок?
  15. Какие существуют виды группировок?
  16. Как определяется число групп?
  17. Какие бывают интервалы?
  18. Что понимается под классификацией в статистике?
  19. Как определяется величина интервала при группировке по количественному признаку?
  20. Что представляет собой статистический ряд распределения? Его элементы.
  21. Что такое полигон, гистограмма, кумулята и огива, как они строятся и что они характеризуют?
  22. В чем сущность метода вторичной группировки?
  23. Что такое статистическая таблица, из каких элементов она состоит?
  24. Назовите виды статистических таблиц и правила их составления.
  25. В чем заключается назначение статистических графиков?
  26. Перечислите основные элементы графиков.
  27. Перечислите основные виды статистических графиков.
  28. Дайте определение статистическому показателю.
  29. Какими бывают статистические показатели по форме выражения?
  30. Чем отличается моментный статистический показатель от интервального?
  31. Дайте определение абсолютному показателю.
  32. Что характеризуют относительные величины?
  33. В каких единицах выражаются абсолютные и относительные величины?
  34. Перечислите виды относительных величин. Что они характеризуют?
  35. Дайте определение средней величине. В чем её сущность?
  36. Как определяется средняя величина?
  37. Какие существуют виды средних величин?
  38. В чем специфика расчета средней для сгруппированных и несгруппированных данных?
  39. Перечислите свойства средней арифметической взвешенной.
  40. Дайте определение структурным средним.
  41. Чем обусловлена необходимость изучения вариации признака?
  42. Какими показателями измеряется вариация?
  43. В чем заключается « правило трех сигм »?
  44. Каковы свойства дисперсии?
  45. Какие существуют виды дисперсии и что они характеризуют?
  46. В чем заключается правило сложения дисперсий?
  47. Для чего рассчитывают относительные показатели вариации?
  48. В чем особенности измерения вариации альтернативных признаков?
  49. Назовите основные показатели, характеризующие форму распределения, расскажите о методах их расчета.
  50. Как интерпретируются показатели асимметрии и эксцесса и оценивается их существенность?



Примерный вариант тестов по модулю 2

  1. Подлежащее статистических таблиц содержит:
    1. перечень единиц совокупности по признаку;
    2. группировку единиц совокупности по одному признаку;
    3. группировку единиц совокупности по нескольким признакам.
  2. Чему равна межгрупповая дисперсия, если признак внутри групп не
    варьирует?
    1. единице;
    2. нулю;
    3. общей дисперсии;
    4. средней из групповых дисперсий.
  3. По предприятию известны следующие данные:

№ цеха
Фонд заработной платы (руб.)
Средняя заработная плата (руб.)

1.

2.

3.
24480

11590

25050
720

610

835

Какую форму средней следует использовать для расчета средней заработной платы по предприятию в целом?
    1. среднюю арифметическую простую;
    2. среднюю арифметическую взвешенную;
    3. среднюю гармоническую простую;
    4. среднюю гармоническую взвешенную;
    5. среднюю геометрическую.
  1. Метод статистических группировок предназначен:
    1. для измерения динамики сложных социально-экономических явлений;
    2. для выделения однородных частей в статистической совокупности;
    3. для анализа взаимосвязей между признаками.
  2. Распределение торговых предприятий города по числу работников характеризуется следующими данными:

Число работников, (чел.)
до 3
4-10
11-20
21-40
41 и более
Итого

Удельный вес предприятий, (%)
9
17
33
35
6
100

Определите модальный интервал:
    1. 4-10;
    2. 11-20;
    3. 21-40.
  1. Три предприятия области имеют следующую производительность труда: первый- 27 у.д.е./чел, 2-й – 31 у.д.е./чел, 3-й – 35 у.д.е./чел. Если производительность в каждом предприятии увеличить на 5%, а численность персонла сократить на 10%, то как изменится средняя производительность по трем предприятиям в целом?
    1. уменьшится;
    2. останется без изменений;
    3. увеличится;
    4. неизвестно.
  2. Совокупность - это:
    1. любое предметное множество явлений природы и общества;
    2. множество элементов, обладающих общими признаками;
    3. реально существующее множество однородных элементов, обладающих общими признаками и внутренней связью;
    4. множество признаков изучаемого социально-экономического явления.
  3. Средняя из внутригрупповых дисперсий характеризует:
    1. вариацию результативного признака "у", обусловленную влиянием всех
      факторов, кроме исследуемого фактора "х";
    2. вариацию результативного признака "у", обусловленную влиянием
      фактора "х";
    3. вариацию внутригрупповых средних относительно общей средней по
      совокупности.
  4. Распределение предприятий отрасли по численности промышленно-производственного персонала характеризуются следующими данными:

Численность ППП (чел.)
До 200
200-400
400-600
600-800
800 и более

Число предприятий
26
23
17
8
7

Определите медианный материал:
    1. до 200;
    2. 200-400;
    3. 400-600.
  1. Известны следующие данные по заработной плате рабочих

Средняя зарплата рабочих бригады (руб.)
Число бригад
Среднее число человек

в бригаде

700-780

780-860

860-940
7

11

3
18

16

11

Данные какой графы будут выступать в качестве весов при расчете средней зарплаты по предприятию в целом?
    1. 2 графы;
    2. 3графы;
    3. 2 и 3 граф ;
    4. 1,2 и 3 граф;
    5. веса не нужны.
  1. По предприятиям имеются следующие данные:

Цена, руб./ед.
Число предприятий
Объем продукции, тыс. шт.

30-34

34-38

38-42
8

16

5
260

235

216

Какую формулу средней необходимо использовать для расчета средней цены в целом по всем предприятиям?
    1. среднюю арифметическую простую;
    2. среднюю арифметическую взвешенную;
    3. среднюю гармоническую простую;
    4. среднюю гармоническую взвешенную;
    5. среднюю геометрическую.
  1. Программа статистического наблюдения включает:
    1. время наблюдения;
    2. критический момент;
    3. способ и метод наблюдения, порядок разработки данных;
    4. систему признаков, подлежащих статистическому наблюдению.
  2. Одним из показателей вариации является:
    1. коэффициент корреляции;
    2. корреляционное отношение;
    3. коэффициент ассоциации;
    4. среднее линейное отклонение.
  3. Какие виды картограмм используются для изображения социально-экономических явлений?
    1. фоновые;
    2. точечные;
    3. знаков-символов.
  4. Выработка 7 членов бригады характеризуется следующими данными (деталей за смену): 18,26, 27,21,21, 24, 28. Определите медианное значение:
    1. 21;
    2. 24;
    3. 23.6.
  5. Ошибки статистического наблюдения бывают:
    1. только случайные;
    2. случайные и систематические;
    3. только ошибки репрезентативности;
    4. ошибок не существует.
  6. Сказуемым статистической таблицы является:
    1. исследуемый объект;
    2. показатели, характеризующие исследуемый объект;
    3. сведения, расположенные в верхних заголовках таблицы.
  7. Инструментарий статистического наблюдения содержит:
    1. только инструкцию;
    2. только формуляр;
    3. только инструкцию и формуляр;
    4. только обращение к субъекту обследования;
    5. макет разработочных таблиц;
  8. Объект статистического наблюдения – это:
    1. единица наблюдения;
    2. статистическая совокупность;
    3. единица статистической совокупности;
    4. совокупность признаков изучаемого социально-экономического явления.
  9. Вариационным называется ряд распределения, построенный:
    1. по количественному признаку;
    2. по качественному признаку;
    3. по качественному и количественному признакам одновременно.
  10. Перечень признаков наблюдения, называется:
    1. статистическим формуляром:
    2. программой наблюдения;
    3. инструментарием наблюдения.
  11. Показатель, характеризующий соотношение между отдельными частями совокупности, называется:
    1. относительным показателем структуры;
    2. относительным показателем координации;
    3. относительным показателем интенсивности;
    4. относительным показателем сравнения.
  12. Признаки элементов статистической совокупности бывают только:
    1. количественные;
    2. количественные и качественные;
    3. качественные;
    4. количественные, качественные и безразмерные,
  13. Темп прироста характеризует:
    1. на сколько единиц в абсолютном выражении уровень одного периода больше (меньше) предыдущего уровня;
    2. во сколько раз уровень данного периода больше (меньше) предыдущего уровня;
    3. на сколько процентов уровень данного периода больше (меньше) уровня предыдущего периода.
  14. В результате сравнения уровня изучаемого явления с размерами среды его распространения получают:
    1. относительный показатель координации;
    2. относительный показатель интенсивности;
    3. относительный показатель сравнения.
  15. Назовите виды графиков, используемых для изображения изменения явлений или процессов во времени;
    1. картограммы:
    2. линейные диаграммы;
    3. фигур-знаков;
    4. секторные диаграммы.
  16. Для оценки однородности совокупности используется:
    1. средняя арифметическая простая величина;
    2. средняя арифметическая взвешенная величина;
    3. мода;
    4. коэффициент вариации;
    5. размах вариации.
  17. Мода – это:
    1. среднее значение изучаемого признака;
    2. наиболее часто встречающееся значение признака;
    3. значение признака, находящееся в середине упорядоченного ряда;
    4. отклонение индивидуального значения от средней величины.
  18. Для изображения интервальных рядов распределения применяются:
    1. полигон;
    2. гистограмма
    3. секторная диаграмма
    4. кумулята
    5. огива.
  19. При уменьшении каждого значения признака в 3 раза, средняя величина:
    1. останется неизменной;
    2. уменьшится в 3 раза;
    3. увеличится в 3 раза;
    4. увеличится в 9 раз;
    5. уменьшится в 9 раз.



Перечень примерных контрольных вопросов по модулю 3

  1. В чем состоит значение рядов динамики в статистическом исследовании?
  2. Что представляет собой статистический ряд динамики, его обязательные элементы.
  3. Какие различают виды рядов динамики?
  4. Какие причины ведут к несопоставимости уровней рядов динамики?
  5. Перечислите способы приведения ряда динамики к сопоставимому виду.
  6. Назовите аналитические (базисные и цепные) показатели рядов динамики.
  7. Как исчисляется средняя хронологическая интервальных и моментных рядов динамики?
  8. Что характеризует: а) средняя хронологическая; б) средний темп роста?
  9. Перечислите компоненты уровня ряда динамики.
  10. Назовите способы определения наличия основной тенденции в ряду динамики.
  11. Какие существуют методы выявления и анализа основной тенденции ряда динамики?
  12. Что такое экстраполяция и интерполяция?
  13. Что в статистике называется индексом?
  14. Что понимается под индексируемой величиной?
  15. Какой индекс называется индивидуальным?
  16. Какие индексы называются общими ( сводными )?
  17. В каких единицах принято измерять индексы?
  18. Что показывает индекс физического объёма продукции?
  19. Что показывает индекс цен?
  20. Что представляет собой разность числителя и знаменателя индексов физического объёма и цен?
  21. Какие веса используются в индексе цен Пааше и Ласпейреса?
  22. Какой индекс называют «идеальный индекс Фишера»?
  23. Какая связь существует между индексом стоимости, физического объёма продукции и цен?
  24. Какие формы средней используются для расчета средних индексов?
  25. Какие бывают системы индексов?
  26. Какая существует связь между базисными и цепными индексами?
  27. Что понимается под индексом переменного состава, постоянного состава и индексом структурных сдвигов?
  28. В чем особенности расчета многофакторных индексов?
  29. Для чего рассчитывают территориальные индексы?
  30. Какие задачи решаются с помощью индекса-дефлятора?
  31. Сформулируйте определение корреляционной связи между признаками, характеризующими социально-экономические явления.
  32. Охарактеризуйте основные виды связи между социально-экономическими явлениями.
  33. Охарактеризуйте критерии оценки существенности связи между социально-экономическими явлениями.
  34. Коэффициент эластичности: способы построения и экономическая интерпретация.
  35. Коэффициенты детерминации: способы построения и экономическая интерпретация.
  36. Приведите формулы построения линейного коэффициента корреляции. Дайте его интерпретацию.
  37. Назовите показатели связи социальных явлений и дайте их экономическую интерпретацию.
  38. Коэффициент Спирмена в оценке связи социально-экономических процессов.
  39. Коэффициент Кендалла в оценке связи социально-экономических процессов.
  40. Дайте понятие выборочного наблюдения.
  41. В чем преимущество выборочного наблюдения?
  42. Дайте характеристику типам отбора.
  43. Дайте характеристику способам отбора.
  44. Сущность собственно-случайной выборки.
  45. Сущность механической выборки.
  46. Сущность типической выборки.
  47. Сущность серийной выборки.
  48. Сущность комбинированной выборки.
  49. В чем отличие выборки от малой выборки.
  50. Как распространяются результаты выборочного наблюдения на генеральную совокупность?

Задание для самостоятельной работы по модулям 2 и 3


Самостоятельная работа состоит из трех задач, для каждой из которых должно быть дано подробное описание хода решения (см. Методические указания к выполнению самостоятельной работы студентов).

Для выполнения расчетных работ необходимо изучить следующие разделы курса “Общая теория статистики”: статистическое наблюдение, сводка, группировка, ряды распределения, статистические таблицы, абсолютные, относительные и средние величины, показатели вариации, графический метод, статистическое изучение вариации в рядах распределения, выборочный метод, оценка статистических гипотез, ряды динамики, статистические методы изучения взаимосвязей; ознакомиться с методическими указаниями к решению каждой задачи, изучить рекомендуемую литературу.

Работа рассчитана на два модуля и выполняется по мере изучения тем.

Примерный вариант тестов по модулю 3

  1. Имеются следующие данные о численности населения города N (на первое января; тыс.чел..)

Год
1993
1994
1995
1996
1997
1998

Тыс. чел.
20.2
19.8
18.4
17.4
15.8
14.5

Средний уровень данного ряда вычисляется по формуле:
    1. средней арифметической простой;
    2. средней арифметической взвешенной;
    3. средней хронологической простой;
    4. средней хронологической взвешенной.
  1. Обследовано 36% продукции предприятия. Ошибка собственно-случайной бесповторной выборки будет меньше ошибки повторной выборки на:
    1. 20%;
    2. 36%;
    3. 25%;
    4. 64%.
  2. Какой из линейных коэффициентов корреляции указывает на наибольшую тесноту связи?
    1. r = 0.80;
    2. r = - 0.45;
    3. r= 0.40;
    4. r = 0;
    5. r =-0,85.
  3. Абсолютное значение одного процента прироста характеризует:
    1. абсолютную скорость роста (снижения) уровней ряда динамики;
    2. интенсивность изменения уровней;
    3. относительное изменение абсолютного прироста уровня ряда динамики;
    4. содержание одного процента прироста в абсолютном выражении.
  4. На лесном массиве в 400 га предполагается определить общий запас древесины. Пробные площади по 0,1 га. На основе предыдущих обследований известно, что по выходу древесины с 0,1 га =5 м3. Какова должна быть численность выборки, чтобы ошибка выборки с вероятностью 0,954 не превышала 1 м3?
    1. 80;
    2. 20;
    3. 50;
    4. 100.
  5. Имеются следующие данные о производстве продукции, млн.т.

год
1992
1993
1994
1995
1996
1997

млн. т.
47.2
46.5
44.2
39.2
35.8
34.1

Средний уровень данного ряда динамики вычисляется по формуле:
    1. средней арифметической простой
    2. средней арифметической взвешенной;
    3. средней хронологической простой;
    4. средней хронологической взвешенной.
  1. Какова должна быть необходимая численность выборки при определении среднего вклада населения в отделениях коммерческих банков города, чтобы с вероятностью 0,954 предельная ошибка выборки не превысила 50 руб.? Ориентировочная дисперсия вкладов равна 200000.
    1. 800
    2. 320
    3. 1600
    4. 160.
  2. Какие значения может принимать эмпирическое корреляционное отношение:
    1. -1
    2. -1 < h < 0
    3. 0
    4. 0 < h < 1
    5. любые положительные.
  3. В 1997г. было произведено 835 тыс. легковых автомобилей, по сравнению с 1994г. темп прироста составил (-13.3%). Определите объем производства легковых автомобилей в 1994 г.
    1. 723.9;
    2. 963.0;
    3. 748.3.
  4. Как определить абсолютный размер экономии (перерасхода) покупателей в результате изменения цен на группу товаров?
    1. невозможно определить;
    2. как разность индекса товарооборота и индекса цен;
    3. как разность числителя и знаменателя индекса цен;
    4. как разность числителя и знаменателя индекса товарооборота.
  5. Продажа мяса птицы на рознично-оптовых рынках города за январь-май увеличилась в 2,15 раза. Определите среднемесячный темп роста продажи:



  6. При уменьшении процента отбора с 36 до 19% и неизменных дисперсии и объеме выборки ошибка выборки увеличится:
    1. в 1,9 раза;
    2. на 26,6%;
    3. на 12,5%;
    4. предсказать результат невозможно.
  7. Формула 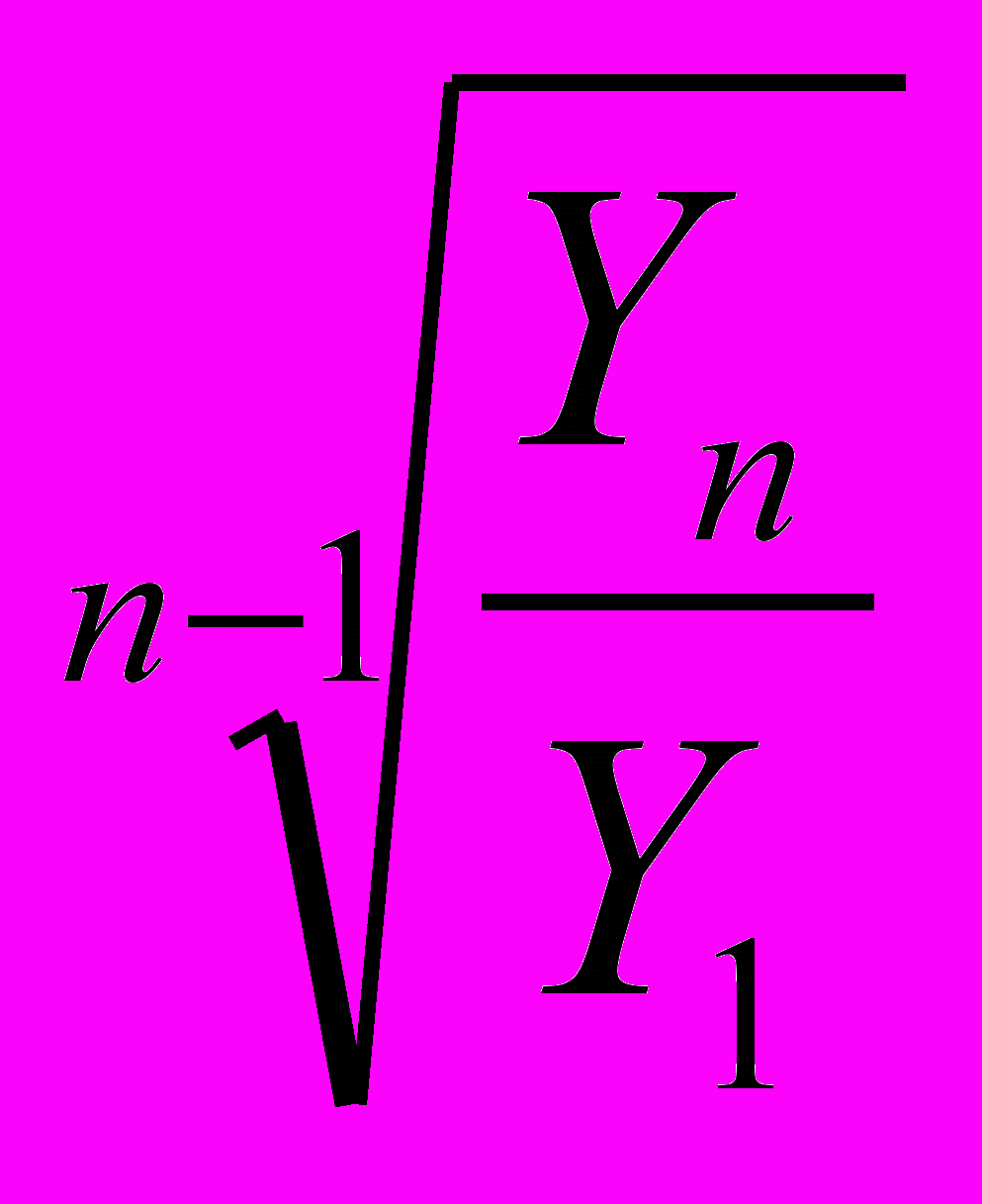используется для расчета:
    1. среднего абсолютного прироста;
    2. среднего темпа роста;
    3. среднего темпа прироста;
    4. среднего уровня ряда.
  8. В отделениях коммерческого банка обследовано 36% валютных счетов вкладчиков. В выборку попало 100 счетов вкладчиков, в том числе: пенсионеров - 60 человек, средний размер вклада X =200 долл. при дисперсии 4800; рабочих и служащих-40 человек, средний размер вклада X =250 долл. при дисперсии 8800. Определите среднюю ошибку типической выборки.
    1. 10;
    2. 6,4;
    3. 4,8;
    4. 8,0.
  9. Себестоимость продукции во втором полугодии выросла на 1.5 % по сравнению с первым при неизменном уровне издержек производства. Определите величину индекса физического объема продукции:
    1. 98.5%;
    2. 101,5%;
    3. 100.0%;
    4. 103.0%;
  10. Какой индекс измеряет динамику среднего уровня экономического показателя?
    1. индекс переменного состава;
    2. индекс фиксированного состава;
    3. цепной индекс;
    4. базисный индекс с переменными весами.
  11. При расчете по одним и тем же исходным данным индекс цен в агрегатной форме будет:
    1. всегда больше индекса цен в средней гармонической форме;
    2. равен индексу цен в средней гармонической форме;
    3. всегда меньше индекса цен в средней гармонической форме;
    4. больше, меньше или равен индексу цен в средней гармонической форме.
  12. Индекс цен фиксированного состава составил 95%, а индекс структурных сдвигов -125 %. Определите, как изменилась средняя цена под влиянием изменения цен отдельных товаров и изменения ассортимента продаж?
    1. снизилась на 24 %;
    2. выросла на 20 %;
    3. выросла на 32 %;
    4. выросла на 19 %,
  13. Идеальный индекс Фишера по форме представляет собой:
    1. среднюю агрегатную;
    2. среднюю арифметическую;
    3. среднюю гармоническую;
    4. среднюю геометрическую,
  14. При перемножении цепных индексов с постоянными весами за весь исследуемый период получают:
    1. базисный индекс с постоянными весами;
    2. базисный индекс с переменными весами;
    3. цепной индекс с переменными весами.
  15. Имеются данные о выпуске одинаковой продукции на двух предприятиях:
1 квартал
II квартал

Предприятие
себестоимость1 изделия

(тыс. руб.)
кол-во

изготовленных изделий

(шт.)
себестоимость

1 изделия

(тыс. руб.)
кол-во

изготовленных изделий

(шт.)

1
17.10
65
17.00
58

2
17.80
25
17.70
32

Как изменилась средняя себестоимость продукции по предприятиям вместе взятым под влиянием структурных сдвигов в производстве?
    1. уменьшилась;
    2. осталась без изменений;
    3. возросла.
  1. Торговое предприятие перевыполнило собственный годовой план по товарообороту на 5 %, при этом объем товарооборота снизился на 2%. Определите относительный показатель плана:
    1. 93.3%;
    2. 107.1%;
    3. 102.9%;
    4. 103.0%.
  2. Каким по своей форме является индекс Струмилина:
    1. средним арифметическим;
    2. средним гармоническим;
    3. средним геометрическим;
    4. агрегатным.
  3. Средний уровень интервального ряда динамики определяется как:
    1. средняя арифметическая;
    2. средняя гармоническая;
    3. средняя хронологическая.
  4. По данным 2%-ного выборочного обследования (n=100) средний стаж работы сотрудников туристических агентств города по специальности равен шести годам при коэффициенте вариации V=30%. Предельная ошибка выборки для среднего стажа работы сотрудников туристических агентств с вероятностью 0,954 равна:
    1. 0,3%;
    2. 3%;
    3. 5%;
    4. 6%.
  5. Проверено 16 проб молока, поступившего на молочный завод для дальнейшей переработки. Средняя жирность молока в пробах хвыб =3,8% при (=0,4%). Какова вероятность того, что средняя жирность поступившего молока не выйдет за пределы 3,7 - 3,9% ?
    1. 0,954;
    2. 0,683;
    3. 0,900;
    4. 0,997.
  6. Товарооборот снизился на 4,5%, а цены возросли на 12%. Как изменился объем продаж?
    1. снизился на 37,5%
    2. снизился на 14,7%
    3. увеличился на 14,7%
    4. увеличился на 17%
  7. При наличии данных на начало каждого месяца, средний уровень показателя определяется по формуле:
    1. средняя арифметическая простая
    2. средняя арифметическая взвешенная
    3. средняя хронологическая простая
    4. средняя хронологическая взвешенная
  8. Индекс средних затрат труда по совокупности компаний составил 1,25. Произошли изменения в структуре производства каждой компании и индекс структурных сдвигов составил 0,98. Как изменилась затраты труда в среднем в каждой компании?
    1. увеличились на 27,6%
    2. снизились на 27,6%
    3. возросли на 22,5%
    4. снизились на 22,5%
  9. Цена на импортный товар возросли на 12%, на аналогичный отечественный цена возросла на 20%. Товарооборот отчетного года соответственно составил 26 и 154 тыс. руб. Определите изменение цен на товар.
    1. снизились на 18,8%
    2. возросли на 18,8%
    3. увеличились на 16%
    4. возросли на 32%



Примерный перечень вопросов к зачету (экзамену) по курсу «Общая теория статистики»

  1. Предмет статистики, ее теоретические основы и связь с другими науками. Основные категории статистической науки.
  2. Статистическое наблюдение, его задачи, этапы проведения и организационные формы.
  3. Виды статистического наблюдения и способы его проведения.
  4. Статистическая сводка, ее задачи и значение. Организация сводки.
  5. Группировка как научная основа сводки, ее задачи и виды.
  6. Виды группировок, их задачи и особенности.
  7. Вторичная группировка.
  8. Ряды распределения, их назначение, элементы и виды.
  9. Статистические таблицы, их назначение и элементы.
  10. Виды статистических таблиц. Правила составления статистических таблиц.
  11. Статистические графики, их назначение и элементы.
  12. Виды статистических графиков.
  13. Абсолютные и относительные величины. Виды абсолютных величин и формы выражения относительных величин.
  14. Относительные величины планового задания, выполнения плана и динамики, их взаимосвязь.
  15. Относительные величины структуры, координации, интенсивности и сравнения.
  16. Понятие средних величин, их особенности. Условия применения средних величин.
  17. Виды средних величин, выбор их формы.
  18. Средняя арифметическая величина и ее свойства.
  19. Средняя гармоническая, средняя квадратическая и средняя геометрическая величины.
  20. Структурные средние величины.
  21. Показатели вариации.
  22. Дисперсия. Виды дисперсий и правило их сложения.
  23. Вариация альтернативного признака.
  24. Понятие экономического индекса, сфера применения индексов. Индивидуальные и общие индексы.
  25. Агрегатные индексы.
  26. Система индексов физического объема продукции, цен и стоимости продукции, их взаимосвязь. Расчеты изменения стоимости продукции за счет отдельных факторов.
  27. Система индексов физического объема товарооборота, цен и товарооборота, их взаимосвязь. Расчет изменения товарооборота за счет отдельных факторов.
  28. Система индексов себестоимости продукции, физического объема продукции и издержек производства, их взаимосвязь. Расчет изменения издержек производства за счет отдельных факторов.
  29. Средние индексы.
  30. Средний арифметический индекс физического объема.
  31. Средний гармонический индекс цен.
  32. Базисные и цепные индексы, их взаимосвязи. Системы индексов с постоянными и переменными весами.
  33. Индексы себестоимости продукции переменного и постоянного состава, их экономический смысл и взаимосвязь.
  34. Индексы цен переменного и постоянного состава, их экономический смысл и взаимосвязь.
  35. Многофакторные индексы.
  36. Территориальные индексы.
  37. Понятие рядов динамики, их виды и элементы ряда динамики.
  38. Аналитические показатели ряда динамики.
  39. Средние показатели ряда динамики.
  40. Понятие общей тенденции развития, методы ее выявления.
  41. Понятие сезонных колебаний и расчет индексов сезонности.
  42. Сопоставимость уровней и смыкание рядов динамики.
  43. Экстраполяция и интерполяция.
  44. Сущность выборочного наблюдения, причины и практика его применения.
  45. Теоретические основы выборочного наблюдения, ошибка репрезентативности.
  46. Доверительные пределы выборочной средней, предельная ошибка выборки.
  47. Способы отбора единиц в выборочную совокупность и виды выборочного наблюдения.
  48. Расчет средней и предельной ошибки выборки при различных видах и способах отбора.
  49. Определение необходимой численности выборки.
  50. Способы распространения результатов выборочного наблюдения на генеральную совокупность.
  51. Сущность корреляционно-регрессионного анализа.
  52. Оценка тесноты связи количественных признаков.
  53. Оценка тесноты связи качественных признаков.
  54. Метод наименьших квадратов.