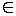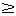Элективный курс по математике
| Вид материала | Элективный курс |
- Элективный курс. «Углубленное изучение некоторых вопросов математики», 64.95kb.
- Элективный курс. «Подготовка к егэ. Решение заданий поля С.» 11 класс, 34 часа, 55.92kb.
- Элективный курс по математике для 11 класса «Решение задач повышенной сложности», 109.29kb.
- Элективный курс «глобальные проблемы человечества», 121.74kb.
- В. А. Ходаков моу воротынская средняя школа Перемышльского района Калужской области, 76.7kb.
- Элективный курс по астрономии, 93.86kb.
- Пояснительная записка Элективный курс «Природа тел Солнечной системы» предназначен, 50.52kb.
- Ф. В. Чижова методическая разработка элективный курс, 490.04kb.
- Элективный курс «Методы решения задач по физике» 10 11 классы 68 часов, 115.81kb.
- Элективный курс по математике «Уравнения и неравенства» учитель: Пономарёва, 19.19kb.
МОУ Стрелецкая сош
Элективный курс по математике
АБСОЛЮТНАЯ ВЕЛИЧИНА
( МОДУЛЬ)
Автор-составитель: Мильшина О.В., учитель математики второй
квалификационной категории
МОУ Стрелецкой СОШ ,
Тамбовской области.
Тамбов- 2010 г.
Автор-составитель: Мильшина О.В., учитель математики второй
квалификационной категории МОУ Стрелецкой СОШ Тамбовской области.
АБСОЛЮТНАЯ ВЕЛИЧИНА (МОДУЛЬ)
(программа элективного курса по математике
для учащихся 9-11 классов общеобразовательных школ)
Пояснительная записка
Понятие абсолютной величины (модуля) является одной из важнейших характеристик
числа как в области действительных, так и в области комплексных чисел.
Это понятие широко применяется не только в различных разделах школьного курса
математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ.
Программой школьного курса математики не предусмотрены обобщение и системати-
зация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Это и позволит сделать элективный курс «Абсолютная величина (модуль)».
Курс рассчитан на учащихся 9-11 классов общеобразовательных школ, проявляющих
интерес к изучению математики.
Курс позволит школьникам систематизировать, расширить и укрепить знания, связан-
ные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере.
Учителю курс поможет наиболее качественно подготовить учащихся к математиче-
ским олимпиадам, сдаче ЕГЭ и экзаменов при поступлении в вузы.
Программа элективного курса предполагает знакомство с теорией и практикой рас-
сматриваемых вопросов и рассчитана на 34 часа: 7,5 часов лекций и 26,5 часов практических занятий.
Содержание курса состоит из восьми разделов, включая введение и итоговое занятие.
Учитель, в зависимости от уровня подготовки учащихся, уровня сложности изучаемого материала и восприятия его школьниками, может взять для изучения не все темы, увеличив при этом количество часов на изучение других. Учитель также может изменить уровень сложности представленного материала.
Программа содержит темы творческих работ и список литературы по предложенным
темам. В процессе изучения данного курса предполагается использование различных методов активизации познавательной деятельности школьников, а также различных форм организации их самостоятельной работы. Результатом освоения программы курса является представление школьниками творческих индивидуальных и групповых работ на итоговом занятии.
Цели курса:
· обобщение и систематизация, расширение и углубление знаний по теме «Абсолютная величина»; обретение практических навыков выполнения заданий с модулем; повышение уровня математической подготовки школьников.
Задачи курса:
· вооружить учащихся системой знаний по теме «Абсолютная величина»;
· сформировать навыки применения данных знаний при решении разнообразных задач
различной сложности;
· подготовить учащихся к ЕГЭ;
· сформировать навыки самостоятельной работы, работы в малых группах;
· сформировать навыки работы со справочной литературой, с компьютером;
· сформировать умения и навыки исследовательской работы;
· способствовать развитию алгоритмического мышления учащихся;
· способствовать формированию познавательного интереса к математике.
Требования к уровню усвоения учебного материала
В результате изучения программы элективного курса «Абсолютная величина (мо-
дуль)» учащиеся получают возможность знать и понимать:
· определение абсолютной величины действительного числа;
· основные операции и свойства абсолютной величины;
· правила построения графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;
· алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содер-
жащих переменную под знаком модуля.
Уметь:
· применять определение, свойства абсолютной величины действительного числа к ре-
шению конкретных задач;
· читать и строить графики функций, аналитическое выражение которых содержит знак абсолютной величины;
· решать уравнения, неравенства, системы уравнений и неравенств, содержащих пере-
менную под знаком модуля.
Содержание курса
(1 ч в неделю, всего 34 ч)
1. Введение (1 ч).
Цели и задачи элективного курса. Вопросы, рассматриваемые в курсе и его структура.
Знакомство с литературой, темами творческих работ. Требования, предъявляемые к
участникам курса. Аукцион «Что я знаю об абсолютной величине?».
2. Абсолютная величина действительного числа а (4 ч).
Абсолютная величина действительного числа а. Модули противоположных чисел. Геометрическая интерпретация понятия модуля а. Модуль суммы и модуль разности конечного числа действительных чисел. Модуль разности модулей двух чисел. Модуль произведения и модуль частного. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля. Применение свойств модуля при решении олимпиадных задач.
3. Графики уравнений (в т.ч. функций), аналитическое выражение которых со-
держит знак абсолютной величины (5 ч).
Применение компьютерной программы «Advanced Grapher» при построении графиков
функций, аналитическое выражение которых содержит знак модуля. Правила и алго-
ритмы построения графиков уравнений, аналитическое выражение которых содержит
знак модуля. Графики уравнений
Графики некоторых простейших функций, заданных явно и неявно, аналитическое
выражение которых содержит знак модуля. Графики уравнений (в т.ч. функций), ана-
литическое выражение которых содержит знак абсолютной величины в олимпиадных
заданиях.
4. Уравнения, содержащие абсолютные величины (11 ч).
Основные методы решения уравнений с модулем. Раскрытие модуля по определению,
переход от исходного уравнения к равносильной системе, возведение в квадрат обеих
частей уравнения, метод интервалов, графический метод, использование свойств аб-
солютной величины. Уравнения вида
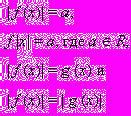
Метод замены переменных при решении уравнений, содержащих абсолютные вели-
чины. Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вида
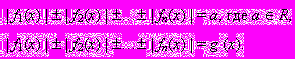
Способ последовательного раскрытия модуля при решении уравнений, содержащих
«модуль в модуле». Графическое решение уравнений, содержащих абсолютные вели-
чины. Использование свойств абсолютной величины при решении уравнений. Уравнения с параметрами, содержащие абсолютные величины. Защита решенных олимпиадных заданий.
5. Неравенства, содержащие абсолютные величины (7 ч).
Неравенства с одним неизвестным.
Основные методы решения неравенств с модулем.
Неравенства вида
Неравенства вида
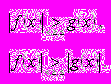
Метод интервалов при решении неравенств, содержащих знак модуля. Неравенства с
параметрами, содержащие абсолютные величины. Неравенства с двумя переменными.
6. Системы уравнений и неравенств, содержащие абсолютные величины (4 ч).
7. Другие вопросы, при решении которых используется понятие абсолютной
величины (1 ч).
8. Итоговое занятие (1 ч).
Учебно - тематический план
| № п/п | Название разделов и тем | Количество часов | Форма проведения | Образовательный продукт | ||
| всего | теории | практики | ||||
| 1. | Введение | 1 | 0,5 | 0,5 | аукцион знаний | анкета, записи |
| 2. | Абсолютная величина действительного числа а | 4 | 1 | 3 | | |
| 2.1. | Абсолютная величина действительного числа а. Основные теоремы | 1 | 1 | | лекция | опорный конспект |
| 2.2. | Операции над абсолютными величинами | 1 | | 1 | тренинг с применением ПК | распечатка решений |
| 2.3. | Упрощение выражений, содержащих переменную под знаком модуля | 1 | | 1 | практикум | решенные задания |
| 2.4. | Применение свойств модуля при решении олимпиадных задач | 1 | | 1 | семинар-практикум | реферат, решенные задания |
| 3. | Графики уравнений, аналитическое выражение которых, содержит знак абсолютной величины | 5 | | 5 | | |
| 3.1. | Применение компьютерной программы «Advanced Grapher» при построении графиков функций, аналитическое выражение которых содержит знак модуля | 1 | | 1 | исследова- тельская работа с применением ПК | распечатка построенных графиков |
| 3.3. | Правила и алгоритмы построения графиков (в т.ч. функций), аналитическое выражение которых содержит знак модуля | 1 | | 1 | семинар-практикум | памятка с правилами и алгоритмами построений |
| 3.3. | Графики уравнений 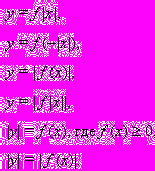 | 1 | | 1 | тренинг | выполненные построения |
| 3.4. | Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля | 1 | | 1 | мастерская | рефераты, опорный конспект, выполненные построения |
| 3.5. | Графики уравнений, аналитическое выражение которых содержит знак абсолютной величины в олимпиадных заданиях | 1 | | 1 | практикум, защита решений | опорный конспект, выполненные построения |
| 4 | Уравнения, содержащие абсолютные величины | 11 | 3 | 8 | | |
| 4.1. | Основные методы решения уравнений с модулем | 3 | 3 | | лекции | конспект, алгоритмы решений |
| 4.2. | Уравнения вида 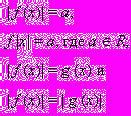 | 1 | | 1 | практикум | решенные задания |
| 4.3. | Метод замены переменных при решении уравнений, содержащих абсолютные величины | 1 | | 1 | семинар-практикум | реферат, памятка, опорный конспект, решенные задания |
| 4.4. | Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вида 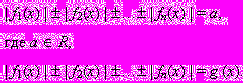 | 1 | | 1 | семинар-практикум | реферат, памятка, опорный конспект, решенные задания |
| 4.5. | Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле» | 1 | | 1 | практикум | реферат, памятка, опорный конспект, решенные задания |
| 4.6. | Графическое решение уравнений, содержащих абсолютные величины | 1 | | 1 | тренинг с применением ПК | распечатка решений |
| 4.7. | Использование свойств абсолютной величины при решении уравнений | 1 | | 1 | семинар-практикум | опорный конспект, решенные задания |
| 4.8. | Уравнения с параметрами, содержащие абсолютные величины | 1 | | 1 | Семинар-практикум | опорный конспект, решенные задания |
| 4.9. | Защита решенных олимпиадных заданий | 1 | | 1 | Защита решений | решенные задания |
| 5 | Неравенства, содержащие абсолютные величины | 7 | 2 | 5 | | |
| 5.1. | Неравенства с одним неизвестным. Основные методы решения неравенств с модулем | 2 | 2 | | лекция | конспект |
| 5.2. | Основные методы решения неравенств с модулем | 1 | 1 | | семинар | реферат |
| 5.3. | Неравенства вида 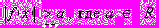 | 1 | | 1 | практикум | решенные задания |
| 5.4. | Неравенства вида 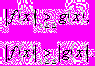 | 1 | | 1 | практикум | решенные задания |
| 5.5. | Неравенства с параметрами, содержащие абсо6лютные величины | 1 | | 1 | практикум | решенные задания |
| 6 | Системы уравнений и неравенств, содержащие абсолютные величины | 4 | | 4 | практикум | схемы решений, решенные задания |
| 7 | Другие вопросы, при решении которых используется понятие абсолютной величины | 1 | | 1 | семинар-практикум | реферат, опорный конспект, решенные задания |
| | Итого: | 34 | 7,5 | 26,5 | | |
Литература
1. Башмаков М.И. Уравнения и неравенства. – М.: ВЗМШ при МГУ, 1983.
2. Виленкин Н.Я. и др. Алгебра и математический анализ. 11 кл. – М.: Просвещение,
1993.
3. Гайдуков И.И. Абсолютная величина. – М.: Просвещение, 1968.
4. Галицкий М.Л. и др. Сборник задач по алгебре 8 – 9 кл. – М.: Просвещение, 1995.
5. Говоров В.М. и др. Сборник конкурсных задач по математике.– М.: Просвещение,
1983.
6. Горнштейн П.И. и др. Задачи с параметрами. – М.: Илекса, Харьков: Гимназия, 2003.
7. Колесникова С.И. Математика. Интенсивный курс подготовки к Единому Государст-
венному экзамену. М.: Айрис-пресс, 2004.
8. Мерзляк А.Г. и др. Алгебраический тренажер. – М.: Илекса, 2001.
9. Мордкович А.Г. Алгебра. 8 кл. – М.: Мнемозина, 2000.
10. Нешков К.И. и др. Множества. Отношения. Числа. Величины. – М.: Просвещение,
1978.
11. Никольская И.Л. Факультативный курс по математике. – М.: Просвещение, 1995.
12. Олехник С.Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10 –
11 кл. – М.: Дрофа, 1995.
13.Шарыгин И.Ф. Факультативный курс по математике 10 – 11 кл. – М.: Просвещение,
1989.
14. Электронный учебник «Алгебра 7 – 11».
15. Ястребинецкий Г.А. Задачи с параметрами. – М.: Просвещение, 1986.
Темы творческих работ
1. Применение модуля в механике и векторной алгебре.
2. Модуль в определении предела.
3. Погрешности.
4. Проект памятки правил и алгоритмов построения графиков уравнений (в т.ч. функций), аналитическое выражение которых содержит знак модуля.
5. Изготовление игры «Математическое лото» по теме «Графики уравнений, аналитическое выражение которых содержит знак модуля».
6. Проект опорных сигналов по способам решения уравнений и неравенств с модулем.
7. Простейшие функции, заданные явно и неявно, аналитическое выражение которых
содержит знак модуля, и их графики.
Урок:
Цель: формирование умений решения неравенств с модулем.
Задачи:
Обучающая - познакомить с методом решения неравенств с модулем, Развивающая - развитие познавательной активности, логического мышления.
Воспитательная - воспитание организованности, внимания, математической наблюдательности.
ТСО: Интерактивная доска, компьютер. Диск с приложениями №1,№2. Переносная доска.
Ход урока:
I. Актуализация знаний и проверка домашнего задания.
Вступительное слово учителя.
Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Единственное отличие, пожалуй, связано с тем, что, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.
Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки (границами этих промежутков являются нули подмодульных выражений), а затем неравенство решается на каждом из промежутков.
Этот метод работает всегда. Правда, в отдельных случаях может быть затруднена его техническая реализация, например, очень тяжело или невозможно найти корни подмодульных выражений и пр. Однако, это сложности иного плана. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях конкурсного экзамена важен не только результат, но и то время, которое потрачено на его получение.
Актуализация знаний:
Абсолютной величиной (модулем) называется функция, которая каждому числу
ставит в соответствие число
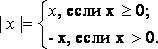
Величина |х| равна расстоянию от точки х до начала координат.
Пусть х и у — действительные числа. Приведем (в виде формул) свойства модуля.
1) |x|
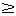 0.
0.2) |x| = 0
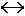 x = 0.
x = 0.3) |x
 y| = |x|
y| = |x|  |y|.
|y|.4) |x : y| = |x| : |y|, где у
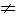 0 .
0 .5)
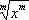 = |x|, где m - четное число (2, 4, 6,...).
= |x|, где m - четное число (2, 4, 6,...).6) |x|n = xn, где n - четное число (2, 4, 6,...).
7) |x + y|
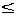 |x| + |y|.
|x| + |y|.8) |x - y|
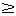 |x| - |y|.
|x| - |y|.Разбор заданий:
1. Стандартный способ.
Стандартный способ решения неравенств, содержащих модуль, состоит в том, что, зная промежутки, на которых функция, находящая под знаком модуля принимает значения определенных знаков, снимают знак модуля.
В общем случае при решении неравенств этим способом поступают так:
а) Находят ОДЗ неравенства.
б) Находят точки в которых функции, стоящие под знаком модуля, равны 0.
в) Полученные точки разделяют ОДЗ на несколько множеств.
г) На каждом, из полученных множеств, определяют знак каждой функции, согласно определению модуля, снимают знак модуля.
д) Решают каждое из полученных неравенств.
е) Полученные множества объединяют.
Задача 1. Решить неравенство |x2 - 3x + 2| + |2x +1| < 5.
Решение.
ОДЗ неравенства R.
x2 - 3x + 2 = 0;
x1 = 1, x2 = 2;
2x + 1 = 0;
x = -0,5;
Три числа -0,5; 1 и 2 разделяют множество действительных чисел на четыре множества. Поэтому рассмотрим четыре случая.
- (-
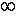 ; -0,5]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 < 0,
; -0,5]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 < 0,
x2 - 5x - 4 < 0;
D = 25 + 16 = 41 > 0, следовательно, x1 =
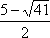 ; x2 =
; x2 = 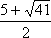 ;
;x
 -0,5,
-0,5, 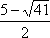 < x <
< x < 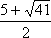 ;
;Решение этого неравенства на этом промежутке x
 (
(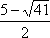 ; -0,5]
; -0,5]2) (-0,5; 1]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 > 0,
тогда x2 - 3x + 2 + 2x + 1 < 5;
x2 - x - 2 < 0;
D = 1 + 8 = 9 > 0, x1 = -1; x2 = 2;
-
 0,5< x
0,5< x 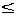 1,
1,-1 < x < 2;
Решение этого неравенства на этом промежутке x (-0,5; 1]
3) (1; 2]. На этом промежутке x2 - 3x + 2 < 0, 2x + 1 > 0;
-x2 + 3x - 2 + 2x + 1 > 5;
-x2 + 5x - 6 > 0;
x2 - 5x + 6 > 0;
D =25 - 24 = 1 > 0, x1 = 2; x2 = 3;
1
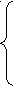 < x
< x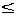 2,
2,x < 2,
x > 3;
Решение этого неравенства на этом промежутке x (1; 2)
4) (2; + ). . На этом промежутке x2 - 3x + 2 > 0, 2x + 1 > 0;
x2 - 3x + 2 + 2x + 1 < 5;
x2 - x - 2 < 0;
x1 = -1; x2 = 2
x
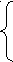 > 2,
> 2,-1 < x < 2,
Решение этого неравенства на этом промежутке x
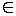
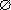 .
.Объединим полученные множества (
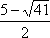 ; -0,5]
; -0,5]  (-0,5; 1]
(-0,5; 1] 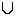 (1; 2)
(1; 2) 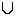
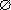 ;
;x
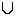 (
(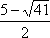 ; 2).
; 2).Ответ: (
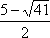 ; 2).
; 2).2. Неравенства вида |f(x)| > g(x) (
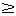 , <,
, <,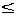 ) рекомендуем решать одним из двух способов, которые рассмотрены ниже.
) рекомендуем решать одним из двух способов, которые рассмотрены ниже.1). Из определения модуля следует, что изучаемые неравенства равносильны совокупности либо системе следующих неравенств:
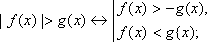
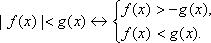
Если неравенства, находящиеся слева от знаков "
 ", являются нестрогими, то и в правой части эквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х)
", являются нестрогими, то и в правой части эквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х)  а = const, неравенство где эквивалентно следующему:
а = const, неравенство где эквивалентно следующему:Пример 2. Решить неравенство |х + 5| > 4.
Решение.
ОДЗ: х
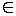 R. Согласно восьмой строке таблицы
R. Согласно восьмой строке таблицы|x + 5| > 4
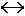 x + 5 < -4 или x + 5 > 4
x + 5 < -4 или x + 5 > 4 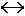 x < -9 или x > -1.
x < -9 или x > -1.Ответ: х
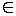 (-; -9)
(-; -9) 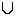 (-1; +).
(-1; +). Пример 3. Решить неравенство
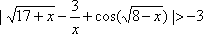 .
.Решение.
Решим систему неравенств
1
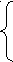 7 + x
7 + x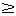 0,
0,8 - x
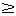 0;
0;x
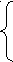
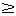 -17,
-17,x
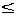 8;
8;Таким образом, ОДЗ функции, стоящей в левой части неравенства, является множество чисел из промежутка [-17; 0)
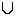 (0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.
(0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.Ответ: [-17; 0)
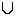 (0; 8].
(0; 8].Пример 4. Решить неравенство |x2 -6x + 5|
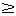 x + 5.
x + 5.Решение.
Это неравенство равносильно совокупности неравенств
x
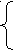 2 - 6x + 5
2 - 6x + 5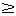 x + 5,
x + 5,x2 - 6x + 5
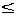 -x - 5;
-x - 5;x
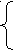 2 - 7x
2 - 7x 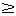 0,
0,x2 - 5x + 10
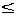 0;
0;Упростим каждое из неравенств полученной совокупности
x
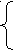 (х - 7)
(х - 7) 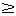 0,
0,x2 - 5x + 10
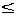 0
0Решением первого неравенства является множество чисел (-; 0] [7; +).
Квадратный трехчлен x2 - 5x + 10 имеет отрицательный дискриминант, поэтому принимает только положительные значения и, следовательно, второе неравенство решений не имеет.
Ответ: (-; 0]
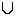 [7; +).
[7; +).2). В ряде случаев (например, если g(х) — квадратный корень либо абсолютная величина, либо любая непрерывная функция, принимающая на всей области определения неотрицательные значения), рассматриваемые неравенства удобнее всего решать возведением в квадрат. Как и в неравенствах |f{x)| > g(х) (
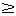 ,
,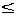 1, <), это можно сделать на множестве g(х) > 0. Для тех х из ОДЗ, где g(х) < 0, неравенство проверяется устно. Далее возможен следующий порядок действий (знак ">" выбран для определенности).
1, <), это можно сделать на множестве g(х) > 0. Для тех х из ОДЗ, где g(х) < 0, неравенство проверяется устно. Далее возможен следующий порядок действий (знак ">" выбран для определенности). Алгоритм решения неравенства |f{x)| > g{х), если g(х) > 0
1. Почленно возвести в квадрат |f(x)|2 > (g(x))2, используя свойство 6, получим неравенство равносильное данному (f{x)2 > (g(х))2
2. Перенести (g{х))2 в левую часть (f(x))2 - {g(x))2 > 0
3. Воспользоваться формулой (f(x) - g(х)) (f(x) + g(x)) > 0
4. Применить метод интервалов
Пример 5. Решить неравенство |x2 - 5x + 9| < |x - 6|.
ОДЗ неравенства R. Так как левая часть неравенства есть модуль от функции, правая часть неравенства есть функция принимающая только положительные значения, то возведем обе части неравенства в квадрат.
|x2 - 5x + 9|2 < |x - 6|2.
(x2 - 5x + 9)2 - (x - 6)2 < 0.
(x2 - 5x + 9 -(x - 6))(x2 - 5x + 9 +(x - 6)) < 0.
(x2 - 6x + 15)(x2 - 4x + 3) < 0.
Дискриминант квадратного трехчлена x2 - 6x + 15 отрицателен (62 - 60 = -24) поэтому на всей области определения он принимает только положительные значения.
Дискриминант квадратного трехчлена x2 - 4x + 3 положителен (42 - 12 = 4), он имеет два корня и они равны 1 и 3. Отрицательные значения квадратный трехчлен принимает, если 1 < х < 3.
Ответ: 1 < x < 3.
3. Способ подстановки.
Введение вспомогательной переменной иногда позволяет намного упростить решение неравенства.
Пример 6. Решить неравенство
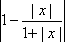
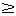

Решение.
Пусть t = |x|, так как |x| 0, то t 0.
Тогда
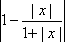
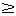
 ;
;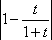
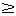
 ;
;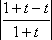
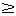
 ;
;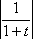
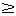
 ;
;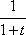
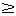
 ;
;t + 1
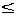 2; t
2; t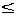 1.
1.Произведем обратную замену. |x|
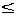 1, откуда -1
1, откуда -1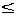 х
х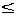 1.
1.Ответ: -1
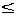 х
х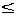 1.
1.Домашнее задание:
Подобрать и решить 3 уравнения с модулем, 3 неравенства с модулем и 3 неравенства с модулем. Можно придумать самим.
Урок:
Тема: Решение неравенств с модулем, содержащих параметр.
Цель урока: формирование умений решения неравенств с модулем, содержащих параметр.
Задачи:
Обучающая - познакомить с методом решения неравенств с модулем, содержащих параметр.
Развивающая - развитие познавательной активности, логического мышления.
Воспитательная - воспитание организованности, внимания, математической наблюдательности.
ТСО: Интерактивная доска, компьютер. Дискета со приложениями №1,№2. Переносная доска.
Наглядность: таблица с формулами
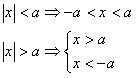
Ход урока:
I. Актуализация знаний и проверка домашнего задания.
Вступительное слово учителя.
Задачи с параметром встречаются на ЕГЭ в группе «С» под номерами 3 и 5.
Так как среди вас есть те, кто претендует на высокий балл, то тема важна для изучения. Начнем с повторения ключевых задач по теме «Решение неравенств с модулем».
Назовите идею решения неравенств, записанных на доске, и решите их: Ответы.

На переносной доске работает ученик
Решить неравенство:
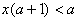
Приходилось ли вам встречать и другие способы решения неравенств?
Ответ: графический. Приложение 1.
Рассмотрим, в чем заключается графический способ решения.
Решить неравенство :
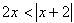
Ученик: – строим графики функций
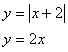
Отмечаем точку пересечения графиков А.
Знак > понимаем так, что 1 график выше графика 2 и пишем ответ: X < 2
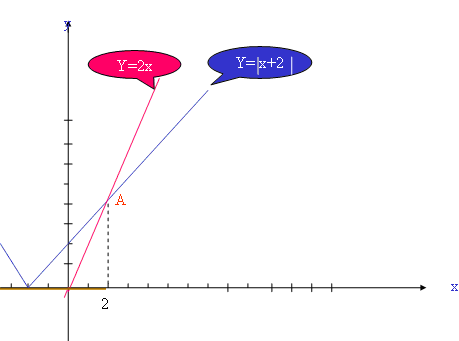
Приложение 1.
Повторим алгоритм решения линейных неравенств с параметром:
Ученик. объясняет решение на переносной доске.
x(a+1)
если
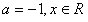
если
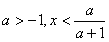
если
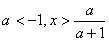
II. Изучение новой темы:
Учитель: рассмотрим методы решения типовых примеров.
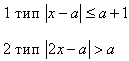
В числовых неравенствах, заменив число на букву, получим неравенство с параметром.
Рассмотрим методы решения этих неравенств. Они аналогичны рассмотренным способам решения неравенств с модулем.
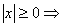
Т.к. знак модуля определён, т.е.
Решение зависит от выражения а+1
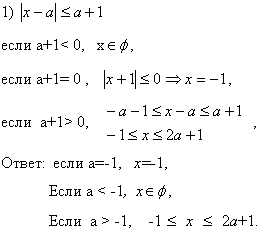
Учитель: решим следующее неравенство:
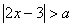
Ответ:
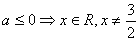
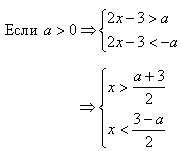
Учитель: Решим 3 пример.
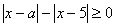
Какими способами можно решить неравенство, если бы вместо буквы а стояло число?
Ответ: возведение обеих частей неравенства в квадрат, методом «промежутков».
Те же способы применяются и для неравенства с параметром.
Методом «промежутков» пойдет решать ( ФИО)
Методом возведения в квадрат (ФИО)
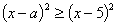 ,
,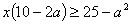 ,
,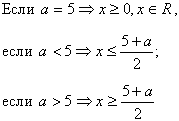
Проверили решения данного примера.
Каким еще способом можно решить данное неравенство?
Ответ: графический.
Показывается приложение 2.
1.Строим графики функций
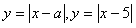
Найдем те значения переменной Х, когда первый график лежит выше второго.
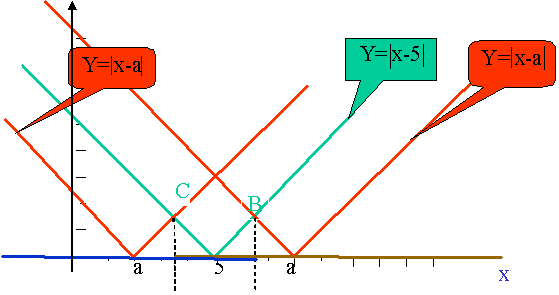
Приложение 2.
Возможны варианты, когда а < 5 и а > 5
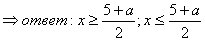
Рассмотрев различные способы решения, сделаем вывод- какой метод наиболее рациональный? Какими методами можно решить неравенства с параметром?
Вывод:
Методы решения неравенств с модулем, содержащие параметр, аналогичны тем, что применяются при решении числовых неравенств с модулем: по определению модуля, возведение обеих частей в квадрат, метод интервалов, графический. Необходимо выбирать наиболее рациональный.
Домашнее задание:
Подобрать и решить 3 уравнения с модулем, 3 неравенства с модулем и 3 неравенства с модулем, содержащие параметр. Можно придумать самим.