Geum.ru

Статистические величины

Вид материалаЛекция

Содержание


Для правильного применения использования абсолютных и относительных величин необходимо
Средние величины
Подобный материал:

Лекция 2

Статистические величины.


Основные понятия:


Статистические ряды и таблицы.

Статистические величины, характеризующие массы или совокупности единиц, называют обобщающими показателями, использование которых в статистическом исследовании позволяет:

  • Давать сводную и концентрированную характеристику совокупностям единиц, изучаемых общественных явлений.
  • Выражает существующие между явлениями связи, зависимости и обеспечивает таким образом взаимосвязанное изучение явлений.
  • Характеризовать происходящие в явлениях изменения, закономерности их развития, а именно осуществлять экономическо-статистический анализ рассматриваемых явлений в том числе на основе расчленения самых обобщающих величин на составляющие определяющие их факторы.
  • Исчисление статистических величин и анализ данных об изучаемых явлениях это и есть завершающий этап статистического исследования.


Виды статистических величин:

  1. Абсолютные.
  2. Относительные.
  3. Средние.


Абсолютные и относительные величины:


Абсолютными величинами называются количественные показатели, которые характеризуют размеры, изучаемых общественных явлений.

При этом различают абсолютные величины:
  • Индивидуальные – признаки отдельных единичных явлений например, выработка одного рабочего. Получают из наблюдений за отдельными единицами явлений.
  • Итоговые (обобщающие) – характеризуют совокупности явлений. Получают подсчетом при подведении итогов индивидуальных абсолютных величин. Итоговые служат характеристики численности массовых явлений по состоянию на определенный момент времени. Либо объема или уровня совокупности явлений за соответствующий объем времени.


Абсолютные величины имеют различные измерители:

  • Натуральные (кг, шт, т)
  • Условно-натуральные (количество тракторов мощностью 65 л.с.)
  • Трудовые (чел./час и др.)
  • Денежные


Относительные величины:


Выражаются соотношением между явлениями в виде степени, доли, темпа.

Знаменатель (основание сравнения, база) – это величина, с которой производится сравнение.

Сравниваемая (отчетная, текущая) величина – это величина, которая сравнивается.

Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случае относительная величина показывает, сколько единиц одной величины приходится на единицу другой.

Важное свойство – относительная величина абстрагирует различия абсолютных величин и позволяет сравнивать такие явления, абсолютные размеры которых непосредственно несопоставимы.


Относительные величины:
  • Выполнения плана
  • Структура
  • Координации
  • Интенсивности



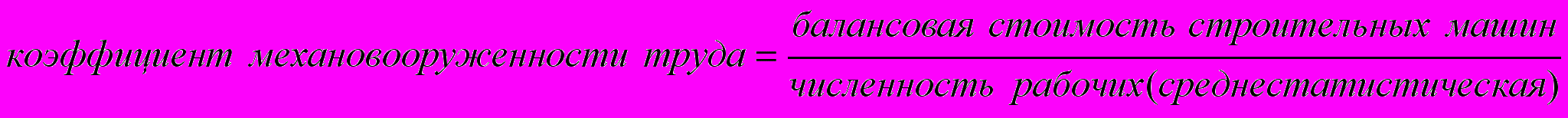
коэффициент текучести рабочей силы – отношение числа рабочих, уволенных по собственному желанию к среднему числу рабочих;


коэффициент оборачиваемости оборотных средств – отношение объема СМР к среднему остатку оборотных средств;


основные фонды переносят свою стоимость в течении длительного периода частями;


относительные величины сравнения характеризуют одноименные абсолютные величины относящиеся к разным объектам;


относительные величины динамики характеризуют степень развития изучаемого явления во времени;


Для правильного применения использования абсолютных и относительных величин необходимо:
  1. учитывать специфику явлений при выборе и расчете величин.
  2. обеспечивать сопоставимость сравниваемой и базисной, абсолютных и относительных величин с точки зрения объема и состава представляемых ими явлений.
  3. комплексно использовать в процессе анализа относительные и абсолютные величины.



Средние величины



Дают сводную или итоговую характеристику массовых общественных явлений.

Количественный показатель характерного типичного уровня массовых однородных явлений.

Взаимозависимость между определяющими показателями и средним выражается следующим образом, если все значения усредняемого признака заменить их средними значениями, то сумма или произведение не изменит определяющего показателя.


Особенности расчетов и выбора средних величин:


Среднеарифметическая:
  • простая
  • взвешенная

Заработная плата (тыс. руб.)

х
Численность рабочих (чел.)

f
Общая заработная плата (тыс. руб.) х*f

203
1
203

214
2
428

232
5
1160

255
3
765

264
2
528

276
1
276

Итого:
14
3360


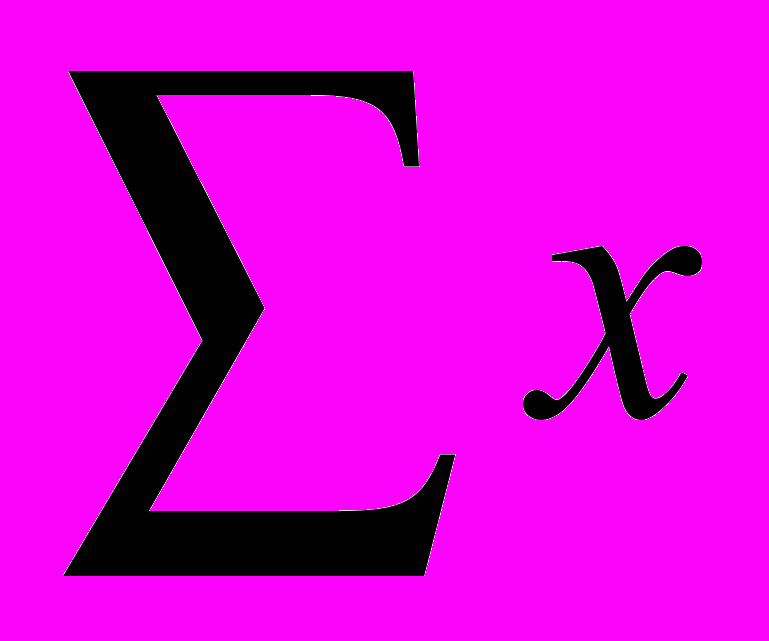- общее значение усредняющего признака

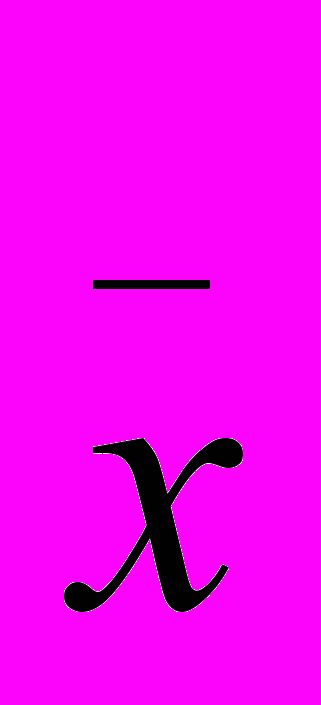- средняя величина

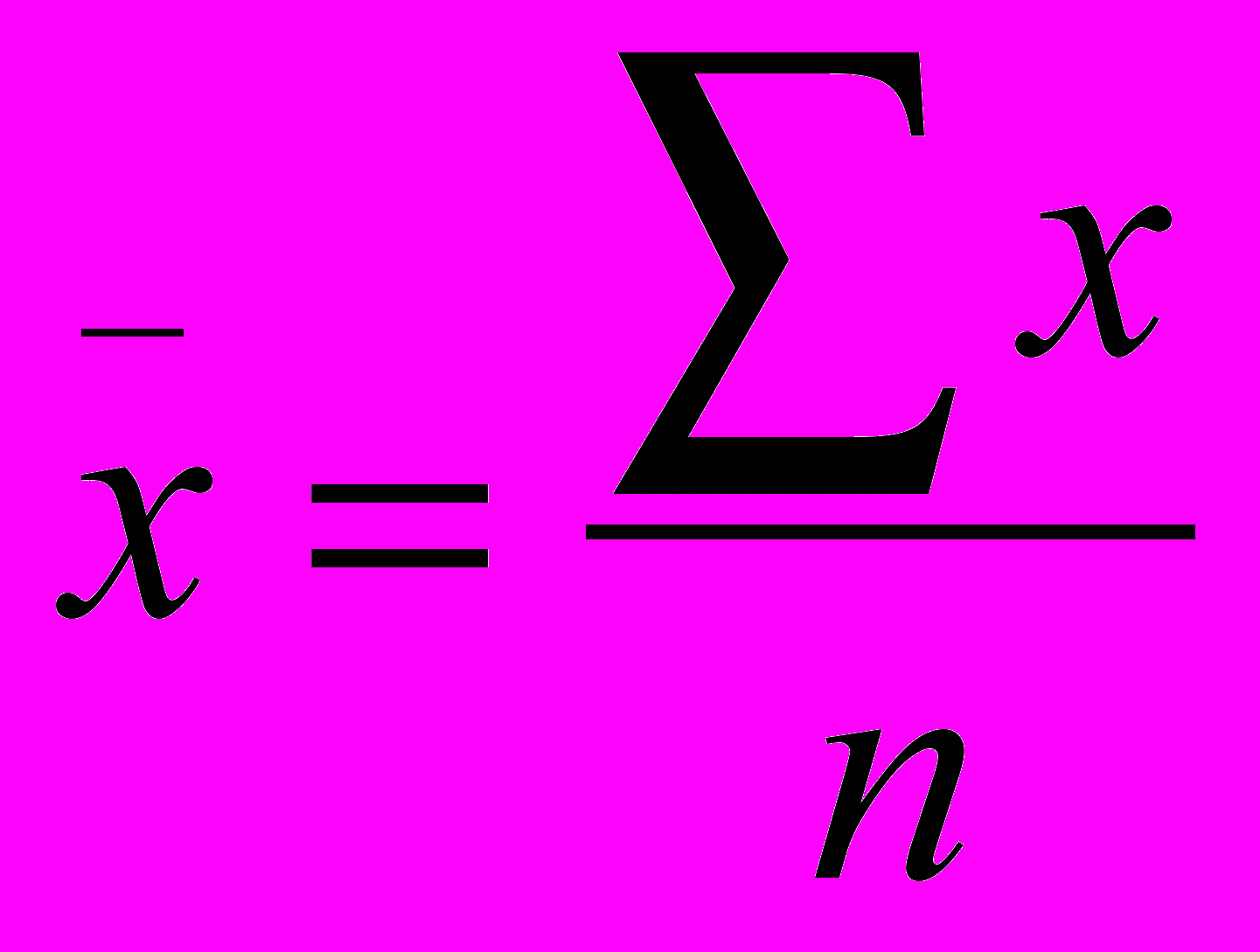- средняя арифметическая простая, где n – численность рабочих

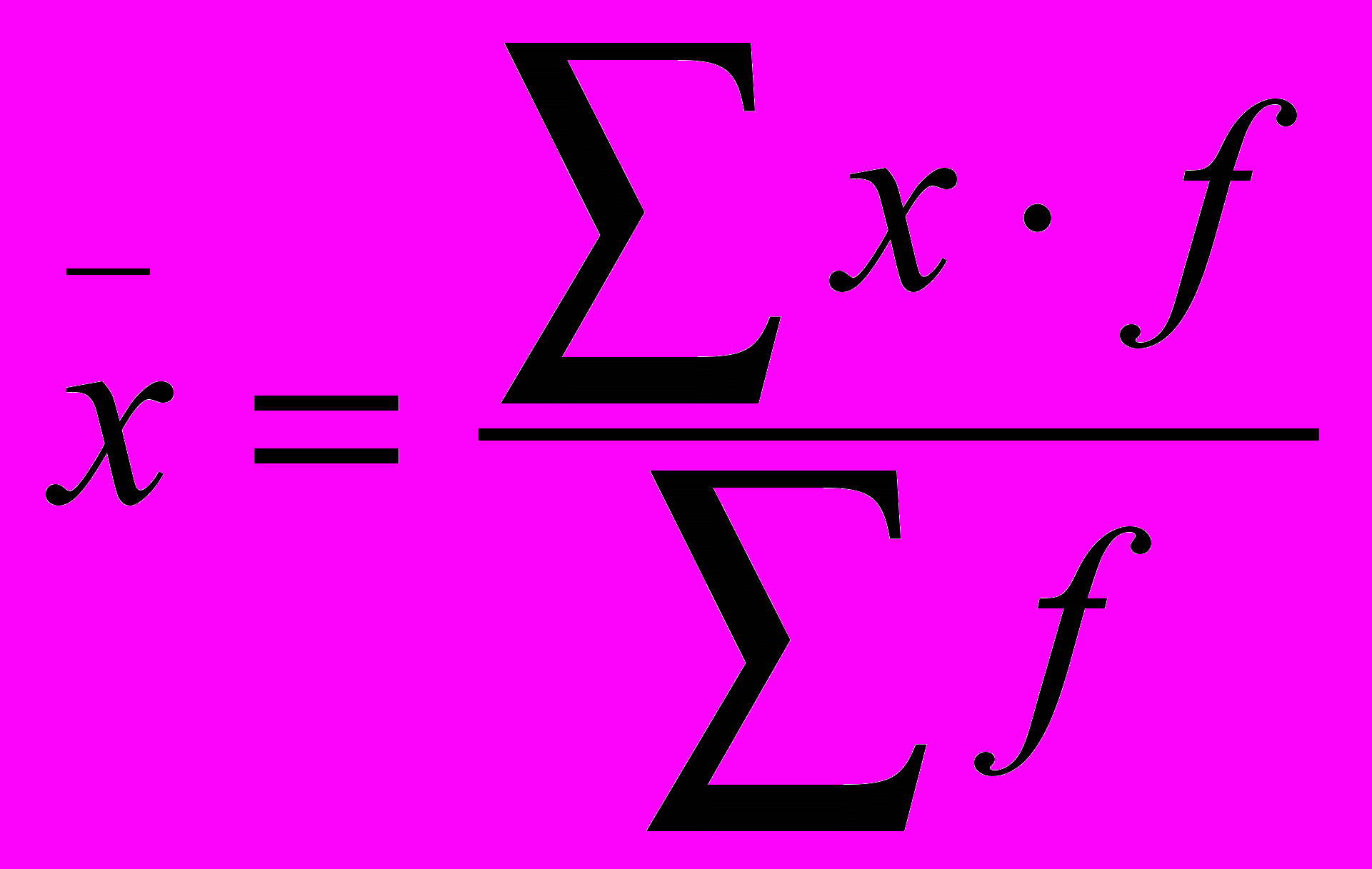- среднее арифметическое взвешенное, где f – количество единиц.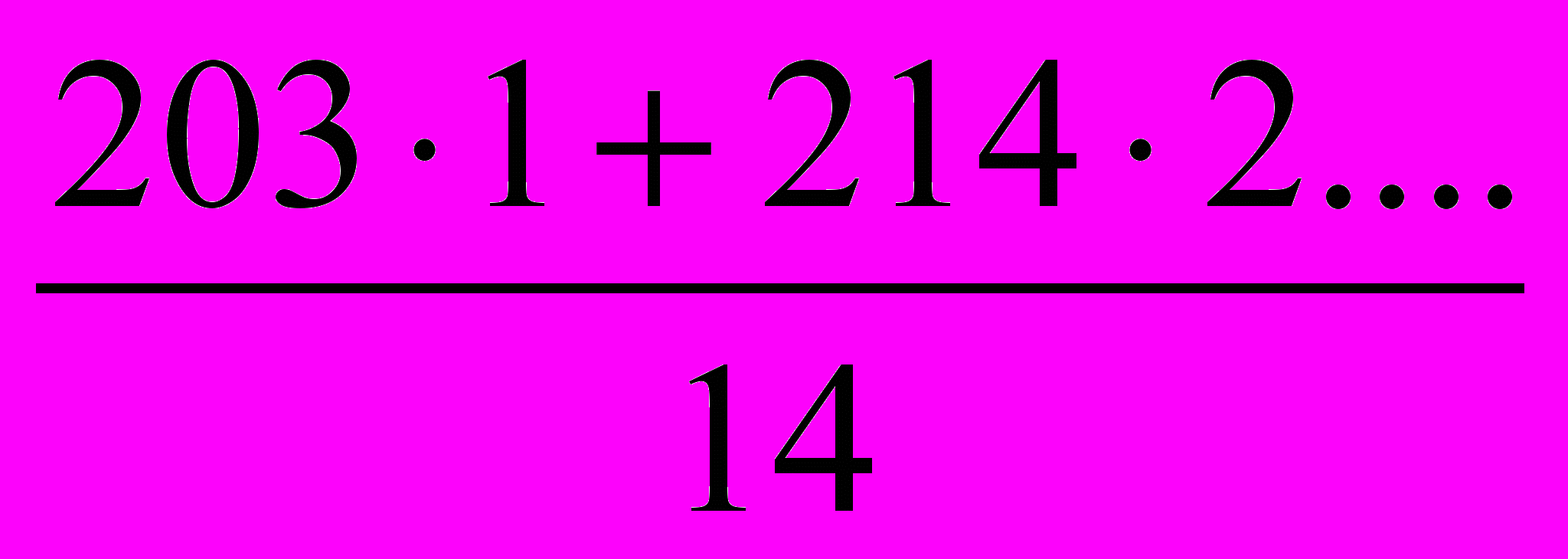




Объект строительства
Сметная стоимость строительства, млн. руб.
Продолжительность строительства (мес)

f
n
x

1
600
20

2
800
40

3
1400
80


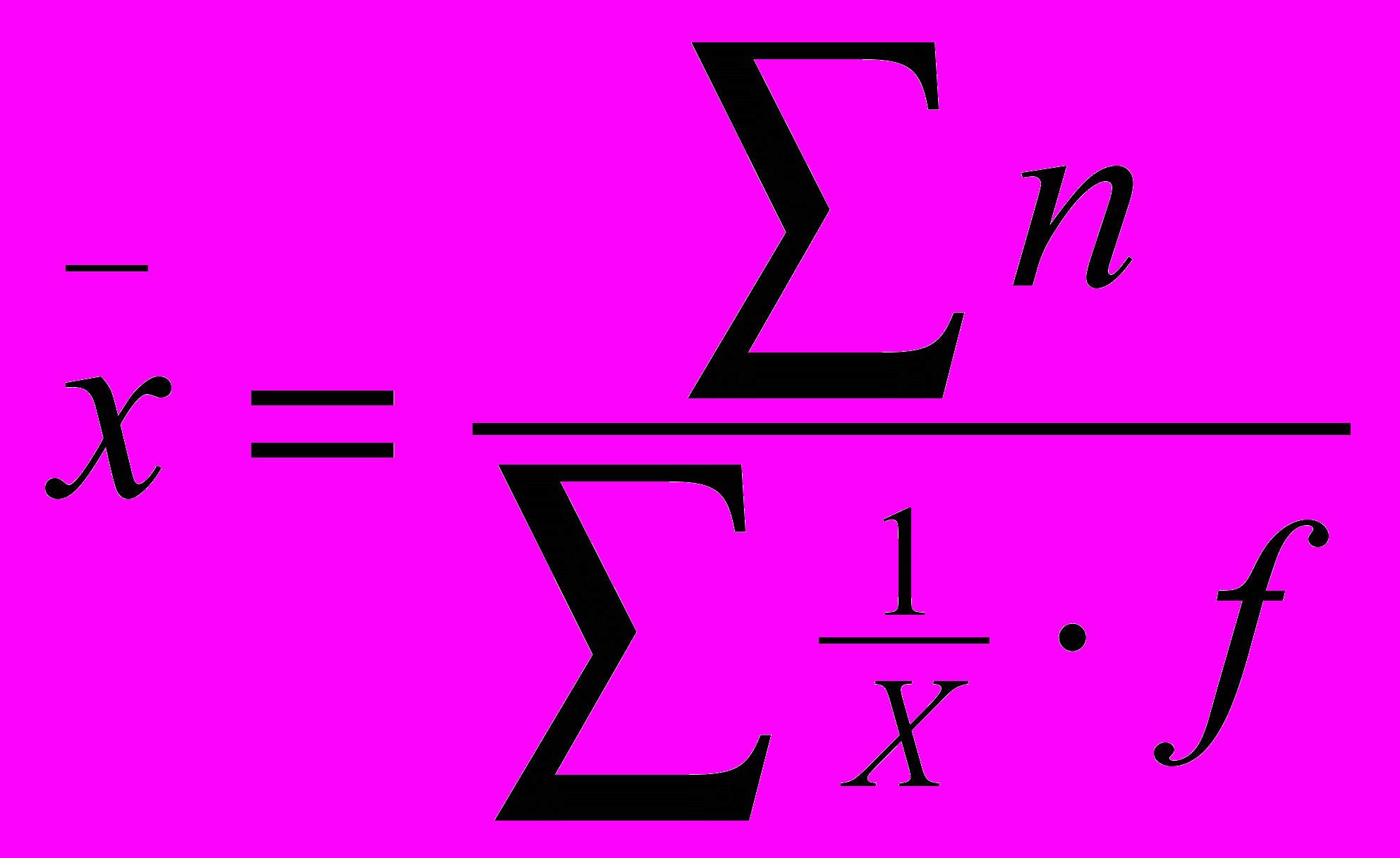- простая среднегармоническая

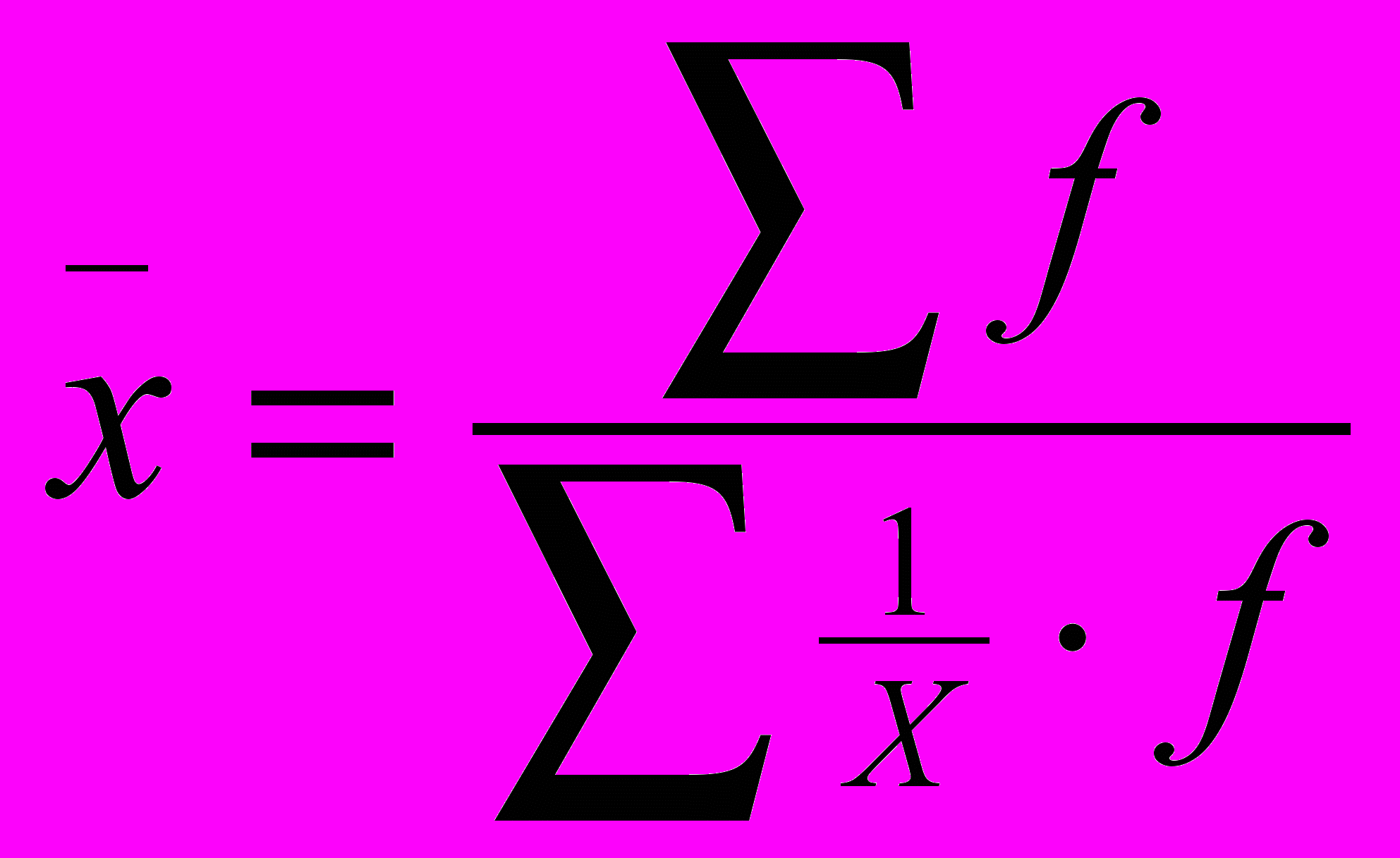- сложная средневзвешенная гармоническая

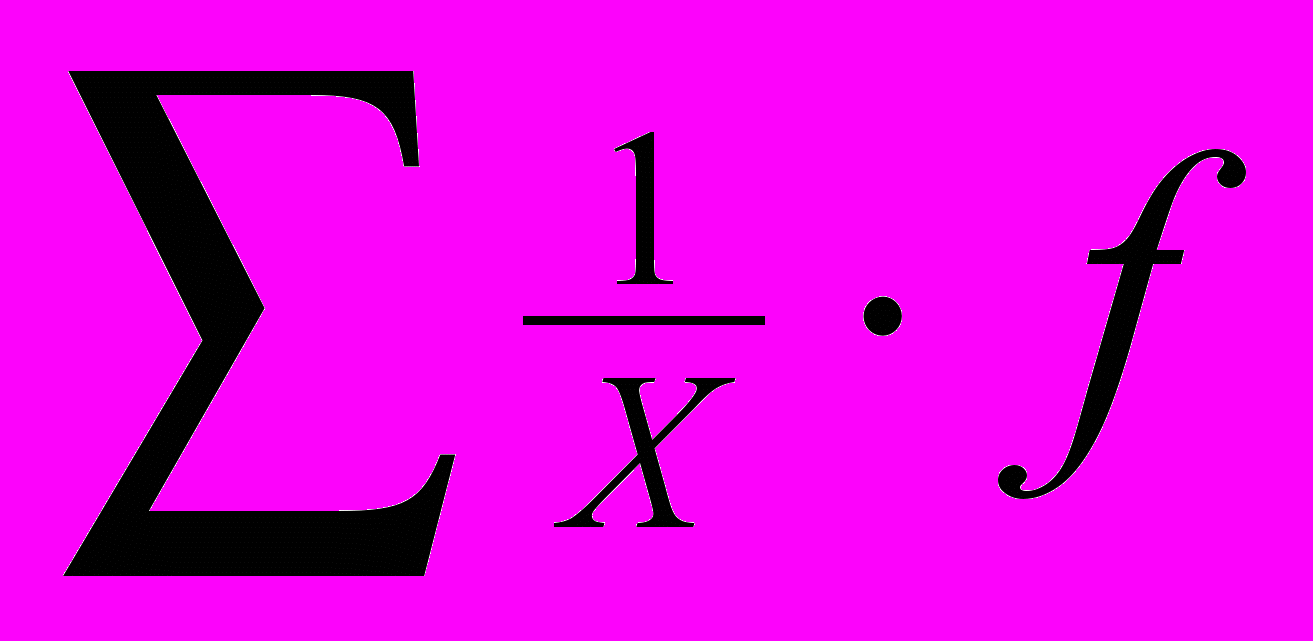- общее значение обратных величин усредняемого признака


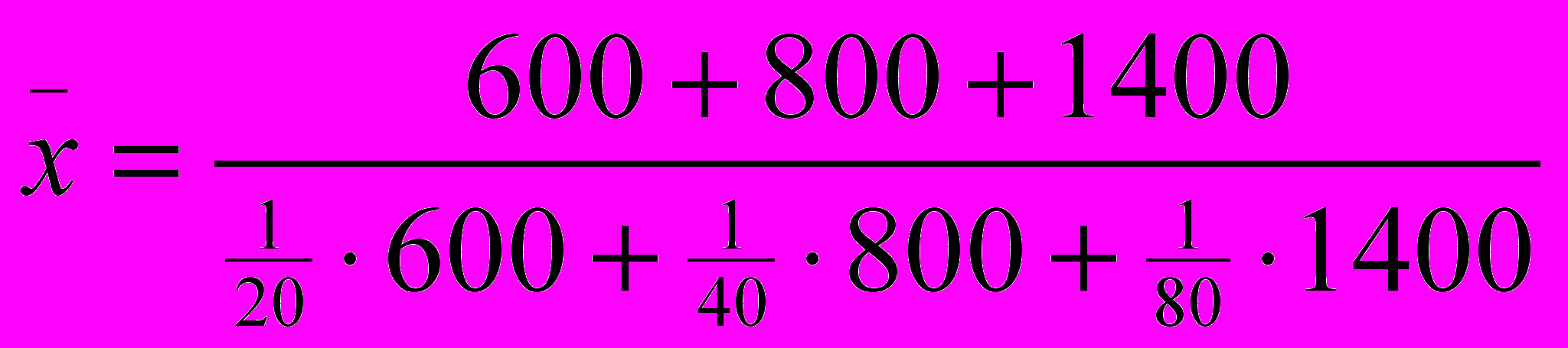- простая

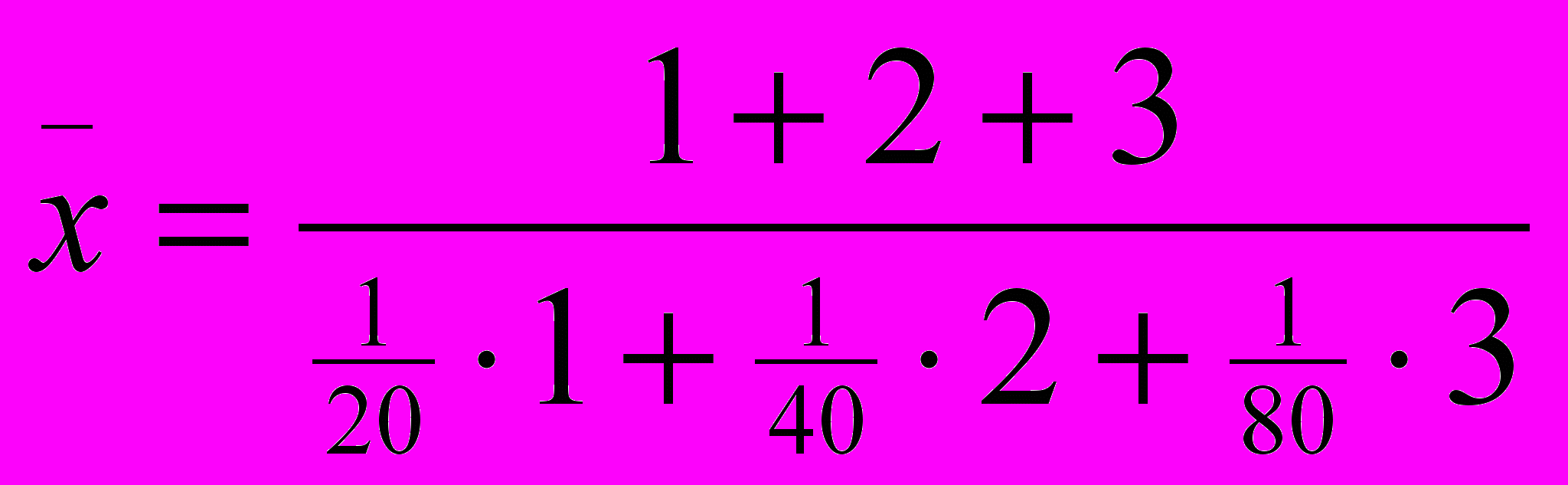- сложная


Среднегеометрическая:


Года
Объем выполняемых работ (млн. руб.)
Коэффициент роста. Отношение объема работ данного года к объему предыдущего

базисный
2500



1
2625
1,05

2
2810
1,07

3
3060
1,09




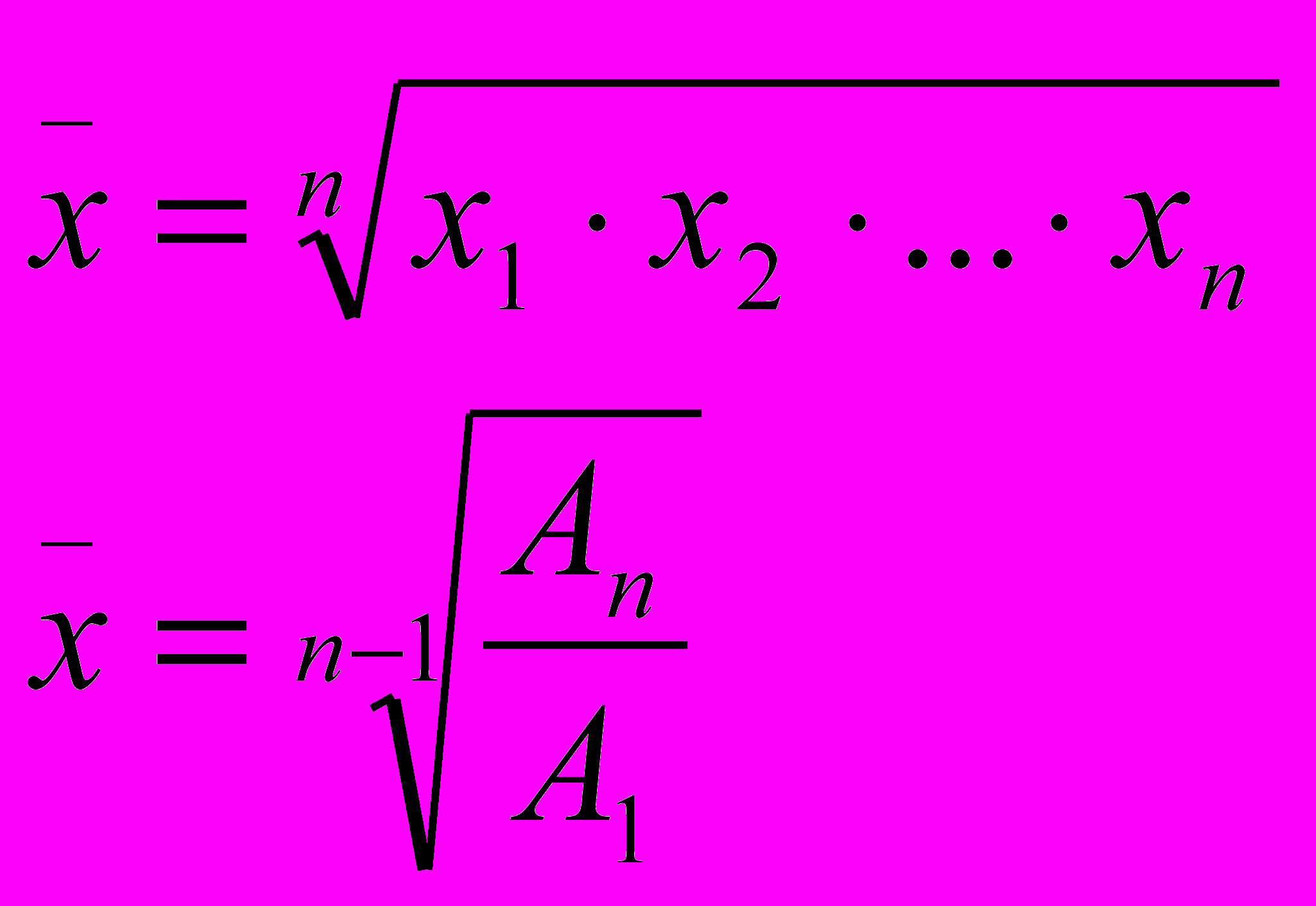
- среднегеометрическое (при изучении рядов динамики (роста, темпа роста))


Мода и медиана.


Для дискретного вариационного ряда:

Мода представляет собой наиболее часто встречающееся значение признака, встречающееся в вариационном ряду, у которого наибольшая частота.

Меридиана – значение признака, находящееся в середине и возрастающего или убывающего вариационного ряда.

В дискретном вариационном ряду моду можно найти по наибольшей частоте, а для определения порядка номера медианы достаточно к общей численности ряда прибавить единицу и полученное число разделить пополам


Интервальный вариационный ряд:






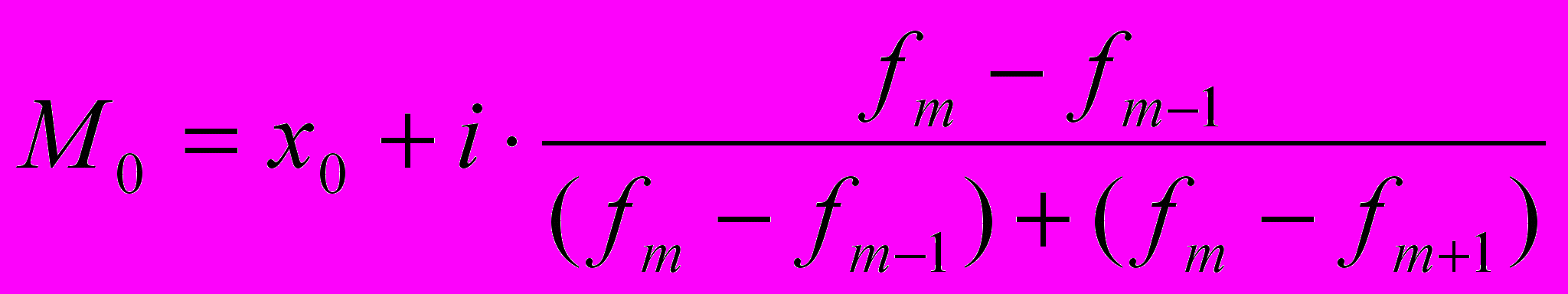
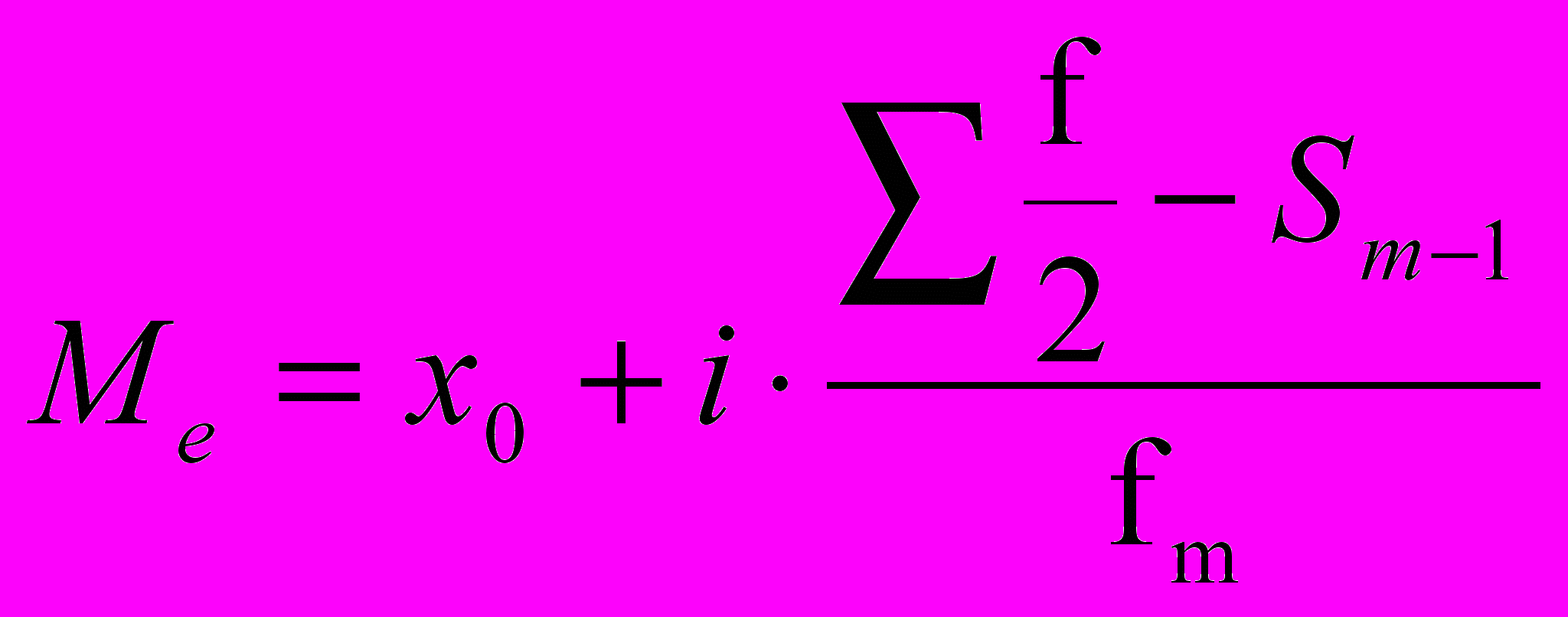
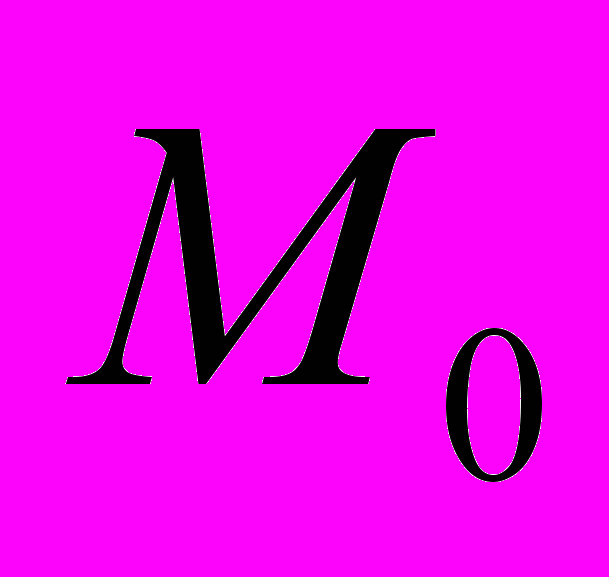- мода

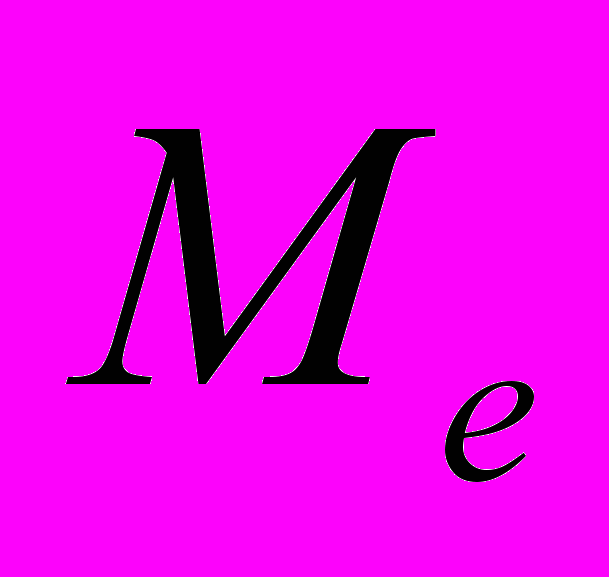- медиана

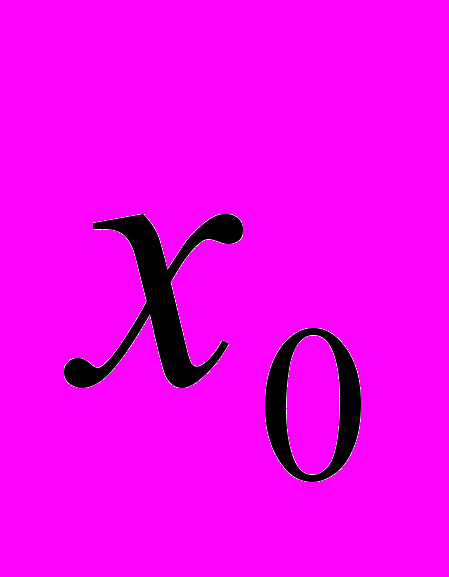- нижняя граница модального (медиального) интервала

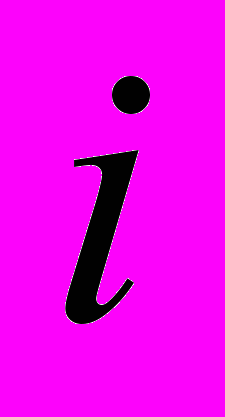- величина модального (медиального) интервала

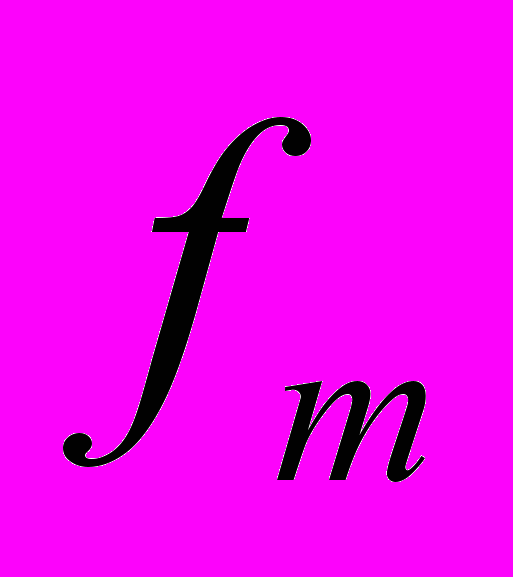- частота модального или медиального интервала

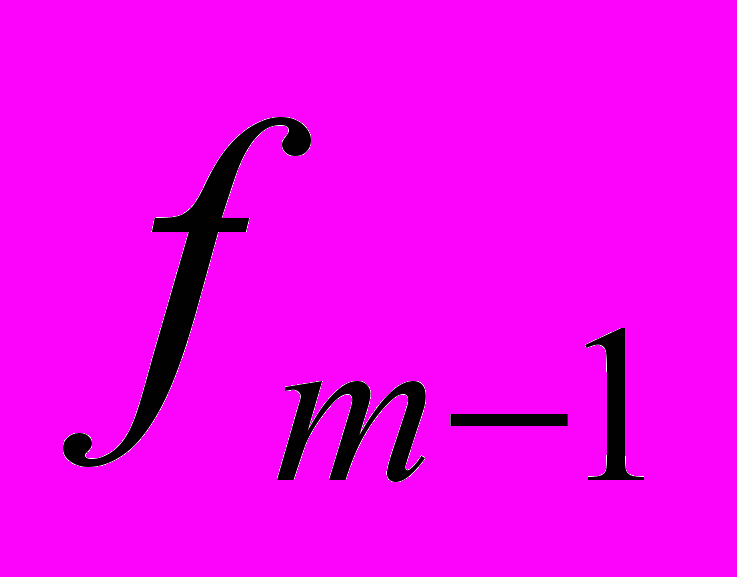- частота предшествующего интервала

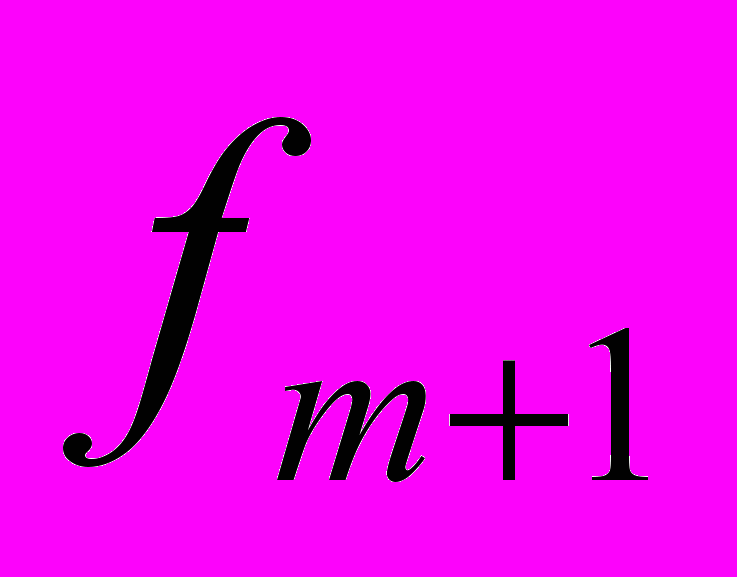- частота интервала следующего за модальным

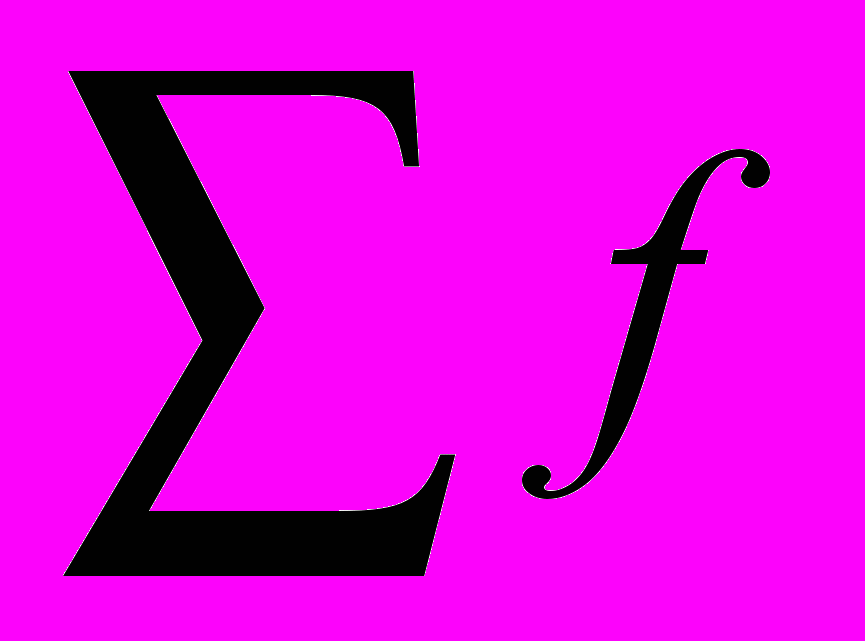- сумма частот ряда

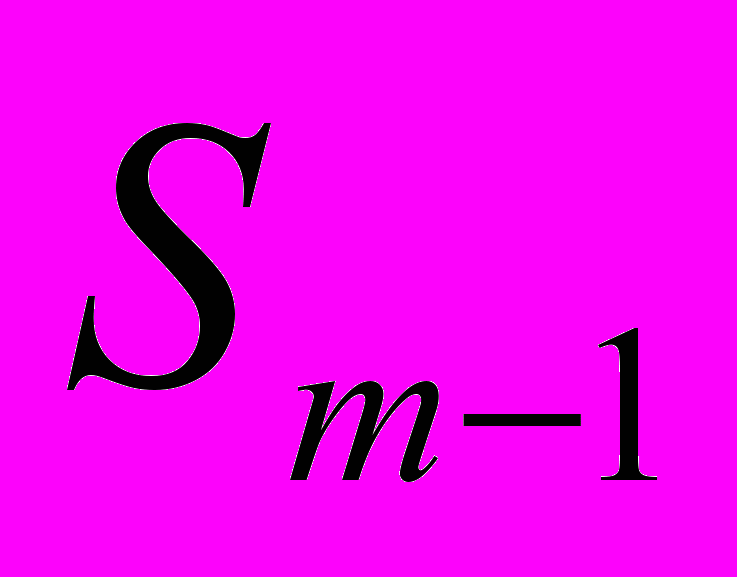- сумма частот в интервалах предшествующего медиальному



Выработка в год на одного рабочего
Количество организаций

До 9500
4

9500-10000
28

10000-10500
40

10500-11000
20

Свыше 11000
8

Итого:
100






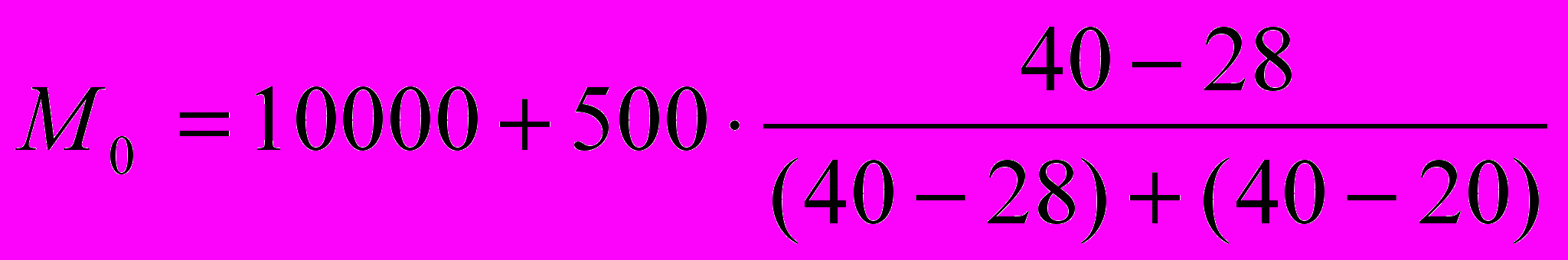
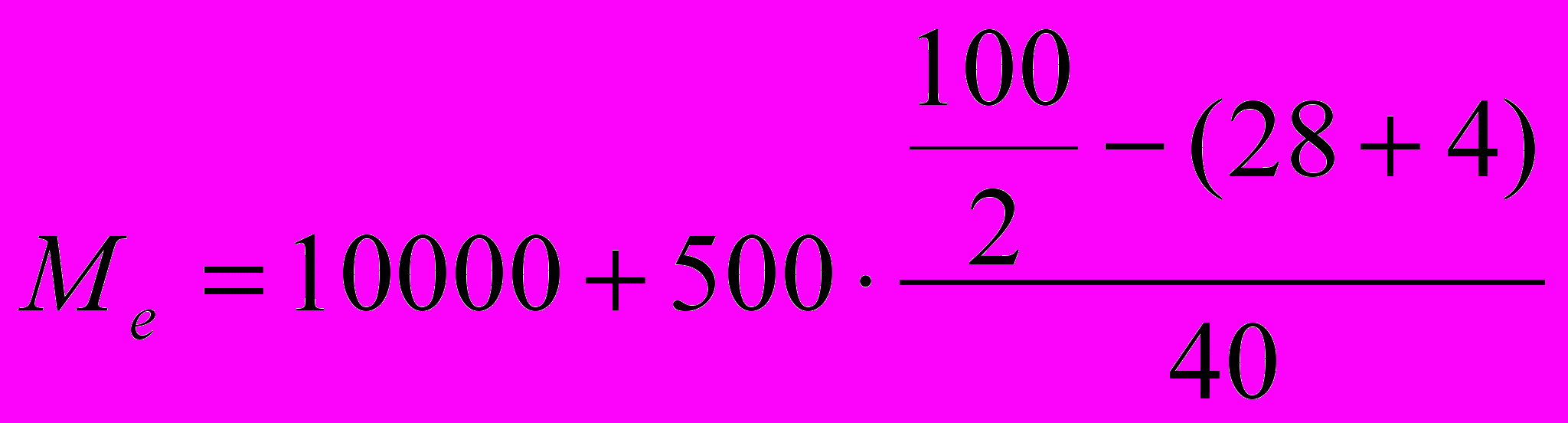
Мода позволяет выявить наиболее распространенный размер или уровень изучаемого явления.


Медиана характеризует деление уровня совокупности явления на 2 части, одна из которых выше или ниже определенного уровня.