Математическое ожидание М(Х) и дисперсия D(Х). Найти закон распределения этой случайной величины

Вид материала

Закон

Подобный материал:

• Вопросы к экзаменам 3-й курс вмк вопросы для темы, 70.75kb.
• Темы лекций по высшей математике элементы теории вероятностей. Относительная частота, 8.28kb.
• Математическое ожидание дискретной случайной величины, 141.8kb.
• Вопросы к экзамену по дисциплине: " Теория вероятностей и математическая статистика", 14.73kb.
• Случайные величины и функции распределения, 49.56kb.
• Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
• Фонд контролирующих материалов по курсу, 53.58kb.
• Закон распределения случайной величины F(X), 330.07kb.
• Числовые характеристики случайных величин, 50.29kb.
• Задание на курсовую работу по дисциплине «математическая статистика» для студентов, 35.79kb.

1. Дискретная случайная величина Х может принимать только два значения: x₁ и x₂ причем x₁ < x₂ . Известны вероятность p₁ возможного значения x₁, математическое ожидание М(Х) и дисперсия D(Х). Найти закон распределения этой случайной величины.

p₁=0,7 М(Х)=3,3 D(Х)=0,21.


Сумма вероятностей всех возможных значений дискретной случайная величины равна единице, поэтому вероятность того, что Х примет значение х₂, равна:

p₂ = 1- p₁ =1-0,7=0,3

Напишем закон распределения

Х	x1	x2
р	0,7	0,3

Запишем математическое ожидание:

М(Х)= 0,7*x₁+0,3*x₂

По условию задачи М(Х)=3,3, следовательно

3,3= 0,7*x₁+0,3*x₂ (1)

Запишем дисперсию:

D(Х)=М(Х²)-[M(X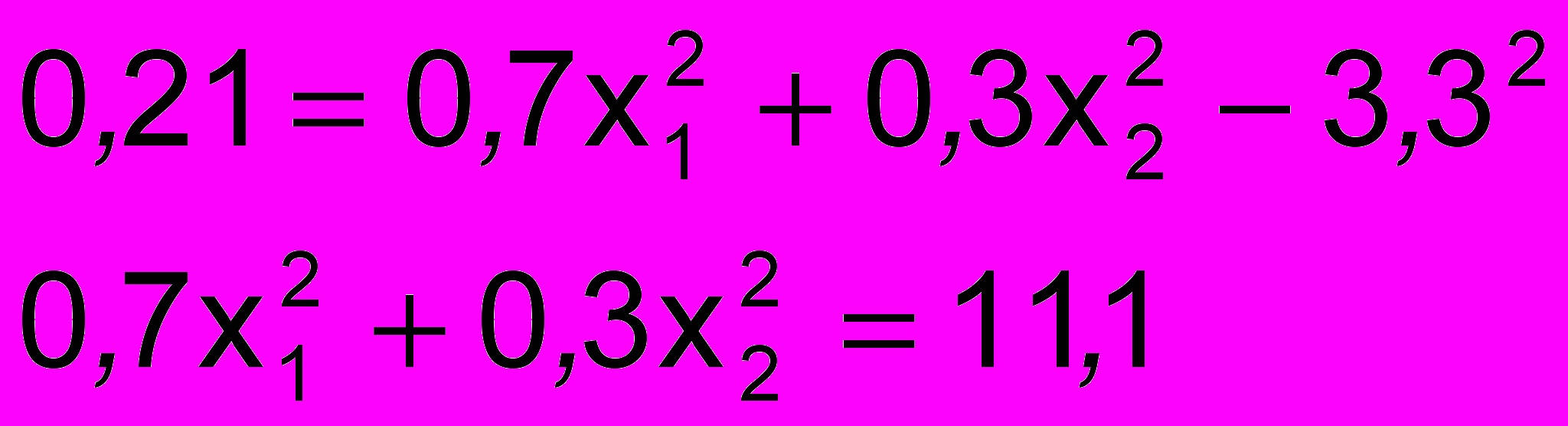)]²

₍₂₎

Решим совместно уравнения (1) и (2)



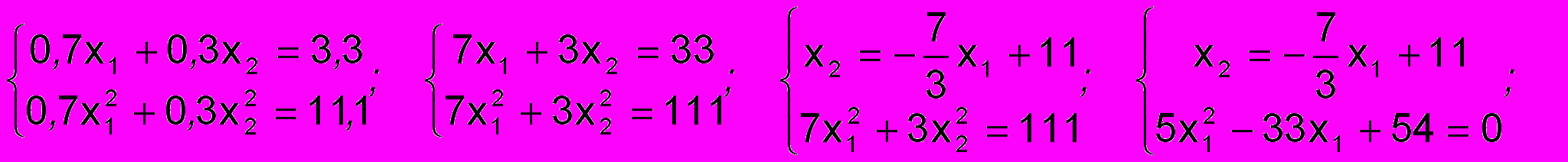
Получаем два решения системы уравнени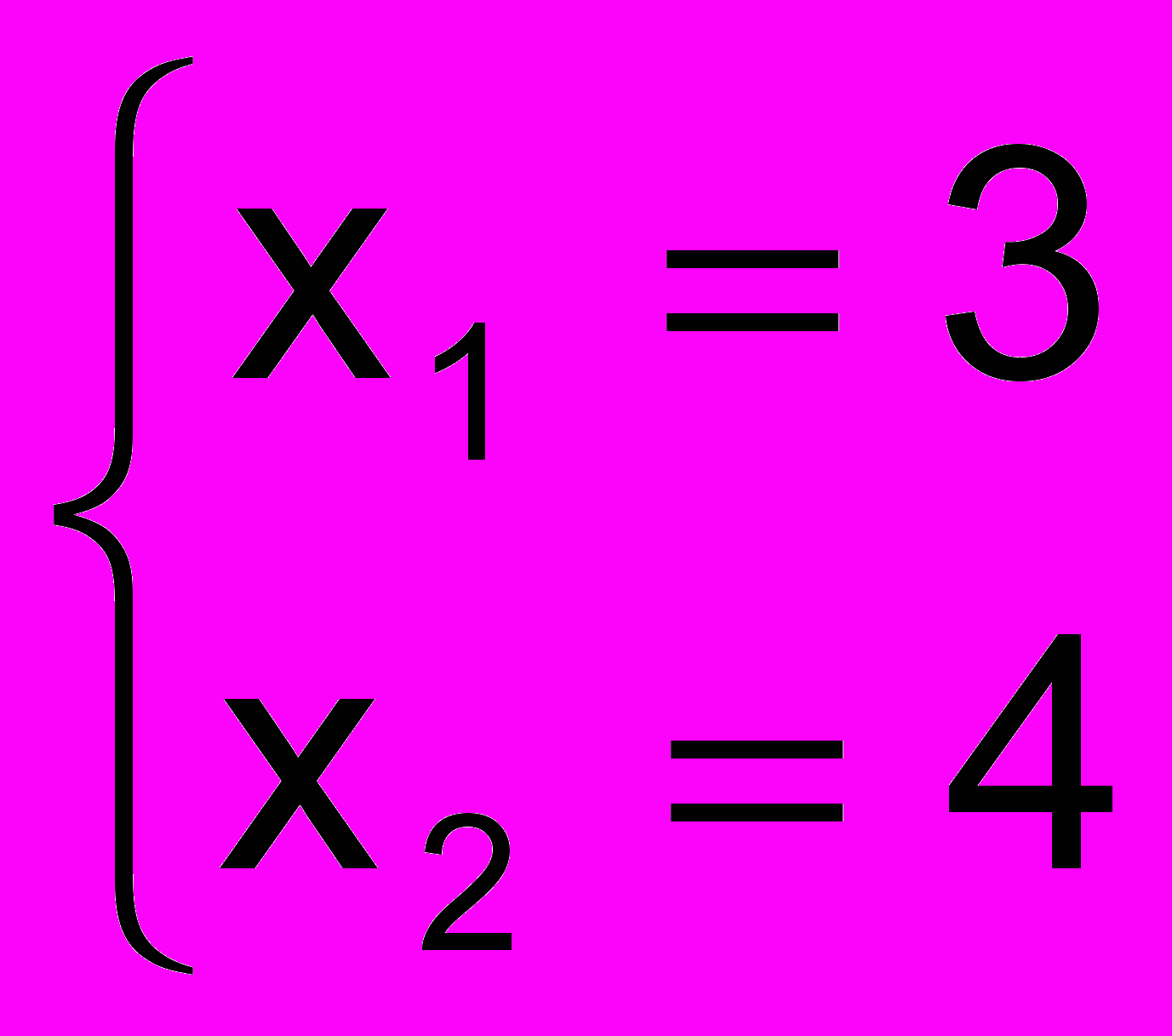й

и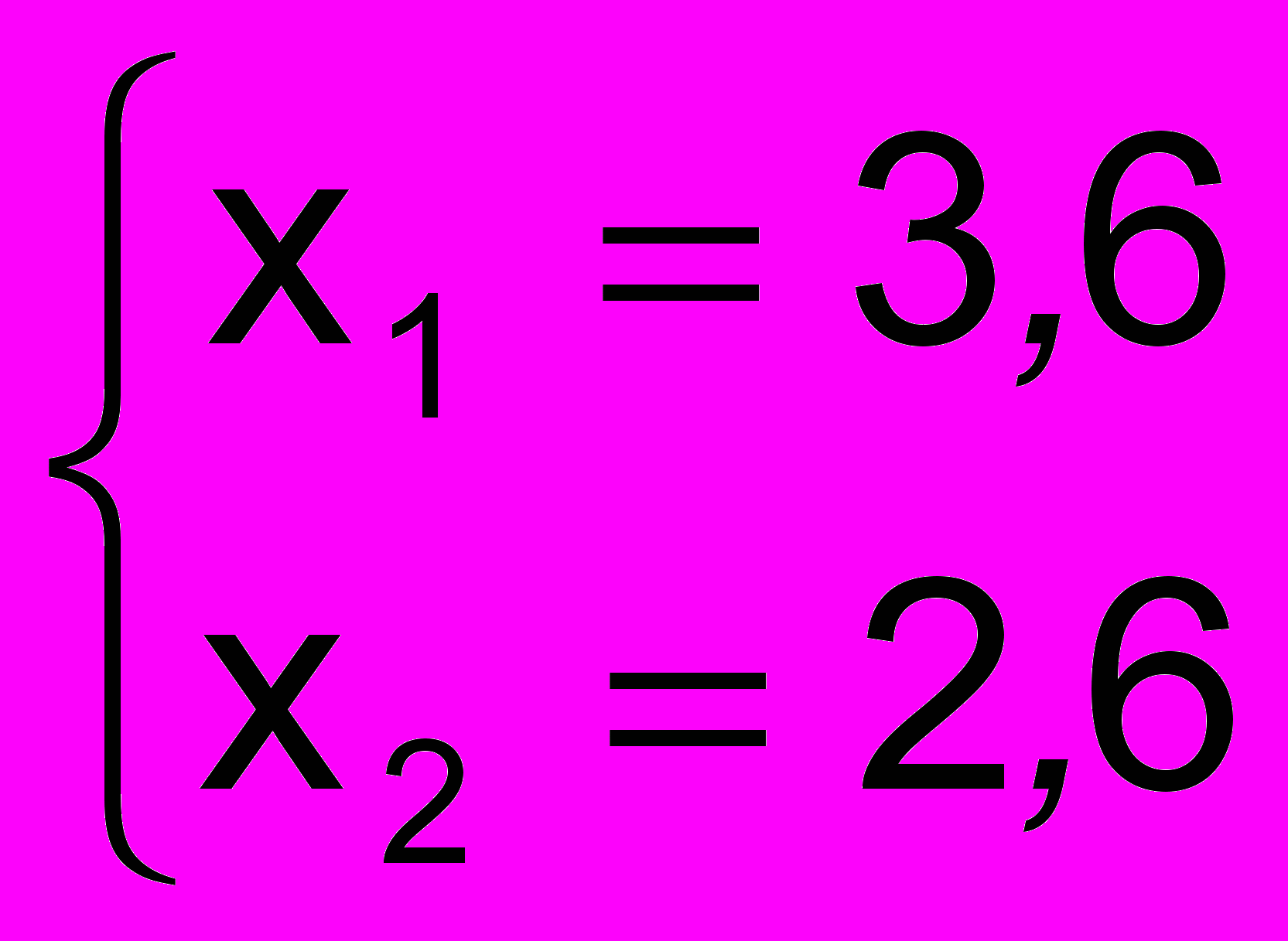

Второе решение отбрасываем, так как по условию задачи x₁ < x₂. Записываем искомый закон распределения случайной величины:

Х	3	4
р	0,7	0,3

2. Случайная величина Х задана следующим законом распределения:

xI	1	3	6	8
pI	0,2	0,1	0,4	0,3

1. построить полигон распределения вероятностей;
   
2. составить интегральную функцию распределения и нарисовать ее график;
   
3. найти М(х) – математическое ожидание, D(x) – дисперсию, (х) – среднее квадратическое отклонение случайной величины Х.
   

Решение

1. Построим полигон распределения вероятностей:
   

		р
		0,4
		0,3
		0,2
		0,1
			1		3			6		8		10					х

2) Составим интегральную функцию распределения:

Если х<1, то F(x)=0.

Если 1х<3, то F(x)=0,2.

Если 3х<6, то F(x)=0,2+0,1=0,3.

Если 6х<8, то F(x)=0,2+0,1+0,4=0,7.

Если х>8, то F(x)=0,2+0,1+0,4+0.3=1.

		F(x)
		1
		0,7
		0,3
		0,2
			1		3			6		8		10					х

3) Математическое ожидание M(X);



= 1*0,2+3*0,1+6*0,4+8*0,3= 0,2+0,3+2,4+2,4=5,3

M(X) = 5,3

б) дисперсия D(X);



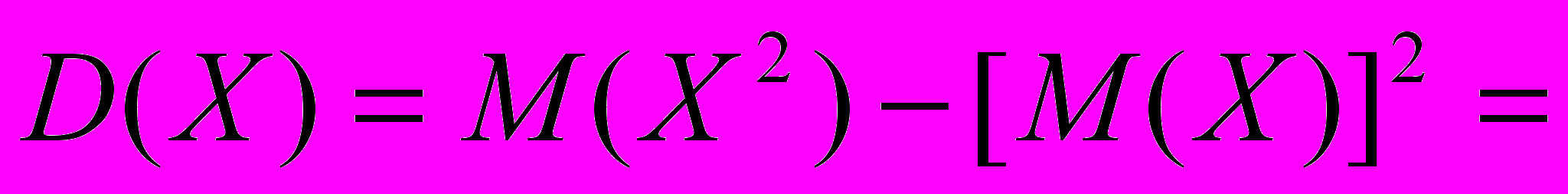
= X₁ ² *P₁ +X₂ ² *P₂ +X₃² *P₃ + X₄² *P₄ - [M(X)] ² =

= 1*0,2+9*0,1+36*0,4+64*0,3-5,3² = 6,61

в) среднее квадратическое отклонение  (X).

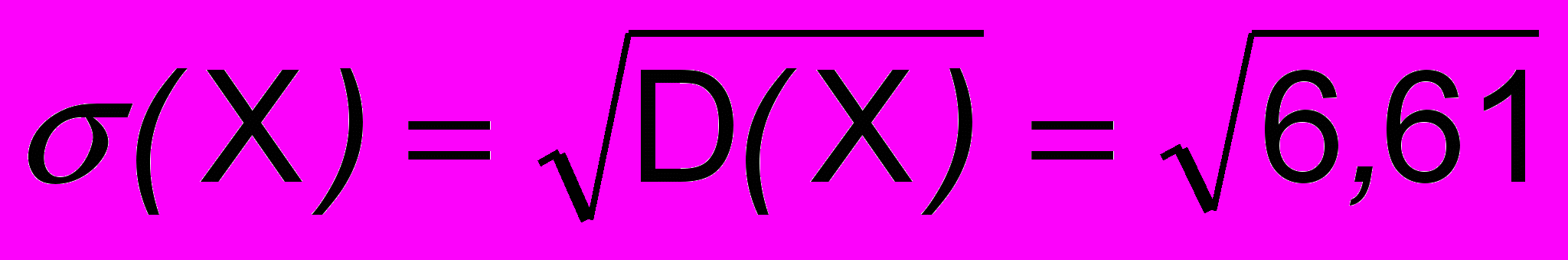 2,57