Geum.ru

Задание на курсовую работу по дисциплине «математическая статистика» для студентов групп специальности «ЗИ» (группа «зи-51», семестр 2011/2012 учебного года)

Вид материалаДокументы

Содержание


Проверяться не будут
Подобный материал:
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
ДЛЯ СТУДЕНТОВ ГРУПП СПЕЦИАЛЬНОСТИ «ЗИ»
(группа «ЗИ-51», семестр 2011/2012 учебного года)

Распределение Пуассона. Вероятность задана значениями .

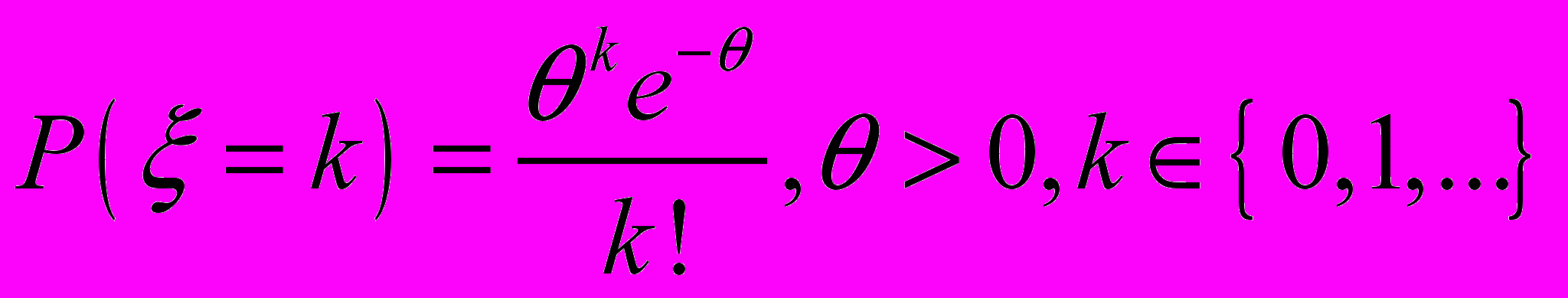Значение 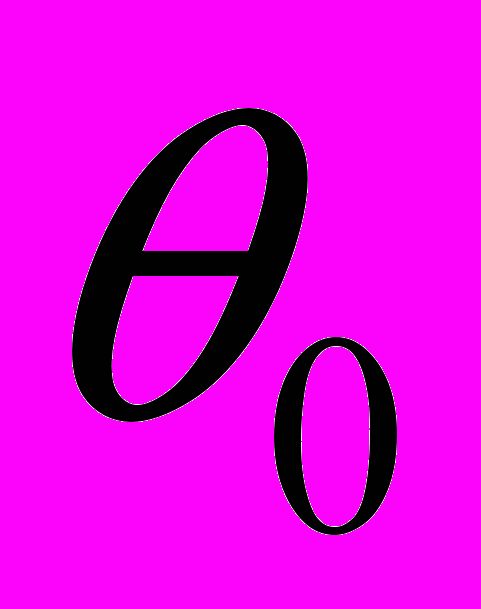оцениваемогопараметра 15;


Уровень доверия ;


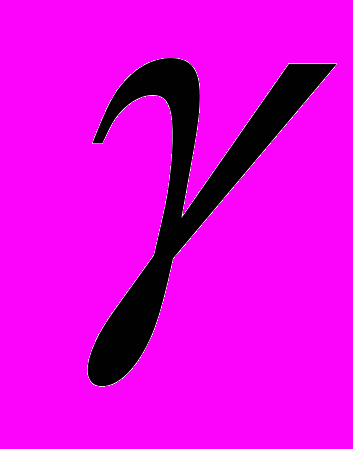
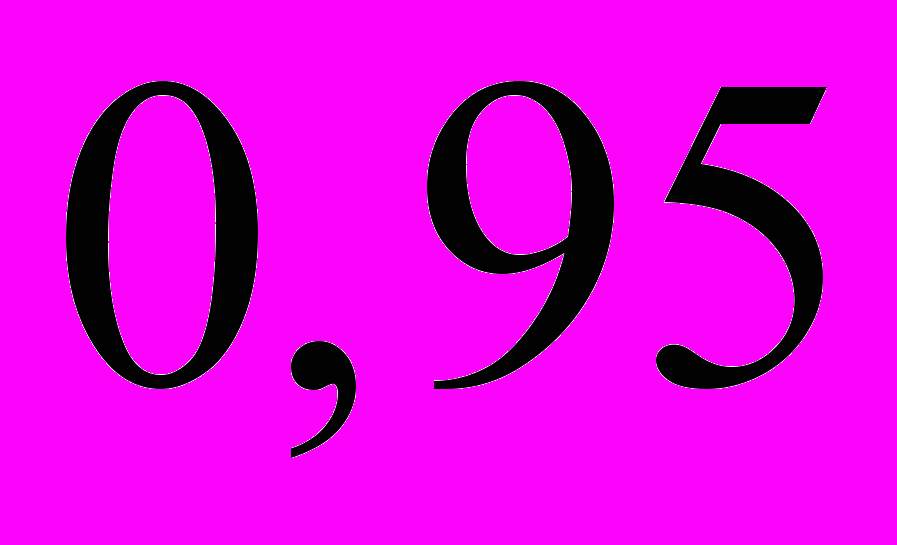В задании указан закон распределения случайной величины (плотность или вероятность), зависящий от неизвестного параметра , а также значение параметра , равное .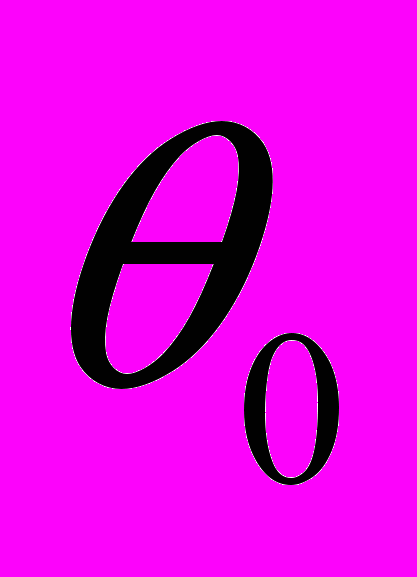


I. Теоретическая часть

Для указанного закона распределения требуется:
  • указать (если это возможно) способ моделирования случайной величины , приведённой в задании, из случайной величины 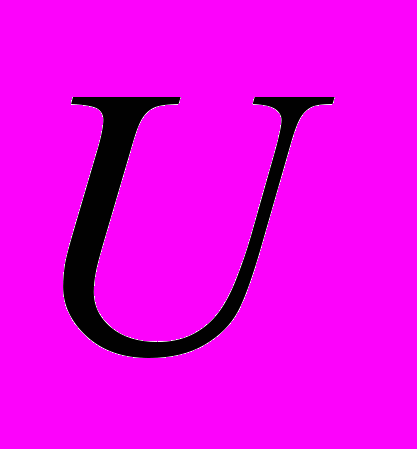с распределением 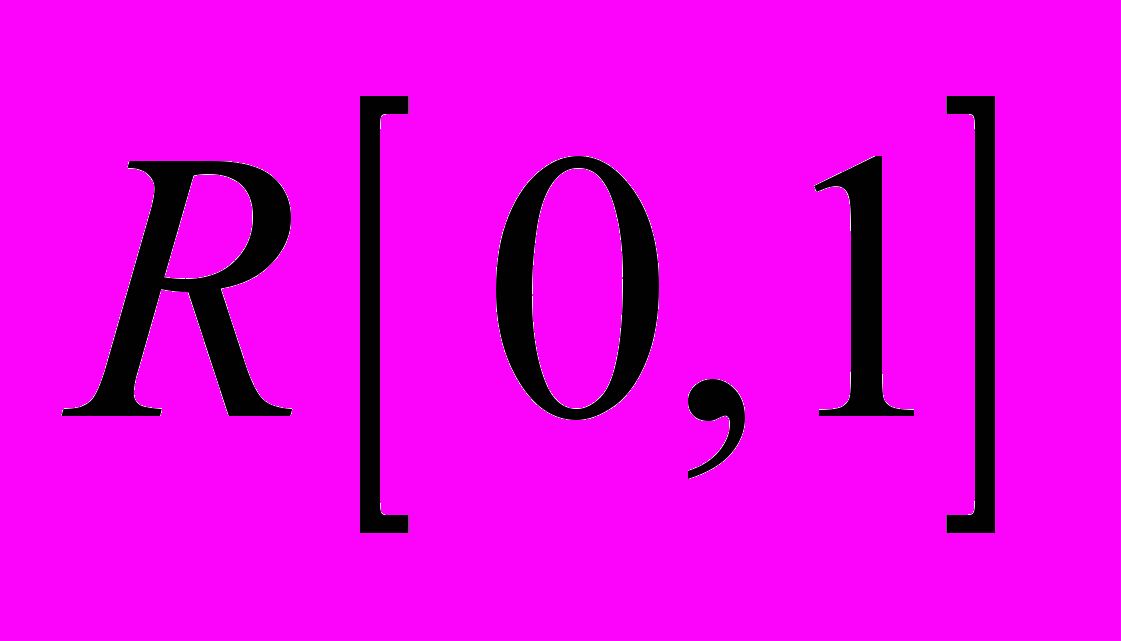(то есть требуется найти соответствующее функциональное соотношение );
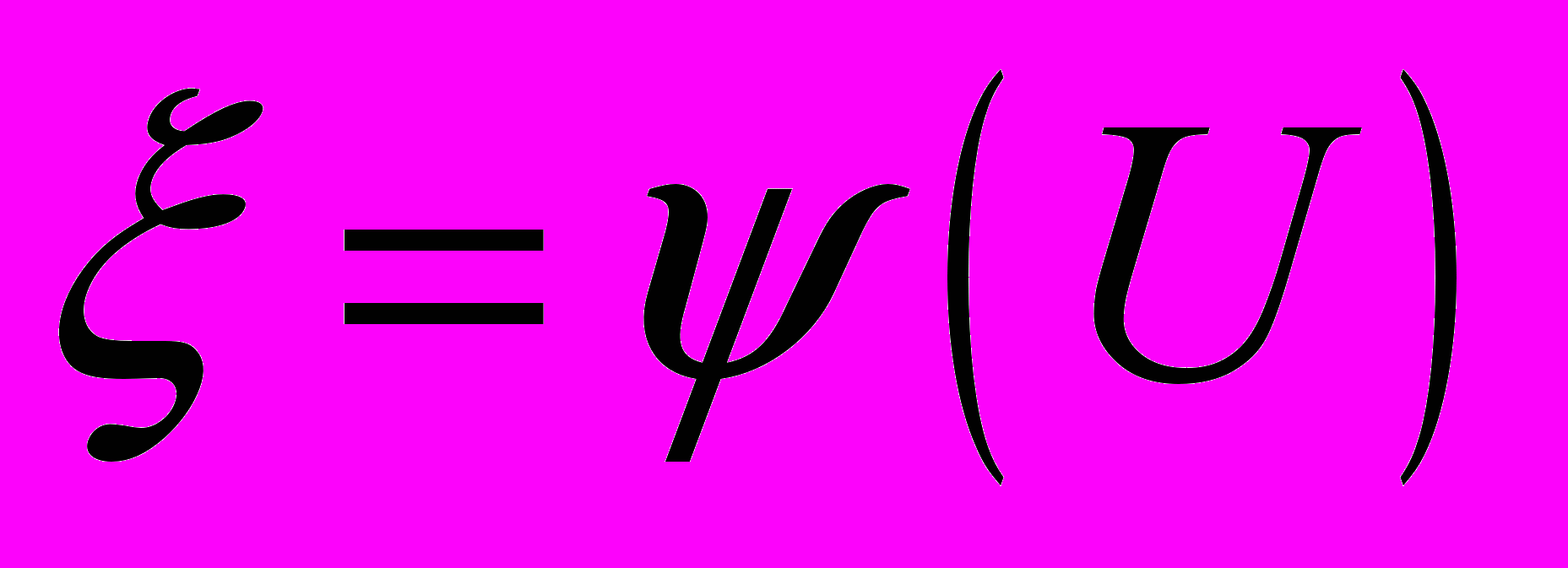  • найти функцию распределения случайной величины ;
  • найти математическое ожидание и дисперсию случайной величины ;
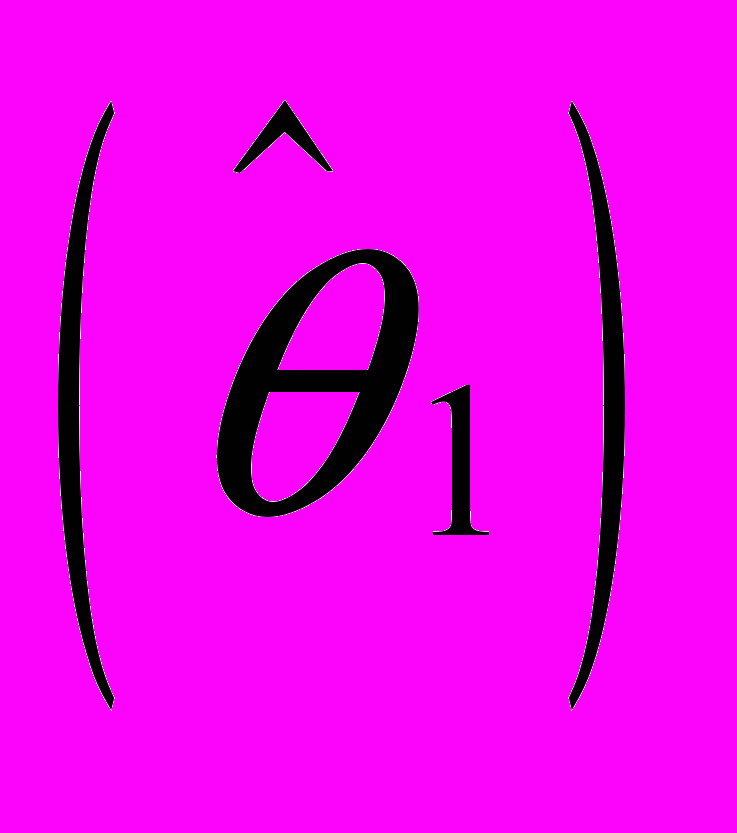  • найти оценки неизвестного параметра методом моментов и методом максимального правдоподобия 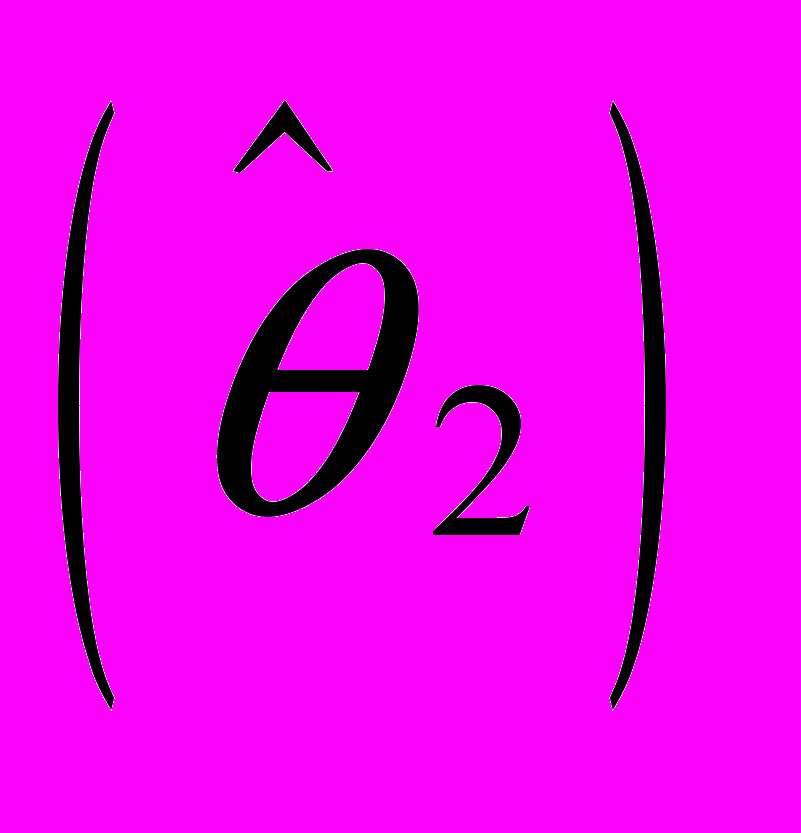. Выяснить, являются ли полученные оценки несмещёнными и состоятельными. Если оценки смещены, то найти несмещённые оценки (если это возможно), зависящие от оценок 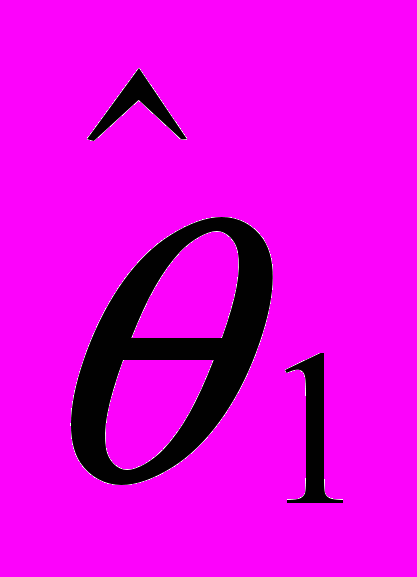и 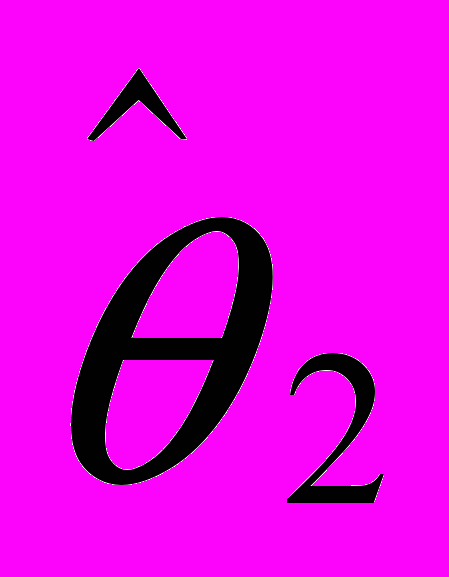. Найти дисперсии несмещённых оценок (если оценки существуют);
  • выяснить, существуют ли параметрические функции 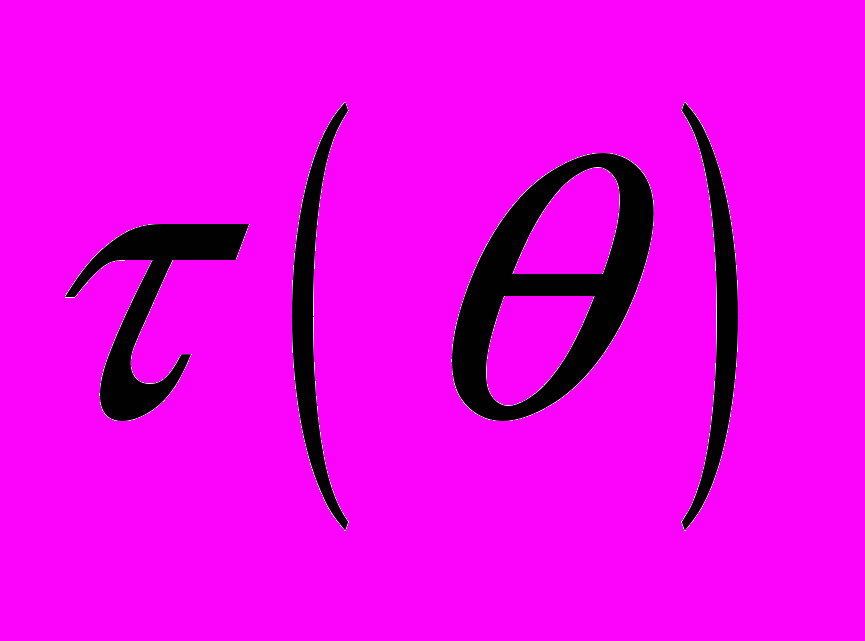, для которых можно найти эффективные оценки. Определить класс таких параметрических функций и вид эффективной оценки;
  • найти оптимальную оценку 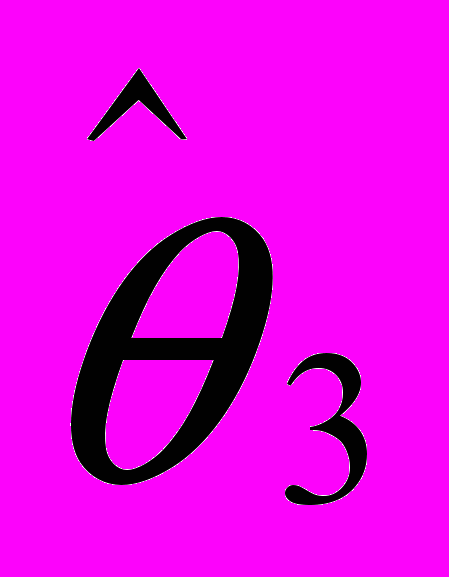неизвестного параметра (если она существует);
  • для неизвестного параметра построить доверительный интервал уровня (значение приведено в задании);
  • для непрерывных распределений – построить критерий Неймана-Пирсона для проверки двух простых параметрических гипотез: 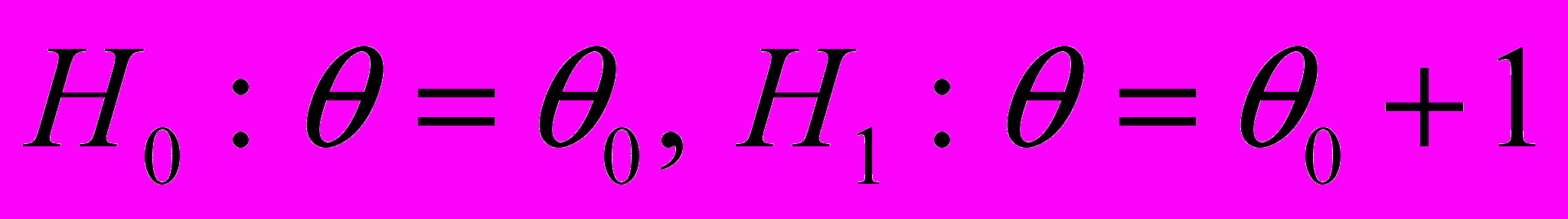( 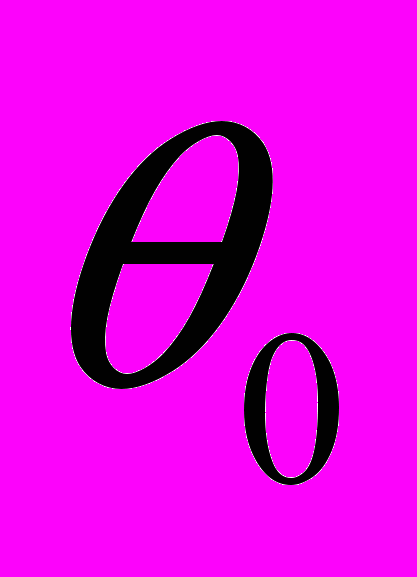– указанное в задании значение параметра ). Вероятность ошибки первого рода положить равной 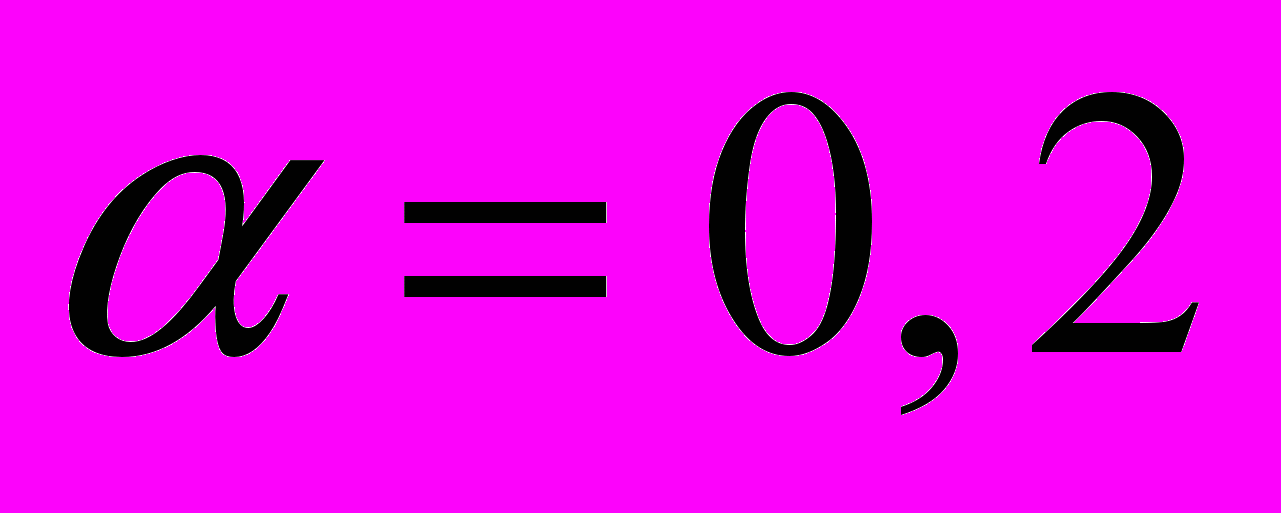. Найти вероятность ошибки второго рода .
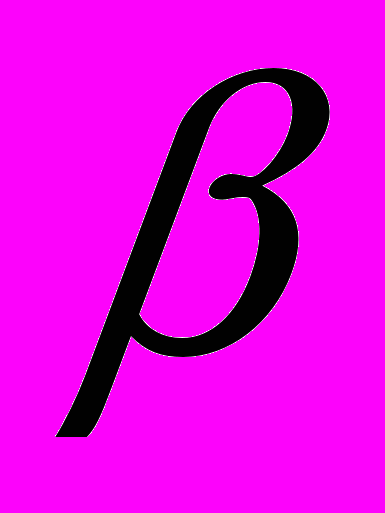  • для дискретных распределений – построить критерий согласия хи-квадрат для проверки гипотезы о том, что истинным параметром распределения является 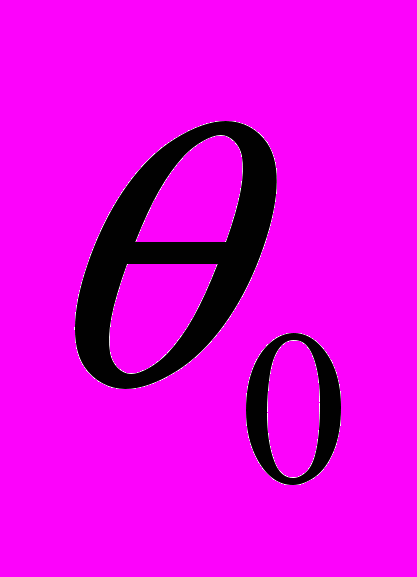. Уровень значимости критерия положить равным .



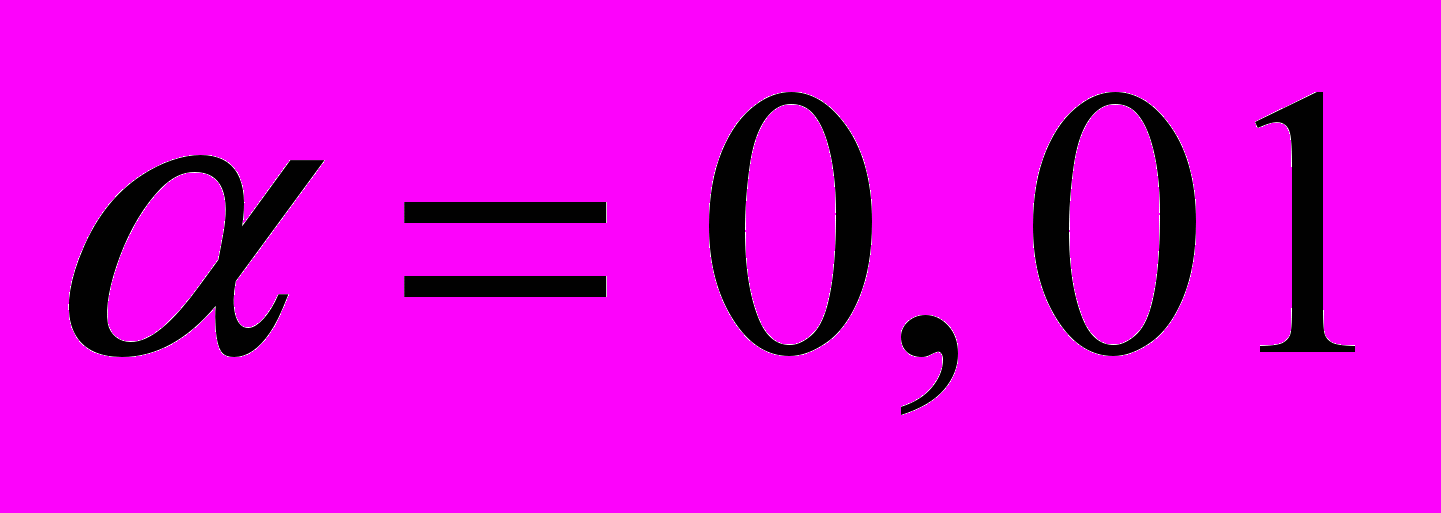II. Работа на компьютере
  1. Смоделировать выборку объёма 200 из заданного закона распределения для заданного значения параметра 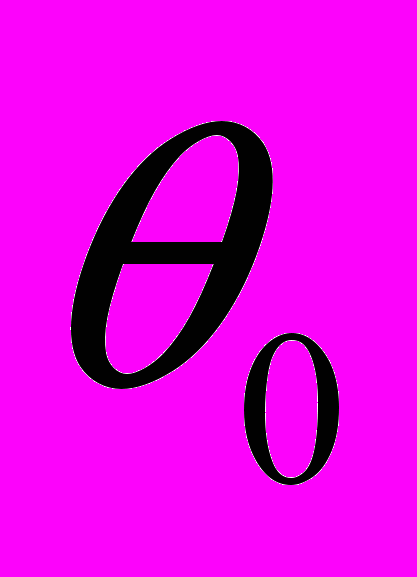. Построить вариационный ряд выборки и эмпирическую функцию распределения .
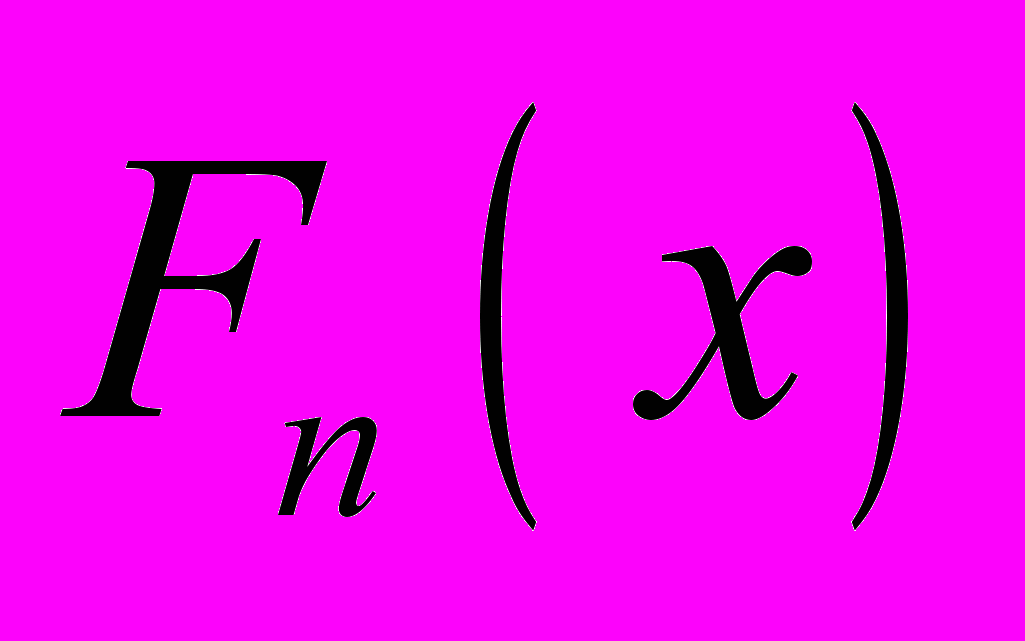  2. По смоделированной в п. 1 выборке найти численные значения оценок 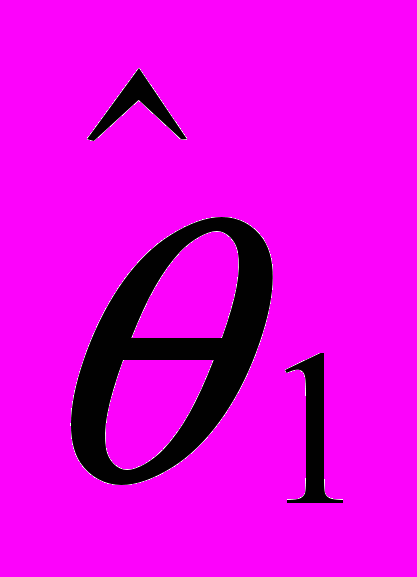, 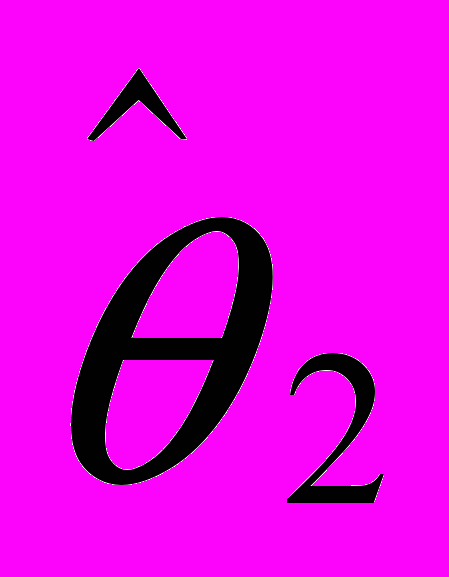и .
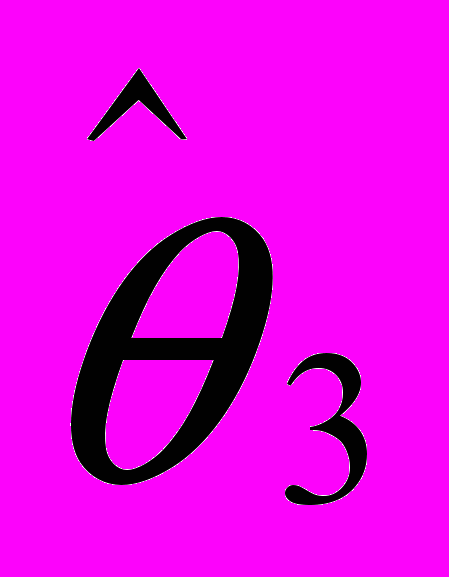  3. Построить доверительный интервал для параметра доверительного уровня , значение которого указано в задании.
  4. Смоделировать 10 выборок объёмом 100 каждая. Для каждой выборки найти численные значения оценок 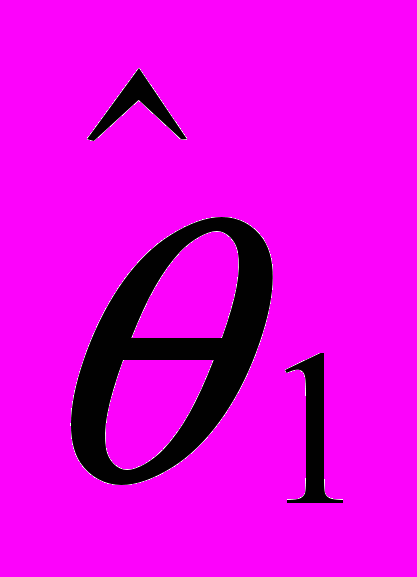, 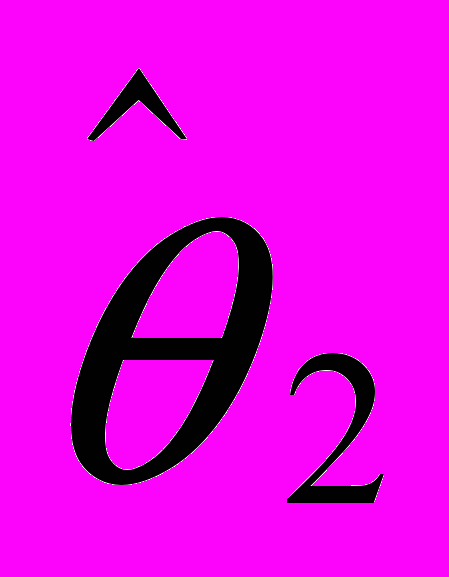и 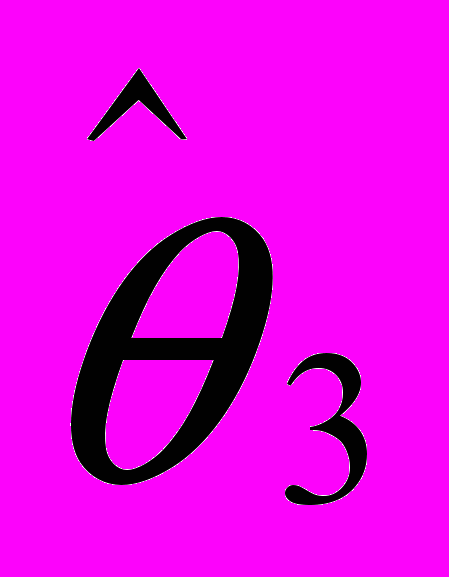, а также численные значения границ доверительного интервала уровня . Найти значения выборочных средних и выборочных дисперсий полученных оценок.
  5. Проверить гипотезу о том, что смоделированная выборка получена из указанного в задании закона распределения, применив критерий согласия хи-квадрат. Уровень значимости критерия положить равным .



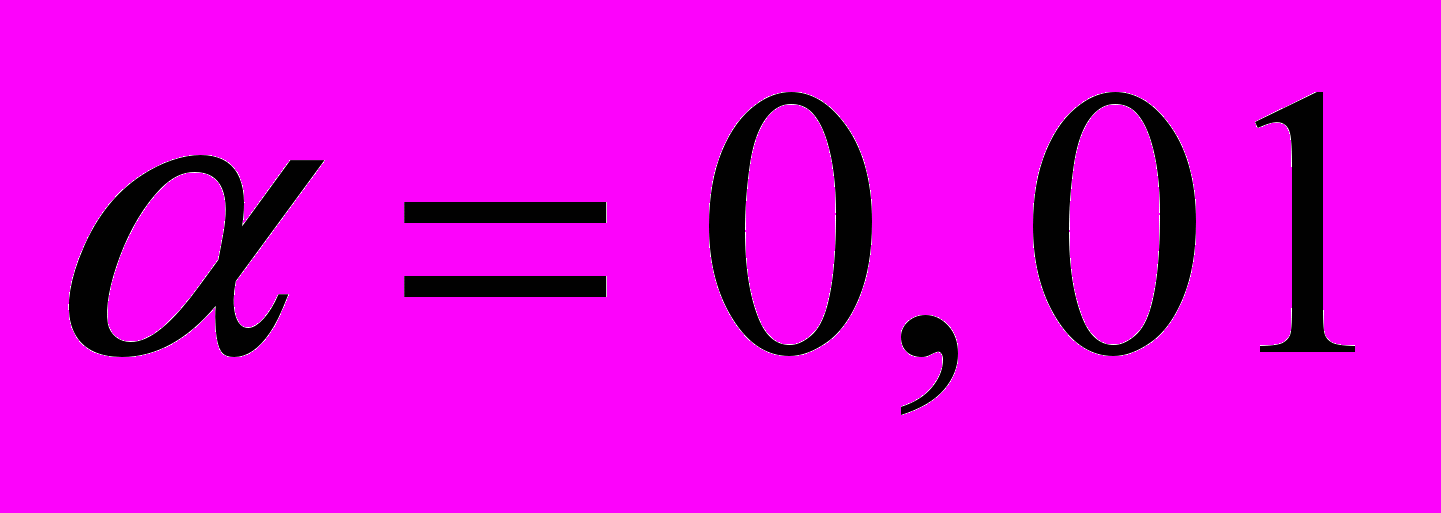III. В Отчёте по курсовой работе должны:

  • присутствовать ВСЕ теоретические выкладки;
  • присутствовать вариационный ряд выборки и график эмпирической функции распределения;
  • присутствовать таблицы полученных выборок, численные значения выборочных характеристик, оценок, а также значения границ доверительных интервалов.



IV. Отчёт по курсовой работе должен быть оформлен на листах формата A4 (желательно – в одном из текстовых редакторов – «MSWORD», «TeX», либо в форматах PDF, PS, DJVU), с титульным листом, фамилиями студента и преподавателя (образец приложен к заданию).


В Н И М А Н И Е !!!

Отчёты, не соответствующие требованиям п. IV,
ПРОВЕРЯТЬСЯ НЕ БУДУТ


Сдача отчёта является необходимым условием
при получении зачёта по курсу!!!




ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Кафедра «Информационная безопасность»







КУРСОВАЯ РАБОТА
по дисциплине «Математическая статистика»
(Распределение )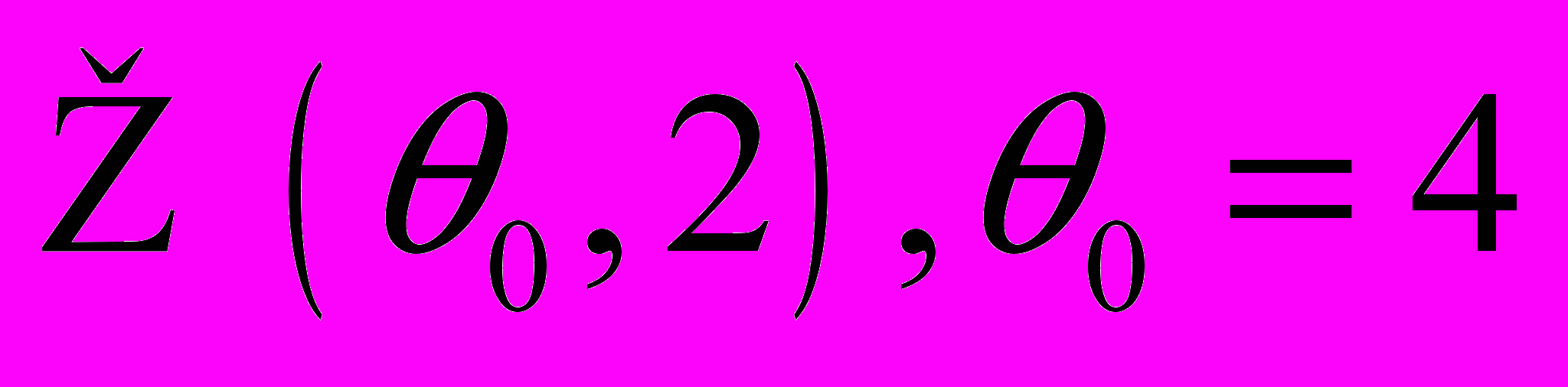


Выполнил:

студент группы ЗИ-51

Базаров И.П.

Проверил: доцент Иванов А.В.


МОСКВА – 2011