Лекция №1. Предмет физики. Физические измерения
| Вид материала | Лекция |
- Программа курса лекций (3 курс, 6 сем, 32 ч, зачет) ( 4 курс, 7 семестр, 36 ч, экзамен), 34.63kb.
- «Физические величины и их измерения», 92.58kb.
- Тема: Физика наука о природе. Физические тела и физические явления, 82.49kb.
- Концепциифизик и, 1687.81kb.
- Лекция Экспериментальные методы измерения равновесной адсорбции, 296.24kb.
- Ядерно-физические методы в решении проблем нефтяной отрасли и экологии Казахстана 01., 579.83kb.
- Программа дисциплины радиофизические измерения Специальность: Радиофизика и электроника, 92.83kb.
- Структура и содержание программы Структура деятельности студентов Контролирующие материалы., 231.8kb.
- 2. Т84. Государственные поверочные схемы т 84 Измерения геометрических величин, 3468.15kb.
- Физические основы механики, 237.04kb.
ЛЕКЦИЯ №1.
ПРЕДМЕТ ФИЗИКИ. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ.
1. ФИЗИКА – в переводе с греческого означает «природа», и как трудно дать краткое внятное определение понятию «природа», так трудно дать определение и предмету «физика» из-за чрезвычайной широты области знания, изучаемой этой наукой.
Если отвлечься от частностей, то можно согласиться с определением, в соответствии с которым предметом физики является изучение простейших и вместе с тем наиболее распространенных видов движения простейших элементов материи.
Такое «амебное» определение предмета просто означает, что физика интересуется в первую очередь такими объектами, как молекулы, атомы и их конгломераты, ядра атомов, электроны и т.п., различные силовые поля. Конечно, мы не забываем, что из этого-то и состоим мы и все, что нас окружает…
2. В современных условиях быстрого и все возрастающего темпа развития науки и техники инженеру, исследователю все чаще приходится сталкиваться с качественно новыми для него областями физических явлений. Эти физические явления часто входят составной частью в технологии получения новых материалов или являются основой реконструкции старых производств, являются теоретической основой элементов новой техники – базы технологического прогресса общества. Поэтому для будущего инженера важно не столько описательное знакомство с обширным кругом разнообразных физических явлений, сколько твердое усвоение иерархии основных физических законов и понятий, позволяющее эффективно их использовать в конкретных ситуациях, при решении конкретных инженерных и технологических задач.
3. ФИЗИКА – наука опытная. Хотя современные физические теории (например, квантовая механика, теория поля) выглядят как сложные абстрактные конструкции из математических предположений, математических выкладок и выводов в виде математических формул, однако все эти теории опираются на опыт, и только опыт является критерием их достоверности.
Физическим опытом называется только такое измерение, в котором все воздействия на исследуемую систему поддаются учету и измерению. Это требование необходимо выполнять, чтобы реализовать главное свойство опыта – его воспроизводимость.
Примеры «антиопытов» – телепатия, телекинез.
Процесс познания в физике начинается либо с наблюдения некоторого (обычно – повторяющегося) явления в естественных условиях, либо со специально поставленных опытов-экспериментов. На основе накопленного экспериментального материала путем обобщения строится некоторое предварительное предположение – гипотеза. Гипотеза требует проверок, подтверждений и доказательств достоверности. Не все гипотезы выдерживают проверок (светоносный эфир, флогистон и др.). Гипотезы, выдерживающие проверку, превращаются в законы.
Физические теории, как правило, базируются на нескольких физических законах, и способны не только удовлетворительно объяснять известные явления, но и могут предсказывать новые явления и закономерности.
Появление достоверного опыта, не согласующегося с существующей теорией, является побудительным толчком к созданию новой, более совершенной теории или к уточнению существующей. Как правило, «хорошие» теории не отвергаются полностью, а входят как составная часть или предельный случай существующей (пример – классическая и релятивистская механика). Реализуется известный принцип развития вверх по спирали, что можно прокомментировать схемой рис.1.1.
НАБЛЮДЕНИЕ
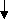
ОПЫТЫ, ЭКСПЕРИМЕНТЫ


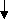
ГИПОТЕЗА
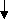
ФИЗИЧЕСКИЙ ЗАКОН
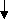
ФИЗИЧЕСКАЯ ТЕОРИЯ
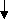
НЕОЖИДАННОЕ НАБЛЮДЕНИЕ

Рис.1.1. Схема развития физического знания.
4. Все физические измерения производятся с ограниченной точностью. Поэтому при каждом физическом измерении указывают не только величину полученного результата, но и точность или величину доверительного интервала.
Одним из самых точных опытов в физике является измерение (с использованием эффекта Мёссбауэра) изменение величины энергии гамма-кванта на долю 10-17 под действием силы тяжести Земли при подъеме на 3 метра (опыт Паунда и Реббки). Повышение точности измерений расширяет возможности познания окружающего мира и поэтому является важнейшей научной и технической проблемой, но, начиная с некоторого предела, стоит недешево. Например, определение величины ускорения свободного падения g с точностью до 7-8 знака после запятой (м/с2) потребовало применения в качестве «падающего предмета» сверхточного лазера. Эти эксперименты дают замечательные результаты при гравиметрической разведке полезных ископаемых и расходы вполне оправданы. Вообще же при решении конкретной инженерной задачи нужно стремиться к тому, чтобы точность была лишь достаточной. И не более того.
Обработка наблюдений и представление результатов эксперимента.
Задачей эксперимента является определение истинного значения физической величины. Истинное значение измеряемой величины является объективным, наиболее полным отражением определенных свойств этой величины, как в количественном, так и в качественном отношениях. В однократном опыте, однако, истинное значение определить невозможно.
Процесс измерения подвержен воздействию ряда факторов, называемых помехами или возмущениями, приводящих к отличию результатов измерения от истинного значения измеряемой величины. Эти факторы, в большинстве своем не зависящие от исследователя, могут быть как известными, так и неизвестными. Они могут быть обусловлены различными причинами: нестабильностью и собственными шумами аппаратуры, внешними воздействиями (колебаниями температуры в помещении, колебаниями напряжения сети и источников питания), ограниченной точностью измерительных приборов, личными качествами исследователя и т.п.
Воздействие помех на процесс измерения приводит к тому, что результаты измерения всегда отличаются от истинного значения измеряемой величины и по этим результатам определить истинное значение нельзя. Поэтому вместо него в опыте находят некоторое приближенное к нему значение, называемое результатом измерения или действительным значением физической величины.
Разность между результатом измерения и истинным значением измеряемой величины называется истинной погрешностью или просто погрешностью измерения. В силу того, что истинное значение неизвестно, неизвестной является и истинная погрешность.
Определение величины погрешностей и их снижение является обязательной и насущной необходимостью любого экспериментатора, поэтому методологии измерений всегда уделяется большое внимание.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Прямым называется измерение, при котором значение измеряемой величины непосредственно считывается со шкалы прибора, проградуированного в соответствующих единицах измерения. Уравнение прямого назначения имеет вид
Y=cx,
где Y - значение измеряемой величины, с - цена деления шкалы прибора в единицах измеряемой величины, х - отсчет по индикаторному устройству и делениях шкалы.
Примерами прямых измерений являются: измерение длины предмета с помощью линейки с миллиметровыми делениями, штангенциркуля или микрометра измерение тока амперметром, напряжения - вольтметром, температуры - термометром и др.
Косвенным называется измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью. Уравнение косвенного измерения имеет вид
Y=f(x1,x2,…,xn),
где Y искомая величина, являющаяся функцией величин х1, х2, ..., xn, измеряемых прямым методом. Можно сказать, что косвенное измерение - это измерение, результат которого рассчитывается по формуле.
Примерами таких измерений являются: определение радиуса шара R == D/2 , площади его поверхности S =D2 или объема V =D3/6 по прямо измеренной величине - диаметру шара D.
Теория погрешностей: классификация, происхождение,
признаки, методы снижения.
Учитывая, что ни истинное значение физической величины, ни истинную погрешность в опыте определить невозможно, задачу нахождения истинного значения формулируют как задачу нахождения некоторого приближенного к истинному значения с указанием возможных небольших отклонений этого приближенного значения от истинного.
По влиянию на результаты измерений погрешности подразделяются на систематические, случайные и промахи.
Систематическая погрешность - это составляющая погрешности измерения, которая остается постоянной или закономерно меняется при повторных измерениях.
Признак систематических погрешностей – мало изменяются по величине и не меняются по знаку.
К систематическим погрешностям относятся, например, погрешности градуировки шкалы, смещение нуля измерительного прибора и др. Одной из основных задач обработки результатов эксперимента является выявление и оценка величины всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче постоянных. Для выявления постоянной систематической погрешности необходимо выполнив измерений хотя бы двумя различными способами или методами. Обнаруженные и оцененные систематические погрешности исключаются из результатов (или уменьшается их влияние) путем введения поправок.
Наблюдаются различные виды систематических погрешностей.
1. Погрешности метода или модели, которые обычно называют методическими погрешностями. Например, определение плотности вещества без учета имеющихся в нем примесей и пустот, использование в нем формул, не совсем точно описывающих явление (влияние силы Архимеда при взвешивании, тепловое расширение при определении линейных размеров и т.п.). Если возникает подозрение, что сама физическая модель, подвергаемая измерению, неадекватно отражает сущность, то единственный путь уточнения измерений – проведение его принципиально отличающимся методом. Сюда же относятся погрешности, к сожалению, неизвестные экспериментатору.
2. Погрешности воздействия внешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей.
3. Погрешности, возникающие из-за неточности действия или личных качеств оператора (экспериментатора), называемые личностными погрешностями.
4. Инструментальные или приборные погрешности, обусловленные конструктивными и технологическими несовершенствами средства измерения. Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов эксплуатации, неправильное положение приборов и т.п.
В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных выше факторов, многие из которых невозможно рассчитать, подавить или выявить в данном эксперимента. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученного с помощью серийного (рабочего) и более точного, образцового прибора. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности был бы слишком дорогим. На практике поэтому различные составляющие систематической погрешности пытаются устранить с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений при условии, что погрешность данного вида по величине и знаку известна.
ПОЛОСА ПОГРЕШНОСТЕЙ И КЛАСС ТОЧНОСТИ ПРИБОРА
Приборными (инструментальными) погрешностями средств измерений называют такие, которые принадлежат данному средству измерений (СИ), определены при его испытаниях и занесены в его паспорт.
Теоретическая погрешность СИ есть разница между значением величины, полученным при помощи этого средства, и истинным значением. Вместо неизвестного истинного значения на практике обычно используется значение, полученное при помощи более точного СИ. По точности СИ делят на рабочие (серийные), образцовые и эталонные. Для рабочего СИ более точным является образцовое, а для образцового СИ – эталонное.
Инструментальные погрешности делят на основные и дополнительные. Основная погрешность это погрешность СИ в нормальных условиях его применения, а дополнительная - в условиях, отличных от нормальных. Нормальные условия (температура, влажность, частота и напряжение питающей сети, положение прибора и др.) оговариваются в паспорте СИ и в инструкции по эксплуатации. Обычно нормальными считаются: температура (293 5) К; атмосферное давление (100 ± 4) кПа; влажность (65 ± 15) %; напряжение сети питания (220 ± 22)В.
Приборная погрешность зависит от условий и длительности эксплуатации СИ, и ее значение в каждом данном измерении неизвестно, поэтому на практике обычно указывают интервалы (- Qх, +Qх) возможных значений погрешности прибора или полосу погрешностей, которую определяют экспериментально не для данного прибора, а для партии приборов данной серии. Границу Qx полосы погрешностей прибора называют нормированным значением приборной погрешности или пределом допускаемой погрешности данного СИ.
Измерительные приборы делят по точности на классы. Точность СИ - характеристика, отражающая близость его погрешности к нулю. Чем меньше погрешность, тем точнее СИ.
Класс точности - характеристика СИ, выраженная пределами его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности указывается на шкале прибора. Его обозначение зависит от способа нормирования основной допускаемой погрешности прибора и обозначается числом из следующего ряда: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01. Обозначение имеет вид либо числа, заключенного в кружок, либо просто числа, либо двух чисел, разделенных косой чертой. Остановимся на этих случаях
1. Класс точности , указанный в виде числа, заключенного в кружок, обозначает максимальную относительную погрешности результата измерения, выраженную в процентах. Абсолютная погрешность в этом случае
Qх = x/100,
где х - отсчет физической величины по шкале прибора.
2. Если класс точности указан просто числом, то он равен максимальной погрешности прибора (границе погрешности), выраженной в процентах от максимального xmax показания шкалы прибора, по которой производится отсчет. В этом случае
= (Qx/xmax)100 и Qx=xmax/100.
Если прибор имеет нулевую отметку не в начале, а в другой точке шкалы, то предел измерений равен протяженности шкалы. Например, для амперметра со шкалой от
(-30) А до (+60) А, xmax = 60 - (-30) == 90 А. Если нулевая отметка находится на краю шкалам или выходит за ее пределы, то xmax принимается равным верхнему пределу диапазона изменений. Так, если амперметр имеет шкалу от 0 до 60А или от 30А до 60А, то хmax=60А.
3. Если класс точности прибора не указан, то его максимальная погрешность Qх принимается равной половине цены деления шкалы.
Случайная погрешность - это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Она обусловлена влиянием на результаты измерения большого числа изменяющихся случайным образом факторов и проявляется в хаотическом изменении результатов повторных наблюдений. Ее причиной могут служить, в частности физическая и нервная реакция самого экспериментатора (попробуйте в строго определенный момент нажимать кнопку секундомера).
Признак случайной погрешности – она непредсказуемо по знаку изменяется от опыта к опыту в узких пределах численных значений.
Случайную погрешность нельзя исключить из результатов. Однако, пользуясь статистическими методами, можно учесть ее влияние на оценку истинного значения измеряемой величины.
Промах — это вид грубой погрешности, зависящей от наблюдателя и связанный с неправильным обращением со средствами измерений: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора, путаницей номеров образцов и т. п. Промахи обнаруживаются нестатистическими методами и результаты наблюдений, содержащие промахи, как заведомо неправильные, исключив из рассмотрения. Простой, но досаточно грубый метод выявления промахов будет указан ниже.
Все составляющие погрешности, как правило, не зависят друг от друга, что допускает их раздельное рассмотрение.
Отметим, что приведенная классификация определяет составляющие погрешности измерения или составляющие погрешностей отдельных наблюдений. Сами погрешности (являющиеся суммой указанных составляющих) могут быть подставлены в виде абсолютной, относительной или нормированной.
Абсолютная погрешность - это погрешность измерения, выраженная в единицах измеряемой величины. Наряду с абсолютной погрешностью используется термин абсолютное значение погрешности, под которым понимают значение погрешности без учета её знака. Эти два понятия различны.
Относительная погрешность - это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения.
Приведенная погрешность - это погрешность, выраженная отношением погрешности средства измерения (приборной погрешности) к некоторой постоянной величине, называемой нормирующим значением и имеющей размерность измеряемой величины. В качестве нормирующего множителя может выступать, например, максимальное значение шкалы прибора (верхний предел показаний прибора). Понятие приведенной погрешности относится только к средствам измерений.
Относительная и приведенная погрешности являются безразмерными величинами. Одни составляющие погрешности могут быть устранены из результатов измерений, а другие - нет. Все виды неустранимых погрешностей вносят вклад в полную погрешность измерения, и для ее нахождения должны быть просуммированы по определенным правилам.
НЕКОТОРЫЕ ПРЕДСТАВЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ И
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ, ИСПОЛЬЗУЕМЫЕ ПРИ ОБРАБОТКЕ
РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ.
Выполняя измерения, мы всегда имеем дело с погрешностями, являющимися суммой рассмотренных выше составляющих. Среди этих составляющих присутствует случайная составляющая, в силу чего при обработке результатов мы должны пользоваться методами математической статистики.
В основе любых измерений лежат прямые измерения, в ходе которых находят некоторое числовое значение физической величины. Для этого ее измеряют несколько раз. Каждая такая, измерительная операция называется наблюдением, а получаемое при этом значение физической величины - результатом наблюдения.
При наблюдении реализуется некоторое возможное значение физической величины. Все множество возможных значений измеряемой величины, которые она может принимать в эксперименте, называется генеральной совокупностью. Это множество может быть как конечным, так и бесконечным. Большинство физических величин имеет непрерывный набор возможных значений, множество которых является бесконечным. Говорят, что такие величины имеют генеральную совокупность бесконечного объема.
Генеральная совокупность несет полную информацию об измеряемой величине и позволяет (в отсутствие не выявленных систематических погрешностей), несмотря на случайный характер результатов отдельных наблюдений, найти истинное значение х0 физической величины. В случае физической величины с непрерывным набором значений для нахождения ее истинного значения необходимо провести бесконечное число наблюдений, что невозможно. Поэтому на практике ограничиваются конечным числом наблюдений (от единиц до нескольких сотен, в нашей учебной физической лаборатории - обычно от 3 до 10). Полученный при этом ряд значений физической величины: х1, х2,...., хN называют выборкой из генеральной совокупности или просто выборкой. Число N результатов наблюдений в выборке называют объемом выборки.
Ввиду ограниченного числа наблюдений в выборке по ней нельзя найти ни истинное значение измеряемой величины, ни погрешность измерения, и задача сводится к нахождению по выборке наилучших выборочных оценок (наилучших приближенных значений) истинного значения и погрешности измерения.
Сравнивая значения, полученные в конкретной выборке, легко заметить некоторое рассеяние.
ПРИМЕР. Будем рассматривать все расчеты и рассуждения применительно к конкретному примеру.
Задача – измерение ускорения свободного падения g путем измерения продолжительности свободного падения тела с высоты h.
Без учета сопротивления воздуха
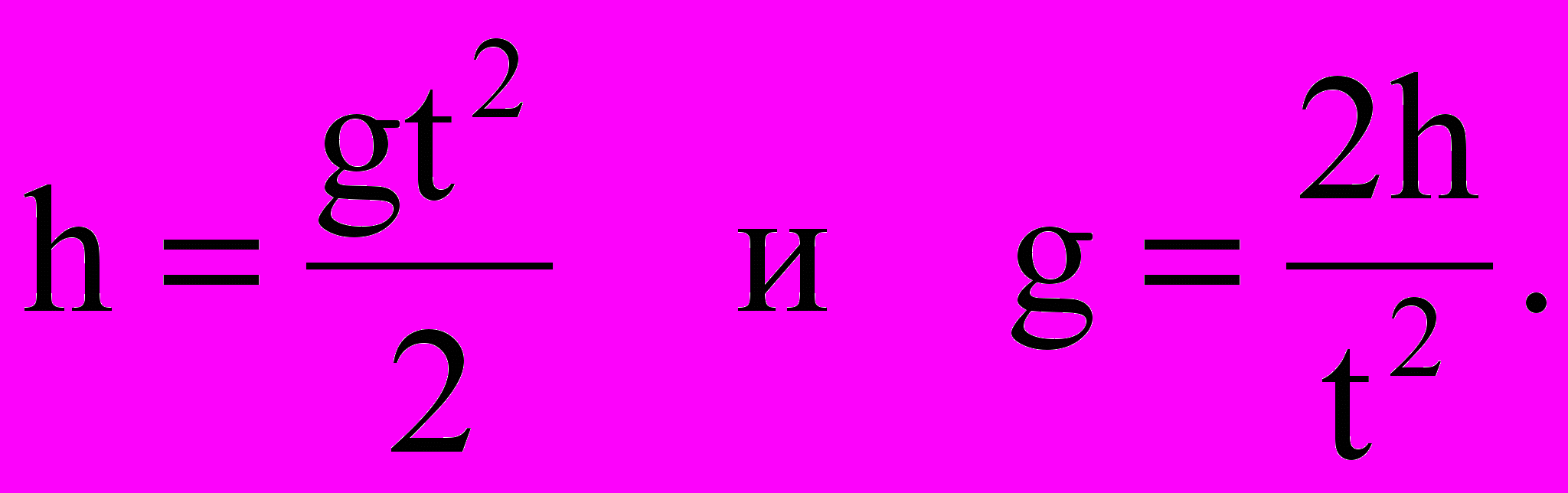
Измерения высоты производится линейкой с ценой деления с=1 см, а время измеряется секундомером с погрешностью 0,01 секунды.
Прямыми измерениями получена серия данных:
| h, м | 0,70 | 0,70 | 0,70 | 0,70 | 0,70 |
| t, c | 0,34 | 0,36 | 0,40 | 0,38 | 0,37 |
Видно, что появление того или иного значения – случайное явление в некотором диапазоне значений, группирующихся около среднеарифметического значения выборки (в нашем случае
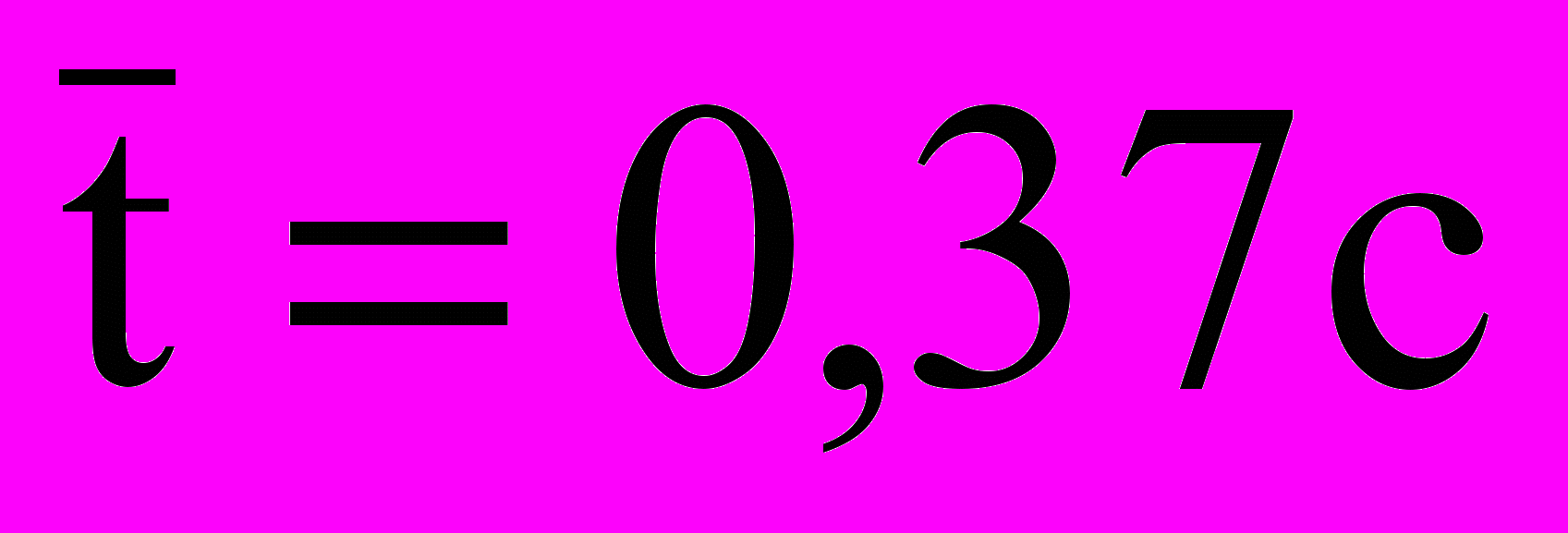 ).
).Известны различные математические законы распределения случайных величин. Наиболее широко распространены нормальный (гауссов) закон и закон равномерного распределения. Ограничимся лишь кратким рассмотрением нормального закона (более подробно вопрос можно изучить с помощью методических указаний авторов Петрунин В.А., Громов В.Е., Березовский В.Н., Мальцев В.Д. «Обработка наблюдений и представление результатов эксперимента», Новокузнецк, СибГИУ,1999, 45 с. или с помощью указанной там литературы). Отметим, что значительная часть приведенной в этой лекции теории заимствована из этих методуказаний.
В соответствии с теорией, при нормальном законе распределения средних значений выборки (и абсолютных погрешностей измерения) сама величина среднеарифметического значения
 при N,
при N, где
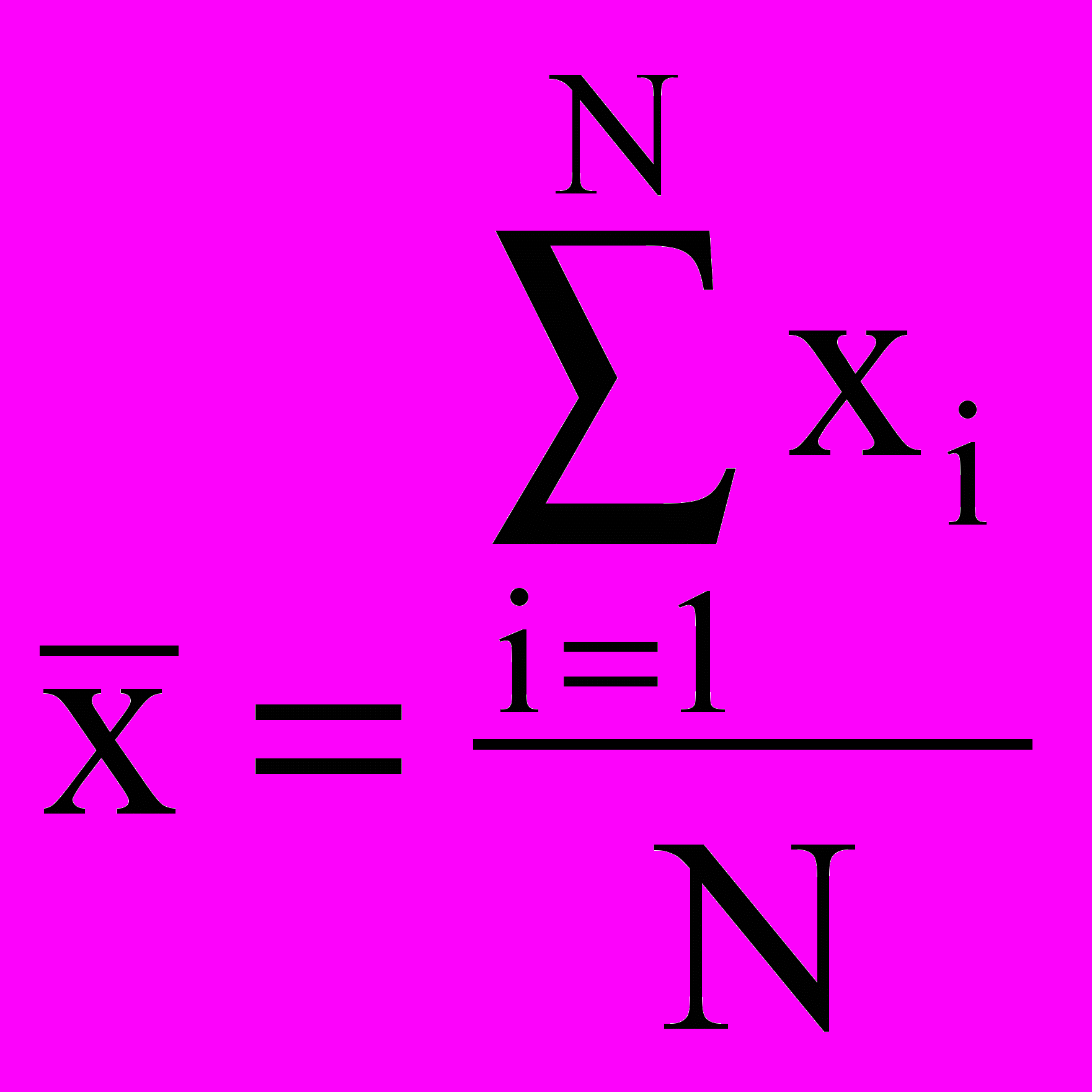 , (1.1)
, (1.1)х0 – истинное значение величины, а N – число произведенных измерений. Из-за ограниченного числа измерений рассчитанная величина
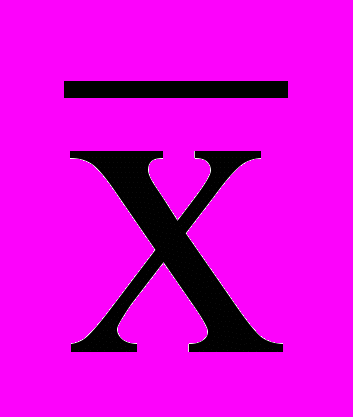 отличается от х0 в принципе тем больше, чем меньшее число измерений произведено.
отличается от х0 в принципе тем больше, чем меньшее число измерений произведено. Корректное представление результата измерений требует указания границ интервала, в которых, скорее всего, будут лежать результаты измерений другого исследователя, если он будет измерять эту же величину этим же методом. Принято вычислять границы доверительного интервала х с указанием вероятности Р попадания в него результата измерения.
Результат записывают обычно в виде хх0=
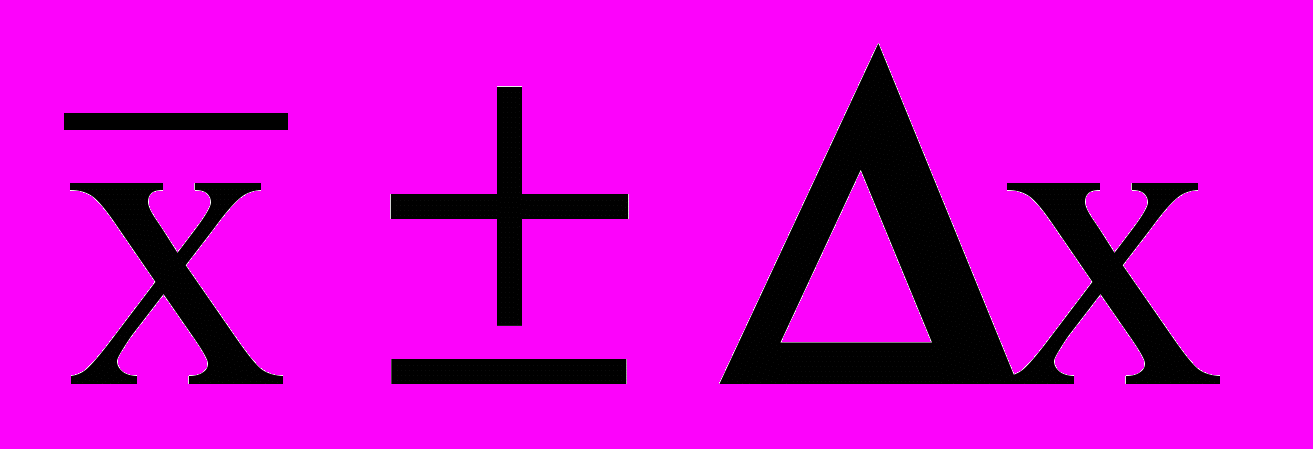 с вероятностью Р.
с вероятностью Р.Доля случайной погрешности в результатах измерений определяется с помощью выражения
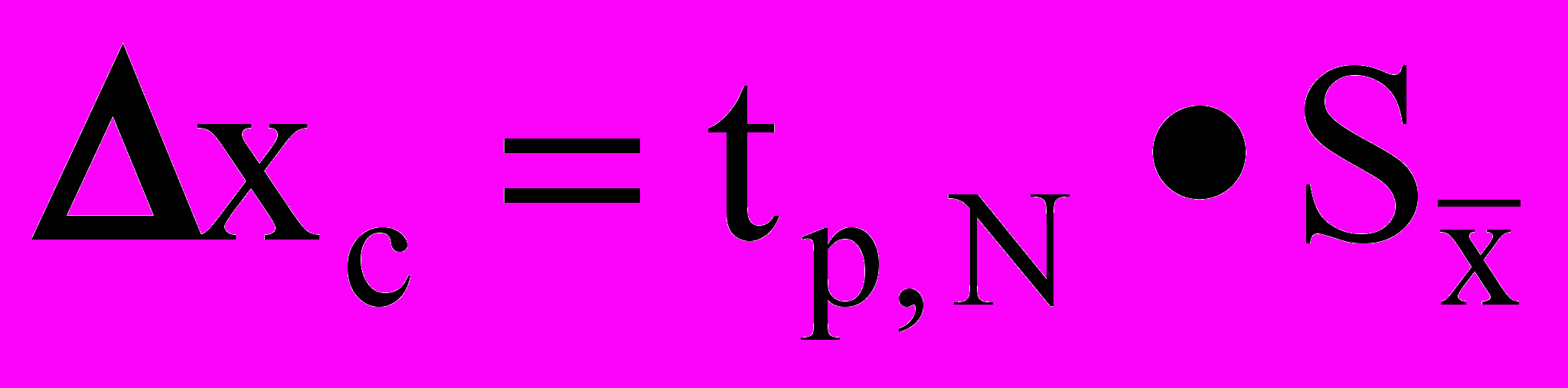 , (1.2)
, (1.2) где tp,N – коэффициенты распределения Стьюдента, определяемые из таблицы для числа опытов N при заданной вероятности р. Часто выбирают «стандартную» вероятность 0,7 и тогда ее не указывают. В студенческой практике широко применяется вероятность 0,95.

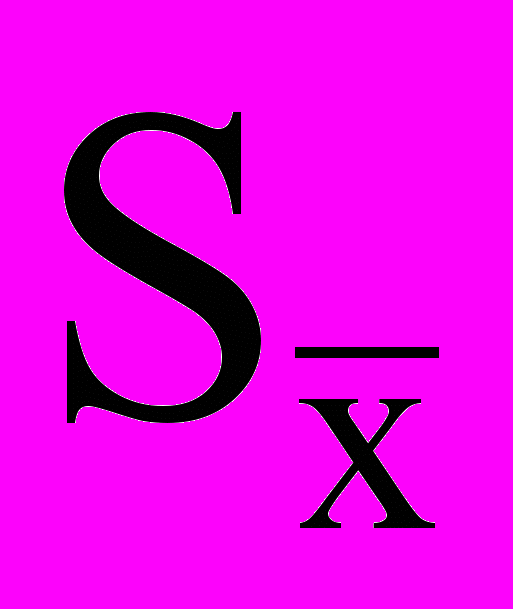 - среднее квадратичное отклонение среднего
- среднее квадратичное отклонение среднего 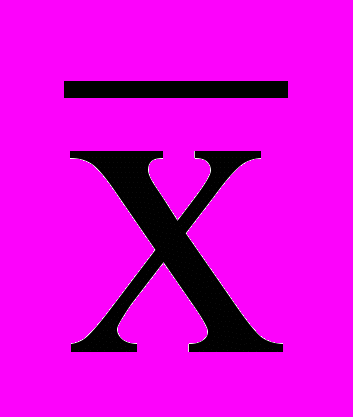 , вычисляемое по формуле
, вычисляемое по формуле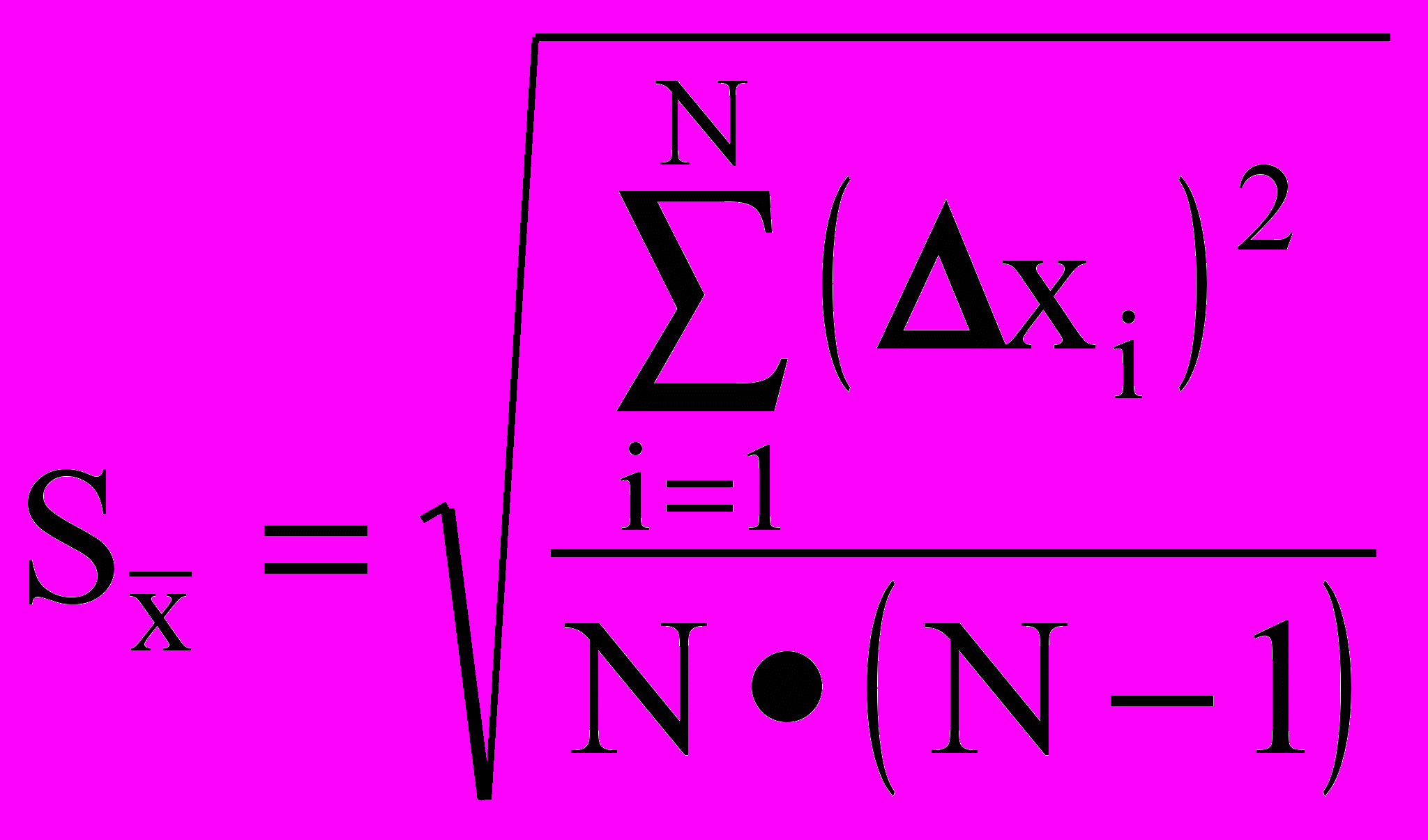 , (1.3)
, (1.3)xi – абсолютная погрешность i-ого измерения.
Величину
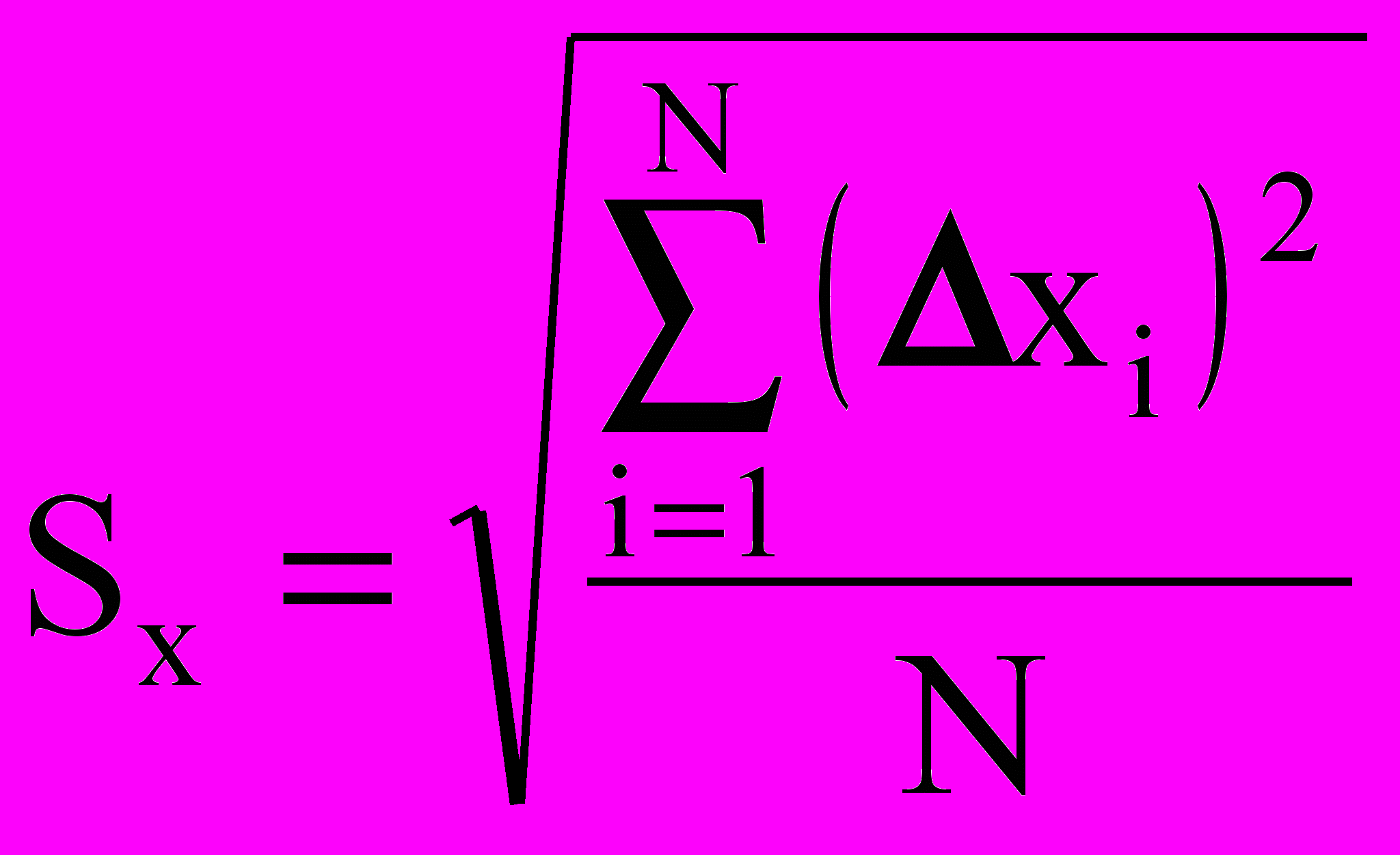 (1.4)
(1.4)называют среднеквадратичным отклонением результата наблюдений от среднего значения, она близка по смыслу к математическому понятию дисперсия распределения и может применяться для приближенного выявления промахов.
А именно: если разность
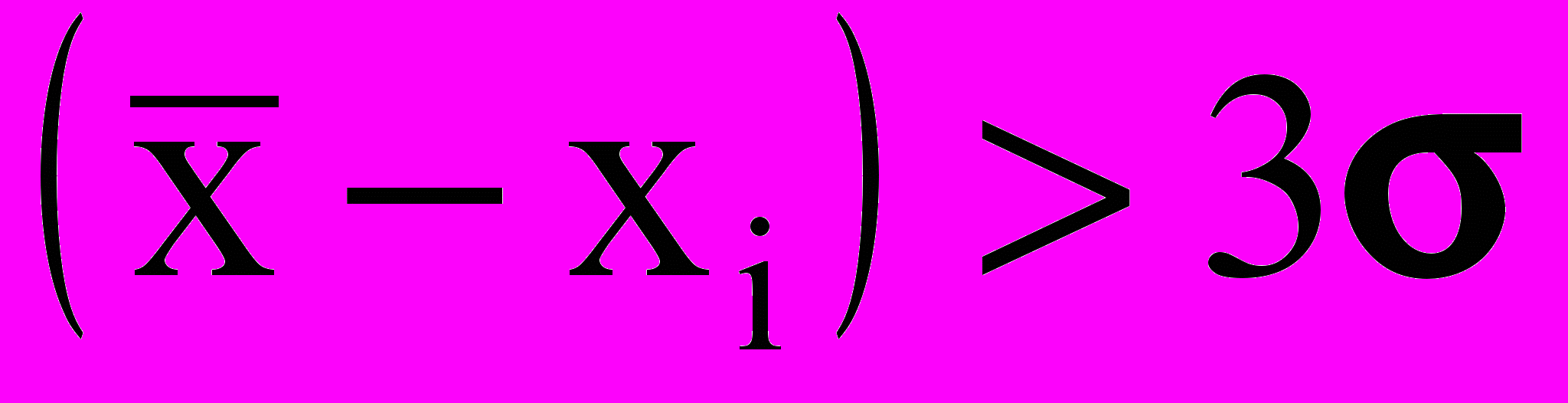 для некоторого i-того измерения, то этот результат следует признать промахом.
для некоторого i-того измерения, то этот результат следует признать промахом.Долю приборной (систематической) погрешности определяют из соотношения
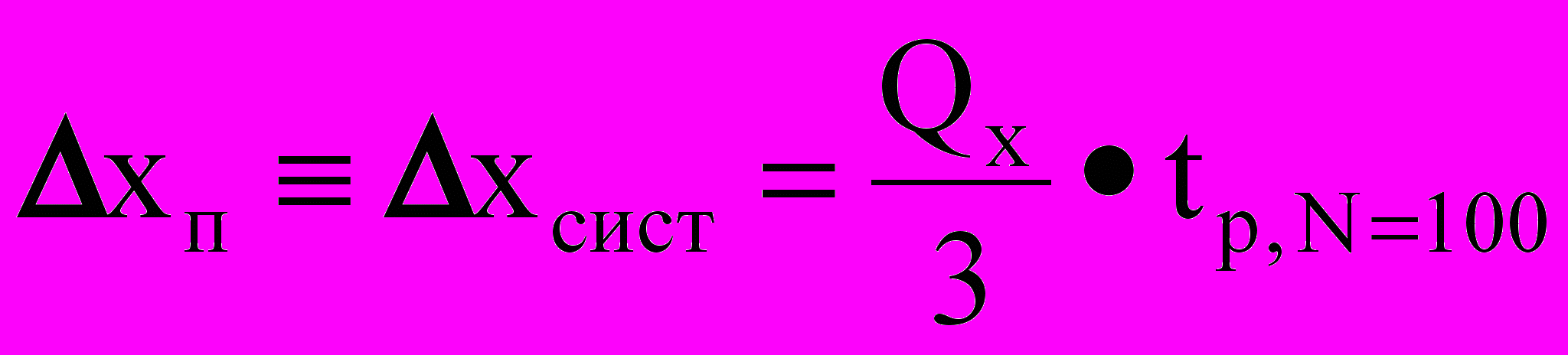 . (1.5)
. (1.5)Окончательно границы доверительного интервала серии прямых измерений определяют из соотношения
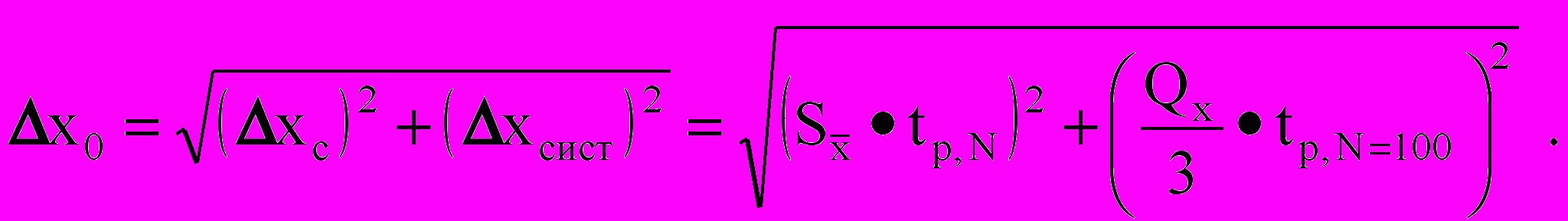 (1.6)
(1.6)При использовании табличных результатов, результатов, полученных другими авторами, а также трансцендентных чисел (, е – основание натурального логарифма и т.п.) необходимо учитывать ошибки, вносимые округлениями и отбросом части чисел. Например, если указано значение плотности вещества 2700 кг/м3, то погрешность составляет половину следующего (за последним указанным) порядка, т.е. 0,5 кг/м3.
Все вышеизложенное предопределяет некоторый обязательный набор вычислительных операций при анализе результатов физических измерений, характеризующийся отличиями при обработке результатов прямых и косвенных измерений.
ПОРЯДОК ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Предполагается измерение некоторой физической величины по формуле. Часть физических величин, входящих в расчетную формулу, измеряется непосредственно. Часть физических величин измерена другими экспериментаторами. Предполагаются также нормальные исходные распределения.
Необходимые операции:
1. Исключение известных систематических погрешностей из результатов наблюдений для всех измеряемых величин.
2. Вычисление средних арифметических по исправленным результатам наблюдений. Среднее арифметическое принимается за результат измерения.
3. Вычисление среднего квадратичного отклонения результата наблюдений для всех измеряемых величин.
4. Вычисление доверительных границ случайных погрешностей.
5. Вычисление границ неисключенных систематических погрешностей.
6. Вычисление границ погрешностей для величин входящих в расчётные формулы, но измеренных другими экспериментаторами.
7. Вычисление доверительных границ общих погрешностей.
8. Вычисление среднего значения косвенно измеренной величины.
9. Вычисление доверительной погрешности косвенно измеренной величины.
ПОРЯДОК РАСЧЁТА РЕЗУЛЬТАТОВ ПРЯМОГО ИЗМЕРЕНИЯ
Как видно из предыдущего пункта, этот этап обязательно присутствует в любых измерениях.
Результатами измерения являются среднее значение и доверительный интервал. Результаты наблюдений удобно представлять в форме таблицы. N - объём выборки (число измерений). Предполагается нормальное распределение наблюдений.
1. Вычисление среднего для измеряемой величины Х
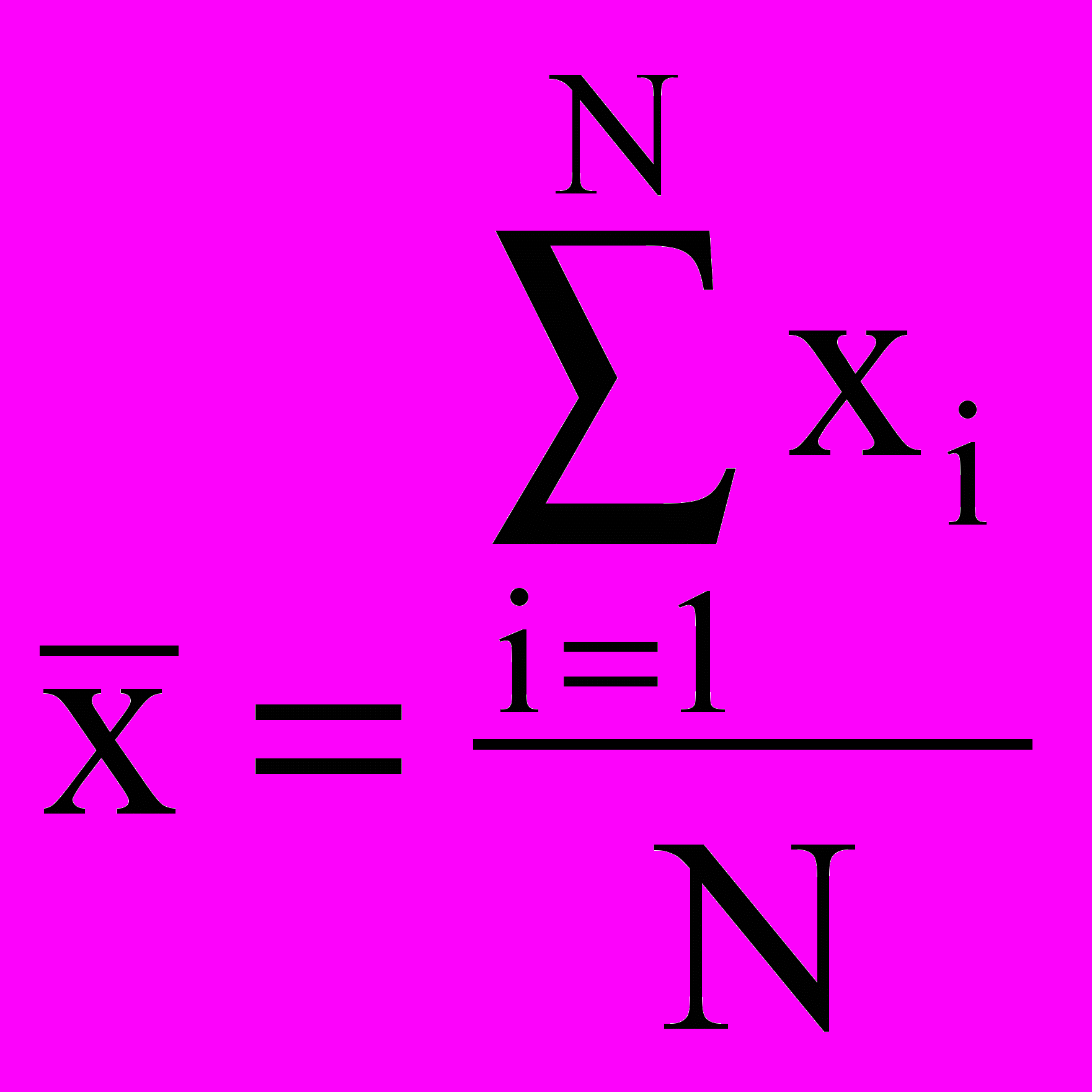 .
.2. Вычисление погрешностей всех N наблюдений
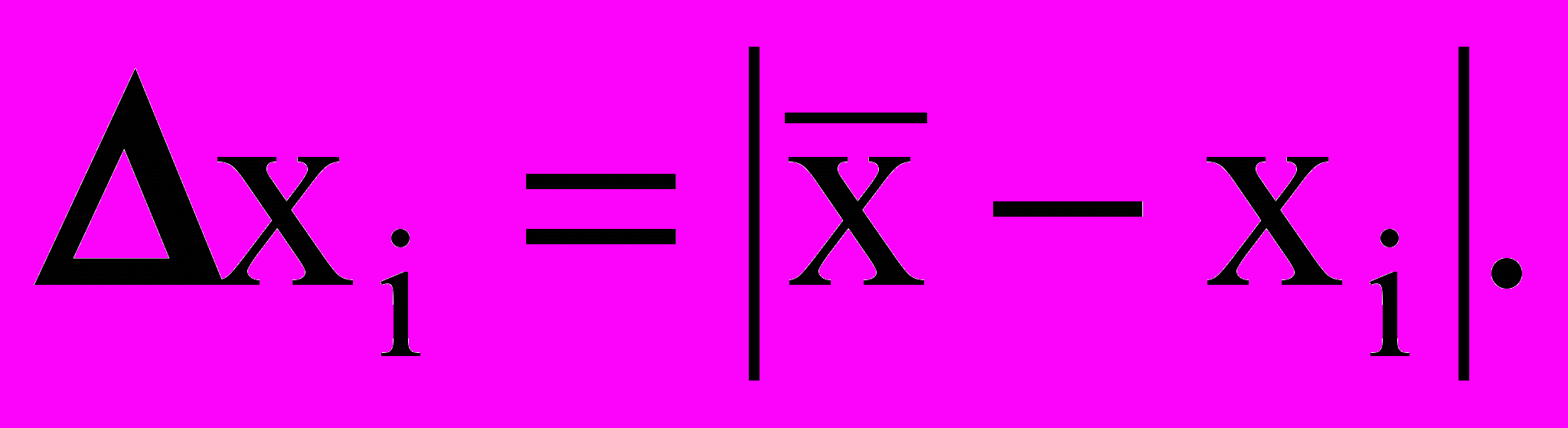
3. Вычисление квадратов погрешностей всех N измерений
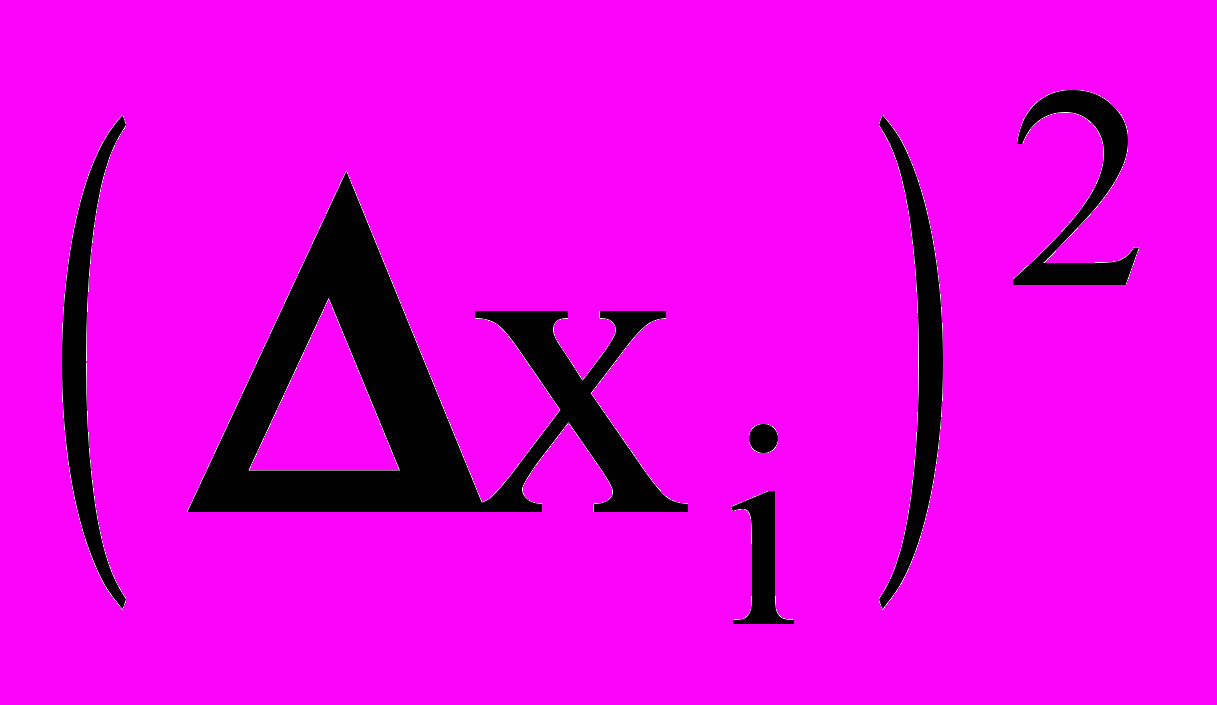 .
.4. Вычисление среднего квадратичного отклонения выборки
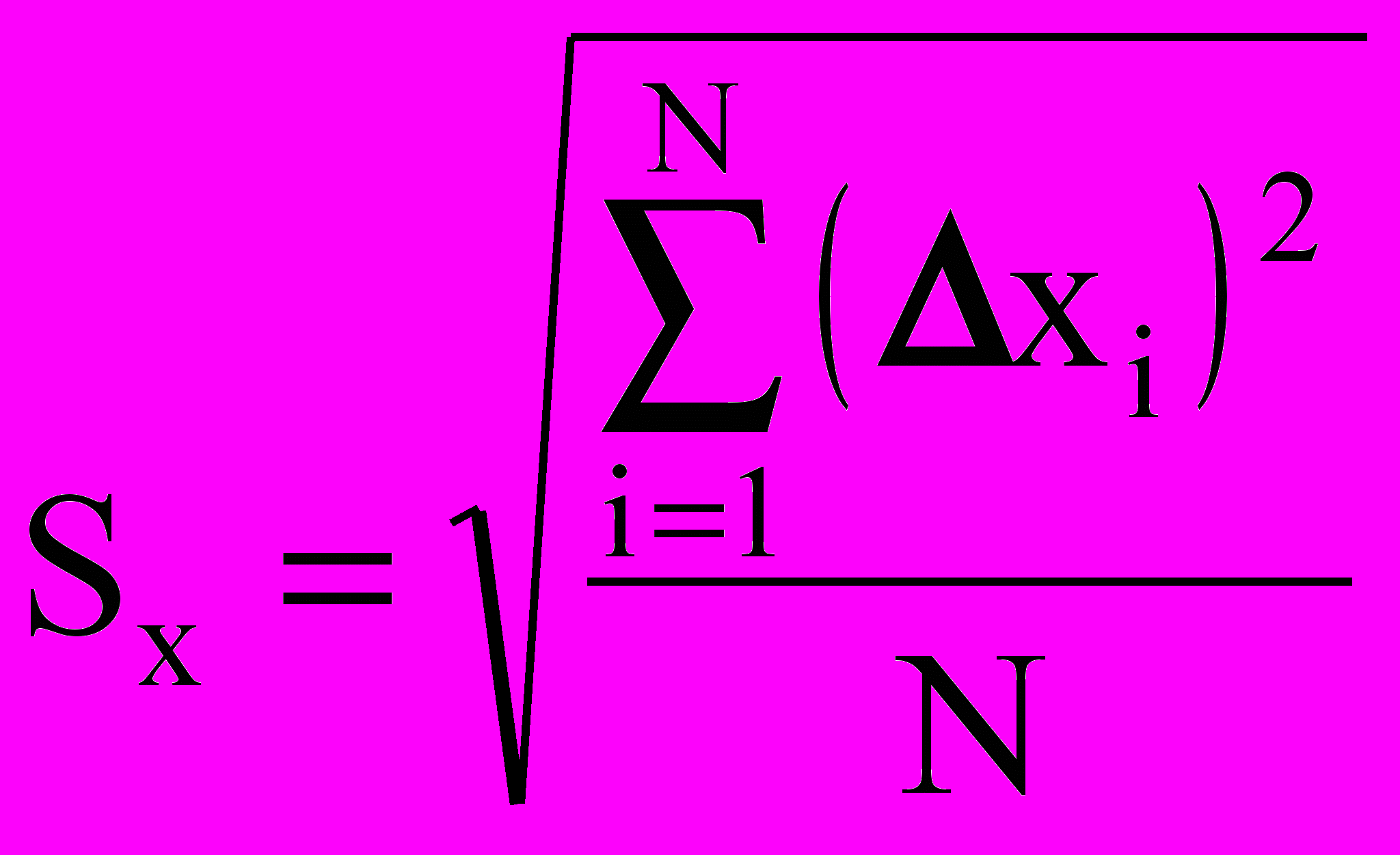 .
.5. Проверка экстремальных наблюдений критериями промахов «3». Исключение промахов.
6. Повторение операций 1 - 4 с укороченной выборкой.
7. Вычисление среднего квадратичного отклонения среднего
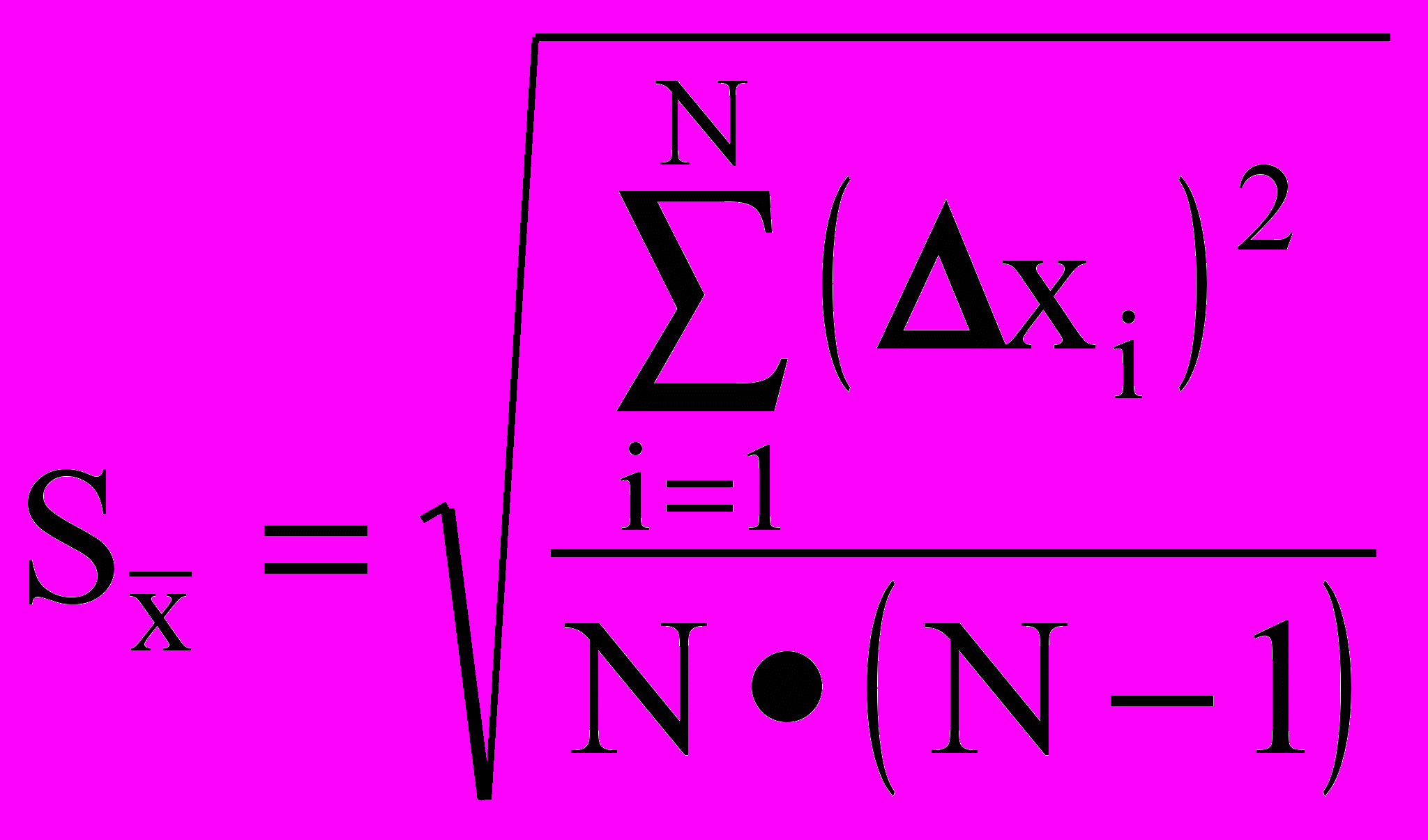 .
.8. Вычисление предельной приборной погрешности Qх по классу точности или цене деления прибора.
9. Определение коэффициентов Стьюдента tP,N и tP,N=100 по соответствующей таблице приложения для доверительной вероятности р=0,95.
10. Вычисление общей доверительной погрешности результата измерения
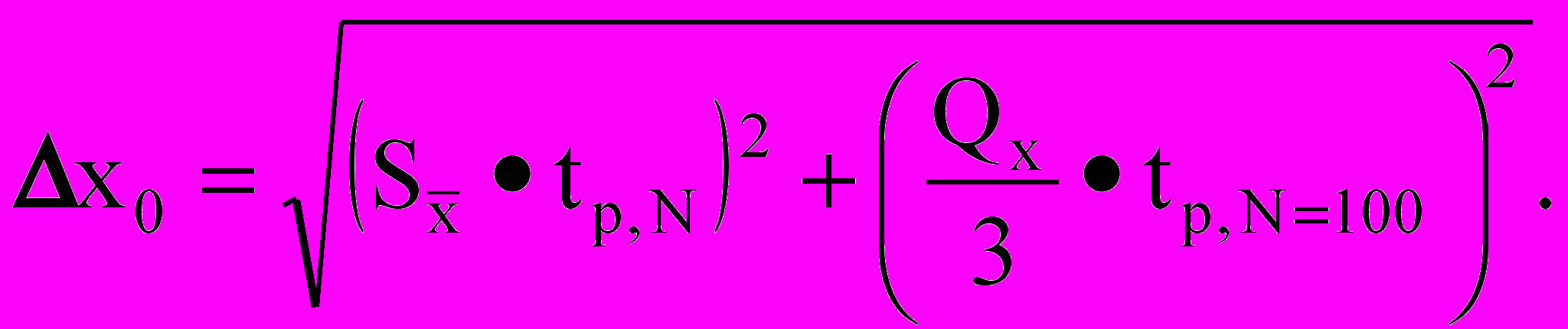
11. Представление результата измерения в форме
х =
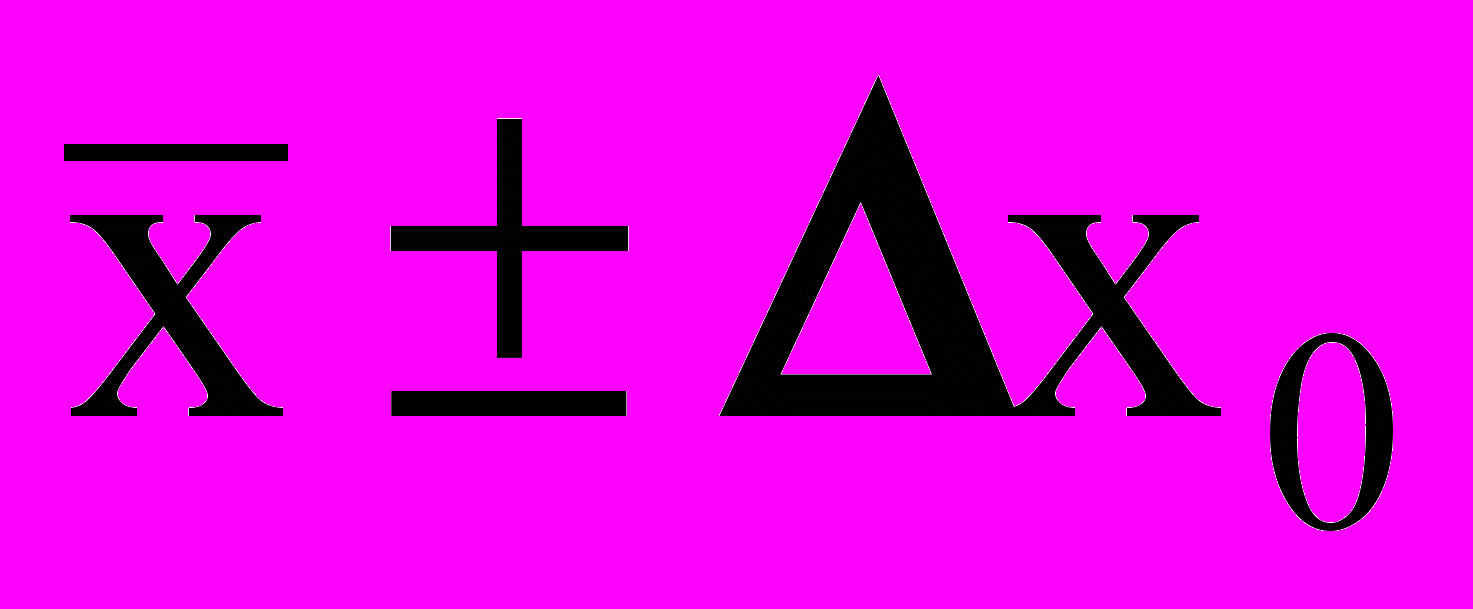 .
.12. Оценка относительной погрешности результата измерения
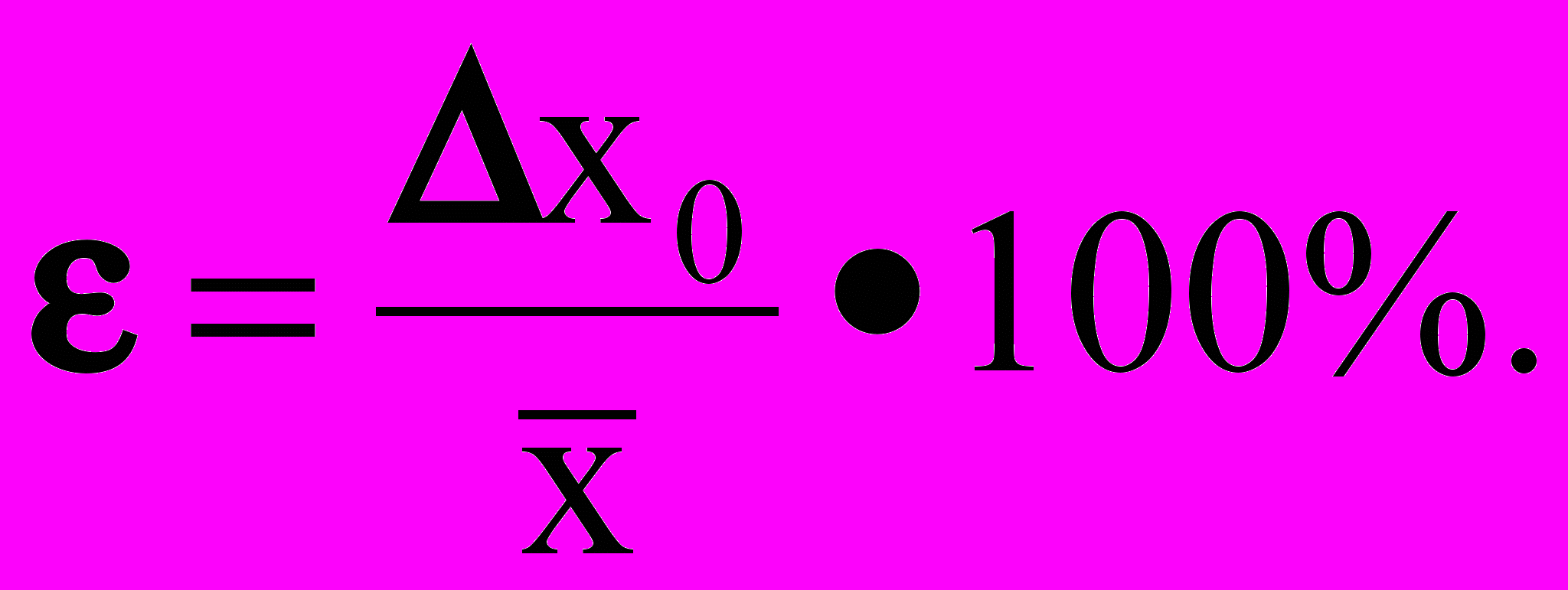
ПОРЯДОК РАСЧЕТА РЕЗУЛЬТАТА КОСВЕННОГО ИЗМЕРЕНИЯ
Используются 2 способа обработки результатов косвенного измерения: метод перенесенной погрешности и выборочный метод, дающие близкие результаты.
МЕТОД ПЕРЕНОСА ПОГРЕШНОСТЕЙ
Этот метод применяется в том случае, когда измеренные прямо значения величин х, у, z..., которые будем называть аргументами функции Ф, образуют выборки.
Отклонения результатов отдельных наблюдений хi, yi, zi, ... от соответствующих истинных значений х0, у0, z0 включают в себя как случайные, так и систематические составляющие. Благодаря этому измеренные значения
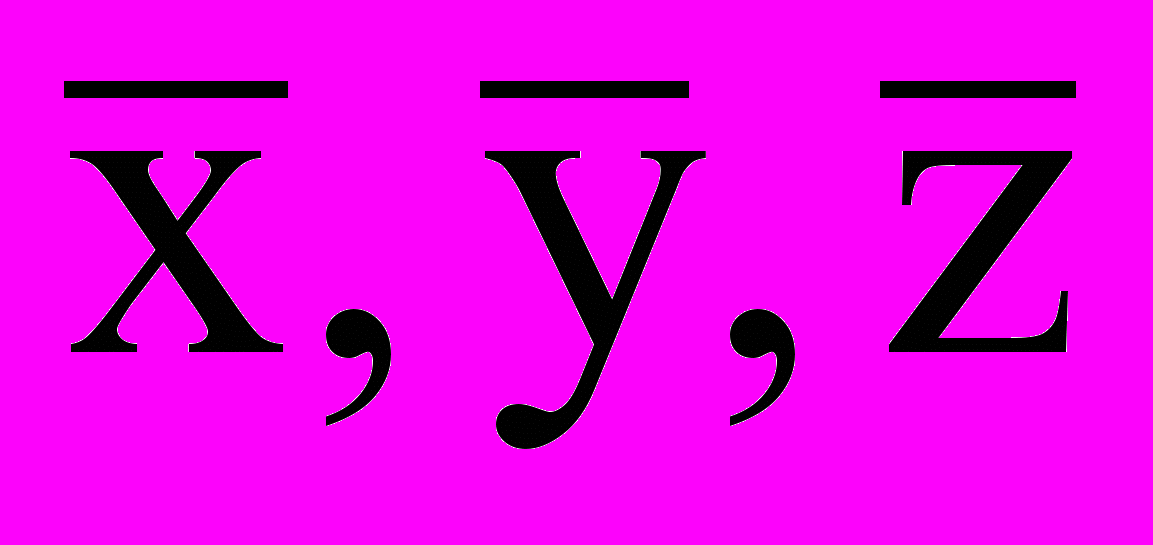 аргументов обладают как случайными x,y,z…, так и систематическими при6орными Qx,Qy,Qz … погрешностями, а погрешность функции Ф также состоит из двух компонент: случайной Ф и систематической QФ. Величина Ф определяется случайными погрешностями аргументов, а QФ - систематическими приборными.
аргументов обладают как случайными x,y,z…, так и систематическими при6орными Qx,Qy,Qz … погрешностями, а погрешность функции Ф также состоит из двух компонент: случайной Ф и систематической QФ. Величина Ф определяется случайными погрешностями аргументов, а QФ - систематическими приборными. Рассмотрим принципы расчета.
Систематические приборные погрешности аргументов мы считаем постоянными. В этом случае все результаты наблюдений каждого аргумента, а также его среднее значение смещены относительно его истинного значения на одну и туже величину, равную систематической погрешности. Взаимное же расположение результатов наблюдений друг относительно друга, а также относительно среднего значения, остается таким же, как и в отсутствие приборной погрешности. Например, все хi, и
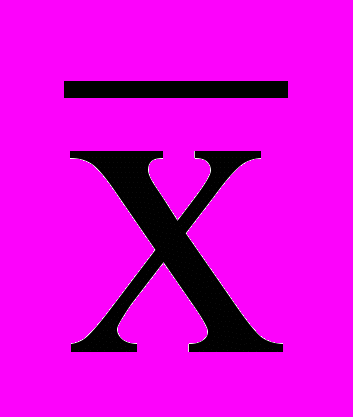 сдвинуты относительно x0 на одну и туже величину Qx, все yi и
сдвинуты относительно x0 на одну и туже величину Qx, все yi и 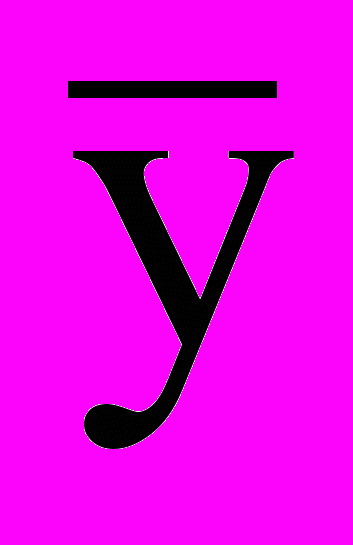 - на величину Qy и т. д. В такой ситуации случайные и приборные погрешности каждого аргумента оказываются независимыми и могут рассматриваться отдельно.
- на величину Qy и т. д. В такой ситуации случайные и приборные погрешности каждого аргумента оказываются независимыми и могут рассматриваться отдельно.Пусть измеряемая величина определяется по расчетной формуле
y=y(x1,x2,…,xm),
где x1,x2,…,xm – аргументы.
j – номер аргумента, m – число аргументов, измеренных с погрешностью (включая округленные иррациональные числа).
Расчетные операции:
- Производится расчет средних
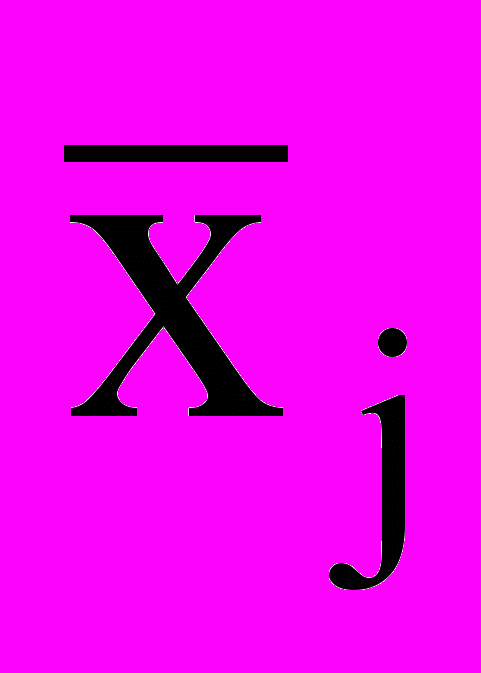 и доверительных интервалов для всех m аргументов.
и доверительных интервалов для всех m аргументов.
- Расчет среднего значения у при средних значениях всех аргументов
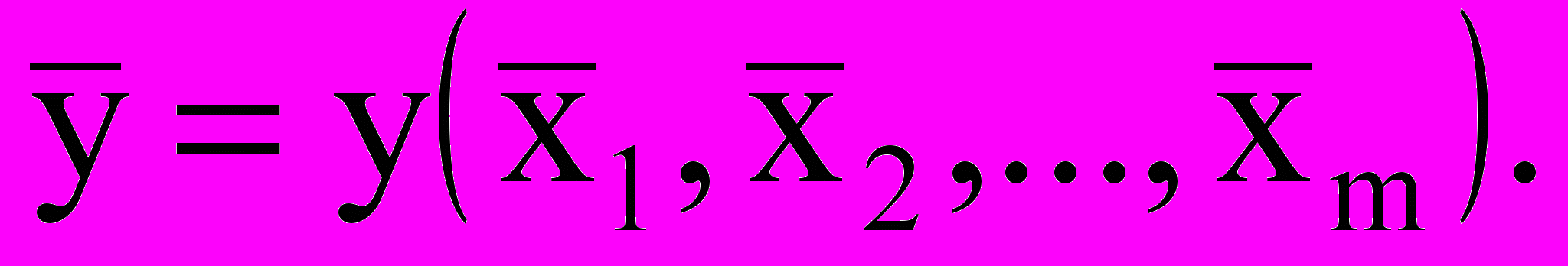
- Вывод формулы для абсолютной погрешности по алгоритму
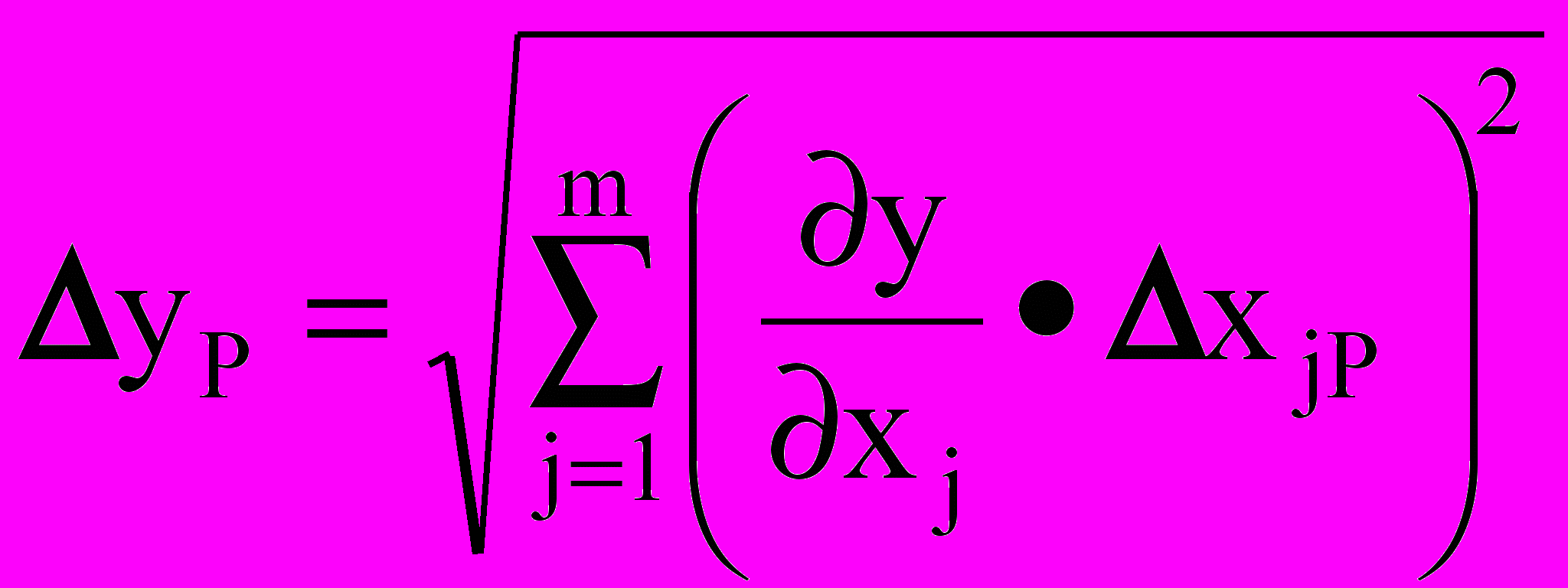
или для относительной погрешности по алгоритму
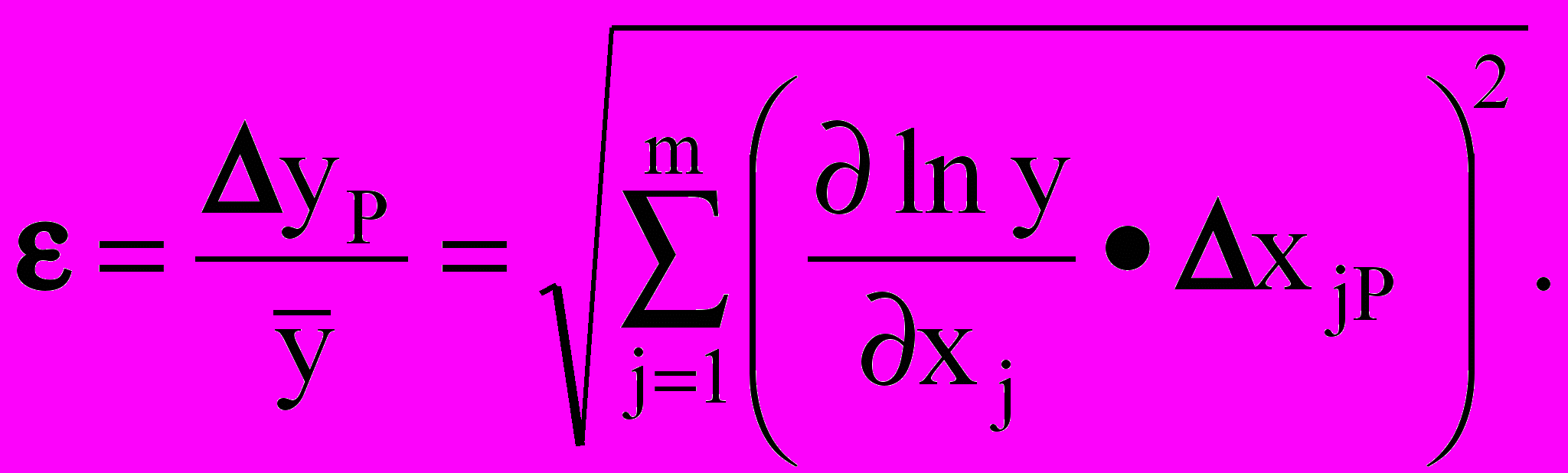
Отметим:
а) Берутся частные производные по всем параметрам.
б) по относительной погрешности можно вычислить абсолютную погрешность
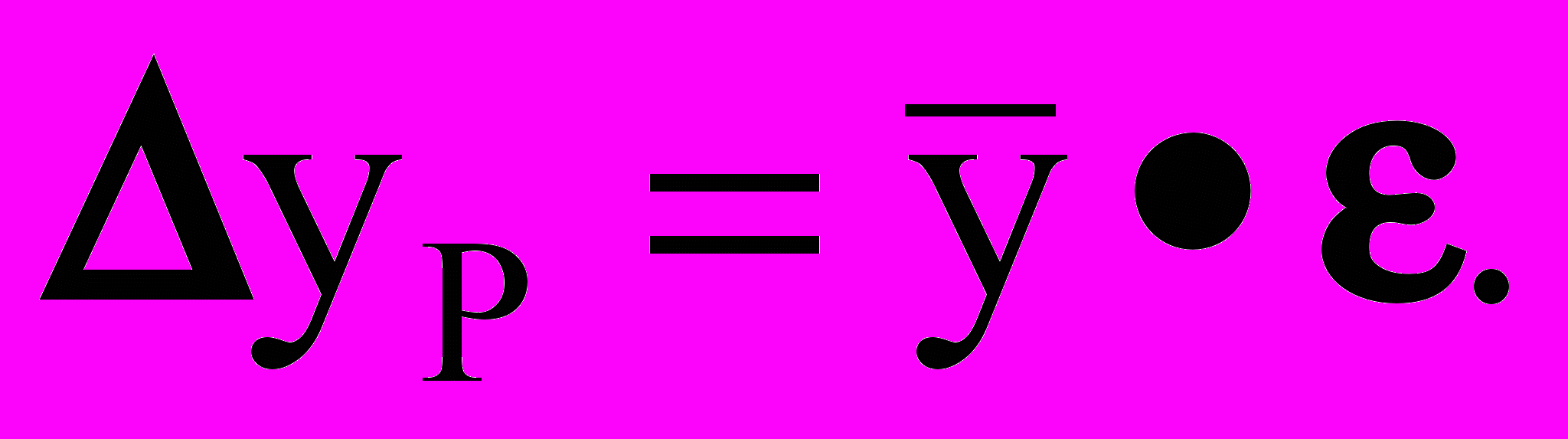
- Вычисление абсолютной погрешности по одной из полученных формул путем подстановки средних значений аргументов.
- Представление результата измерения в форме
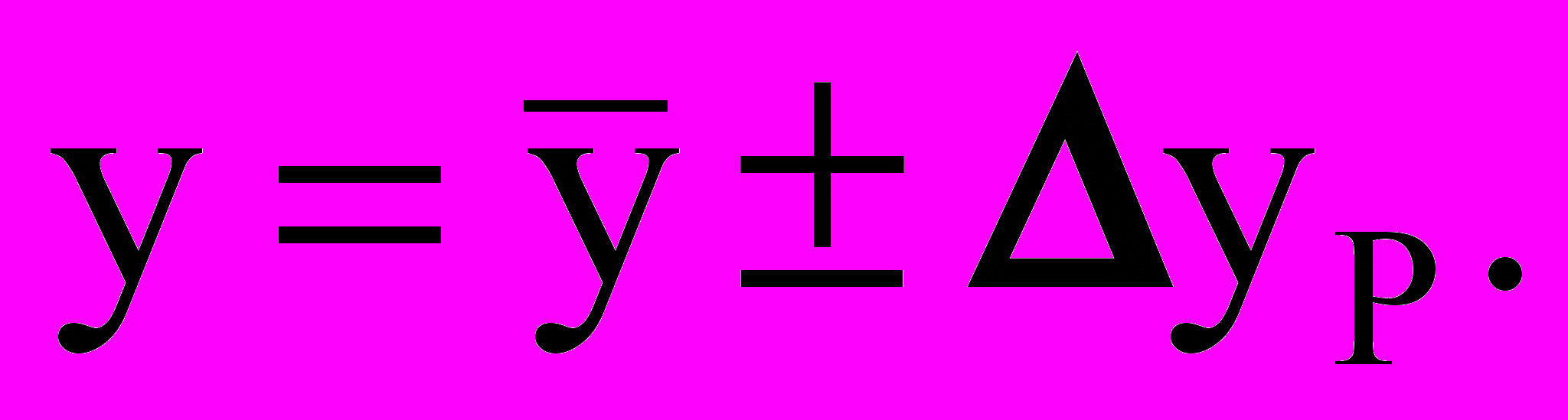
- Оценка относительной погрешности
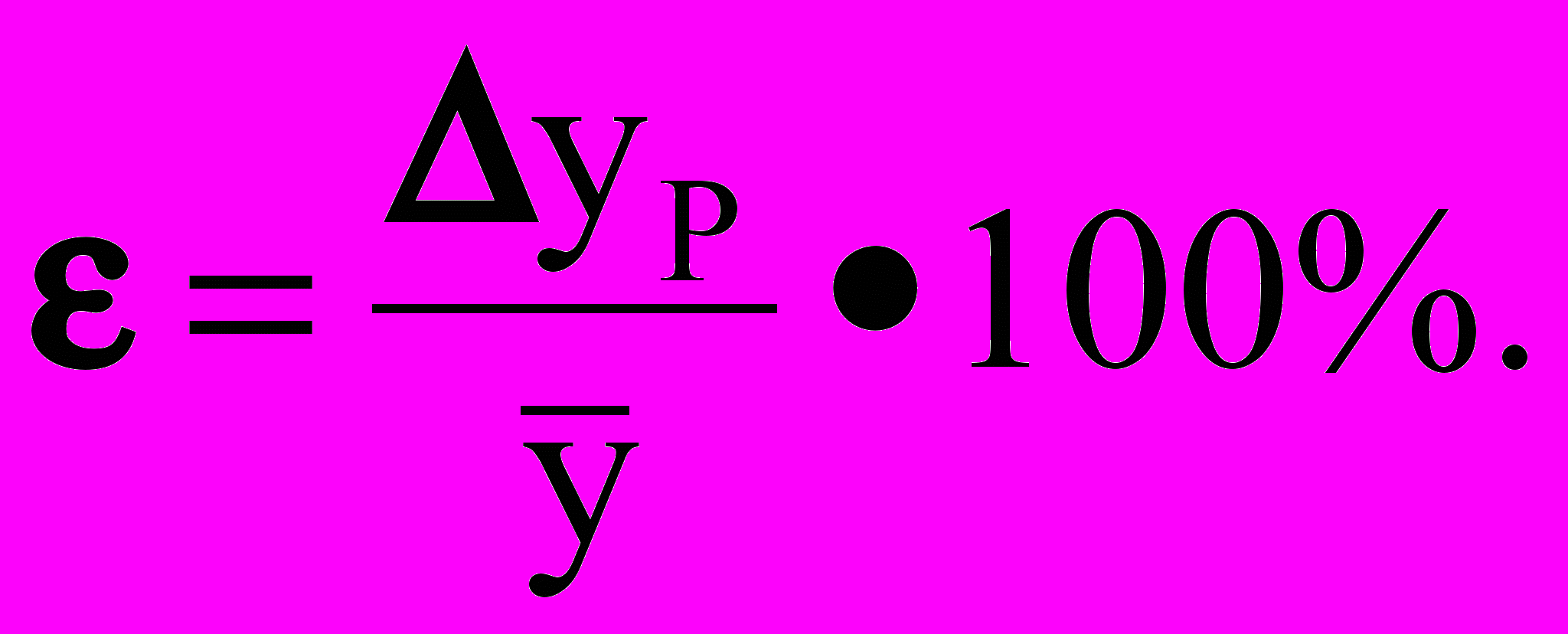
ВЫБОРОЧНЫЙ МЕТОД
Пусть Ф=Ф(х, у, z...) и для х, у, z... имеются выборки по N членов. Тогда можно получить выборку Ф
Фi==Ф(хi, уi, zi, …)
и поступить с ней как с результатами прямых измерений.
Вычислить среднее значение
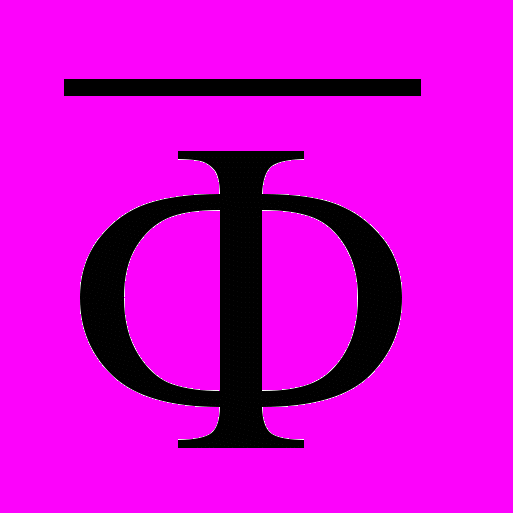
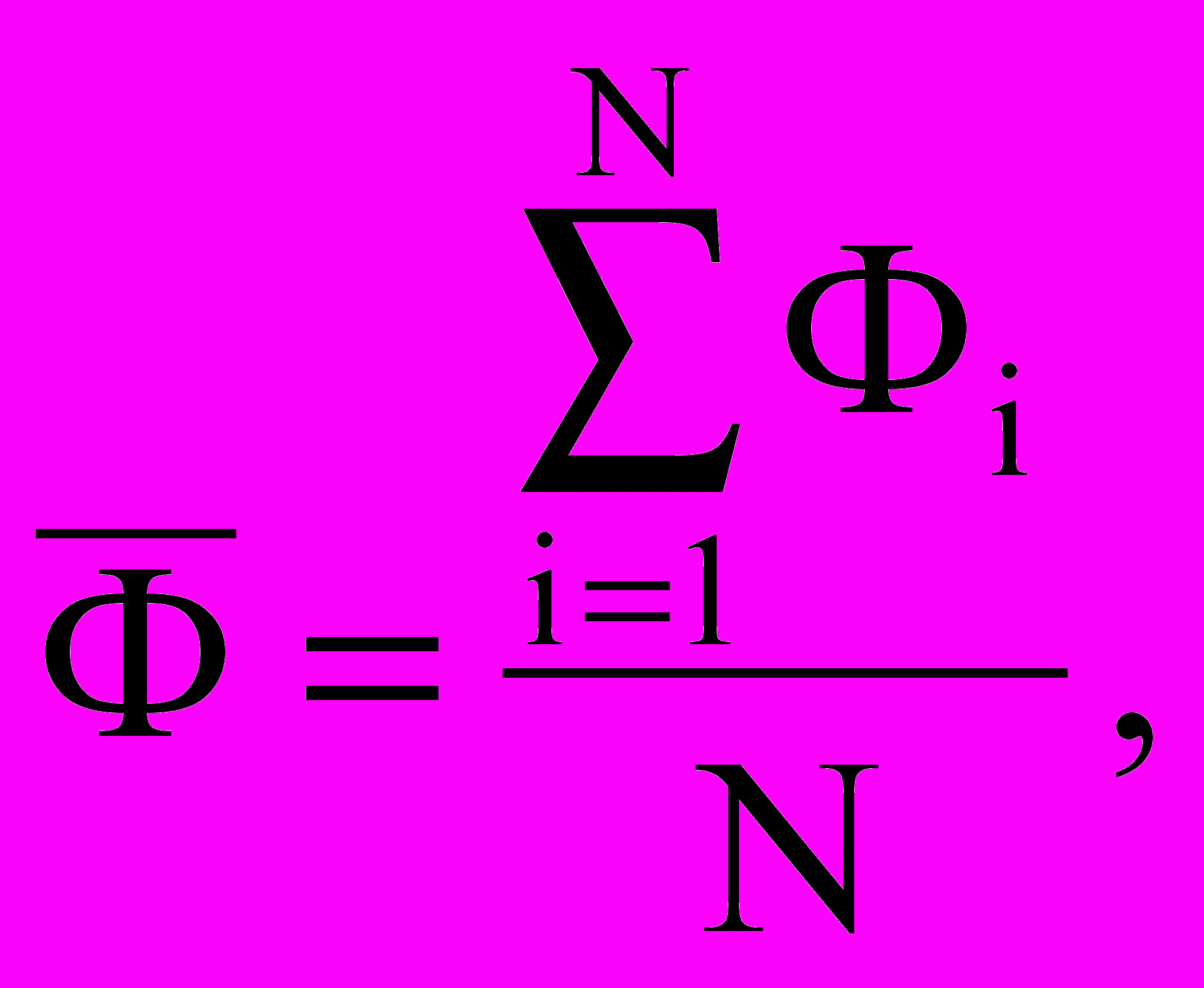
и среднеквадратичное отклонение среднего
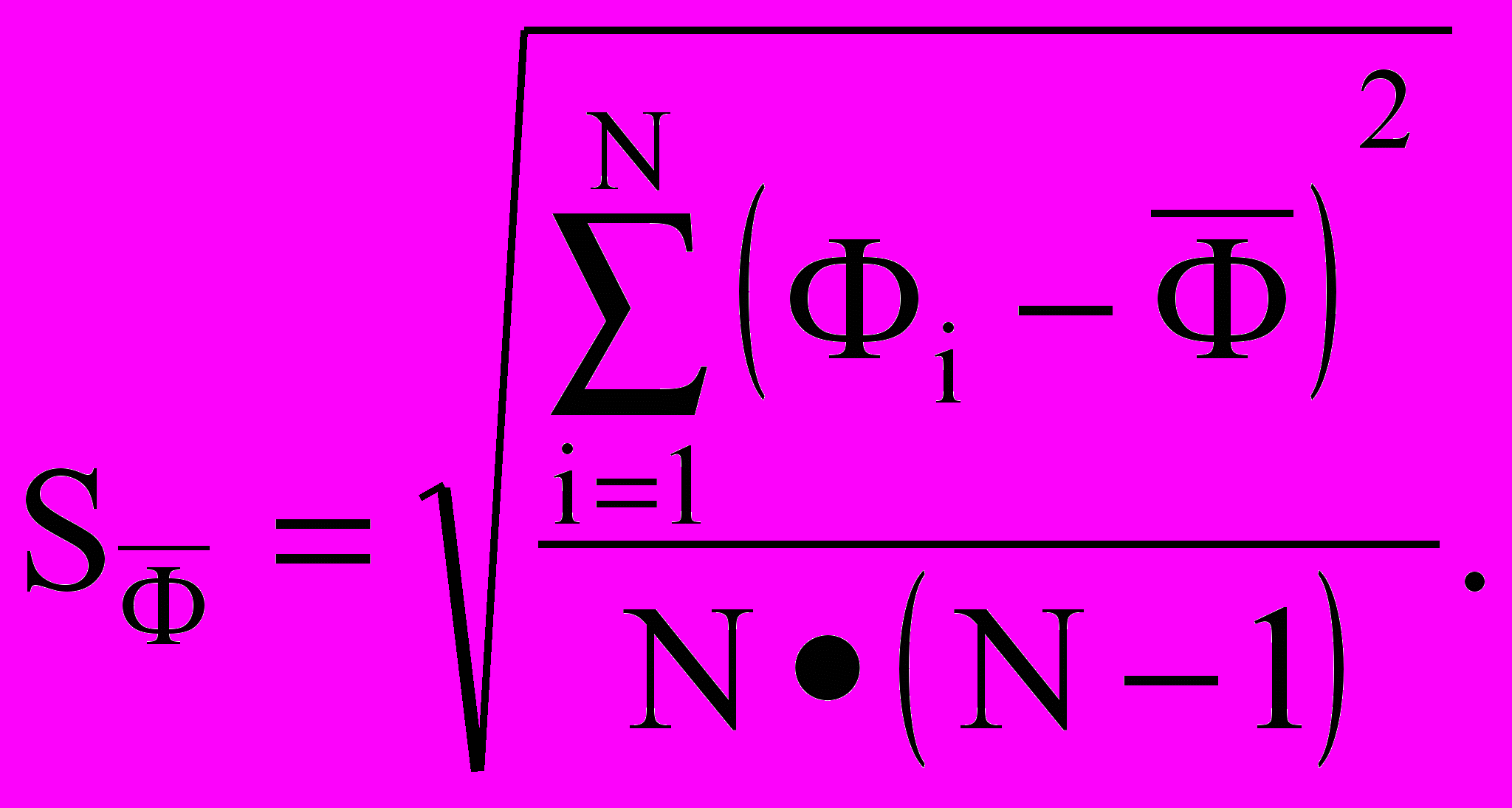
Для заданных Р и N взять из таблицы коэффициент Стьюдента tP,N, вычислить доверительную погрешность (предполагается нормальное распределение).
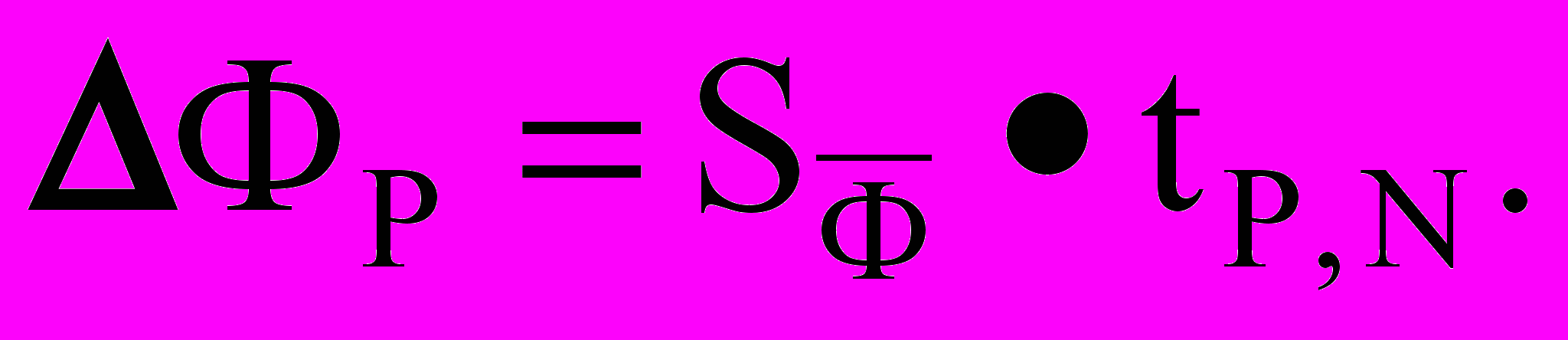
Записать результат в виде
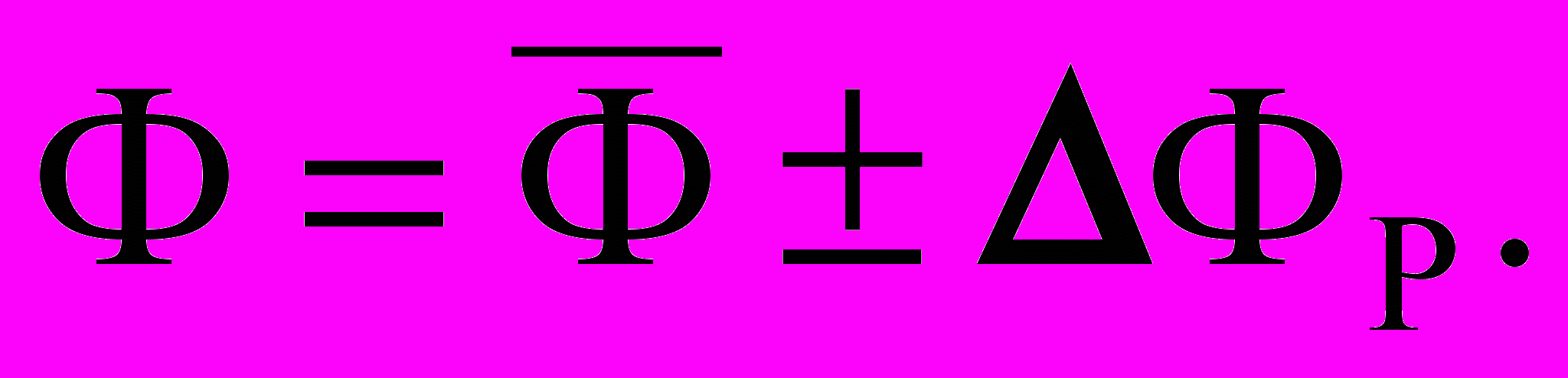
Вычислить относительную погрешность
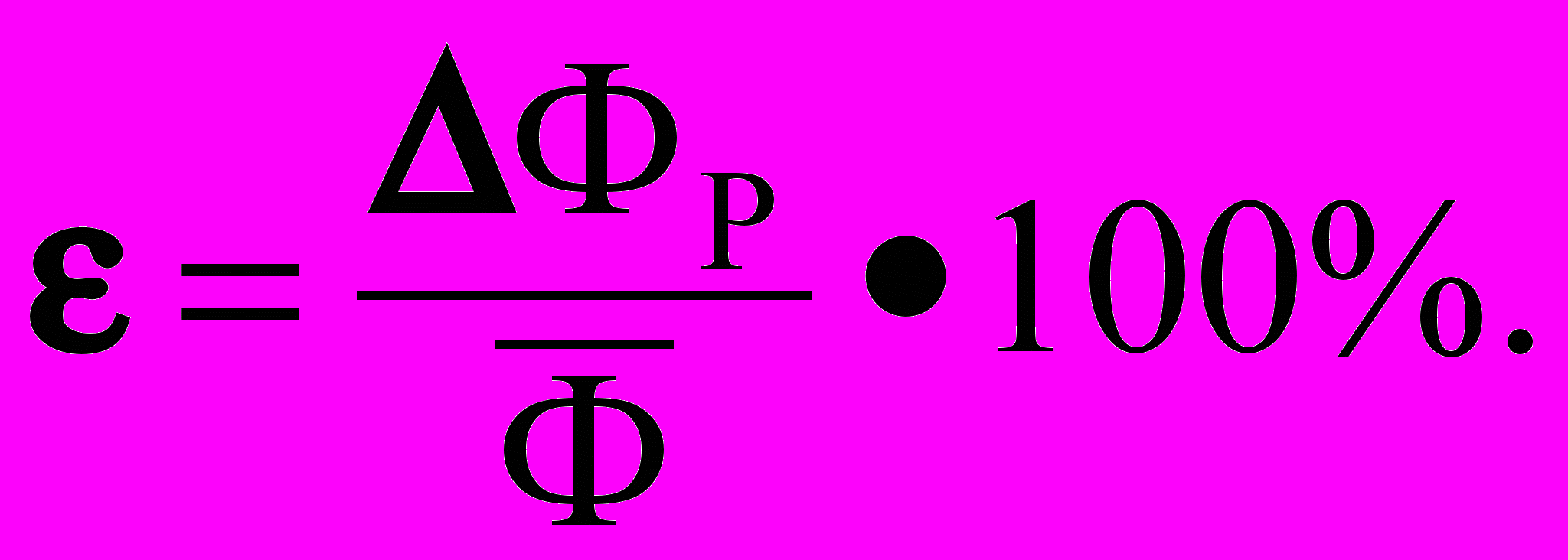
ПРИМЕР ОБРАБОТКИ ДАННЫХ
ПРИ КОСВЕННОМ ИЗМЕРЕНИИ
Вернемся к рассмотрению выбранного нами примера.
ПРИМЕР. Будем рассматривать все расчеты и рассуждения применительно к конкретному примеру.
Задача – измерение ускорения свободного падения g путем измерения продолжительности свободного падения тела с высоты h.
Без учета сопротивления воздуха
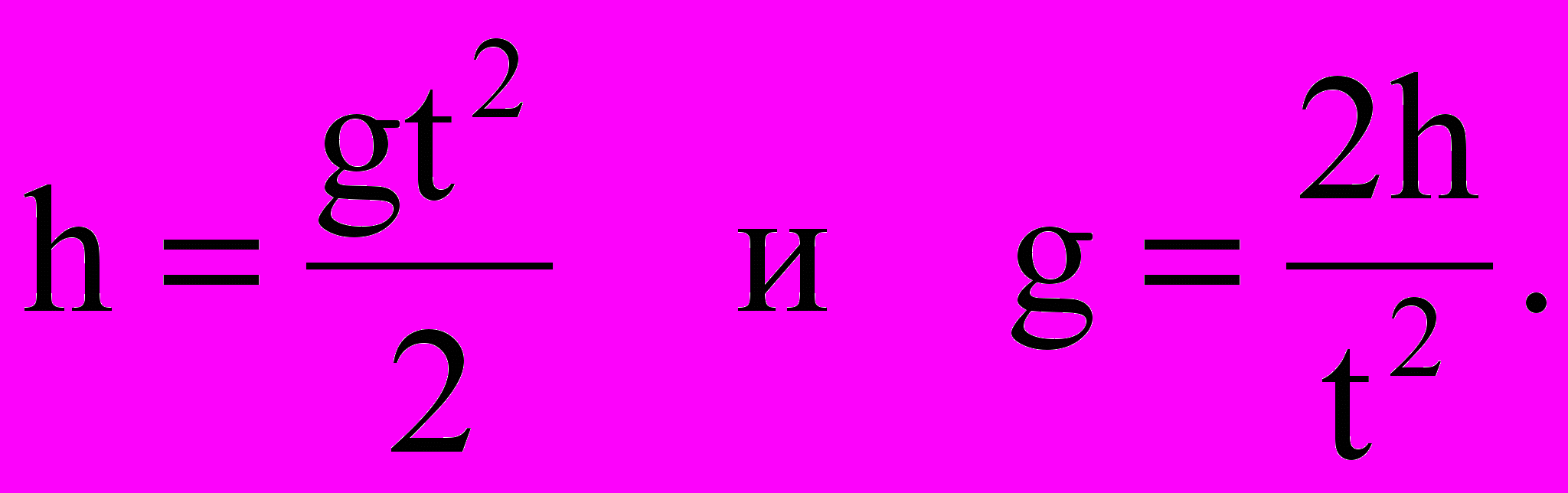
Измерения высоты производится линейкой с ценой деления с=1 см, а время измеряется секундомером с погрешностью 0,01 секунды.
Прямыми измерениями получена серия данных:
| h, м | 0,70 | 0,70 | 0,70 | 0,70 | 0,70 |
| t, c | 0,34 | 0,36 | 0,40 | 0,38 | 0,37 |
| t,c | -0,03 | -0,01 | 0,03 | 0,01 | 0 |
| (t)2,c2 | 910-4 | 10-4 | 910-4 | 10-4 | 0 |
Принимаем:
Qh = 0,005м, Qt= 0,01 с.
Следуем рекомендованному порядку для метода переноса погрешностей:
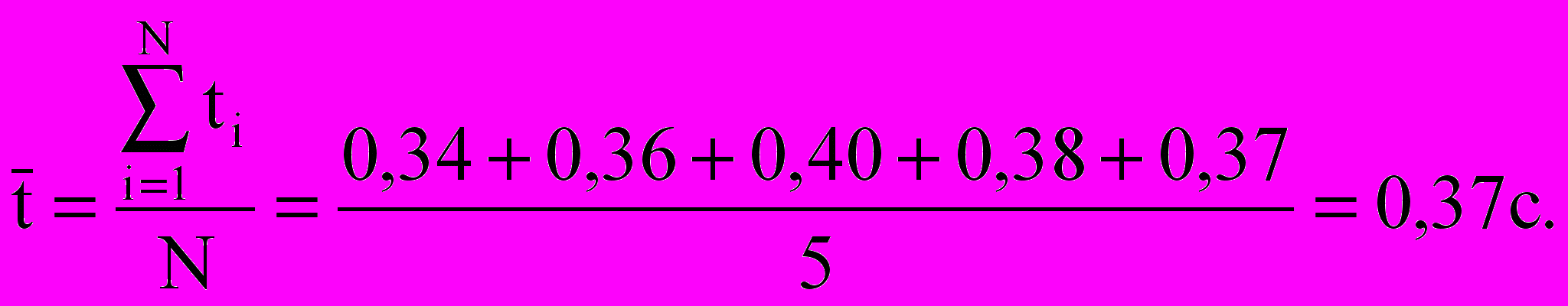
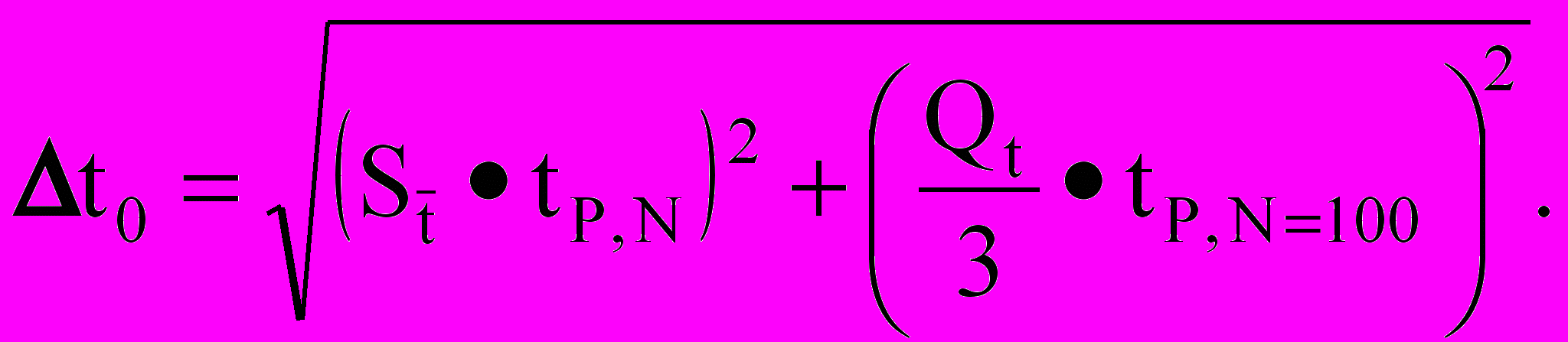
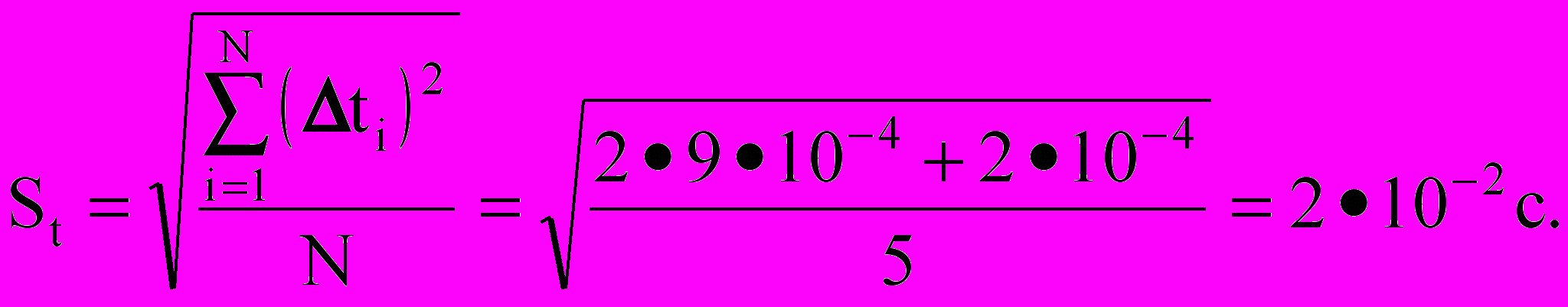
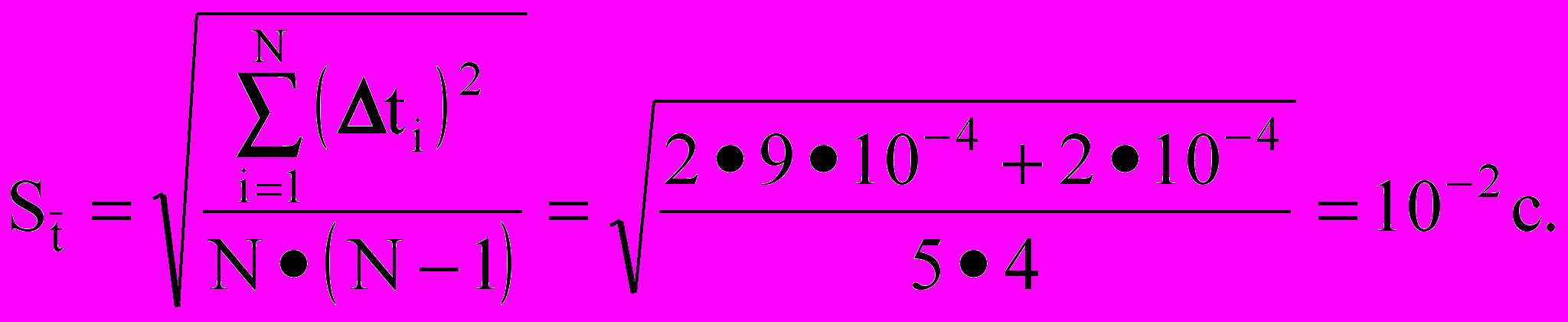
Если Р = 0,95, то tP,N = 2,8; tP,100 =2 и
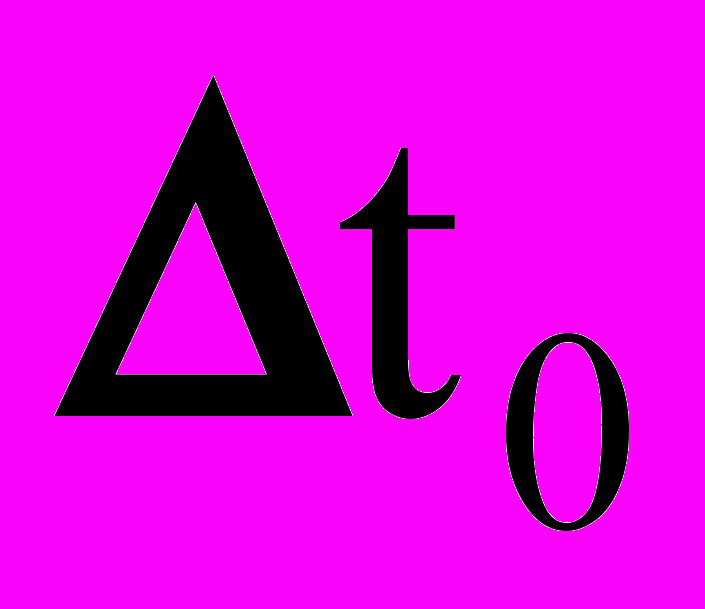 =0,029c.
=0,029c.h = 0.70м; h0 =
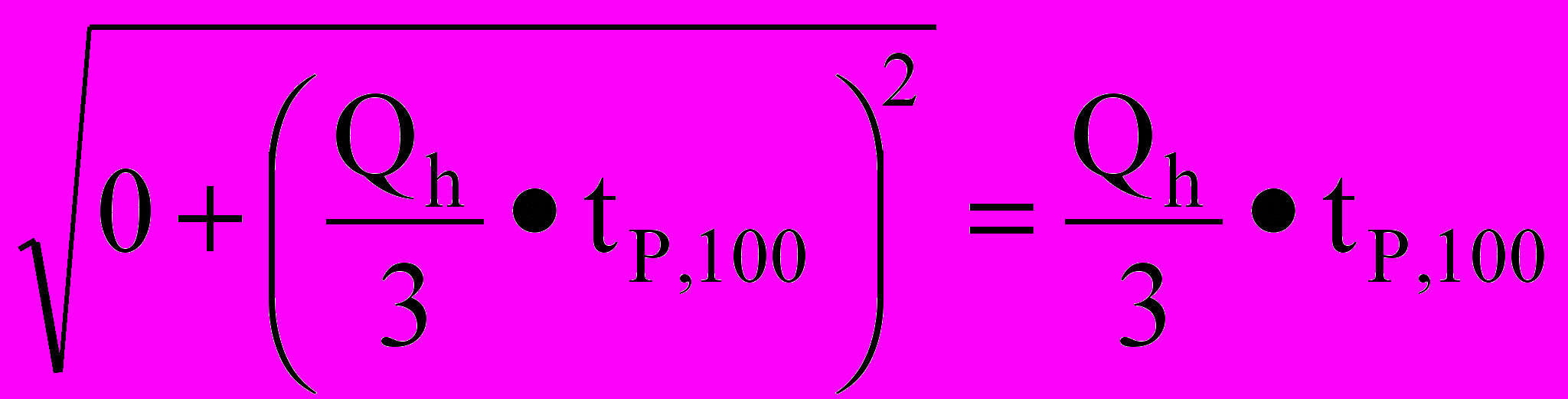 =
= 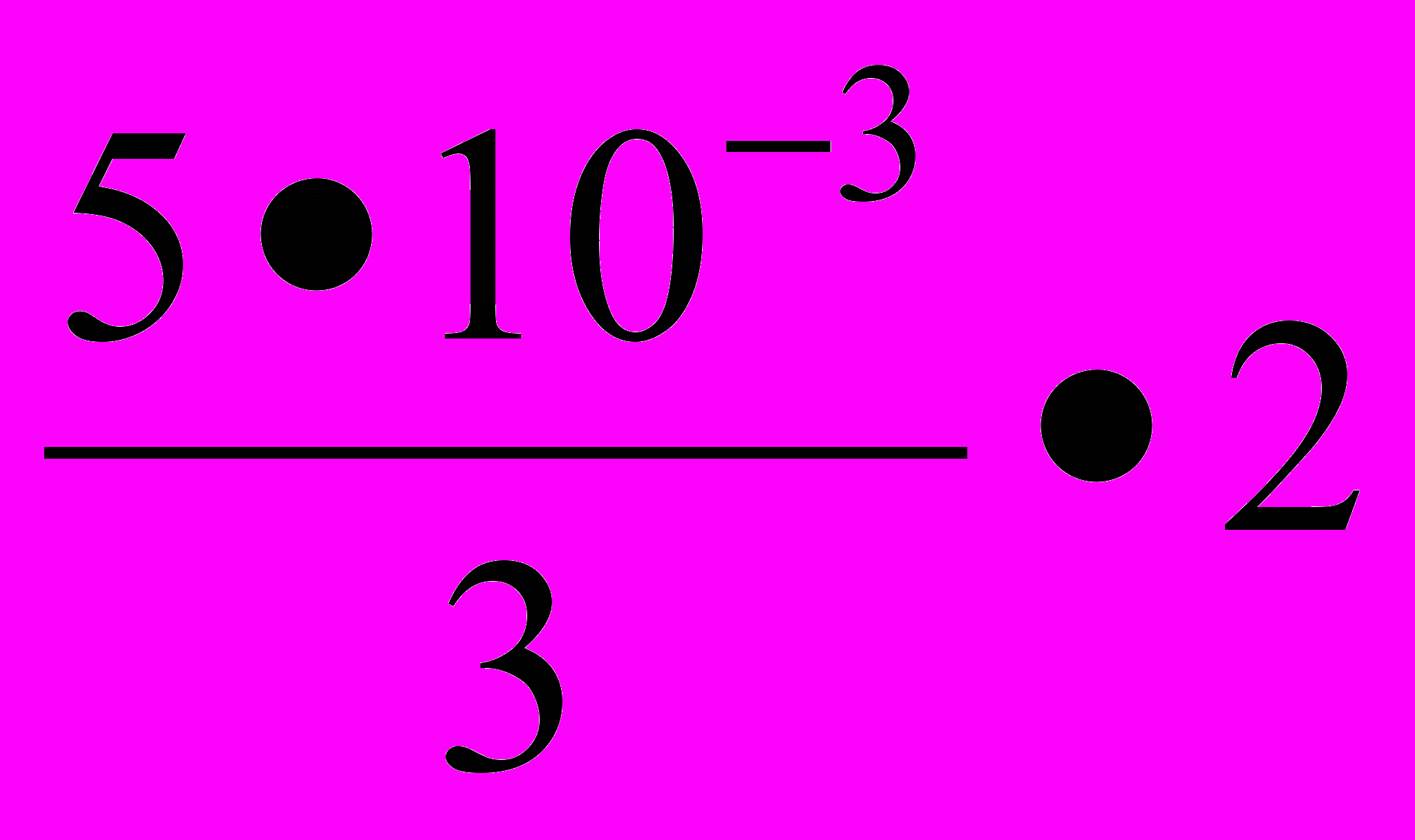 .
. h0 = 0.0033м =0,33 см.
Промахи не проявляются.
Вычисляем среднее значение искомой величины:
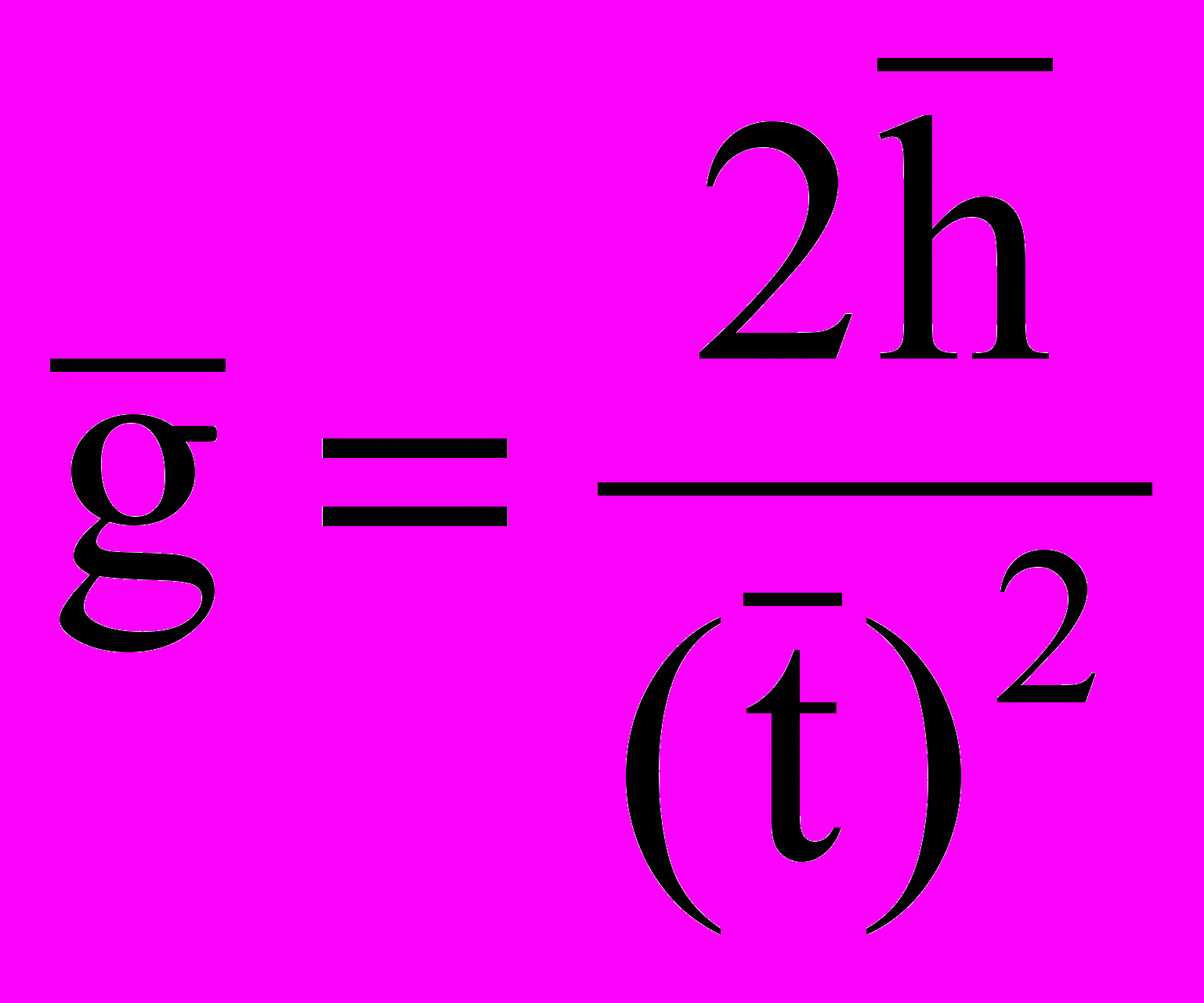 ,
, 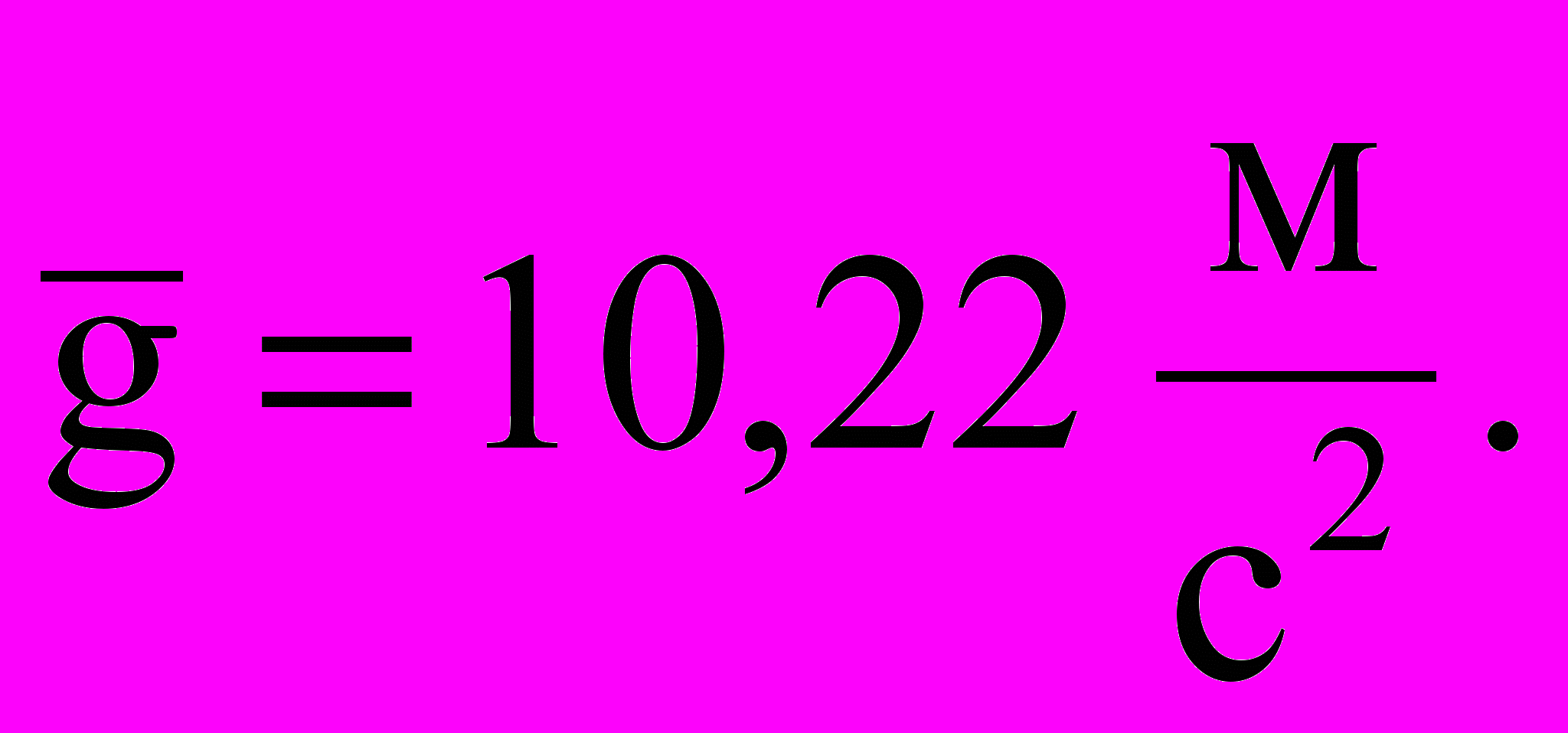
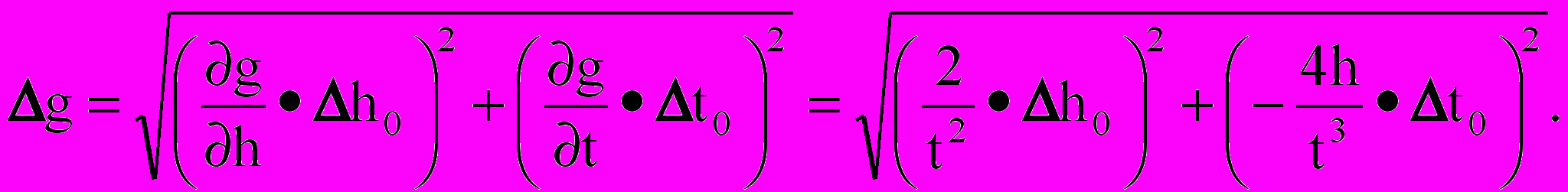
Вычислим полученное выражение при средних значениях
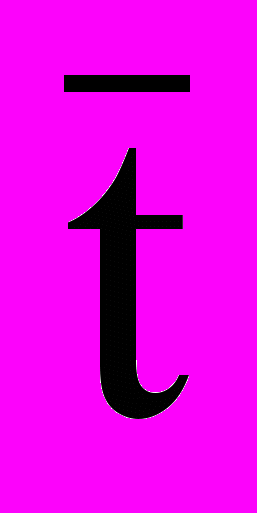 и
и 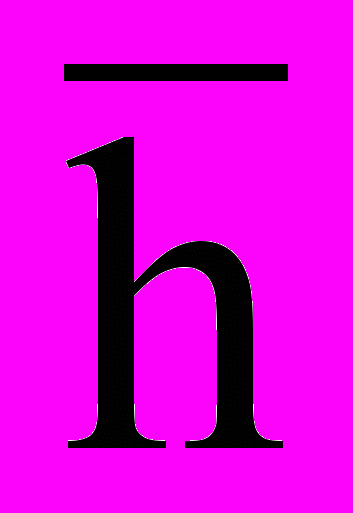 и с использованием уже найденных t0 и h0.
и с использованием уже найденных t0 и h0.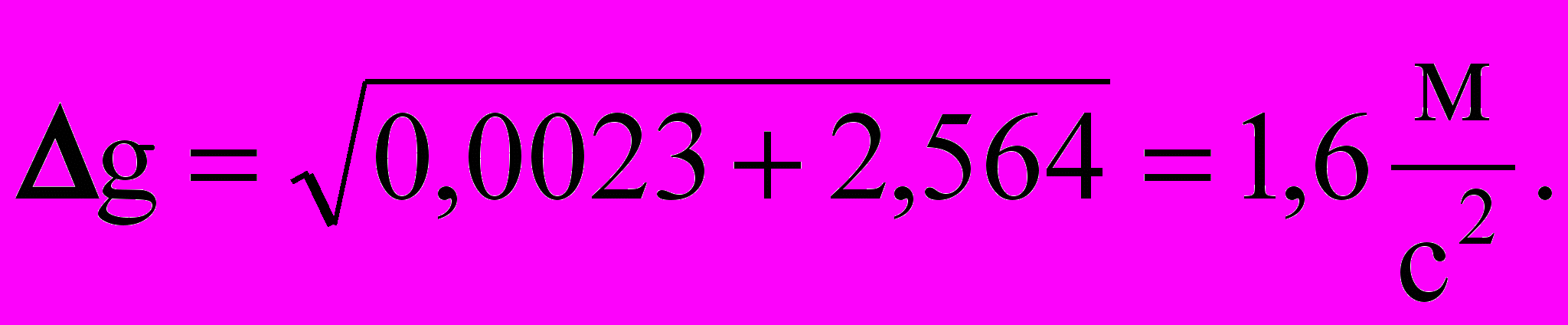
Итак, результат составляет
g =(10,21,6) м/с2 или 8,6 м/с2g11,8 м/с2, Р=0,95
Относительная ошибка составляет
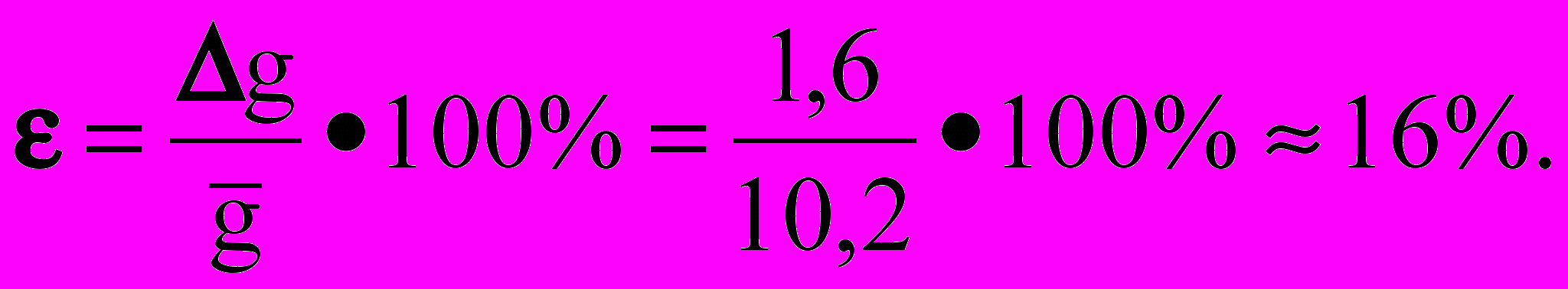
Решим ту же задачу выборочным методом.
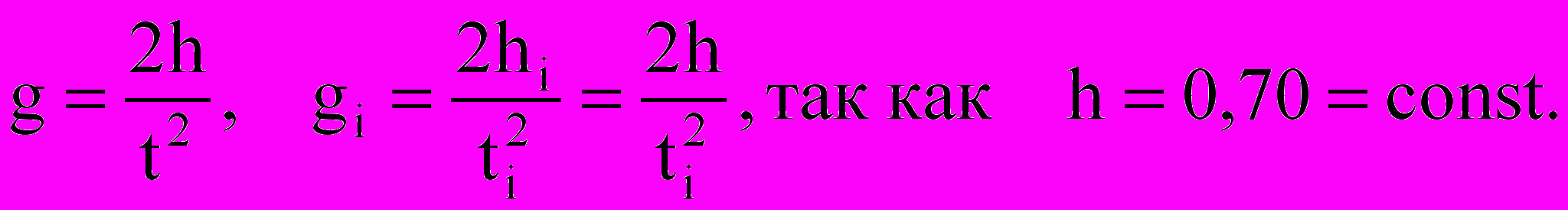
| ti2, c2 | 0,1156 | 0,1296 | 0,1600 | 0,1444 | 0.1369 |
| gi, м/с2 | 12,11 | 10,80 | 8,750 | 9,695 | 10,23 |
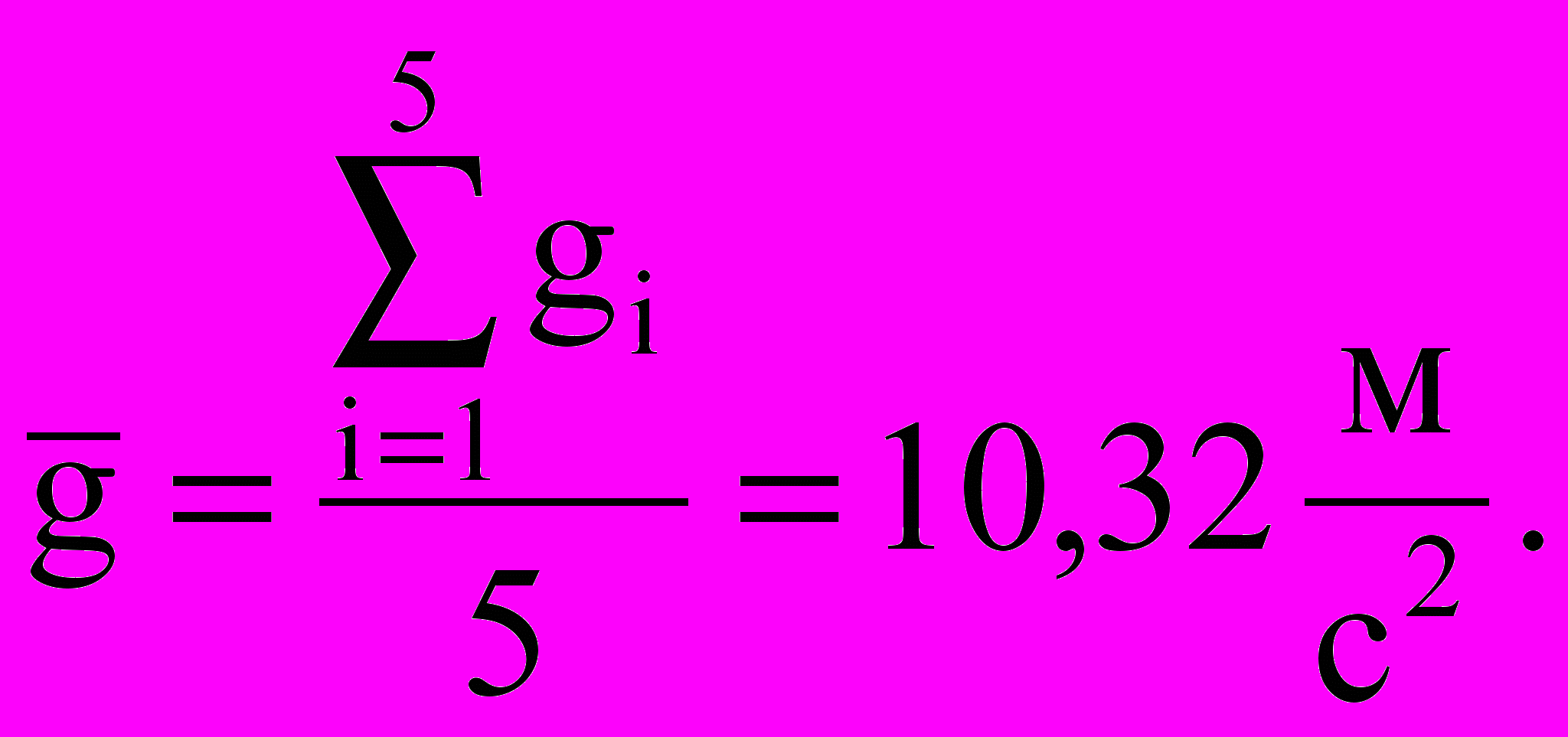
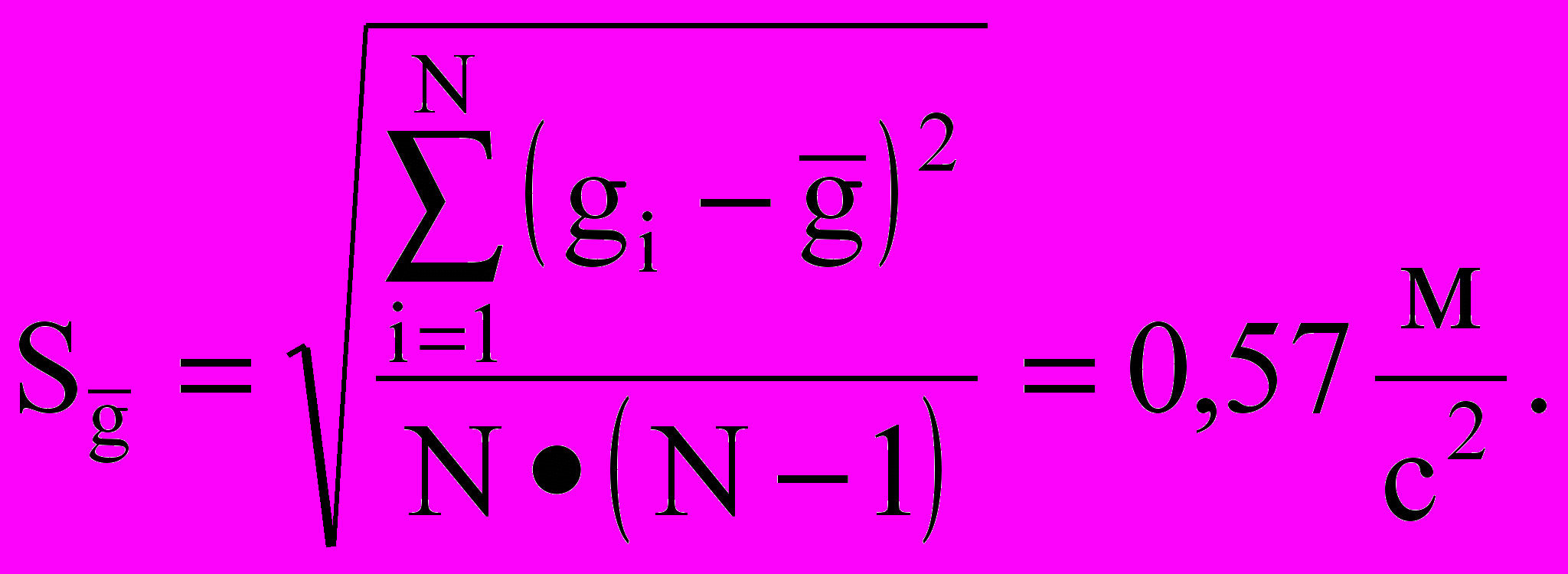
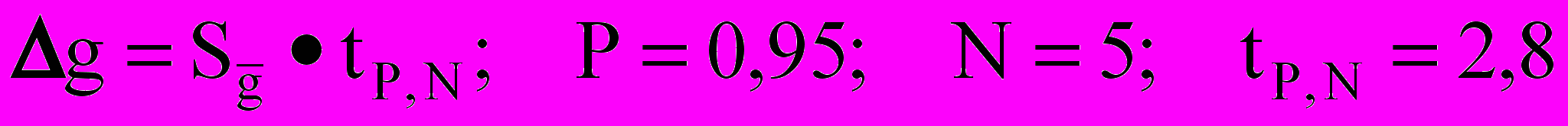
g=0,572,8 м/с2=1,6 м/с2.
g = (10,31,6) м/с2.
Доверительные интервалы, рассчитанные по методам переноса погрешностей и выборочному методу, перекрываются. Результаты неразличимы с вероятностью 0,95.
