Самостоятельная работа студентов Знакомство с MathCad Основной экран MathСad

Вид материала

Самостоятельная работа

Содержание Курсор ввода Ввод формул. Математические выражения. Операция присваивания. Знак присваивания Имена переменных Математические выражения Для редактирования формул Десятичный формат Содержание работы 1 6. Вычислите значения приведенных ниже математических выражений. При наборе старайтесь использовать клавиатурный вариант для зна 2. Ввод и использование функций. Построение графиков функций Ранжированные (дискретные переменные), вектора и матрицы График функции Форматирование графиков Equal scales Legend Lable Color — цвет линии и точек данных: red (красный), blu (синий), grn (зеленый), cya (голубой), brn (коричневый), blk (черный), wht Weight — толщина линии и точек данных. При помощи вкладки Labels М3,2 = 3.Пример. Содержание работы 2

Подобный материал:

• Самостоятельная работа студентов под руководством преподавателя Самостоятельная работа, 1542.41kb.
• Самостоятельная работа студентов под руководством преподавателя Самостоятельная работа, 1755.62kb.
• Самостоятельная работа студентов самостоятельная работа студентов по курсу «Теории, 66.51kb.
• MathCad Mathcad, 7.16kb.
• Самостоятельная работа студентов 2 курса (письменные ответы по общебиологическим разделам), 261.09kb.
• Самостоятельная работа студентов под руководством преподавателя Самостоятельная работа, 1853.91kb.
• Самостоятельная работа студентов допущено Редакционно-издательским советом тгу имени, 375.14kb.
• Контрольная работа (типовой расчет) №2 "расчет сложной цепи периодического синусоидального, 29.02kb.
• Самостоятельная работа студентов 1 курса впо по дисциплине «Русский язык и культура, 350.15kb.
• Самостоятельная работа с учебником Цель: Уточнить представления о модели Земли глобусе, 40.96kb.

Самостоятельная работа студентов

1. Знакомство с MathCad

Основной экран MathСad. Внешний вид экрана Mathcad является типовым для пакетов, работающих в среде Windows, здесь находится: строка заголовка; строка меню; стандартная панель; панель форматирования; рабочее поле программы; строка состояния; математические панели инструментов.

Специфическими для Mathcad являются математические панели. Имеется главная математическая панель Math (Математика). Она содержит кнопки для открытия математических панелей более низкого уровня:

Calculator (калькулятор); Graph (графика); Matrix (векторные и матричные операции); Evaluation (операторы управления вычислениями); Calculus (математический анализ (операторы дифференцирования, интегрирования, суммирования и др.)); Boolean (булево (логические операторы)); Programming (программирование); Greek (греческие символы); Symbolic (символика).

Если панель Математика отсутствует на экране, то ее можно открыть с помощью команды меню Вид – Панели инструментов (View – Toolbars). Этой же командой открываются и закрываются и другие панели.

Курсор ввода (крестик красного цвета) указывает место рабочей области, где в данный момент могут вводиться или создаваться объекты информации: формулы, текст, графики или данные. Положение курсора устанавливается в рабочем поле с помощью мыши или клавишами управления курсора на клавиатуре. Последний вариант позволяет размещать объекты строго на одной строке или друг под другом.

В рабочей области экрана могут находиться математические выражения, таблицы, графики, а также текстовые поля. В текстовых полях помещается информация, с помощью которой можно отображать ход и результаты решения задачи — комментарии. Если при вводе текста русские буквы отображаются неправильно, то необходимо установить кириллическую гарнитуру с помощью панели Форматирование (Formatting).

Любой объект в рабочей области MathCad часто называют регион. Одинарный щелчок мыши позволяет выделить регион прямоугольной рамкой. Выделенный регион можно масштабировать (с помощью специальных маркеров на рамке) или перемещать (указатель мыши установленный на рамке приобретает форму ладони).

Выполните для примера пункт 1 задания к работе.

Ввод формул. Математические выражения строятся из чисел, переменных, функций и символов математических операций. Символы основных арифметических операций и цифры имеются на панели Калькулятор, но лучше их вводить с клавиатуры. Для убыстрения процесса ввода желательно использовать клавиатурный вариант ввода и других часто встречающихся символов. Если подвести указатель мыши к некоторой кнопке, то появится подсказка: название кнопки и ее клавиатурный аналог. Например, для кнопки «Х^У» — возведение в степень , т. е. для ввода верхнего индекса нужно использовать сочетание клавиш «Shift 6».

В арифметических выражениях могут применяться встроенные стандартные функции. Используются три способа их ввода:

1) выбор с панели Калькулятор (Calculator), если они на ней имеются;

2) ввод имени функции с клавиатуры (в скобках, если требуется, – аргумент);

3) выбор функции из списка команды меню Вставка – Функция (Insert – Function) или  кнопки f(x) на cтандартной панели.

Следует обратить внимание, что не все функции имеют имена, совпадающие с принятыми в математике, например, тангенс — tan.

Математические выражения создаются как отдельные регионы в процессе ввода символов с клавиатуры или выбора их с панелей. При вводе формулы появляется прямоугольная рамка (шаблон ввода), в которой помещается вычисляемое выражение. Курсор ввода представляет собой уголок синего цвета.

Горизонтальная сторона курсора ввода подчеркивает тот символ или часть формулы, по отношению к которым выполняется очередная операция. Ширина уголка и его высота (для «многоэтажных» выражений) увеличивается при каждом нажатии клавиши пробела.

При выполнении некоторых операций, таких, как деление, извлечение корня, возведение в степень и заключение в скобки, требуется выделять группу символов, для которых будет выполняться операция. Выделение группы символов производится при щелчке мышью на формуле с последующим нажатием клавиши пробел для увеличения уголка. Для отмены выделения и возврата к минимальной ширине полки нужно снова щелкнуть мышью в место, где будет происходить ввод.

Обычно уголок повернут вправо, если он повернут влево (клавишей управления курсором или мышью) ввод будет происходить перед курсором. Если применить деление к части формулы, выделенной правым курсором — она будет помещена в числитель дроби, если выделение левым уголком — в знаменатель.

Mathcad может автоматически преобразовать некоторые круглые скобки в квадратные. На результат вычислений это не влияет.

Для получения результата (вывода его на экран) необходимо набрать знак «=». Слева от знака равенства появится результат выражения или значение заданной ранее переменной.

По умолчанию действует режим автоматического вычисления. В этом режиме при любом изменении программы или данных автоматически производится пересчет решения задачи. Для включения (или отмены) режима автоматического вычисления используется флажок команды Автоматическое вычисление (меню Tool – Calculation – Automatic Calculation). Если режим автоматического вычисления отменен, то для каждого запуска программы нужно выбрать команду Выполнить (Calculate Now) (та же цепочка команд) или нажать кнопку « = » на стандартной панели инструментов.

Выполните для примера пункт 2 работы.

Математические выражения. Операция присваивания. Для того, чтобы задать значение переменной используется операция присваивания, обозначаемая специальным символом «:=». Общий вид оператора присваивания:

< Имя переменной > := < Математическое выражение >.

Здесь сначала вычисляется математическое выражение справа от знака «:=», а затем результат присваивается переменной (матрице или вектору), имя которой указано слева от знака присваивания.

Знак присваивания выбирается с панели Калькулятор (Calculator) или вводится с клавиатуры — набирается двоеточие (для латинской раскладки), знак « = » добавляется автоматически.

Имена переменных могут состоять из букв и цифр, но начинаться должны с буквы. MathCad различает строчные и прописные символы. Например, Х и х; Val, VAL и val — разные переменные.

Математические выражения составляются с помощью арабских цифр, латинских и греческих букв (панель инструментов Греческие символы — Greek), символов математических операций и др. В простейшем случае — это одно число.

Например: x := 2.18 s := sin(1.5) + 0.45 12 := tan(x2) – 0.3xs .

Операция умножения обычно не подразумевается, а пишется явно. Так, операцию умножения следует записать xs, а не xs, что будет воспринято как имя из двух букв. В MathСad допускается (хотя это не рекомендуется) набирать без символа умножения произведение числа на переменную (например — 0.3х) или на выражение в скобках. Произведение переменной на число без знака умножения недопустимо (например — x2, хотя допустимо — 2x).

Для получения результата следует ввести имя переменной и знак «=».

Все переменные должны быть определены (им должно быть присвоено какое-то значение) до того, как они будут использованы.

MathCad читает и выполняет программу слева направо и сверху вниз. Т. е., в приведенном выше примере нельзя поменять местами регионы или набирать «12 =» выше (результат выведен не будет).

Выполните для примера пункт 3 работы.

Для редактирования формул, созданных с помощью редактора формул Mathcad, требуется определенный навык работы. Для внесения исправлений применяются следующие рекомендации:

1) для вставки курсора в место изменения, нужно щелкнуть в этом месте кнопкой мыши, перемещать курсор в формуле можно с помощью клавиш управления курсором на клавиатуре;

2) для удаления ненужных скобок нужно поместить курсор справа от левой удаляемой скобки и нажать клавишу Backspase.

3) иногда проще удалить часть формулы или весь регион и набрать заново.

Заметим, что если горизонтальная сторона уголка подчеркивает все выражение, включая символ «:=» и левую часть формулы, то ввод символов в формулу не производится. Необходимо с помощью мыши вернуть уголок к размеру, не превышающему ширины правой части выражения.

Для копирования и перемещения формул или фрагментов формул используются команды Вырезать (Cut), Копировать (Copy), Вставить (Paste) меню Правка (Edit) или соответствующие кнопки стандартной панели.

Для применения команд к нескольким регионам, их следует выделить рамкой выделения (появятся пунктирные рамки) Для выделения разрозненных регионов можно щелкнуть мышью на каждом из них при нажатой клавише Shift.

В MathCad нет явного понятия строчек, и иногда бывает трудно установить мышью курсор ввода точно в нужном месте. Если, к примеру, сначала переменной присвоено значение, а затем набирается формула с использованием этой переменной — регионы желательно набрать друг за другом. Если второй регион расположен правее, но хоть немного выше — он будет читаться MathCad раньше.

Можно выровнять группу выделенных регионов по горизонтали или вертикали с помощью команд меню Формат – Выровнять регионы (Format – Align Regions) или с помощью специальных кнопок стандартной панели, которые становятся активными при выделении нескольких регионов.

Выполните для примера пункт 4 работы.

Результат расчетов может быть представлен в различных форматах. Десятичный формат (Decimal)  это обычная форма записи дробного числа, только вместо десятичной запятой используется десятичная точка. Научный формат (Scientific) обычно применяется для очень больших и очень малых чисел и включает число в десятичном формате (мантисса), умноженное на число 10 в определенной степени (порядок).

По умолчанию MathCad сам выбирает наиболее подходящую форму представления результата — формат Общий (General). Изменить тип формата, увеличить число выводимых после десятичной точки цифр и изменить другие параметры представления результата можно с помощью команды меню Формат – Результат (Format – Result). Изменения будут относиться к выделенным формулам или ко всему документу, если выделений нет.

Выполните для примера пункт 5 работы.

В процессе работы с редактором формул на экране часто появляются лишние символы («мусор»), которые на самом деле в программе отсутствуют. Если нажать клавиши Ctrl + R или меню Вид – Обновить (View – Refresh), то все лишние символы исчезнут.

Выполните для примера пункт 6 работы.

Содержание работы 1

1. Установив курсор в центре рабочей области вставьте текстовый регион (меню Вставить – Область текста), введите заголовок «Лабораторная работа 1». Выделите и переместите регион в верхний левый угол, потренируйтесь его масштабировать.

2. Введите следующее выражение, внимательно следя за формой курсора ввода



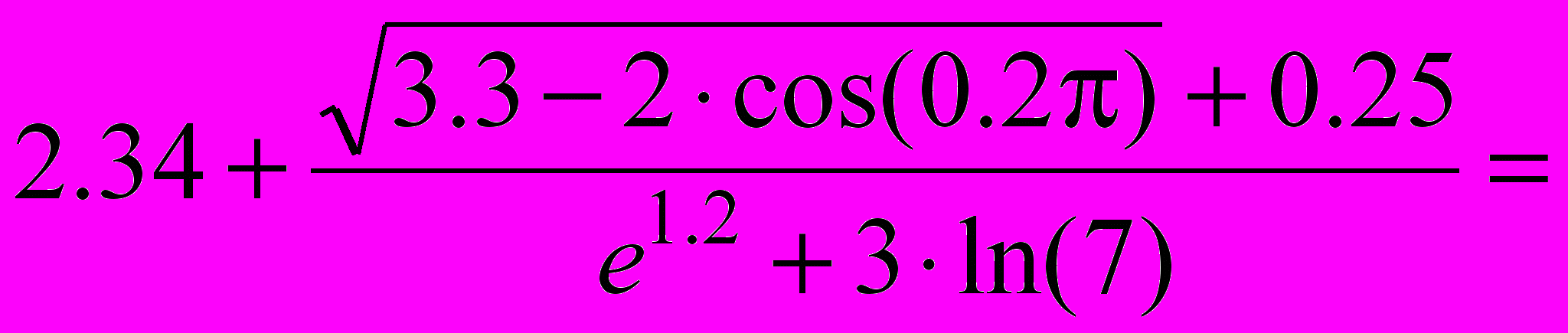
(сравните получившийся результат с верным:  2.509).


3. Введите следующие выражения

x := 2.18 а := –3.610 ^{– 3}

b:= 5 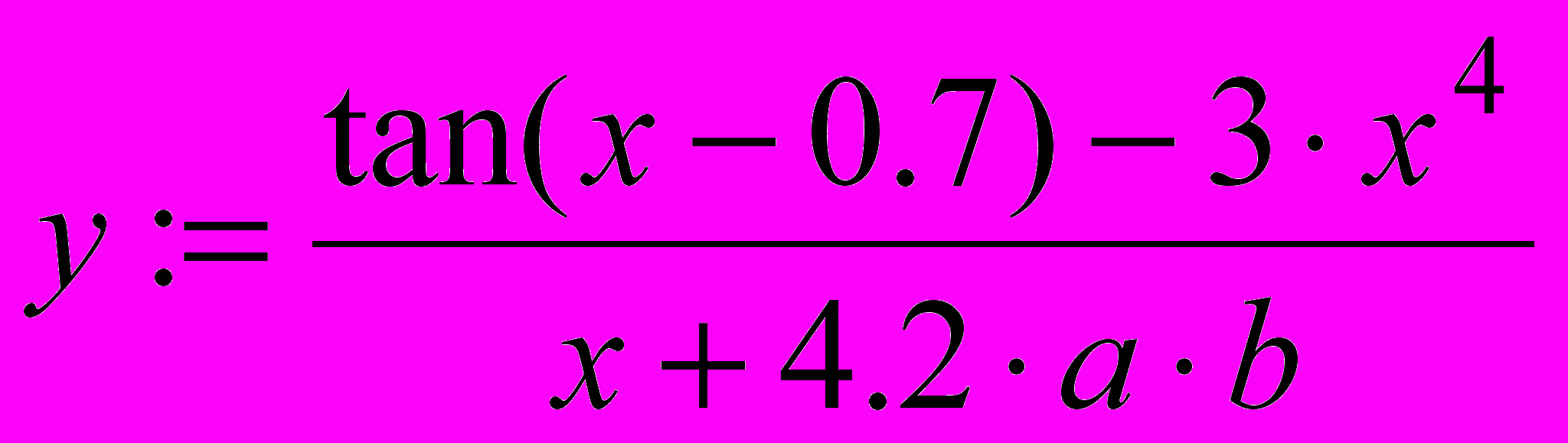y = 

(сравните получившийся результат с верным y = –26.978).

4. Переместите выражение «b:= 5» по вертикали вниз (немного ниже строки с регионом «y:= …»), обратите внимание на то, что результат расчета пропал и в выражении переменная b стала красного цвета (сообщение об ошибке — неизвестная переменная). Выделите регионы «b:= 5», « y:= …» и «y= …» и выровняйте их по горизонтали с помощью специальной кнопки на стандартной панели. Потренируйтесь выравнивать регионы по вертикали и горизонтали.

5. Выведите значение переменных х, а и b в одну строку: наберите «х = » и, не выходя из этого региона, используйте стрелку перемещения курсора вправо с клавиатуры.

Обратите внимание на то, в каком виде MathCad вывел значения переменных. Измените формат вывода (меню  Формат – Результат) на десятичный, увеличьте число десятичных позиций до 5; выберите научный формат результата.

6. Вычислите значения приведенных ниже математических выражений. При наборе старайтесь использовать клавиатурный вариант для знака присвоения «:=» — «:» (Shift ж), для набора верхнего индекса — «» («Shift 6»); при переходе от одного региона к другому — клавиши управления курсором.

Исходные данные:

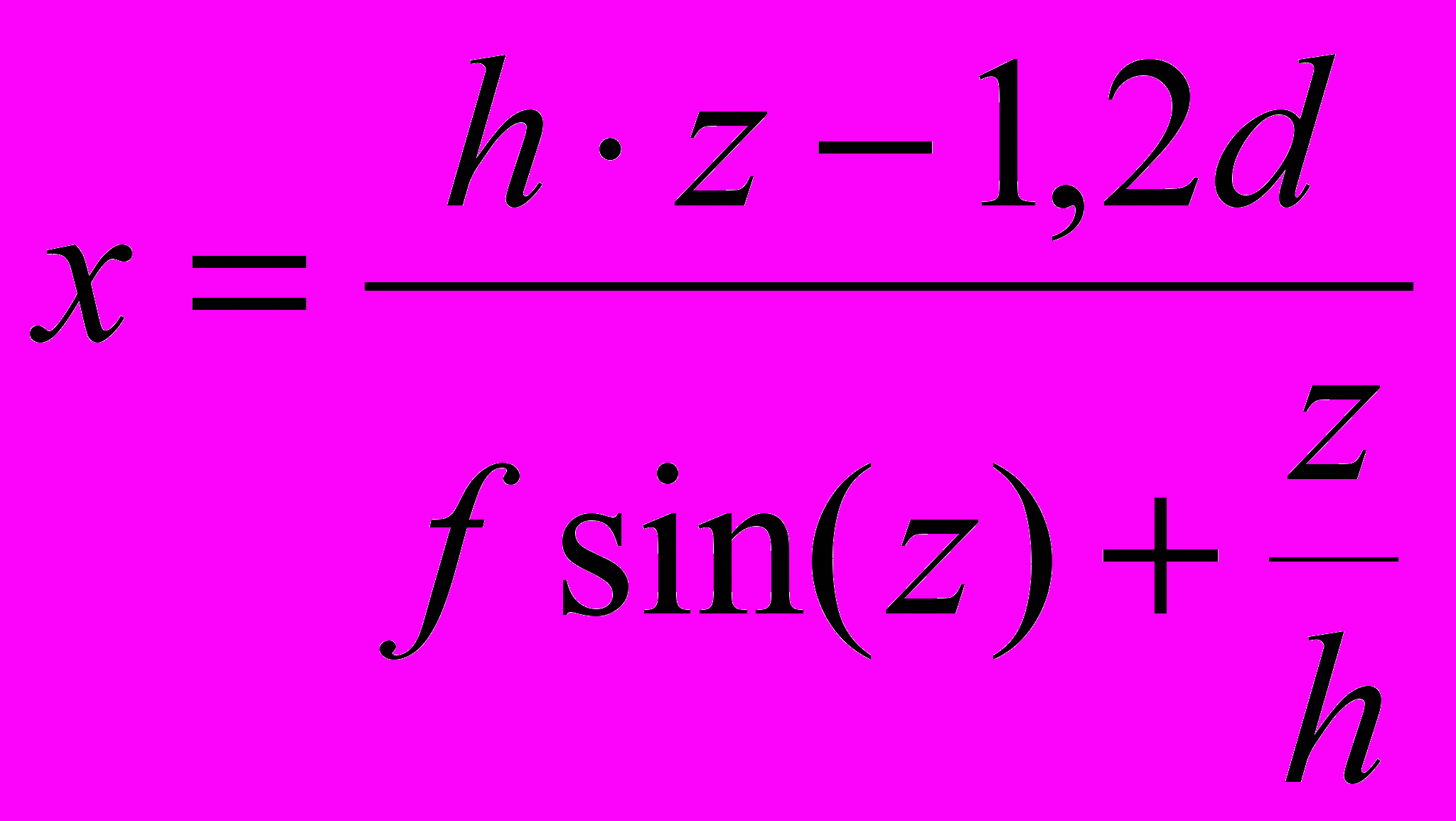
при 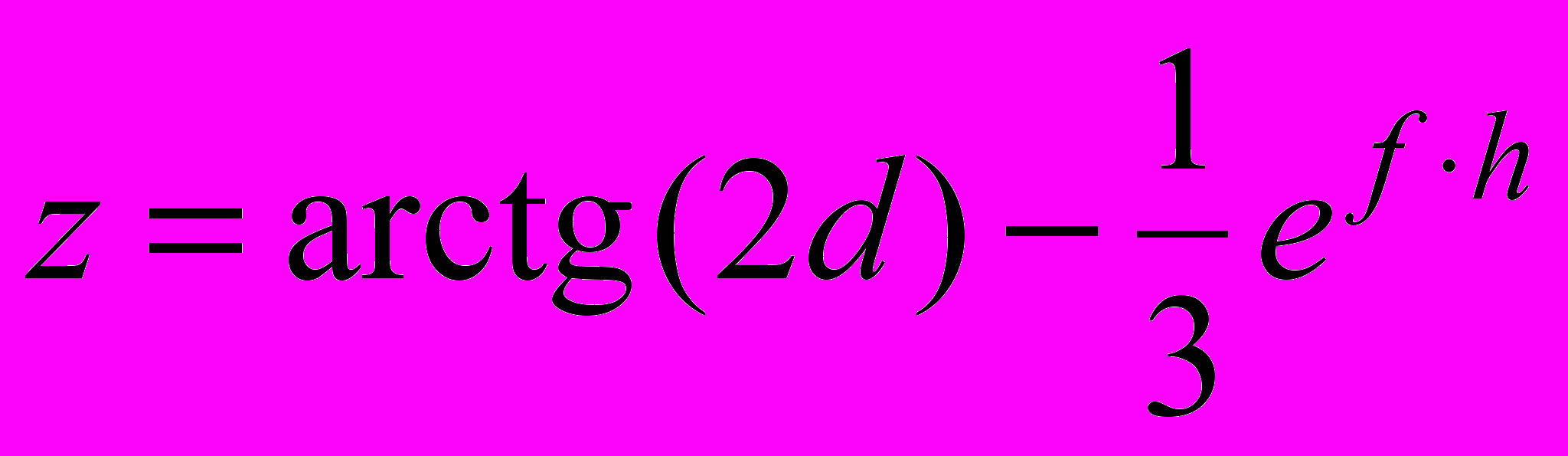, h = –5, d = 0,08 , f = 4,310 ^{– 4}

2. Ввод и использование функций. Построение графиков функций Ранжированные (дискретные переменные), вектора и матрицы

Функции пользователя. В MathCad можно задавать любые функции, зависящие от произвольного числа аргументов. Такая функция, задаваемая пользователем, может быть определена с использованием других функций, в том числе и стандартных. MathCad имеет большое число стандартных встроенных функций, лишь малая часть которых приведена на панели инструментов Калькулятор.

При задании вида функции нужно записать ее имя, за которым в круглых скобках указать аргумент (или аргументы через запятую), затем знак присвоения и необходимое выражение. Конкретное значение аргумента заранее задавать не обязательно. Например:

f(x) := (x² + 2)sin(3x); .

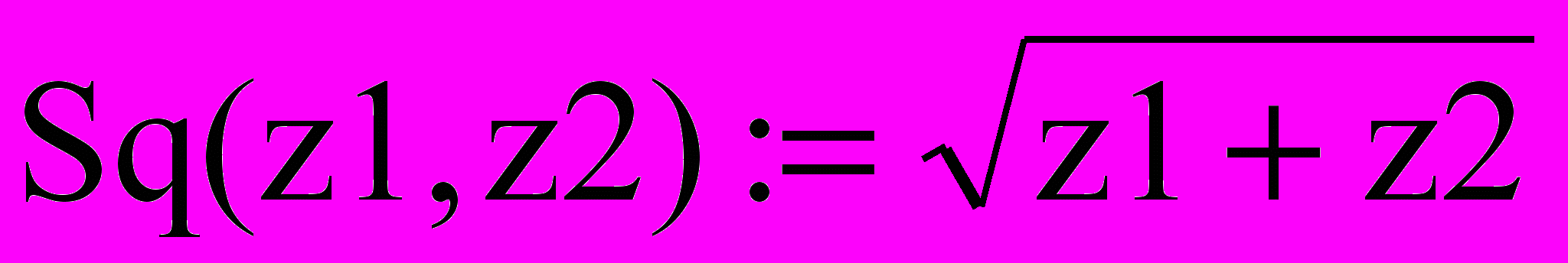Необходимо следить, чтобы имя аргумента слева и справа от знака присвоения было одно и то же. Например, в результате невнимательности при наборе может возникнуть такая запись g(z) := (у² + 2). Это будет воспринято программой как запись функции, которая  является константой и не зависит от аргумента z (y — не аргумент, а переменная, значение которой MathCad потребует задать заранее).

Обращение к функции (вызов функции) осуществляется по имени, после которого в скобках указывается конкретный аргумент. Это может быть непосредственно значение, переменная (обычная или ранжированная), значение которой задано ранее, или выражение. Используются функции пользователя, как и стандартные, в любых выражениях или для непосредственного вычисления (слева от знака «=»).

Следует обратить внимание, что имя переменной, задающей фактическое значение аргумента, может и не совпадать с именем аргумента при описании функции (формальный аргумент лишь определяет вид функции, а не ее конкретные значения).

Например, заданные выше функции могут быть использованы следующим образом.

a:= 2 Vr:=3, 3.5 .. 5 x:= –7 Sq(2.5, 4x) =

Din:= cos(5a) + (f(a) – f(x)) Din= f(Vr)=

Последний результат будет представлять собой пять чисел — значение функции f в точках 3, 3.5, 4, 4.5 и 5.

Выполните пункт 1 работы.




Ранжированная переменная (Range Variable):

Дискретная переменная, переменная интервального типа, диапазон значений, множество упорядоченных равноотстоящих значений

Соответствует математической записи типа

k = 1,2,3 … 10 b = 2,3; 2,4; 2,5 … 3,1

Переменная задается следующим образом:

x := первое значение[,второе значение] .. конечное значение

[ ] – необязательный параметр; второе значение – это первое значение + шаг, если не задано, то шаг = 1

.. – знак диапазона, используется кнопка m..n панели «Матрицы» или с клавиатуры «;», нельзя набирать точки с клавиатуры


x:= 3,4 .. 8 или x:= 3 .. 8 reg:=1.1, 1.2 .. 1.9






При определении ранжир. переем. могут использоваться не только непосредств. значения, но и переменные или выражения, заданные ранее:

X0:= 3.7 Xh:= 0.05 Xend:= 4 rx:= X0, X0+Xh .. Xend




Задать переменную, принимающую 5 равноотстоящих значений от 10 до 100: (между первым и пятым значением – 4 шага)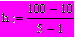




h = 22.5 H:= 10, 10+h .. 100


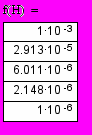
Ранжированная переменная может использоваться как аргумент функции, результат – табл. значений функции.



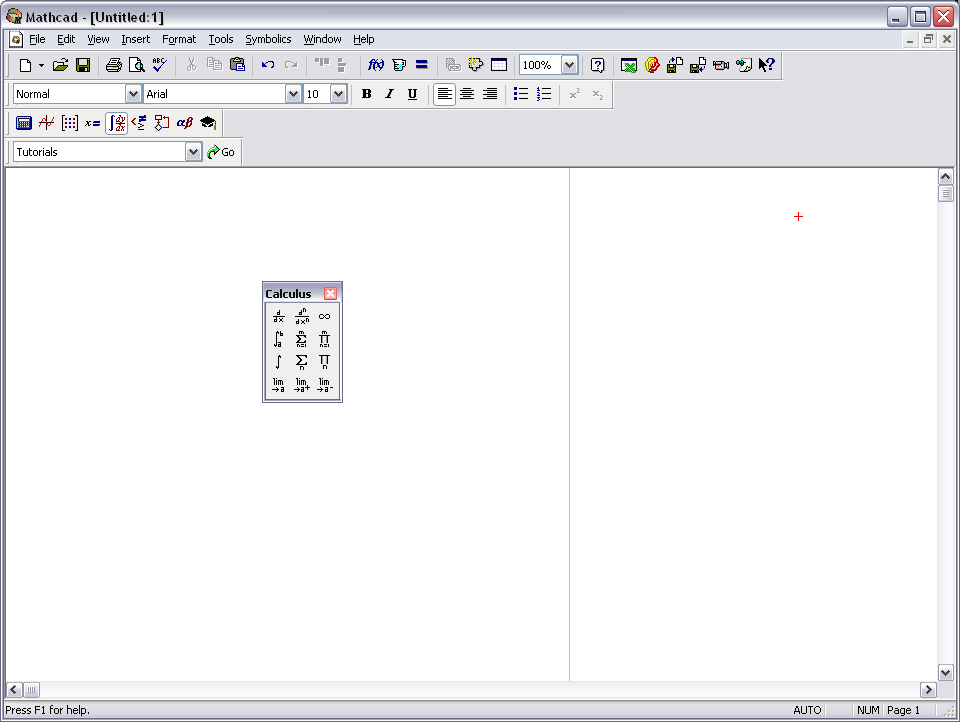Можно вычислить сумму/произведение всех значений ранжированной переменой, а также сумму/произведение всех значений выражения или функции с ранжированной переменной.

Используются соотв. кнопки панели «Математический анализ».






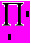
i:= 1, 1.2 .. 6 m:= 2,7 .. 32



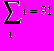
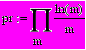
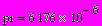
Если для суммы/произведения используется шаблон с верхним и нижним пределами, то переменную по которой ведется суммирование заранее определять не надо, она будет принимать значения в заданных пределах с шагом 1.

i:= 1, 2 .. 6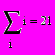

или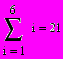

Переменная заданная непосредственно в шаблоне вне этого региона не определена (not defined)






Любые действия с ранжированной переменной используют все ее значения, нельзя отдельно получить только некоторые из этих значений. Работать с отдельными элементами позволяют переменные матричного типа.

Выполните пункт 2 работы.


График функции позволяет в наглядной форме представить результаты решения задачи, найти начальные данные для некоторого вида задач, исследовать поведение функции и т. д.

До построения графика следует задать вид функции. Затем установить курсор в том месте экрана, где должен быть левый верхний угол графика и нажать кнопку
Декартов график (x-Y Plot) панели Графики (Graph) или использовать соответствующую команду меню Вставка – График (Insert – Graph). Появится регион, внутри которого расположена прямоугольная область собственно для графика, в шаблоне под ней нужно ввести имя аргумента, в шаблоне слева — имя функции с тем же аргументом, затем следует щелкнуть мышью вне региона графика или нажать клавишу Enter.

Если аргумент не был задан заранее, то график будет построен в пределах, определенных MathCad (по-умолчанию). Чаще всего это отрезок [–10; 10]; для функции с положительной  областью определения — [0; 10] и т. д.

Форматирование графиков осуществляется с помощью диалогового окна, вызываемого двойным щелчком мыши по графику или меню Формат – График – Декартов график (Format – Graph – X-Y Plot).

Окно форматирования имеет четыре вкладки, содержащие параметры:

• X-Y Axes (Оси X-Y) — отображение осей;
  
• Traces (Графики) — отображение линии графика;
  
• Labels (Надписи) — отображение надписей на графике;
  
• Defaults (По умолчанию).
  

На вкладке X-Y Axes представлены основные параметры, относящиеся к осям абсцисс и ординат декартова графика.

Область Axis Style (Стиль осей) содержит переключатели, позволяющие задавать стиль координатных осей: Boxed (Рамка) — в виде прямоугольника; Crossed (Крест) — в форме креста; None (Нет) — оси отсутствуют.

Выбор параметра Equal scales (Равный масштаб) приведет к заданию одинакового масштаба осей.)

Параметры областей Axis X и Axis Y позволяют модифицировать оси X и Y и устанавливать:

Log scale — логарифмический масштаб; Grid lines — линии сетки; Numbered — цифровые данные по осям; Auto scale — автоматическое масштабирование графика; Show markers — маркеры на осях; Auto grid — автоматический вывод линий сетки; Number of grids — задание вручную числа линий сетки (опция недоступна, если включен параметр Auto grid).

Вкладка Traces содержит список параметров всех линий, построенных в данной графической области. Чтобы модифицировать линию достаточно выделить ее в списке и настроить соответствующие установки:

Legend Lable — имя выбранной линии (по умолчанию trace 1, trace 2 и т. д.);

Symbol — символ, которым обозначаются отдельные точки данных;

Line — стиль линии: solid (сплошная), dot (пунктирная), dash (штриховая), dadot (штрихпунктирная);

Color — цвет линии и точек данных: red (красный), blu (синий), grn (зеленый), cya (голубой), brn (коричневый), blk (черный), wht (белый).

Type — тип линии: lines (линии), points (точки), error (ошибка), bar (столбец), step (шаг), draw (рисунок), stem (стержень), solid bar (гистограмма);

Weight — толщина линии и точек данных.

При помощи вкладки Labels осуществляется создание надписей на графике (вводится заголовок графика, подписей под осями).

Особенности построения графиков

Если переменная, указанная на графике как аргумент (внизу по центру), ранее в документе не была задана, график будет построен для аргумента от -10 до 10 (или от 0 до 10 для положительно определенных ф-ций …). При этом аргумент автоматически изменяется с таким мелким шагом, чтобы график выглядел плавной линией (если задать тип линии – точки, они сольются в сплошную линию). Поменять пределы изменения аргумента можно непосредственно на графике (числа слева и справа внизу области графика). Аналогичные изменения границ для оси У не приводят к построению нового графика (может измениться только масштаб), если границы расширить, то над/под графиком останется пустое пространство, если уменьшить, то рисунок будет «обрезан».

Внимание: при построении графика, как и при вычислении значений функции, переменная-аргумент не обязана совпадать с переменной, которая использовалась для определения ф-ции. Например, задавали 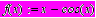(здесь х не определяет никаких значений, а только задает вид функции, т.е. является формальным аргументом), а график можно строить от ха1, тогда и по оси У указать f(ха1) (ха1 – фактический аргумент с конкретными значениями).

Если перед графиком аргумент был задан как ранжированная переменная, график будет построен в соответствующих пределах. При этом, значения функции определяются только в точках, задаваемых ранжированной переменной, которые на графике соединяются участками прямой. Так, если шаг крупный, график будет ломаной линией, для исправления такой картины нужно уменьшить шаг. Если задать тип линии – точки (для лучшего отображения увеличить толщину или выбрать символы), то на графике будут видны только точки, соответствующие ранжированной переменной. Если теперь непосредственно на графике расширить границы аргумента, то слева и справа останется свободное место (новые значения не появятся). Сузить границы можно на графике или изменив ранжированную переменную.

Аргумент может быть задан и как вектор, тогда график можно строить как и с ранжир. переменной (для всех значений вектора), или поэлементно: указывается диапазон изменения индексов вектора и в качестве аргумента переменная с индексом (например, k:=2..7, а на графике z_k и f(z_k)). Если и значение функции – вектор (функция задана таблично), то по оси У указывается имя этого вектора, если аргумент задан с индексом, то и по оси У – переменная с индексом.

Внимание: Для одного графика переменная по оси Х должна точно совпадать с аргументом функции, записываемой по оси У. Нельзя смешивать переменные с индексом и целый вектор, нельзя по одной оси указывать ранжированную переменную, а по другой – вектор.

На одних осях может быть построено несколько графиков (функции записывают через запятую, при этом они автоматически располагаются друг под другом вдоль оси У). Если аргументы разные, их тоже записывают через запятую. Порядок записи аргументов должен строго соответствовать порядку записи функций. Если количество аргументов меньше, то последний аргумент относится ко всем последующим функциям. Например, по оси У указано f(а), g(a), y_j по оси Х соответственно а, а, х_j; если поменять порядок функций: y_j, f(а), g(a), то по оси Х можно записать х_j, а , что равнозначно записи х_j, а, а. Границы изменения аргумента и функции на графике автоматически определятся по максимальным значениям (если для разных функций значения сильно отличаются, то лучше не строить их вместе, иначе какие-то графики могут быть очень маленькими).

Выполните пункт 3 работы.


Вектора и матрицы. Переменной может быть присвоено значение матрицы или вектора (вектор-столбец). Для этого используем панель «Матрицы», задав нужное число строк и столбцов, получим шаблон для заполнения конкретными значениями. Для получения шаблона вектора, число столбцов задать равным 1.




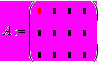
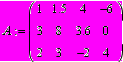
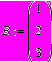
С матрицами можно проделать все допустимые операции: вычислить обратную матрицу, транспонировать матрицу, складывать и вычитать матрицы. Можно вычислить определитель матрицы, скалярное и векторное произведение.

Доступ к элементу матрицы прозводится по индексу, отсчитываему от 0.

Вектор-столбец имеет один индекс, для перехода к нижнему индексу надо нажать кнопку Xn , или с клавиатуры – [.



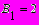
Двумерный массив имеет уже два индекса, также отсчитываемые от 0, первый из них нумерует строки, второй – столбцы, Индексы разделяются запятыми.

Можно вычислить сумму элементов вектора, используя кнопку с панели «матрицы», например:

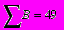
Для вычисления произведения элементов вектора или суммы/произведения эл-ов матрицы используются кнопки панели «мат. анализ»:



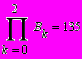
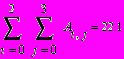
Эти же операции могут выполняться не для всех эл-ов, например для первых двух строк и последних двух столбцов





Аналогичные действия можно выполнить и с помощью других шаблонов, где индексы – это целочисленные ранжированные переменные



Индексы могут изменяться и с шагом больше 1.

Например, просуммируем элементы 0-го и 2-го столбцов



Вектора и матрицы можно также задавать поэлементно или используя общую формулу для всех элементов с заданным диапазоном номеров. Незаданные значения = 0. Например:

Пример: Задать матрицу 5 на 4, каждый элемент которой равен сумме его номера строки и столбца: m:= 0 .. 4 n:=0 .. 3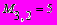

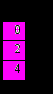
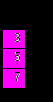
Ранжированная переменная, задающая номера элементов матрицы может изменяться и с шагом, больше 1 (только целым).


<sub>Чтобы поменять начальный номер элементов матриц используется команда ORIGIN:=первый номер

ORIGIN:=1 теперь для той же матрицы М3,2 = 3.


Пример. Определим вектор х из 10 равноотстоящих элементов от 0.2 до π,</sub>

вектор у – соответствующие значения функции sin. Сначала вычислим шаг

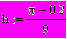
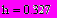
Вектор х можно задать несколькими способами:

способ 1	способ 2	способ 3	результат
			…

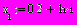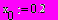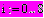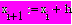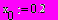<sub>Вектор у можно задать двумя способами:

сразу или поэлементно



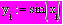
Если нумерация с 1: ORIGIN:=1</sub>








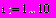
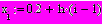
или


_или







Выполните пункты 3 и 4 работы.

Содержание работы 2

1. Задайте функцию в соответствии с исходными данными. Вычислите их значения для аргументов, заданных разными способами: непосредственные числа (из второго столбца таблицы); переменные и выражения (из третьего столбца); ранжированная переменная, изменяющаяся в заданных пределах с шагом (из последнего столбца).

Вид функции	Значение аргументов
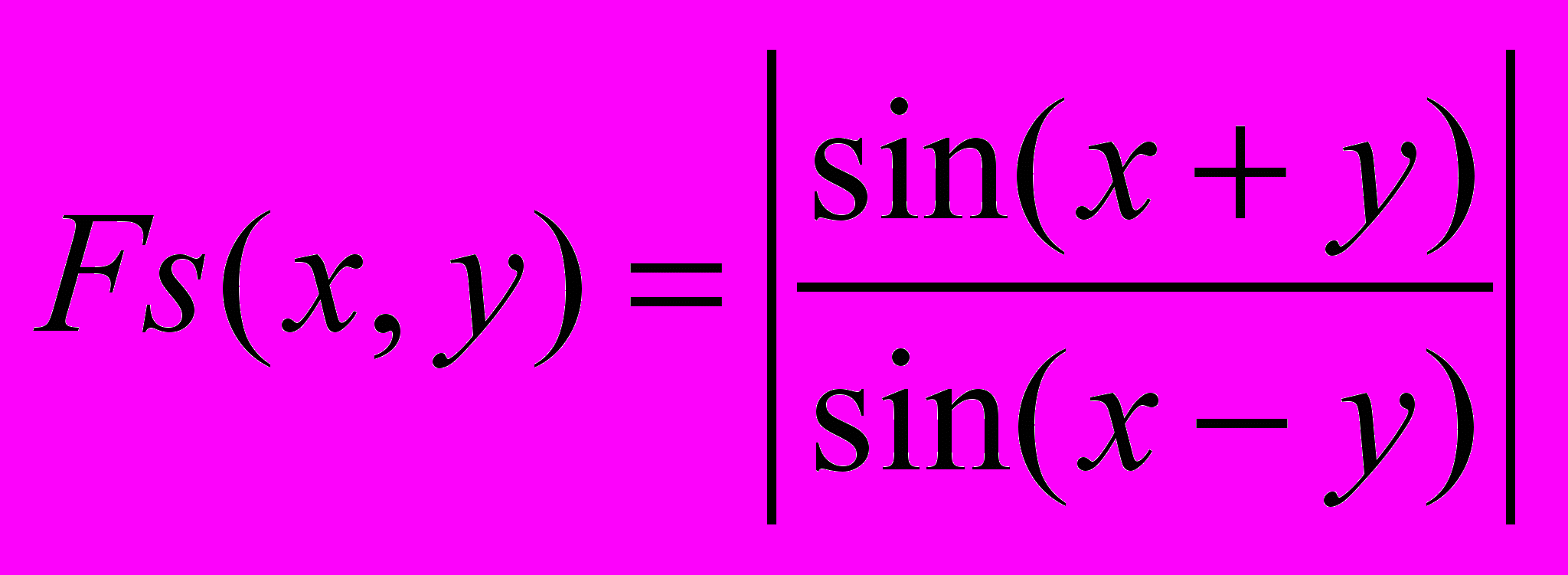	(0,6; 1) (–2; 3)	 = /4;  = –/6 (/3+2; /2 – )	x = 1 y[1; 2] h = 0,1

2. Задать ранжированную переменную x на отрезке [0,8; 1,8] с шагом 0,1. Распечатать значения x и соответствующие значения функции f(x) из п.2 Вычислить отношение суммы значений функции f(x) к произведению значений x.

3. Задать функцию f(x)=.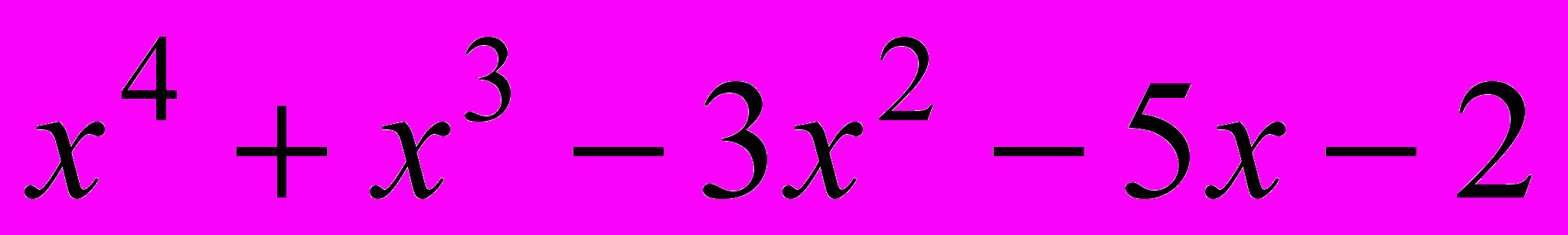

Построить ее график и отформатировать его в полном соответствии с рисунком (график f(x) — красного цвета, линии сетки — зеленые);


4. Задать вектор x на отрезке [0,8; 1,8] с шагом 0,1 и вектор у, значения которого у_i равны f(x_i) из п.2. Распечатать элементы векторов. Вычислить сумму первых пяти элементов вектора у и произведение элементов вектора x с нечетными номерами.