Исследование характера и диапазона изменения

Вид материала

Исследование

Содержание 5.1. Исследование характера и диапазона измененияхарактеристик в области эксплуатационных режимовработы двигателя 5.2. Расчёт характеристик ГР с учётом и без учёта колебательных процессов, сравнительный анализ результатов 5.3. Влияние закона движения толкателя на динамику МГР 5.4. Методика синтеза, структура и элементыавтоматизированного программного комплекса 5.5. Результаты и выводы

Подобный материал:

• Великой Отечественной Войны. Данное исследование, 132.59kb.
• Морфофункциональные изменения при хроническом гастрите у собак и воздействии эми квч, 342.08kb.
• Аналитическое исследование, 321.69kb.
• Исследование энергодинамических и регулировочных характеристик гидропривода с гидромоторным, 310.64kb.
• Артеменко Юрий Николаевич исследование и разработка информационно-измерительной системы, 450.64kb.
• Влияние электромагнитного облучения терагерцового диапазона на частотах молекулярного, 338.37kb.
• Лампы серии Pure Light Стандартные автомобильные лампы в качестве оригинального оборудования, 92.99kb.
• Применение электромагнитных волн миллиметрового диапазона в ортопедии и травматологии, 15.01kb.
• Общественное мнение о деятельности судебных и правоохранительных органов в Республике, 79.71kb.
• Изучая географию, вы не раз осуществляли самостоятельный поиск (исследование), 53.74kb.

ГЛАВА 5. СИНТЕЗ ХАРАКТЕРИСТИК ГАЗОРАСПРЕДЕЛЕНИЯ ДВИГАТЕЛЯ, РАБОТАЮЩЕГО В ЗАДАННОМ ПОЛЕ РЕЖИМОВ

В данном разделе исследован характер и диапазон изменения характеристик ГР на различных эксплуатационных режимах, а также влияние ограничений высших производных от перемещения толкателя по углу поворота кулачка на показатели динамики. Представлена методика синтеза характеристик ГР на основе совместного решения задач формирования закона движения толкателя, математического моделирования динамики МГР и рабочих процессов двигателя с учётом его работы в заданном поле эксплуатационных режимов. Приведены примеры и произведён сравнительный анализ результатов.

5.1. Исследование характера и диапазона изменения
характеристик в области эксплуатационных режимов
работы двигателя

Среди показателей, определяющих надёжность кулачковой пары, важнейшими являются гидродинамические условия смазки сопряжения кулачок-толкатель. На рис. 5.1.а в качестве примера приведены характерные диаграммы скорости скольжения V_ск по углу поворота кулачка, рассчитанные для сопряжения впускной кулачок - толкатель тракторного дизеля 8ЧВН15/16 на различных скоростных режимах работы. Используемые для её вычисления расчётные зависимости при различных кинематических схемах механизма приведены в разделе 2.2. Значения скорости и ускорения толкателя, необходимые для расчёта характеристик, приведённых на рис. 5.1 и 5.2, определялись путём численного дифференцирования со сглаживанием таблично заданного на чертеже закона перемещения толкателя с учётом кинематики качающегося рычага.

Величина V_ск пропорциональна угловой скорости вращения кулачка , поэтому при оценке тепловой напряжённости и склонности сопряжения к износу используют также отношение V_ск/. Из представленных графиков следует, что неблагоприятная зона наибольших значений V_ск соответствует отрицательному участку и области перемены знака ускорения толкателя. При этом существенно влияние асимметрии закона качания рычага толкателя (для рассматриваемой схемы МГР с рычажным толкателем), взаимодействующего с симметричным кулачком, на характер изменения V_ск по углу поворота кулачка. Так, максимальное значение скорости скольжения для рассматриваемого клапанного привода имеет место на стороне профиля, соответствующей подъёму толкателя, как это видно на рис. 5.1.а. В реальных конструкциях МГР величина V_ск может достигать 3 - 5 м/с, а для ряда быстроходных двигателей даже превышать 6 м/с.

Рис.5.1. Характеристики сопряжения кулачок-толкатель по углу поворота кулачка при значениях угловой скорости его вращения 89 (1), 110 (2) и 130 (3) рад/с: скорость относительного скольжения (а), гидродинамически эффективная скорость (б), контактное напряжение (в)

Рис. 5.2. Толщина масляной плёнки в сопряжении кулачок-толкатель по углу поворота кулачка: а) - при значениях угловой скорости его вращения 89 (1), 110 (2) , 130 (3) рад/с и вязкости масла 0,012 Нс/м2; б) - при значениях угловой скорости его вращения 89 рад/с и вязкости масла 0,012 (1), 0,008 (2), 0,006 (3) Нс/м2

Условия работы кулачковой пары существенно зависят также от такой кинематической характеристики, как гидродинамически эффективная скорость V_г. Чем больше по модулю величина V_г, тем лучше гидродинамические условия смазки, так как при этом увеличивается толщина масляной плёнки согласно (1.1). Из расчётных формул для V_г (см. раздел 2.2) следует, что её величина пропорциональна угловой скорости  вращения кулачка.

Неблагоприятные условия смазки сопряжения кулачок-толкатель обычно соответствуют участку отрицательного ускорения толкателя, о чём свидетельствуют приведённые на рис. 5.1.б характерные диаграммы изменения V_г по углу поворота кулачка, рассчитанные для МГР двигателя 8ЧВН15/16. При этом, также как и для скорости скольжения V_ск, существенное влияние на протекание характеристики V_г оказывает асимметрия закона движения толкателя. Так, на стороне его подъёма значения гидродинамически эффективной скорости существенно меньше, чем на стороне опускания, причём в двух точках участка отрицательного ускорения при его подъёме она даже равна нулю. Именно в таких точках, как показываю результаты ряда исследований [213, 384, 451, 471], наблюдаются максимальные износы профиля кулачка.

На рис. 5.2.а приведены диаграммы минимальной толщины масляной плёнки h_min в сопряжении кулачок-толкатель, рассчитанной по (1.1) для различных скоростных режимов работы двигателя. При этом значение действующей в сопряжении силы, используемое для вычисления h_min и контактного напряжения  (см. рис. 5.1 в и 5.2), определялось по (2.33) для облегчённого варианта клапанного механизма (приведённая масcа M принималась равной 0,694 кг). Величина h_min, используемая для оценки гидродинамических условий смазки сопряжения кулачок-толкатель и рассчитываемая по формулам контактной гидродинамики, оказывает существенное влияние на износостойкость рассматриваемого сопряжения и изменяется в выполненных конструкция в пределах от нескольких десятых до единиц микрометров в различных точках профиля. Сопоставление рисунков 5.1.б и 5.2.а позволяет сделать вывод о сходном характере изменения V_г и h_min. Однако величина h_min зависит на только от гидродинамически эффективной скорости V_г и свойств материалов, но также от вязкости масла ₀ и действующей силы. В случае квазистационарного расчёта, результаты которого приведены на рис. 5.2, изменение нагрузки слабо влияет на h_min вследствие малого показателя степени в формуле (1.1) для действующей силы, равного (-0,13). Однако изменение вязкости может оказать заметное влияние на величину h_min, что иллюстрируется диаграммой на рис. 5.2.б. При этом уменьшение ₀ может быть обусловлено ростом температуры в контакте, связанным с увеличением скорости скольжения V_ск, максимальные значения которой приходятся, как уже отмечалось, на те же участки профиля кулачка, где не высоки значения гидродинамически эффективной скорости V_г. Кроме того, вязкость масла зависит также от температурного режима работы двигателя. Приведённые на рис. 5.2.б диаграммы, соответствующие номинальному скоростному режиму двигателя 8ЧВН15/16, дают возможность количественно оценить влияние вязкости масла на h_min.

Рассмотрим приведённые на рис. 5.1.в характеристики контактного напряжения  по углу поворота кулачка на различных скоростных режимах работы двигателя, полученные на основе квазистационарного расчёта. Для кривой 1 характерен максимальный уровень контактного напряжения в области вершины кулачка, постоянный на значительном протяжении профиля.

С увеличением частоты вращения кулачка максимальная величина  уменьшается в связи с ростом по модулю отрицательных значений ускорения. Приведенные на рис. 5.1.в расчётные диаграммы позволяют количественно оценить это изменение. При этом уровень контактного напряжения в районе вершины кулачка уже не остаётся постоянным.

Следует также отметить, что на участке положительного ускорения толкателя с увеличением частоты вращения кулачка контактное напряжение растёт. Однако здесь его уровень невысок в связи с большим радиусом кривизны профиля. Поэтому на боковых поверхностях кулачка величина  не достигает максимальных значений даже при значительном росте частоты вращения кулачка.

Из сказанного следует, что при работе двигателя на скоростных режимах меньше номинального (например, на режиме максимального крутящего момента) контактное напряжение в районе вершины кулачка может достигать своих максимальных значений. Однако для быстроходных двигателей при недостаточной жёсткости клапанного привода следует считаться с ростом нагруженности сопряжения кулачок-толкатель в связи с колебательными процессами в МГР.

Таким образом, выявлены закономерности изменения основных характеристик сопряжения кулачок-толкатель по углу поворота кулачка в области эксплутационных режимов работы двигателя. Приведённый анализ позволяет сделать вывод, что наиболее тяжёлые условия работы сопряжения кулачок-толкатель МГР ДВС по контактной прочности, гидродинамическим условиям смазки, тепловой напряжённости и склонности к износу соответствуют области отрицательного ускорения толкателя.

5.2. Расчёт характеристик ГР с учётом и без учёта колебательных процессов, сравнительный анализ результатов

Для решении задачи выбора характеристик ГР представляется важным исследовать влияние возникающих в упругом клапанном приводе колебательных процессов на его нагруженность и на показатели, определяющие прочность и надёжность МГР.

Выполненные многочисленные расчётные и экспериментальные исследования позволяют сделать вывод, что отклонения действительного перемещения клапана от теоретического, вызванные деформацией клапанного привода и возникающими колебательными процессами, даже в МГР с нижним расположением распределительного вала не превышают нескольких десятых миллиметра и не изменяют существенно значение время-сечения клапана. На протекание процессов газообмена может оказать влияние лишь изменение фаз газораспределения, обусловленное наряду с отмеченными факторами также и наличием теплового зазора в механизме.

Отклонения в процессе колебаний аналога скорости клапана от теоретических значений более существенны и могут достигать нескольких миллиметров на радиан. В связи с этим определение действительной скорости клапана необходимо для оценки условий посадки клапана на седло.

Для быстроходных двигателей колебательные процессы в МГР вносят существенные изменения в закон изменения ускорения ведомого звена, увеличивают нагруженность клапанного привода и могут быть причиной разрыва кинематической цепи в процессе работы механизма. Действительные значения ускорений элементов и сил в связях могут быть определены на основе математического моделирования динамики МГР.

На рис. 5.3 приведены действительный и теоретический (без учёта колебательных процессов) законы изменения аналога ускорения впускного клапана двигателя 8ЧВН15/16 на номинальном скоростном режиме при использовании серийного кулачка. Приведённые диаграммы получены на основе адекватной модели динамики клапанного привода, идентифицированной по экспериментальным данным (см. раздел 6.2). Величина теплового зазора в механизме на стороне толкателя принималась равной 0,1 мм.

Рис. 5.3. Аналог ускорения клапана по углу поворота кулачка при n= 1700 об/мин с учётом (1) и без учёта (2) колебаний в клапанном приводе

Согласно полученным данным максимальное теоретическое значение аналога ускорения клапана равно 83 мм/рад², в то время как его действительное максимальное значение без учёта ударных ускорений при посадке клапана составляет 142 мм/рад². Таким образом, коэффициент динамичности по ускорению равен 1,71, а среднеквадратичное отклонение последнего от теоретических значений составляет 27 мм/рад². Эти значения увеличиваются при недостаточной жёсткости привода и с ростом частоты вращения распределительного вала.

На рис. 5.4 приведены расчётные диаграммы сил в связи коромысло-клапан (между элементами 3 и 4 на рис. 3.4) при работе двигателя на различных скоростных режимах. Квазистатическое значение силы вычислялось по формуле

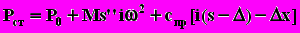, (5.1)

где - начальное усилие клапанных пружин;

M - масса движущихся частей механизма, приведённая к клапану;

- аналог ускорения толкателя;

i - передаточное число коромысла;

 - угловая скорость вращения кулачка;

с_пр - жёсткость клапанных пружин;

s - перемещение толкателя;

 - тепловой зазор на стороне толкателя;

x - квазистатическая деформация клапанного привода, вычисляемая по формуле

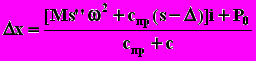, (5.2)

где c - жёсткость привода.

Из рисунков следует, что если при n= 800 об/мин максимальные усилия в приводе возникают в районе вершины кулачка, то с ростом частоты вращения этот максимум перемещается в область положительных ускорений на стороне подъёма толкателя как при квазистационарном расчёте, так и при учёте колебательных процессов в механизме. При этом в первом случае (кривая 2) уменьшение максимального усилия при n= 1250 об/мин (рис. 5.4.б) по сравнению с n= 800 об/мин (рис. 5.4.а) объясняется увеличением по модулю отрицательного ускорения на вершине кулачка.

Получаемые на основе математического моделирования динамики результаты не только позволяют сделать качественный вывод об усилении колебательных процессов в МГР с ростом частоты вращения коленчатого вала, но и оценить их количественно. Сравнительные показатели динамики МГР на различных скоростных режимах приведены в таблице 5.1.

Следует отметить, что важно определить не только максимальные усилия в приводе в процессе его работы, но и минимальные, характеризующие возможность разрыва кинематической цепи и неуправляемого движения клапана.

На рис. 5.5 наряду с усилиями в коромысле на стороне клапана (кривые 1) приведены также диаграммы силы, сжимающей штангу толкателя (кривые 2) и силы, действующей в стержне клапана (кривые 3) на различных скоростных режимах. В последнем случае определяется ударная сила в паре седло - клапан при посадке клапана. С использованием таких графиков оценивается нагруженность, прочность и устойчивость элементов МГР.

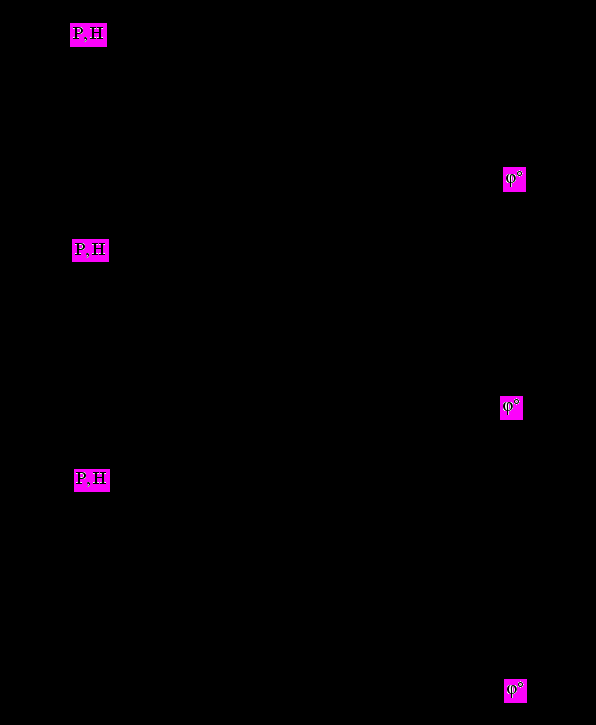Рис. 5.4. Сила в МГР по углу поворота кулачка при n= 800 (а), 1250 (б) и 1700 (в) об/мин: 1 - с учётом колебаний; 2 - квазистатическое значение

Таблица 5.1 Показатели динамики клапанного привода по действующим силам Частота вращения коленчатого вала n, об/мин Максимальная квазистатическая сила в приводе Pmax2, Н Максимальная сила в приводе Pmax1, H Коэффициент динамичности по силам Среднеквадратичное отклонение силы от квазистатических значений P, H 800 808 836 1,03 54,9 1250 763 935 1,22 105,7 1700 887 1205 1,36 137

На основе математического моделирования динамики МГР наряду с действующими силами определяются также перемещения, скорости, ускорения элементов и контактные напряжения в сопряжениях. Так, на рис. 5.6

приведены диаграммы контактного напряжения в сопряжении кулачок-толкатель на различных скоростных режимах, полученные с помощью упомянутой математической модели динамики МГР двигателя 8ЧВН15/16. Расчёт контактного напряжения выполнен по известным формулам Герца (см., например, (2.22) или (2.28)) с учётом и без учёта колебаний. В последнем случае требуемая для расчёта сила вычислялась по формуле

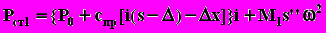, (5.3)

где M₁ - масса клапанного механизма, приведённая к толкателю.

Максимальные значения контактного напряжения возникают при подъёме толкателя в области отрицательного ускорения около точки перемены его знака. В таблице 5.2 приведены оценочные показатели динамики МГР по контактному напряжению.

Таблица 5.2 Показатели динамики клапанного привода по контактному напряжению в сопряжении кулачок-толкатель Частота вращения коленчатого вала n, об/мин Максимальное квазистатическое напряжение max2, MПа Максимальное контактное напряжение max1, МПа Коэффициент динамичности по контактному напряжению Среднеквадратичное отклонение , МПа 800 383 410 1,07 14,1 1250 357 426 1,2 27,6 1700 333 411 1,23 36,7

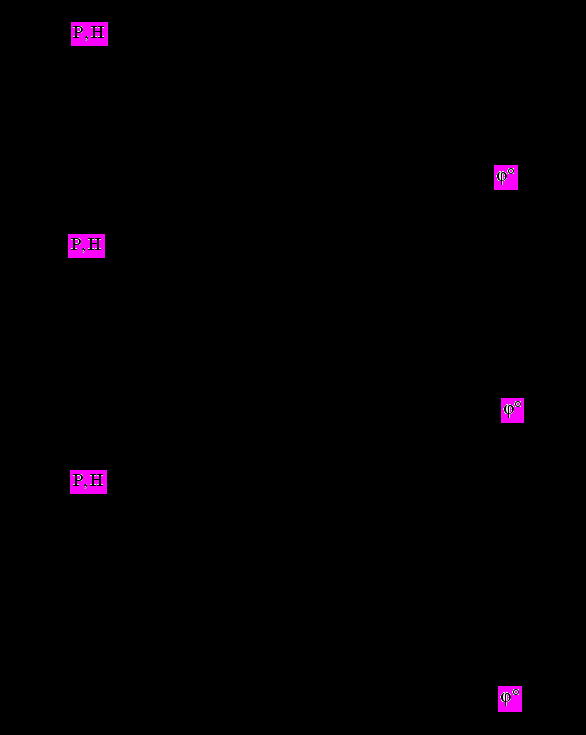Рис. 5.5. Силы в элементах МГР по углу поворота кулачка при n= 800 (а), 1250 (б) и 1700 (в) об/мин: 1 - на стороне клапана (между коромыслом и клапаном); 2 - на стороне толкателя (между толкателем и коромыслом); 3 - в стержне клапана

Сопоставление диаграмм, приведённых на рис. 5.6, позволяет сделать следующий вывод. С увеличением частоты вращения кулачка контактное напряжение в районе его максимальных значений в квазистационарном расчёте (кривые 2) снижается в связи с ростом по модулю отрица-

Рис. 5.6. Контактное напряжение в сопряжении кулачок-толкатель по углу поворота кулачка при n= 800 (а), 1250 (б) и 1700 (в) об/мин: 1 - с учётом колебаний; 2 - квазистатическое значение

тельного ускорения. Однако при этом одновременно увеличивается амплитуда колебаний, что в конечном итоге приводит к примерно одинаковому уровню максимального контактного напряжения при различных скоростных режимах работы двигателя. Действительно, огибающие максимальных пиков контактного напряжения в области его максимальных значений на рис. 5.7 практически совпадают при различных частотах вращения n.

Рис. 5.7. Контактное напряжение в сопряжении кулачок-толкатель по углу поворота кулачка: 1 - при n= 1700 об/мин; 2 - при n= 1250 об/мин; 3 - при n= 800 об/мин.

Рассмотрим характеристики гидродинамики смазки в сопряжении кулачок-толкатель. Из формул, приведённых в разделе 2.2, следует, что колебательные процессы в механизме не оказывают влияния на гидродинамически эффективную скорость и скорость скольжения. Однако толщина масляной плёнки зависит также и от действующей силы, достоверное определение которой связано с учётом динамических процессов в механизме. Методика такого расчёта и анализ влияния колебательных процессов в механизме на толщину масляной плёнки рассмотрены в разделе 3.3.

Таким образом, при оценке действительной нагруженности упругого клапанного привода и определении показателей, связанных с его надёжностью, необходимо учитывать колебательные процессы в механизме. Эта задача может быть решена на основе математического моделирования динамики МГР.

5.3. Влияние закона движения толкателя на динамику МГР

Многочисленные расчётные и экспериментальные исследования показывают, что закон движения толкателя, в частности, изменение ускорения по углу поворота кулачка, оказывает существенное влияние на динамику клапанного механизма. Так, установлено, что виброактивность кулачка МГР, работающего в широком диапазоне скоростных режимов, тем ниже, чем существует большее количество производных от перемещения толкателя по углу поворота кулачка. При этом для обеспечения плавного движения толкателя в быстроходных двигателях важно как обеспечить отсутствие разрывов ускорения и производных перемещения толкателя более высоких порядков, так и ограничить их экстремальные значения, что способствует уменьшению колебаний звеньев привода и особенно клапанных пружин. Именно поэтому функцию ускорения часто составляют из отрезков синусоид и косинусоид. Законы такого типа имеют слабые гармоники высших порядков, что снижает интенсивность колебаний клапанных пружин [306]. Однако на границах таких отрезков могут быть разрывы высших производных. Кроме того, такие законы не обеспечивают максимальную эффективность ГР, определяемую время-сечением клапана.

Анализ влияния характера изменения ускорения толкателя на показатели динамики клапанного механизма в простых случаях может быть выполнен аналитически. Так, в [219] c использованием операционного метода, основанного на преобразованиях Лапласа, такой анализ выполнен для различных законов кинематического возбуждения одномассового упругого кулачкового привода при отсутствии демпфирования для чисто инерционной нагрузки. При этом получены выражения для коэффициента динамичности по ускорениям, равного отношению максимального модуля ускорения выходного звена с учётом упругости связи к соответствующему значению для жёсткого привода. Полученные результаты свидетельствуют о преимуществах в динамическом отношении неразрывных и гладких законов движения толкателя.

Однако более точный анализ динамики конкретного клапанного механизма в заданном поле скоростных режимов при использовании различных законов кинематического возбуждения может быть выполнен с помощью адекватной математической модели. При этом могут быть также определены действующие силы, контактные напряжения, оценена надёжность силового замыкания звеньев.

В данном разделе в качестве примера расчётно исследована динамика МГР при использовании трёх законов изменения аналога ускорения, приведённых на рис. 5.8. Соответствующие симметричные законы движения толкателя, разработанные численным методом, имеют верхний выстой при максимальном перемещении толкателя 10 мм, и угловую протяжённость 100. Исследование проведено в диапазоне изменения частоты вращения коленчатого вала двигателя 1250  2000 об/мин с использованием адекватной динамической модели привода впускного клапана двигателя 8ЧВН15/16, идентифицированной по экспериментальным данным (см. раздел 6.2). Величина теплового зазора в механизме на стороне толкателя принималась равной 0,1 мм.

Рис. 5.8. Аналог ускорения толкателя по углу поворота кулачка: 1 - с ограничениями на ; 2 - с ограничениями на и ; 3 - с ограничениями на , и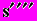

При использовании пошагового численного метода формирования закона движения толкателя плавность закона изменения его ускорения определяется задаваемыми ограничениями на аналог ускорения и его производные согласно (2.7). Разрывный закон ускорения 1 на рис. 5.8 сформирован с учётом ограничения вида (2.7), действующего на всей области изменения угла поворота кулачка  как при подъёме, так и при опускании толкателя:

-20 мм/рад² 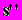  50 мм/рад². (5.4)

Значение площади под кривой перемещения толкателя для кулачка 1 равно 12,38 мм²рад.

Трапецеидальный закон 2 на рис. 5.8 сформирован с учётом ограничения (5.4) и дополнительного ограничения вида (2.7), также действующего на всей области изменения угла поворота кулачка  как при подъёме, так и при опускании толкателя:

-500 мм/рад³ 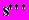  500 мм/рад³. (5.5)

Значение площади под кривой перемещения толкателя для кулачка 2 составляет 11,87 мм²рад.

Наконец, гладкий закон ускорения 3 на рис. 5.8 сформирован с учётом ограничений (5.4), (5.5) и дополнительного ограничения вида (2.7), также действующего на всей области изменения угла поворота кулачка  как при подъёме, так и при опускании толкателя:

-5000 мм/рад⁴ 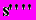  5000 мм/рад⁴. (5.6)

Значение площади под кривой перемещения толкателя для кулачка 3 равно 10,83 мм²рад.

На рис. 5.9. приведены графики изменения максимального усилия P_max в клапанном приводе на стороне клапана и максимального контактного напряжения _max в сопряжении кулачок-толкатель в зависимости от частоты вращения коленчатого вала n для трёх изображённых на рис. 5.8 законов движения толкателя. С увеличением n значения P_max, приходящиеся на начало движения толкателя, монотонно возрастают для законов 1, 2 и 3. При этом на всех скоростных режимах с увеличением плавности изменения ускорения от закона 1 до закона 3 значения P_max уменьшаются.

Максимальные значения контактного напряжения _max имеют место, как правило, на участке отрицательного ускорения вблизи точки перемены его знака на стороне подъёма толкателя. Следует отметить, что величина _max зависит как от отрицательных ускорений, возрастающих с ростом n, так и от колебательных процессов в механизме. В диапазоне изменения n= 1250  1800 об/мин сохраняется закономерность уменьшения _max с увеличением плавности изменения ускорения от закона 1 до закона 3 (см. рис. 5.9.б). При n > 1800 об/мин эта закономерность нарушается, что может быть объяснено некоторым снижением интенсивности колебаний (см. рис. 5.10.б) для закона 1, вызванным особенностями частотных характеристик привода клапана и закона движения толкателя (например, соотношением частоты собственных колебаний привода и протяжённости положительного участка кривой ускорения [192]). Для разрывной кривой ускорения 1 значение _max сначала возрастает с ростом n, а затем убывает (рис. 5.9.б). Но чем более плавно изменяется ускорение (законы 2 и 3), тем монотоннее и в более узких пределах изменяются значения _max. В связи с этим в целом можно сделать вывод о более благоприятных характеристиках изменения _max для неразрывных кривых ускорения при работе двигателя в диапазоне эксплуатационных режимов.

То же относится и к характеристикам интенсивности колебаний, приведённым на рис. 5.10. Среднеквадратичные отклонения силы в клапанном приводе и контактного напряжения в сопряжении кулачок-толкатель от соответствующих квазистатических значений (то есть вычисленных без учёта колебательных значений) определялись по формуле (3.65). Подъёмы и провалы характеристик на отдельных скоростных режимах уменьшаются с ростом плавности изменения ускорения толкателя. Кроме того, для закона с разрывной кривой ускорения 1 уже при n= 1250 об/мин наблюдаются разрывы кинематической цепи клапанного привода в процессе его работы, в то время как для закона 3 такие разрывы отсутствуют во всём исследуемом диапазоне изменения скоростных режимов.

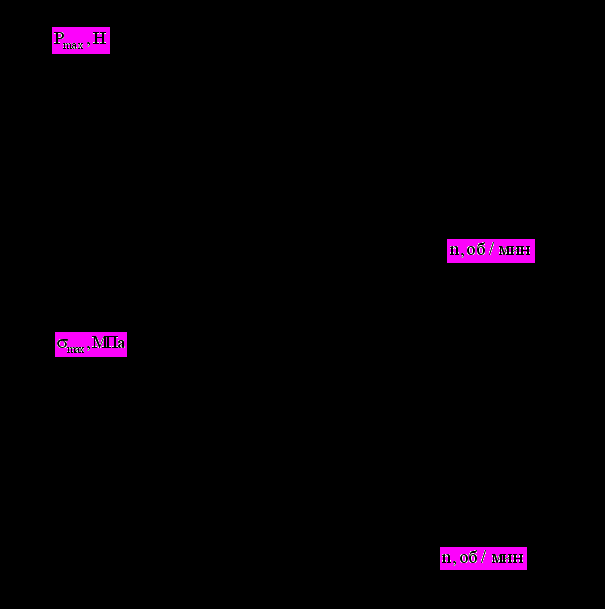Рис. 5.9. Характеристики МГР двигателя 8ЧВН15/16 по частоте вращения коленчатого вала для законов движения толкателя, изображённых на рис. 5.1 : а) - максимальная сила в приводе; б) - максимальное контактное напряжения в сопряжении кулачок- толкатель

Таким образом, плавность изменения ускорения толкателя, определяемая для численного метода профилирования кулачка ограничениями на высшие производные от перемещения толкателя по углу поворота кулачка, оказывают значительное влияние на динамические характеристики клапанного привода и, следовательно, могут служить эффективным рычагом их улучшения. Разработанные численные методы, алгоритмы и компьютерные программы позволяют оперативно в автоматизированном режиме получать соответствующие качественные и количественные результаты.

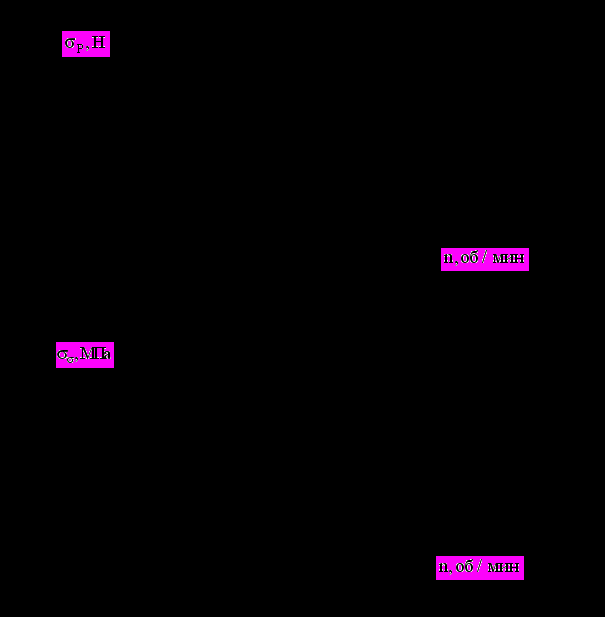Рис. 5.10. Характеристики МГР двигателя 8ЧВН15/16 по частоте вращения коленчатого вала для законов движения толкателя, изображённых на рис. 5.1 : среднеквадратичные отклонения силы в клапанном приводе (а) и контактного напряжения в сопряжении кулачок-толкатель (б) от соответствующих квазистатических значений

5.4. Методика синтеза, структура и элементы
автоматизированного программного комплекса

Рассмотрим комплексную методику синтеза характеристик ГР, базирующуюся на разработанных обобщённых численных методах пошагового формирования закона движения толкателя, моделирования динамики и газообмена. Соответствующая укрупнённая схема алгоритма приведена на рис. 5.11, а структура используемого автоматизированного диалогового программного комплекса - на рис. 5.12.

Рис. 5.11. Схема алгоритма синтеза характеристик ГР ДВС

Рис. 5.12. Структура диалогового автоматизированного программного комплекса для проектирования МГР

Содержание файлов исходных данных изложено в приведённых выше описаниях соответствующих методов и программных комплексов. Состав общей базы данных представлен на рис. 5.12. Кроме того, для проведения расчёта необходимо определить диапазоны изменения скоростных режимов работы двигателя и варьирования фаз газораспределения.

Выбор диапазонов варьирования значений фаз осуществляется по результатам анализа их влияния на показатели двигателя для различных эксплуатационных режимов работы. При этом могут быть использованы регрессионные зависимости, аналогичные полученным в разделе 4.3.

Значения текущих значений фаз (процедура 3 на рис. 5.11) определяются методом сканирования с заданным шагом либо на основе использования известных методов оптимизации. Возможно также применение методов планирования эксперимента для сокращения количества исследуемых сочетаний фаз и последующего получения регрессионных зависимостей.

Затем согласно процедуре 4 выполняется синтез законов движения толкателя для впускного и выпускного приводов клапанов на основе численного метода, описанного в главе 2 (комплекс программ САМ на рис. 5.12).

Рассматриваемая методика формирования оптимальных характеристик предполагает первоначальный выбор проектировщиком тех или иных ограничений (2.7) на высшие производные, обеспечивающих требуемую плавность закона движения толкателя в соответствии с быстроходностью двигателя. Так, например, для двигателей малой быстроходности на основе существующих рекомендаций может быть выбран один из следующих вариантов: разрывная кривая ускорения с ограничиваемой величиной его скачка, трапецеидальный закон изменения ускорения. Для двигателей средней и высокой быстроходности ограничения на высшие производные задаются таким образом, чтобы была сформирована неразрывная или гладкая кривая ускорения толкателя. Наконец, если двигатель предназначен для работы на одном скоростном режиме или в узком диапазоне изменения частоты вращения коленчатого вала, то возможна динамическая настройка закона движения толкателя. При этом во всех случаях обеспечивается максимизация время-сечения клапана. Кроме того, в исходных данных для формирования законов движения толкателей задаются требуемые ограничения на прочностные, гидродинамические, технологические, кинематические характеристики, параметры сбега с учётом кинематики МГР при возможной реализации описанных во второй главе особенностей.

Процедура 5 на рис. 5.11 предусматривает проверку отсутствия встречи клапанов с поршнем для исследуемых законов движения в соответствии с текущими значениями фаз газораспределения при заданных размерах и кинематике МГР, а также кривошипно-шатунного механизма двигателя. Соответствующая компьютерная программа входит в состав программного комплекса (ELEM на рис. 5.12). При наличии встречи осуществляется соответствующая коррекция закона движения толкателя либо переход к следующим значениям фаз в соответствии с законом их варьирования (см. процедуру 3).

Моделирование динамики МГР (процедура 6 на рис. 5.11) выполняется на основе разработанной обобщённой математической модели, представленной в третьей главе (комплекс программ D на рис. 5.12). Серия динамических расчётов проводится в заданном диапазоне скоростных режимов работы двигателя с установленным шагом по частоте вращения коленчатого вала двигателя. Для привода выпускного клапана моделируется сила от давления газов на тарелку клапана, действующая в начальной фазе его открытия на заданном нагрузочном режиме. В случае неудовлетворительной динамики клапанного привода (повышенная нагруженность, разрывы звеньев, превышение допускаемых контактных напряжений и др.) формируется соответствующее сообщение в выходной файл и осуществляется возврат к процедуре 4 - синтезу законов движения толкателя.

При этом производится коррекция соответствующих исходных данных (процедура 8 на рис. 5.11) с целью повышения плавности кривой ускорения толкателя и улучшению динамических характеристик. Расчёты согласно данной методике продолжаются до тех пор, пока формируемый закон движения толкателя не будет удовлетворять заданным требованиям во всём исследуемом диапазоне режимов. Изложенный алгоритм может быть реализован как в диалоговом, так и в автоматизированном режиме.

На следующем этапе согласно процедуре 9 на рис. 5.11 осуществляется моделирование рабочих процессов ДВС, определение показателей газообмена, индикаторных и эффективных показателей двигателя на основе обобщённого метода, описанного в четвёртой главе (комплекс программ GAS на рис. 5.12). Данное исследование проводится в рассматриваемом диапазоне режимов работы двигателя, а критериальным показателем в этом случае может служить удельный эффективный среднеэксплуатационный расход топлива. При этом с целью сокращения затрат машинного времени показатели газообмена и характеристики двигателя могут быть определены с использованием полученных ранее регрессионных зависимостей. Следует также отметить, что результаты моделирования рабочих процессов двигателя в заданном поле режимов работы при различных фазах газораспределения могут быть использованы, например, при разработке систем газораспределения с изменяемыми фазами.

Последовательность действий, соответствующих процедурам 4  9, выполняется для всех исследуемых согласно процедуре 3 сочетаний фаз газораспределения, после чего выбирается вариант, соответствующий минимуму выбранного критерия качества. Затем с помощью комплекса программ TECHNOLOGY, описанного в разделе 2.6, осуществляется подготовка данных, необходимых для изготовления и контроля профилей кулачков в соответствии с той или иной кинематической схемой.

Наряду с упомянутыми программами, автоматизированный программный комплекс VG для проектирования МГР содержит также программы PROF профилирования кулачка и выбора закона движения толкателя традиционными методами, используемые для выполнения сравнительных расчётов. В частности, во второй главе приведены результаты исследования характеристик кулачков Курца и трёхдуговых кулачков с разрывным ускорением, рассчитанных с помощью данных программ. Кроме того, рассматриваемый комплекс VG содержит также программы DIFF для расчёта закона движения толкателя и характеристик профиля при табличном задании перемещения толкателя по углу поворота кулачка с некоторым шагом (так обычно задаются профили кулачков на чертежах распределительных валов).

Так как шаг по углу поворота кулачка приводимых в исходной таблице значений перемещения толкателя зачастую бывает чрезмерно большим для численного дифференцирования, разработанная и реализованная в комплексе программ DIFF методика предусматривает на первом этапе интерполирование таблично заданной функции с помощью интерполяционного процесса Эйткена - Лагранжа [292] при заданной точности итераций. Затем выполняется расчёт характеристик скорости и ускорения толкателя на основе численного дифференцирования функции его перемещения, заданной таблицей значений в равноотстоящих точках по формулам Лагранжа с пятью узлами [292].

Как известно, операция численного дифференцирования не является достаточно устойчивой и приводит к некоторому разбросу результатов. В связи с этим целесообразно, как показывают многочисленные расчёты, после каждой процедуры численного дифференцирования проводить двукратное сглаживание. Для этого используется специальная подпрограмма сглаживания функции, заданной таблицей значений в равноотстоящих точках, с помощью многочлена первой степени, построенного по трём последовательным точкам методом наименьших квадратов.

Наконец, после определения функций скорости и ускорения толкателя выполняется расчёт характеристик МГР в соответствии с используемой кинематической схемой (см. раздел 2.2). При необходимости производится пересчёт закона движения толкателя и характеристик для других кинематических схем МГР и его размеров, как это показано в 2.2 и 2.6.

Объединение в единый комплекс VG программ, предназначенные для разработки и проектирования элементов МГР, математического моделирования его динамики, а также процессов газообмена в ДВС позволяет организовать их оперативное взаимодействие (обмен данными) и эффективное использование. Результаты использования разработанной комплексной методики проектирования кулачков для разработки и совершенствования системы газораспределения двигателя 8ЧН15/16 свидетельствуют об её эффективности.

5.5. Результаты и выводы

1. Определён характер и диапазон изменения характеристик, связанных с работоспособностью и надёжностью системы ГР на различных скоростных режимах без учёта и с учётом колебательных процессов в клапанном приводе.
   
2. Качественно и количественно оценено влияние различных законов движения толкателя с разрывным и неразрывным ускорением, сформированных пошаговым численным методом, на динамику и нагруженность клапанного привода в широком диапазоне скоростных режимов.
   
3. Разработана методика синтеза характеристик ГР двигателей, работающих в заданном поле эксплуатационных режимов, основанная на совместном решении задач формирования закона движения толкателя, математического моделирования динамики МГР и рабочих процессов двигателя.
   
4. Создан автоматизированный комплекс компьютерных программ, позволяющий эффективно решать перечисленные задачи.