Конспект лекцій до дисципліни Безпека програм та даних

Вид материала

Конспект

Содержание Лекция 3. Контроль целостности информации 1.1 Криптография. Классификация криптоалгоритмов Симметричные криптоалгоритмы 1.3 Симметричные криптоалгоритмы 1.3.2 Блочные шифры Общие сведения о блочных шифрах Название алгоритма Сеть Фейштеля Лекция 6. Защита программ от взлома

Подобный материал:

• Конспект лекцій з дисципліни „Радіоекологія для студентів спеціальності 040106  „Екологія,, 1393.76kb.
• Конспект лекцій Хмельницький, 2005 Снозик О. В. Безпека життєдіяльності, 909.72kb.
• Конспект лекцій Удвох частинах Частина 2 Суми, 1998.47kb.
• Конспект лекцій Удвох частинах Частина 1 Суми, 2323.63kb.
• Конспект лекцій Суми Видавництво Сумду 2010, 2423.29kb.
• Конспект лекцій з дисципліни „ Управління інноваційним розвитком" для студентів факультету, 2082.69kb.
• Конспект лекцій з дисципліни «Оподаткування підприємств», 2062.58kb.
• Конспект лекцій з дисципліни "Дослідна робота", 768.49kb.
• Конспект лекцій з дисципліни Правознавство Харків − хнамг − 2006 Міністерство освіти, 3534.27kb.
• Як конспект лекцій Дніпропетровськ Нметау 2008, 735.01kb.

JBOD

А что делать, если нужен просто один логический диск гигантского размера? Без всяких зеркалирований, чередования и четности? Тогда это уже не RAID, а JBOD – Just A Bunch Of Disks. Реализовать этот режим способен простейший контроллер или даже программная реализация контроллера.

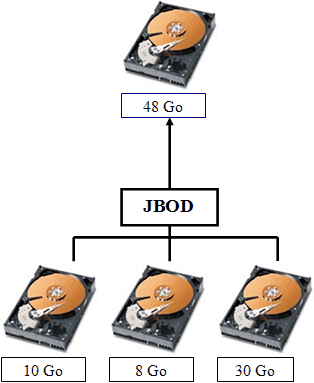Объединение дисков в один логический

Есть ли у него преимущества, если JBOD не повышает ни быстродействия, ни надежности? Есть. По крайней мере, для работы используется все доступное пространство жестких дисков. И еще: в случае выхода из строя одного из жестких дисков, информация на других не повреждается.

Сведем основные характеристики наиболее распространенных уровней в таблицы.

Распространенные single RAID массивы

	RAID 0	RAID 1	RAID 3	RAID 5	RAID 6
Технология	Чередование	Зеркали- рование	Чередование, четность	Чередование, четность	Чередование, четность
Контроллер	Все	Все	Аппаратный	Аппаратный Hi-End	Специали- зированный
Кол-во жестких дисков	2, 4	2	3 и больше	3 и больше	3 и больше
Доступное рабочее пространство, %	100	50	66 для 3, 75 для 4	66 для 3, 75 для 4	33 для 3 50 для 4 60 для 5
Стойкость при отказе диска	Нет	Высокая	Высокая	Высокая	Очень высокая
Восстановление данных	Нет	Очень быстрое	Быстрое	Быстрое	Очень быстрое
Скорость случайного чтения	Очень хорошая	Хорошая	Хорошая	Очень хорошая	Очень хорошая
Скорость случайной записи	Очень хорошая	Хорошая	Плохая	Нормальная	Плохая
Скорость линейного чтения	Очень хорошая	Хорошая	Очень хорошая	Очень хорошая	Хорошая
Скорость линейной записи	Очень хорошая	Хорошая	Хорошая	Хорошая	Средняя
Цена	Самая низкая	Низкая	Средняя	Средняя	Высокая

Распространенные multi-RAID массивы

	RAID 0+1	RAID 1+0	RAID 5+0	RAID 5+1
Технология	Чередование, зеркали- рование	Чередование, зеркали- рование	Чередование, четность	Чередование, четность, зеркали- рование
Контроллер	Почти все	Почти все	Специали- зированный	Специали- зированный
Кол-во жестких дисков	4 min	4 min	6 min	6 min
Доступное рабочее пространство, %	50	50	66 для 2 страйпов по 3 диска	33-40
Стойкость при отказе диска	Очень хорошая	Отличная	Хорошая	Отличная
Восстановление данных	Быстрое	Очень быстрое	Среднее	Быстрое
Скорость случайного чтения	Очень хорошая	Очень хорошая	Очень хорошая	Очень хорошая
Скорость случайной записи	Хорошая	Хорошая	Хорошая	Хорошая
Скорость линейного чтения	Очень хорошая	Очень хорошая	Очень хорошая	Очень хорошая
Скорость линейной записи	Хорошая	Хорошая	Хорошая	Хорошая
Цена	Относительно высокая	Относительно высокая	Высокая	Очень высокая

Лекция 3. Контроль целостности информации


Контроль целостности программной структурыв процессе эксплуатацииКонтроль целостности программ и данных выполняется одни-ми и теми же методами. Исполняемые программы изменяютсякрайне редко на этапе их эксплуатации. Существует достаточноширокий класс программ, для которых все исходные данные илиих часть также изменяются редко. Поэтому контроль целостноститаких файлов выполняется так же, как и контроль программ.Контроль целостности программных средств и данных осуще-ствляется путем получения (вычисления) характеристик и сравне-ния их с контрольными характеристиками. Контрольные характе-ристики вычисляются при каждом изменении соответствующегофайла. Характеристики вычисляются по определенным алгорит-мам. Наиболее простым алгоритмом является контрольное сум-мирование. Контролируемый файл в двоичном виде разбиваетсяна слова, обычно состоящие из четного числа байт. Все двоичныеслова поразрядно суммируются с накоплением по mod2, образуя врезультате контрольную сумму. Разрядность контрольной суммыравняется разрядности двоичного слова.


Алгоритм полученияконтрольной суммы может отличаться от приведенного, но, какправило, не является сложным и может быть получен по имею-щейся контрольной сумме и соответствующему файлу.Другой подход к получению характеристик целостности свя-зан с использованием циклических кодов [63]. Суть метода со-стоит в следующем. Исходная двоичная последовательностьпредставляется в виде полинома F(x) степени п-1, где п - числобит последовательности. Для выбранного порождающего поли-нома Р(х) можно записать равенство:110где m - степень порождающего полинома, G(x) - частное, a R(x) -| остаток от деления F(x) • хш на Р(х).Из приведенного соотношения можно получить новое выра-I жение:Из последнего выражения можно сделать вывод: если исход-ный полином увеличить на хш (сдвинуть в сторону старших раз-рядов на m разрядов) и сложить с остатком R(x) по модулю 2, тополученный многочлен разделится без остатка на порождающийполином Р(х).При контроле целостности информации контролируемая по-следовательность (сектор на диске, файл и т. д.), сдвинутая на mразрядов, делится на выбранный порождающий полином, и запо-минается полученный остаток, который называют синдромом.Синдром хранится как эталон.


При контроле целостности к поли-ному контролируемой последовательности добавляется синдром иосуществляется деление на порождающий полином. Если остатокот деления равен нулю, то считается, что целостность контроли-руемой последовательности не нарушена. Обнаруживающая спо-собность метода зависит от степени порождающего полинома ине зависит от длины контролируемой последовательности. Чемвыше степень полинома, тем выше вероятность определения из-менений d, которая определяется из соотношения: d =l/2m.Использование контрольных сумм и циклических кодов, как идругих подобных методов, имеет существенный недостаток.


Алгоритм получения контрольных характеристик хорошо известен, ипоэтому злоумышленник может произвести изменения таким об-разом, чтобы контрольная характеристика не изменилась (напри-мер, добавив коды).Задача злоумышленника усложнится, если использовать пере-менную длину двоичной последовательности при подсчете кон-трольной характеристики, а характеристику хранить в зашифро-ванном виде или вне КС (например, в ЗУ Touch Memory).Рассмотрим пример использования циклических кодов дляконтроля целостности двоичной последовательности.Пусть требуется проконтролировать целостность двоичнойпоследовательности А=1010010. Используется порождаемый по-лином вида: Р(х)=х3+х+1.111А. Получение контрольной характеристики.При вычислении синдрома RA(X) действия выполняются поправилам деления полиномов, заменяя операцию вычитания опе-рацией сложения по модулю:Двоичная последовательность с синдромом имеет вид :А' = 1010010011 (синдром подчеркнут).


ПоследовательностьА' хранится и(или) передается в КС.Б. Контроль целостности информации.Если изменений последовательности А' = 1010010011 не про-изошло, то соответствующий ей полином должен разделиться напорождающий полином без остатка:Результат произведенных вычислений свидетельствует о це-лостности информации.112Если синдром отличен от нуля, то это означает, что произошлаошибка при хранении (передаче) двоичной последовательности.Ошибка определяется и в контрольных разрядах (в синдроме).Существует метод, который позволяет практически исключитьвозможность неконтролируемого изменения информации в КС.Для этого необходимо использовать хэш-функцию. Под хэш-функцией понимается процедура получения контрольной харак-теристики двоичной последовательности, основанная на кон-трольном суммировании и криптографических преобразованиях.Алгоритм хэш-функции приведен в ГОСТ Р34.11-94.


Алгоритм неявляется секретным, так же как и алгоритм используемого приполучении хэш-функции криптографического преобразования,изложенного в ГОСТ 28147-89 [9].Исходными данными для вычисления хэш-функции являютсяисходная двоичная последовательность и стартовый вектор хэши-рования. Стартовый вектор хэширования представляет собой дво-ичную последовательность длиной 256 бит. Он должен быть не-доступен злоумышленнику.

Вектор либо подвергается зашифро-ванию, либо хранится вне КС.Итерационный процесс вычисления хэш-функции Н преду-сматривает:• генерацию четырех ключей (слов длиной 256 бит);• шифрующее преобразование с помощью ключей текущегозначения Н методом простой замены (ГОСТ 28147-89);• перемешивание результатов;• поразрядное суммирование по mod2 слов длиной 256 бит ис-ходной последовательности;• вычисление функции Н.В результате получается хэш-функция длиной 256 бит. Значе-ние хэш-функции можно хранить вместе с контролируемой ин-формацией, т. к., не имея стартового вектора хэширования, зло-умышленник не может получить новую правильную функциюхэширования после внесения изменений в исходную последова-тельность. А получить стартовый вектор по функции хэширова-ния практически невозможно.


Лекция 4. Основны криптографической защиты информации

1.1 Криптография.

Классификация криптоалгоритмов

Сама криптография не является высшей ступенью классификации смежных с ней дисциплин. Наоборот, криптография совместно с криптоанализом (целью которого является противостояние методам криптографии) составляют комплексную науку – криптологию.

Необходимо отметить, что в русскоязычных текстах по данному предмету встречаются различные употребления основных терминов, таких как "криптография", "тайнопись" и некоторых других. Более того, и по классификации криптоалгоритмов можно встретить различные мнения. В связи с этим автор не претендует на то, что его вариант использования подобных терминов является единственно верным.

В отношении криптоалгоритмов существует несколько схем классификации, каждая из которых основана на группе характерных признаков. Таким образом, один и тот же алгоритм "проходит" сразу по нескольким схемам, оказываясь в каждой из них в какой-либо из подгрупп.

Основной схемой классификации всех криптоалгоритмов является следующая:

1. Тайнопись.
   Отправитель и получатель производят над сообщением преобразования, известные только им двоим. Сторонним лицам неизвестен сам алгоритм шифрования. Некоторые специалисты считают, что тайнопись не является криптографией вообще, и автор находит это совершенно справедливым.
   
2. Криптография с ключом.
   

Алгоритм воздействия на передаваемые данные известен всем сторонним лицам, но он зависит от некоторого параметра – "ключа", которым обладают только отправитель и получатель.

1. Симметричные криптоалгоритмы. Для зашифровки и расшифровки сообщения используется один и тот же блок информации (ключ).
   
2. Асимметричные криптоалгоритмы. Алгоритм таков, что для зашифровки сообщения используется один ("открытый") ключ, известный всем желающим, а для расшифровки – другой ("закрытый"), существующий только у получателя.
   

Весь дальнейший материал будет посвящен криптографии с ключом, так как большинство специалистов именно по отношению к этим криптоалгоритмам используют термин криптография, что вполне оправдано. Так, например, любой криптоалгоритм с ключом можно превратить в тайнопись, просто "зашив" в исходном коде программы некоторый фиксированный ключ. Обратное же преобразование практически невозможно.

В зависимости от характера воздействий, производимых над данными, алгоритмы подразделяются на:

1. Перестановочные
   Блоки информации (байты, биты, более крупные единицы) не изменяются сами по себе, но изменяется их порядок следования, что делает информацию недоступной стороннему наблюдателю.
   
2. Подстановочные
   Сами блоки информации изменяются по законам криптоалгоритма. Подавляющее большинство современных алгоритмов принадлежит этой группе.
   

Заметьте: любые криптографические преобразования не увеличивают объем информации, а лишь изменяют ее представление. Поэтому, если программа шифрования значительно (более, чем на длину заголовка) увеличивает объем выходного файла, то в ее основе лежит неоптимальный, а возможно и вообще некорректный криптоалгоритм. Уменьшение объема закодированного файла возможно только при наличии встроенного алгоритма архивации в криптосистеме и при условии сжимаемости информации (так, например, архивы, музыкальные файлы формата MP3, видеоизображения формата JPEG сжиматься более чем на 2-4% не будут).

В зависимости от размера блока информации криптоалгоритмы делятся на:

1. Потоковые шифры.
   Единицей кодирования является один бит. Результат кодирования не зависит от прошедшего ранее входного потока. Схема применяется в системах передачи потоков информации, то есть в тех случаях, когда передача информации начинается и заканчивается в произвольные моменты времени и может случайно прерываться. Наиболее распространенными предствателями поточных шифров являются скремблеры.
   
2. Блочные шифры
   Единицей кодирования является блок из нескольких байтов (в настоящее время 4-32). Результат кодирования зависит от всех исходных байтов этого блока. Схема применяется при пакетной передаче информации и кодировании файлов.
   

1.3 Симметричные криптоалгоритмы

1.3.1. Скремблеры

Скремблерами называются программные или аппаратные реализации алгоритма, позволяющего шифровать побитно непрерывные потоки информации. Сам скремблер представляет из себя набор бит, изменяющихся на каждом шаге по определенному алгоритму. После выполнения каждого очередного шага на его выходе появляется шифрующий бит – либо 0, либо 1, который накладывается на текущий бит информационного потока операцией XOR.

1.3..2. Блочные шифры

Блочные шифры шифруют целые блоки информации (от 4 до 32 байт) как единое целое – это значительно увеличивает стойкость преобразований к атаке полным перебором и позволяет использовать различные математические и алгоритмические преобразования.

1.3.1 Скремблеры

В последнее время сфера применения скремблирующих алгоритмов значительно сократилась. Это объясняется в первую очередь снижением объемов побитной последовательной передачи информации, для защиты которой были разработаны данные алгоритмы. Практически повсеместно в современных системах применяются сети с коммутацией пакетов, для поддержания конфиденциальности которой используются блочные шифры. А их криптостойкость превосходит, и порой довольно значительно, криптостойкость скремблеров.

Суть скремблирования заключается в побитном изменении проходящего через систему потока данных. Практически единственной операцией, используемой в скремблерах является XOR – "побитное исключающее ИЛИ". Параллельно прохождению информационного потока в скремблере по определенному правилу генерируется поток бит – кодирующий поток. Как прямое, так и обратное шифрование осуществляется наложением по XOR кодирующей последовательности на исходную.

Генерация кодирующей последовательности бит производится циклически из небольшого начального объема информации – ключа по следующему алгоритму. Из текущего набора бит выбираются значения определенных разрядов и складываются по XOR между собой. Все разряды сдвигаются на 1 бит, а только что полученное значение ("0" или "1") помещается в освободившийся самый младший разряд. Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным ее битом (см. рис.1).


Рис.1.

Из теории передачи данных криптография заимствовала для записи подобных схем двоичную систему записи. По ней изображенный на рисунке скремблер записывается комбинацией "10011₂" – единицы соответствуют разрядам, с которых снимаются биты для формирования обратной связи.

Рассмотрим пример кодирования информационной последовательности 010111₂ скремблером 101₂ с начальным ключом 110₂.

скремблер код.бит инф.бит рез-т

1 1 0 _

\ \ \_

1 1 1 _ \_

\ \ \_ 0 XOR 0 = 0

0 1 1 _ \_

\ \ \_ 1 XOR 1 = 0

1 0 1 \_

\ \ 1 XOR 0 = 1

и т.д.

Как видим, устройство скремблера предельно просто. Его реализация возможна как на электронной, так и на электрической базе, что и обеспечило его широкое применение в полевых условиях. Более того, тот факт, что каждый бит выходной последовательности зависит только от одного входного бита, еще более упрочило положение скремблеров в защите потоковой передачи данных. Это связано с неизбежно возникающими в канале передаче помехами, которые могут исказить в этом случае только те биты, на которые они приходятся, а не связанную с ними группу байт, как это имеет место в блочных шифрах.

Декодирование заскремблированных последовательностей происходит по той же самой схеме, что и кодирование. Именно для этого в алгоритмах применяется результирующее кодирование по "исключающему ИЛИ" – схема, однозначно восстановимая при раскодировании без каких-либо дополнительных вычислительных затрат. Произведем декодирование полученного фрагмента.

Как Вы можете догадаться, главная проблема шифров на основе скремблеров - синхронизация передающего (кодирующего) и принимающего (декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация необратимо теряется. Поэтому, в системах шифрования на основе скремблеров очень большое внимание уделяется методам синхронизации. На практике для этих целей обычно применяется комбинация двух методов: а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении такого бита активно начать поиск синхронизации с отправителем, и б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить декодирование принимаемых битов информации "по памяти" без синхронизации.

Число бит, охваченных обратной связью, то есть разрядность устройства памяти для порождающих кодирующую последовательность бит называется разрядностью скремблера. Изображенный выше скремблер имеет разрядность 5. В отношении параметров криптостойкости данная величина полностью идентична длине ключа блочных шифров, который будет проанализирован далее. На данном же этапе важно отметить, что чем больше разрядность скремблера, тем выше криптостойкость системы, основанной на его использовании.

При достаточно долгой работе скремблера неизбежно возникает его зацикливание. По выполнении определенного числа тактов в ячейках скремблера создастся комбинация бит, которая в нем уже однажды оказывалась, и с этого момента кодирующая последовательность начнет циклически повторяться с фиксированным периодом. Данная проблема неустранима по своей природе, так как в N разрядах скремблера не может пребывать более 2^N комбинаций бит, и, следовательно, максимум, через, 2^N-1 циклов повтор комбинации обязательно произойдет. Комбинация "все нули" сразу же исключается из цепочки графа состояний скремблера – она приводит скремблер к такому же положению "все нули". Это указывает еще и на то, что ключ "все нули" неприменим для скремблера. Каждый генерируемый при сдвиге бит зависит только от нескольких бит хранимой в данный момент скремблером комбинации. Поэтому после повторения некоторой ситуации, однажды уже встречавшейся в скремблере, все следующие за ней будут в точности повторять цепочку, уже прошедшую ранее в скремблере.

Возможны различные типы графов состояния скремблера. На рисунке 2 приведены примерные варианты для 3-разрядного скремблера. В случае "А" кроме всегда присутствующего цикла "000">>"000" мы видим еще два цикла – с 3-мя состояниями и 4-мя. В случае "Б" мы видим цепочку, которая сходится к циклу из 3-х состояний и уже никогда оттуда не выходит. И наконец, в случае "В" все возможные состояния кроме нулевого, объединены в один замкнутый цикл. Очевидно, что именно в этом случае, когда все 2^N-1 состояний системы образуют цикл, период повторения выходных комбинаций максимален, а корреляция между длиной цикла и начальным состоянием скремблера (ключом), которая привела бы к появлению более слабых ключей, отсутствует.


Рис.2.

И вот здесь математика преподнесла прикладной науке, каковой является криптография, очередной подарок. Следствием одной из теорем доказывается (в терминах применительно к скремблированию), что для скремблера любой разрядности N всегда существует такой выбор охватываемых обратной связью разрядов, что генерируемая ими последовательность бит будет иметь период, равный 2^N-1 битам. Так, например, в 8-битном скремблере, при охвате 0-го, 1-го, 6-го и 7-го разрядов действительно за время генерации 255 бит последовательно проходят все числа от 1 до 255, не повторяясь ни разу.

Схемы с выбранными по данному закону обратными связями называются генераторами последовательностей наибольшей длины (ПНД), и именно они используются в скремблирующей аппаратуре. Из множества генераторов ПНД заданной разрядности во времена, когда они реализовывались на электрической или минимальной электронной базе выбирались те, у которых число разрядов, участвующих в создании очередного бита, было минимальным. Обычно генератора ПНД удавалось достичь за 3 или 4 связи. Сама же разрядность скремблеров превышала 30 бит, что давало возможность передавать до 2⁴⁰ бит = 100 Мбайт информации без опасения начала повторения кодирующей последовательности.

ПНД неразрывно связаны с математической теорией неприводимых полиномов. Оказывается, достаточно чтобы полином степени N не был представим по модулю 2 в виде произведения никаких других полиномов, для того, чтобы скремблер, построенный на его основе, создавал ПНД. Например, единственным неприводимым полиномом степени 3 является x³+x+1, в двоичном виде он записывается как 1011₂ (единицы соответствуют присутствующим разрядам). Скремблеры на основе неприводимых полиномов образуются отбрасыванием самого старшего разряда (он всегда присутствует, а следовательно, несет информацию только о степени полинома), так на основе указанного полинома, мы можем создать скремблер 011₂ с периодом зацикливания 7(=2³-1). Естественно, что на практике применяются полиномы значительно более высоких порядков. А таблицы неприводимых полиномов любых порядков можно всегда найти в специализированных математических справочниках.

Существенным недостатком скремблирующих алгоритмов является их нестойкость к фальсификации. Подробнее данная проблема рассмотрена на следующей лекции, применительно к созданию целых криптосистем.

1.3.2 Блочные шифры

1.3.2.1. Общие сведения о блочных шифрах   ( 19 кб )
На сегодняшний день разработано достаточно много стойких блочных шифров. Практически все алгоритмы используют для преобразований определенный набор биективных (обратимых) математических преобразований

1.3.2.2. Сеть Фейштеля
Сетью Фейштеля называется метод обратимых преобразований текста, при котором значение, вычисленное от одной из частей текста, накладывается на другие части. Часто структура сети выполняется таким образом, что для шифрования и дешифрования используется один и тот же алгоритм – различие состоит только в порядке использования материала ключа.

1.3.2.3. Блочный шифр TEA
Блочный алгоритм TEA приведен как пример одного из самых простых в реализации стойких криптоалгоритмов.

1.3.2.4. AES : cтандарт блочных шифров США c 2000 года
В 1998 году был объявлен открытый конкурс на криптостандарт США на несколько первых десятилетий XXI века. Победителем конкурса был признан бельгийский блочный шифр Rijndael. Скорее всего он станет стандартом де-факто блочного шифрования во всем мире.

Общие сведения о блочных шифрах

Характерной особенностью блочных криптоалгоритмов является тот факт, что в ходе своей работы они производят преобразование блока входной информации фиксированной длины и получают результирующий блок того же объема, но недоступный для прочтения сторонним лицам, не владеющим ключом. Таким образом, схему работы блочного шифра можно описать функциями Z=EnCrypt(X,Key) и X=DeCrypt(Z,Key)

Ключ Key является параметром блочного криптоалгоритма и представляет собой некоторый блок двоичной информации фиксированного размера. Исходный (X) и зашифрованный (Z) блоки данных также имеют фиксированную разрядность, равную между собой, но необязательно равную длине ключа.

Блочные шифры являются основой, на которой реализованы практически все криптосистемы. Методика создания цепочек из зашифрованных блочными алгоритмами байт позволяет шифровать ими пакеты информации неограниченной длины. Такое свойство блочных шифров, как быстрота работы, используется асимметричными криптоалгоритмами, медлительными по своей природе. Отсутствие статистической корреляции между битами выходного потока блочного шифра используется для вычисления контрольных сумм пакетов данных и в хешировании паролей.

Следующие разработки всемирно признаны стойкими алгоритмами и публикаций о универсальных методах их взлома в средствах массовой информации на момент создания материала не встречалось.

Название алгоритма	Автор	Размер блока	Длина ключа
IDEA	Xuejia Lia and James Massey	64 бита	128 бит
CAST128		64 бита	128 бит
BlowFish	Bruce Schneier	64 бита	128 – 448 бит
ГОСТ	НИИ ***	64 бита	256 бит
TwoFish	Bruce Schneier	128 бит	128 – 256 бит
MARS	Корпорация IBM	128 бит	128 – 1048 бит

Криптоалгоритм именуется идеально стойким, если прочесть зашифрованный блок данных можно только перебрав все возможные ключи, до тех пор, пока сообщение не окажется осмысленным. Так как по теории вероятности искомый ключ будет найден с вероятностью 1/2 после перебора половины всех ключей, то на взлом идеально стойкого криптоалгоритма с ключом длины N потребуется в среднем 2^N-1 проверок. Таким образом, в общем случае стойкость блочного шифра зависит только от длины ключа и возрастает экспоненциально с ее ростом. Даже предположив, что перебор ключей производится на специально созданной многопроцессорной системе, в которой благодаря диагональному параллелизму на проверку 1 ключа уходит только 1 такт, то на взлом 128 битного ключа современной технике потребуется не менее 10²¹ лет. Естественно, все сказанное относится только к идеально стойким шифрам, которыми, например, с большой долей уверенности являются приведенные в таблице выше алгоритмы.

Кроме этого условия к идеально стойким криптоалгоритмам применяется еще одно очень важное требование, которому они должны обязательно соответствовать. При известных исходном и зашифрованном значениях блока ключ, которым произведено это преобразование, можно узнать также только полным перебором. Ситуации, в которых постороннему наблюдателю известна часть исходного текста встречаются повсеместно. Это могут быть стандартные надписи в электронных бланках, фиксированные заголовки форматов файлов, довольно часто встречающиеся в тексте длинные слова или последовательности байт. В свете этой проблемы описанное выше требование не является ничем чрезмерным и также строго выполняется стойкими криптоалгоритмами, как и первое.

Таким образом, на функцию стойкого блочного шифра Z=EnCrypt(X,Key) накладываются следующие условия:

1. Функция EnCrypt должна быть обратимой.
   
2. Не должно существовать иных методов прочтения сообщения X по известному блоку Z, кроме как полным перебором ключей Key.
   
3. Не должно существовать иных методов определения каким ключом Key было произведено преобразование известного сообщения X в сообщение Z, кроме как полным перебором ключей.
   

Давайте рассмотрим методы, с помощью которых разработчики блочных криптоалгоритмов добиваются одновременного выполнения этих трех условий с очень большой долей достоверности.

Все действия, производимые над данными блочным криптоалгоритмом, основаны на том факте, что преобразуемый блок может быть представлен в виде целого неотрицательного числа из диапазона, соответствующего его разрядности. Так, например, 32-битный блок данных можно интерпретировать как число из диапазона 0..4'294'967'295. Кроме того, блок, разрядность которого обычно является "степенью двойки", можно трактовать как несколько независимых неотрицательных чисел из меньшего диапазона (рассмотренный выше 32-битный блок можно также представить в виде 2 независимых чисел из диапазона 0..65535 или в виде 4 независимых чисел из диапазона 0..255).

Над этими числами блочным криптоалгоритмом и производятся по определенной схеме следующие действия (слева даны условные обозначения этих операций на графических схемах алгоритмов) :

Биективные математические функции
	Сложение	X'=X+V
	Исключающее ИЛИ	X'=X XOR V
	Умножение по модулю 2N+1	X'=(X*V) mod (2N+1)
	Умножение по модулю 2N	X'=(X*V) mod (2N)
Битовые сдвиги
	Арифметический сдвиг влево	X'=X SHL V
	Арифметический сдвиг вправо	X'=X SHR V
	Циклический сдвиг влево	X'=X ROL V
	Циклический сдвиг вправо	X'=X ROR V
Табличные подстановки
	S-box (англ. substitute)	X'=Table[X,V]

В качестве параметра V для любого из этих преобразований может использоваться:

1. фиксированное число (например, X'=X+125)
   
2. число, получаемое из ключа (например, X'=X+F(Key))
   
3. число, получаемое из независимой части блока (например, X₂'=X₂+F(X₁))
   

Последний вариант используется в схеме, названной по имени ее создателя сетью Фейштеля (нем. Feistel).

Последовательность выполняемых над блоком операций, комбинации перечисленных выше вариантов V и сами функции F и составляют "ноу-хау" каждого конкретного блочного криптоалгоритма. Размер блоков и длина ключа современных (1999 год) алгоритмов были нами рассмотрены ранее. Один-два раза в год исследовательские центры мира публикуют очередной блочный шифр, который под яростной атакой криптоаналитиков либо приобретает за несколько лет статус стойкого криптоалгоритма, либо (что происходит неизмеримо чаще) бесславно уходит в историю криптографии.

Характерным признаком блочных алгоритмов является многократное и косвенное использование материала ключа. Это диктуется в первую очередь требованием невозможности обратного декодирования в отношении ключа при известных исходном и зашифрованном текстах. Для решения этой задачи в приведенных выше преобразованиях чаще всего используется не само значение ключа или его части, а некоторая, иногда необратимая (небиективная) функция от материала ключа. Более того, в подобных преобразованиях один и тот же блок или элемент ключа используется многократно. Это позволяет при выполнении условия обратимости функции относительно величины X сделать функцию необратимой относительно ключа Key.

Поскольку операция зашифровки или расшифровки отдельного блока в процессе кодирования пакета информации выполняется многократно (иногда до сотен тысяч раз), а значение ключа и, следовательно, функций V_i(Key) остается неизменным, то иногда становится целесообразно заранее однократно вычислить данные значения и хранить их в оперативной памяти совместно с ключом. Поскольку эти значения зависят только от ключа, то оин в криптографии называются материалом ключа. Необходимо отметить, что данная операция никоим образом не изменяет ни длину ключа, ни криптостойкость алгоритма в целом. Здесь происходит лишь оптимизация скорости вычислений путем кеширования (англ. caching) промежуточных результатов. Описанные действия встречаются практически во многих блочных криптоалгоритмах и носят название расширение ключа (англ. key scheduling)

Сеть Фейштеля

Сеть Фейштеля является дальнейшей модификацией описанного выше метода смешивания текущей части шифруемого блока с результатом некоторой функции, вычисленной от другой независимой части того же блока. Эта методика получила широкое распространение, поскольку обеспечивает выполнение требования о многократном использовании ключа и материала исходного блока информации.

Классическая сеть Фейштеля имеет следующую структуру:


Рис.1.

Независимые потоки информации, порожденные из исходного блока, называются ветвями сети. В классической схеме их две. Величины V_i именуются параметрами сети, обычно это функции от материала ключа. Функция F называется образующей. Действие, состоящее из однократного вычисления образующей функции и последующего наложения ее результата на другую ветвь с обменом их местами, называется циклом или раундом (англ. round) сети Фейштеля. Оптимальное число раундов K – от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптоскойстость любого блочного шифра к криптоанализу. Возможно, эта особенность и повлияла на столь активное распространение сети Фейштеля – ведь при обнаружении, скажем, какого-либо слабого места в алгоритме, почти всегда достаточно увеличить количество раундов на 4-8, не переписывая сам алгоритм. Часто количество раундов не фиксируется разработчиками алгоритма, а лишь указываются разумные пределы (обязательно нижний, и не всегда – верхний) этого параметра.

Сразу же возникает вопрос, – является ли данная схема обратимой ? Очевидно, да. Сеть Фейштеля обладает тем свойством, что даже если в качестве образующей функции F будет использовано необратимое преобразование, то и в этом случае вся цепочка будет восстановима. Это происходит вследствие того, что для обратного преобразования сети Фейштеля не нужно вычислять функцию F^-1.

Более того, как нетрудно заметить, сеть Фейштеля симметрична. Использование операции XOR, обратимой своим же повтором, и инверсия последнего обмена ветвей делают возможным раскодирование блока той же сетью Фейштеля, но с инверсным порядком параметров V_i. Заметим, что для обратимости сети Фейштеля не имеет значение является ли число раундов четным или нечетным числом. В большинстве реализаций схемы, в которых оба вышеперечисленные условия (операция XOR и уничтожение последнего обмена) сохранены, прямое и обратное преобразования производятся одной и той же процедурой, которой в качестве параметра передается вектор величин V_i либо в исходном, либо в инверсном порядке.

С незначительными доработками сеть Фейштеля можно сделать и абсолютно симметричной, то есть выполняющей функции шифрования и дешифрования одним и тем же набором операций.


Лекция 6. Защита программ от взлома


Рассмотрим некоторые тонкости организации защиты на достаточно популярном примере - предполагаем, что программа защищена некоторым кодом (серийным номером, паролем), который сообщается пользователю после соблюдения им определенных условий. До регистрации в этой программе заблокирован ряд каких либо полезных функций, используется надоедливая реклама или ограничен строк работы. После ввода этого кода производится его проверка и при положительном исходе проверки программа начинает нормально работать.