Внешнеэкономических связей, экономики
| Вид материала | Пояснительная записка |
- М. В. Ломоносова Экономический факультет Магистратура Направление «Менеджмент» Программа, 246.76kb.
- Курс II уровень курса Магистратура Тип курса По выбору Семестр(ы), 15.71kb.
- Понятие, формы и способы осуществления внешнеэкономических связей. Предпосылки развития, 35.78kb.
- В г. Тольятти Экономический факультет Кафедра «Мировой экономики» методические рекомендации, 282.77kb.
- Состав, 21.24kb.
- В г. Калининграде А. Котенко Страхование Методические указания, 527.88kb.
- В г. Дзержинске Нижегородской области факультет: юридический Курсовая, 263.16kb.
- Информационное письмо о Всероссийской научно-практической конференции, 162.21kb.
- Понятие, формы и способы осуществления внешнеэкономических связей. Предпосылки развития, 1636.83kb.
- Практическое пособие для предпринимателей г. Ростов-на-Дону 2008г. Оглавление, 1634.23kb.
5. Методы оптимизации в инвестиционном анализе
Методы оптимизации не получили должного распространения при решении задач финансового анализа, так как их применение требует определённой математической подготовки, а также использования высокопроизводительных компьютеров, оснащённых соответствующими пакетами прикладных программ. Вместе с тем возросшие возможности персональных компьютеров и современные достижения в области программного обеспечения открывают новые перспективы для применения методов математической оптимизации в финансово-экономической сфере, делая их доступными широкому кругу специалистов.
В широком смысле процесс оптимизации (выработки оптимального решения) можно трактовать как поиск и выбор наилучшего с некоторой точки зрения варианта среди множества возможных или допустимых.
Математическая оптимизация представляет собой процесс нахождения экстремума (максимума или минимума) функции при заданных ограничениях (условная оптимизация) или без ограничений (безусловная оптимизация). Исследование проблем разработки теоретических и практических методов решения подобных задач осуществляется в рамках специального научного направления — математического программирования [1, 2, 5].
В настоящее время практически все популярные версии табличных процессоров включают встроенные средства решения задач математического программирования. Не является исключением и MS Excel, предоставляющий пользователю специальное средство — «Поиск решения».
« Поиск решения» MS Excel — это мощный инструмент оптимизации и решения уравнений, обладающий «дружелюбным» пользовательским интерфейсом и позволяющий специалисту сформулировать задачу из своей предметной области в режиме диалога. В частности, с его помощью можно быстро и эффективно определить наиболее оптимальный вариант использования ограниченных ресурсов, обеспечивающий максимизацию одних величин (например, прибыли), или же минимизацию других (например, расходов).
Средство « Поиск решения» позволяет анализировать задачи трех типов:
- линейные (все зависимости между переменными задачи линейны);
- нелинейные (между переменными задачи существует хотя бы одна непропорциональная зависимость);
- целочисленные (результаты решения должны быть целыми числами).
Говоря «языком» электронных таблиц, « Поиск решения» удобно использовать в тех случаях, когда необходимо найти оптимальное или заданное значение для отдельной ячейки путем подбора значений других ячеек с учётом возможных или требуемых ограничений.
Процедура поиска решения позволяет найти оптимальное значение формулы содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут ссылаться на другие влияющие ячейки.
Таким образом, чтобы применить « Поиск решения», необходимо сформулировать задачу в терминах MS Excel, т.е. определить в специальном окне диалога целевую ячейку, изменяемые ячейки и ограничения, если последние существуют.
Целевая ячейка (называемая также целевой функцией) — это ячейка рабочего листа, для которой нужно найти максимальное, минимальное или заданное значение. Она должна содержать формулу, прямо либо косвенно зависящую от изменяемых ячеек.
Изменяемые ячейки (искомые переменные) — это ячейки, значения которых будут изменяться до тех пор, пока не будет найдено решение. Как правило, они содержат ключевые переменные модели. В общем случае можно задать до 200 изменяемых ячеек, которые могут содержать как формулы, так и ссылки на блок, либо несмежные ячейки. Несмежные ячейки должны разделяться точкой с запятой.
При сохранении полученного решения формулы в изменяемых ячейках будут заменены постоянными значениями.
Ограничение — это значение ячейки, которое должно находиться в определённых пределах или удовлетворять целевым критериям. Ограничения могут налагаться как на целевую, так и на изменяемые ячейки. Для одной модели могут быть определены по два ограничения для каждой изменяемой ячейки (верхний и нижний пределы), а также до 100 дополнительных. Как правило, ограничения накладываются путем использования операторов сравнения: <=, >=, =. Ограничения целочисленности целесообразно применять в случаях, когда используемая в задаче величина или искомый результат должны принимать одно из двух значений — «Да» или «Нет», 0 или 1, либо когда дробные значения результатов недопустимы (например, при расчёте числа объектов инвестиций, служащих, машин, станков и т.д.).
Ограничения целочисленности могут быть заданы только для целевых ячеек.
Процедура решения оптимизационной задачи предусматривает последовательное выполнение ряда итераций. После каждой итерации происходят перерасчёт значений изменяемых ячеек и проверка заданных ограничений и критериев оптимальности. Выполнение процедуры завершается, если найдено решение с приемлемой точностью, либо если дальнейший поиск решения невозможен. Последнее возникает в случаях, когда модель сформулирована некорректно, выполнено максимально допустимое количество итераций или исчерпано предельное время решения. Можно увеличить количество выполняемых итераций, точность вычислений и время, отведённое на поиск решения, путём корректировки значений, установленных по умолчанию. Корректировка значений выполняется нажатием кнопки [Параметры] диалогового окна «Поиск решения» и указанием требуемых величин в появившемся окне «Параметры поиска решения».
После завершения поиска решения MS Excel предлагает три варианта продолжения работы:
- сохранить полученное решение или восстановить исходные значения на рабочем листе;
- сохранить полученное решение в виде именованного сценария;
- просмотреть один из встроенных отчётов о ходе решения.
Наиболее простые возможности средства « Поиск решения» продемонстрируем на примере задачи анализа предела безопасности при оценке значений потока платежей инвестиционного проекта.
Анализ предела безопасности для оценки потока платежей
В общем случае подобная задача может быть сформулирована следующим образом: определить допустимую величину ошибки оценки значений потока платежей, при которой обеспечивается безубыточность операции (т.е. нулевое значение NPV).
При решении задачи будут использоваться данные из примера 1.1.
Подготовим ЭТ согласно рис. 1.12. Заданные для вычислений формулы приведены в табл. 1.12
В этой таблице используется только одно пользовательское имя — «Ошибка», определённое для ячейки В6, значение которой по умолчанию равно 0. Ячейки блока С11:С16 содержат значения потока платежей, скорректированные на величину ошибки (базовая формула для формирования этого блока задана в ячейке С11 и копируется требуемое число раз). Поскольку по умолчанию величина ошибки равна 0, значения скорректированного потока платежей первоначально совпадают с исходными. Приступим к решению задачи.
Прежде всего, необходимо определить, какая ячейка будет использоваться в качестве целевой. В данном случае это должна быть ячейка, содержащая формулу для вычисления NPV, т.е. С18. Её величина зависит от значений потока платежей (блока ячеек С11:С16) и в результате решения задачи должна стать равной 0.
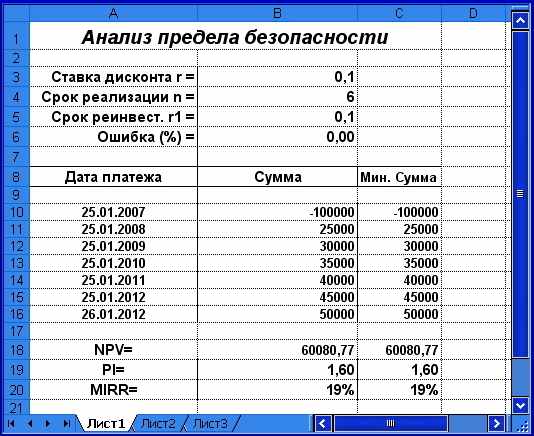
Рис. 1.12. Анализ предела безопасности (исходная электронная таблица)
Таблица 1.12
Формулы таблицы анализа предела безопасности
| Адрес ячейки | Формула |
| C11 | =В11* (1-Ошибка) |
| B18 | =ЧИСТНЗ (В3; В10:В16; А10:А16) |
| B19 | – В18 / В10 + 1 |
| B20 | =МВСД (В10:В16; В3; В5) |
| C18 | =ЧИСТНЗ (ВЗ; С10:С16; А10:А16) |
| C19 | – С18 / С10 + 1 |
| C20 | =МВСД (С10:С16; ВЗ; В5) |
Соответственно в качестве изменяемой следует использовать ту ячейку, которая оказывает непосредственное влияние на значения потока платежей, т.е. ячейку, содержащую величину ошибки — В6.
Выберите в главном меню: меню «Сервис», пункт «Поиск решения» и заполните поля появившегося окна диалога, как показано на рис. 1.13. Если команда «Поиск решения» отсутствует в меню «Сервис», установите в меню «Настройки» флажок в пункте «Поиск решения».
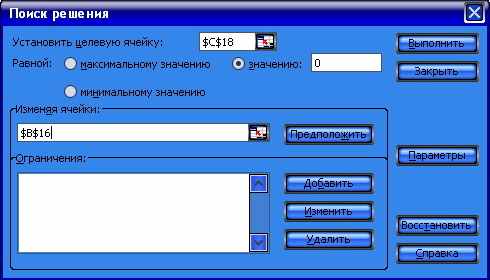
Рис. 1.13. Окно диалога «Поиск решения»
После нажатия кнопки [Выполнить] на экране появится следующее сообщение (рис. 1.14).
Рис. 1.14. Сообщение о результатах решения
Нажимаем кнопку [ОК]. Полученная в результате таблица будет иметь вид, показанный на рис. 1.15.
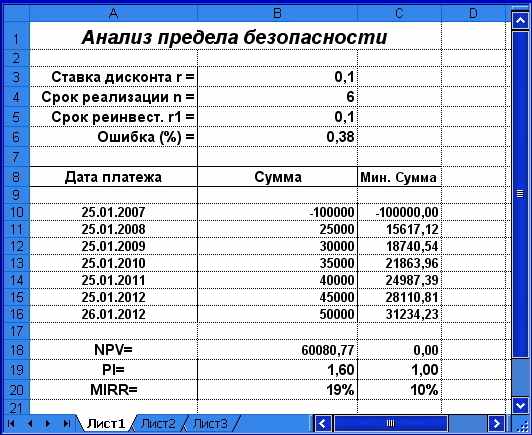
Рис. 1.15. Электронная таблица с результатами решения
Результаты анализа показывают, что проект имеет хороший запас прочности и будет безубыточным, даже если ошибка при оценке значений потока платежей составит 36%.
Очистив блок ячеек В3:В6 и удалив строки 11 – 16, получим шаблон для анализа подобных проблем.
Для решения данной задачи можно было воспользоваться более простым инструментом — « Подбор параметра».
Оптимизация портфеля инвестиций при ограниченном бюджете
Решая проблему выбора инвестиционных проектов в условиях ограниченного бюджета из примера 1.4, был использован индекс рентабельности в качестве ранга с целью отбора вариантов, обеспечивающих максимальную рентабельность вложенных средств. Более эффективный подход к решению подобных проблем заключается в применении методов математического программирования и, в частности, линейной оптимизации.
В общем случае задача линейной оптимизации формулируется в следующем виде [2]:
| A X max | (1.8) |
| C X B | (1.9) |
| Xk 0 (k = 1; n) | (1.10) |
где А — матрица коэффициентов при переменных целевой функции;
X — вектор переменных целевой функции;
С — коэффициенты функции ограничений;
В — вектор ограничений.
Технологию решения задач линейного программирования в среде MS Excel рассмотрим на примере 1.4. Обозначим проект «А» через Х1, проект «В» через Х2 и т.д. (см. табл. 1.11). Тогда целевая функция задачи может быть сформулирована в векторной форме:
| max NVP = | 1   5 00019 000 42 000 45 000 12 000 16 500 | | X 1X2 X3 X4 X5 X6 | (1.11) |
Определим ограничения для этой задачи. По условиям инвестиционный бюджет фирмы ограничен суммой в 250 000 ден. ед. Следовательно, суммарные первоначальные затраты на реализацию проектов не могут быть больше этой суммы:
| 8  0 00060 000 70 000 100 000 40 000 110 500 | × | X  1X2 X3 X4 X5 X6 | 250 000 | (1.12) |
Кроме того, нельзя реализовать отрицательное число проектов, а также конкретный проект более одного раза:
| 0 Xk (k = 1; 6) | (1.13) |
Реализуем модель (1.11) – (1.12) в среде MS Excel. Подготовим рабочий лист согласно рис. 1.16.
Необходимые для этого формулы приведены в табл. 1.13.
Приведём необходимые пояснения. Блоки ячеек В5:В10 и С5:С10 содержат коэффициенты при переменных целевой функции (1.11) и ограничениях (1.12). Произведения коэффициентов и переменных для соотношений (1.11) и (1.12) реализованы формулами в блоках D5:D10 и Е5:Е10 (базовые формулы для формирования этих блоков заданы в ячейках D5 и Е5, которые необходимо скопировать требуемое число раз). Для хранения значений искомых переменных отведен блок ячеек F5:F10. Первоначально их значения неизвестны и предполагаются равными 0. Соотношения модели (1.11) и (1.12) реализованы формулами в ячейках D12 и Е13 (целевая функция и функция ограничения соответственно).
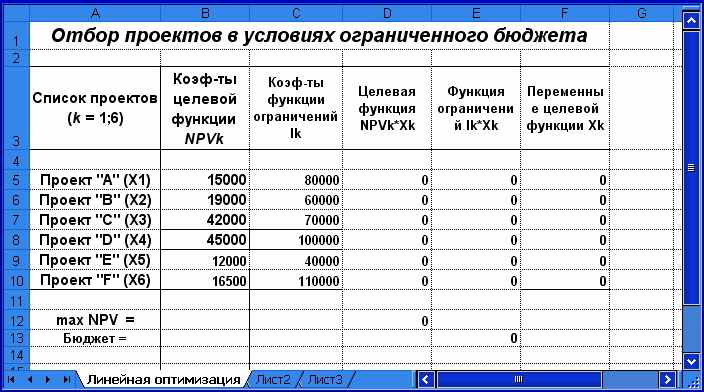
Рис. 1.16. Макет таблицы для линейной оптимизации
Таблица 1.13
Формулы рабочего листа
| Адрес ячейки | Формула |
| D5 | =B5 * F5 |
| E5 | =C5 *F5 |
| D12 | =СУММ (D5:D10) |
| E13 | =СУММ (E5:E10) |
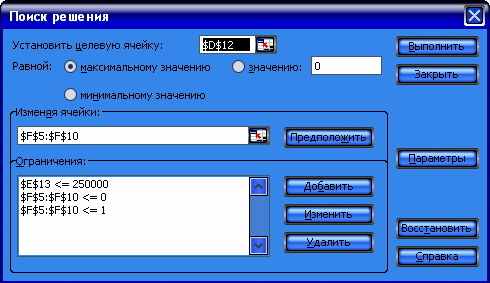
Рис. 1.17. Заполнение окна «Поиск решения» исходными данными
Выберем в главном меню MS Excel ниспадающее меню «Сервис», пункт «Поиск решения» и заполним появившееся окно диалога исходными данными, как показано на рис. 1.17. Для формирования блока ограничений щелкнем мышью по кнопке [Добавить] и заполним поля окна диалога «Добавления ограничений». Последняя операция повторяется требуемое количество раз.
П
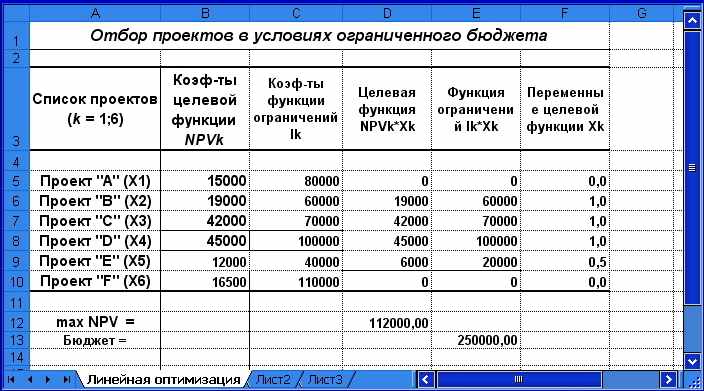олученная после нажатия кнопки [Выполнить] таблица будет иметь вид, представленный на рис. 1.18.Рис. 1.18. Результаты оптимального решения
Из приведённого решения следует, что для достижения максимальной величины NPV =112 000 необходимо реализовать 0,5 проекта «Е», а также проекты «В», «С», «D».
Отметим, что оптимальное решение обеспечивает получение большей NPV по сравнению с полученной методом ранжирования по индексу рентабельности.
Выполнив поиск решения, сохраним все значения, введенные в диалоговых окнах средства « Поиск решения» в виде модели, нажав в диалоговом окне «Параметры поиска решения» кнопку [Сохранить модель]. Таким образом, в последующих сеансах работы с MS Excel не придётся снова заниматься постановкой задачи, чтобы продолжить анализ. Загрузка сохранённой ранее модели осуществляется нажатием кнопки [Загрузить модель] диалогового окна «Параметры поиска решения» с указанием соответствующего блока ячеек.
Ещё удобнее сохранять параметры задачи в виде сценариев под определёнными именами. В диалоговом окне « Результаты поиска решения», приведённом на рис. 1.14, имеется кнопка [Сохранить сценарий]. При её нажатии активизируется специальный инструмент MS Excel «Диспетчер сценариев», который позволяет присвоить имя сценария текущим значениям изменяемых ячеек. Таким образом, можно сохранить несколько сценариев (значений изменяемых ячеек) для каждого листа рабочей книги и использовать их в дальнейшем при проведении многовариантного анализа вида «что будет, если».
MS Excel позволяет также провести дальнейшее исследование полученного решения с помощью генерации отчётов трех типов (рис. 1.14):
- результаты;
- устойчивость;
- пределы.
Генерация этих отчётов осуществляется выбором мышью требуемой позиции в списке «Тип отчёта» диалогового окна «Результаты поиска решения» и последующего нажатия кнопки [ОК]. При этом выбранный тип отчёта автоматически генерируется в виде отдельного листа рабочей книги с соответствующим названием.
В отчёте по результатам приводятся значения целевой ячейки, изменяемых ячеек и ограничений (рис. 1.19). Отчёт состоит из трех таблиц. Для целевой и изменяемых ячеек в соответствующих таблицах показываются их исходные и конечные величины. В таблицу оптимального решения для ограничений включена информация о состояниях:
- связанное, если ограничение выполнено полностью;
- несвязанное, если имеется резерв, величина которого показана в графе «Разница».
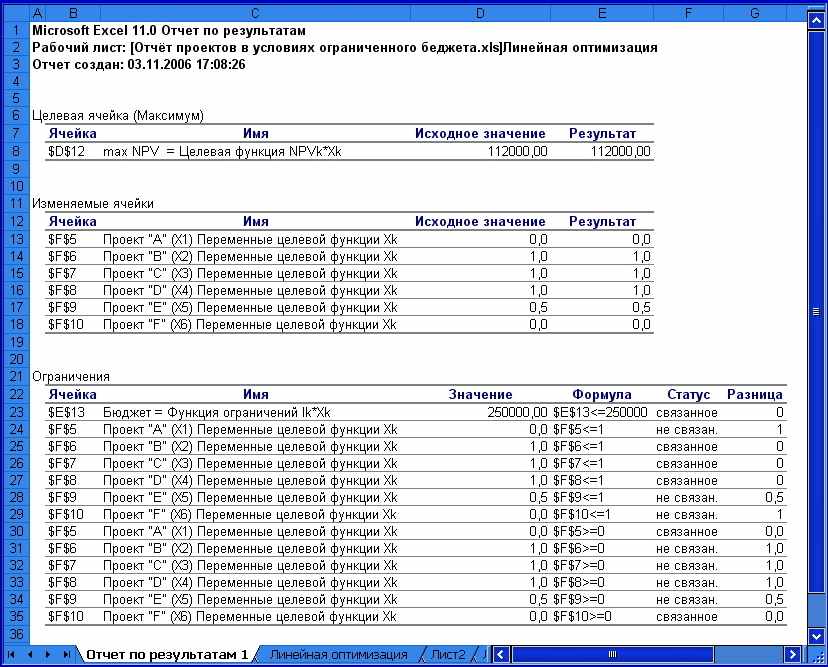
Рис. 1.19. Отчёт по результатам списка «Тип отчёта»
диалогового окна «Результаты поиска решения»
Отчёт об устойчивости содержит информацию о чувствительности целевой ячейки (т.е. полученного решения) к изменениям параметров её формулы (ключевых переменных задачи) и ограничений (рис.1.20). Отчёт содержит два раздела: «Изменяемые ячейки» и «Ограничения». Данные о каждой изменяемой ячейке и ячейке-ограничении выводятся на отдельной строке. Правый столбец каждого раздела содержит информацию об устойчивости решения, т.е. показывает, насколько увеличится (уменьшится) значение целевой ячейки при увеличении (уменьшении) на единицу значения соответствующей изменяемой ячейки или ограничения.
В зависимости от установленного значения параметра « Линейная модель» диалогового окна «Параметры решения» могут быть получены два варианта этого отчёта — для нелинейных задач (параметр отключён) и для линейных (параметр включён).
В отчёте о пределах (ограничениях) приводятся оптимальные значения каждой изменяемой ячейки вместе с нижним и верхним пределами её изменения, при которых не нарушаются ограничения модели (рис.1.21).
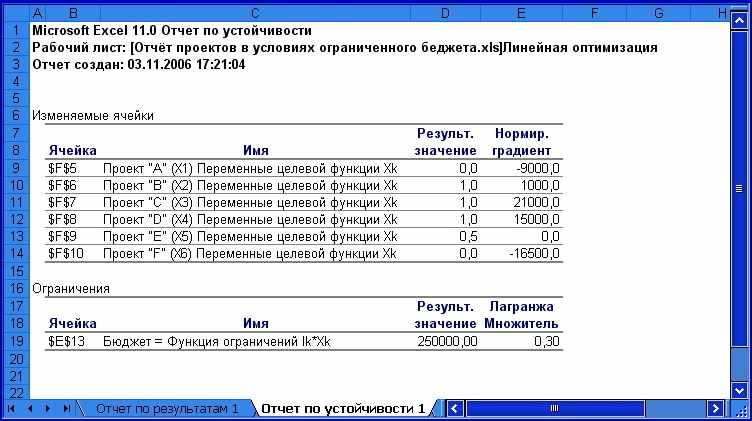
Рис. 1.20. Отчёт по устойчивости списка «Тип отчёта»
диалогового окна «Результаты поиска решения»
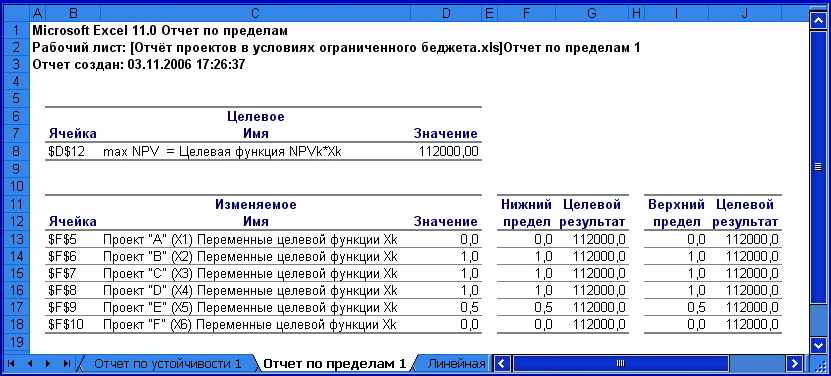
Рис. 1.21. Отчёт по пределам списка «Тип отчёта»
диалогового окна «Результаты поиска решения»
Интерпретация результатов отчётов требует знания основ математической оптимизации и, в частности, понятия двойственности. Детальные сведения о математическом программировании и его применении в различных сферах можно найти в [1, 2, 5].