Внешнеэкономических связей, экономики
| Вид материала | Пояснительная записка |
- М. В. Ломоносова Экономический факультет Магистратура Направление «Менеджмент» Программа, 246.76kb.
- Курс II уровень курса Магистратура Тип курса По выбору Семестр(ы), 15.71kb.
- Понятие, формы и способы осуществления внешнеэкономических связей. Предпосылки развития, 35.78kb.
- В г. Тольятти Экономический факультет Кафедра «Мировой экономики» методические рекомендации, 282.77kb.
- Состав, 21.24kb.
- В г. Калининграде А. Котенко Страхование Методические указания, 527.88kb.
- В г. Дзержинске Нижегородской области факультет: юридический Курсовая, 263.16kb.
- Информационное письмо о Всероссийской научно-практической конференции, 162.21kb.
- Понятие, формы и способы осуществления внешнеэкономических связей. Предпосылки развития, 1636.83kb.
- Практическое пособие для предпринимателей г. Ростов-на-Дону 2008г. Оглавление, 1634.23kb.
2. Метод чистой текущей стоимости (NPV)
Основная идея чистой текущей стоимости (net present value — NPV) заключается в том, чтобы найти разницу между инвестиционными затратами и будущими доходами, выраженную в скорректированной во времени (к началу реализации проекта) денежной величине.
При заданной норме дисконта можно определить современную величину всех оттоков и притоков денежных средств в течение экономической жизни проекта, а также сопоставить их друг с другом. Результатом такого сопоставления будет положительная или отрицательная величина (чистый приток или чистый отток денежных средств), которая показывает, удовлетворяет или нет проект принятой норме дисконта.
Пусть I0 — сумма первоначальных затрат, т.е. сумма инвестиций на начало проекта;
PV — текущая стоимость денежного потока на протяжении экономической жизни проекта.
Тогда чистая текущая стоимость равна:
| NPV = PV-I0 | (1.2) |
Величину PV можно определить по формуле (1.1):
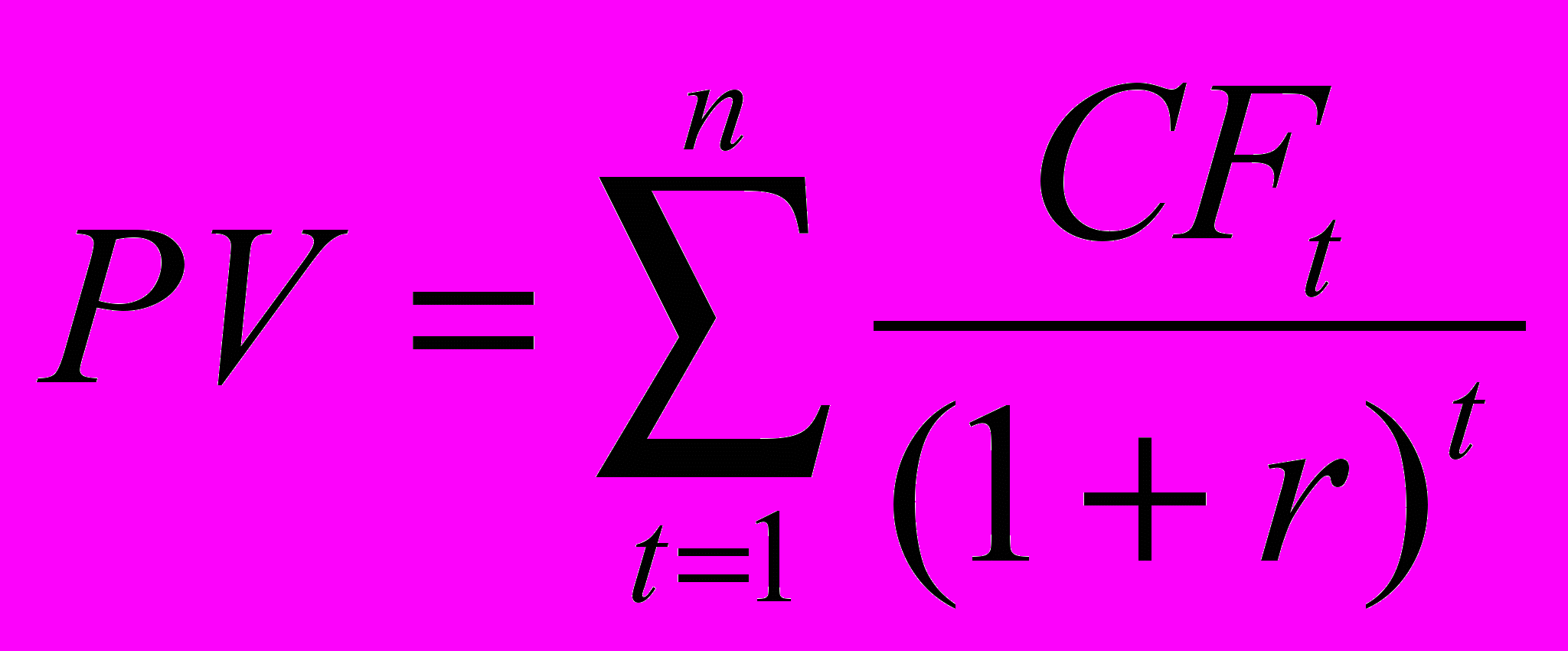 | |
где r — норма дисконта;
n — число периодов реализации проекта;
CFt — чистый поток платежей в периоде t.
Подставив формулу вычисления PV в (1.2), получим:
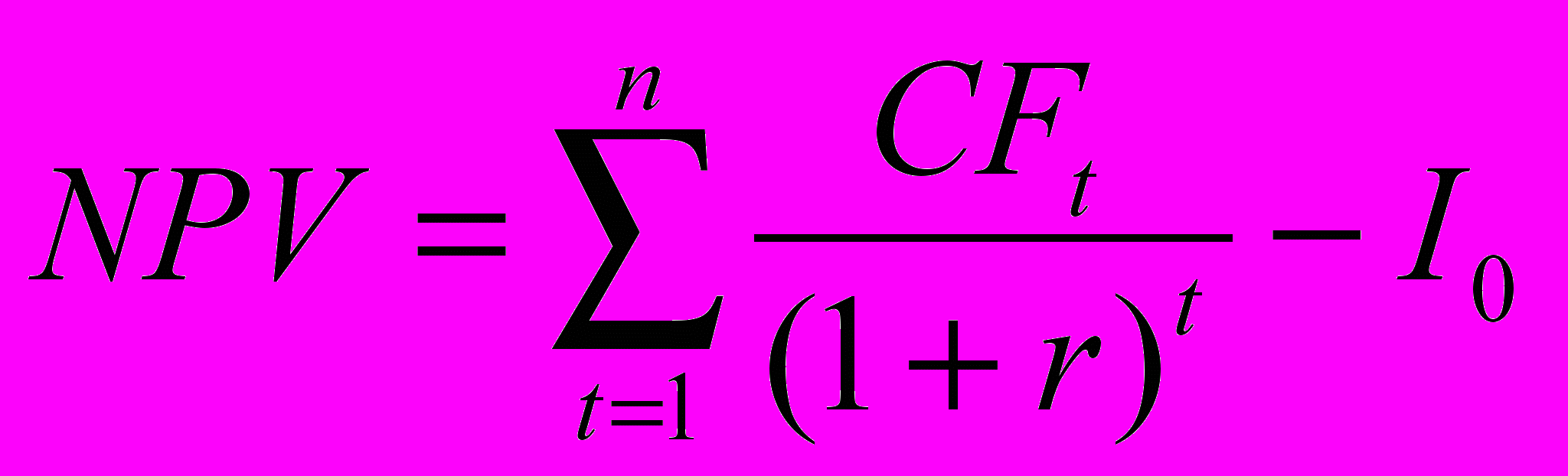 | (1.3) |
Если рассчитанная таким образом чистая текущая стоимость потока платежей имеет положительный знак ( NPV>0) — то в течение своей экономической жизни проект возместит первоначальные затраты I0, обеспечит получение прибыли согласно заданному стандарту r, а также её некоторый резерв, равный NPV. Отрицательная величина NPV показывает, что заданная норма прибыли не обеспечивается и проект убыточен. При NPV = 0 проект только окупает произведённые затраты, но не приносит дохода.
Общее правило при определении чистой текущей стоимости NPV: если NPV > 0, то проект принимается, иначе его следует отклонить.
В простейшем случае денежный поток проекта состоит из суммы первоначальных инвестиций I0 и последующих поступлений средств от его реализации — CFt.
Пример 1.1
Фирма собирается вложить средства в приобретение нового оборудования, стоимость которого вместе с доставкой и установкой составит 100 000 ден. ед. Ожидается, что внедрение оборудования обеспечит получение на протяжении 6 лет чистых доходов в 25 000, 30 000, 35 000, 40 000, 45 000 и 50 000 ден. ед. соответственно. Принятая норма дисконта равна 10%. Определить экономическую эффективность проекта.
В табл. 1.2 приведен полный расчёт NPV этого примера. Как видим, при условии правильной оценки денежного потока проект обеспечивает возмещение произведённых затрат (примерно к концу четвертого года) и получение 10% чистой прибыли, а также дополнительной (сверх установленной нормы) прибыли, равной величине NPV (57 302,37).
Таблица 1.2
Расчёт NPV проекта
| t | I0 | CFt | (1+r)t | PVt (Гр.З : Гр.4) | NPV |
| 0 | -100 000,00 | | 1,0000 | -100 000,00 | -100 000,00 |
| 1 | | 25 000,00 | 1,1000 | 22 727,27 | -77 272,73 |
| 2 | | 30 000,00 | 1,2100 | 24 793,39 | -52 479,34 |
| 3 | | 35 000,00 | 1,3310 | 26 926,02 | -26 183,32 |
| 4 | | 40 000,00 | 1,5041 | 27 320,54 | 1 137,22 |
| 5 | | 45 000,00 | 1,6105 | 27 941,50 | 29 078,68 |
| 6 | | 50 000,00 | 1,7716 | 28 223,70 | 57 302,37 |
| Итого | -100 000,00 | 225 000,00 | | 157 302,37 | 57 302,37 |
Другое объяснение полученного показателя NPV могло бы состоять в следующем: если проект финансировался за счёт долгосрочной ссуды в 100 000 ден. ед., взятой на 6 лет под 10% годовых, её величина и проценты могли бы быть полностью выплачены из поступлений наличности от проекта. Кроме того, после расчётов с кредиторами остаток полученной от проекта наличности составил бы сумму в 57 302,37 ден. ед.
При прогнозировании потоков платежей по периодам должны учитываться все виды поступлений и выплат, связанных с данным проектом, как производственного, так и непроизводственного характера. Например, амортизационные отчисления, высвобождения оборотных средств, поступления от ликвидации либо продажи оборудования по окончанию проекта должны включаться в доходы соответствующих периодов.
Если проект предполагает последовательные начальные вложения средств в течение нескольких лет либо дополнительные инвестиции в какие-то периоды реализации проекта, они также должны быть учтены при расчете NPV.
С учётом вышеизложенного формула расчета NPV для общего случая примет вид:
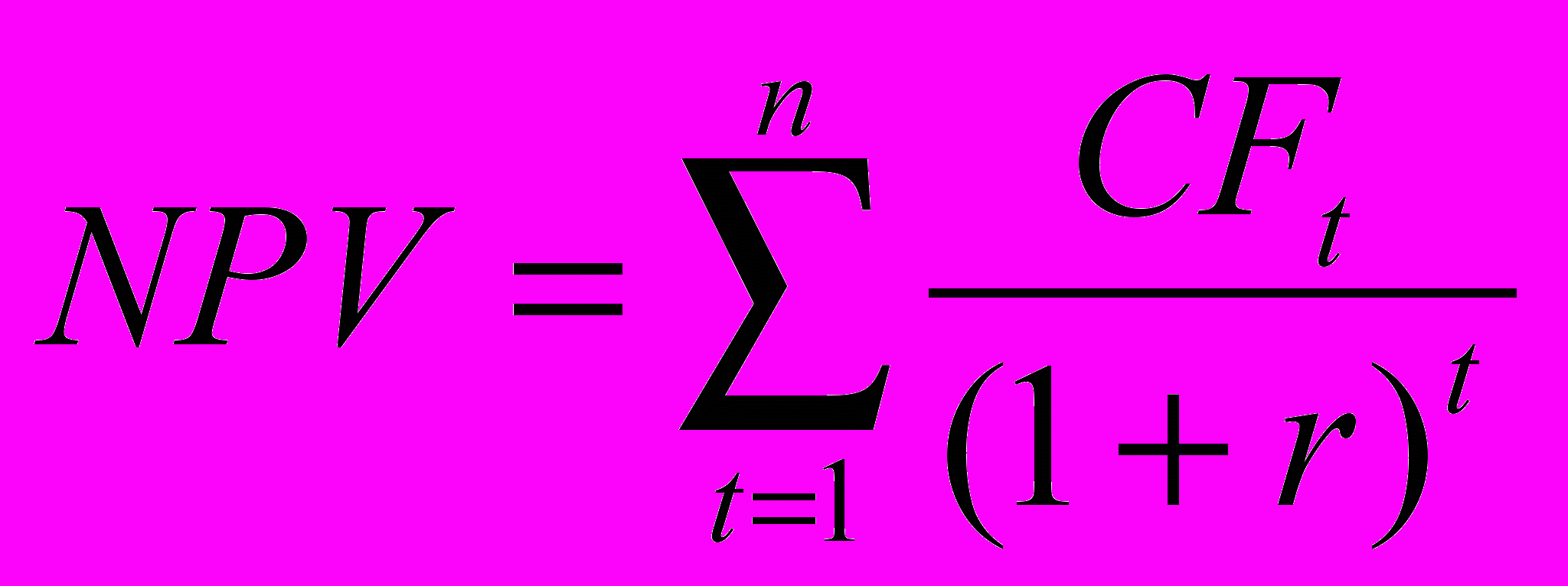 | (1.4) |
Расчёт вручную показателей, базирующихся на дисконтных методах, достаточно трудоёмок. Поэтому при выполнении расчётов пользуются специальной группой финансовых функций MS Excel, предназначенных для автоматизации анализа эффективности инвестиционных проектов (табл. 1.3).
Таблица 1.3
Функции анализа эффективности инвестиционных проектов
| Наименование функции | Формат функции | |
| Оригинальная версия | Локализованная версия | |
| NPV | НПЗ | НПЗ (Ставка; Платежи) |
| IRR | ВНДОХ | ВНДОХ (Платежи; [прогноз]) |
| MIRR | МВСД | МВСД (Платежи; Ставка; Ставка_реинвест) |
| XNPV | ЧИСТНЗ | ЧИСТНЗ (Ставка; Платежи; Даты) |
| XIRR | ЧИСТВНДОХ | ЧИСТВНДОХ (Платежи; Даты; [прогноз]) |
Автоматизация расчёта критерия NPV
Для исчисления чистой текущей стоимости потока платежей в MS Excel реализовано две функции — НПЗ () и ЧИСТНЗ () . Они используют следующие аргументы:
ставка — норма дисконта (процентная ставка);
платежи — значения элементов денежного потока;
даты — даты платежей (только для функции ЧИСТНЗ ().
Рассмотрим технологию применения этих функций для расчёта NPV.
Функция НПЗ (ставка; платежи)
Функция НПЗ () позволяет определить текущую стоимость потока равномерно распределённых во времени платежей (PV) с учётом заданной оценки. Она реализует соотношение (1.1).
Следует обратить внимание на то, что эта функция не учитывает величину первоначальных затрат I0, т.е. инвестиций, сделанных на момент времени t = 0. Поэтому для определения показателя чистая текущая стоимость (NPV) из полученного результата следует вычесть величину первоначальных вложений I0.
При проведении анализа с применением функции НПЗ () удобно задавать I0 как отрицательную величину. Тогда показатель NPV можно рассчитать по формуле:
| NPV = I0 + PV, I0<0. | (1.5) |
Рассчитаем показатель NPV для примера 1.1. Введём данные потока платежей в любой непрерывный блок ячеек электронной таблицы (ЭТ), например с В1 по В6, а в ячейку В7 выражение:
-100000 + НПЗ (0,1; В1.В6) (Результат: 57302,37).
Практическое применение этой функции ограничено случаем равномерного распределения платежей во времени. Данное ограничение позволяет преодолеть другая функция — ЧИСТНЗ ().
Функция ЧИСТНЗ (ставка; платежи; даты)
Функция ЧИСТНЗ () — самая мощная в своей группе. Она позволяет определить показатель NPV для потоков с платежами произвольной величины, осуществляемых за любые промежутки времени. Техника её использования практически аналогична только что рассмотренной. Различие заключается в том, что для каждого платежа должна быть указана предполагаемая дата его осуществления. Кроме того, в отличие от функции НПЗ () , её продвинутый аналог ЧИСТНЗ () корректно учитывает величину первоначальных инвестиций I0 и позволяет рассчитать NPV напрямую, без выполнения дополнительных действий, реализуя соотношение (1.4).
Однако применение данной функции с указанием в качестве аргументов абсолютных величин порождает ряд неудобств, связанных как с вводом (громоздкий и неприглядный вид формулы), так и с заданием аргумента даты. При расчётах MS Excel преобразует даты в их порядковые номера в году, при этом отсчёт ведётся с 1900 г. Например, дата «1 апреля 2006 г.» будет иметь порядковый номер 38808 (т.е. 38808-й день от начала 1900 г.).
Рассмотрим следующий пример.
Пример 1.2
Вложение на дату 12.03.06 суммы в 100 ден. ед. обеспечивает получение 02.07.06 суммы в 50 и 23.08.06 суммы в 70 ден. ед. Определим эффективность операции при норме дисконта в 10%.
=ЧИСТНЗ (0,1; {-100; 50; 70}; {38788; 38900; 38952}) (Результат: 15,62).
Проблема заключается в сложности определения порядковых номеров дат вручную. Существуют два пути её решения:
- использование функций преобразования дат;
- задание аргументов в виде адресов содержащих их ячеек MS Excel.
Первый способ основан на возможности использования функций в качестве аргументов других функций. В частности, в примере 1.2 вместо порядкового номера даты 12.03.06 (38788) можно задать вычисляющую его функцию — ДАТА (), имеющую формат:
=ДАТА (год; месяц; день)
Тогда формула вычисления показателя NPV примет вид:
=ЧИСТНЗ (0,1; {-100; 50; 70}; {ДАТА(2006; 3; 12); 38900; 38952}) (Результат: 15,62).
Фигурные скобки в MS Excel, означают данные типа «массив».
Таким же образом могут быть заданы и две остальные даты. Однако в случае большого числа платежей формула станет слишком длинной и малопонятной.
Более удобен и эффективен второй способ. Для его реализации необходимо ввести исходные данные в смежные ячейки электронной таблицы. При этом все необходимые преобразования MS Excel выполнит автоматически. Пусть даты введены в ячейки с A1 по АЗ (т.е. в блок А1:АЗ), а величины платежей — с В1 по ВЗ (В1:ВЗ). Тогда формула расчёта примет вид:
=ЧИСТНЗ(0,1; В1.ВЗ; А1.АЗ) (Результат: 15,62).
Помимо компактности и наглядности такой способ задания аргументов функций имеет еще одно важнейшее достоинство — обеспечивает возможность быстрого и эффективного проведения многовариантного анализа путём изменения данных в ячейках таблицы. Это замечательное свойство табличных процессоров понадобится в дальнейшем, при анализе показателей на чувствительность. А пока построим электронную таблицу для решения примера 1.1 с использованием только что рассмотренных функций.
Для упрощения предположим, что платежи по этому проекту осуществляются один раз в году, в один и тот же день. Дата покупки оборудования — 30.01.07.
Подготовим таблицу, как показано на рис. 1.3.
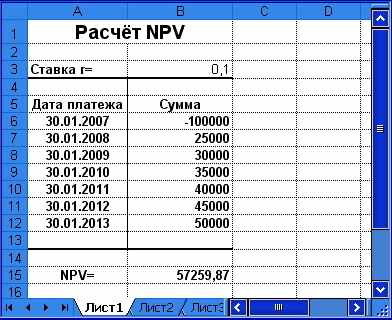
Рис. 1.3. Расчёт NPV (пример 1.1)
Можно ускорить процесс создания данной таблицы, воспользовавшись командой «Заполнить» из темы главного меню «Правка». Для этого следует ввести первую дату — 30.01.07 — в ячейку А6. Выделим блок А6:А12. Выберем команду «Заполнить», подпункт «Прогрессия». После появления окна диалога (рис. 1.4), установим переключатель «Прогрессия» в положение по столбцам, переключатель «Тип» — в положение «дата», переключатель «Единица даты» — в положение «год». В поле «Предельное значение» введём последнюю дату — 30.01.13.
Результатом выполнения этих действий должно стать заполнение блока ячеек А6:А12 значениями дат платежей. Введите в блок ячеек В6:В12 данные потока платежей (поскольку значения платежей отличаются друг от друга на постоянную величину — 5000, здесь также можно воспользоваться командой «Заполнить» — для этого следует ввести первую величину чистого дохода — 25000 — в ячейку B7.).
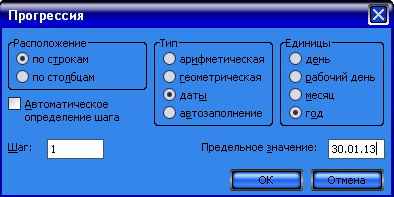
Рис. 1.4. Окно диалога подпункта «Прогрессия»
Формула для вычисления NPV в ячейках В15 имеет вид:
=ЧИСТНЗ(ВЗ; В6:В12; А6:А12) (Результат: 57153,74)
Функция ЧИСТНЗ () учитывает реальное число дней в каждом году.
Таблицу сохраним на магнитном диске, поскольку она будет использоваться в дальнейшем при изложении материала.
На практике после определения показателей эффективности инвестиций осуществляют анализ их чувствительности (sensitivity analysis) к изменениям возможных условий. В общем случае подобный анализ сводится к исследованию изменений полученной величины в зависимости от различных значений параметров рекуррентных соотношений. Решим пример 1.1 при норме дисконта 20% (рис. 1.5).
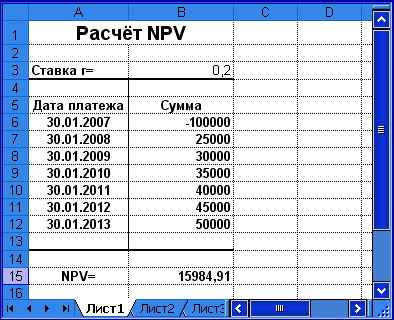
Рис. 1.5. Чувствительность NPV к изменению нормы дисконта
Величина NPV по-прежнему положительна, однако она уменьшилась до 15984,91. Если увеличить норму дисконта до 30%, величина NPV примет отрицательное значение (проверьте это самостоятельно).
Следовательно, норма дисконта r оказывает прямое влияние на срок окупаемости проекта и обратное — на величину NPV.
В рассматриваемом примере приток денежной наличности от реализации проекта увеличивается с 25 000,00 до 50 000,00 в течение 6 лет. Рассмотрим обратный случай.
Пусть денежный поток последовательно уменьшается с 50 000,00 до 25 000,00 ден. ед. в течение 6 лет с тем же интервалом. Норма дисконта равна 10%.
Поскольку меняется лишь порядок поступления платежей, воспользуемся операцией « Сортировка данных». Для этого выделим блок ячеек В7:В12 и щелкнем мышью по кнопке «Обратная сортировка» на панели инструментов.
—
 кнопка [Обратная сортировка].
кнопка [Обратная сортировка].Расчет NPV для данного случая приведен на рис. 1.6. Проведённые расчёты показывают увеличение NPV.
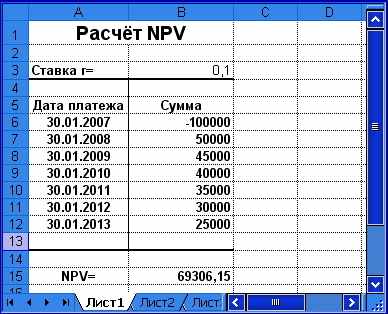
Рис. 1.6. Чувствительность NPV к изменению структуры потока
Таким образом, наряду с нормой дисконта на величину NPV существенное влияние оказывает структура денежного потока. Чем больше притоки наличности в первые годы экономической жизни проекта, тем больше конечная величина NPV и соответственно тем скорее произойдет возмещение произведённых затрат.
Эксперименты свидетельствуют, что в целом показатель NPV должным образом отражает соотношение между притоками и оттоками денежных средств в течение определенного периода времени, а также дает представление как о возмещении произведённых затрат, так и о достижении заданной нормы доходности вложения средств.
Являясь абсолютным показателем, NPV обладает важнейшим свойством — свойством аддитивности (NPV различных проектов можно суммировать).
NPV(A, B, C) = NPV(A) + NPV(B) + NPV(C)
К числу других важнейших свойств этого критерия следует отнести более реалистические предположения о ставке реинвестирования поступающих средств. В методе NPV неявно предполагается, что средства, поступающие от реализации проекта, реинвестируются по заданной норме дисконта r.
Использование критерия NPV теоретически обоснованно, и в целом он считается наиболее корректным измерителем эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др.) может приводить к затруднениям при принятии управленческих решений.
Пример 1.3
Предположим, что рассматриваются два проекта. Принятая норма дисконта составляет 10%. Соответствующие оценки денежных потоков и расчёт NPV приведены в табл. 1.4.
Таблица 1.4
Условия реализации проектов (пример 1.3)
| Проект | I0 | CFt | PV | NPV |
| X | -10 000,00 | 16 500,00 | 15 000,00 | 5 000,00 |
| Y | -100000,00 | 115 000,00 | 105 000,00 | 5 000,00 |
Чистая текущая стоимость обоих проектов составляет 5000 и в случае необходимости выбора не позволяет однозначно определить лучший вариант. Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используются также и относительные — индекс рентабельности и внутренняя норма доходности.
