А. Ю. Каргашина и А. С. Миркотан под редакцией > Ю. М. Баяковского

Вид материала

Книга

Содержание Арифметика чисел с плавающей точкой

Подобный материал:

• Баринова Анна Юрьевна учитель английского языка Как правильно готовить проект к урок, 42.88kb.
• Учебник под редакцией, 9200.03kb.
• Рабочая программа по русскому языку 11 класс По учебно-методическому комплексу под, 152.57kb.
• Рабочая программа По технологии для 5, 7, 8, 9 класса на 70 часов в год, 619.15kb.
• Зинченко П. И. Непроизвольное запоминание / Под редакцией В. П. Зинченко и Б. Г. Мещерякова, 260.23kb.
• Рабочая программа по литературе для 6 классе по программе под редакцией Коровиной, 194.25kb.
• Рабочая программа по русскому языку 9 класс По учебно-методическому комплексу под редакцией, 544.8kb.
• Гарифуллиной Светланы Рафаэльевны 2011-2012 учебный год пояснительная записка, 795.91kb.
• П. А. Сорокина Москва Санкт-Петербург Сыктывкар 4-9 февраля 1999 года Под редакцией, 6816.25kb.
• Н. В. Кузнецова Директор О(с)ош л. И. Лобанова бюджетное муниципальное образовательное, 428.15kb.

Арифметика чисел с плавающей точкой

До сих пор мы рассматривали только арифметику чисел с фиксированной точкой. Точка в ней указывает на основание системы счисления. В системе счисления с основанием, или базой, равной десяти, точка аналогична обычной десятичной точке. Так же как столбцы, расположенные слева от десятичной точки, обозначают соответствующее количество умножений на десять, столбцы, расположенные справа, обозначают число делений на десять. Так, запись D 12.34 означает 1(десять)+2(один)+3(одна десятая)+4(одна десятая от одной десятой).

Такое же изображение чисел возможно относительно любого основания, причем в приведенном описании десятка должна быть всюду заменена на величину основания. Например, O 12.34 в десятичной записи есть 1(восемь)+2(один)+3(одна восьмая)+4(одна восьмая от одной восьмой)=8+2+3/8+4/64. Здесь мы использовали восьмеричную систему счисления.

Подобным же образом можно применять двоичную систему. Например, B 0.(10)=B 0.101010...=D 1/2+1/8+1/32+...=D 2/3 (вычислите сумму геометрической прогрессии)²¹.


УПPАЖНЕНИЕ. Найдите двоичное представление числа 1/10. Используя его, разработайте другой метод выполнения операции деления на десять.


Точка в подобной записи фиксирована в том смысле, что, если она присутствует, программист знает точно, в каком месте она расположена. Умножение числа D 123456 на D 234567 можно выполнить теми же машинными командами, что и умножение числа D 12345600 на D 0.0234567. В действительности же при перемножении целых чисел на ЭВМ учитываются все значащие цифры сомножителей. Иначе программа должна хранить положение точки. В предыдущем примере мы имели десятичную точку. Если же для нормализации чисел используются команды сдвига, то необходимо знать положение двоичной точки.

Макроассемблер MACRO-11 имеет обеспечение, позволяющее работать с числами в специальном формате с плавающей точкой, который согласован с аппаратными возможностями дополнительных плат, поставляемых к большинству процессоров. Представление чисел в плавающем формате системы PDP-11 включает три поля. Двоичная точка, отмечающая начало дробной части, располагается слева от шестого бита первого слова, где хранится число. Дробная часть располагается вправо до нулевого бита и дальше на столько слов, сколько содержит используемое представление. Последнее может быть рассчитано на одно, два или четыре слова. Так, если мы используем два слова, то имеем



Значение дробной части числа с плавающей точкой зависит от выбора порядка. Например, в десятичной записи число 123.45 можно представить как 0.12345 X 103 или как 0.012345 X 104 и т.д. до бесконечности. Первая форма записи, характеризующаяся наличием отличной от нуля цифры сразу после точки, называется нормализованной формой представления числа в плавающем формате. Процессоры серии PDP-11 работают исключительно с нормализованным двоичным представлением чисел. В такой записи первый бит после двоичной точки должен быть равен 1. Он отсутствует в машинном представлении плавающего числа (так называемый скрытый бит). Нужно подразумевать, что 6-му биту первого слова предшествует двоичное число 0.1.

Десятичные числа с плавающей точкой можно задавать ассемблеру в виде последовательности десятичных знаков, включая по необходимости десятичную точку. Порядок записывается в виде буквы E, после которой следует целое число (возможно, отрицательное или нуль). Числа в таком формате описываются директивой .FLT2 (два слова на число) или .FLT4 (четыре слова на число). Например, в результате трансляции строки MEM:

.FLT2 -2.1E-3

ассемблер заведет нормализованное двоичное представление в плавающем формате числа D —0.0021, отведя под него ячейки памяти, начиная с метки MEM.

Старший бит первого слова, как и обычно, является знаковым. В битах с 7-го по 14-й кодируется двоичный порядок числа. Для положительных плавающих чисел этот код представляет собой истинный порядок числа, увеличенный на O 200. Рассмотрим, к примеру, число D 1/10. Легко показать, что

D 1/10 = 3/32(1+1/16+1/64+...) =

= B 0.0001100110011...

= 2^-3B 0.110011001100...

Таким образом, поле порядка должно содержать O 200—3=175=B 01111101 Помня, что нужно отбросить первую единицу дробной части, получим первое слово нашего числа:



т.е. 037314. Второе слово имеет вид



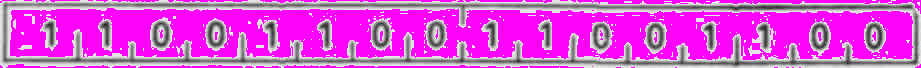
или 146314. Последняя восьмеричная цифра второго слова на самом деле во время трансляции будет округлена до пяти.

Нулем считается любое число, меньшее по абсолютной величине чем D 2^-127, причем подразумевается, что всякое представление, содержащее нуль в поле порядка, соответствует числу с порядком —128.

Ясно, что арифметические операции с плавающей точкой должны выполняться командами, в которых учитываются особенности представления таких чисел. Возьмем, к примеру, сумму D 27+3 и посмотрим, как она вычисляется, если слагаемые записаны в плавающем формате. Используя восьмеричное представление для дробной части, имеем следующее нормализованное представление этих чисел: D 27=O 33=2⁵O 0.66; D 3=2²O 0.6. Сначала представление числа с меньшим порядком изменяется так, чтобы порядки оказались равными. В нашем случае это приведет к записи числа 3 в виде: D 3=2⁵O 0.06. (Конечно, это уже не нормализованное представление.) Теперь выполняется сложение:

2⁵O 0.66 + 2⁵O 0.06 = 2⁵O 0.74

Так же как и для их суммы, для обоих слагаемых возможен укороченный плавающий формат. Для перевода числа в этот формат в ассемблере имеется специальный оператор F (стрелка вверх, затем F), за которым должно быть записано число в десятичном виде:

MOV F27,MEM

Программа, выполняющая рассмотренное выше сложение, могла бы начинаться со сдвига дробной части представления числа D 3 на три бита вправо для выравнивания порядков слагаемых. «Скрытый» бит при этом, конечно, должен быть представлен явно. Тогда сложение дробных частей даст корректный уже нормализованный результат.

В общем случае, однако, подобный метод не годится. Рассмотрим сложение D 27+6, причем будем считать, что оба числа представлены в укороченном плавающем формате. Поле порядка первого числа содержит O 205. Двоичная запись дробной части, округленная до восьми разрядов, есть 0.11011000. Опуская первую единицу, получаем 7-разрядное представление дробной части: O 130. Поле порядка числа D 6 равно O 203, а поле дробной части в нормализованном виде — O 100. После сдвига этого поля для выравнивания порядков на два разряда имеем в дробной части число O 60 (не забывайте об отброшенном разряде). Сложение дробных частей приводит теперь к результату O 210, который перекрывает поле порядка.

Подобные вычисления лучше производить с помощью процессора плавающей арифметики, если он входит в состав вашего ЦП. К тому же он выполняет операции существенно быстрее, чем при программной реализации. Здесь мы можем только очень коротко проиллюстрировать то, как им пользоваться.

Процессор плавающей арифметики работает только с нормализованным представлением плавающих чисел длиной в два или четыре слова и выдает результат в той же форме. Действия над этими числами выполняются особыми командами ассемблера, которые автоматически обращаются к соответствующим схемным реализациям. Так, команда ADDF выполняет сложение плавающих чисел длиной в два слова, а команда ADDD—длиной в четыре слова.

Для сложения плавающих чисел необходимо, чтобы одно из них было занесено в один из четырех сумматоров внутри процессора. На самом деле в него входит более четырех сумматоров, но остальные не могут использоваться для передачи данных между памятью и процессором. Обращение к ним такое же, как к первым четырем регистрам центрального процессора: аппаратура сама разбирается в том, какие регистры имеются в виду. Однако, чтобы самому не запутаться, лучше положить

F0=%0

и т.д. Также часто применяется и мнемоника AC0 и т. п.

Проделаем вычисления, которые прежде показались бы нам трудновыполнимыми. Во-первых, устанавливаем плавающий формат слагаемых:

MEM: .FLT2 27

.FLT2 6 ;в MEM+4

Теперь мы должны занести одно из них на сумматор, который имеет соответствующую длину, командой загрузки плавающего числа

LDF MEM,F0

Результат сложения всегда остается на сумматоре:

ADDF MEM+4,F0

Наконец, результат можно записать в память:

STF F0,WRD

Хотя ранее расчеты на всех вычислительных машинах осуществлялись подобным образом через сумматор, сейчас уже таких машин осталось немного. Так что процессорное устройство плавающей арифметики демонстрирует всплеск ностальгии по благополучно угасающей традиции.