Geum.ru

Старинные задачи 3 этап 1 задание. Моу «Кормиловский лицей»

Вид материалаЗадача

Содержание


3. Задача Альбрехта Дюрера.
Способы составления магических квадратов
4. Задача Озанама
Подобный материал:
Старинные задачи 3 этап 1 задание. МОУ «Кормиловский лицей»

1. Чешская задача: “Если бы я дала первому жениху половину слив из этой корзины и еще одну сливу, второму жениху половину оставшихся слив и еще одну сливу, а оставшиеся сливы поделила пополам и половину их и еще три сливы дала бы третьему жениху, то корзина опустела бы”. Сколько слив в корзине?

Ответ: 30 слив.
  1. 1). 30:2+1=16; 2). 30-16=14; 3). 14:2+1=8; 4). 14-8=6; 5). 6:2+3=6; 6). 6-6=0.



  1. ½* (1/2* (х/2-1) -1) -3=0;

1/2*(х/2-1)-1=6;

1/2*(х/2-1)=7;

х/2-1=14;

х/2=15;

х=30.

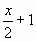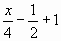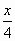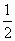
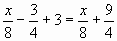III. Пусть первоначально в корзине было х слив. Первый жених получил слив, второй - = + слив, третий - слив.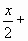

,

,

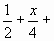
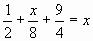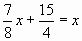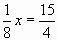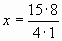, , х = 30.

Ответ: 30 слив.

2.Задача Леонардо Пизанского: Некто купил 30 птиц за 30 монет. Куропатки стоят по 3 монеты, голуби – по 2 и пара воробьев – по монете. Спрашивается, сколько птиц каждого вида.

1). Если число куропаток, голубей и воробьев обозначить буквами x, y, z соответственно, то решение сведется к нахождению тройки натуральных чисел, удовлетворяющих системе уравнений



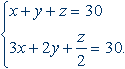
Исключив z и выразив затем x через y, получим x = 6 – 3/5 y. Единственное возможное значение y равно 5, тогда x = 3, z = 22.

Ответ: 3 куропатки, 5 голубей, 22 воробья.

Автор «Liber abaci» рассматривал задачу на сплав достоинства 1, который должен получиться из трех целочисленных количеств достоинством 3, 2 и 1/2. Эта же задача, но с чуть измененными числовыми данными (стоимость птиц разного вида выражается обратными числами: 1/3, 1/2 и 2) разбиралась еще в одном сочинении Леонардо.


3. Задача Альбрехта Дюрера.

Построить магический квадрат 4 * 4 для натуральных чисел от 1 до 16, чтобы два числа в нижних средних клетках указывали на год создания талисмана (1514), а сумма чисел четырех центральных клеток образовывали магическую сумму (34).

Решение.

16
3
2
13

5
10
11
8

9
6
7
12

4
15
14
1



В средние века магические квадраты приобрели необычайную популярность. В XI в. о них узнали в Индии, а затем в Японии. Им была посвящена обширная литература. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера, изображенный на его знаменитой гравюре «Меланхолия» (рис.). Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки.

III. СПОСОБЫ СОСТАВЛЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ

Общий метод построения квадратов неизвестен, хотя широко применяются различные частные алгоритмы. Некоторые из них я представляю ниже.

Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата:
  • нечетный;
  • четный, порядок которого равен степени числа 2;
  • четный, порядок которого равен удвоенному нечетному;
  • четный, порядок которого равен учетверенному нечетному.

4. Задача Озанама : Трое хотят купить дом за 26000 ливров. Они условились, что первый даст половину, второй – одну треть, а третий – одну четверть. Сколько даст каждый?


I. 1). х/2+х/3+х/4=26000; 13х/12=26000; х=26000*12:13=24000; 24000:2=12000ливров-I;

24000:3=8000ливров-II; 24000:4=6000ливров-III.

Ответ: 12000ливров-I ; 8000ливров-II; 6000ливров-III.


II. ½ +1/3 + ¼ =13/12, что составляет 26000 ливров. Отсюда 1/12 составляет 2000 ливров. Следовательно, первый даст 12000, второй-8000 и третий -6000 ливров.

Рефлексия:

  1. Чем вам понравился данный этап?

Задачи интересные, много узнали о математиках Западной Европы. Вспомнили магические квадраты, которые составляли в 6 классе.
  1. Какие затруднения были, и в каких задачах?

Затруднения были в выборе математика (о многих хотелось рассказать).