Итоги деятельности гану «Институт прикладных исследованйЙ» ан рб за 2010 год Стерлитамак 2010
| Вид материала | Документы |
- Итоги деятельности банковской сферы алтайского края за 2010 год, задачи на 2011 год, 221.93kb.
- Анализ работы методического центра за 2009-2010 учебный год, 492.93kb.
- Публичный доклад о результатах деятельности профессионального лицея №43 за 2010-2011, 625.2kb.
- Развитие физической культуры и спорта в современных условиях Материалы межрегиональной, 5260.81kb.
- Итоги науных научной деятельности сотрудников академии за 2011 год. Вуза за 2010 год, 345.27kb.
- Итоги работы учебно-образовательного процесса за 2009-2010 учебный год, 456.21kb.
- С. Ф. Жилкина подвел итоги работы за 2010 год. 16 февраля 2011 года в головном офисе, 47.68kb.
- Лицензия турагента: ав 157766 Донецкая обл г. Краматорск ул. Шкадинова,, 311.56kb.
- Стерлитамак Республики Башкортостан на 2010-2014 годы Во исполнение Федерального закон, 242.79kb.
- Заместитель директора рунмц мо рб, кандидат педагогических наук, 1386.8kb.
Математика
а) Исследован полностью вопрос о корректной постановке задачи Дирихле для уравнения смешанного типа с характеристическим вырождением (для уравнения Келдыша)
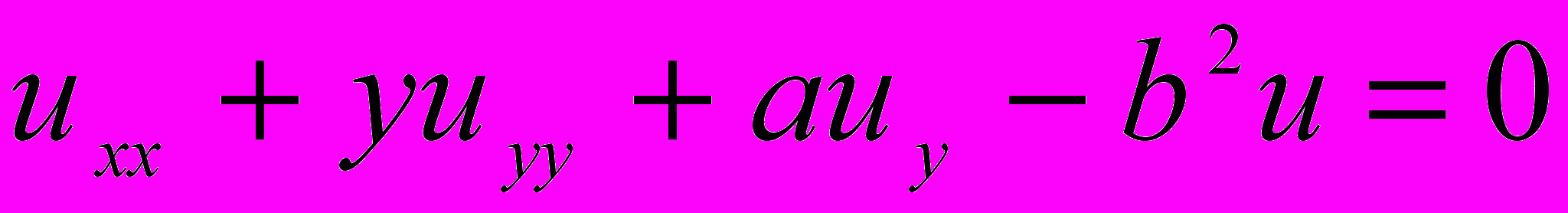 | (1) |
в прямоугольной области
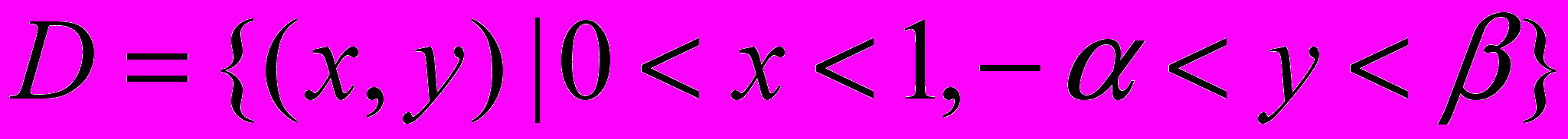
в зависимости от коэффициента
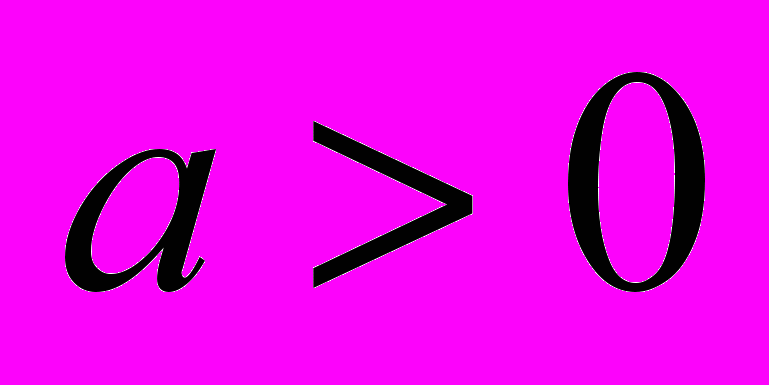и параметров 
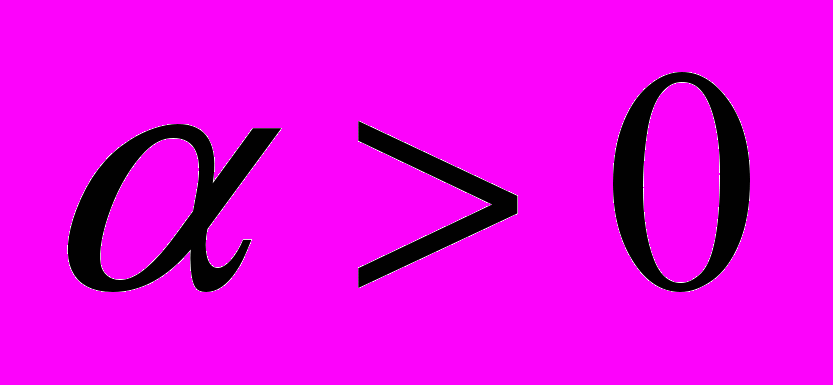и 
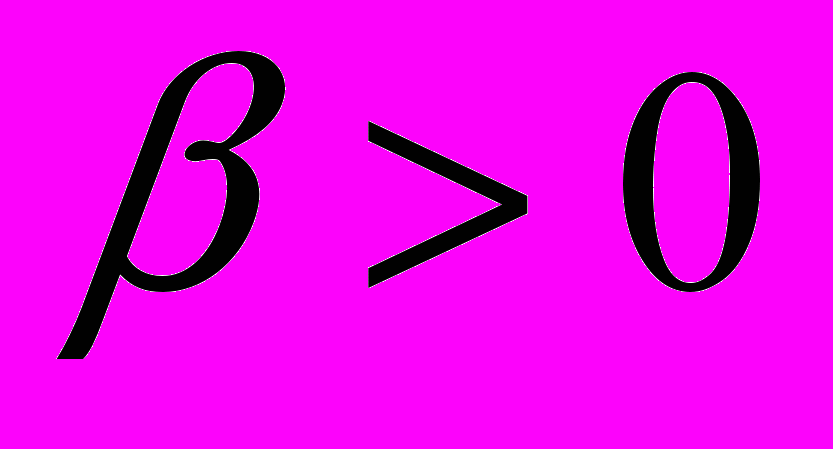. При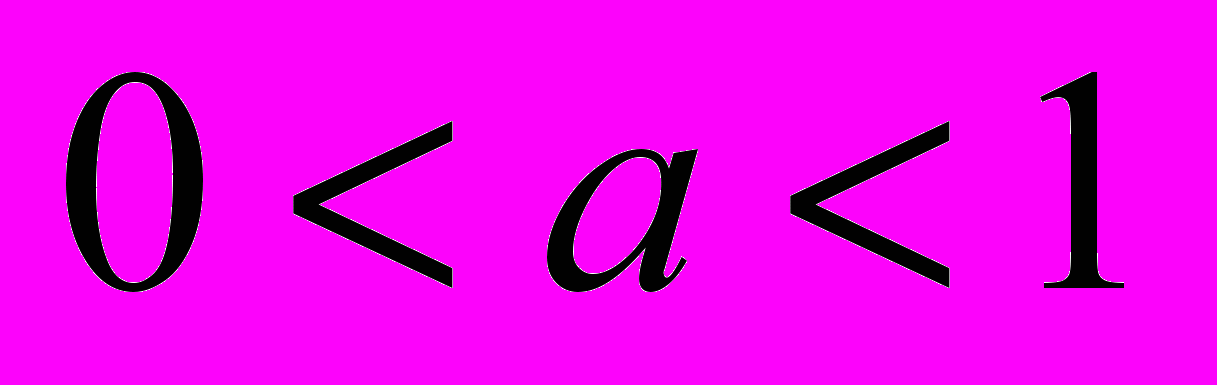 
установлен критерий единственности решения задачи Дирихле для уравнения (1) в области 
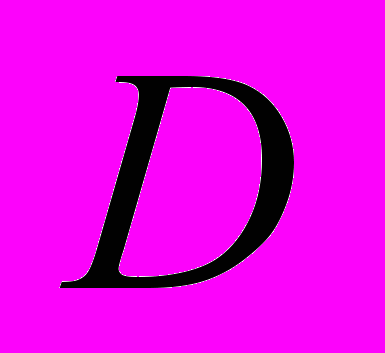. Само решение при некоторых ограничениях на 
и 
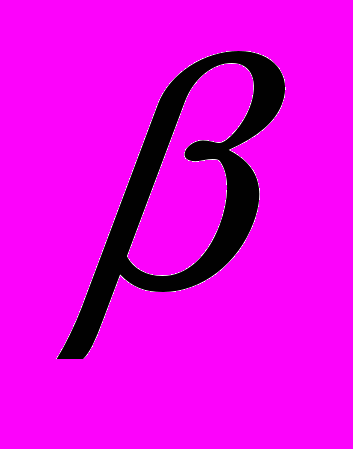построено в виде суммы ряда по собственным функциям соответствующей одномерной спектральной задачи. При 
и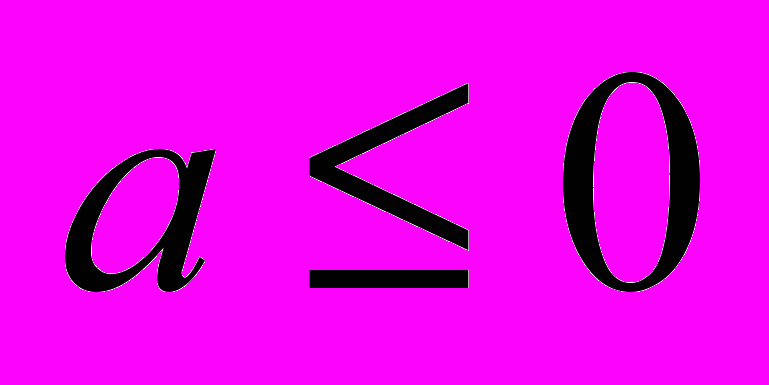 
показано, что задача Дирихле в классической постановке поставлена не корректно. В связи с этим найдены новые постановки видоизмененных задач и доказаны соответствующие теоремы единственности и существования. Решения этих задач также построены в виде суммы ряда по собственным функциям.б) Для уравнения типа Чаплыгина
 | (2) |
где
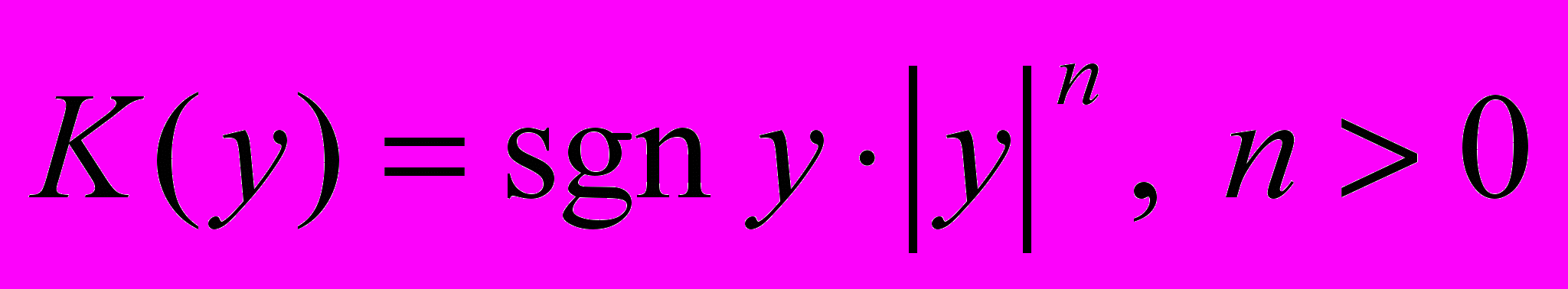в прямоугольной области 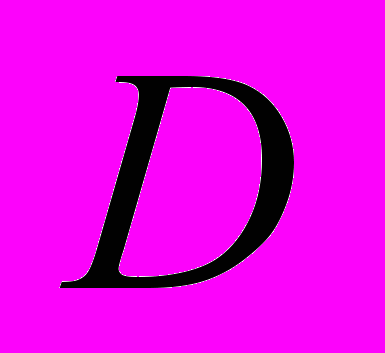изучена краевая задача с нелокальным интегральным условием:  | |
 | |
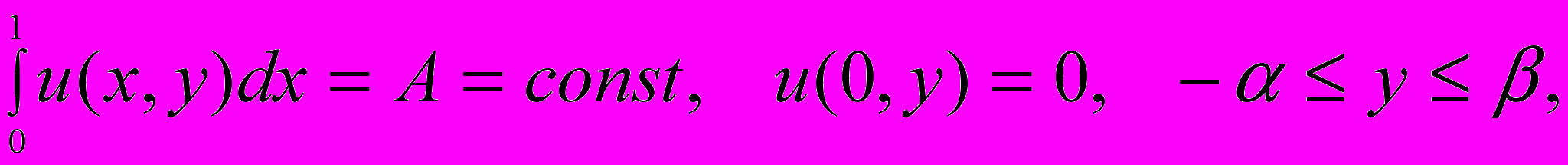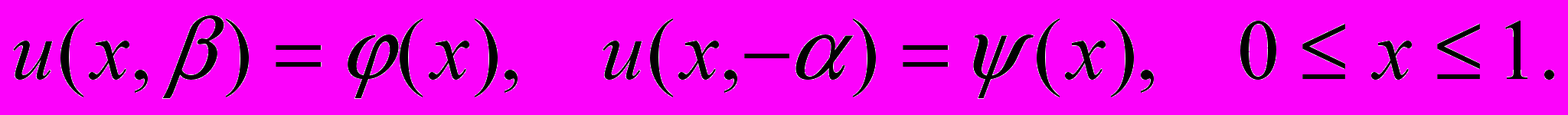Методом спектральных разложений установлен критерий единственности решения задачи при всех
Построена соответствующая система корневых функций одномерной спектральной задачи, которая является полной и образует базис в пространстве 
Решение поставленной задачи построено в виде суммы биортогонального ряда. При некоторых ограничениях на заданные функции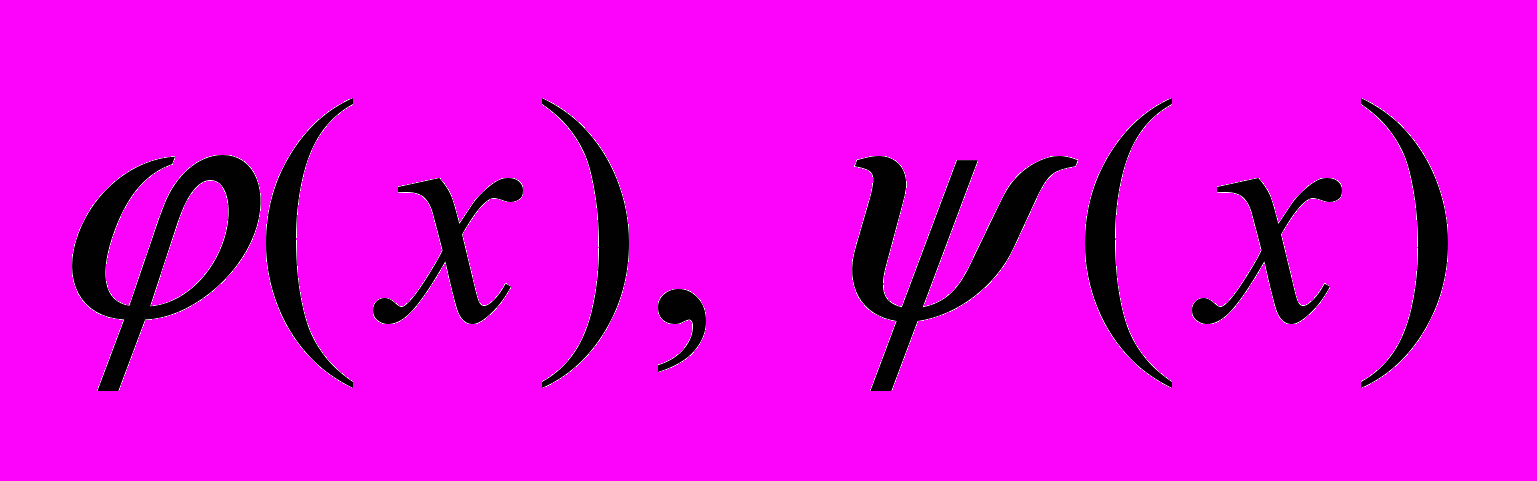 
и число доказана сходимость ряда в пространстве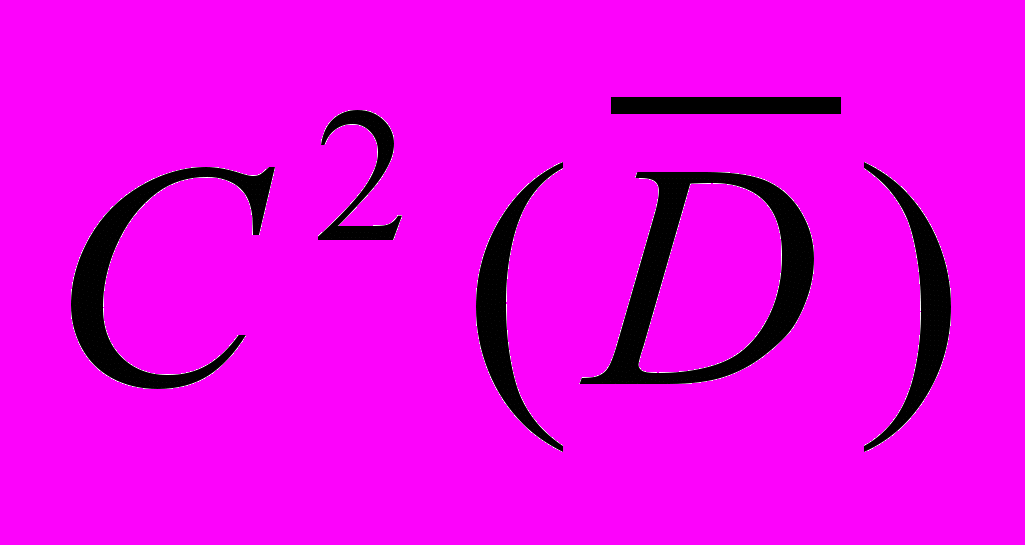 
.в) Для уравнения параболо-гиперболического типа
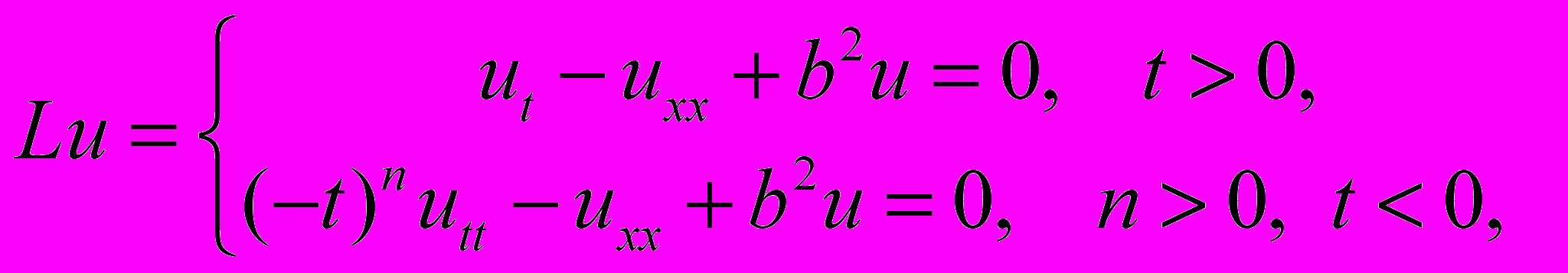 | (3) |
в прямоугольной области
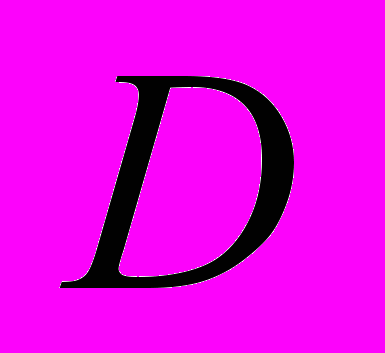исследована задача с нелокальными граничными условиями:  | |
 | |
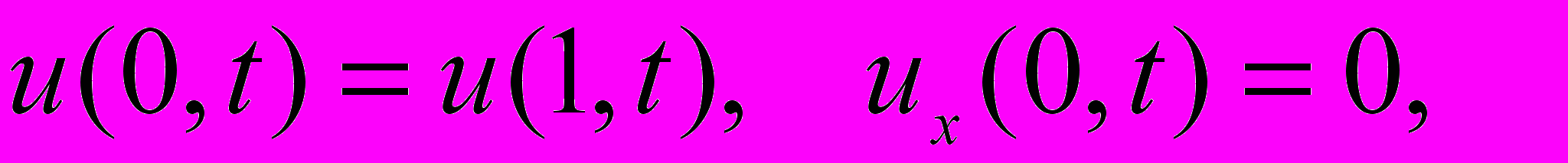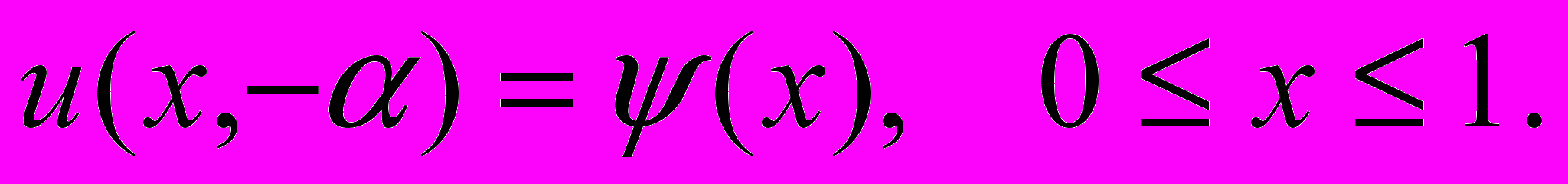Для указанной задачи установлены необходимые и достаточные условия единственности решения. Решение задачи построено в виде суммы биортогонального ряда и найдены достаточные условия относительно функций
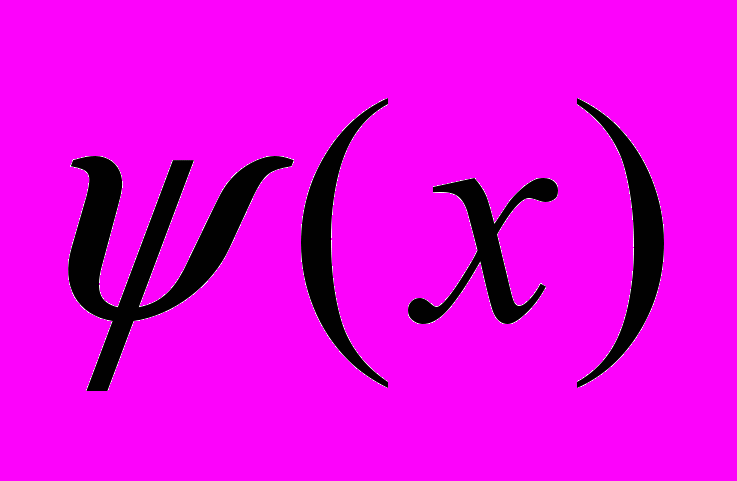и числа для обоснования сходимости построенного ряда.г) Для уравнения смешанного параболо-гиперболического типа (3) в прямоугольной области
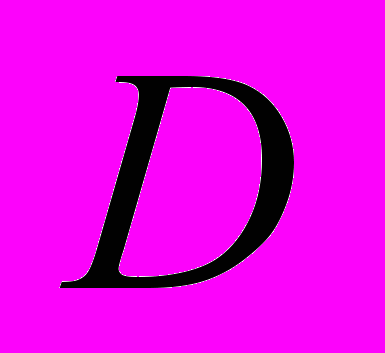при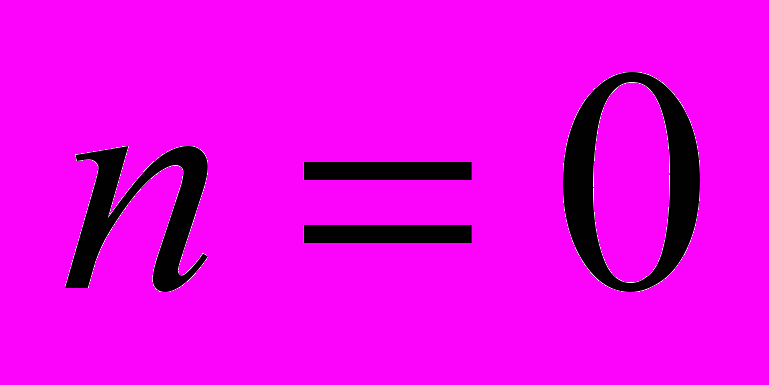 
изучены обратные задачи, связанные с поиском правой части:  | (4) |
т.е. требуется найти функци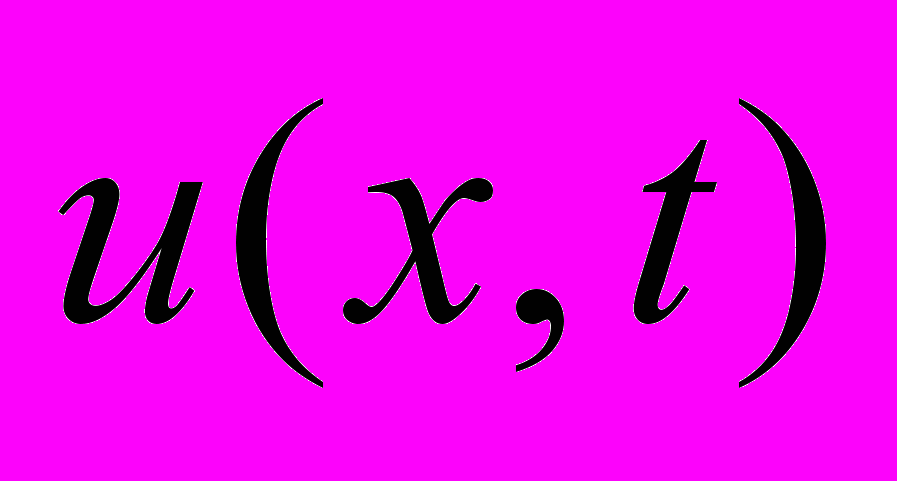и
и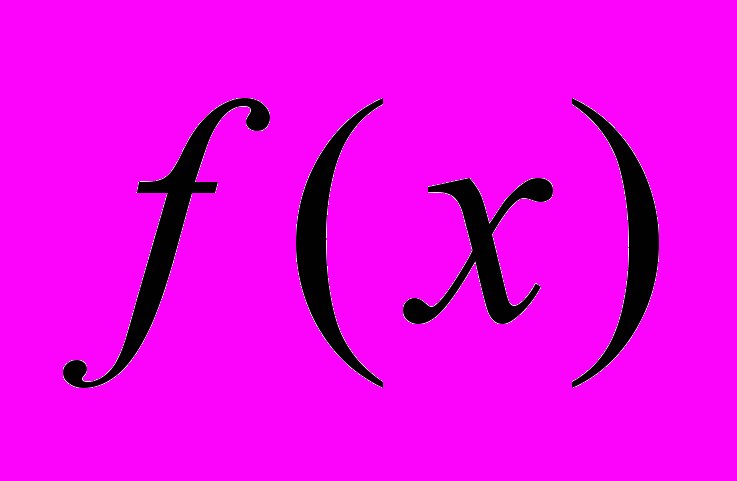 
удовлетворяющие на множестве 
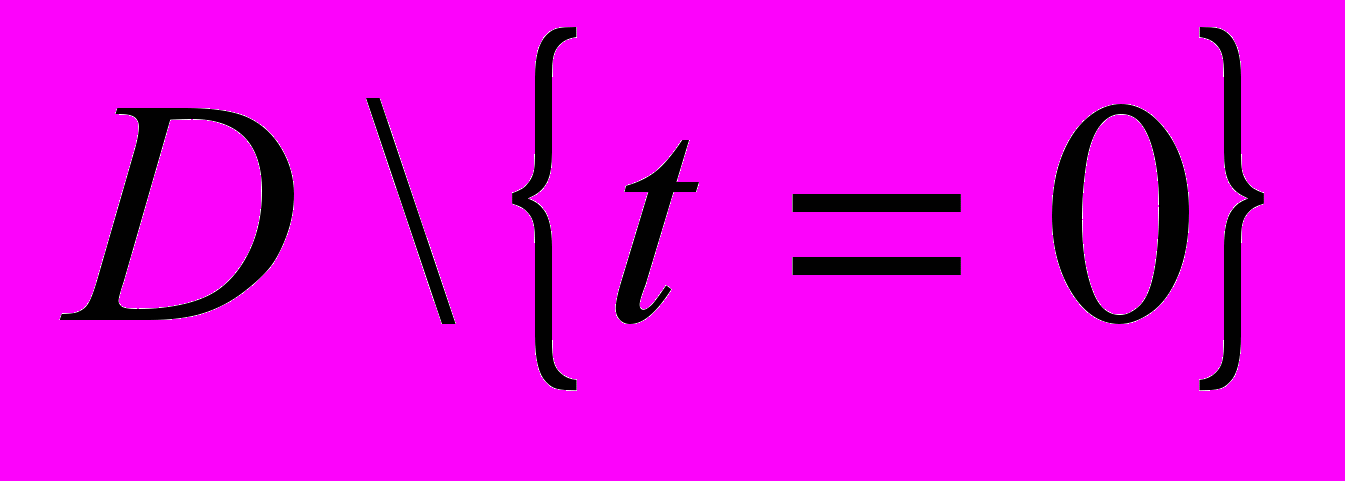уравнению (4) и граничным условиям:  | |
 | |
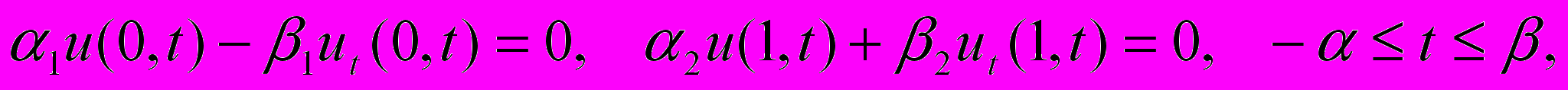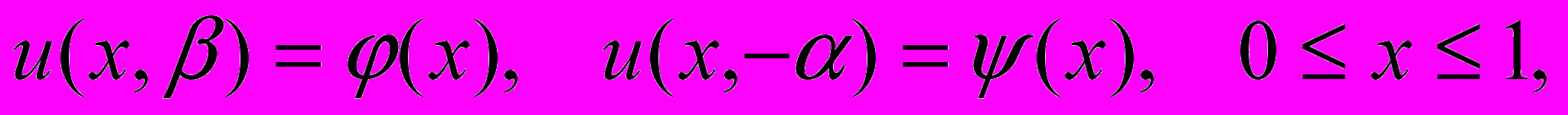где
и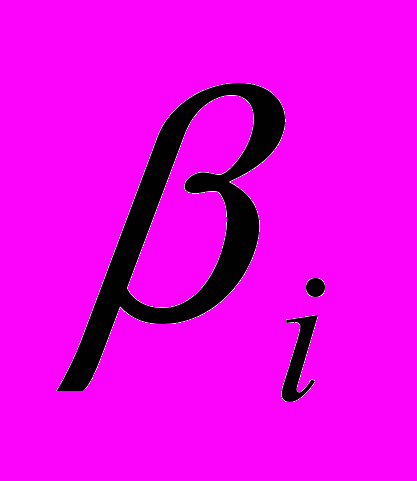
, 
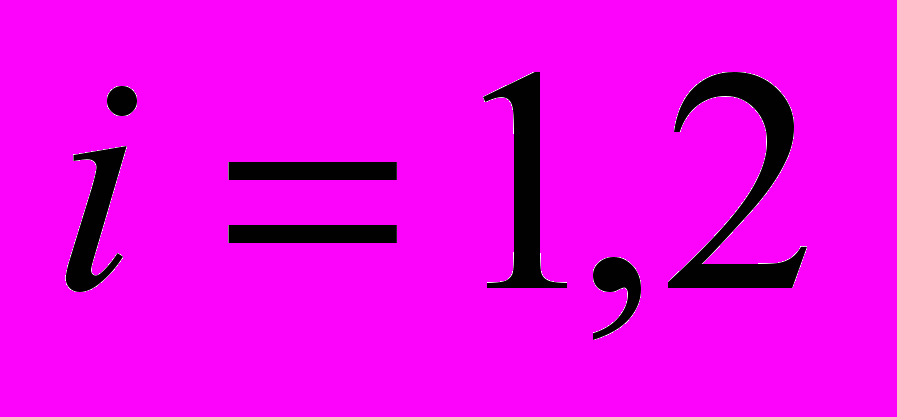, заданные действительные числа, которые не обращаются в нуль одновременно.Методом спектрального анализа установлен критерий единственности решения поставленной обратной задачи с граничными условиями первого – третьего родов на сторонах
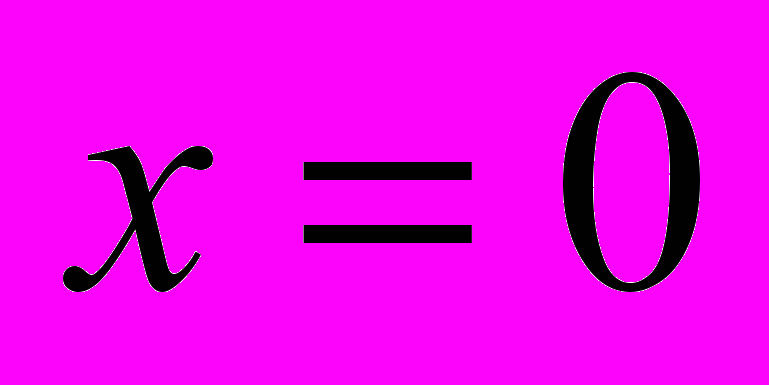и
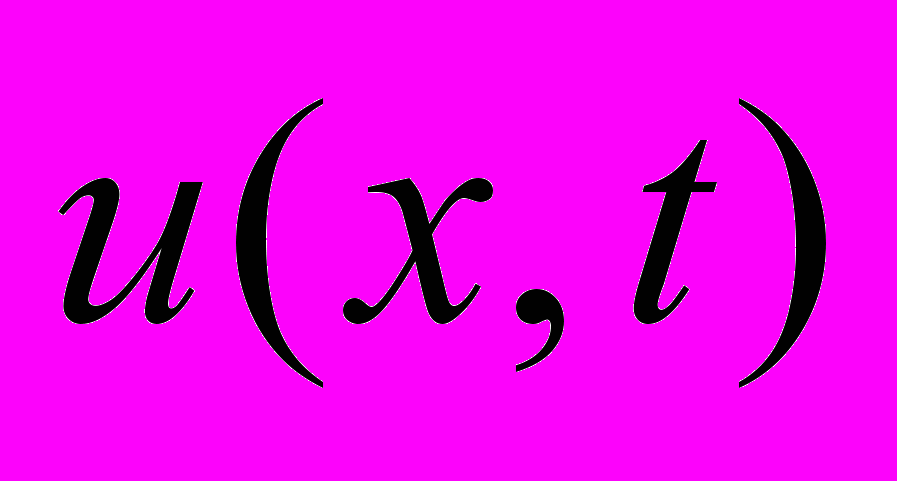. Неизвестные функции и 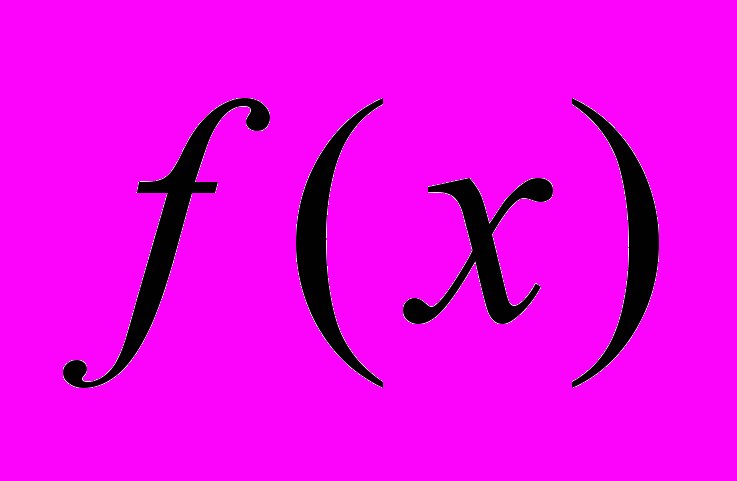построены в виде суммы ряда по системе собственных функций соответствующей одномерной спектральной задачи. д) При обосновании существования решения поставленных прямых и обратных задач для уравнений смешанного типа методом спектральных разложений возникает проблема знаменателей. В связи с чем установлены оценки отделимости от нуля малых знаменателей в зависимости от размеров прямоугольной области и коэффициентов рассматриваемых уравнений (Сабитов К.Б., Трегубова А.Х., Сабитова Ю.К., Сафин Э.М.).
е) Для квазилинейных эллиптических уравнений с финитной правой частью
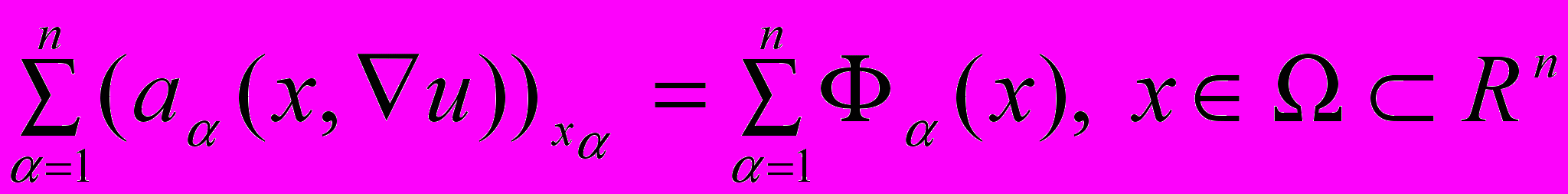
в областях с некомпактными границами получены оценки скорости убывания на бесконечности решения задачи Дирихле и установлена точность этих оценок.
Для квазилинейных параболических уравнений
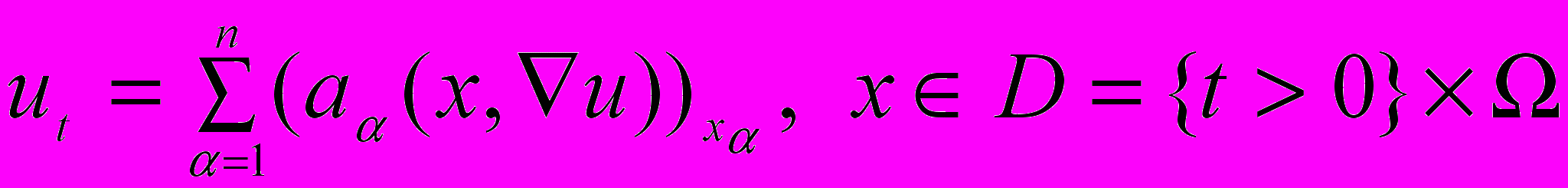
установлены оценки скорости стабилизации решения первой смешанной задачи с финитной начальной. В случае слабо квазилинейных параболических уравнений доказана точность полученных оценок (Кожевникова Л.М., Каримов Р.Х.)