Задачи: Повторить основные понятия логики. Решить задачи: на построение логических формул; нахождения значений сложных высказываний с помощью ти
| Вид материала | Урок |
- Логика высказываний. Основные понятия и определения. Логические функции одной и двух, 6.36kb.
- Алгебра логики. Определение формы сложных высказываний, построение таблиц истинности, 132.48kb.
- Задачи урока: повторить свойство монотонности и ограниченности показательной функции;, 91.6kb.
- Функции алгебры логики, 47.25kb.
- Программа дисциплины Математическая логика Семестр, 13.41kb.
- Элементы математической логики, 189.46kb.
- Значение формулы логики предикатов, 9.17kb.
- Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
- 5. 11. Как упростить логическую формулу?, 21.9kb.
- Ложь с позиции информатики, 105.56kb.
Мастер-класс по теме «Использование интерактивной доски на уроках информатики и ИКТ»,
учитель информатики и ИКТ Показаньева И.А.
Образовательный модуль «Логические основы построения компьютера»
У

рок с использованием интерактивной доски
по теме «Построение таблиц истинности»
В

данном уроке использованы следующие элементы интерактивности:
1. «Электронное перо» - решение задач, заполнение таблиц истинности, заполнение кроссворда и т.д.
2. «Найди пару» - передвижение объектов-слов к соответствующим объектам-рисункам.
3. «Подбери верное» - подобрать данным объектам-понятиям правильные объекты-определения (перетаскивание объектов).
4. «Открой и узнаешь» - ответ на вопрос спрятан за прямоугольником на экране.
Цель: Научить строить таблицы истинности для нахождения значений сложного высказывания с использованием учебного алгоритма.
Задачи:
- Повторить основные понятия логики.
- Решить задачи:
- на построение логических формул;
- нахождения значений сложных высказываний с помощью ТИ.
План урока:
- Организационный момент. Цель, задачи урока – 3 мин.
- Разминка «Что такое логично?» в форме задания «Сделай выбор!» – 2 мин.
- Повторение. Восстановление решения задачи предыдущего урока (открой и узнаешь) – 2 мин.
3.1. Задание «Найди пару!». Привести в соответствие слова и рисунки – 3 мин.
3.2. Задание «Подбери верное!». Даны два столбца «Понятия», «Определения», передвигая объекты на интерактивной доске поставить в соответствие данным определениям – понятия – 2 мин.
- Простое высказывание
- Логическая операция
- Логическая переменная
- Логическая формула
- ТИ
3.3. Задание «Заполни!» - заполнение таблиц истинности основных логических операций электронным пером – 3 мин.
3.4. Задание «Восстанови порядок!» - алгоритм построения ТИ (электронное перо) - 2 мин.
3.6. Кроссворд – обобщение «Основные понятия логики» – 3 мин. (электронное перо).
- Решение задач
- Разбор задачи с построением ТИ – 5 мин.
4.2. Самостоятельное решение задач в тетрадях, на доске – 10 мин.
- Обобщение, анализ, оценка результатов (достижение поставленной цели), домашнее задание – 5 мин.
Ход урока:
Слайд №1
- Организационный момент. Цель, задачи урока – 3 мин.
Здравствуйте, ребята! Мы продолжаем работать над темой «Логика в курсе информатики». Наше сегодняшнее занятие является логическим продолжением предыдущего и может быть условно разделено на 2 части:
- теоретическая часть - повторение основных понятий и алгоритмов, необходимых для построения ТИ и
- практическая часть – решение задач построения ТИ.
Слайд №2
Итак, цель сегодняшнего урока – ……………..
Задачи:……………..
Каждый из вас на сегодняшнем уроке должен будет работать самостоятельно, и в конце урока критично и аргументировано оценить свою деятельность по предложенным критериям. Вы должны будете убедить всех присутствующих в том, что логично будет вам поставить именно ту оценку, на которую вы себя оценили.
А что значит ЛОГИЧНО? В начале урока сразу небольшая разминка.
Слайд №3
2. Разминка «Что такое логично?» в форме задания «Сделай выбор!» – 2 мин. (на доске вычеркивает учитель) На доске - множество слов. Какие из перечисленных понятий наиболее близки понятию л о г и ч н о?
четко аналитично правдоподобно
кратко обоснованно «супер»
красив "железно" доказательно
громко истинно добросовестно
закономерно вероятно разумно
Слайд №4
3. Повторение
Вспомним решение задачи предыдущего урока -2 мин.
Мы с вами на прошлом уроке познакомились с алгоритмом построения таблицы истинности и реализовали его на решении конкретной задачи. Восстановим это решение:
В классе оказалось разбито стекло. Учитель объясняет директору: Это сделал Коля или Саша. Но Саша этого не делал, так как в это время сдавал мне зачет. Следовательно, это сделал Коля. Прав ли учитель?
Мы с вами формализовали условие задачи, составив логическую формулу, и построили ТИ, для того, чтобы найти все значения, которые может принимать данное сложное высказывание. Е=(K v C) & ¬C =>K
К = Это сделал Коля.
С = Это сделал Саша.
| 1 | 2 | 3 | 4 | 5 | 6 |
| К | С | НЕ С | К V C | 4&3 | 5=>1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Слайд №5
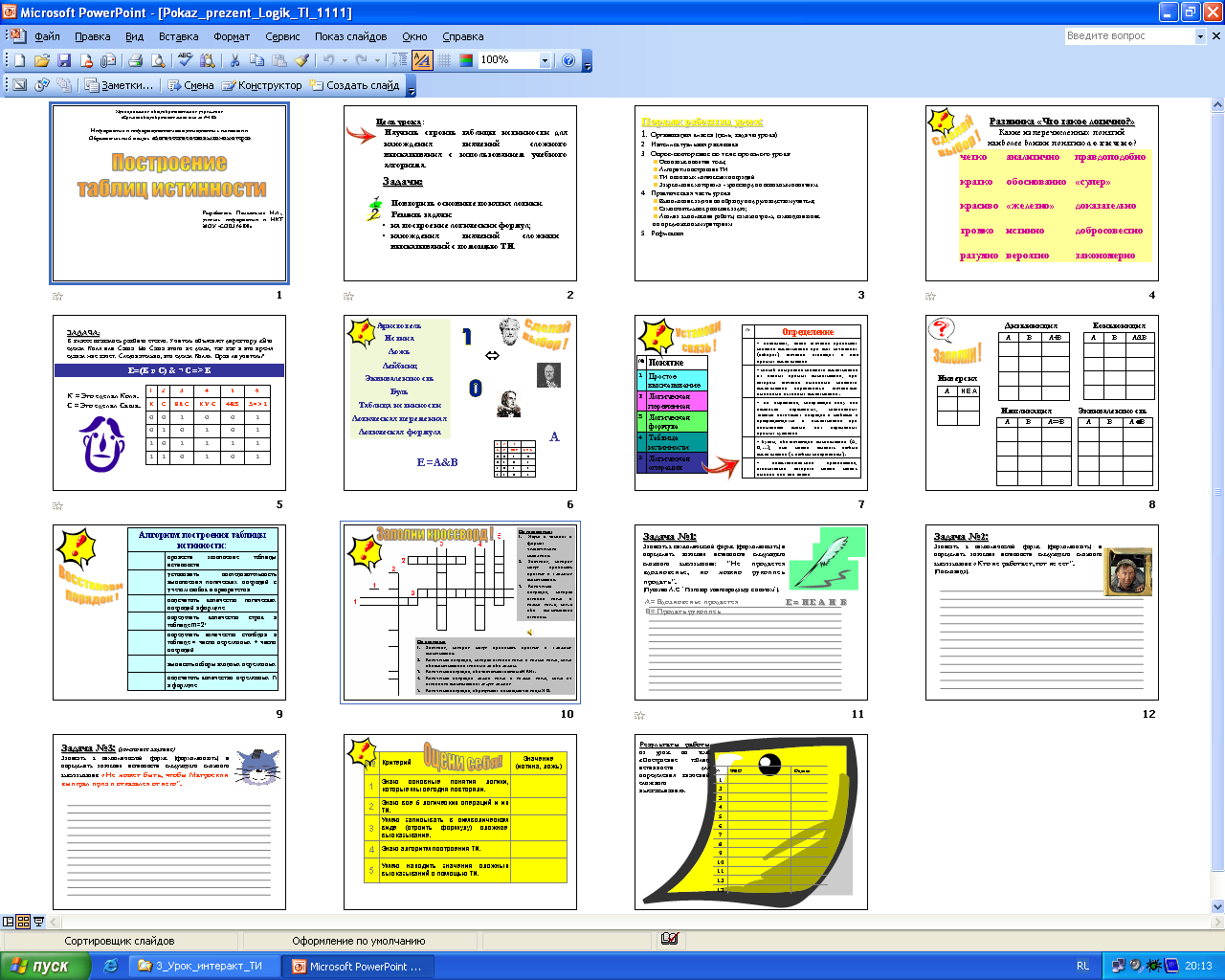
3.1. Решение задачи вспомнили, чтобы идти дальше, вам предлагается выполнить задание «Найди пару»: нужно передвинуть слова к соответствующим рисункам.
Молодцы! А вот теперь выберите из этого множества пар ТЕ, которыми мы пользовались при решении задачи. Вы будете выбирать, я буду их обводить кружочком.
Аристотель Логическая операция Эквивалентность Логическая переменная
Логическая формула Таблица истинности Истина Ложь
Совершенно верно, именно эти понятия нам оказались необходимы. Теперь все вместе вспомним их определения, выполним задание на следующем слайде.
Слайд №6
3
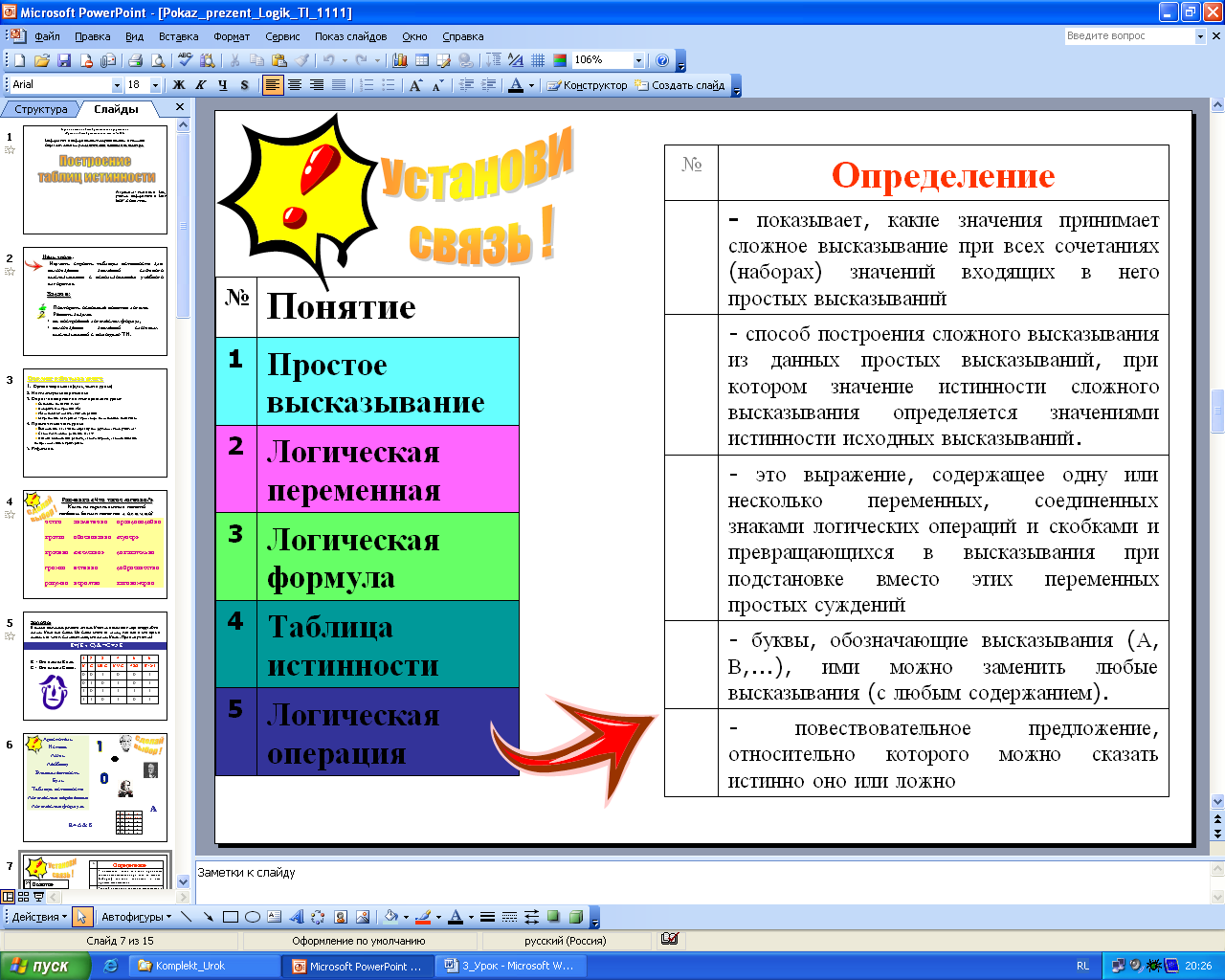
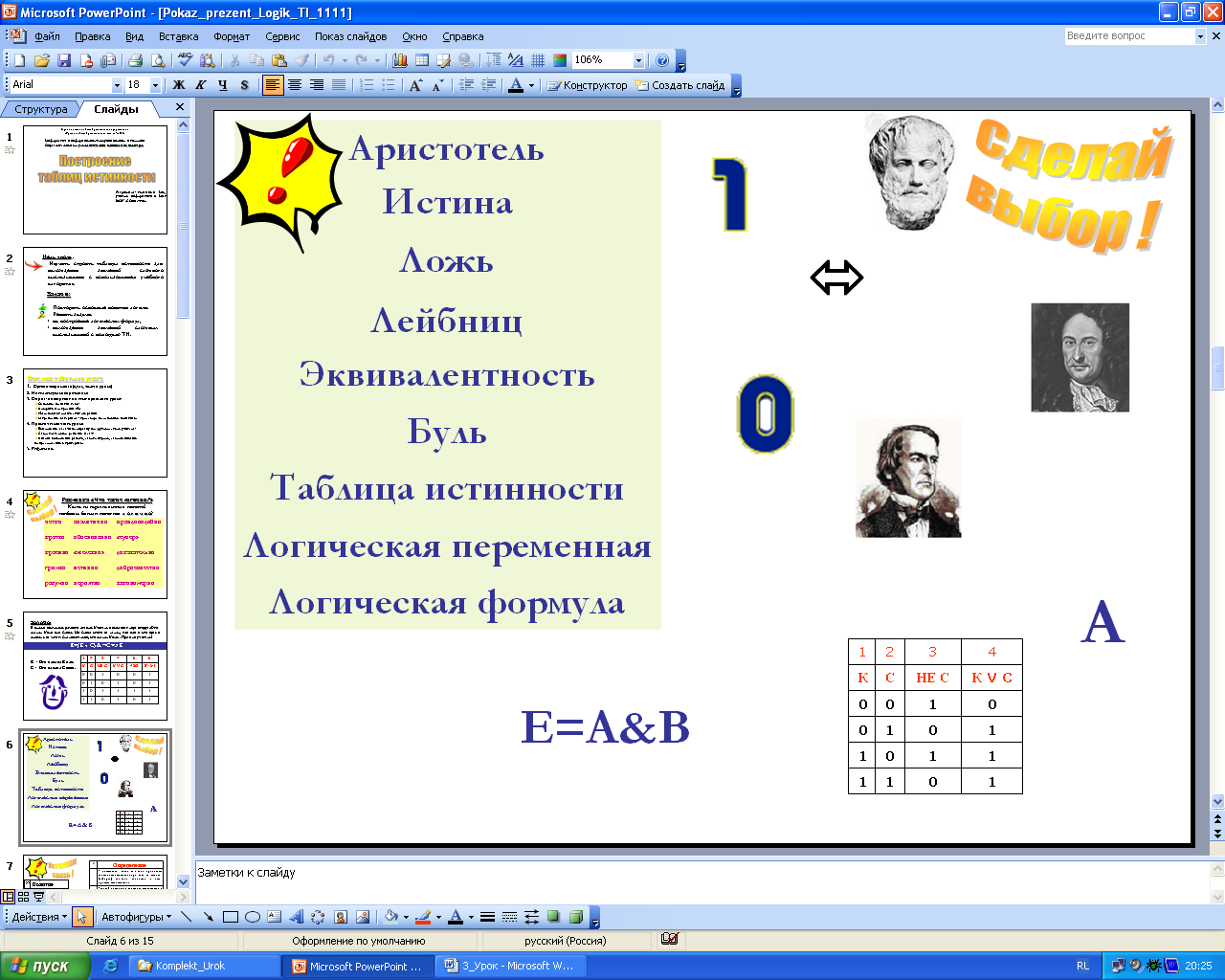
.2. Поработаем в режиме «Подбери верное». Даны два столбца «Понятия», «Определения» (передвигая объекты на экране подобрать данным определениям соответствующие понятия) – 3 мин.
| № | Определение |
| 4 | - показывает, какие значения принимает сложное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний |
| 5 | - способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний. |
| 3 | - это выражение, содержащее одну или несколько переменных, соединенных знаками логических операций и скобками и превращающихся в высказывания при подстановке вместо этих переменных простых суждений |
| 2 | - буквы, обозначающие высказывания (А, В,...), ими можно заменить любые высказывания (с любым содержанием). |
| 1 | - повествовательное предложение, относительно которого можно сказать истинно оно или ложно |
Ответ:
Последнее понятие в нашей таблице – логическая операция. Какие вы знаете логические операции. В следующем задании нужно заполнить ТИ этих операций.
Слайд №7
- Задание «Заполни!» - заполнение ТИ электронным пером – 3 мин.
- Наконец, самое главное - повторение алгоритма построения ТИ сложного высказывания в форме «Проставь порядок выполнения» (электронное перо)- 2 мин.
Слайд №8
| Алгоритм построения таблицы истинности: | |
| 7 | провести заполнение таблицы истинности |
| 5 | установить последовательность выполнения логических операций с учетом скобок и приоритетов; |
| 3 | подсчитать количество логических операций в формуле; |
| 2 | определить количество строк в таблице m=2n; |
| 4 | определить количество столбцов в таблице: число переменных + число операций; |
| 6 | выписать наборы входных переменных |
| 1 | подсчитать количество переменных n в формуле; |

Ответ:
Слайд №9
- В

качестве небольшой музыкально-интеллектуальной паузы – обобщения предлагаю вам заполнить небольшой кроссворд. Причем заполнить нужно коллективно, пока звучит музыка – 3 мин. Как только музыка закончится, заполнение прекращаем. Ваша задача – успеть вписать как можно больше слов. Если успеваете всё, каждый может записать по 1 баллу в свою копилку. Ответ:
П
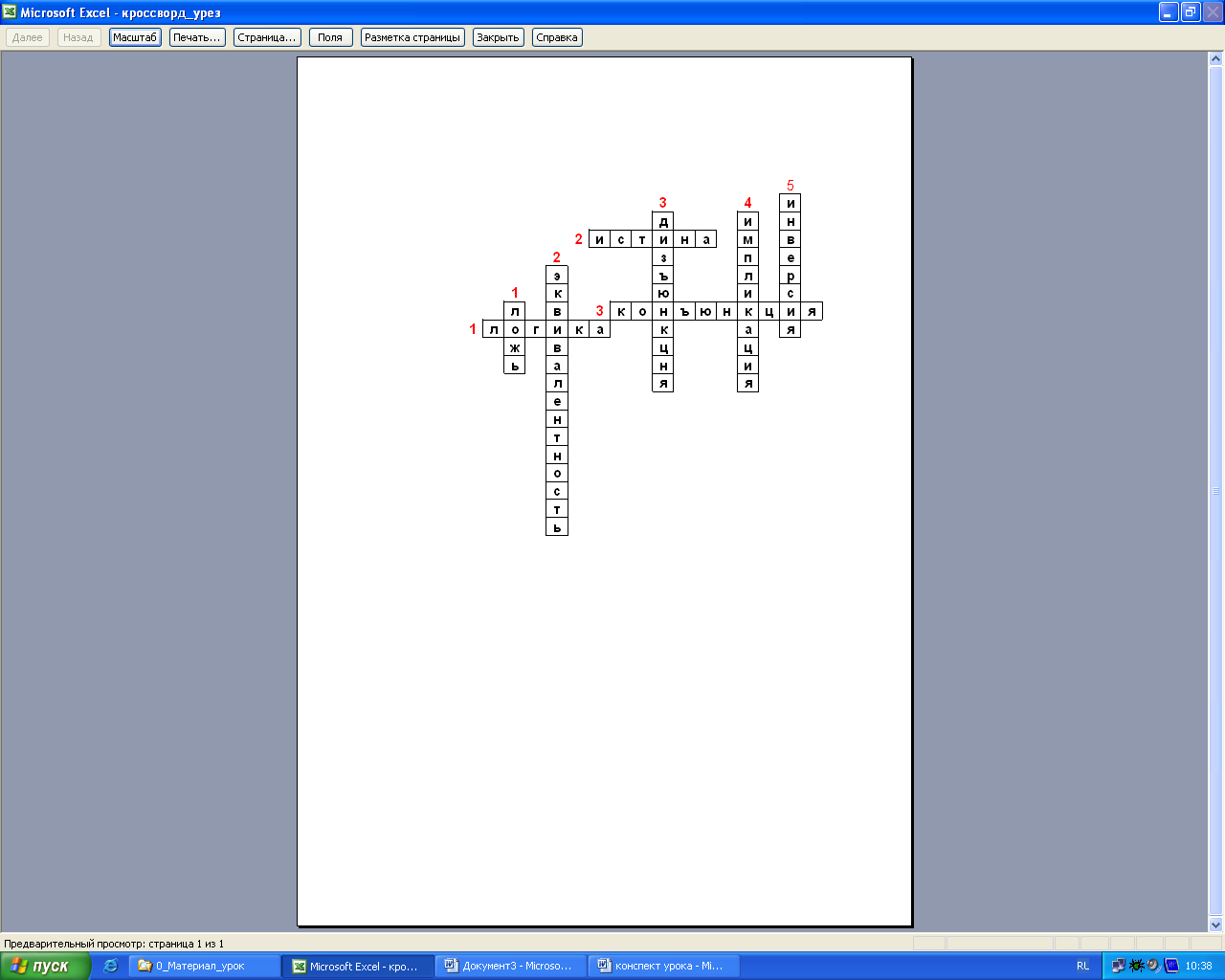
о горизонтали:
- Наука о законах и формах человеческого мышления.
- Значение, которое могут принимать простые и сложные высказывания.
- Логическая операция, которая истинна тогда и только тогда, когда оба высказывания истинны.
По вертикали
- Значение, которое могут принимать простые и сложные высказывания.
- Логическая операция, которая истинна тогда и только тогда, когда оба высказывания истинны или оба ложны.
- Логическая операция, обозначаемая союзом «ИЛИ».
- Логическая операция ложна тогда и только тогда, когда из истинного высказывания следует ложное
- Логическая операция, образуемая с помощью частицы НЕ.
4. РЕШЕНИЕ ЗАДАЧ - Разбор задачи с построением ТИ – 5 мин.
4
| А | В | НЕ А | НЕ А И В |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
.1. Задача №1
Записать в символической форме (формализовать) и найти значения истинности следующего высказывания: "Не продается вдохновенье, но можно рукопись продать".
Пушкин А.С. "Разговор книгопродавца с поэтом").
А = Вдохновенье продается
В= Продать рукопись
Е = Не А И В
- Решение задач самостоятельно – 10 мин.
Задача №2
Вам предлагается самостоятельно (в тетрадях, желающие – на доске) решить аналогичную задачу. Вспомните, в комедии Леонида Гайдая «Операция Ы и другие приключения Шурика», одна из новелл называлась «Напарник». Хулиган-верзила Федя – герой этой новеллы сказал Шурику: «Кто не работает, тот ест», изменив тем самым известную пословицу. Давайте проверим истинность народной поговорки «Кто не работает, тот не ест».
Задача №3
Записать в символической форме (формализовать) и определить значения истинности следующего сложного высказывания: «Не может быть, чтобы Матроски выиграл приз и отказался от него".
- Подведение итогов, оценка результатов (по предложенным критериям) – 2 мин. Поставить 1, если данное высказывание истинно и 0 – если ложно.
- Знаю основные понятия логики, которые мы сегодня повторяли.
- Знаю все 5 логических операций и их ТИ.
- Умею построить формулу сложного высказывания.
- Знаю алгоритм построения ТИ.
- Умею находить значения сложных высказываний с помощью ТИ.
Кол-во «1» будет являться вашей оценкой. «0» укажет вам на необходимость ликвидации этого пробела в дальнейшем. Учащиеся выставляют себе оценки на страницу электронного журнала, комментируя за что поставили себе «1» и «0».
Учитель: самым сложным наверное, является свободное владение ТИ логических операций. Кстати, на следующих уроках мы познакомимся с прикладной программой, которая облегчит нам построение ТИ – это ЭТ Excel. В них, при правильно введенной формуле логической операции автоматически выдается значение «истина», «ложь».
6. Домашнее задание -
учащимся, которые будут сдавать экзамен по информатике в 9 классе или планируют сдавать ЕГЭ в 11 классе.
Задание части А
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
Какое выражение соответствует F?
- ¬X/\¬Y/\Z
- ¬X\/¬Y\/Z
- X\/Y\/¬Z
- X\/Y\/Z
*Дополнительно (резерв, если позволяет время, по вариантам)
Записав следующие два суждения в символической форме, постройте таблицу истинности для каждого из них.
- Кто не играет, тот не выигрывает.
А = Кто-то играет В = Кто-то выигрывает Е= НЕ А => НЕ В
| А | В | НЕ А | НЕ В | НЕ А =>НЕ В |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
- Кто играет, тот выигрывает.
А = Кто-то играет В = Кто-то выигрывает Е= А => В
| А | В | А =>В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| | | |