Geum.ru

Размышления об Эйлере, навеянные думами о прошлом, в свете проблемы устойчивости

Вид материалаДокументы
Подобный материал:
  1   2   3

Размышления об Эйлере, навеянные думами о прошлом,
в свете проблемы устойчивости

Н. В. Валишвили

Грузинский государственный университет, Кутаиси, Грузия

Мыслитель, ученый, математик, механик и инженер, академик Санкт-Петер-бургской и Берлинской Академий наук Л. Эйлер по совету своего учителя Даниила Бернулли в 1744 году стал закладывать основы науки устойчивости на примере упругих стержней. Она оказалась по существу вечной, неиссякаемым кладезем поисков, сомнений, успехов и неудач. Вызывает удивление и восхищение сила духа, воли и таланта Эйлера, который в условиях начала зарождения современной математики и полного отсутствия каких-либо вычислительных методов и средств, облегчающих расчеты, сумел заложить основы науки устойчивости и получить результаты, эталонные и образцовые, критически обсуждаемые и поныне.

Но не меньшее удивление вызывает тот факт, что в нынешних условиях, когда существуют развитая математика и компьютерная техника, способная считать быстрее человека со скоростью миллиардов операций в секунду, мир продолжает мыслить и считать по образу и подобию Л. Эйлера. Так как считаю эту проблему заслуживающей интереса, не столько математической, сколько философской и психологической, хочу сообщить некоторые свои новые результаты, которые породили желание поделиться мыслями.

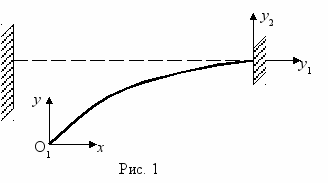
Меня сегодня заботит не столько механика и тем более устойчивость тонкостенных систем. Мои думы заняты состоянием устойчивости таких сфер человеческого бытия, как просвещение, которым я непрерывно занимаюсь последние 50 лет, задачи которого в отличие от задач механики являются «мягкими», трудно решаемыми, но как я убедился на собственном опыте, не безнадежными и не бесперспективными. В механике тонкостенных конструкций сейчас говорю только о продольном изгибе стержней и пластин, но хочу верить, что моя новая компьютерная технология окажется полезной в самых разных областях прикладной механики и экономики для изучения неоднозначных, расщепляющихся решений.

Для изучения закономерности нелинейного деформирования стержня, рис. 1, рассмотрим его элемент длиною ds и используем нелинейные дифференциальные уравнения оболочек, [2, стр. 10 – 12]. При этом, опустив лишнее для прямого стержня, которое суть системы и её порядок, шестой, не меняет, получим:

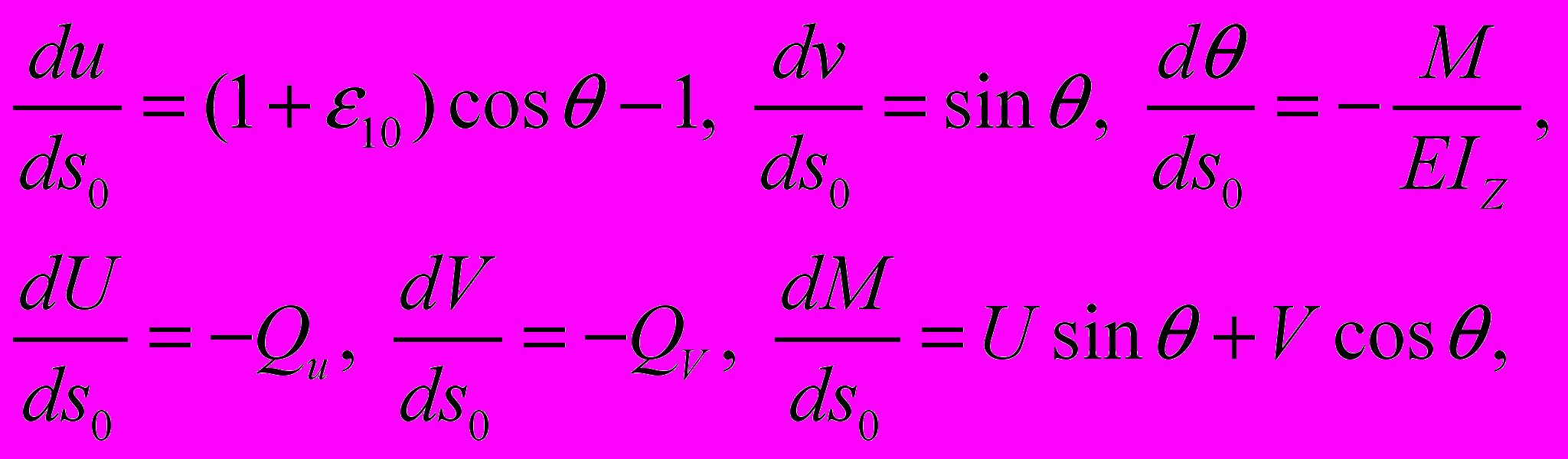(1)

где: u, v, θ – горизонтальное и вертикальное линейные перемещения точек срединной линии и угол поворота сечения стержня в той же точке; ε10 – деформация волокон, расположенных вдоль центральной оси; U, V, M – горизонтальная и вертикальная составляющие внутреннего усилия, а также изгибающий момент, Qu и Qv – интенсивности распределенных продольных и поперечных нагрузок.

Изменение длины стержня, как правило, не учитывается, но здесь для первого уравнения исключение сделано не случайно. Покажем такую необходимость в некоторых нелинейных задачах, преобразовав первое уравнение системы (1)

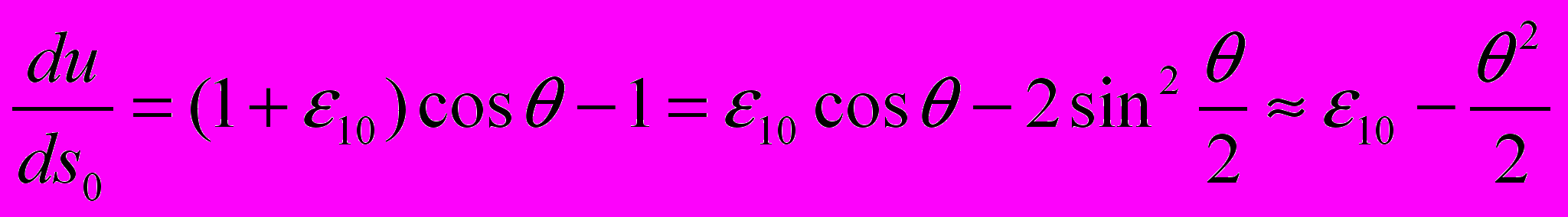(2)

В таком представлении априори сказать, что больше или меньше: первое слагаемое в правой части уравнения или второе, – невозможно.

Введем безразмерные неизвестные, параметры и аргумент:

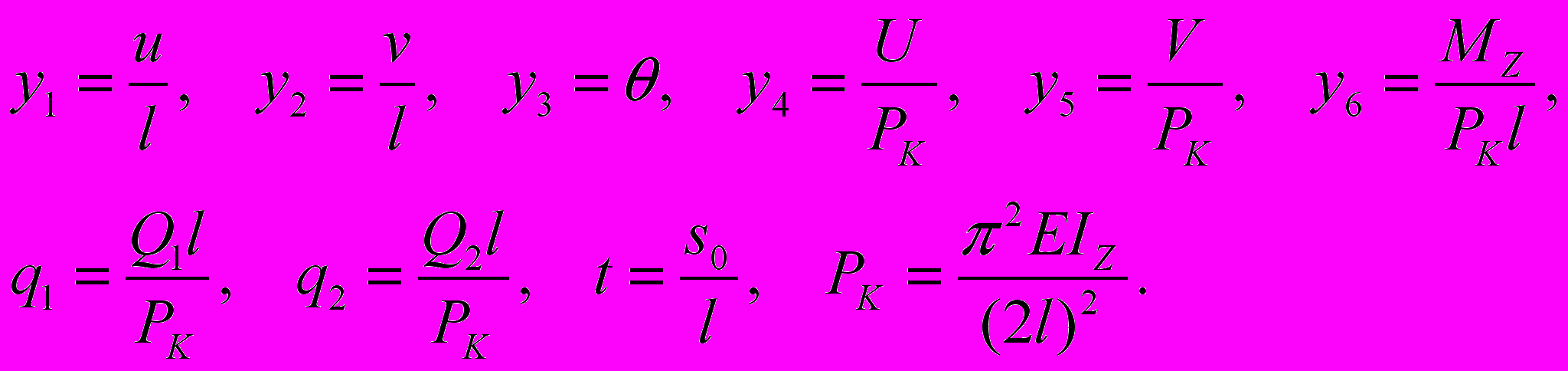(3)

где PK – первая критическая эйлерова сила для консольного стержня длиною l.

Неизвестная ε10, так же как и θ, является безразмерной величиной, но в отличие от неё, является зависимой от нормальной силы. В системе новых независимых переменных эта зависимость имеет вид

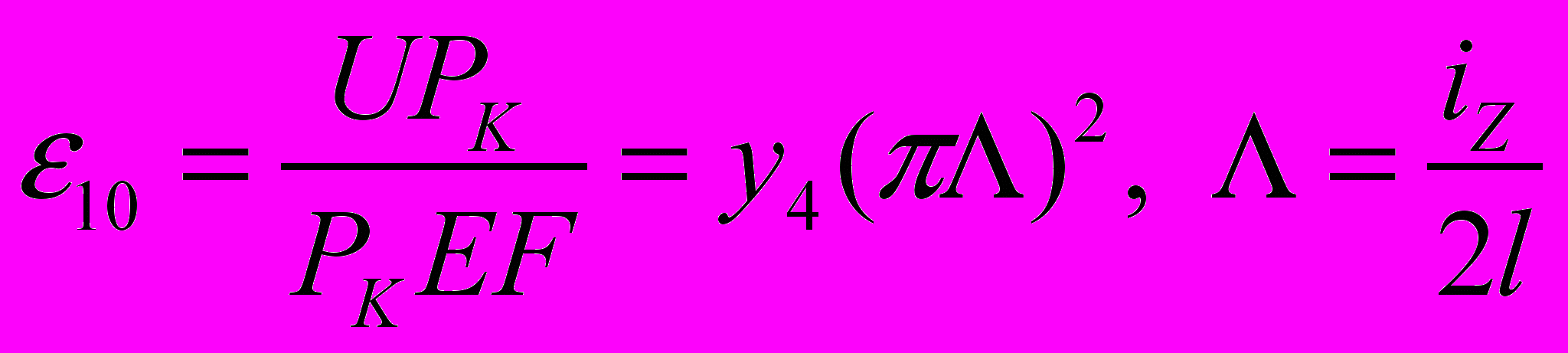. (4)

Тот, кто учтет соотношения (4) и оценит роль каждого из двух слагаемых правой части уравнения (2), являющихся мерой укорочения стойки и половины квадрата угла поворота поперечного сечения, без соответствующих предварительных расчетов пренебрежимо малой величиной, будет самонадеянным или наивным простаком. Роль ни того, ни другого уже десятки лет назад, в 1976 году, меня не прельщала. Поэтому уже тогда я пошел наперекор распространенному мнению и в своей книге заранее не дал предпочтение ни одному из них, [2, стр. 10 – 17], хотя в дальнейшем, в конкретных случаях, поступал по обстоятельствам, – то учитывал, то нет какую-нибудь из них.

Учтя свой опыт, и теперь не буду спешить и так выпишу систему уравнений (1) без упрощений в безразмерном виде:

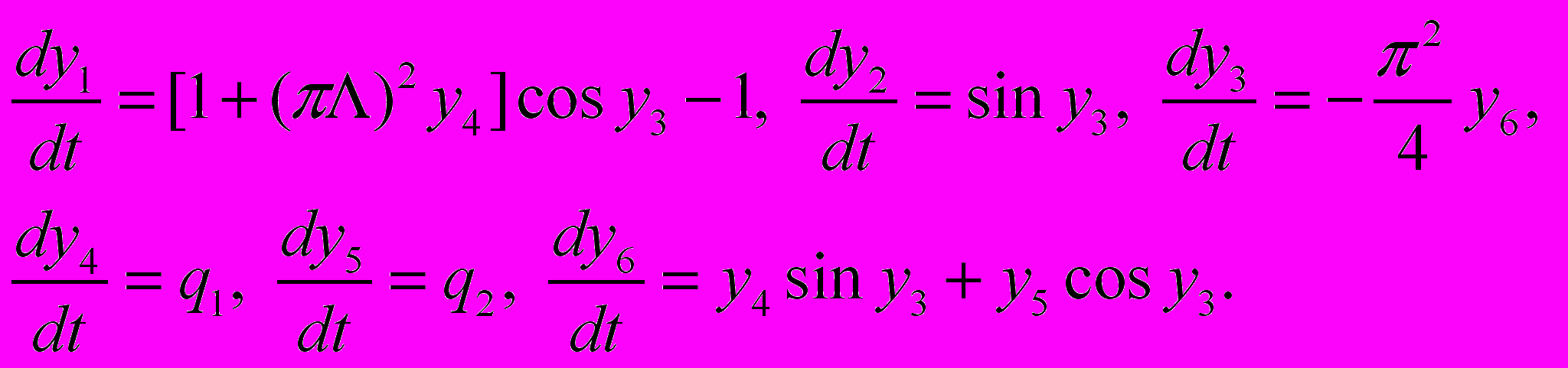(5)

В первом уравнении системы (5) учтено изменение длин волокон вдоль центральной оси стержня [2, стр. 10]. Хотя такая система не является общепризнанной, но этой проблеме позже, в 1985 году, была посвящена всемирная встреча ученых Евромех–197, которая посчитала её основой новой нелинейной теории тонкостенных элементов, назвав её теорией конечных поворотов конструктивной механики. Труды этой встречи были изданы в 1986 году одновременно в Германии, США, Англии, Франции и Японии, [6, стр. I – X].

Для решения задач в дальнейшем используем две прямоугольные координатные системы: первую неподвижную y1Oy2 с началом в точке заделки стержня, а вторую подвижную, двигающуюся по кривой изогнутой оси в процессе деформирования стержня. Начало движения подвижной системы, то есть начало процесса интегрирования уравнений поместим на свободном конце стержня О1 (в точке с координатой t = 0 и номером N = 1), а конец интегрирования – в точке заделки О (в точке с координатой t = 1 и номером N = 2), рис. 1.

Для решения системы (5) учтем условия на свободном конце стержня, ведущим параметром сделаем y3(0) = A(8,1), а ведомыми определим параметры, которые соответствуют краевым условиям на свободном конце стержня:

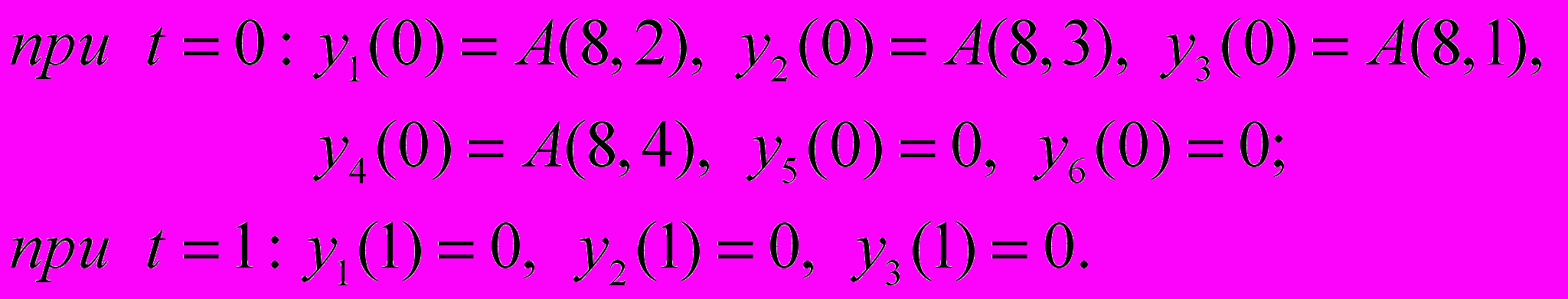
(6)

Взяв начальные параметры и осуществив численное интегрирование в соответствии с граничными условиями (6), составим три численные нелинейные уравнения для определения ведомых параметров А(8,2), А(8,3), А(8,4):

y1(1) ≡ F1{A(8,1), A(8,2), A(8,3), A(8,4)} = 0

y2(1) ≡ F2{A(8,1), A(8,2), A(8,3), A(8,4)}  = 0 (7)

y3(1) ≡ F3{A(8,1), A(8,2), A(8,3), A(8,4)}  = 0

В начальных условиях (6) соотношение y4(0)  = A(8,4) соответствует действию сосредоточенной силы. В случае отсутствия сосредоточенной илы, когда на стержень действуют только продольные распределенные нагрузки, это условие заменится нулевым условием y4(0) = 0.

За прошедшее время я решил большое количество нелинейных задач с помощью своего численного метода, который создал и опубликовал почти полвека назад [1, стр. 1089 – 1092]. Я назвал его просто, без всяких прикрас и претензии – «Алгоритм решения нелинейных краевых задач», не посчитав нужным отметить в его характере свойство непрерывности или способности продолжения решения при следовании за параметром, как за поводырем, хотя все это правда, а не выдумка в отношении моего метода. Тем более, я никогда не говорил о непременной связи метода с большими перемещениями оболочек вращения. Все это вместо меня сделали другие, которые старались «улучшить» мой метод внесением в него изменений косметического характера, не пытаясь вникнуть и понять его суть.

Уже на исходе старого тысячелетия и позже, в начале нового столетия, моим методом я вместе с сотрудниками опубликовал [7, 8, 14 – 18] решения ряда нелинейных задач образования, здравоохранения, газодинамики, теплопередачи и аэродинамики. А теперь постараюсь представить решение нелинейных задач, в которых не может быть разговора о непрерывности и продолжении по параметру, так как еще Эйлер сотни лет назад обнаружил свойство бифуркации решения, в своей основе противоречащее понятию непрерывности, означая разрыв и разветвление решения.

С помощью моего метода я рассмотрел и решил задачи Эйлера об устойчивости консольного стержня для случая, когда действующее на стержень продольное сжимающее усилие, определяющее нормальную силу в стержне, изменяется по параболическому закону: N = Рtn = A(8,4)tn. При этом в частном случае, когда показатель степени равен нулю, имеем дело со сосредоточенной сжимающей силой N = P = А(8,4) = const.

Нетерпеливый критик Эйлера и меня, заодно с ним, своего современника не пожалеет и воскликнет: «Зачем объединять две задачи, когда первую из них Эйлер решил, а на второй зуб сломал?»

Не буду сердиться, помнить русскую пословицу, что «на сердитых воду возят», сохранять спокойствие и с умным видом разъяснять нетерпеливому критику, почему не могу последовать его совету.

Действительно, Эйлер не только решил задачу устойчивости стержня для случая сосредоточенной силы, но и постарался решить задачи для параболического характера, начав со случая устойчивости стойки–стержня под действием собственного веса, n = 1. Более того, он несколько раз решил эту задачу и полученные результаты опубликовал. Но каждый раз убеждался, что его решение неверно. Он так и умер, но не довел до конца решение этой злополучной задачи.

В этой истории заключается не вина, а беда Эйлера, который своим уникальным мышлением намного опередил время. Сегодня в компьютерный век, когда возникли благоприятные условия, и задача практически решена в общем виде, благородно ли нам делить этот класс задач Эйлера на части? Что касается меня, когда привожу результаты решения подобных задач, мысленно их увязываю с именем Эйлера, а себя мыслю как исполнителя его завещания. Я всегда помню и не забываю, что, если бы не было Эйлера, сомнительно было бы и появление моих результатов, которые получены решением системы (5), укороченной согласно рассматриваемой задаче и представленной в виде:

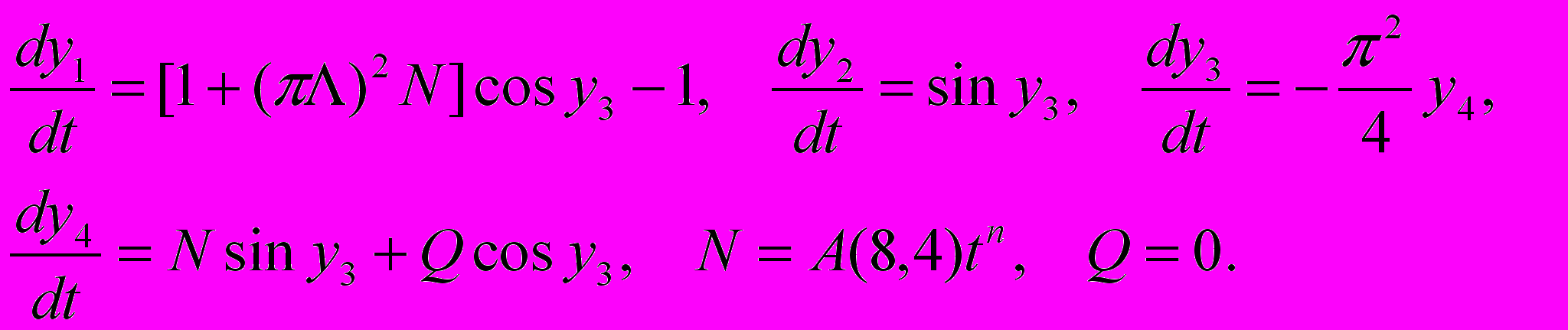(8)

При этом граничные условия для системы (8) представляются следующим образом:

t = 0: y1(0) = A(8,2), y2(0) = A(8,3), y3(0) = A(8,1), y4(0) = 0;

t = 1: y1(1) = 0, y2(1) = 0, y3(0) = 0. (9)

В таблице 1 приведены критические значения параметров нагрузки, которые определены прямым компьютерным методом и программой. При этом они не требуют специального учета бифуркационных скачков и разрывов в решениях. Мой метод, неверно окрещенный самозваными крестными отцами, которых никто не приглашал и не просил, методом непрерывного следования за поводырем–параметром, сам, без посторонней помощи, обнаруживает точки бифуркации и, в случае необходимости, для получения критических сил совершает скачки на необходимую для получения решения высоту, если она даже равна тысячам единиц.

Таблица 1

n
0
1
2
3
4
5

PK
1.00000
3.17647
6.52523
11.0470
16.7386
23.6045

n
6
7
8
9
10
11

PK
31.6424
40.8526
51.2306
62.7948
75.5195
89.4076

n
12
13
14
15
16
17

PK
104.477
120.719
138.130
156.715
176.463
197.410