Geum.ru

Размышления об Эйлере, навеянные думами о прошлом, в свете проблемы устойчивости

Вид материалаДокументы
Подобный материал:
1   2   3
(11)

где .

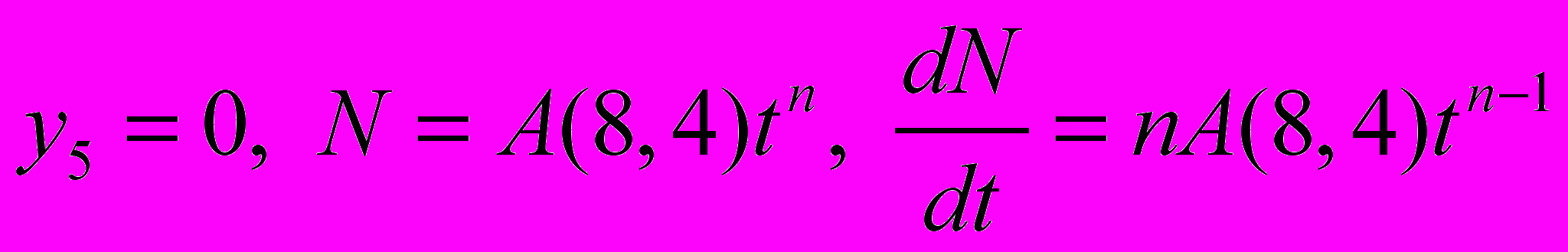Для этой необычной системы уравнений граничные условия тоже необычные и странные, так как изгибающий момент на конечной опоре вместо нуля равен неизвестной величине А(8,3):

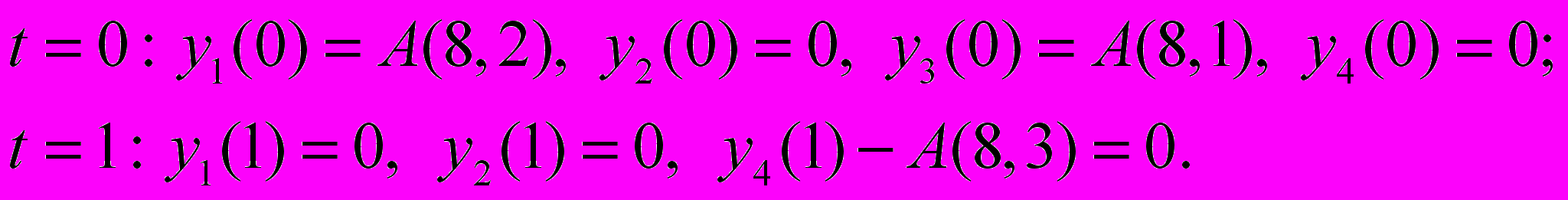(12)

Полученные в результате решения системы (11) – (12) значения критических усилий для разных значений нагрузочного параметра n приведены в таблице 5.

Таблица 5

n
0
1
2
3
4
5

PK
1.00000
1.92062
3.13417
4.64084
6.43850
8.53278

n
6
7
8
9
10
11

PK
10.9180
13.5358
16.5674
19.8317
23.3889
27.2392

n
12
13
14
15
16
17

PK
31.3824
35.8186
40.5477
45.5699
50.8850
56.4931


Таблицу 5 начал составлять еще Эйлер. Первую задачу, которой соответствуют значения параметра нагрузки n = 0 и критической силы в безразмерном виде PK = 1, он решил, и это решение сегодня общеизвестно. Но, чтобы напомнить его, переведем безразмерное значение критической силы для двухопорной балки с сосредоточенной сжимающей силой в привычный для всего технически грамотного честного народа размерный вид:

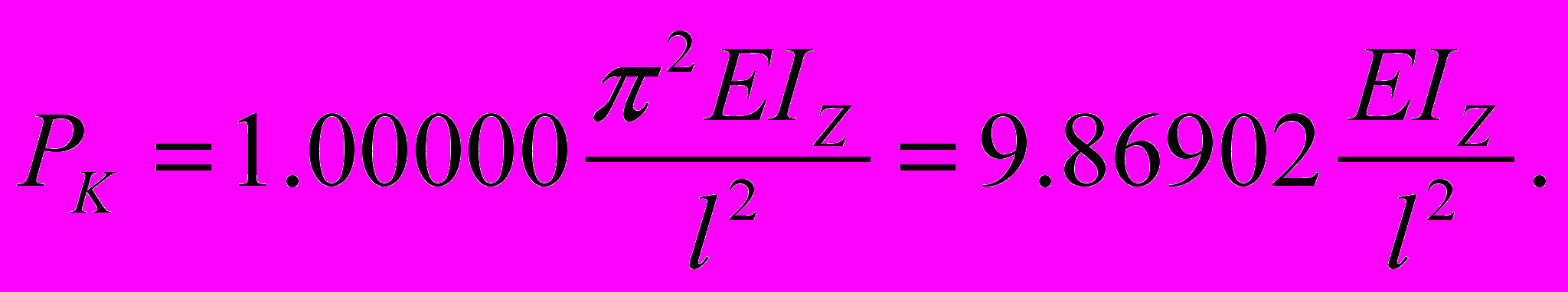(13)

Не забудем упомянуть и вторую задачу таблицы 5 (n = 1), которую начал решать Эйлер, но не успел закончить, так как не учел, что жизнь человека является мгновением в быстротечном периоде существования живого на земле. Для безразмерной критической силы двухопорной стойки, теряющей устойчивость под действием собственного веса, в таблице 5 приведено непривычное для общества безразмерное значение PK = 1.92062, которому также соответствует формула в непривычном размерном виде

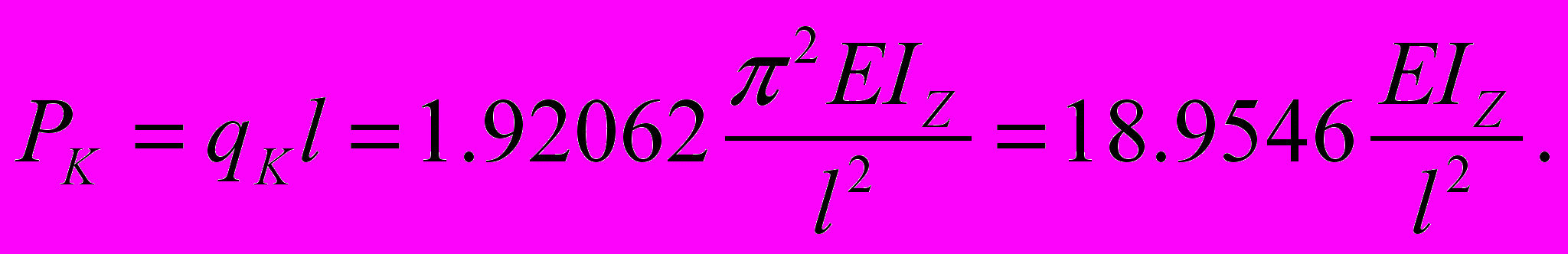(14)

Я близкий этому результат получил и раньше, составив алгоритм и программу счета на основе уже известной численной методики, которую привел в учебнике для студентов [14, стр. 483 – 485] не случайно. Я считаю, что эта методика сегодня является вчерашним днем и имеет не научное, а познавательное значение:

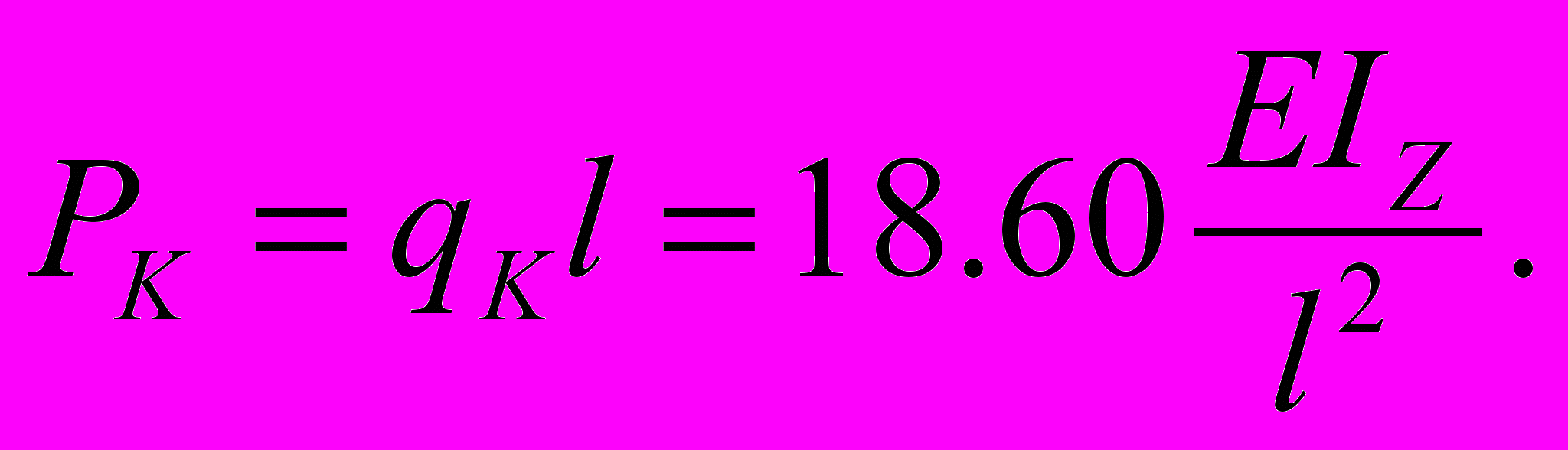(15)

Хотя этот результат почти совпадает с точным численным решением (14) и получен тоже на компьютере раньше его на десятки лет, я его научным достижением не считаю, так же, как не считаю вкладом в науку решения подобных задач в специальных функциях. Уверен, что не все согласятся со мной, но я утверждаю, что тот внес вклад в науку устойчивости, кто хоть на полшажка продвинул учение Эйлера вперед. В таких размышлениях нахожусь, когда думаю о необычном характере системы уравнений (11) и краевых условий (12).

Свой учебник я начинаю [14, стр. 21 – 24] с изложения принципов, которые лежат в основе сопротивления материалов и конструкции. При этом, говоря о принципе сохранения начальных размеров, отмечаю роль исключений, среди которых, как видно из уравнений (11) и краевых условий (12), особую роль играют задачи устойчивости.

Когда на стержень действуют продольные распределенные сжимающие силы, до начала потери устойчивости стержень находится в исходном, горизонтальном положении между двумя опорами и никаких изгибающих моментов в нем не возникает. Не возникает он и в надопорных сечениях, в которых следует удовлетворить краевым условиям. Но с началом процесса потери устойчивости стержень начинает отклоняться от горизонтального положения вместе с распределенными силами. При этом эти силы, оставаясь параллельными исходной горизонтальной оси, создают вертикальные реакции на опорах, которые должны друг друга уравновесить, так как других вертикальных сил нет в системе. Но при этом чистый изгиб сменяется поперечным изгибом, при котором исключается явление эффекта потери устойчивости Эйлера.

Положение только кажется безвыходным, но выход все-таки есть: разрешающие уравнения устойчивости надо записать в начальном положении системы и менять их в процессе потери устойчивости и отклонения стержня от исходного положения, учетом изменения опорных реакциях при численном счете. При этом возникающий в процессе счета надопорный реактивный изгибающий момент, хотя является фиктивным, уравновешивает момент активных сил, исключая появление вертикальных взаимно уравновешивающих друг друга опорных реакций и создавая условие для чистого изгиба, обязательного для компьютерного метода определения критической силы. При аналитических и некоторых численных процессах этот эффект не дает о себе знать, но мой метод, который особенно чувствителен к непорядкам в системе счета, сразу сигнализирует, отказываясь продолжать расчет.

Для исключения нежелательного явления у правой опоры к стержню следует приложить сосредоточенный неизвестный, изменяющийся в ходе процесса счета изгибающий момент А(8,3), который в начале процесса потери устойчивости равен нулю, а в ходе процесса счета возникает, полностью уравновешивая моменты от продольных сил и тем самым исключая возникновение вертикальных опорных реакций и обеспечивая условие чистого изгиба для стержня. Чудак момент, как появится неожиданно в начале процесса потери устойчивости, так и внезапно исчезнет во тьме неизвестности, став равным нулю, после завершения процесса потери устойчивости и исполнения своей роли.

Когда размышляю об этом, то невольно вспоминаю капитальный обзорный труд академика И. И. Воровича, который, подводя итог исследованиям в области нелинейной теории пологих оболочек, упомянул и мои работы с сотрудниками, которые по тематике и выводам являются исключением из тысяч исследований, проведенных в мире в прошлом веке. Речь идет о круглых пластинах, для которых только мы и американская пара исследователей смогли выявить неоднозначные решения для осесимметричного нагружения [5], в то время как другие исследователи не могли теоретически доказать возможность существования в этом случае нескольких решений [15, стр. 267 – 268].

Это мне напоминает китайскую притчу о поисках черной кошки в темной комнате, где её нет. Другие ученые, которые также исследовали проблему, в отличие от меня и моих сотрудников, А. К. Твалчрелидзе и Д. Ш. Георхелидзе, искали несколько решений в классе осесимметричных решений при действии поперечной нагрузки. Мы их нашли, когда изучили неосесимметричные деформирования осесимметричного нагружения пластинки так же, как и другие, поперечными силами.

Тот, кто подумает, что я сказал главное, ошибется. На самом деле я хотел спросить, чем характеризуются и отличаются друг от друга пластина, пологая оболочка и вообще оболочечные тонкостенные конструкции? Если речь идет об оболочках, то тот же И. И. Ворович в своей книге правильно пишет, что многочисленные примеры получения неоднозначных решений для оболочек можно найти в работах, которые я выполнил один или с сотрудником [15, стр. 288 – 289]. При этом он ссылается на мою книгу, в которой кроме оболочек рассматриваются круглые пластинки и определяются также критические значения при осесимметричном нагружении пластинки продольными силами. При этом пластинка теряет устойчивость по осесимметричной форме, которую для пластинки при поперечном нагружении ученые всего мира безуспешно ищут, так как ее не существует.

Видимо, мой друг Иосиф Израилевич суть пологости конструкции, как все, считает чисто геометрическим понятием, но мне кажется, что, если рассматривать её в отрыве от характера нагрузки, можно попасть впросак и утверждать, что при нагружении пластинки продольными осесимметричными силами круглая пластинка не теряет устойчивости. Примерно такая история случилась с Эйлером, но он не поверил своему решению, что стойка под действием собственного веса не теряет устойчивости, и оказался прав. Мы тоже поступим как Эйлер и не поверим утверждению, что круглая пластинка по осесимметричной форме не потеряет устойчивости при осесимметричном нагружении, и с помощью моего метода и компьютерной программы исследуем устойчивость круглой пластинки на основе уравнений пологих оболочек Рейсснера-Феодосьева.

Аналогично работе [2, стр. 139] постараемся получить наиболее простую форму разрешающих уравнений для симметричного относительно центральной оси деформирования круглых пластин. В этом случае для безразмерных параметров, аргумента и неизвестных получим формулы, в которых для размерных и безразмерных величин при необходимости используем одинаковые символы. При этом для их отличия у размерных величин в верхнем индексе поместим звездочку:

(16)

Здесь w, θ – нормальные перемещения и угол поворота нормали в точках срединной поверхности, удаленных от центра пластины на расстояние r; N1, N2, M1, M2 – радиальные и окружные нормальные силы и изгибающие моменты, соответственно; Ф, Θ – разрешающие функции, через которые выражаются нормальные силы и изгибающие моменты; μ – коэффициент Пуассона; P – интенсивность радиальных усилий у контура пластины.

Применив эти соотношения к общим уравнениям оболочек вращения [2, стр. 17 – 21] и преобразовав их применительно к пластинке, получим:

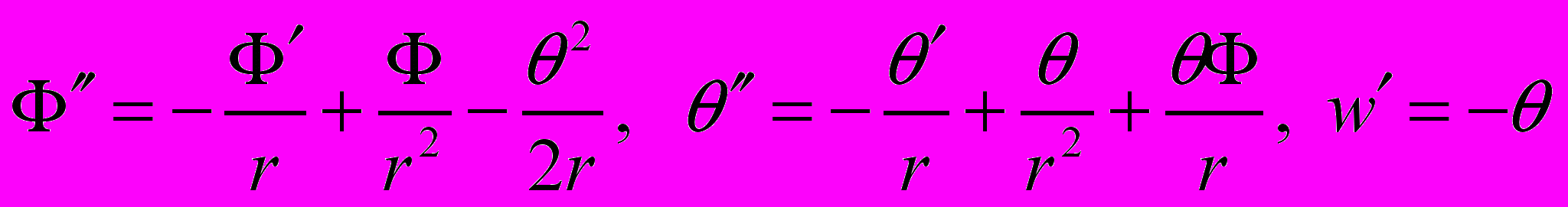. (17)

Штрихом в уравнениях (17) обозначается производная по r. Наличие продольных распределенных нагрузок нелинейная теория Рейсснера-Феодосьева, которой, в основном, я пользовался всегда, не предусматривает, и поэтому их нет в системе (17).

Запишем граничные условия на наружном контуре пластинки r = 1, если на контуре имеется шарнирно подвижная опора и приложена равномерно распределенная нагрузка интенсивностью P, (задача 1):

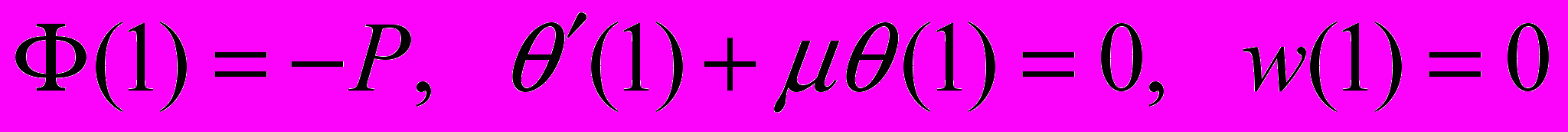. (18)

Если на контуре крепление пластинки исключает поворот нормали в меридиональной плоскости, но позволяет свободу движения в радиальном направлении, то граничные условия на контуре, при r = 1, имеют вид (задача 2)

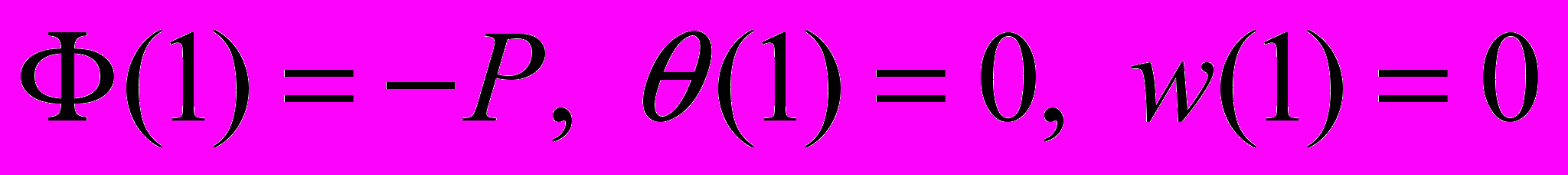. (19)

При численном решении задачи для пластинки необходимо иметь также выражения, характеризующие поведение разрешающих функций в малой окрестности центра пластинки 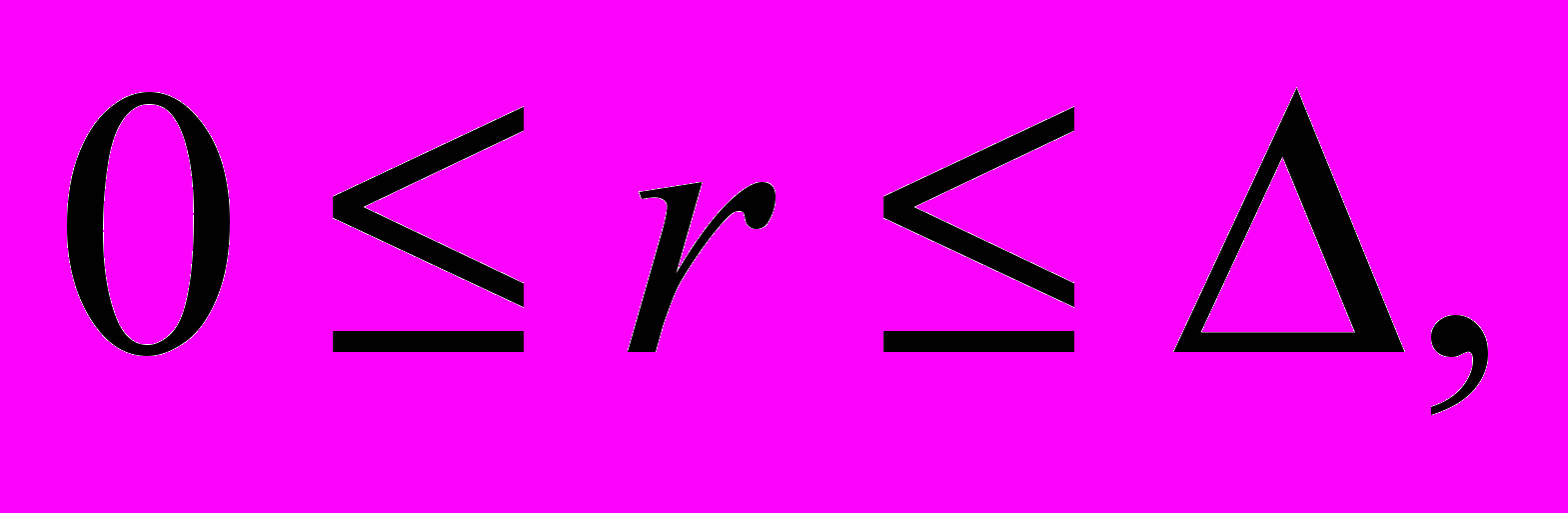которые имеют вид

(20)

Для удобства осуществления расчетов целесообразно перевести (17) в систему из пяти уравнений первых порядков с помощью формул

(21)

При этом получим систему нелинейных дифференциальных уравнений:

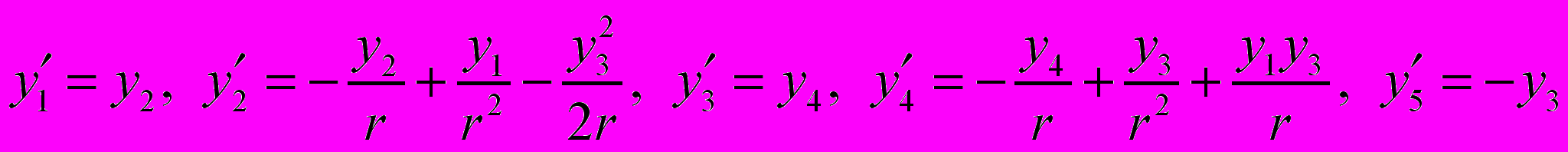(22)

Изучение устойчивости круглых осесимметричных пластин начнем с пластинки, имеющей шарнирно подвижный внешний контур и подвергающейся по нему сжатию в плоскости пластинки равномерно распределенной радиальной нагрузкой интенсивности P. При этом граничные условия представляются соотношениями (18) и (20), которые для новых неизвестных (21) принимают вид:

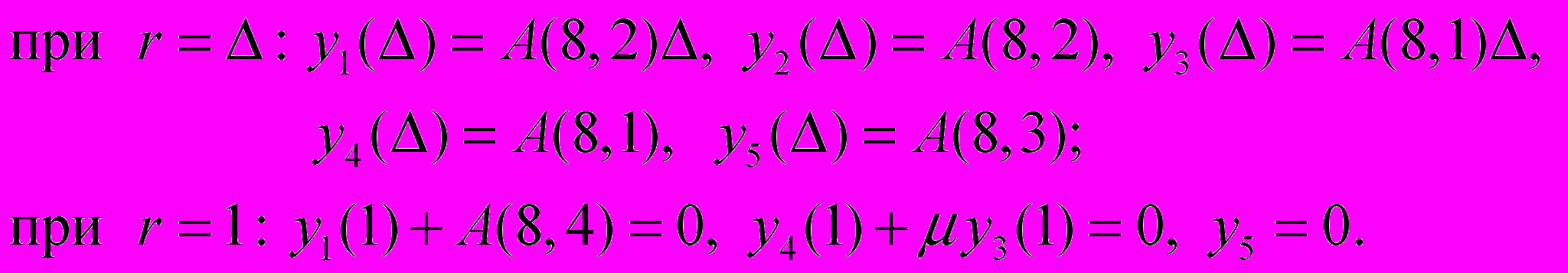(23)

Таким образом, мы получили интегрально-дифференциальную нелинейную краевую задачу с четырьмя параметрами А(8,1), А(8,2), А(8,3) и А(8,4), среди которых первый ведущий, а три остальные – ведомые. В то же время мы имеем точно такое же количество условий в конце отрезка интегрирования, что позволяет определить все три ведомых параметра, в том числе и критическую силу при фиксированном бесконечно малом с инженерной точки зрения значения ведущего параметра А(8,1).

Из элементарного анализа системы уравнений и граничных условий видно, что если критическая сила для пластинки при действии продольных сил существует, то её надо определять в зависимости от коэффициента Пуассона, который присутствует в краевых условиях первой задачи, а во второй он вообще отсутствует. Что касается нагрузки, то она в обеих задачах присутствует вопреки логике и здравому смыслу только в краевых условиях. Несмотря на это, я провел расчеты новым численным методом для обеих задач и получил значения критических сил во всем диапазоне возможного изменения коэффициента Пуассона и для полученных численно значений критических сил составил таблицу 6.

Из таблицы следует вывод, что я как бы обделил вторую задачу, решив для неё только одну задачу, в то время как первой уделил целых восемь!

Таблица 6

μ
0.00
0.10
0.20
0.25
0.30
0.35
0.40
0.50

Задача 1
3.38991
3.66875
3.93791
4.06900
4.19780
4.32436
4.44872
4.69100

Задача 2
14.6825

Я не случайно сказал в отношении второй задачи, что как бы обделил её. На самом деле я для неё предложил формулу определения критической силы, которая справедлива при любых значениях коэффициента Пуассона μ, модуля упругости E, толщины h и радиуса пластины c:

(24)

Что касается первой задачи, то для неё я посчитал критические силы только для нескольких значений коэффициента Пуассона. По ним в лучшем случае можно построить кривую зависимости критической силы от коэффициента Пуассона.

Таким образом, в современных условиях, когда почти не сталось нерешенных задач, решения которых могут быть определены аналитическими методами, ведущая роль в получении точных решений постепенно переходит от человека к компьютеру. Поэтому форма записи исходных уравнений для численного решения часто определяет точность численного решения, а не точность в традиционном понимании.

Когда я над этим думаю, то невольно вспоминаю противоестественное понятие пологости оболочки, анализу которого посвящаются капитальные труды серьезных ученых, в то время как настоящие оболочки остаются на задворках человеческого мышления. Для пологих оболочек и пластин были специально придуманы функции, которые упростили уравнения, но взамен коэффициент Пуассона загнали в краевые условия, а распределенные продольные нагрузки вовсе исключили из уравнений оболочек, в то время как именно они по сути пологости должны в первую очередь определять критические силы Эйлера.

И вспоминаю 70-е годы прошлого столетия, которые оказались судьбоносными для меня, в значительной мере определившими мою дальнейшую судьбу, о чем я не жалею, но часто в сомнениях размышляю. Эти размышления бесконечны и бескрайни. Поэтому их сейчас ни мысленно охватить, ни, тем более, письменно изложить. Но, когда я узнал о семинарах по актуальным проблемам нелинейной теории механики оболочек в Казани, я вспомнил казанский семинар 1969 года.

Тогда я жил в Москве и работал в МВТУ профессором вместе с Всеволодом Ивановичем Феодосьевым, который решал вопрос о возможности моего допуска к защите докторской диссертации. Он мне посоветовал: «Нодар, я специалист – практик ракетостроения. Теоретический центр нелинейной механики тонкостенных конструкций находится в восточной столице России Казани. Его возглавляет Хамид Музафарович Муштари, которого я близко не знаю, но его научному уровню доверяю. Если он одобрит твою работу и согласится оппонировать тебе, то я тоже к нему присоединюсь. Другого пути к вершинам науки у тебя нет».

С таким напутствием я приехал в незнакомый мне тогда город Казань и явился в институт, который возглавлял Хамид Музафарович Муштари, но узнал, что научный руководитель организации тяжело болен, давно на службе не появлялся и не знает никто, когда позволят ему приступить к работе врачи. Я от неожиданности растерялся и не знал, что делать. Но меня успокоили заместители директора, которые на второй день назначили внеочередное заседание научного семинара, чтобы заслушать мой доклад. В этот день в конференц-зале института собрались ученые института, и председательствующий предоставил мне слово. Но я не успел сказать слова, как открылась дверь, и вошел Муштари, который молча под одобрительные возгласы зала направился к своему месту председателя и, как ни в чем не бывало, продолжил заседание.

Мой доклад присутствующие встретили многими вопросами, но сдержанно в оценках. Только председательствующий молчал, словно набрал в рот воды. Наконец, когда увидел, что все желающие задать вопросы и выступить удовлетворены, заговорил тихим, спокойным голосом, обращаясь как бы ко мне и одновременно к залу: «Я вас, молодой человек, не знаю, но верю, так как ознакомился с вашей работой, которая мне понравилась, в журнале Академии Наук СССР, и, хотя я не занимаюсь вычислительными методами, но понял, что вы не все секреты своего метода раскрыли. Поэтому, когда я узнал, что назначено внеочередное заседание семинара для вашего доклада, врачи не смогли задержать меня в постели, я явился на семинар, надеясь услышать новое по сравнению с уже знакомым мне из журнальной статьи. Действительно я услышал кое-что новое, но чувствую, что не все, что вы знаете или в будущем узнаете о своем методе, я услышал. Мне доложили, что вас интересует мое мнение о вашей работе как о докторской диссертации. Я внимательно слушал ваш доклад и наблюдал за реакцией на него ученых нашего центра. Поэтому посчитаю за честь приглашение в МВТУ вашим оппонентом лично или как руководителя коллектива. А сейчас, пока нет никакой официальной просьбы из МВТУ, дадим вам только положительный отзыв на ваш доклад, который составит мой заместитель и представит мне на подпись дома или в больнице».

Когда я вернулся в Москву из Казани и представил отзыв Д. Х. Муштари в МВТУ, все мои вопросы, связанные с защитой докторской диссертацией, автоматически решились. Хамид Музафарович в Москву приехать не смог из-за болезни, но никому не уступил право защищать мои интересы, сам подписал отзыв, как руководитель коллективного оппонента, на мою докторскую диссертацию.

После той памятной поездки в Казань Муштари больше я не встречал, так как он тяжело болел и вскоре скончался. С тех пор прошло сорок лет, но помню, его благородный и мужественный поступок по отношению ко мне, когда он, превозмогая болезнью и сопротивление врачей, явился на мой доклад, где не только похвалил, но также пророчески сказал, что я что-то скрываю или не договариваю. Поверьте, я ничего не скрывал, но сейчас через сорок лет думаю, не был ли Муштари пророк, который увидел в моем методе то, что я тогда не видел и только сейчас увидел и доложил – возможность обнаружения точек бифуркации и определения критических сил моим методом. Когда об этом думаю, то невольно смотрю на свой метод глазами Муштари и называю его методом со скрытыми возможностями, познать которые до конца никому, в том числе мне, не дано.

Литература.

1. Валишвили Н.В. Об одном алгоритме решения нелинейных краевых задач // Прикладная математика и механика. – Т. 32. – Вып. 6. – 1968.

2. Валишвили Н.В. Методы расчета оболочек вращения на ЭЦВМ. Серия «Библиотека для расчётчика». – М.: Машиностроение, 1976.

3. Валишвили Н.В. Устойчивость сжатых и изогнутых стержней при действии следящих нагрузок // Труды МВТУ № 332. Динамика и прочность машин. – 1980.

4. Valishvili N.V., Gavrushin S.S. Finite difference analysis of geometrically nonlinear thin elastic shells. Casopis pre problemy mechaniky v strojnictve. Veda. Vydavatelstvo Slovenskej Akademie vied. Strojnicky Casopis. Cislo 4. Roc. 33. 1982.

5. Валишвили Н.В., Гиорхелидзе Д.Ш., Твалчрелидзе А.К. Об устойчивости оболочек вращения при конечных перемещениях // Тр. Всесоюзной конф. по теории пластин и оболочек. Часть первая. – Таллин. – 1983.

6. Valisvili N.V., Tvalchrelidze A. K. Numerical analysis of thin-walled structure winite displasments. Finit Rotations in Structural Mechanics // Proseedings of the Euromech Colloquim 197. Jablonna. Poland, 1985. Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo. – 1986.

7. Автандилов Г.Г., Валишвили Н.В., Вольмир А.С. , Нацвлишвили Р.М. Об одной математической модели обучения // Тр. первого Всесоюзного симпозиума АН СССР «Нелинейная теория и биомеханика». Кутаиси – Ткибули, 22 – 24 мая 1985 г. – Тбилиси: Изд-во Тбилисского ун-та, 1985.

8. Валишвили Н.В., Нацвлишвили Р.М. Организация интенсивного обучения базовым дисциплинам с применением вычислительной техники // Тр. научно-исследовательского института проблем высшей школы Министерства Высшей школы и среднего специального образования СССР. – М., 1987.

9. Валишвили Н.В., Кавтарадзе Р. З., Петриченко М.Р. Вторичные течения как адиабатизирующий фактор равновесного пограничного слоя в закрученном потоке вязкой жидкости // Фундаментальные исследования в технических университетах. Материалы IV Всероссийской научно-методической конф. – Санкт Петербург, 2000.

10. Валишвили Н.В., Петриченко М.Р., Кавтарадзе Р.З. Теплообмен при вращательном движении жидкости над неподвижной плоскостью // Вестник МГТУ им. Н.Э. Баумана. Серия «Машиностроение». – № 2 (47). – 2002.

11. Валишвили Н.В., Кавтарадзе Р.З., Петриченко М.Р. Расщепляющие в нелинейных задачах теплообмена и пограничного слоя // Тр. 13 школы-семинара РАН под руководством академика А.И. Леонтьева. 2000.

12. Petrichenko M.R., Valishvili N., R.Z. Kavtaradze. Boundary laver in a vortex flow over the stationary plane // Thermophysics and Aeromechanics. – N. 3. – Vol. 9. – 2002.

13. Труды Международной конференции «Неклассические задачи механики», проведенной в Грузинском Государственном университете 25 – 27 октября 2007 г. в двух томах. – Кутаиси, 2007.

14. Валишвили Н.В., Георхелидзе Д.Ш. Сопротивление материалов и конструкций. Учебник на грузинском языке. – Тбилиси, 2008.

15. Ворович И.И. Математические проблемы нелинейной теории пологих оболочек. М.: Наука. Гл. ред. физ.-мат. лит-ры, 1989.

16. Глушков Г.С. Инженерные методы расчетов на прочность и жесткость. Издание второе, переработанное и дополненное. – М.: Государственное научно-техническое изд-во машиностроительной литературы, 1962.

17. Валишвили Н.В., Глушков Г.С. Универсальные формулы для расчета ступенчатых балок. – М.: Машгиз, 1964.

18. Валишвили Н.В. Формулы для расчета рам со стойками переменного сечения. – М.: Машиностроение, 1965.