Geum.ru

Размышления об Эйлере, навеянные думами о прошлом, в свете проблемы устойчивости

Вид материалаДокументы
Подобный материал:
1   2   3


Новым методом задачи решаются для любого показателя степени n, и получаются значения соответствующих критических параметров для тонкостенных конструкций. Но при необходимости, исследования бифуркации решения могут быть осуществлены этим методом и в других областях человеческого бытия: политике, экономике, просвещении, здравоохранении и других сферах.

Как показывает практика расчета и составления таблицы 1 в выборе значения n ограничений нет. Более того, выбор параболической степенной зависимости для описания характера изменения нормальной нагрузки является условным, так что в принципе он может быть любым. Критические нагрузки, представленные в таблице, определены на компьютере прямо, «в лоб», и для этого не понадобились дополнительные итерационные методы при поиске корней нелинейных уравнений.

После смерти Эйлера проходят века, но страсти вокруг его исследований не утихают. Сменяются поколения ученых, но критика Эйлера, что он не учел свойства материала и еще кое-что и поэтому значения его критических сил недостоверны, не прекращаются. Досужие критики вопреки Эйлеру, вводят понятия приведенных характеристик площади поперечного сечения, модулей упругости, секущего и разгрузки, обсуждают «проблему»: уменьшается или растет сжимающая сила в ходе потери устойчивости стержнем и многое еще другое кое-что. Но Эйлер создал и оставил такой незаменимый и неизмеримый кладезь мудрости, что в нем до конца пока не может разобраться никто. Человечество навсегда останется верным здравому смыслу и не откажется от мудрости Эйлера, несмотря на то, что некоторые ученые все не унимаются и без конца пытаются «улучшать» творение Эйлера внесением в его учение «новшеств» косметического характера, пытаясь «запудрить» мозги обществу.

Чтобы, я тоже, как иной критик, не попал впросак, буду осторожен, вернусь к таблице 1 и в компьютерный век, используя свою технологию определения критической силы, постараюсь вникнуть в суть гибкости стержня. Именно откуда следуют понятия короткого, среднего и длинного стержней, которые являются основным яблоком раздора в оценке значения научного наследия Эйлера. При этом использую понятие коэффициента жесткости , являющееся величиной, обратной гибкости: 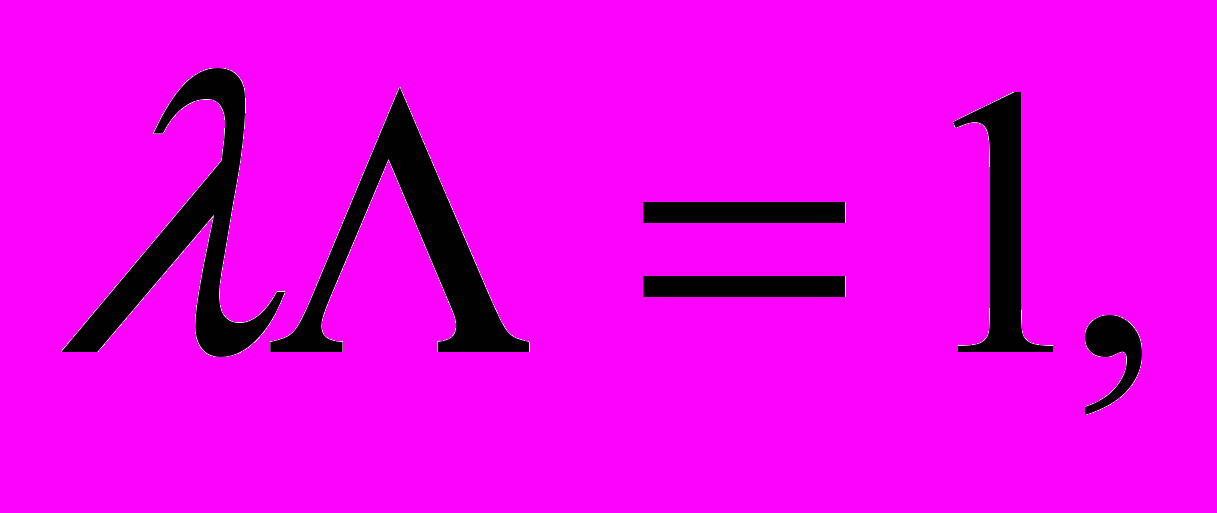которая в основном применяется при исследованиях устойчивости стержней.

При переходе от системы (1) – (2) к системе (4) все неизвестные величины были приведены к безразмерному виду за исключением двух неизвестных: угла поворота сечения θ и деформации срединного волокна в продольном направлении ε, – которые сами по себе являются безразмерными величинами. Что касается первого из них, то его безразмерная форма органически вписывается в общий ряд введенных безразмерных неизвестных и поэтому автоматически играет должную роль в определение результатов расчетов. Со второй неизвестной дело обстоит сложнее. Ее учет возможен только изменением длины отрезка интегрирования [0, 1], что до определения значения критической силы невозможно, да и не целесообразно. Во-первых, ее величина зависит от другой неизвестной, нормальной силы, но сама она непосредственно ни на что не влияет.

Во-вторых, я поостерегся распространенного досужего мнения, что укорочение стержня не играет существенной роли при деформировании стержней вообще и при определении критических нагрузок в частности. Так, оставшись в плену общественного мнения, я временно «забыл» рекомендацию международной встречи ученых Евромех–197 о необходимости учета продольной деформации срединных волокон в нелинейных соотношениях тонкостенных конструкций. Видимо, вместе со временем изменился и я, так как во время издания своей книги, на десять лет раньше «сабантуя» ученых, я был молод и неосторожен и поэтому начал свой труд с учета именно этого спорного парадокса [2, стр. 10 – 12].

Поэтому учту и вторую русскую пословицу, которая гласит, что «лучше поздно, чем никогда», и позже, во вторую очередь все же уточню значения критических сил таблицы 1 при учете укорочения стержня.

Таблица 2
n
0
1
2
3
4
5
6

PK
1.000000
3.17647
6.52523
11.0470
16.7386
23.6045
31.6424

0.00
b
1.000000
1.000000
1.000000
1.000000
1.000000
1.000000
1.000000

0.01
b
0.999900
0.998841
0.999782
0.999724
0.999665
0.999607
0.999548

0.02
b
0.999960
0.998365
0.999130
0.998895
0.998661
0.998426
0.998192

0.03
b
0.999100
0.998271
0.998042
0.997514
0.996987
0.996459
0.995932

0.04
b
0.998400
0.997459
0.996520
0.995581
0.994644
0.993705
0.992767

0.05
b
0.997500
0.996029
0,994526
0.993096
0.991630
0.990165
0.988699

0.06
b
0.996400
0.994282
0.992169
0.990058
0.987947
0.985836
0.983726

0.08
b
0.993600
0.989835
0.986079
0.982325
0.978572
0.974820
0.971069

0.10
b
0.990000
0.984118
0.978246
0.972383
0.966519
0.960655
0.954795


В таблице 2 я повторил часть значений критических сил из таблицы 1, снабдив их соответствующими значениями укороченной длины стержня, r = b, жесткости и показателя характера нагрузки n. В этой таблице, как и в таблице 1, критические силы рассчитаны без учета укорочения стержня, но в дальнейшем эти укорочения будут учтены в граничных условиях, и новым расчетом опять с помощью компьютерного метода будут уточнены значения критических сил, которые вместе с процентом уточнения результата приведены в таблице 3.

Из приведенных здесь результатов видно, что для определения значения критической силы учет укорочения стержня так же важен, как учет характеристик нагрузки и жесткости или гибкости.

Любой здравомыслящий человек, который проанализирует приведенные в таблицах результаты, согласится со мной, что Эйлер создал безупречную математическую теорию устойчивости, завещав нам, потомкам построение на её основе прикладной теории. В ней нам следует учесть и представить воедино все факторы, влияющие на устойчивость систем, в том числе разные нелинейности (геометрическую и физическую), свойства конструкции, среды и материала.

Иного дотошного критика, который справедливо упрекнет меня за некорректное определение укорочения стержня без учета пластичности материала, прошу простить меня и посчитать, что я, как Эйлер, теорию пластичности не знаю. Поэтому полученные результаты привожу не для руководства, а для размышлений.

После изучения влияния конструктивного и силового параметров на значение критических сил консольного стержня, рассмотрим место среды в проблеме устойчивости. Для этого расширим систему (8), и представим её в виде системы пятого порядка:

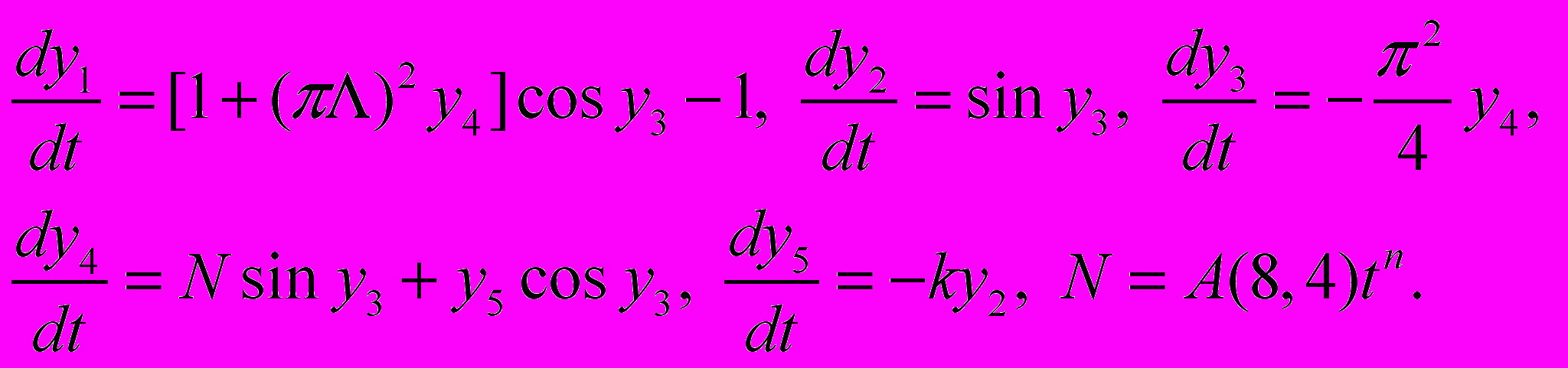(9)

Эта расширенная система нелинейных уравнений предназначена для исследования устойчивости консольного стержня, который помещен в упругую среду, соответствующей модели Винклера и имеющей характеристику жесткости k. Согласно этой модели взаимодействие стержня и среды определяется соотношением q2 = – k y2.

Таблица 3
n
0
1
2
3
4
5
6

0.00
PK
1.00000
3.17647
6.52523
11.0470
16.7386
23.6045
31.6424

%
0%
0%
0%
0%
0%
0%
0%

0.01
PK
1.00021
3.18754
6.53137
11.0623
16.7734
23.6709
31.5189

%
0%
0%
0%
0%
0%
0%
0%

0.02
PK
1.0081
3.19210
6.53137
11.1082
16.8749
23.8676
32.1051

%
0%
0%
0%
1%
1%
1%
1%

0.03
PK
1.00181
3.19300
6.57693
11.1853
17.0456
24.1098
32.4169

%
0%
1%
1%
1%
2%
2%
2%

0.04
PK
1.00322
3.20081
6.61720
11.2943
17.2879
24.5102
33.5352

%
0%
1%
1%
2%
3%
4%
6%

0.05
PK
1.00503
3.21461
6.67043
11.4364
17.6064
25.0364
34.5552

%
1%
1%
2%
3%
5%
6%
9%

0.06
PK
1.00725
3.23158
6.73404
11.6129
18.0027
26.0842
36.0814

%
1%
2%
3%
5%
7%
10%
12%

0.08
PK
1.01293
3.27533
6.90195
12.0763
19.0627
28.2190
40.0177

%
1%
3%
5%
9%
12%
16%
21%

0.10
PK
1.0231
3.33274
7.12568
12.7074
20.5354
31.2607
30.9279

%
2%
5%
8%
13%
18%
24%
31%

Граничные условия изменятся и примут вид:

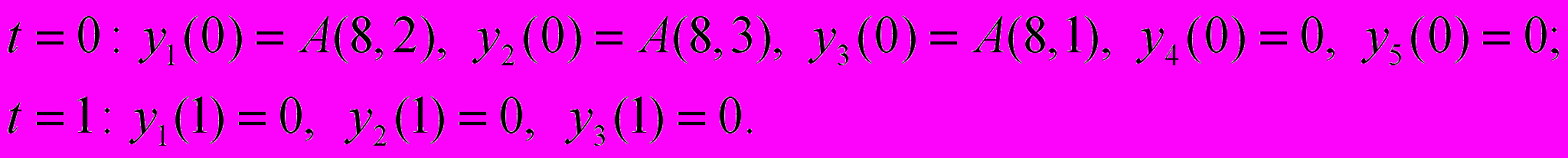(10)

В таблице 4 приведены значения критической силы для укороченного за счет сжатия консольного стержня, находящегося в упругой среде с различными значениями коэффициента постели k и параметра изменения нагрузки n.

Таблица 4

k\n
0
1
2
3
4
5
6
7

0
1.00000
3.17467
6.52567
11.0470
16.7397
23.6031
31.6412
40.8536

2
1.35490
4.43587
9.06204
15.0645
22.3485
30.8666
40.5912
51.5155

4
1.68491
5.69029
11.5567
18.8520
27.3947
37.1273
48.0316
60.1029

6
1.99081
6.93798
14.0015
22.3974
31.9121
42.5262
54.2545
67.1125

8
2.27351
8.17867
16.3938
25.7082
35.9545
47.2047
59.5198
72.9376

10
2.53447
9.41121
18.7271
28.7802
39.5669
51.2797
64.0246
77.8534


Гораздо сложнее обстоит дело с той задачей Эйлера, которая касается устойчивости двух шарнирно опертой стойки, подвергающейся сжатию распределенными по параболическому закону продольными силами. Эту задачу Эйлер решал всю жизнь, но неоднократно терпел неудачу, «ломал зуб», пытаясь решить задачу устойчивости стойки под действием собственного веса, так как каждый раз получал ответ, что такая стойка не потеряет устойчивость. Я грешным делом в «Сопротивление материалов и конструкций», неубедительно толковал неудачу Эйлера, пытаясь убедить студентов, что наш мудрый предок не смог правильно решить эту задачу из-за неучета возникающих при потере устойчивости стойкой взаимно уравновешивающих друг друга горизонтальных опорных реакций [14, стр. 482 – 485].

Когда сейчас думаю о прошлом, прихожу к выводу, что Эйлер, который прекрасно думал и считал, в условиях равновесия ошибку допустить не мог. Но он слишком рано родился и не знал «психологию» компьютера, а его задачи устойчивости для двухопорных стоек принципиально отличаются от задач консольного стержня, для которых вид нагрузки не имеет значение, так как не требуется удовлетворения условию равенства нулю изгибающего момента над обеими опорами. Поэтому сегодня, в компьютерную эпоху, и во времена Эйлера отношение к действию распределенных сжимающих нагрузок должно быть принципиально разным. В их различии может разобраться только компьютер, которого во времена Эйлера не было и в помине.

С тем, кто мне возразит и скажет, что Эйлер ведь решил задачу устойчивости для балки на двух опорах в случае действия продольной сосредоточенной силы, спорить не стану. Но скажу, что эта задача является исключением из правил, так как в этом случае сила, всегда оставаясь у опоры в процессе потери устойчивости и не меняя направления, не создает изгибающий момент над второй опорой. В этом случае решение задачи упрощается, так как условие равенства нулю момента над обеими опорами автоматически выполняется и число неизвестных параметров с трех уменьшается до двух.

Я, как и любой мало-мальски знакомый с современной вычислительной техникой человек, знаю, что компьютер не сам формирует свою психологию и нравы. Он является детищем, рабом творчества и копией разума человека и не более того. Поэтому в его «мышлении» и «логике» есть только то, что в него заложил человек. Но, кроме этого я, полвека учивший вместе с компьютером машинный язык и логику счета, и то знаю, что количественные изменения в скорости действий и принятии решений постепенно переросли в качественное противостояние в психологии творца и творения, создав зону непонимания и отчуждения между человеком и машиной.

Я несколько раз пытался проследить «логику» в действиях компьютера при реализации моего метода решения нелинейных уравнений для обнаружения точек бифуркации и расчета критических сил. При этом каждый раз добивался успеха только в тех случаях, когда задача имела решение в известных математике функциях, например, тригонометрических, эллиптических или функциях Бесселя. Но, когда этого не было, я не мог понять ахинею компьютера, которая позволяла ему получать решение задачи, хотя в основе его действий был заложен мой метод. Сегодня одному Богу известно, как мыслит и что делает компьютер в своем бездонном и бездушном чреве, когда для решения задачи не существует специальных функций. Что будет завтра, – поживем, увидим...

Однако пора и честь знать, вспомнить еще одну русскую пословицу: «Соловья баснями не кормят», – и выписать чудные уравнения и краевые условия задачи Эйлера в компьютерном варианте для стойки с двумя опорами, которые по понятным причинам не мог знать Эйлер. Сегодня мы обязаны знать и не удивляться, что компьютерный вариант уравнений и краевых условий отличается от тех же выражений для аналитического решения задачи.

Итак, система уравнений для изучения устойчивости стержня, который лежит на двух шарнирных опорах в сжатом продольными силами состоянии, имеет вид: