«Применение ит в обработке медицинских изображений»
| Вид материала | Реферат |
- Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
- Нелинейная цифровая фильтрация лазерных изображений при регистрации и обработке, 242.95kb.
- Экспресс-контроль цветовых характеристик мясного сырья и мясопродуктов, основанный, 316.99kb.
- Вопросы патентных отношений при получении разрешений на применение новых медицинских, 32.57kb.
- Уждается применение предварительной обработки для повышения качества декодирования, 27.18kb.
- Алгоритмы восстановления изображений при томографической обработке проекций, 48.43kb.
- Мультимедийный 24'' монитор Benq g2400WD, 292.01kb.
- Рассматривается проблема коррекции изображений документов, снятых цифровой фотокамерой,, 33.11kb.
- Некоторые методы распознавания изображений, 261.7kb.
- Обработка и передача изображений, 149.44kb.
Глава 2 Проблема выделения средних линий
2.1 Свойства средних линий
В этом пункте рассматриваются различные свойства средних линий, которые были получены путем анализа литературы и различных приложений скелетов в компьютерной графике и визуализации.
Гомотопность (сохранение топологии)
Средние линии должны быть топологически эквивалентны исходному объекту [4][8]. Сохранение топологии может быть сформулировано следующим образом: Два объекта имеют одинаковую топологию, если они имеют одинаковое число связных компонент и полостей.
Однако для средних линий отсутствует понятие полости (из-за одномерности). Поэтому в [10] было предложено следующее определение гомотопности: Скелет сохраняет топологию исходного объекта, если он содержит то же самое число связных компонент и имеет по крайней мере одну петлю для каждой полости в исходном объекте.
Циклы в скелете могут быть найдены с помощью алгоритма поиска в глубину, а наличие полостей в исходном объекте можно определить, используя метод, предложенный в [9].
Инвариантность относительно изометрических преобразований
Обозначим изометрическое преобразование (преобразование, в котором сохраняются расстояния между точкам) через T, рассматриваемый объект через O, объект, подвергшийся преобразованию T(O), а его скелет
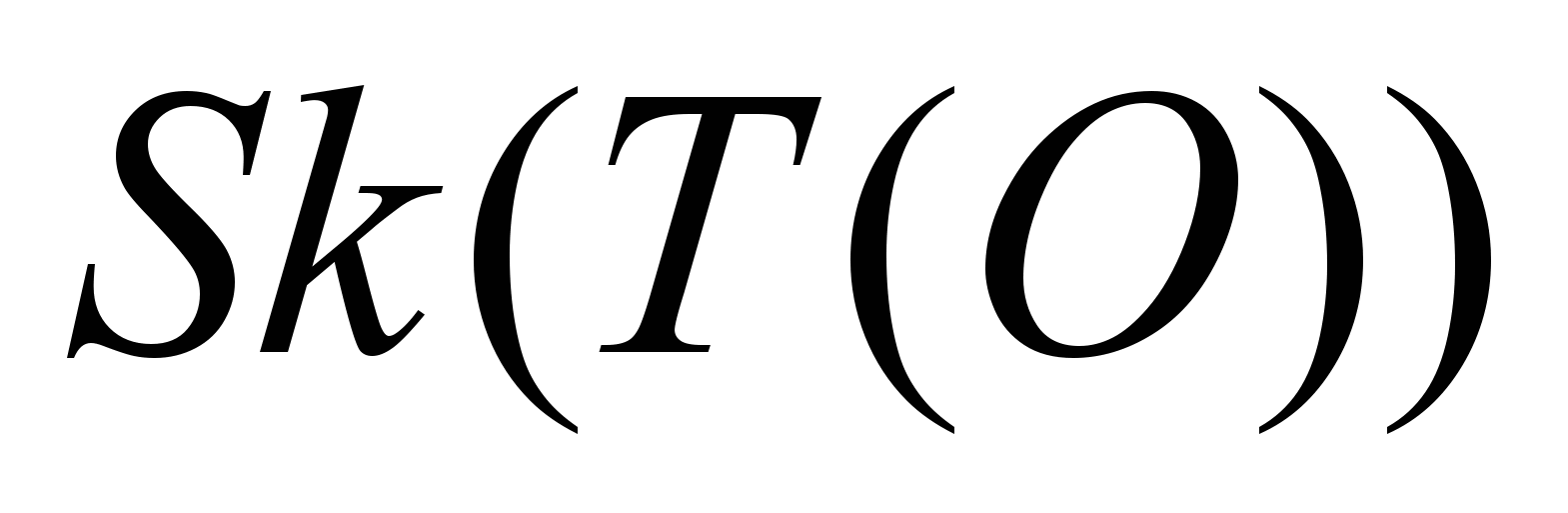должен быть таким же, как и трансформированный скелет исходного объекта, т.е. критерий инвариантности можно переписать| | 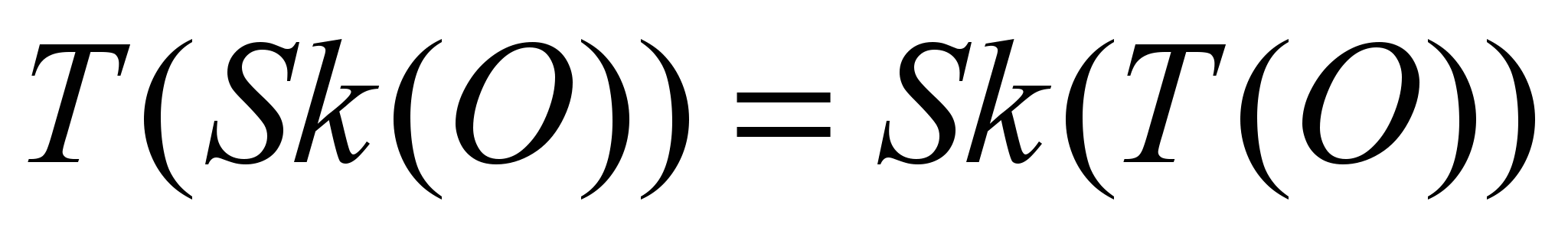 | (2.1) |
Это свойство очень важно для приложений, где средние линии используются для описания объекта.
Восстанавливаемость
В [11][12] рассматривают способность некоторых скелетов восстанавливать исходный объект из скелета. Учитывая определение средних линий как множества центров максимальных вписанных шаров, очевидным решением восстановления является вычисление и хранение для каждой точки скелета расстояния до ближайшей точки границы. Если обозначить функцию восстановления через
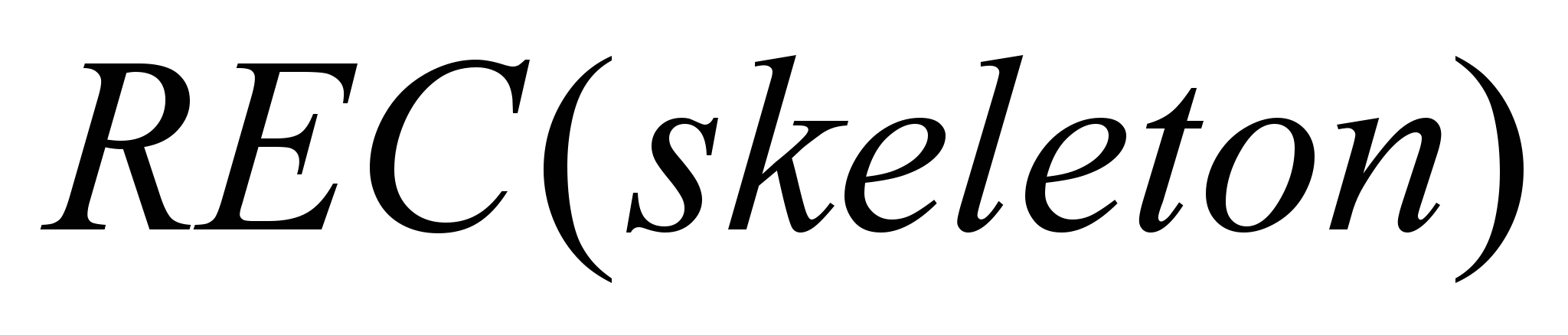, тогда точное восстановление означает| |  | (2.2) |
Трехмерный объект может быть полностью восстановлен из его представления средними линиями. Это свойство часто используется в приложениях для сжатия объектов, а также для визуализации [13]. В тоже время в общем случае, полное восстановление из-за дискретности множества вокселей не всегда возможно.
Толщина
Желательно, скелет должен быть одномерным, т.е. шириной в один воксель во всех направлениях, исключая точки сочленения различных ветвей.
Можно выделить три типа точек скелета [22]: регулярные точки, которые имеют ровно два соседних вокселя; конечные точки, имеющие ровно один соседний воксель, и точки соединения, которые могут иметь три или более соседей.
Тонкость и восстанавливаемость являются двумя противоречащими друг другу свойствами. Даже для объектов, в средних поверхностях которых фактически содержатся только кривые (например, для трубчатых объектов), скелет шириной в один воксель может не содержать все необходимые центры максимальных шаров для точной реконструкции объекта.
Центрированность
Важной характеристикой средней линии является его центрированность в пределах объекта. Для достижения идеальной центрированности необходимо, чтобы средняя линия находилась на медиальной поверхности, а сама медиальная поверхность была сосредоточена в пределах объекта. Кроме того, требуется, чтобы средняя линия находилась по центру медиальной поверхности [10]. Это свойство очень важно в приложениях сжатия изображений, а также в некоторых научных приложениях, например, в вычислении средней линии вихря [11]
Тем не менее, в большинстве случаев, точной центрированности извлеченного скелета не требуется или нежелательно (с учетом известной чувствительности скелета к малым возмущениям на границе объекта) [6] [7]. Приближенной центрированности достаточно для многих приложений, таких как виртуальная навигация или визуализация. Например, в виртуальной колоноскопии, надежность (см. ниже) и гладкость пути более важны, чем точная центрированность [14].
Покомпонентная дифференциация
С помощью средних линий можно различать различные компоненты исходного объекта, т.е. логические компоненты объекта должны быть биективны логическим компонентам средних линий.
Покомпонентная дифференциация отличается от гомотопности в том, что она касается логического восприятия составных частей единого объекта, в то время как последняя связана с геометрической составляющей компонентов, образующих различные объекты.
Проверка, удовлетворяет ли скелет этим свойствам, является сложной задачей, так как определение компоненты объекта не является достаточно точным, а определяется с участием человеческого восприятия, которое по своей сути субъективно.
Связность
Это свойство является следствием гомотопии. Если средняя линия соответствует односвязной компоненте, то она должна быть связной.
Помехоустойчивость
Как показано на рисунке 2 (б), средняя линия очень чувствительна к небольшим изменениям на границе. Желательное свойство скелета – слабая чувствительность к шуму на границе объекта, то есть, скелет объекта без шума и скелет того же объекта с шумом должны быть аналогичны.
Гладкость
Гладкость не только эстетическое свойство, но на самом деле полезно в некоторых приложениях. Например, в виртуальной навигации, которая использует среднюю линию как путь прохода камеры. Путь должен быть как можно более плавным, чтобы избежать резких изменений в изображении.
Иерархичность
Средняя линия сложных объектов может отражать естественную иерархию сложных объектов [15]. Иерархический подход является полезным, поскольку он может создать набор средних линий разных сложностей, которые могут быть использованы в различных приложениях. В строгой иерархии, скелет на определенном уровне в иерархии содержит все средние линии слоев ниже в иерархии в качестве подмножества. Такая строгая иерархия полезна в приложениях с использованием различных разрешений.
2.2 Существующие алгоритмы выделения средних линий
Существует много различных алгоритмов выделения средних линий для двумерного и трехмерного случаев. Хотя некоторые из 2D алгоритмы распространяются на 3D, мы ограничиваем наше рассмотрение алгоритмов, специально предназначенных для трехмерного случая.
В современной литературе обычно используется схема классификации, в которой выделяются следующие классы [16]: основанные на топологическом утоньшении, на использовании дистанционных карт (поиск точек хребта), а также на использовании диаграмм Вороного. Тем не менее, существуют методы, которые принадлежат нескольким классам одновременно (например, методы, основанные на дистанционных преобразованиях, которые используют топологическое утоньшение для «обрезки» получившегося скелета).
2.2.1 Топологическое утоньшение
Методы топологического утоньшения строят скелет путем удаления вокселей границы объекта до тех пор, пока не будет получена необходимая тонкость. Все утоньшающие алгоритмы функционируют в дискретных пространствах и основываются на концепте «простой» точки, введенной Morgenthaler в 1981 [17]. «Простая» точка [18] это воксель, который может быть удален без изменения топологии объекта. Важное свойство «простых» точек состоит в том, что они могут быть определены локально, то есть путем анализа локальной окрестности, что делает алгоритмы топологического утоньшения более эффективными.
Процесс утоньшения начинается от границы объекта и продолжается, пока не останется «простых» точек. На каждой итерации, каждый граничный воксель проверяется на принадлежность множеству «простых» точек. Условия обычно реализованы как шаблоны (или маски) размера 3x3x3 или более. Центр маски совмещается с рассматриваемым вокселем и анализируется окрестность этого вокселя. Все воксели в маске имеют величины «0», «1» или «не опреден». Величина «0» соответствует вокселю границы, «1» – вокселю объекта, «не определен» может принадлежать как границе, так и объекту.
В то же время, удаление всех «простых» точек объекта приводит к укорочения самого скелета, потому что концевые точки скелеты сами являются «простыми».
Существуют несколько подклассов утоньшающих алгоритмов, различающихся по способу определения «простых» точек, а также порядком их удаления.
- методы направленного утоньшения удаляют воксели строго с одного направления на каждом шаге (например, север-юг-верх-низ-запад-восток) используя различные вариации направлений и условий обнаружения конечных точек [19]. Эти методы чувствительны к выбору порядка направлений.
- методы последовательного утоньшения подполей – методы, делящие дискретное пространство на несколько подмножеств, называемых подполями, и на каждой подитерации удаляются воксели, принадлежащие определенному подполю. Используется различное число подполей: 2 [20], 4 [21] or 8 [22]. Например, для подхода деления на 2 подполя [20], два вокселя находятся в разных подполях, если они разъединены границей объекта.
- полностью параллельные методы [23] – алгоритмы, рассматривающие все граничные точки для удаления в одной итерации. В целях сохранения топологии рассматривается как правило окрестность из 26 соседей.
На рисунке 3 представлен пример топологического утоньшения.
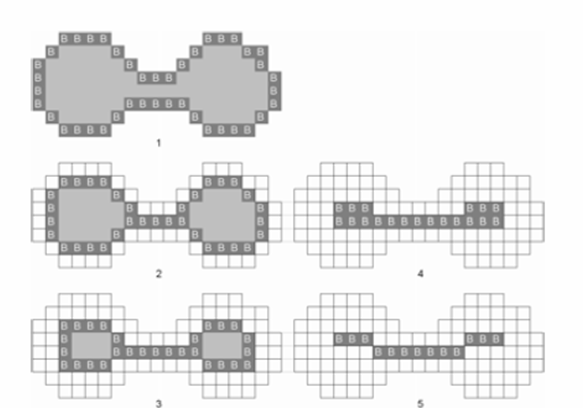
Рисунок 3 – Пример алгоритма утоньшения для двумерного случая. Граничные точки, помечаются «B» и затем удаляются, если они «простые»
2.2.2 Использование дистанционных преобразований
Дистанционное преобразование – преобразование, которое каждой точке изображения ставит в соответствие расстояние в заданной метрике до ближайшей точки фона (Рис. 4). Формальная запись:
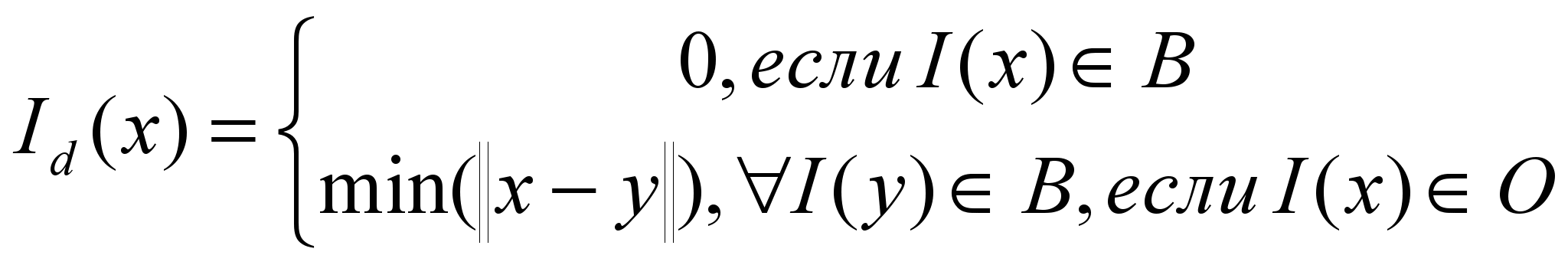| |  , | (2.3) |
где
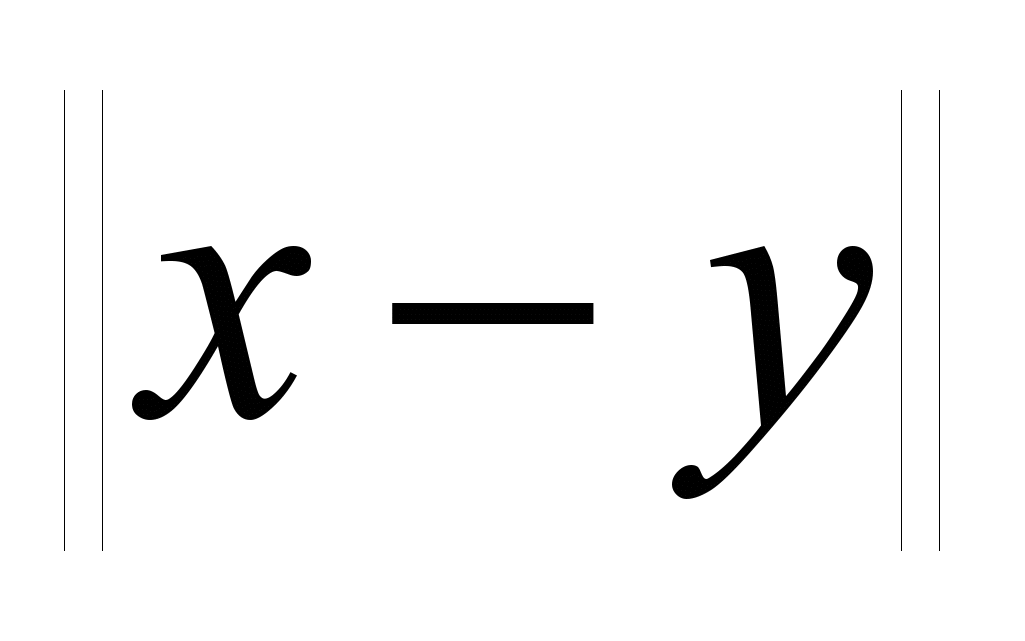– некоторая метрика.Алгоритмы для построения карт расстояний могут быть классифицированы по нескольким критериям.
Классификация по способу вычисления расстояния:
Чамферные дистанционные преобразования [24], где новое значение расстояния для вокселя вычисляется из расстояний его соседей и соответствующих весов маски.
- Векторные дистанционные преобразования [25], в котором для каждого обработанного вокселя хранится вектор ближайших точек границы, а для необработанного вокселя этот вектор строится, используя вектора соседей из шаблонной окрестности.
- Дистанционные преобразования на основе решения эйконального уравнения [26], где расстояние находится из конечных разностей первого или второго порядков расстояний соседних вокселей
- Квадратное евклидово дистанционное преобразование [27], в котором вместо расстояния до ближайшей точки фона хранится квадрат этого расстояния, что позволяет воспользоваться некоторыми преимуществами.
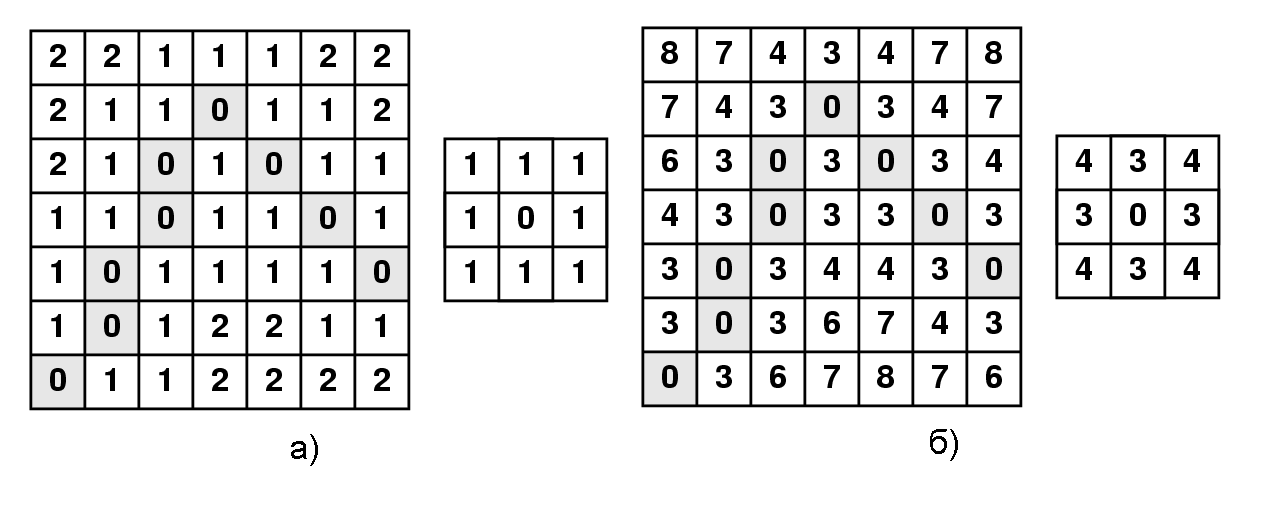
Рисунок 4 – Дистанционные карты с использованием а) шахматной метрики
б) (3,4)-метрики Чамфера
Хребтовые точки дистанционной карты соответствуют вокселям, которые находятся в центре объекта. Они выступают в качестве потенциальных кандидатов точек средних линий. Ниже перечислены некоторые подходы, использующиеся для поиска вокселей-кандидатов:
- методы утоньшения, использующие дистанционную карту для определения приоритета выбора вокселей для удаления [28]
- методы поиска градиента [29] предполагающие выявление районов неоднородного градиента и маркировки таких вокселей в качестве кандидатов на удаление.
- методы вычисления дивергенции используют в [30] в качестве функции приоритета для удаления «простых» вокселей с малым значением дивергенции.
- методы адаптивного утоньшения характеризуются сравнениями между значением дистанционной карты в вокселе и средним значением дистанционной карты его соседей [31].
Множество вокселей-кандидатов обычно имеет большую размерность и следующий шаг как правило заключается в уменьшении их количества.
Для связности большинство алгоритмов используют минимальные остовные деревья [32], кратчайшие пути [33] или другие алгоритмы на графах.
Некоторые методы сначала используют объединение, затем удаление вокселей путем нахождения кратчайшего пути в связанном множестве [29].
Основное преимущество этих методов в том, что вычисление дистанционной карты происходит очень быстро (за линейное время от числа вокселей), что очень важно во многих приложениях.
2.2.3 Использование диаграмм Вороного.
Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек более близких к одному из элементов множества S, чем к любому другому элементу множества [41].
Пример диаграммы Вороного продемонстрирован на рисунке 5.
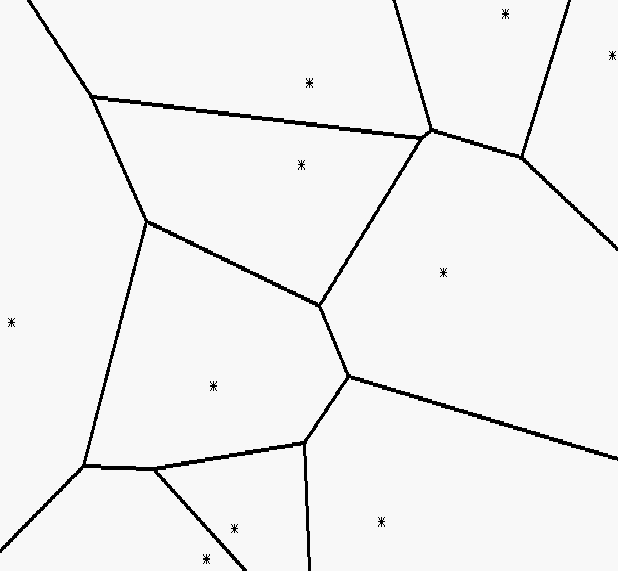
Рисунок 5 – а) 10 сгенерированных точек и б) построенная для них диаграмма Вороного.
Популярный подход состоит в использовании диаграмм Вороного [34], порожденых вершинами трехмерной полигональной сетки или непосредственно точками границы. Внутренние ребра и грани диаграммы Вороного, могут быть использованы для выделения средних линий и плоскостей. Средняя линия может быть получена из медиальной плоскости путем утоньшения последней. В работе [35], определяется число "шаровых областей " (непересекающихся максимальные шары), центры которых позднее объединеняются в среднюю линию, используя информацию медиальной поверхности. В работе [36], средняя линия рассчитывается путем морфологической эрозии диаграмм Вороного на основе геодезической функции.
2.2.4 Общеполевые методы
Кроме дистанционных карт могут использоваться другие типы карт, построенные с помощью функций, отличных от функции расстояния.
В этот класс включена обобщенная потенциальная функция поля [37] [38] [15], где потенциал во внутренней точке объекта определяется как сумма потенциалов, возникающих на границе объекта. В дискретном случае [15], граничные воксели считаются точечными зарядами, генерирующими потенциальное поле. Функция электростатического поля используется в [38] для создания потенциала внутри объекта. Также используется частный случай потенциального поля – сила отталкивания – в работах [37] [38] и [15] (Рис. 6).
Скелет строится через определение локальных экстремумов построенного поля и объединения их.
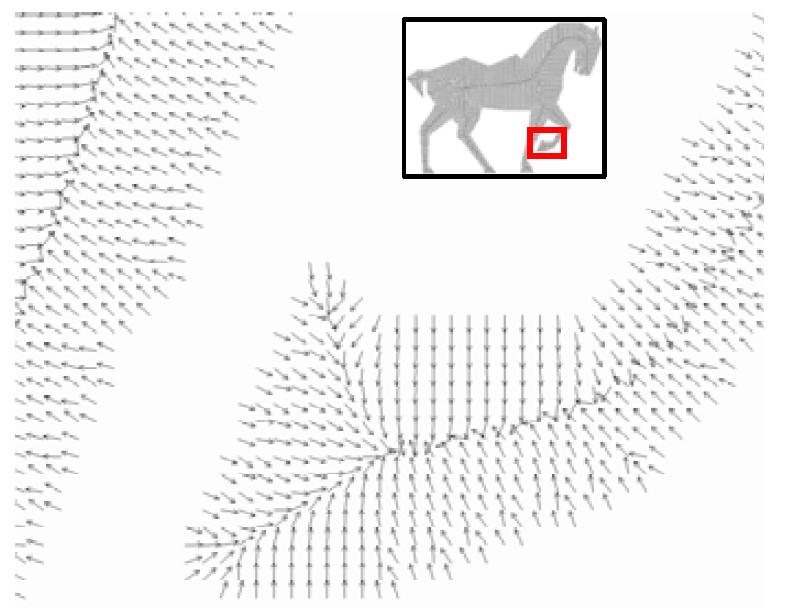
Рисунок 6 – Поле сил отталкивания двумерного изображения.
Локальные экстремумы могут быть найдены за счет критических точек векторного поля [15] или обнаружения локальных максимумов вдоль эквипотенциальных контуров [2]. Другие методы непосредственно используют «силовые» алгоритмы, начиная в нескольких стартовых точках («семенах») и используя тот факт, что вычисляемые силы затухают в пиковых точках.
Основным преимуществом этих функций перед функцией расстояния является то, что они могут выделять сглаженные линии на медиальных поверхностях. Это происходит потому, что они принимают во внимание большие приграничные районы, а не только ближайшие точки на границе. Это также создает эффект усреднения, который делает эти алгоритмы менее чувствительны к шумам на границе. Тем не менее, вычислительная сложность у них гораздо выше.
2.3 Сравнение существующих методов
В этом пункте рассмотрены различные подходы к построению средних линий и их воздействие на различные свойства, описанные в пункте 2.2.
Гомотопность
Алгоритмы утоньшения обеспечивают гомотопность, поскольку удаляются только те воксели, которые не меняют топологию объектов.
Поскольку методы, основанные на дистанционных картах, не выделяют скелет напрямую, сохранение топологии зависит от последующих шагов – обрезки и связывания. Очевидно, что алгоритмы, основанные на минимальных остовых деревьях не сохраняют топологию, потому что они не могут создавать петель.
Средние линии, построенные алгоритмами, основанными на общеполевых методах, могут быть несвязными даже для односвязных объектов [15], так как этот класс алгоритмов сильно зависит от разрешения изображений, а также от погрешностей при вычислениях.
Инвариантность при изометрических преобразованиях
Направленные методы утоньшения чувствительны к ориентации объекта. Окончательный результат (конечные точки, число ветвей и их местоположение) зависит от порядка, в котором обработаны различные направления. Дистанционные карты, диаграммы Вороного и методы, основанные на характеристиках полей, не зависят от ориентации объекта.
Во всех случаях, затрагивающих дискретные представления объектов, конечное представление воксельной сетки допускает небольшую погрешность при преобразовании объектов. В результате даже при том, что алгоритмы выделения средних линий не чувствительны к ориентации, сами входные данные уже несут некоторую погрешность из-за преобразования. Эта погрешность обнаруживается на границе преобразованного объекта, и этот эффект подобен эффекту поверхностного шума.
Восстанавливаемость
Средняя линия или средняя поверхность трехмерного объекта захватывает локальное симметричное представление в объекте через различные типы элементов: участки поверхности в скелете представляют симметрические пластинчатые области исходной формы, в то время как отдельные кривые в скелете соответствуют цилиндрическим (трубчатым) областям формы. Очевидно, что независимо от используемого метода выделения, полная и точная реконструкция исходного объекта не возможна при наличии информации, сохраненной в одной только средней линии. Так как скелет содержит только сегменты кривой, плоские части объекта не могут быть восстановлены от него.
Цилиндрические формы (то есть, формы, которые могут быть точно представлены обобщенными цилиндрами), представляют специальный класс объектов, которые могут быть точно восстановлены от одного только скелета. Общие формы могут только быть приближены обобщенной цилиндрической реконструкцией. Ясно, что более плотный скелет кривой приведет к более точному результату. При восстановлении с помощью подхода наращивания шаров [31] необходима информация дистанционной карты для определения радиуса шара, который будет выращен из каждого вокселя скелета. В этом отношении, методы, основанные на дистанционных картах, имеют преимущество перед другими методами, потому что эта информация доступна.
Толщина
Алгоритмы утоньшения могут непосредственно построить тонкий скелет (при использовании утоньшающих шаблонов). Параллельные алгоритмы утончения, которые удаляют все простые воксели сразу, возможно, не в состоянии достигнуть соответствующего представления из-за ограничений топологии. На рисунке 4 имеем прямоугольник, ширина которого четное число вокселей. На последнем шаге процесса утоньшения средняя линия будет шириной в 2 вокселя. Хотя все воксели этой кривой «простые» точки, удаляя их полностью, мы бы удалили всю среднюю линию. На данном этапе никакие другие «простые» точки не могут быть удалены, и скелет не представлен в 1D. У направленных методов утончения предусмотрена эта проблема: один ряд вокселей в средней линии будет удален, а второй ряд будет сохранен в последующих шагах.
Методы, основанные на дистанционных картах и диаграммах Вороного не представляют скелет в 1D. Для обоих методов необходима постобработка по уменьшению количества вокселей [39].
Центрированность
Алгоритмы утоньшения и методы полевых характеристик не гарантируют центрированность. В случае направленного утоньшения, центрированность зависит от порядка применения различных направлений. В случае общеполевых методов, которые рассматривают области, отличные от ближайших точек границы, центрированность также не гарантируется.
Методы, использующие дистанционные карты могут лучше достигать центрированности, потому что информация о центрах (максимальных шаров) включена в дистанционную карту.
Геометрические методы напрямую вычисляют контактные точки (точки, которых касаются границы максимальных вписанных сфер) также могут достигать центрированности.
Методы, основанные на диаграммах Вороного, зависят от выбора плотности поверхности объекта: плотный объект дает более отцентрированную среднюю линию, но увеличивает время работы. Проблемы с центрированностью возникают [39] особенно в регионах, где топология объекта изменяется между последовательными множествами уровней. Это также зависит от разрешения (расстояние между двумя последовательными множествами уровней).
Покомпонентная дифференциация
Способность различать различные компоненты средней линии зависит от способности обнаруживать точки сочленения, т.е. точки, в которых соединяются две или более линии.
Алгоритмы утоньшения непосредственно могут классифицировать обрабатываемые точки как точки сочленения.
Методы, основанные на дистанционных картах сами по себе не могут определять тип точек построенного скелета. Обычно данная классификация происходит на этапе постобработки [19]. Тем не менее, переход размещения для этих классов методов чувствителен к шуму.
Метод множеств уровня может также непосредственно определить точки сочленения (как центры построенных множеств уровней).
Связность
Связность обычно гарантируется всеми классами алгоритмов. Некоторые алгоритмы (утоньшения, алгоритм множеств уровня) явно поддерживают связность во время выполнения, тогда как для других необходима постобработка.
Надежность
Алгоритмы утоньшения, а также алгоритмы, основанные на дистанционных картах и диаграммах Вороного, чувствительны к шумам и генерируют много ненужных ответвлений в скелете. Некоторые подходы используют постобработку получившихся скелетов [28].
Общеполевые подходы менее восприимчивы к шуму из-за большого количества включенных усредняющих основных вычислений. Эти методы являются более чувствительными к разрешению, поскольку средняя линия в объектах может привести к неустойчивости в численных расчетах.
Многие из этих алгоритмов, описанных в литературе, как правило, иллюстрируется лишь несколькими примерами и не протестированы на большой базе данных общих 3D объектов (например, базы данных 3D-моделей [40]). Таким образом, остается неясным, как надежны в целом эти алгоритмы в отношении выбора их параметров.
Гладкость
Из-за дискретного характера объектов, алгоритмы утоньшения не дают плавных средних линий.
Методы, основанные на дистанционной карте, на местах имеют тот же недостаток, потому что в процессе построения карты нет усреднения. Однако в дальнейшем, при обрезке и связывании, можно включать некоторые алгоритмы сглаживания. Алгоритмы на основе диаграмм Вороного ведут себя подобным образом.
В случае общеполевых методов, усреднение используется при расчете векторного поля. Хотя в некоторых алгоритмах можно провести шаг постобработки, независимо от алгоритма выделения скелета, для сглаживания линий.
Иерархичность
Иерархичность (способность создавать семейства средних линий различной сложности), не достижима при использовании алгоритмов утоньшения, поскольку при воксельной обработке существует только два варианта: сохранить его или удалить его. Скелет получается только на последней итерации алгоритма.
Методы, основанные на дистанционных картах, могут быть иерархичными, варьируя число кандидатов-вокселей на шаге обрезки. Для того, чтобы получить скелет строгой иерархии (т. е. скелет одного уровня, входит полностью в скелет более высокого уровня), на шаге связывания необходимо принимать во внимание скелет предыдущего уровня.
Общеполевые методы также могут выделять иерархичные средние линии, варьируя количество исходных точек («семян»), используемых для построения отдельных сегментов средних линий.
Эффективность
Алгоритм топологического утоньшения – практически линейный процесс относительно числа вокселей объекта. Большинство вокселей входного объекта удаляются, когда они обрабатываются впервые (в качестве «простых» точек); «непростые» точки обрабатываются повторно. Сложность анализа таких алгоритмов затруднено, так как конечный результат зависит от входных данных.
Дистанционная карта может быть построена также за линейное время. Последующие шаги обрезки и стыковки могут иметь большую сложность, однако, они оперируют гораздо меньшим множеством вокселей.
Вычислительная сложность построения диаграмм Вороного для множества из n точек в худшем случае
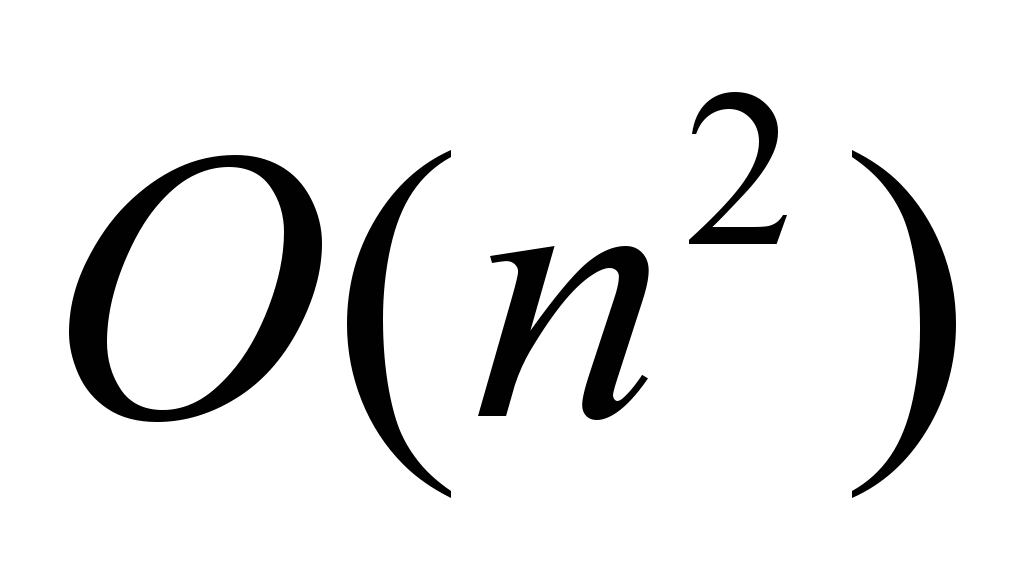, хотя на практике она почти линейна [4]. Как и в случае с дистанционными картами, здесь необходима постобработка.Сложность вычисления потенциального поля
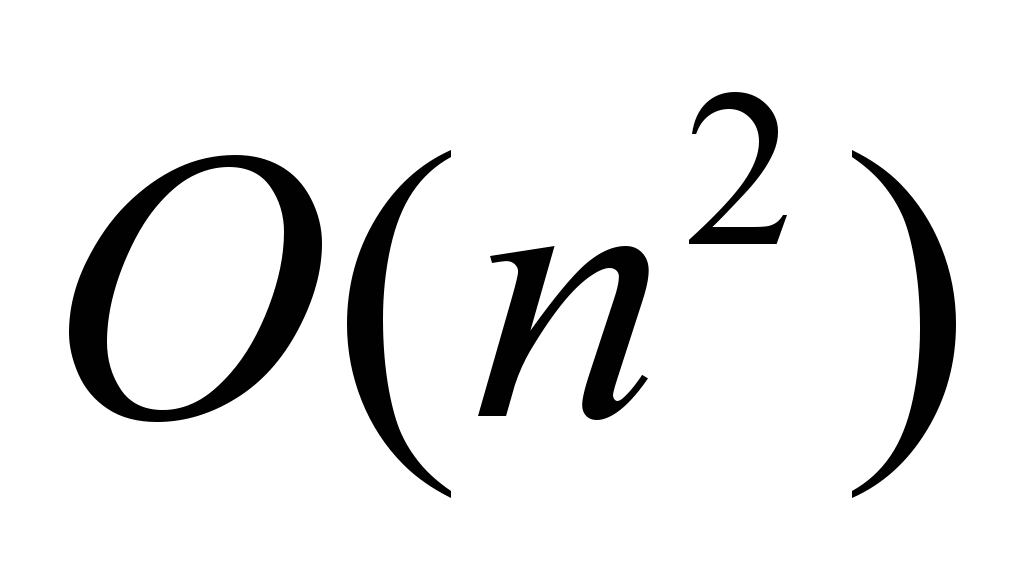[15], где n – общее число вокселей. Для больших объектов или объектов с высоким разрешением этот метод работает очень долго.Краткие выводы
В таблице 1 для каждого класса алгоритмов представлены достигаемые или недостигаемые свойства. «Да» означает то, что класс алгоритма гарантирует сохранение того или иного свойства, «Нет» в противном случае. Пустые места оставлены, если свойство сохраняется только некоторыми алгоритмами в классе или в случае, когда свойство слишком сложно для анализа подхода определенного класса (как было показано выше)
Таблица 1 – Свойства, достижимые различными классами алгоритмов.
| Свойство | Утоньшение | Дистан-ционные карты | Диаграммы Вороного | Обще-полевые методы |
| Гомотопность | Да | | Да | Нет |
| Инвариантность | | Да | | Да |
| Восстанавли-ваемость | Нет | | Нет | Нет |
| Тонкость | | | | Да |
| Определение сочленений | | | Да | Да |
| Связность | Да | | | |
| Надежность | Нет | Нет | Нет | Да |
| Гладкость | | | | Да |
| Иерархичность | Нет | | | Да |
| Эффективность | Да | Да | Да | Нет |