Некоторые методы распознавания изображений

I. A. Mikhaylov

Постановка задачи

Рассматривается задача распознавания изображений цифровых символов. Будем работать только с растровыми чёрно-белыми изображениями. Пусть задан алфавит изображений-образцов и одно тестовое изображение. Размеры изображений: как образцов, так и теста могут быть различны. Задача состоит в том, чтобы для тестового изображения найти наиболее похожее на него изображение-образец из заданного алфавита. Степень сходства двух изображений будем определять как значение метрики или функции различия для этих изображений. Функция различия есть такое обобщение метрики, для которого выполнение неравенства треугольника не является обязательным.

Предложенные методы решения задач

Метод срезов

В этом разделе даётся описание метода распознавания, получившего название метода срезов. Раздел содержит определения бесконечного вектора, линейного образа и определения используемых метрик.

Под бесконечным вектором будем понимать вектор, размерность которого бесконечна, причём для каждого бесконечного вектора V существует такое n ≥ 0, что v_i ≥ 0 для i  n и v_i = 0 для i > n, где v_i — i-й элемент вектора V. Заметим, что допускается нулевое значение n.

Пусть V, V — бесконечные векторы.

Метрикой на множестве бесконечных векторов будем называть

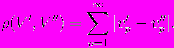
Пусть имеется матрица изображения A = (a_ij) размера nm. Для каждого i: 1  i  n определим множество индексов S(A, i):
S(A, i) = {s₁, s₂, … , s_k} = {j:a_ij = 1  (j = 1  a_i,_j-1 = 0), 1  j  m}.
Будем считать, что s₁ < s₂ < … < s_k.

Вектором разности для тройки (A, i, N), где 1  i  n, N —натуральное, будем называть бесконечный вектор действительных чисел, построенный следующим образом:

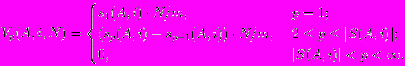
Линейным образом матрицы изображения A = (a_ij) размера nm с частотой сечения N, где N — натуральное, будем называть мультимножество векторов разности для этой матрицы
L(A, N) = {l_p: l_p = V(A, np/N, N), 1  p  N}.

Пусть L(A₁, N), L(A₂, N) — линейные образы матриц изображений A₁ и A₂ с частотой сечения, равной N.

Метрикой на множестве линейных образов матриц изображений с частотой сечения N будем называть

Легко проверить, что выполняются соответствующие свойства метрики.

Метод, основанный на модификации метрики Хаусдорфа

Метрика Хаусдорфа находит свое применение в задаче распознавания изображений как мера близости множеств [2]. При использовании данной метрики изображения рассматриваются как конечные множества точек (пикселей), причём точки одного изображения привязываются к точкам другого. В этом разделе описывается подход к решению задачи распознавания, использующий модификацию метрики Хаусдорфа для определения близости изображений.

Для того чтобы показать отличие предлагаемой функции различия от оригинальной метрики Хаусдорфа, приведём вначале полное определение последней.

Расстоянием множества из одной точки {x'₀} от компактного множества G будем называть

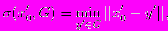
где x'₀ - y' — расстояние между точками x'₀ и y'.
Отклонением множества G₁ от G₂ называется
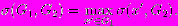
Метрикой Хаусдорфа называется
(G₁, G₂) = max {(G₁, G₂), (G₂, G₁)}.

Отличия предлагаемой функции различия от метрики Хаусдорфа содержатся во втором и третьем пунктах.

Отклонением множества G₁ от G₂ будем называть
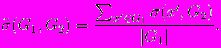
hm-функцией различия будем называть

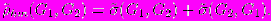
Необходимые свойства предложенной функции различия следуют из определения.

Метод радиальных окрестностей

В этом разделе даётся описание метода распознавания, названного методом радиальных окрестностей. Данный метод имеет некоторые общие черты с CL-подходом, описанным в работе [3].

Дадим определения используемых структур, а затем описания функций различия для этих структур. Пусть имеется изображение A, заданное матрицей (a_ij) размера mn. Под радиальной окрестностью точки с координатами (i, j) и коэффициентом нормирования s будем понимать упорядоченный набор из четырех бинарных векторов (v^l, v^r, v^t, v^b), построенных следующим образом:

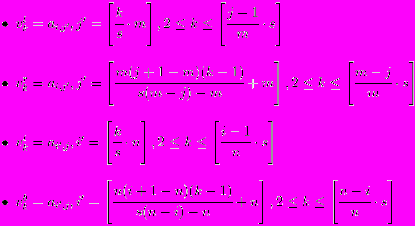
При этом v^l₁ = v^r₁ = v^t₁ = v^b₁ = 1. Таким образом, радиальная окрестность содержит масштабированные части строк и столбцов, проходящих через центр окрестности.

Под радиальным образом изображения A будем понимать множество радиальных окрестностей, построенных для каждого элемента соответствующей матрицы (a_ij).

Введем теперь функции различия на множестве бинарных векторов, радиальных окрестностей и радиальных образов изображений.

bm-функцией различия на множестве бинарных векторов будем называть

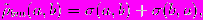
где

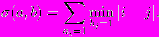
Заметим, что при использовании данной функции для сравнения бинарных векторов радиальных окрестностей указанный минимум всегда может быть найден, так как каждый такой вектор имеет, по крайней мере, один ненулевой элемент по построению.

Введем функцию различия на множестве радиальных окрестностей:

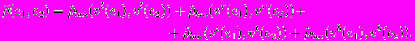
Введем pp-функцию различия на множестве радиальных образов:

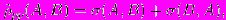
где

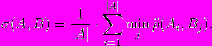
Здесь A_i — i-я окрестность образа A, B_j — j-я окрестность образа B. Необходимые свойства для всех приведенных функций различия следуют из их определения.

Описание проведённых экспериментов

Для оценки эффективности методов были проведены три эксперимента. Отметим, что в алгоритме метода срезов частота сечений бралась равной 100, в алгоритме метода радиальных окрестностей коэффициент нормирования s брался равным 100, а в алгоритме метода, основанного на модификации метрики Хаусдорфа, в качестве расстояния между точками на плоскости использовалась сумма модулей разностей координат. Кроме того, при использовании метода, основанного на модификации метрики Хаусдорфа, до вычисления значения функции различия тестовое изображение приводилось к размеру образца с помощью алгоритма масштабирования, описанного в работе [4].

В каждом из экспериментов был использован также корреляционный алгоритм (см. [1]), применяемый на предприятии «Славнефть-ЯНОС» для распознавания бортовых номеров железнодорожных цистерн. При описании результатов будем использовать следующие обозначения:

Corr — метод, использующий корреляционный алгоритм;
Slice — метод срезов;
MHaus — метод, основанный на модификации метрики Хаусдорфа;
Radial — метод радиальных окрестностей.

Теперь опишем каждый эксперимент в отдельности.

Эксперимент № 1

В первом эксперименте алфавит образцов включал в себя 10 изображений символов '0'—'9' высотой 14 пикселей, полученных с помощью шрифта Times New Roman.

Тестовые изображения строились с использованием 4 моделей искажения. Высота построенных тестовых изображений также равнялась 14 пикселям. В конце описания каждой модели будем давать её условное обозначение, необходимое нам при сравнении результатов.

Нанесение на изображение-образец одиночных пикселей. Расположение каждого пикселя выбиралось случайно. Цвет всех пикселей совпадал с цветом контура. Их количество варьировалось от 1 до 50. Обозначение — NoisePoint.
Нанесение на изображение-образец прямых линий. Направление, длина и толщина линий были случайны; длина колебалась в пределах от 1 до 7 пикселей, толщина - от 1 до 3 пикселей. Цвет половины из них совпадал с цветом фона, цвет остальных совпадал с цветом символа. Обозначение — NoiseLine.

Алгоритмы искажения контура, описанные далее, на входе получают последовательность узлов контура (или цепь), построенную вручную. Узел представляет собой координаты некоторой точки контура. Цепь в среднем содержит 25 узлов, распределенных по всему контуру. В цепь символа-образца вносились изменения, затем она отображалась в растр.

Сдвиг каждого узла цепи на случайный вектор. При этом координаты изменялись не более, чем на 20% от размеров изображения. Обозначение — ContourSimple.
Разбиение контура символа на несколько сегментов, поворот каждого сегмента относительно узла, случайно выбранного в данном сегменте. Количество сегментов выбиралось случайно в диапазоне от 2 до 6. Угол поворота лежал в пределах от -/6 до /6. Обозначение — ContourSecTurn.

При использовании каждой модели было построено 5000 тестовых изображений (500 для каждого из 10 образцов).

Эксперимент № 2

Во втором эксперименте набор образцов остался прежним, а в качестве тестов был взят набор изображений цифр, вырезанных с фотографий номеров цистерн после их бинаризации. Данный набор применялся для тестирования корреляционного алгоритма распознавания, описанного в работе [1]. Он содержит изображения всех цифр, кроме единицы. Общее количество изображений в наборе — 493. Средний размер тестов — 814 пикселей. В таблице 1 показаны некоторые изображения из этого набора.

Таблица 1. Примеры тестовых изображений

Эксперимент № 3

В третьем эксперименте в качестве образцов был взят набор изображений, вырезанных из бинаризованных фотографий цистерн. Этот набор также использовался в упомянутой выше работе [1]. Набор включает в себя 55 изображений всех цифр за исключением единицы. Тестовые изображения остались такими же, как во втором эксперименте.

Результаты экспериментов и заключение

Опишем теперь результаты проведенных экспериментов, представив их в табличной форме: первый столбец содержит номер эксперимента (а также название модели искажения для первого эксперимента), в каждой строке представлено соответствующее число верно распознанных тестов для четырёх алгоритмов (в процентах).

Таблица 2. Результаты экспериментов

№ эксперимента		Corr	Slice	MHaus	Radial
1	NoisePoint	99,68	88,12	96,64	93,62
	NoiseLine	96,70	89,54	90,42	87,72
	ContourSimple	61,90	61,50	80,98	85,88
	ContourTurnSec	64,94	66,78	71,44	61,46
2		60,24	39,35	75,05	82,75
3		94,73	91,28	93,71	95,94

Подведём итоги. Разработаны три алгоритма распознавания изображений алфавитно-цифровых символов, для проверки эффективности которых проведены три эксперимента. В ходе экспериментов было установлено, что:

метод срезов является самым быстрым из предложенных;
метод, основанный на модификации метрики Хаусдорфа, и метод радиальных окрестностей показывают неплохие результаты при распознавании реальных зашумленных изображений, используя при этом ограниченный набор эталонов;
расширение набора эталонов позволяет повысить эффективность всех предложенных методов.

Найденные решения с большим или меньшим успехом можно использовать в таких задачах, как распознавание номеров железнодорожных цистерн, распознавание регистрационных номеров автомобилей, распознавание печатных и рукописных символов. Результаты опубликованы в работах [4, 5].

Литература

Распознавание номеров железнодорожных цистерн с использованием корреляционного алгоритма / А.К. Карлин, А.Н. Малков, Е.А. Тимофеев, Г.П. Штерн // Математика, кибернетика, информатика. Труды международной научной конференции, посвящённой памяти профессора А.Ю. Левина (Ярославль, 25—26 июня, 2008) / Под ред. С.А. Кащенко, В.А. Соколова; Яросл. гос. ун-т. —Ярославль: ЯрГУ, 2008.—C. 103—110.
Хмелев, Р.В. Совместное использование структурного анализа и метрики Хаусдорфа при сравнении объекта и эталона/ Р.В. Хмелев // Компьютерная оптика. В.27.—2005.—сс. 174—176.
Abou-zeid, Hatem M.R. Computer Recognition of Unconstrained Handwritten Numerals/ Hatem M.R. Abou-zeid, Akrem S. El-ghazal, and Ammar A. Al-khatib // Circuits and Systems. Proceedings of the 46th IEEE International Midwest Symposium on.—2003.—pp. 969—973.
Михайлов, И.А. Об одном методе распознавания изображений/И.А. Михайлов // Моделирование и анализ информационных систем. Т. 14, № 4. /Под ред. В.А. Соколова.—Ярославль: Изд-во Яросл. гос. ун-та
им. П.Г. Демидова, 2007.—сс. 7—12.
Михайлов, И.А. Некоторые методы распознавания изображений/ И.А. Михайлов // Моделирование и анализ информационных систем. Т. 15, № 4. /Под ред. В.А. Соколова.—Ярославль: Изд-во Яросл. гос. ун-та
им. П.Г. Демидова, 2008.—сс. 56—64.

Blog

Некоторые методы распознавания изображений

Содержание