Geum.ru

Програма фахових вступних випробувань Програма розроблена на підставі програми державної атестації студентів сну ім. В. Даля за напрямом підготовки

Вид материалаДокументы

Содержание


Програма фахових вступних випробувань
Рівняння математичної фізики
Критерії оцінювання
Рівень підготовки
Дуже низький
Порядок проведення фахового вступного випробування
Подобный материал:
  1   2


Східноукраїнський національний університет
імені Володимира Даля

кафедра прикладної математики


Затверджую


Ректор _______________ О.Л. Голубенко


“_____”_____________ 2012


Пояснювальна записка

щодо проведення фахового вступного випробування для осіб,
які вступають на навчання за освітньо-професійними програмами підготовки СПЕЦІАЛІСТІВ або МАГІСТРІВ зі спеціальності
"Прикладна математика"

на базі раніш здобутого освітньо-кваліфікаційного рівня бакалавр або спеціаліст


Пояснювальна записка складається з:

"Програми фахових вступних випробувань";

"Вимог до рівня підготовки вступників";

"Переліку рекомендованої літератури";

"Критеріїв оцінювання";

"Порядку проведення фахового вступного іспиту".


Луганськ – 2012


Програма фахових вступних випробувань


Програма розроблена на підставі програми державної атестації

студентів СНУ ім. В. Даля за напрямом підготовки

« Прикладна математика »


Алгебра та геометрія

1. Дослідження і розв’язання систем 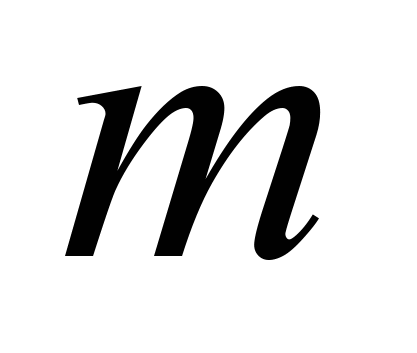лінійних рівнянь з 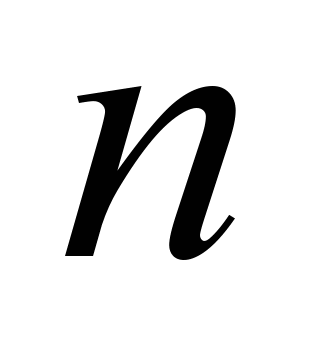невідомими методом Гауса.

2. Визначники 2-го і 3-го порядку. Метод Крамера розв’язання СЛАР.

3. Перестановки й підстановки. Інверсії, парні й непарні перестановки, їхнє число. Множення перестановок, цикли. Подання підстановок у вигляді добутку підстановок і транспозиції.

4. Визначення й властивості визначника 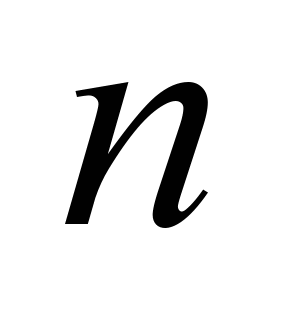-го порядку.

5. Мінори й алгебраїчні доповнення. Теорема про розкладання визначника по рядку (або стовпцеві). Обчислення визначників, теорема Лапласа. Правило Крамера.

6. Алгебра матриць. Лінійні операції, їх властивості. Множення прямокутних матриць. Обернені матриці. Визначник добутку матриць. Запис і розв’язання системи 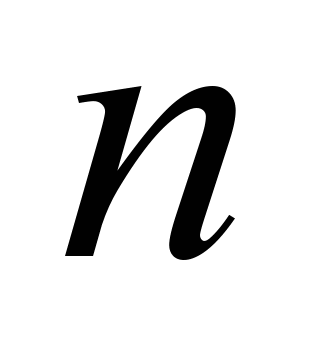лінійних рівнянь з 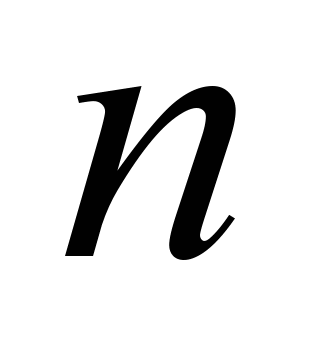невідомими в матричній формі.

7. Арифметичний 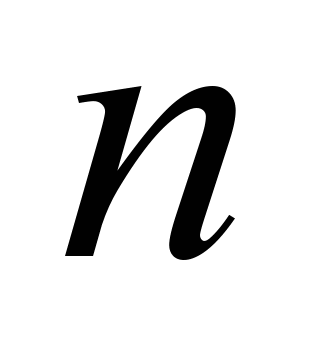-вимірний простір. Лінійні операції і їхні властивості. Лінійна залежність і незалежність векторів.

8. Ранг матриці. Теорема про ранг матриці.

9. Векторна алгебра на площині й у просторі. Лінійні операції, їхні властивості. Афінний базис на площині й у тривимірному просторі. Координати вектора.

10. Скалярний добуток векторів. Визначення й властивості. Вираження скалярного добутку через координати в ортонормованому базисі. Довжина вектора. Кут між векторами. Умова ортогональності. Направляючі косинуси вектора.

11. Орієнтація двох векторів на площині і трьох у просторі. Векторний добуток векторів, його властивості. Вираз векторного добутку через координати співмножників у правому ортонормованому базисі.

12. Змішаний добуток векторів, його властивості. Вираження змішаного добутку через координати співмножників. Об’єм паралелепіпеда, тетраедра. Умова компланарності.

13. Рівняння площини в просторі, прямої на площині. Різні види рівняння прямої і площини. Взаємне розташування площин. Відстань від точки до площини в просторі і до прямої на площині.

14. Рівняння прямої у просторі. Канонічні й параметричні рівняння. Взаємне розташування прямих і площин. Задачі на пряму й площину.

15. Криві другого порядку. Еліпс. Визначення й властивості. Виведення канонічного рівняння. Гіпербола, визначення й властивості. Виведення канонічного рівняння.

16. Визначення й властивості параболи. Виведення канонічного рівняння. Ексцентриситет, фокуси й директриси кривих другого порядку.

17. Перетворення ортонормованого базису на площині. Приведення рівняння кривої другого порядку до канонічного виду. Класифікація кривих другого порядку.

18. Поверхні другого порядку. Класифікація поверхонь другого порядку. Канонічні рівняння основних типів поверхонь другого порядку (еліпсоїди, гіперболоїди, параболоїди, конус і циліндри).

19. Цілі числа. Подільність, властивості подільності. Прості числа. Основна теорема арифметики. Найбільший загальний дільник і найменше спільне кратне.

20. Побудова комплексних чисел. Алгебраїчна й тригонометрична форма комплексного числа. Операції над комплексними числами. Добування кореня 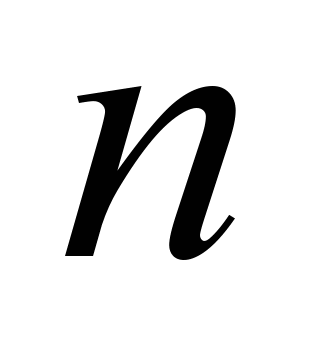-ого ступеня, корені з одиниці.

21. Поняття алгебраїчної операції, групи, підгрупи, алгебри. Ізоморфізм і гомоморфізми. Числові кільця і поля.

22. Кільце многочленів над числовим полем. Операції над многочленами, подільність многочленів, теорема про подільність із залишком. Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда.

23. Корінь многочлена й ділення на лінійний двочлен. Схема Горнера. Кратні корені. Відділення кратних множників многочлена. Можливість розв'язання в радикалах рівнянь другого й третього ступеня. Формули Кардано. Дискримінант. Можливість розв'язання рівняння четвертого ступеня. Нерозв'язність рівнянь ступеня .

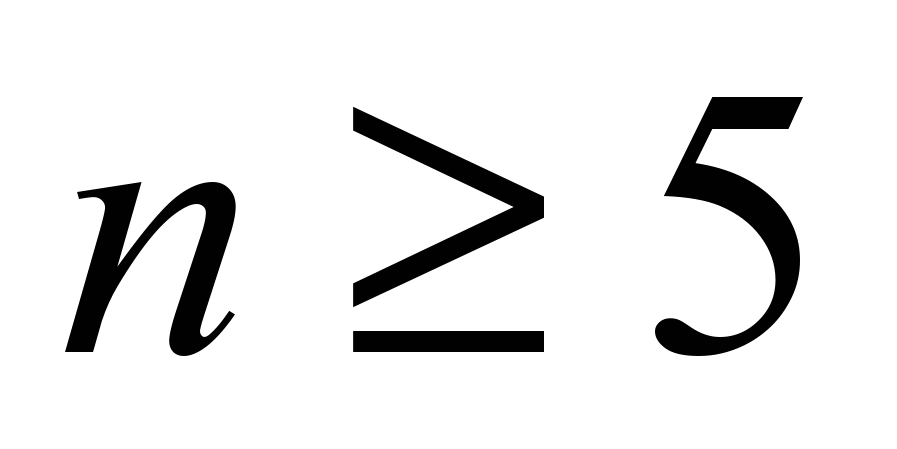24. Многочлени над полем комплексних чисел. Основна теорема алгебри й наслідки з неї, наслідок про многочлени над полем дійсних чисел. Формули Вієта.

25. Границі коренів. Метод Штурма відділення дійсних коренів многочленів із дійсними коефіцієнтами.

26. Многочлени над полем раціональних чисел. Критерій Эйзенштейна. Раціональні корені многочленів з раціональними коефіцієнтами.

27. Лінійні простори. Лінійна залежність і незалежність векторів. Ізоморфізм лінійних просторів однакової розмірності. Скінченні простори. Базис і розмірність.

28. Підпростори; підпростори натягнуті на вектори. Перетинання й сума підпросторів, розмірність суми.

29. Лінійні оператори. Завдання лінійного оператора матрицею. Матриця переходу, матриця лінійного оператора в різних базисах. Перетворення координат вектора при зміні базису.

30. Операції над лінійними перетвореннями. Кільце лінійних операторів і кільце матриць. Їхній ізоморфізм. Власні вектори і власні значення.

31. Характеристичний многочлен матриці, характеристичний многочлен лінійного оператора, його інваріантість щодо базису.

32. Евклідів простір. Скалярний добуток. Нерівність Коші – Буняковського. Довжина вектора, кут між векторами. Ортонормований базис. Процес ортогоналізації. Ізоморфізм евклідових просторів.

33. Ортогональні матриці й ортогональні перетворення евклідових просторів. Симетричні перетворення і матриці.

Дискретна математика

1. Поняття множини. Порожня й універсальна множини. Операції об'єднання, перетинання, доповнення, їхні властивості.

2. Декартовий добуток множин, n-арні, бінарні відношення. Відображення, функції, алгебраїчні операції. Бієктивні й ін'єктивні відображення. Операції над відношеннями, зворотне відношення, властивості

3. Відношення еквівалентності. Теорема про розбивку множин на класи по даному відношенню еквівалентності й зворотна. Частково впорядкована множина, ізоморфізм. Теорема про ізоморфне подання частково впорядкованої множини в алгебрі підмножин.

4. Визначення лінійного порядку. Цілком упорядкована множина. Аксіома індукції й еквівалентні їй твердження. Визначення ґрат. Дистрибутивні ґрати. Булеві алгебри. Поняття про аксіоматичну побудову булевих алгебр. Ізоморфне подання булевих алгебр в алгебрі підмножин.

5. Потужність множини. Злічені множини, їхні властивості. Незліченність континуума. Теорема про потужності всіх підмножин довільної множини Порівняння потужностей. Аксіома вибору й еквівалентні їй твердження. Трансфінитна індукція.

6. Алгебра висловлень. Логічні операції над висловленнями. Таблиці істинності. Формули алгебри висловлень. Тавтології, протиріччя. Повні системи логічних зв'язувань.

7. Досконалі кон'юнктивні нормальні форми, диз'юнктивні нормальні форми. Подання функцій у такому вигляді. Подання одних логічних операцій через інші.

8. Поняття предиката. Одномісні й 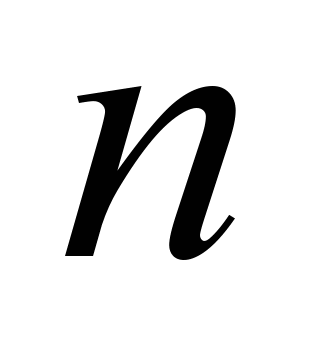-місні предикати. Рівносильні предикати. Логічні операції над предикатами. Формули обчислення предикатів.

9. Квантори. Вільні й зв'язані змінні. Тавтології із кванторами. Теорії I-го порядку. Інтерпретація, виконанність й істинність. Несуперечність обчислення предикатів I-го порядку.

10. Поняття про аксіоматичну побудову обчислення висловлень і предикатів. Аксіоми, формули, правила виводу. Виводимість формул. Теорема дедукції. Наслідки. Теорема Геделя про неповноту.

11. Основні функції алгебри логіки, истинностні таблиці. Рівносильні функції, фіктивні й істотні змінні. Суперпозиція функцій.

12. Канонічні форми булевих функцій. Теорема розкладання. Арифметичні операції в алгебрі логіки. Многочлени Жегалкіна. Подання довільної функції многочленом Жегалкіна, його єдиність.

13. Функціонально замкнені класи. Базис і порядок замкненого класу. Принцип подвійності.

14. Теорема Поста. Критерій повноти довільної системи функцій. Таблиці Поста. Наслідки з теореми Поста.

15. Поняття про загальну теорію функціонально замкнених класів.

16. Основні комбінаторні схеми. Правила суми й добутки. Розміщення, перестановки й сполучення з повтореннями й без повторень.

17. Біном Ньютона. Деякі властивості сполучень. Поліноміальна формула.

18. Задача Фібоначчі. Числа Фібоначчі, їхні властивості. Рекурентні співвідношення. Порядок співвідношення, загальне й частинний розв’язок. Властивості розв’язків лінійних рекурентних співвідношень із постійними коефіцієнтами.

19. Розв’язання лінійних рекурентних співвідношень 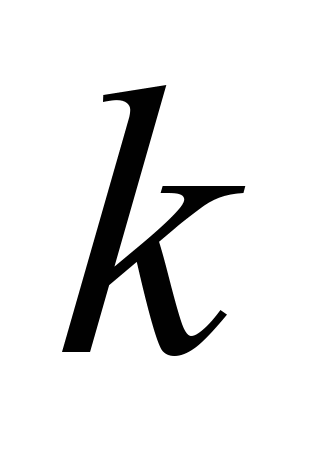-го порядку з постійними коефіцієнтами.

20. Основні визначення теорії графів. Зв'язні графи. Суграфи й підграфи. Ізоморфізми графів. Задачі, що послужили основою теорії графів. Ейлерові цикли.

21. Цикломатичне число графа. Дерева. База незалежних циклів.

22. Плоска реалізація графа. Ейлерова характеристика плоского зв'язного графа. Теорема про ейлерову характеристику площини. Теорема Понтрягіна-Куратовського.

23. Алгоритмічні задачі в графах. Відшукання ейлерова циклу, знаходження найкоротшого шляху. Поняття про двочасткові графи.

24. Проблема 4-х фарб. Поняття про ейлерову характеристику двовимірної замкненої поверхні. Теорема про п'ять фарб.

25. Алфавіт, стани. Визначення кінцевого автомата. Автомати Мура й Милі.

26. Еквівалентні автомати. Морфізми автоматів. Ізоморфізми автоматів.

27. Проблеми мінімізації автоматів. Еквівалентні й 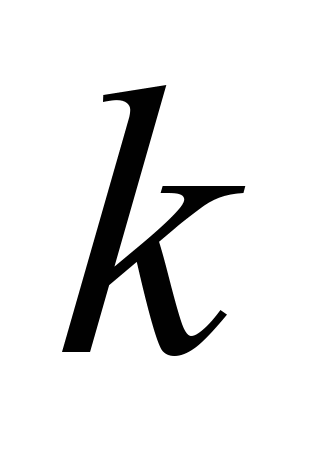-еквівалентні стани автоматів. Визначення еквівалентних станів.

28. Алгоритм побудови мінімального автомата для повністю визначеного автомата.

29. Експерименти по розпізнаванню автоматів. Поняття про структурний синтез автоматів. Машина Т'юрінга й кінцевий автомат.

30. Концепція алгоритму. Нормальні алгоритми Маркова.

31. Машини Поста-Т'юрінга. Алгоритми Поста-Т'юрінга.

32. Примітивно рекурсивні й частково рекурсивні функції. Алгоритми Кліні-Черча.

33. Еквівалентність різних визначень алгоритму.

34. Приклади конкретних алгоритмів. Алгоритмічно нерозв'язні проблеми.

Математичний аналіз

1. Елементи теорії множини: поняття множини, порожня множина, дії над множинами, закони подвійності, декартовий добуток множини. Відображення множини, прообраз, суперпозиція відображень, зворотне відображення, ін’єкція, сюр’єкція, бієкція. Еквівалентні множини, скінченні, злічені і незлічені множини.

2. Аксіоми дійсних чисел і наслідки з них. Обмежена і необмежена множина: верхні і нижні межі множини. Точна верхня межа, точна нижня межа. Принцип вкладених відрізків, лема про покриття, лема про граничну точку.

3. Числові послідовності, границя послідовності. Основні теореми про збіжні послідовності. Нескінченно малі. Критерій Коші збіжності послідовностей. Підпослідовності, частинні границі. Монотонні послідовності. Теорема Вейерштраса. Число .

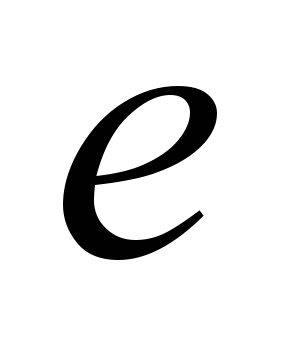4. Елементарні функції. Границя функції в точці. Основні теореми про границі. Критерій Коші. Односторонні границі. Нескінченно малі і нескінченно великі функції. Неперервність функції в точці. Неперервність елементарних функцій. Важливі границі.

5. Класифікація точок розриву. Властивості функцій неперервних на відрізку. Неперервність обернених функцій. Рівномірна неперервність. Теорема Кантора.

6. Означення похідної. Фізична і геометрична інтерпретація похідної. Правила обчислення похідних, похідна складної функції. Таблиця похідних.

7. Диференційовність, диференціал, інваріантність форми диференціала. Похідні вищих порядків. Теорема Лейбніца. Диференціали вищих порядків.

8. Поняття екстремуму. Теорема Ферма. Теорема Ролля. Теорема Коші. Теорема Лагранжа. Ознаки монотонності. Правило Лопіталя.

9. Формула Тейлора. Різні форми залишкового члена у формулі Тейлора. Формули Маклорена елементарних функцій.

10. Достатні умови екстремуму в термінах першої і другої похідних. Найбільше і найменше значення функції на відрізку.

11. Опуклість функції. Точки перегину. Достатні умови опуклості. Асимптоти. Дослідження функцій і побудова їх графіків.

12. Векторні функції. Похідна і диференціал вектор-функції. Дотична, нормаль.

13. Первісна і невизначений інтеграл. Основні властивості. Таблиця інтегралів. Інтегрування частинами. Інтегрування методом заміни змінною.

14. Комплексні числа і дії над ними. Корені многочленів. Розкладання многочлена на множники. Раціональні дроби і розкладання правильного дробу на прості.

15. Інтегрування раціональних дробів. Метод Остроградського.

16. Інтегрування тригонометричних функцій. Інтегрування деяких ірраціональних функцій, інтегрування диференціальних біномів.

17. Інтеграл Рімана. Інтегральні суми. Верхня і нижня суми і їх властивості. Критерії інтегровності.

18. Класи інтегровних функцій. Властивості визначеного інтеграла. Теорема про середнє для інтеграла Рімана.

19. Визначений інтеграл як функція верхньої границі і його властивості. Формула Ньютона-Лейбніца. Інтегрування частинами. Заміна змінною. Інтегрування вектор-функції.

20. Криві. Довжина кривої. Формула для обчислення довжини кривою.

21. Площа криволінійної трапеції. Площа криволінійного сектора (у полярних координатах). Об'єм тіла. Об'єм тіла обертання. Площа поверхні.

22. Статичні моменти. Координати центру тяжіння. Невласні інтеграли.

23. Числові ряди. Сума ряду, збіжність ряду. Необхідні умови збіжності ряду. Критерій Коші збіжності ряду. Властивості рядів, що збігаються. Залишок ряду. Властивості залишку.

24. Ряди з додатними членами. Ознака порівняння. Ознака Коші. Ознака Даламбера. Інтегральна ознака.

25. Ряди з довільними членами. Ознака Лейбніца. Оцінка залишку ряду Лейбніца. Перетворення Абеля. Ознака Абеля. Ознака Дирихле. Абсолютна збіжність. Властивості рядів, що збігаються абсолютно. Теорема Рімана.

26. Функціональні послідовності і ряди. Рівномірна збіжність функціональної послідовності. Критерії рівномірної збіжності. Ознака Вейерштраса рівномірної збіжності функціонального ряду. Ознака Абеля і Дирихле рівномірній збіжності ряду.

27. Неперервність, інтегровність, диференційованість функціонального ряду.

28. Степеневі ряди. Основна теорема збіжності степеневого ряду. Властивості суми степеневого ряду.

29. Ряд Тейлора. Збіжність ряду Тейлора. Аналітичні функції. Розкладання елементарних функцій в ряд Тейлора-Маклорена. Застосування степеневих рядів для наближених обчислень. Формула Стірлінга. Ряд Тейлора вектор-функції.

30. Функції декількох змінних. 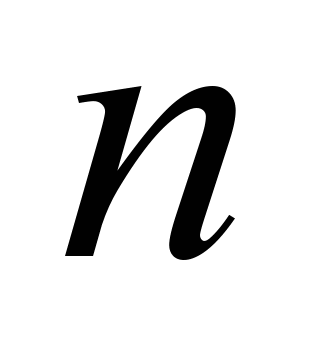-вимірні простори. Метрика. Евклідовий простір. Нерівність Коші - Буняковського. Множини в 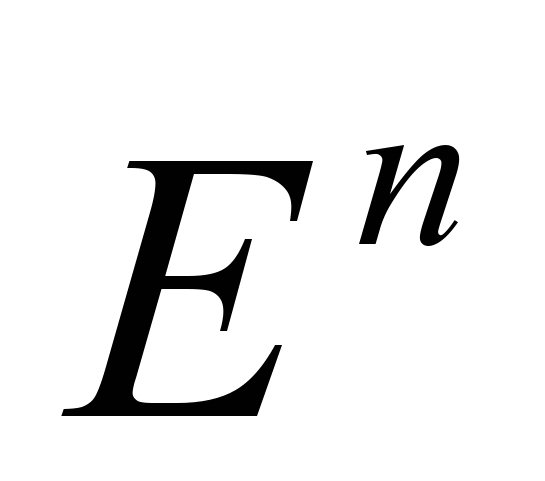. Околи точки. Збіжність послідовності точок в 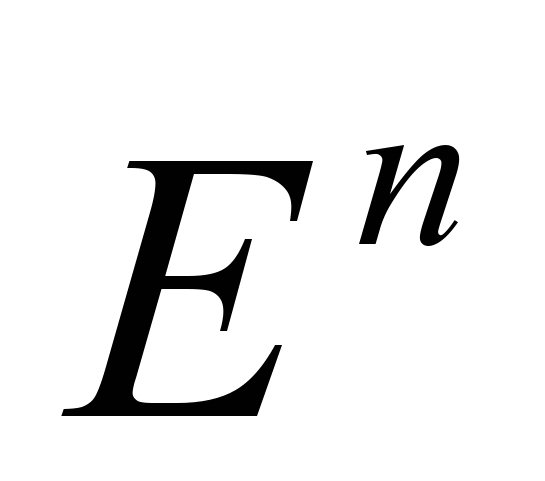. Відкриті, замкнені, лінійно-зв'язні множини. Компакти.

31. Відображення з 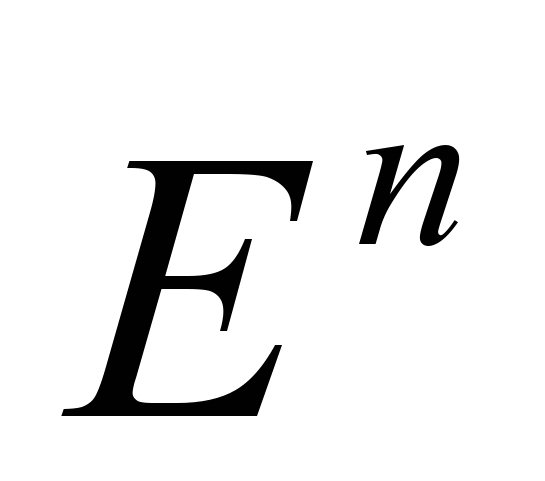в 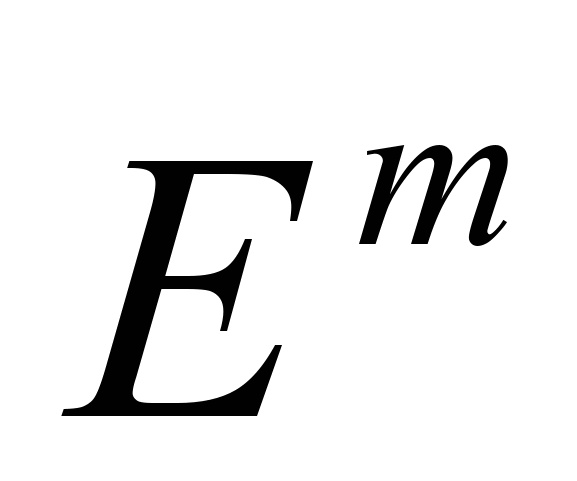. Лінійні відображення. Границя функції декількох змінних. Неперервні функції і відображення, їх властивості. Властивості функцій неперервних на компакті. Рівномірна неперервність. Теорема Кантора.

32. Частинні похідні і частинні диференціали. Диференційовність функції в точці. Похідна відображення. Диференціал. Похідна складної функції. Градієнт функції. Похідна за напрямком.

33. Частинні похідні вищих порядків. Похідні вищих порядків відображень. Диференціали вищих порядків.

34. Формула Тейлора функції декількох змінних.

35. Екстремуми функції декількох змінних. Необхідні умови екстремуму. Достатні умови екстремуму.

36. Теорема про зворотну функцію. Неявні функції. Теорема про неявну функцію. Диференційовність неявної функції.

37. Умовний екстремум. Метод множників Лагранжа. Достатні умови умовного екстремуму.

38. Інтеграли, залежні від параметра. Власні інтеграли, залежні від параметра. Неперервність, диференційовність.

39. Невласні інтеграли, залежні від параметра. Рівномірна збіжність. Ознака Вейерштраса рівномірної збіжності. Критерій Коші рівномірної збіжності. Ознаки Абеля і Дирихле. Властивості інтегралів, залежних від параметра. Неперервність, інтегровність і диференційовність. Приклади.

40. Бета і гамма - функції і їх основні властивості. Формула Стірлінга.

41. Метричні простори. Приклади метричних просторів. Відкрита і замкнена множина в метричних просторах. Фундаментальні послідовності. Повні метричні простори. Неперервні відображення в метричних просторах. Зв'язна множина.

42. Лінійні простори. Лінійні оператори в нормованих просторах. Лінійні функціонали. Норма оператора. Скалярний добуток. Теорема Рісса. Ортонормовані базиси.

43. Ряди Фур'є по ортонормованих системах. Коефіцієнти Фур'є.

44. Тригонометричні ряди Фур'є. Лема Рімана. Ядро Дирихле. Ознака Діні.

45. Комплексна форма тригонометричних рядів Фур'є.

46. Перетворення Фур'є і його основні властивості. Приклади. Обернене перетворення Фур'є. Інтеграл Фур'є. Ознаки збіжності.

47. Криволінійні інтеграли I і II -го роду і їх застосування.

48. Міра Жордана в 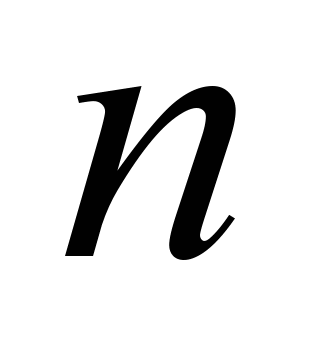- мірному просторі і її властивості.

49. Означення кратного інтеграла. Існування кратного інтеграла. Властивості кратного інтеграла.

50. Обчислення кратних інтегралів через повторні.

51. Заміна змінних в кратних інтегралах. Якобіан і його геометричний зміст.

52. Поверхневі інтеграли I - го роду. Орієнтація поверхні. Поверхневі інтеграли II - го роду. Векторне поле. Потік векторного поля.

53. Теореми Гаусса-Остроградського і Стокса. Дивергенція і ротор векторного поля. Умови незалежності криволінійного інтеграла від шляху інтегрування.

54. Потенціальні і соленоїдні векторні поля.

Теорія ймовірностей

1. Визначення ймовiрностi (класичне, частотне, геометричне).

2. Властивості ймовірностей.

3. Умовні ймовiрностi, незалежні події.

4. Формули повної ймовiрностi i Байєса.

5. Означення випадкової величини.

6. Функція розподілу, щiльнiсть.

7. Числові характеристики випадкових величин: математичне сподiван ня, дисперсiя.

8. Основні розподіли: бiномiальний, Пуассона, геометричний, рiвномiрний, показниковий, нормальний та їх числові характеристики.

9. Незалежнi випадковi величини, коефiцiєнт кореляцiї.

10. Характеристичнi функцiї та генератриси.

11. Закон великих чисел та центральна гранична теорема.

12. Дискретний ланцюг Маркова. Класифiкацiя станів дискретного ланцюга Маркова.

13. Знаходження ергодичного розподілу.

Математична статистика

1. Детерміновані та стохастичні процеси.

2. Загальні принципи моделювання та побудова математичних моделей.

3. Засоби зображення даних, описна статистика.

4. Типи залежностей, частотні розподілення.

5. Постановка мети та вибір методу дослідження. Вибірковий метод.

6. Випадковість та надійність.

7. Чисельні характеристики випадкових величин.

8. Точечне та iнтервальне оцінювання.

9. Поняття статистичної гіпотези.

10. Критерiї узгодження.

11. Основнi принципи прийняття рішень.

12. Перевірка статистичної гіпотези.

Диференціальні рівняння

1. Математичне моделювання і диференціальні рівняння.

2. Задачі, що приводяться до диференціальних рівнянь.

3. Основні поняття і геометричне тлумачення рівнянь .

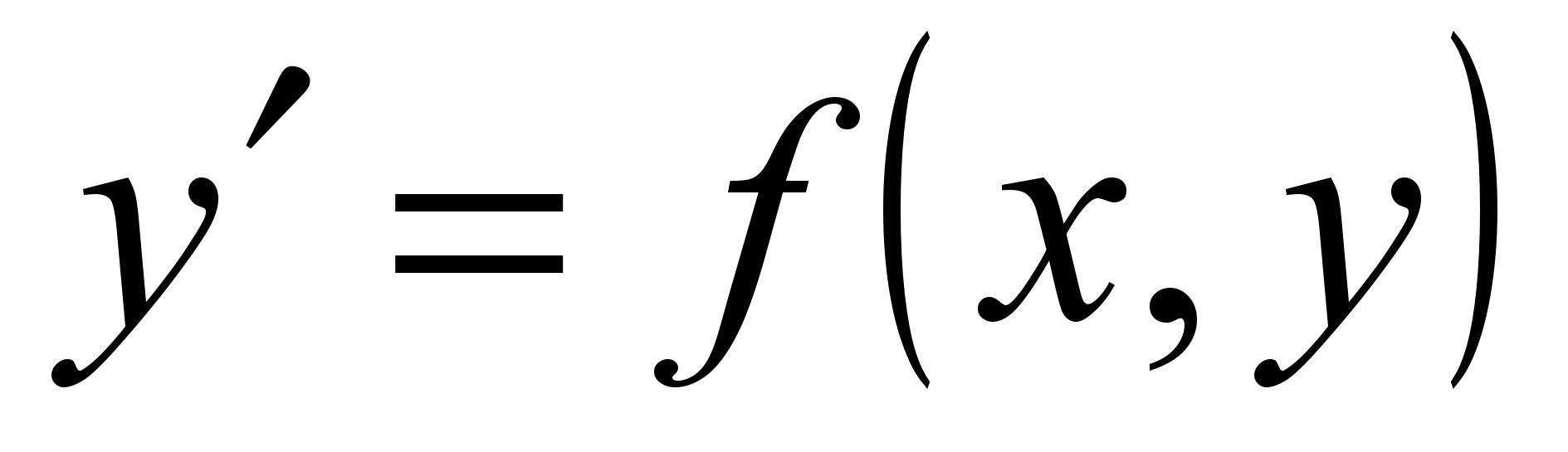4. Інтегрування диференціальних рівнянь з відокремленими та відокремлюваними змінними, однорідних диференціальних рівнянь першого порядку і тих, що до них зводяться. Узагальнене однорідне рівняння.

5. Лінійні диференціальні рівняння першого порядку. Властивості лінійного рівняння і його розв’язків. Методи інтегрування лінійних рівнянь першого порядку.

6. Рівняння, що зводяться до лінійних.

7. Рівняння в повних диференціалах. Інтегруючий множник і його знаходження.

8. Рівняння першого порядку не розв’язувані відносно похідної.

9. Теореми існування і єдиності рішення задачі Коші для рівнянь розв’язуваних і не розв’язуваних відносно похідної.

10. Особливі точки диференціальних рівнянь першого порядку і їх класифікація.

11. Особливі розв’язки диференціальних рівнянь першого порядку.

12. Задача про траєкторії.

13. Основні поняття, теорема існування і єдиності розв’язку задачі Коші для диференціальних рівнянь вищих порядків.

14. Деякі типи диференціальних рівнянь вищих порядків. Теорія лінійних диференціальних однорідних рівнянь, що інтегруються в квадратурах.

15. Пониження порядку диференціальних рівнянь.

16. Лінійні диференціальні рівняння вищих порядків. Теорія лінійних диференціальних однорідних рівнянь.

17. Розв’язки лінійних однорідних диференціальних рівнянь n-го порядку з постійними коефіцієнтами.

18. Лінійні неоднорідні рівняння. Теорема про вид загального розв’язку. Метод варіації довільних постійних.

19. Розв’язки лінійних неоднорідних диференціальних рівнянь із спеціальною правою частиною.

20. Рівняння, що приводяться до рівнянь з постійними коефіцієнтами.

21. Інтегрування диференціальних рівнянь за допомогою степеневих рядів. Рівняння Бесселя.

22. Застосування лінійних диференціальних рівнянь 2-го порядку до дослідження коливальних процесів.

23. Канонічна і самоспряжена форми лінійного однорідного рівняння 2-го порядку.

24. Коливальні і не коливальні розв’язки. Теореми Штурма.

Методи оптимізації

1. Класифікація задач оптимізації. Основні визначення. Разноманітні типи математичних моделей оптимізації.

2. Основні математичні поняття. Лінійний векторний простір. Евклідов простір. Опуклі множини. Функції багатьох змінних. Лінійна залежність векторів, базис векторного простору.

3. Необхідні відомості з лінійної алгебри. Системи лінійних алгебраїчних рівнянь. Метод Жордана-Гаусса.

4. Функція однієї змінної. Умови екстремума. Необхідні і достатні умови екстремума функції багатьох змінних.

5. Загальна задача лінійного програмування. Форми математичних моделей, їхні еквівалентні перетворення. Графічний метод розв’язування задачі лінійного програмування.

6. Симплекс-метод розв’язування задачі лінійного програмування. Основні теореми й алгоритм симплекс-методу.

7. Симплекс-метод із штучним базисом. Основна теорема М-задачі.

8. Прикладні технічні задачі лінійної оптимізації (задача оптимального розкрою і т.п.).

9. Застосування симплекс-методу для розв’язування економічних задач оптимізації (задачі оптимального планування виробництва і т.п.).

10. Двоїстість у лінійному програмуванні. Симетричні і несиметричні двоїсті задачі. Економічна інтерпретація двоїстих задач.

11. Властивості розв’язків взаємноподвійних задач. Основні теореми двоїстості. Двоїстий симплекс-метод, його алгоритм.

12. Додатки теорії подвійності. Застосування двоїстого симплекс-методу для аналізу усталеності і чутливості оптимального розв’язку.

13. Постановка параметричних задач. Розв’язання лінійних параметричних задач двоїстим симплекс-методом.

14. Лінійні розподільні задачі. Транспортна задача. Методи побудови опорного плану транспортної задачі. Метод потенціалів, основна теорема й алгоритм розв’язання транспортної задачі.

15. Задача цілочиселього (дискретного) програмування. Метод Гоморі.

16. Основи комбінаторних методів. Комбінаторні методи розв’язування задач цілочиселього програмування. Метод гілок і меж.

17. Задача булевого лінійного програмування. Адитивний алгоритм її розв’язування.

18. Метод динамічного програмування. Принцип оптимальності Белмана. Обчислювальні аспекти динамічного програмування.

19. Прикладні задачі, розв'язувані методом динамічного програмування (задача керування запасами, мережні задачі, задача оптимального управління т.п.).

20. Загальна задача нелінійного програмування. Необхідні і достатні умови оптимальності розв’язку.

21. Класичні методи одновимірної оптимізації. Методи багатовимірної оптимізації.

22. Класифікація методів нелінійного програмування. Властивості опуклих множин і опуклих функцій. Опукле програмування. Теорема Куна-Таккера.

23. Чисельні методи оптимізації. Методи пошуку безумовного екстремума. Градієнтні методи. Метод Н’ютона (метод других похідних).

24. Методи оптимізації при наявності обмежень. Аналітичні методи. Метод множників Лагранжа.

25. Метод проекції градіенту. Метод умовного градіенту. Метод штрафних функцій.

26. Оцінка ефективності методів оптимізації. Критерії і тестові задачі, застосовувані при порівнянні методів розв’язання задач нелінійного про-грамування.

27. Основні поняття теорії матричних ігор. Теорема про мінімакс. Зв'язок матричних ігор із лінійним програмуванням.

28. Основні поняття про задачі оптимального керування. Застосування принципу оптимальності Белмана для побудови оптимального керування. Поняття принципу максимуму Понтрягіна.

Випадкові процеси

1. Визначення випадкового процесу. Основні поняття і співвідношення. Задача аналізу тимчасових рядів. Критерії випадковості. Екстремальні точки.

2. Закон розподілу випадкових процесів. Ймовірностні характеристики випадкових процесів. Закони розподілу. Загальні властивості законів розподілу випадкових функцій. Кореляційна функція випадкового процесу і її властивості.

3. Векторний випадковий процес. Взаємна кореляційна функція і її властивості. Комплексний випадковий процес. Неперервність випадкового процесу. Диференціювання випадкового процесу. Інтегрування випадкового процесу.

4. Вимірні випадкові функції. Неперервні випадкові функції. Стаціонарні випадкові процеси.

5. Диференціювання стаціонарного випадкового процесу. Періодичні стаціонарні процеси. Стаціонарні тимчасові ряди. Стаціонарні випадкові функції. Неперіодичний стаціонарний процес і його спектральне подання. Властивості спектральної щільності стаціонарного процесу.

6. Спектральне розкладання стаціонарних випадкових функцій. Спектральне подання лінійних операцій. Лінійний фільтр. Ергодичний стаціонарний випадковий процес. Нормальні випадкові процеси. Гаусові випадкові функції.

7. Корелограма. Автокореляційна функція. Спектральна функція. Фільтри і передатні функції, частинні автокореляції. Прогноз і фільтрація стаціонарних процесів.

8. Спектральне подання кореляційної функції стаціонарного процесу. Спектральний аналіз. Спектральна теорія. Гармонійний аналіз. Негармонійні коливання. Згладжування спектра. Нерівні тимчасові інтервали.

9. Тимчасові ряди. Тренд. Визначення тренда. Ковзні середні. Аналіз тренда. Сезонні коливання. Процеси з незалежними збільшеннями. Неперервна складового процесу з незалежними збільшеннями. Процес броунівського руху.

Теорія функції комплексного змінного

1. Комплексні числа та дії над ними.

2. Стереографічна проекція і сфера Рімана.

3. Топологія комплексної площини. Лема Гейне-Бореля-Лебега.

4. Послідовності комплексних чисел. Принцип Больцано-Вейерштраса, критерій Коши.

5. Поняття функції комплексного змінного; структура областей та їх меж.

6. Неперервність та рівномірна неперервність функції комплексного змінного.

7. Діференційовність функції комплексного змінного; умови Коши-Рімана.

8. Поняття аналітичної функції; геометричний зміст модуля і аргументу похідної функції комплексного змінного.

9. Поняття конформного відображення; зв'язок між аналітичними функціями і конформними відображеннями.

10. Дрібно-лінійна функція; степенева і показникова функції.

11. Поняття поверхні Рімана. Функція Жуковського і тригонометричні функції комплексного змінного.

12. Інтеграли по комплексному змінному; основні властивості таких інтегралів.

13. Теорема Коші.

14. Визначений і невизначений інтеграли.

15. Формула Коші. Інтеграл типу Коші.

16. Існування похідних всіх порядків для функції, аналітичної в області.

17. Теорема Морера.

18. Формула Сохоцкого. Інтеграл Пуассона.

19. Ряди аналітичних функцій, що рівномірно збігаються; теорема Вейерштраса.

20. Перша теорема Абеля. Область збіжності і радіус збіжності степеневого ряду; друга теорема Абеля.

21. Ряд Тейлора; теорема Тейлора; теорема єдиності аналітичних функцій.

22. Ряд Лорана; теорема Лорана; класифікація ізольованих особливих точок.

23. Поведінка аналітичних функцій в околі усуненої особливої точки. Теореми Сохоцкого і Пікара.

24. Цілі і мероморфні функції.

25. Логарифмічні лишки, принцип аргументу, теорема Руше.

26. Розкладання мероморфних функцій на суму простих дробів.

27. Обчислення контурних інтегралів і деяких визначених інтегралів за допомогою лишків.

28. Основні критерії збіжності нескінченних добутків, нескінченні добутки, що абсолютно збігаються.

29. Нескінченні добутки, що рівномірно збігаються, нескінченний добуток Вейерштраса і його властивості.

30. Зображення цілих і мероморфних функцій за допомогою нескінченних добутків.

31. Основні принципи аналітичного продовження; поняття повної аналітичної функції.

32. Аналітичне продовження функції дійсного змінного на комплексну площину.

33. Загальні принципи теорії конформних відображень; принцип збереження області; принцип взаємовідповідної відповідності; принцип симетрії Рімана-Шварца.

34. Комфортне відображення многокутників; формула Кристоффеля-Шварца.

35. Відображення напівплощини на прямокутник; поняття про еліптичні функції

36. Плоскопаралельні векторні поля і їх зв'язок з аналітичними функціями; комплексний потенціал.

37. Застосування аналітичних функцій в гідромеханіці, електростатиці, теорії теплопровідності.

Диференціальні рівняння (спец. курс)

1. Поняття про крайові задачі. Задача Штурма-Ліувілля. Поняття про власні числа і власні функції.

2. Функція Гріна і розв'язання крайових задач.

3. Системи звичайних диференціальних рівнянь. Основні поняття. Канонічна, нормальна і симетрична форма систем. Теорія існування й єдиності розв'язку задачі Коші.

4. Приведення диференціальних рівнянь вищих порядків до систем диференціальних рівнянь і обернена задача.

5. Методи інтегрування систем.

6. Теорія лінійних систем диференціальних рівнянь.

7. Метод Ейлера побудови фундаментальної системи однорідних лінійних систем.

8. Матричний метод розв’язування однорідних систем.

9. Методи розв’язування лінійних неоднорідних систем: метод варіації постійних інтегрованих комбінацій, розв'язання лінійних неоднорідних систем зі спеціальною частиною.

10. Основні поняття стійкості Ляпунова.

11. Стійкість розв'язку автономних систем. Найпростіші типи точок спокою.

12. Нелінійні системи. Стійкість за першим наближенням.

13. Другий метод Ляпунова. Теореми Ляпунова і Чєтаєва.

14. Критерії стійкості: Гурвіца, Л'єнара-Шиппара, Михайлова.

15. Основні поняття лінійних диференціальних рівнянь у частинних похідних другого порядку.

16. Лінійні рівняння з двома незалежними змінними. Метод характеристик.

Рівняння математичної фізики

1. Поняття характеристик. Класифікація рівнянь в частинних похідних.

2. Формула Даламбера.

3. Загальний розвязок задачі Коші.

4. Задачі з даними на характеристиках. Функція Рімана.

5. Постановка крайових задач для рівнянь коливань. Поняття інтеграла енергії.

6. Задача Штурму-Ліувіля. Властивості власних функцій і власних значень.

7. Параболічні рівняння. Принцип максимуму. Теорема єдиності.

8. Задача Коші для рівняння теплопровідності.

9. Метод розподілу змінних для рівняння теплопровідності в прямокутнику, колі, циліндрі.

10. Еліптичні рівняння. Постановка крайових задач.

11. Рівняння Лапласа.

12. Загальні властивості гармонійних функцій. Фундаментальний розв’язок рівняння Лапласа.

13. Метод функцій Гріна.

14. Перша і друга формули Гріна.

15. Теорія потенціалів.

16. Інтегральне рівняння Фредгольма. Метод послідовних наближень.

Математична економіка

1. Споживач і система його переваг.

2. Функція корисності.

3. Модель поведінки споживача.

4. Задача споживацького вибору для деяких функцій корисності.

5. Рівняння Слуцького.

6. Висновки з рівняння Слуцького.

7. Виробничі множини і виробничі функції.

8. Теорія фірми.

9. Фірма і її дії на конкурентному ринку в умовах монополії і при податках; дії споживачів при стягуванні податків.

10. Моделі економічної взаємодії на простих ринках.

11. Ігрові моделі співпраці і конкуренції.

12. Моделі ринків.

13. Модель міжгалузевого балансу – одна з глобальних моделей виробництва.

14. Модель Неймана – глобальна модель виробництва.

Вимоги до рівня підготовки вступників


Учасник іспиту повинен:

Алгебра та геометрія

Знати:

– різні методи дослідження і розв’язання системи лінійних рівнянь, у тому числі метод Гауса і метод Крамера для будь-яких лінійних систем 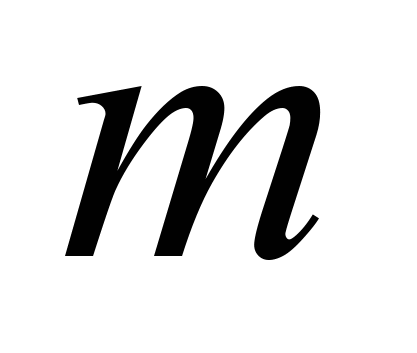рівнянь з 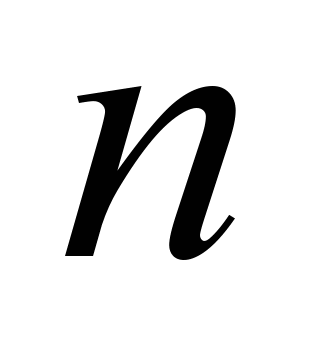невідомими;

– визначники 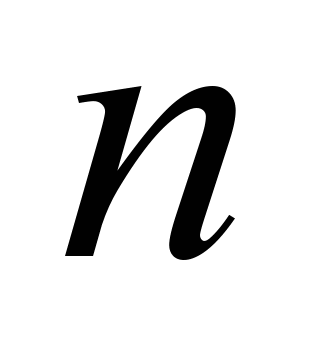-го порядку, їхні властивості, методи обчислення, ранг матриці, різні методи його визначення. Алгебру матриць, оборотність матриць, запис і розв’язання системи 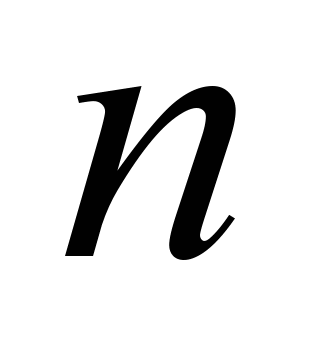лінійних рівнянь з 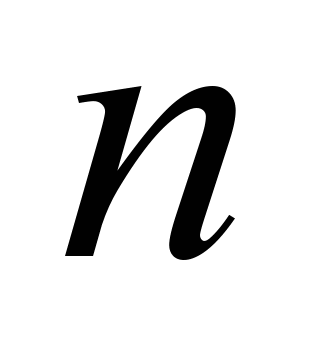невідомими в матричній формі;

– векторну алгебру, вектори на площині й у просторі, лінійні операції, координати. Скалярний, векторний і змішаний добуток векторів, їхнє вираження в координатах в ортонормованому базисі, геометричний зміст, застосування до розв’язання геометричних завдань. Рівняння площин і прямих, розв’язання геометричних задач на прямі й площини, криві другого порядку, їхні характеристики: ексцентриситет, фокуси, директриси. Поверхні другого порядку, класифікація, дослідження форми по канонічному рівнянню;

– побудову комплексних чисел, алгебраїчна й тригонометрична форми, операції над ними;

– поняття про алгебраїчну операцію, групи кільця, поля. Ізоморфізм і гомоморфізми. Числові кільця та поля, кільця многочленів над числовими полями;

– основну теорему алгебри й наслідки з неї. Можливість розв'язання в радикалах рівнянь ступеня 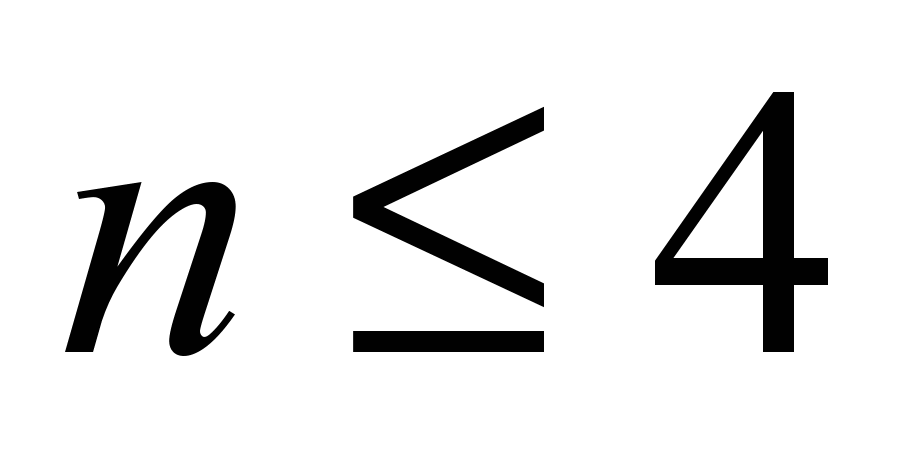. Нерозв'язність у радикалах рівнянь ступеня ;

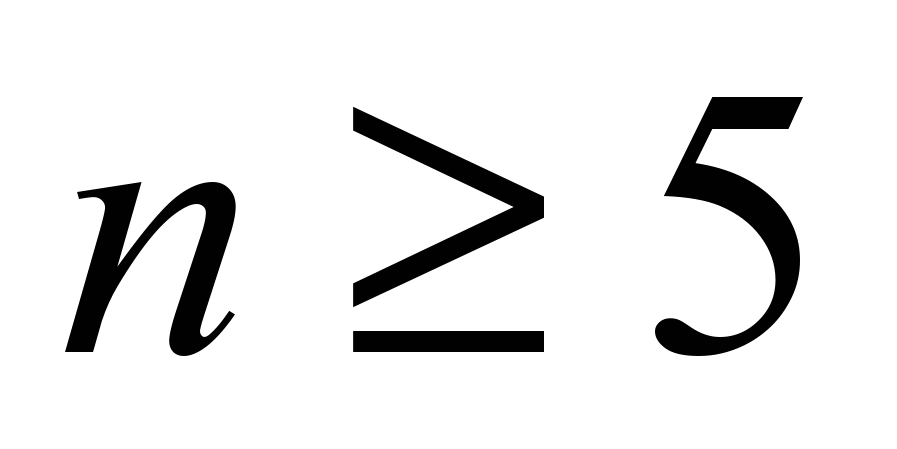– подільність у кільці многочленів над довільним числовим полем. Алгоритм ділення з залишком, найбільший спільний дільник і найменше спільне кратне, алгоритм Евкліда. Відділення кратних множників. Корені і подільність на лінійні множники, метод Штурма відділення дійсних коренів многочленів із дійсними коефіцієнтами. Наближене обчислення дійсних коренів. Існування многочленів, що не приводяться, будь-якого ступеня над полем раціональних чисел. Критерій Эйзенштейна. Знаходження раціональних коренів многочленів із раціональними коефіцієнтами;

– алгебраїчні й трансцендентні розширення полів. Побудова простого алгебраїчного розширення. Поняття лінійного простору, базис і розмірність. Підпростір, натягнутий на вектори, розмірність суми й перетинання підпросторів. Скалярний добуток, евклідового простору. Ізоморфізм лінійних і евклідових просторів. Ортонормовані базиси, процес ортогоналізації. Лінійні перетворення й матриці. Перетворення координат при зміні базису й зміна матриці перетворення при зміні базису;

– лінійні перетворення евклідових просторів, ортогональні й симетричні матриці.

Уміти:

– досліджувати і розв’язувати СЛАР з 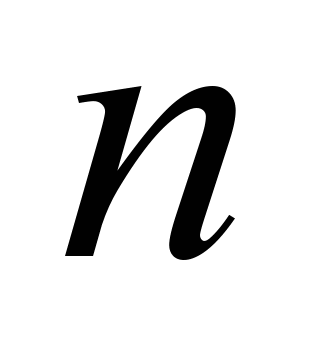невідомими методом Гауса і методом Крамера;

– обчислювати визначники 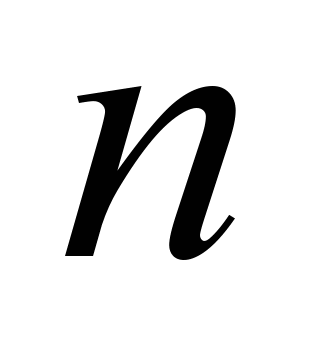-го порядку різними методами;

– володіти матричною алгеброю і векторною алгеброю;

– розв’язувати стандартні задачі з геометрії із застосуванням векторної алгебри, приводити рівняння другого ступеня до канонічного виду;

– розв’язувати в радикалах алгебраїчні рівняння ступеня не вище четвертого;

– відокремлювати дійсні корені многочленів з дійсними коефіцієнтами й обчислювати їх із необхідною точністю;

– знаходити раціональні корені многочленів із раціональними коефіцієнтами;

– користуватися алгоритмом Евкліда і відокремлювати кратні множники многочленів;

– позбуватися від ірраціональності в знаменнику дробу;

– визначати базис і розмірність підпростору, знаходити матрицю лінійного оператора, координати вектора при зміні базису;

– знаходити ортогональну проекцію й ортогональне доповнення вектора на підпростір евклідового простору.

Дискретна математика

Знати:

– способи завдання множин; операції над множинами і їхні властивості, декартови добутку множин, 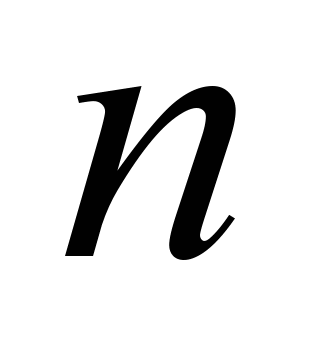-арні й бінарні відносини, операції над ними; відношення еквівалентності на множині й розбивка множини на класи. Відображення й функції. Частково впорядковані множини. Лінійний порядок і цілком упорядковані множини, аксіому індукції й еквівалентні їй твердження. Визначення ґрат, дистрибутивні структури з доповненнями. Булеві алгебри. Ізоморфні подання булевих алгебр в алгебрі підмножин;

– потужність множини, зліченні множини і їхні властивості, незліченність континуума. Теорема про потужності всіх підмножин довільної множини. Порівняння потужностей. Кардинальні й ординальні числа, їхні властивості. Аксіома вибору й еквівалентні їй твердження;

– алгебру висловлень, логічні операції над висловленнями; формули висловлень, тавтології, протиріччя, повні системи зв'язувань;

– аксіоматичні побудови вирахування висловлень, системи аксіом, правило висновку, виводимість формул. Теорема дедукції;

– досконалі диз'юнктивні й кон’юнктиві нормальні форми;

– алгебру предикатів, одномісні, багатомісні предикати, множина істинності предикатів, операції над предикатами, формули вирахування предикатів. Квантори. Тавтології із кванторами. Теорії I-го порядку, інтерпретація, виконаннітсь й істинність моделі. Несуперечність вирахування предикатів I-го порядку, повнота й незалежність теорії I-го порядку.

– функції алгебри логіки від декількох змінних. Рівносильні функції, суперпозиція функцій. Арифметичні операції й многочлени Жегалкіна, реалізація функцій релейно-контактними схемами, проблема мінімальності. Функціонально замкнені класи булевських функцій. Принципи подвійності. Самодвоїсті, монотонні й лінійні функції. Теорема Поста. Критерії повноти системи функцій;

– основні комбінаторні схеми. Правила суми й добутки;

– розміщення, перестановки й сполучення з повтореннями й без повторень. Деякі властивості сполучень, біном Ньютона і його узагальнення. Поліномінальная формула. Рекурентні співвідношення. Розв’язання лінійних рекурентних співвідношень 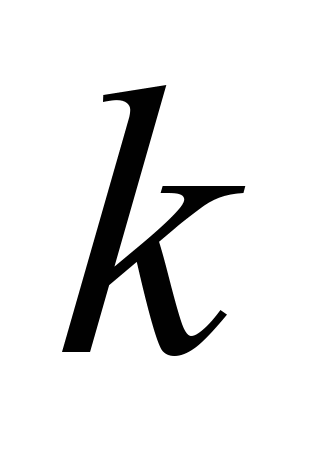-го порядку з постійними коефіцієнтами. Загальні й приватні рішення. Числа Фібоначчі. Виробляючі функції, їхнє застосування до рішення комбінаторних задач;

– основні поняття теорії графів. Цикломатичне число графа, дерева. Ейлерові цикли;

– теорема Ейлера про існування ейлерових циклів. Проблема чотирьох фарб, задача комівояжера, існування гамільтонових циклів. Плоскі графи, ейлерова характеристика. Теорема Понтрягіна-Куратовського. Алгоритмічні задачі теорії графів. Теорема про п'ять фарб;

– алфавіт, слова, функції й алгебраїчні операції. Кінцеві автомати Милі й Мура. Еквівалентні стани, морфізми й ізоморфізми автоматів. Задача мінімізації повністю визначеного автомата. Задача структурного синтезу автоматів;

– машини Т'юрінга. Концепція алгоритму. Нормальні алгоритми Маркова. Алгоритмічно нерозв'язні задачі. Примітивно-рекурсивні функції й множини. Алгоритми Кліні-Черча й алгоритми Т'юрінга-Поста. Еквівалентність різних визначень алгоритму.

Уміти:

– доводити різні властивості операцій над множинами; знаходити добутки бінарних відношень, зворотні відношення, визначати, якими із заданих властивостей володіють задані відношення. По заданому відношенню еквівалентності знаходити фактор-множину й по заданій розбивці множини знаходити відношення еквівалентності. Орієнтуватися в типах відношень порядку, уміти знаходити ізоморфні впорядковані множини. Користуватися методом індукції. Доводити еквівалентність множин, користуватися канторовським діагональним методом;

– уміти знаходити суми й добутки кардинальних й ординальних чисел, використати таблиці істинності, знаходити тавтології й доводити, що деяка формула є тавтологією, використовуючи властивості логічних операцій;

– вільно орієнтуватися в поняттях пряма, зворотна й протилежна теореми, користуватися законом контрапозиції й іншими законами логіки, необхідними й достатніми умовами, методами доведень. Використовуючи мову логіки предикатів, досліджувати логічну структуру математичних визначень і теорем;

– визначати рівносильні булеві функції, подавати одні логічні операції через інші, подавати будь-яку логічну функцію в диз'юнктивній або кон'юнктивній нормальній формі, многочленом Жегалкіна. Становити таблиці Поста й виділяти повні системи функцій з довільно заданих;

– користуватися основними комбінаторними схемами. Використати формулу бінома Ньютона й поліноміальну формулу, використати виробляючі функції для виводу деяких властивостей відповідних послідовностей і розв’язання деяких комбінаторних задач;

– знаходити ейлерові цикли в графах, якщо вони існують; знаходити цикломатичне число графа, ейлерову характеристику, з'ясувати, чи є заданий граф плоским. Описати роботу кінцевого автомата й машини Т'юрінга; визначати еквівалентні автомати, знаходити еквівалентні 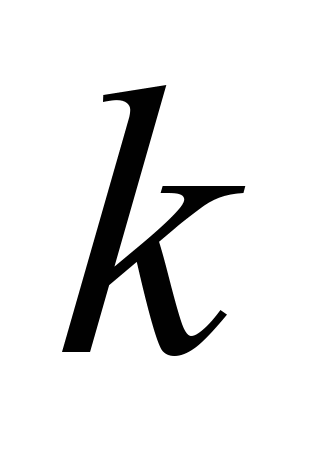-еквівалентні стани автоматів;

– мінімізувати довільно заданий автомат. Скласти програму роботи машини Т'юрінга, що обчислює деякі арифметичні функції.

Математичний аналіз

Знати:

– аксіоматичну теорію дійсного числа;

– теорію числових послідовностей;

– границя функції в точці;

– неперервність функції в точці;

– диференціальне обчислення функції однією змінною;

– теорію інтеграла Рімана;

– диференціальне обчислення функцій декількох змінних;

– теореми існування і диференціювання неявної функції;

– теорію екстремуму і умовного екстремуму функції декількох змінних;

– ознаки збіжності числових рядів;

– рівномірну збіжність функціональних послідовностей;

– ознаки рівномірної збіжності функціональних рядів;

– критерій розкладання функції в степеневий ряд;

– ознаки збіжності невласного інтеграла першого і другого роду;

– ознаки рівномірної збіжності невласного інтеграла залежного від параметра;

– інтеграли Ейлера;

– кратні інтеграли;

– теорему про незалежність криволінійного інтеграла від шляху інтегрування;

– поверхневі інтеграли першого і другого роду;

– формули Гріна, Гауса – Остроградського, Стокса;

– основи теорії поля , , ;

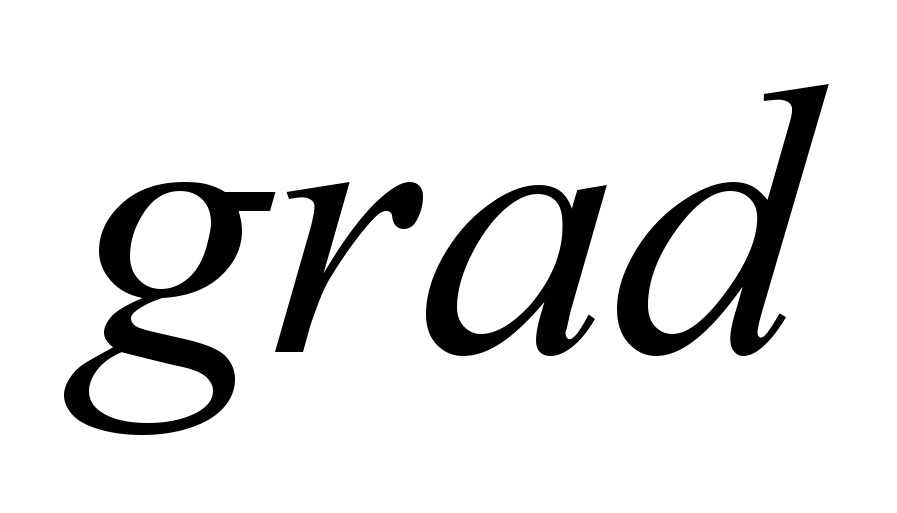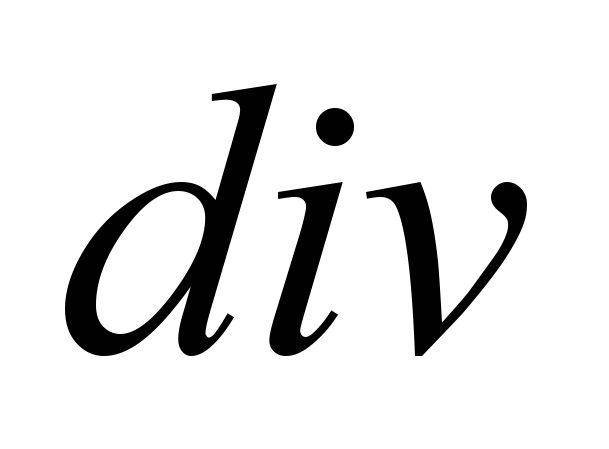– ряд Фур’є і ортонормовані системи;

– нерівність Бесселя і рівність Парсеваля;

– ознака поточкової збіжності тригонометричних рядів Фур’є;

– ознака рівномірної збіжності рядів Фур’є;

– перетворення Фур’є;

Уміти:

– знаходити границю числової послідовності;

– застосовувати визначні границі для знаходження границь функцій;

– перевіряти функцію на неперервність і рівномірну неперервність;

– диференціювати складні і обернені функції;

– розкладати функцію в ряд Тейлора і Маклорена;

– знати формулу Лейбніца;

– користуватися правилом Лопіталя;

– досліджувати функцію на екстремум;

– знаходити проміжки монотонності;

– досліджувати функцію на опуклість;

– знаходити точки перегину;

– знаходити асимптоти;

– будувати графік функції за загальною схемою;

– користуватися таблицею первісних для знаходження невизначеного інтеграла;

– володіти методами інтегрування;

– перевіряти функцію на інтегровність по Ріману;

– знати основні теореми і основні формули інтегрального обчислення;

– користуватися інтегралом Рімана в геометрії, механіці і фізиці;

– диференціювати функцію декількох змінних;

– диференціювати неявно задані функції;

– досліджувати на екстремум і умовний екстремум функцію декількох змінних;

– досліджувати на абсолютну і умовну збіжність числові ряди;

– досліджувати на рівномірну збіжність функціональні послідовності і функціональні ряди;

– розкладати функції в ряд Тейлора;

– досліджувати на абсолютну, умовну збіжність невласні інтеграли;

– досліджувати на рівномірну збіжність невласні інтеграли, залежні від параметра;

– обчислювати інтеграли за допомогою гамма-функції і бета-функції;

– обчислювати кратні інтеграли;

– виконувати заміну змінних в подвійних і потрійних інтегралах;

– застосовувати кратні інтеграли в геометрії і механіці;

– обчислювати криволінійні інтеграли;

– застосовувати криволінійні інтеграли в геометрії і фізиці;

– обчислювати поверхневі інтеграли;

– користуватися формулами Гріна, Стокса, Гауса - Остроградського;

– обчислювати , , ;

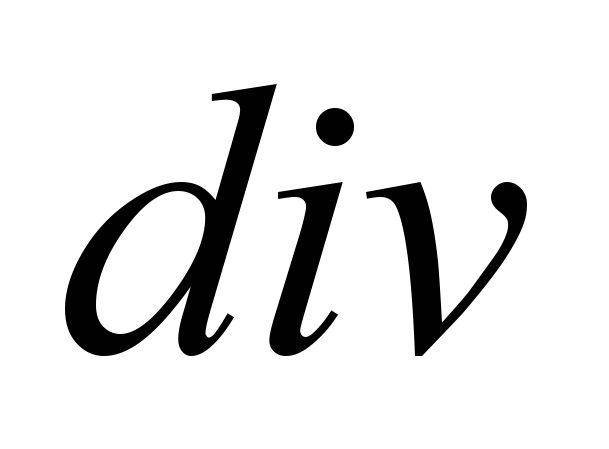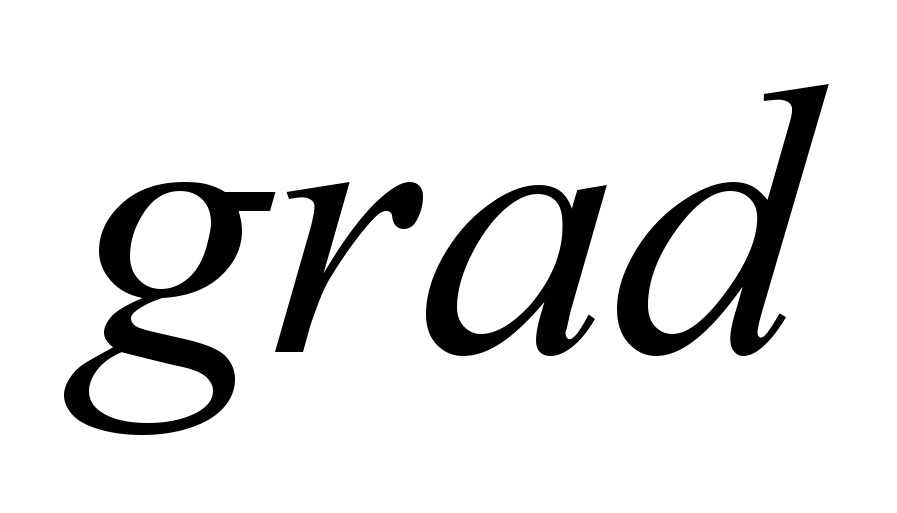– розкладати функцію в ряд Фур'є;

– застосовувати перетворення Фур'є.

Теорія ймовірностей

Знати:

– визначення ймовiрностi (класичне, частотне, геометричне);

– властивості ймовірностей, умовні ймовiрностi, незалежні події, формули повної ймовiрностi і Байєса;

– означення випадкової величини, функція розподілу, щiльнiсть, числові характеристики випадкових величин: математичне очікування, дисперсiя;

– основні розподіли: бiномiальний, Пуасона, геометричний, рiвномiрний, показниковий, нормальний та їх числові характеристики;

– незалежні випадкові величини, коефіцієнт кореляцiї;

– характеристичні функції та генератриси;

– закон великих чисел та центральна гранична теорема;

– стани дискретного ланцюга Маркова, ергодичний розподiл.

Уміти:

– знаходити ймовiрностi випадкових подiй;

– користуватися формулами повної ймовiрностi та Байеса;

– знаходити математичне очікування, дисперсiю і коефiцiєнт кореляцiї випадкових величин;

– знаходити розподіли функцій від випадкових величин;

– застосовувати закон великих чисел та центральну граничну теорему для перевiрки збiжностi випадкових величин;

– робити класифiкацiю станiв дискретного ланцюга Маркова, знаходити ергодичний розподiл.

Математична статистика

Знати:

– визначення математичної статистики;

– властивості статистики, задачі математичної статистики;

– означення випадкової величини, функція розподілу, щільність, числові характеристики випадкових величин: математичне сподівання, дисперсія;

– основнi розподіли: Пуассона, геометричний, рівномірний, показниковий, нормальний та їх числовi характеристики;

– незалежнi випадковi величини, коефiцiєнт кореляцiї;

– закон великих чисел та центральна гранична теорема;

– понняття статичної гіпотези;

– основні задачi математичної статистики;

– основнi методи оцiнки невiдомих параметрiв: метод моментiв, метод максимальної правдоподiбностi;

– перевiрка незмiщеностi та ефективностi оцiнок;

– iнтервальне оцiнювання невiдомих параметрiв;

– критерiї згоди: Колмогорова, 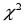, Колмогорова-Смiрнова;

– критерiй Неймана-Пiрсона;

– метод найменших квадратiв, лiнiйна регресiя.

Уміти:

– знаходити розподіли частот вибірок;

– будувати емпiричну функцiю розподiлу, гiстограму;

– знаходити вибiрковi середнє, дисперсiю, коефiцiєнт кореляцiї;

– знаходити точковi та iнтервальнi оцiнки невiдомих параметрiв;

– перевiрити їх незмiщенiсть та ефективнiсть;

– використовувати критерiй 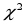, Колмогорова для перевiрки статистичних гiпотез;

– будувати лінійну регресію.

Диференціальні рівняння

Знати:

– принципи побудови математичних моделей на підставі теорії диференціальних рівнянь;

– теорію диференціальних рівнянь першого порядку розв’язуваних і не розв’язуваних відносно похідної;

– основні типи диференціальних рівнянь вищих порядків, що інтегруються в квадратурах і методи їх інтегрування;

– теорію лінійних диференціальних рівнянь п -го порядку;

–методи інтегрування лінійних диференціальних рівнянь п-го порядку і тих, що до них зводяться.

Уміти:

– використовувати знання диференціальних рівнянь в задачах математичного моделювання;

– знаходити розв’язки типів диференціальних рівнянь першого порядку, що інтегруються;

– інтегрувати і знижувати порядок деяких рівнянь вищих порядків;

– вирішувати як однорідні, так і неоднорідні лінійні диференціальні рівняння 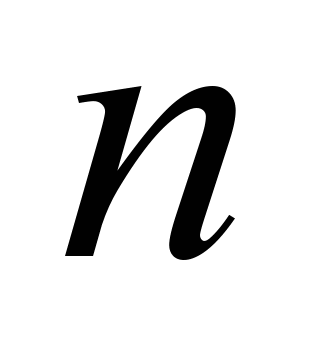-го порядку і ті, що до них зводяться.

Методи оптимізації

Знати:

– теорію і методи розв’язування лінійних задач оптимізації;

– теорію подвійності лініного програмування;

– симплекс-метод та его модифікації;

– основи теорії і методи розв’язування задач цілочиселього програмування;

– основні поняття про динамічне програмування;

– загальну теорію розв’язування нелінійних задач оптимізації;

– чисельні методи нелінійного програмування.

Уміти:

– ставити і аналізувати оптимізаційні моделі прикладних задач економічного і технічного змісту;

– розв’язувати задачі лінійного програмування симплекс-методом і подвійним симплекс-методом;

– розв’язувати задачі транспортного типу;

– розв’язувати задачі цілочиселього програмування методом Гоморі і комбінаторними методами;

– застосовувати принцип оптимальності Белмана при розв’язуванні задач динамічного програмування;

– розв’язувати задачі нелінійного програмування чисельними методами.

Випадкові процеси

Знати:

– задачу аналізу тимчасових рядів, критерії випадковості;

– ймовірностні характеристики, закони розподілу й усереднені характеристики випадкових функцій;

– векторний випадковий процес, взаємна кореляційна функція і її властивості.

– комплексний випадковий процес, неперервність випадкового процесу, диференціювання випадкового процесу, інтегрування випадкового процесу;

– стаціонарні випадкові процеси, диференціювання стаціонарного випадкового процесу, періодичні стаціонарні процеси;

– спектральне подання лінійних операцій, лінійний фільтр;

– ергодичний стаціонарний випадковий процес, нормальні випадкові процеси;

– фільтри і передатні функції, частинні автокореляції;

– спектральне подання кореляційної функції стаціонарного процесу, спектральний аналіз;

– спектральну теорію, гармонійний аналіз, негармонійні коливання;

– процеси з незалежними збільшеннями.

Уміти:

– використовувати основні поняття і співвідношення аналізу тимчасових рядів;

– використовувати на практиці критерії випадковості;

– знаходити екстремальні точки і закон розподілу випадкового процесу;

– визначати ймовірносні характеристики випадкового процесу;

– знаходити кореляційну функцію випадкового процесу і практично використовувати її властивості;

– знаходити взаємну кореляційну функцію;

– диференціювати й інтегрувати випадковий процес;

– виділяти періоди стаціонарності випадкового процесу;

– знаходити спектральну щільність стаціонарного процесу;

– визначати ергодичність стаціонарного випадкового процесу;

– знаходити автокореляційну і спектральну функції;

– будувати фільтри і передатні функції;

– використовувати результати обробки для прогнозу стаціонарних процесів;

– знаходити тренд, використовувати аналіз тренда для виділення сезонних коливань;

– визначати неперервну складового процесу з незалежними збільшеннями;

– ставити практичні задачі стосовно до процесу броунівського руху.

Теорія функції комплексного змінного

Знати:

-– систему аксіом теорії комплексних чисел;

– поняття комплексного змінного і функції комплексного змінного;

– теорему Коші і інтеграл Коші;

– теорему рядів аналітичних функцій;

– теорію лишків;

– поняття нескінченних добутків і їх застосування до аналітичних функцій;

– принцип аналітичного продовження;

– загальні принципи теорії конформного відображення.

Уміти:

– виконувати дії над комплексними числами;

– використовувати умови Коши-Рімана для встановлення аналітичної функції комплексного змінного;

– виконувати конформні відображення, використовуючи лінійні, дрібно-лінійні і інші елементарні функції;

– розкладати функції комплексного змінного в степеневі ряди і ряди Лорана;

– класифікувати особливі точки;

– обчислювати лишки;

–користуватися формулою Кристоффеля-Шварца.

Диференціальні рівняння (спец. курс)

Знати:

– основи теорії диференціальних рівнянь і лінійних систем;

– методи розв’язання систем;

– методи розв’язання систем диференціальних рівнянь з постійними коефіцієнтами;

– перший і другий методи Ляпунова дослідження стійкості;

– критерій стійкості Гурвіца, Л'єнара-Шиппара, Михайлова.

Уміти:

– розв'язувати системи диференціальних рівнянь методом послідовних наближень, методом виключення, методом комбінацій, що інтегруються;

– розв'язувати лінійні неоднорідні системи методом варіації довільних постійних;

– знаходити загальний розв'язок лінійних однорідних систем з постійними коефіцієнтами матричним методом;

– користатися методом Ейлера розв’язування лінійних однорідних систем з постійними коефіцієнтами;

– розв'язувати лінійні неоднорідні системи диференціальних рівнянь з постійними коефіцієнтами методом невизначених коефіцієнтів, методом Даламбера;

– використовувати перший і другий методи Ляпунова для дослідження стійкості розв'язків.

Рівняння математичної фізики